אז מה זה עניין P=NP, בעצם?

כפי שחששתי, החדשות על ההוכחה ש-P שונה מ-NP היו נכונות אך מוקדמות מדי. הקונצנזוס שהולך ומסתמן בבלוגים שעוסקים בעניין - לאחר שכמה מטובי מדעני המחשב והמתמטיקאים בעולם שיתפו פעולה בבחינת ההוכחה - הוא שבהוכחה יש בעיות שלא ניתנות לתיקון, ושככל הנראה גם לא יהיה ניתן להפיק ממנה דרך חדשה ומבטיחה להתמודדות עם הבעיה. בקיצור, מהומה רבה על לא מאומה. לא אכנס כאן לפרטים הטכניים של ההתנגדויות להוכחה - גם כי איני בקיא בהם לחלוטין וגם כי עדיף לקרוא פשוט את מה שהמומחים אמרו, אך יש נקודה אחת מבין ההתנגדויות ששווה לציין - לעת עתה, לא ברור כלל למה ההוכחה - שמראה שבעיה מסויימת היא “קשה” (עוד מעט אסביר בפירוט במה העניין) - לא עובדת באותו האופן גם על בעיות אחרות שידוע שהן דווקא קלות. במילים אחרות, כרגע ההוכחה מוכיחה גם דברים שאינם נכונים, ומכאן שודאי שיש בה בעיה.

החשש שכעת מביעים חלק מהדוברים בעניין הוא שההוכחה הזו היא הסנונית הראשונה לבוא עידן שבו הוכחות-שגויות-שנראות-רציניות לכך ש-P שונה מ-NP יצוצו לעתים קרובות יחסית. ברור שמאמץ הירואי של בדיקת הוכחה - שבו חוקרים מהשורה הראשונה עוזבים את כל מה שהם עוסקים בו ושוברים את הראש על מאמר לא פשוט של 100 עמודים - לא יוכל לחזור על עצמו שוב ושוב ושוב. מכאן שצעקת ה”זאב” הראשונה הזו עלולה לגרום לבעיות לא פשוטות בהמשך, כשיצוצו הוכחות נוספות. כפי שהעיר מישהו (איני מוצא כעת את הציטוט המדויק), כל המהומה הזו היא מה שקורה כשמישהו כותב בראש המאמר שלו “P שונה מ-NP” במקום “גישה חדשה להתמודדות עם בעיית P נגד NP”, שכנראה הייתה מובילה לבדיקה יותר איטית ושפויה של ההוכחה - אולי גם יותר מועילה.

אבל, מצד שני, ההוכחה הזו גם עשתה דבר מה מועיל מאוד - היא עוררה עניין בבעיית P נגד NP וסיפקה לה קצת יחסי ציבור מוצלחים. בארץ זה הורגש הרבה פחות - עד כמה שראיתי, אף כלי תקשורת מרכזי לא התייחס לעניין ולו ברמז. אבל זה לא שציפיתי לכך. אני בכל זאת רוצה לנצל את ההזדמנות הזו ולהזכיר, במילים פשוטות ככל הניתן, מה בעצם הבעיה ולמה פתרון הוא כזו סנסציה.

בשורה אחת (שכמובן, כוללת שקרים למכביר), השאלה האם P=NP היא השאלה האם לפתור את תרגילי הבית זה לא קשה יותר מאשר להעתיק אותם. זו השאלה האם לפרוץ הצפנה זה לא קשה יותר מאשר לפענח אותה באופן לגיטימי. זו השאלה האם להוכיח משפט מתמטי זה לא קשה יותר מאשר לקרוא ולהבין את ההוכחה. זו השאלה האם למצוא את הכימיקל שיתן לנו חיי נצח לא קשה יותר מאשר להשתמש בו ולבדוק שהוא עובד. זו השאלה אם לבדוק האם קיים או לא קיים אלוהים לא קשה יותר מאשר להשתכנע שהוא כאן אם הוא יוכיח זאת באותות ומופתים…

טוב, נסחפתי.

מדעי המחשב עוסקים בבעיות שניתנות לתיאור באופן מדוייק יחסית. לא שאלות של קיום אלוהים או או אהבה או חיי נצח, אלא דברים פרוזאיים יותר כמו “איך אפשר לפרק את המספר הזה לגורמים?” ו”האם אפשר להרכיב מערכת שעות שבה אף קורס לא מתנגש מתוך רשימת הקורסים הבאה?”. אולי יום אחד נוכל לנסח גם שאלות כמו קיום אלוהים באופן שבו מדעי המחשב יודעים לטפל - אבל לעת עתה זה לא רלוונטי ואולי טוב שכך.

מדעני מחשב משתמשים באות P כדי לתאר בעיות חישוביות שניתנות לפתרון באופן יעיל, כש”יעילות” נמדדת במונחי פרק הזמן שהמחשב צריך לעבוד כדי לפתור את הבעיה. ההגדרה המדוייקת של “יעיל” אינה מסובכת אך לא אכנס אליה כאן כי השיקולים שהנחו את בחירתה אינם כה פשוטים להסבר מיידי. בתיאוריה, העובדה שבעיה שייכת לקבוצת הבעיות P לא אומרת שהיא בהכרח קלה לפתרון, אלא רק שהיא “לא קשה באופן מבהיל” לפתרון. עם זאת, בפועל, מרבית הבעיות המעשיות שב-P אכן ניתנות לפתרון בזמן יעיל למדי. בעיות לדוגמה הן מציאת מקסימום או מינימום של קבוצת איברים; מיון של קבוצת איברים; ביצוע פעולות החשבון הבסיסיות; חישובים קצת יותר מתוחכמים כמו הוצאת שורש; חיפוש מילים בטקסטים ארוכים; פתרון של מערכות משואות לינאריות, ושל בעיות אופטימיזציה לינאריות; ותוצאה אחת חדשה יחסית ומלהיבה יחסית - בדיקת ראשוניות.

גם כאן, יש שקר בסיסי שטבוע בהגדרת P, שמפריד בין משמעותה התיאורטית ומשמעותה המעשית. P מתארת בעיות שקיים להן פתרון דטרמיניסטי, שהוא יעיל גם במקרה הגרוע ביותר. בעולם האמיתי הדרישות הללו חשובות פחות - אלגוריתמים הסתברותיים מצויינים לבדיקת ראשוניות היו ידועים הרבה לפני שהוכח שבדיקת ראשוניות היא ב-P; ובעיות שכנראה אינן שייכות ל-P נפתרות מדי יום ביומו בעזרת אלגוריתמים לא מושלמים, שבמקרים מסויימים עשויים לעבוד גרוע מאוד, אבל עבור המקרים הממוצעים שמגיעים אליהם הם דווקא יעילים למדי; ועם זאת, שייכות ל-P היא עדיין חותם די מובהק של “הבעיה הזו היא קלה יחסית”. התכונה החשובה ביותר של בעיות קלות היא שהן נשארות קלות יחסית גם כשמפעילים אותם על קלטים מסדרי גודל מפלצתיים - כך למשל האלגוריתם של גוגל צריך לטפל במטריצה שמתארת “את כל האינטרנט” - מטריצה ענקית בגודלה, אבל שאפשר לטפל בה בזמן סביר יחסית כי טיפול במטריצות הוא ב-P (ושוב - אני משקר פה על ימין ועל שמאל אבל אתם סולחים לי).

ומאיפה האות P הגיעה בכלל? מהמילה Polynomial - פולינומי, שניתן לתיאור באמצעות פולינום. זהו שם טכני - “זמן ריצה יעיל” מזוהה עם “זמן ריצה שניתן לחסימה באמצעות פולינום” וממש לא נורא אם לא תבינו למה הכוונה כאן.

כעת ל-NP. בלבול מאוד נפוץ הוא לחשוב ש-NP פירושו “לא ב-P” (כלומר, שה-N מסמן “Not”). המשמעות האמיתית היא שוב טכנית - Nondeterminsitic Polynomial. מה קשור אי דטרמיניזם לכאן - זה כבר לדיון אחר, והסיבות הן בעיקר היסטוריות. המשמעות של NP, שהיא מה שחשוב כאן, היא זו: בעיות שקל לבדוק את פתרונן. וכאן מתאימה דוגמה - אם אומרים לי “הפירוק לגורמים של 35 הוא 5 ו-7”, קל לי לבדוק זאת - אני כופל את 7 ו-5 ומקבל 35, כצפוי. עם זאת, לא ידוע כיום שום אלגוריתם יעיל לפירוק לגורמים של מספר - כך שזוהי בעיה שקל לבדוק את פתרונה, אך לא קל לפתור (ליתר דיוק - לא ידוע אם קל לפתור אותה). גם בעיית לוח הזמנים שדיברתי עליה למעלה היא כזו - אם נותנים לכם רשימה ארוכה של קורסים שיש לשבץ בכיתות ובשעות שלא יתנגשו, תחת אילוצים מסויימים, יכול להיות מאוד קשה למצוא מערכת שעות מוצלחת; אבל אם מישהו כבר מביא לכם כזו, קל לבדוק שהיא אכן מוצלחת.  כפי שאפשר להבין מכך, NP היא מחלקת בעיות גדולה יותר מאשר P; כל מה שקל לפתור, קל גם לבדוק אם הוא פתיר (למי שהטענה הזו נשמעת קצת “חשודה”, אל חשש - כשמביאים הגדרות מתמטיות מדוייקות למחלקות אלו, המשפט הזה מקבל משמעות יותר מדוייקת שנכונותה ברורה למדי).

השאלה האם P=NP או שמא P שונה מ-NP היא השאלה האם שתי הקבוצות הללו זהות, כלומר האם כל בעיה ב-NP היא גם ב-P, כלומר האם כל בעיה שמתאפיינת בכך שקל לבדוק פתרונות שלה, היא בעיה שקל לפתור?

ניסוח שקול הוא זה: האם העובדה שאנו יודעים לבדוק בקלות האם פתרון לבעיה מסויימת הוא נכון אומרת שאנחנו גם יכולים למצוא בקלות פתרון שכזה?

זוהי השאלה המרכזית במדעי המחשב כיום, אחת מ”שבע בעיות המילניום” של מכון קליי, ולטעמי אחת מהשאלות החשובות ביותר שהמין האנושי שאל את עצמו מאז ומעולם. ובניגוד לשאלות פילוסופיות, לשאלה הזו קיים פתרון חד משמעי, ויום אחד הוא יהיה בהישג ידינו, או לפחות כך אנו מקווים. והפתרון הזה הוא, על פי כל הרמזים והאותות והנסיון שנצברו בארבעים השנים מאז שהשאלה הפכה למרכזית במדעי המחשב - ש-P שונה מ-NP. שקלות בדיקה אינה גוררת קלות פתרון. שהעולם אינו קסום ופשוט כפי שאולי אפשר היה לקוות.

כדי להמחיש עד כמה P=NP היא תוצאה חזקה באופן מופרז, הנה משחק מחשבתי - חשבו על בעיה כלשהי שהטרידה אתכם, ושקיים לה פתרון שאתם יכולים לשבת ולקרוא ולהבין - נניח, פתרון של מאה עמודים. אם P=NP, אז מחשב יכל לגלות את הפתרון הזה בעצמו, ללא מאמץ מיוחד. נשמע מוזר ומופרך? בוודאי! ראשית, כי אני מציג את הבעיה בצורה מופרכת; אבל שנית, כי התוצאה עצמה היא מופרכת בכוח שלה, ואיננה עד-כדי-כך שונה מהתיאור המטופש שנתתי כאן. הדוגמה על ההצפנה שתיארתי בהתחלה היא אפילו מציאותית למדי - אם יש תוכנית מחשב שבהינתן טקסט מוצפן יודעת לזהות שמשהו הוא הפיענוח הנכון שלו (בעיה שבפני עצמה אינה טריוויאלית בהקשרים מסויימים, אבל בחלקם - בפרט, בכל הנוגע להצפנת מפתח ציבורי - היא כן), אז קיימת תוכנה שבמאמץ לא שונה מהותית תוכל לפרוץ את ההצפנה ולגלות את הפיענוח הנכון. וזו רק דוגמה - התוצאה היא כללית וחזקה בהרבה.

סקוט אהרונסון פרסם מצגת שבה הוא מדבר על בעיית P=NP. הוא מנסה להמחיש עד כמה הוכחה ש-P=NP תהיה מפתיעה לקהילת מדעני המחשב בעזרת גרף שאני חושב שקולע בול לרעיון:

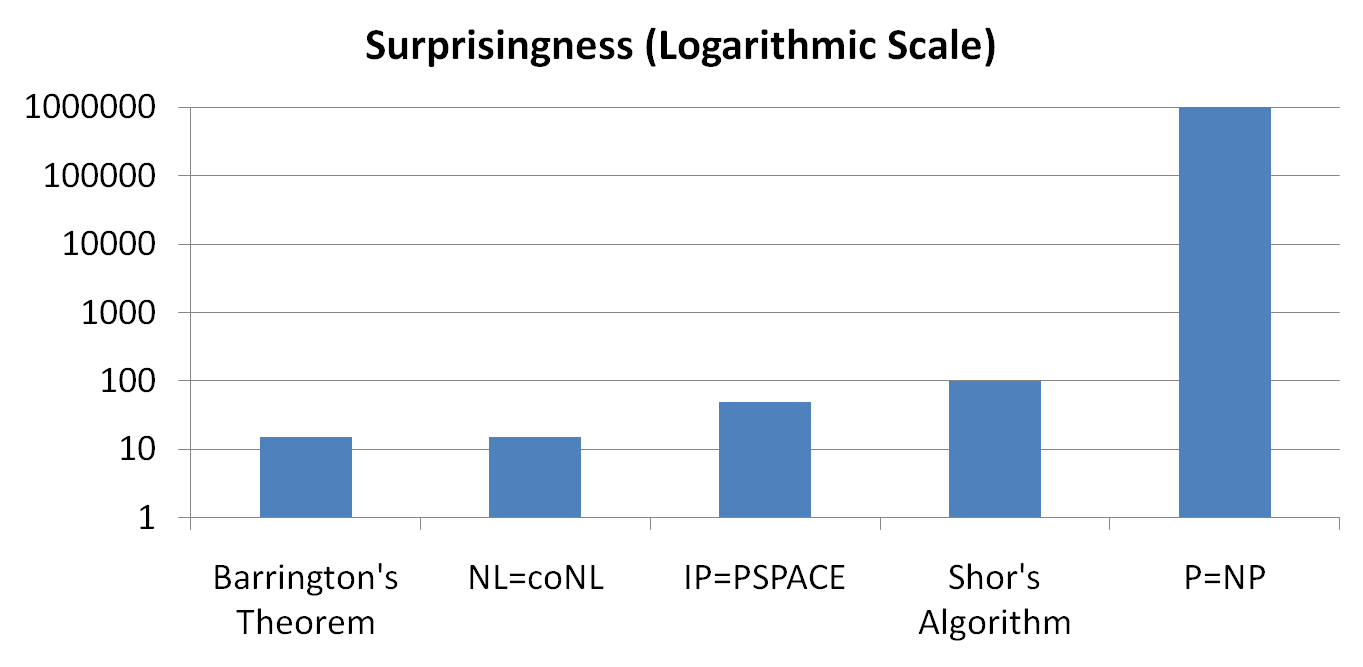שימו לב לסקלה הלוגריתמית! אותה סקלה שבה משתמשים, למשל, במדידת רעידות אדמה. אם אינכם מכירים את התוצאות שמשמאל ל-P=NP, לא נורא - כולן תוצאות מפתיעות ומרתקות בתורת הסיבוכיות (למשל, האלגוריתם של שור הוא אלגוריתם יעיל לפירוק לגורמים במודל המחשב הקוונטי - אלגוריתם זה הקפיץ בצורה דרמטית את ההתעניינות בחישוב קוונטי). אם נמשיך בדוגמת רעידות האדמה - אם נפרש את הגרף כך שגם האלגוריתם של שור בסך הכל מתאים לרעידת אדמה קטנה ומסכנה, שבה בקושי שמים לב שאיזו כוס על השולחן בקומה 20 זזה טיפה לשנייה ואז מפסיקה - אז P=NP יתאים לרעידת אדמה שבה עיר מודרנית שלמה מתמוטטת וקורסת ונבלעת בלב האדמה. עד כדי כך יהיה מדובר על תוצאה מפתיעה.

אבל הוכחה ש-P שונה מ-NP ? התוצאה הזו בהחלט לא תהיה מפתיעה, אלא מה שכולם מצפים לו. היא גם לא תגרור את תרחישי האימה/אוטופיה שתיארתי קודם - מה שלא ידוע לנו כרגע, ימשיך להיות לא ידוע לנו ושום מחשבים לא יעזרו באופן קסום. אז אם כך, למה בכל זאת קמה מהומה כזו סביב ההוכחה האחרונה?

הסיבה למהומה היא שבעיית P נגד NP היא קשה. קשה ברמת “גם אם המוחות הגדולים ביותר בעולם יתכנסו ויחשבו על הבעיה במשך חודשים רצופים, לא ברור שהם בכלל יצליחו לומר עליה משהו בעל ערך”. קשה ברמת “למרות שעברו 40 שנים מאז שנוסחה השאלה במפורש, שום דבר מהשיטות שפותחו עד היום במדעי המחשב לא מסוגלת להתמודד איתה”. יותר מכך - ישנן הוכחות ששיטות מסויימות פשוט לא יוכלו לעבוד. הדרך להראות זאת מזכירה את מה שדיברתי עליו בתחילת הפוסט, כשציינתי שאחת הבעיות בהוכחה הנוכחית היא שהיא “מוכיחה” גם עבור בעיות קלות שהן קשות; אפשר להראות כי שיטות כלליות מסויימות ייכשלו גם הן בביצוע הפרדות שכאלו בין קל וקשה.

התחושה הכללית בקרב מדעני המחשב (וזה נושא שנידון רבות בימים האחרונים, לאור ההוכחה) היא שמדעי המחשב התיאורטיים כפי שהם כיום פשוט אינם מסוגלים להתמודד עם הבעיה. הכלים והרעיונות שפותחו עד כה הם חסרי ערך נגדה. כמו לתקוף טנק מבוצר בעזרת מטאטא נוצות. הדעה הרווחת היא שתידרש גישה חדשה ושונה למדעי המחשב - תיאור מתמטי חדש, או מודל חדש לתיאור חישובים - משהו שיאפשר לראות את הבעיה באופן שונה. אני סבור שהסיטואציה דומה במידת מה למשפט האחרון של פרמה - זהו משפט שהניסוח שלו פשוט למדי ודורש רק ידע בסיסי בחשבון; אך ההוכחה שלו מתבססת על מתמטיקה מתוחכמת ומתקדמת ביותר (רציתי להביא כאן ציטוט מדויק שלו אבל אסתפק בלזרוק לחלל האוויר “עקומים אליפטיים” ו”תבניות מודולריות” כמו שעושים תמיד) - אנחנו צריכים למצוא את המתמטיקה המתוחכמת ומתקדמת שתאפשר לנו להתמודד עם P נגד NP, ודעתם של המומחים כיום היא שאנחנו עדיין רחוקים מאוד משם. לכן הוכחה “אלמנטרית” יחסית, שמשתמשת בכלים מוכרים, תהיה סנסציה. ההוכחה הנוכחית הייתה כזו - הרעיונות שעליהם היא התבססה היו מוכרים יחסית, אם כי נעשה בהם שימוש חדש ולא טרויוויאלי - אך כנראה שגם שגוי.

בדבר אחד אני בטוח, בין אם ההוכחה היא נכונה ובין אם לאו - מדעי המחשב עומדים להמשיך להיות תחום מתמטי מרתק גם בשנים הבאות.