אז מה זה אינטגרל?

מה השטח של עיגול שרדיוסו באורך 1? אלו מכם שלמדו נוסחאות בבית הספר אולי זוכרים שזה צריך להיות \( \pi \), אבל למה? איך מגיעים לזה? הבעיה הזו - מדידת שטח של צורות מסובכות - העסיקה את המתמטיקאים עוד משחר היוולדה של המתמטיקה, ובפרט אצל היוונים הקדמונים. הפתרון הראשון לבעיה הופיע אצל מי שהיה ככל הנראה גדול המתמטיקאים של העת העתיקה - ארכימדס. בשיטה שלו ניתן לראות את ניצני החשבון האינפיניטסימלי, אך מכיוון שאני לא כותב כרגע פוסט היסטורי לא אכנס לפרטים.

בעיה מתמטית נוספת, שצצה בהקשר מודרני יותר, היא הבעיה של מדידת האנרגיה שמועברת לגוף עליו פועל כוח. במכניקה הקלאסית, כוח שפועל על גוף גורם לשינוי במהירות שלו (או יותר במדויק, בתנע שלו, אבל לא כולם מכירים את המושג הזה). אלא ששינוי במהירות אינו בהכרח שינוי באנרגיה של הגוף - ייתכן שהכוח יגרום לשינוי כיוון המהירות אך לא גודלה (זה המצב, למשל, בתנועה מעגלית). אם כן, השינוי באנרגיה נמדד ביחס לאותו חלק מהכוח שפועל בכיוון התנועה של הגוף. מה שמעניין כאן הוא שאין צורך להכניס את מושג הזמן לתמונה: אין צורך להשתמש בטיעון בסגנון “הפעלתי כוח של כך-וכך למשל חמש שניות ולכן העברתי לגוף אנרגיה כזו וכזו”, אלא מספיק לדבר על “הפעלתי כוח של כך-וכך תוך כדי שהגוף עבר מרחק של כך-וכך, ולכן העברתי לגוף אנרגיה כזו וכזו”. במילים אחרות, אם הפעלתי על גוף כוח קבוע \( F \) בכיוון תנועתו, והוא עבר מרחק של \( \Delta x \), אז האנרגיה שהועברה לו היא \( F\cdot\Delta x \). לגודל הזה קוראים העבודה של הכוח על הגוף.

אלא שייתכן שהכוח שפועל על גוף תלוי במיקום שלו ואינו קבוע לכל אורך תנועתו של הגוף. דוגמה קלאסית לכך היא גוף שנמצא בנפילה חופשית מעל כוכב לכת מסויים - ככל שהגוף יתקרב יותר לכוכב הלכת כך כוח המשיכה של אותו כוכב יתגבר. במילים אחרות, ייתכן ש-\( F\left(x\right) \) הוא פונקציה לא קבועה, ואז איך נחשב את העבודה של הכוח?

שתי הבעיות הללו הן למעשה אותה הבעיה, ובשתיהן הפתרון שמציע החשבון האינפיניטסימלי הוא לבצע סכום ממושקל כלשהו, שמובן מסויים יהיה “סכום על מספר לא בן מניה של איברים”. סכום שכזה נקרא אינטגרל. כדי להבין לאן אני חותר, בואו נחזור אל בעיית חישוב השטח של עיגול. עיגול הוא צורה מסובכת ואין לנו מושג איך למדוד את השטח שלו, אז לאיזו צורה אנחנו כן יודעים למדוד שטח? הצורה הפשוטה ביותר היא ככל הנראה מלבן. מלבן שאורכו \( a \) ורוחבו \( b \) הוא בעל שטח של \( a\cdot b \) - זוהי הנחת היסוד בכל הדיון הזה. האינטגרל הוא דרך לקחת את הגדרת השטח הזו ובאמצעות מושג הגבול להחיל אותה לפחות או יותר כל צורה נורמלית שתוכלו לחשוב עליה - רק עבור מקרים “לא נחמדים” יחסית נקבל צורות שלא ניתן למדוד להן שטח באופן הזה.

בואו נניח לצורך פשטות שאפשר לצייר את הצורה שאנחנו רוצים למדוד באופן הבא: מצד אחד, היא תחומה מלמטה על ידי הישר \( y=0 \) (“ציר ה-\( x \)”). מצד שני, היא תחומה מלמעלה באמצעות עקומה כלשהי שמתוארת באמצעות פונקציה \( f\left(x\right) \), שלכל ערך של \( x \) בתחום מסויים (נניח לבינתיים שבין 0 ל-1) מתארת את גובה העקומה. לכאורה זו דרך הצגה קצת מגבילה, כי לא ניתן לתאר כך עיגול, למשל (העקומה שמגדירה עיגול אינה ניתנת לתיאור באמצעות פונקציה כזו כי למרבית ערכי ה-\( x \), העקומה שמקיפה את העיגול אינה פונקציה - יש לה שני ערכים שונים), אבל במקרה של עיגול אין בעיה אמיתית (כי רבע עיגול כן ניתן לתאר כך בקלות: העקומה \( f\left(x\right)=\sqrt{1-x^{2}} \) כש-\( x \) בין 0 ו-1 מתארת בדיוק את רבע עיגול היחידה; גם חצי עיגול ניתן לתאר בקלות אם מרשים ל-\( x \) לרוץ בין מינוס 1 ו-1).

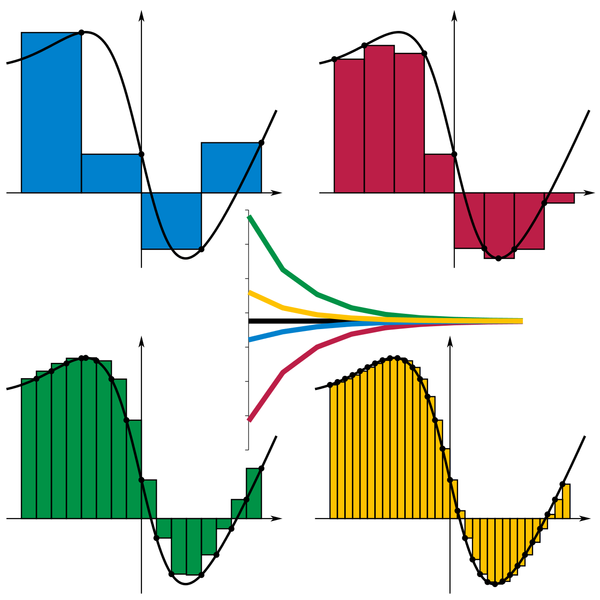
הרעיון כעת הוא פשוט ומבריק - בואו נקרב את הצורה שאנחנו רוצים למדוד באמצעות מלבנים, שאת שטחם אנו יודעים למדוד במדויק. אפשר לחלק את הקטע שבין 0 ו-1 ל-\( n \) מקטעים זהים שאורך כל אחד מהם \( \frac{1}{n} \), ולבנות בכל מקטע שכזה מלבן שרוחב בסיסו הוא \( \frac{1}{n} \), וגובהו נקבע לפיה גובה הפונקציה באותו קטע. כאן מגיע קסם מסויים - לא באמת אכפת לנו איזה גובה לבחור למלבן שלנו, כל עוד זה יהיה גובה של אחת מהנקודות של הפונקציה בקטע; כל עוד הפונקציה “מתנהגת נחמד” לא תהיה עם זה שום בעיה. התוצאה? קירוב, אולי גס, לשטח שלוכדת הפונקציה באותו מקטע.

פורמלית ניתן להגדיר זאת כך: לכל \( 1\le k\le n \) ניקח נקודה \( x_{k} \) בתוך המקטע \( \left[\frac{k-1}{n},\frac{k}{n}\right] \), ונקבע את גובה המלבן להיות \( f\left(x_{k}\right) \). כעת שטח המלבן לאותו מקטע יהיה \( f\left(x_{k}\right)\cdot\frac{1}{n} \), ולכן סכום השטחים של כל המלבנים יהיה \( \sum_{k=1}^{n}f\left(x_{k}\right)\cdot\frac{1}{n} \).

אותו תעלול בדיוק יכול לשמש אותנו גם ככלי להעריך את העבודה שכוח מבצע על גוף בתנועה. נניח שהגוף נע מהנקודה 0 לנקודה 1, ושהכוח שפועל עליו מתואר על ידי הפונקציה \( F\left(x\right) \). נחלק את הקטע \( \left[0,1\right] \) למקטעים מגודל \( n \) ונניח את ההנחה המקלה שבכל מקטע הכוח שפועל על הגוף קבוע ושווה לערך של \( F \) באחת מהנקודות במקטע, נאמר \( x_{k} \); אז אנחנו יודעים בדיוק מה העבודה על הגוף באותו מקטע - היא בדיוק \( F\left(x_{k}\right)\cdot\frac{1}{n} \). לכן סכום העבודה הכולל הוא \( \sum_{k=1}^{n}f\left(x_{k}\right)\cdot\frac{1}{n} \). שתי הבעיות השונות שלנו הפכו לבעיה אחת (עם הבדל אחד - בבעיה שמדבר על כוח, הפונקציה יכולה להיות גם שלילית, אבל הפתרון שנציג עובד גם במקרה זה).

בשני המקרים אנחנו מקבלים קירוב גס בלבד. מתי, אם כן, הסכום יניב את הערך המדויק? ובכן, כאשר לא נקרב את השטח באמצעות מלבנים, אלא באמצעות “מקלות” חסרי רוחב. אלא מה, הכלים המתמטיים הרגילים שלנו לא מאפשרים לנו לתאר מקרים שכאלו - למקלות חסרי רוחב יש שטח 0, ויש מספר לא בן מניה שלהם. אין דרך הגיונית לבצע סכום שלהם באמצעות הכלים שמוכרים לנו. אבל אם אותם מקלות יתרחבו, אפילו טיפ-טיפה, ויהיו בעלי רוחב \( \Delta x \) קטן ככל שנרצה, אז אפשר יהיה לבצע את חישוב השטח של הקירוב הזה בשיא הקלות, כי יש לנו מספר סופי של מחוברים שכולם מלבנים. אם כן, אנחנו מקבלים סדרה אינסופית של קירובים, והשאלה שאנו שואלים את עצמנו היא - האם הסדרה הזו שואפת למשהו? האם יש לה גבול? אם כן, הגבול הזה תופס בדיוק את מושג ה”סכום לא בן מניה של המקלות חסרי הרוחב”; והסכום הזה נקרא האינטגרל של \( f\left(x\right) \) בקטע \( \left[0,1\right] \). פורמלית: \( \int_{0}^{1}f\left(x\right)dx=\lim_{n\to\infty}\sum_{k=1}^{n}f\left(x_{k}^{n}\right)\cdot\frac{1}{n} \), כש-\( n \) ב-\( x_{k}^{n} \) בא לציין שלכל \( n \) יש אוסף נקודות שונה שאנו עשויים לבחור כדי לקרב את \( f\left(x\right) \).

בואו נדבר רגע על הסימון \( \int_{0}^{1}f\left(x\right)dx \). ה-\( \int \), שהוא הסימן המוסכם לאינגטרל, הוא מעין גרסה מוארכת של האות \( S \), מלשון “סכום” (Sum). ה-\( 0,1 \) שרואים למטה ולמעלה הם ה”גבולות” של האינטגרל. ה-\( dx \) שבפנים הוא חסר משמעות מעשית. אינטואיטיבית, הרעיון שמאחוריו הוא זה: מכיוון שאינטגרל הוא הכללה של סכום סופי מהצורה \( \sum f\left(x_{k}\right)\Delta x \), כש-\( \Delta x \) מייצג יחידת מרחק קטנה (בדוגמה שלנו, \( \frac{1}{n} \) כש-\( n \) קטן עוד ועוד), הרי שכשעוברים ל”סכום אינסופי על מספר לא בן מניה של איברים” צריך לעשות שינוי בסימונים שיבהיר את האופי השונה של הסכימה. כשם שאת \( \sum \) הופכים ל-\( \int \), כך גם את \( \Delta x \) הופכים ל-\( dx \) שמציין, אינטואיטיבית “יחידת מרחק קטנה באופן אינפיניטסימלי”. בפועל אין לזה משמעות (כי חישוב של אינטגרל מתבצע באופן שונה מחישוב של סכום סופי - לא באמת כופלים ביחידות שטח אינפיניטסימליות) ולכן ה-\( dx \) בעיקר מסייע להבהיר מי המשתנה שרלוונטי לאינטגרציה, במקרה שבו \( f \) היא פונקציה של כמה משתנים. בבתי הספר משתמשים באותו \( dx \) גם בתור תירוץ טוב להוריד נקודות למי ששכח אותו.

זה שהגדרנו מה זה אינטגרל ממש לא אומר שההגדרה עובדת - האם לכל פונקציה \( f \) אכן קיים הגבול שכתבתי לעיל? התשובה היא שממש, ממש לא. למעשה, העובדה שהשארתי את שאלת “איך בכלל בוחרים את הנקודות \( x_{n}^{k} \) הללו” פתוחה מאפשרת לכל מי שרוצה לעשות צרות “להנדס” סדרה של נקודות שעבורה הגבול הנ”ל בכלל לא יתכנס. דוגמה קלאסית לפונקציה שאין לה אינטגרל היא פונקצית דיריכלה, שמוגדרת להיות 1 על המספרים הרציונליים ו-0 על האי רציונליים. המלכוד הוא בכך שכל קטע שהוא מכיל גם רציונליים וגם לא רציונליים. לכן על ידי בחירה מתאימה של נקודות אני יכול לגרום לכך ש-\( \sum_{k=1}^{n}f\left(x_{k}\right)\cdot\frac{1}{n} \) יהיה שווה 0 (נבחר רק נקודות אי רציונליות בתור \( x_{k} \)) או ש-\( \sum_{k=1}^{n}f\left(x_{k}\right)\cdot\frac{1}{n} \) יהיה שווה 1 (נבחר רק נקודות רציונליות) מה שיחבל בהגדרה של \( \lim_{n\to\infty}\sum_{k=1}^{n}f\left(x_{k}^{n}\right)\cdot\frac{1}{n} \): אוכל לקבל שהגבול הוא 0, או 1, או כלל לא קיים - הכל תלוי בשאלה איך אני בכלל בוחר את הנקודות \( x_{k}^{n} \). לכן הדיון באינטגרלים צריך להתחיל בשאלה - עבור אילו פונקציות ההגדרה בכלל עובדת, ותמיד מספקת את אותו המספר, בלי ליצור בעיות?

מחלקה אחת של פונקציות שעבורה ההגדרה עובדת היא הפונקציות הרציפות שהזכרתי בפוסט קודם. הרציפות של הפונקציה אומרת שהיא מתנהגת “מאוד נחמד” כשמצמצמים אותה לקטעים קטנים - אם אבחר נקודה \( x_{k} \) בתוך קטע, אז \( f\left(x_{k}\right) \) תהיה קרובה מאוד לכל הערכים האפשריים של הפונקציה באותו הקטע, ולכן גודל השגיאה שלי לא יכול להיות משמעותי. למעשה, ההוכחה טיפה יותר מתוחכמת ומסתמכת על תכונה מעט יותר חזקה מ”סתם” רציפות - תכונה שנקראת רציפות במידה שווה - אך מכיוון שזה פוסט מבוא לא אציג לא את התכונה ולא את ההוכחה (אבל כן אעיר שרציפות במידה שווה תמיד מתקיימת עבור פונקציות רציפות בקטע סגור - גם זה משפט לא טריוויאלי לחלוטין שיש להוכיח - ולכן לא באמת שיקרתי לכם).

פונקציות רציפות הן לא סוף הסיפור. ההגדרה עובדת גם עבור פונקציות כלליות יותר, גם אם יש להן מספר נקודות אי רציפות. למשל, כל פונקציה בעלת מספר סופי של נקודות אי רציפות - עובדת. גם מספר אינסופי אך בן מניה של נקודות אי רציפות עובד. הקריטריון הכללי ביותר שניתן לתת מנוסח בעזרת מושג שלא הגדרתי: לפונקציה יש אינטגרל במובן שתיארתי לעיל אם ורק אם קבוצת נקודות אי הרציפות שלה היא ממידה אפס. מה פירוש “ממידה אפס”? לא ניכנס לכך כרגע.

מושג האינטגרל שתיארתי למעלה נקרא אינטגרל רימן, על שם המתמטיקאי בן המאה ה-19. זה נראה קצת מוזר, כי אינטגרלים היו בשימוש כבר על ידי ניוטון ולייבניץ במאה ה-17; העניין הוא בכך שהתיאור הפורמלי באמצעות גבולות לא היה קיים עד למאה ה-19, אז נוסח מחדש החשבון האינפיניטסימלי באופן מדויק ופורמלי יותר. ההגדרה של רימן איננה ההגדרה היחידה - קיימת הגדרה נוספת של דארבו שבה במקום לבחור נקודה “אקראית” מתוך כל קטע כדי לקבוע את גובה המלבן שייבנה עליו, בוחרים את הנקודות הגבוהה והנמוכה ביותר, בונים כך שני קירובים שונים לפונקציה (אחד גדול יותר והשני קטן יותר) ואז משווים ביניהם ורואים האם הם שואפים לאותו הדבר ככל שמעדנים את החלוקה של הקטע. לא השתמשתי בדרך ההצגה הזו כאן כי לדעתי היא מעט פחות אינטואיטיבית (למרות שגם לה יתרונות לא מעטים) ומכיוון שהיא לא מאפשרת לכתוב הגדרה קצרה ונאה כמו \( \lim_{n\to\infty}\sum_{k=1}^{n}f\left(x_{k}^{n}\right)\cdot\frac{1}{n} \).

למעשה, גם ההגדרה של אינטגרל רימן שנתתי ניתנת להכללה כלשהי. אף אחד לא באמת דורש ממני לבצע את החישוב רק על הקטע \( \left[0,1\right] \); אותו רעיון עובד לכל קטע סופי. אף אחד גם לא דורש ממני לפרק את הקטע לחלקים בגודל שווה - העיקר שהוא מפורק ל-\( n \) קטעים כלשהם, ושכשאנחנו משאיפים את \( n \) לאינסוף, גודלם של כל הקטעים שואף לאפס. וכמובן, הסיפור לא נגמר גם כאן. אפשר להגדיר אינטגרלים דו, תלת ו-\( d \)-ממדיים, לכל \( d \); ואפשר להגדיר אינטגרלים על תנועה לאורך מסלול (זו ההגדרה הכללית שבה משתמשים בחישוב עבודה), ואפשר להגדיר אינטגרלים על משטחים; ואפשר להגדיר אינטגרלים על קטעים אינסופיים; וכל זה רק על ידי וריאציות פשוטות על ההגדרה של אינטגרל רימן. יש אינטגרלים יותר מתוחכמים שמוגדרים באופן שמכליל את אינטגרל רימן ופותר חלק מהבעיות שבו - ככל הנראה האינטגרל המפורסם ביותר שמכליל את אינטגרל רימן הוא אינטגרל לבג. כך למשל פונקצית דיריכלה שהצגתי קודם היא אינטגרבילית לבג בצורה פשוטה מאוד (ערך האינטגרל הוא 0, מה שמתאים לאינטואיציה שלנו שה-1-ים שתורמים המספרים הרציונליים הם כאין וכאפס בהתחשב בכך שהרציונליים הם רק בני מניה ואילו כל הקטע \( \left[0,1\right] \) איננו בן מניה). כל המושגים הללו ראויים לפוסטים משל עצמם; אני בפוסט הזה בסך הכל מציג את הבסיס של הבסיס של הבסיס.

אולי אתם מרגישים קצת מרומים - לא הראיתי לכם בסופו של דבר איך מחשבים את השטח של עיגול היחידה עם המושג החדש שהמצאתי. הסיבה לכך היא שטרם הסברתי איך מחשבים את האינטגרל. לצורך כך צריך להכניס לתמונה מושג חדש - האינטגרל הלא מסויים - ולקשר בין מושג האינטגרל למושג הנגזרת. לכך אגיע בהמשך, בפוסט על המשפט היסודי של החדו"א.

לסיכום, גם למי שאיבד את עצמו בסבך הפרטים, הסבר קצר: אינטגרל רימן של פונקציה \( f\left(x\right) \) על קטע \( \left[a,b\right] \) הוא מעין סכום משוקלל אינסופי של כל ערכי \( f\left(x\right) \) בקטע. כאשר \( f\left(x\right) \) חיובית, זה יוצא בדויק השטח שכלוא בין ציר ה-\( x \) ובין גרף הפונקציה באותו קטע. האופן שבו מתבצע חישוב הסכום המשוקלל הזה הוא באמצעות בניית סדרה אינסופית של סכומים משוקללים סופיים ושימוש במושג הגבול כדי לראות לאן הקירובים מתכנסים. ומה שמדהים כל כך כאן הוא שהקירוב הזה עובד. אנחנו מצליחים לחשב במדויק שטחים של צורות מסובכות למדי באמצעות ההגדרה-מבוססת-הקירוב הזו, כמו במקרה של נגזרת, שבה קירבנו “מהירות רגעית” באמצעות סדרה של “מהירויות ממוצעות” על גבי פרקי זמן הולכים וקטנים. זה לטעמי הקסם הגדול ביותר בחשבון האינפיניטסימלי, ואחד מהקסמים הגדולים במתמטיקה: היכולת להפוך את הקירוב הלא מדויק לתשובה סופית מדויקת לחלוטין. לשמחתי זכיתי למספר רב של רגעי “וואו” מתמטיים שבהם נפל לי אסימון והותיר אותי חסר נשימה לרגע. ההוכחה של קנטור לקיום גדלים שונים של אינסוף היא הדוגמה הראשונה שאני חושב עליה תמיד; אבל הקירוב-שהוא-מדויק של אינטגרלים ונגזרות נמצא במקום השני.