פרוייקט "תוצאות מפתיעות בסיבוכיות" יוצא לדרך!

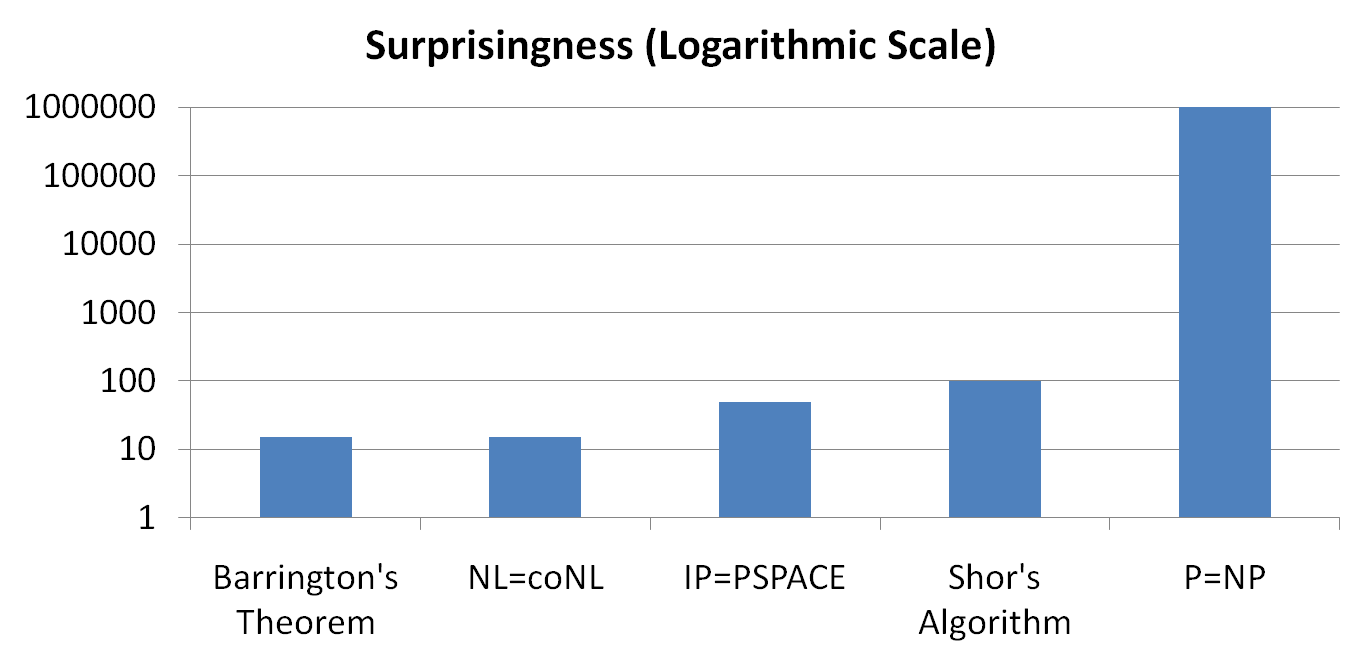
בשלהי מהומת ה”הוכחה” ש-\( \mbox{P}\ne\mbox{NP} \) בקיץ האחרון נתקלתי במצגת של סקוט אהרונסון שניסתה לדבר על בעיית \( \mbox{P}\ne\mbox{NP} \) ומדוע היא כה קשה. אחד מהשקפים ניסה להמחיש עד כמה הוכחה שמתקיים דווקא \( \mbox{P}=\mbox{NP} \) תהיה מפתיעה - הבאתי אותו בבלוג גם בעבר, והנה הוא שוב:

<img class="alignnone size-large wp-image-707" title="pnp_graph" src="/assets/img/2010/08/pnp_graph.png" alt="גרף המציג דירוג "הפתעה" של משפטים במדעי המחשב; ה"משפט" P=NP מדורג בצורה קיצונית מעבר למספר משפטים ידועים ומפתיעים במדעי המחשב" width="450" height="220" />

מנקודת מבטו של מי שמכיר קצת את תורת הסיבוכיות השקף הזה קולע בול: כל התוצאות שמשמאל ל-\( \mbox{P}=\mbox{NP} \) הן תוצאות מפתיעות (גם בפני עצמן וגם במובן זה שהקהילה המדעית אכן הופתעה לגלות אותן). אבל מה על מי שאינו מכיר את תורת הסיבוכיות? ובכן, מכיוון שאני מכיר את כל התוצאות הללו באופן שיאפשר לי (אני מקווה) לכתוב פוסט על כל אחת מהן, אנסה להשלים את הפער.

חייבים להבהיר משהו מראש - כל התוצאות הללו הן לא טריוויאליות. להסביר אותן דורש זמן, ודורש רקע והכרה מוקדמת כלשהי עם מושגים, ודורש כניסה לפרטים טכניים לא פשוטים. הבלוג אמנם לא מתחייב להיות מדויק, אבל כפי שהקוראים הותיקים שמים לב, מדי פעם מתחשק לי להיכנס לעובי הקורה ולהציג משהו לפרטי פרטיו. כך אעשה עם ארבע התוצאות הללו. אני מתחייב להביא כאן הוכחות מלאות של כל ארבעתן, ובתקווה עם כל הרקע הנלווה הנדרש (מה שאומר שכל בעיה תזדקק למספר פוסטים). זה אתגר לא פשוט, ואני מקווה שאצליח לעמוד בו; מכיוון שכל אחת מארבע התוצאות הללו היא יפהפיה בזכות עצמה, אני חושב שזה גם אתגר ראוי.

את הפוסט הזה אנצל כדי להציג סקירה כללית של התוצאות - מה כל אחת מהן אומרת בערך, מה ההקשר ההיסטורי שלה ומה הרעיונות המרכזיים בהוכחה. ונלך משמאל לימין.

משפט ברינגטון:

השאיפה הגדולה של תורת הסיבוכיות היא למצוא חסמים תחתונים. להגיד “את הדבר הזה והזה אי אפשר לעשות בזמן שהוא קצר מ…”. לרוע המזל, מציאת חסמים תחתונים היא קשה ביותר והתוצאות של תורת הסיבוכיות, למרבה הבושה, דלות מאוד. מרבית התוצאות בתורת הסיבוכיות הן מהצורה “אם הדבר הזה קשה, אז גם הדברים הללו קשים”, כש”הדבר הזה” שממנו מתחילים הוא בעיה שיש קונצנזוס כלשהו על הקושי שלה, אך אין הוכחה.

אחת הסיבות שבגללן קשה להוכיח חסמים תחתונים היא שכדי להראות שבעיה היא קשה, צריך להראות שכל נסיון לתקוף אותה הוא מועד לכשלון. איך בדיוק אפשר לכסות את כל דרכי התקיפה האפשריות? ברמה הבסיסית של המושג, ה”כל” הזה בכלל לא מוגדר היטב - האם סיוע מאלוהים או מתרבות חייזרים מתקדמת שהגישה שלה לחישוב שונה לחלוטין משלנו נכלל בתוך ה”כל” הזה? בלית ברירה, מדעני המחשב פונים אל מודל מתמטי קונקרטי לחישוב - מכונת טיורינג, למשל - ומצטמצמים לעיסוק בטענה “כל נסיון לפתור את הבעיה עם מכונת טיורינג ידרוש זמן לא יעיל” (גם מושג ה”יעילות” נזקק להגדרה מתמטית מדויקת). רק מה, מכונת טיורינג היא מודל מורכב למדי ובעל אופני פעולה רבים ושונים, וקשה מאוד למצוא עבורה חסמים תחתונים. לכן מדעני המחשב ממשיכים לחפש אחרי מודלים שעבורם יהיה קל להוכיח חסמים תחתונים. מודל שכזה, שבו נתלו תקוות רבות בעבר והיום כבר הרבה פחות, הוא זה של מעגלים בוליאניים - לא אכנס כאן להגדרה המדויקת אלא אמתין עם זה לפוסט המתאים.

מודל פשוט עוד יותר של חישוב שאליו פנו בתקווה שעליו ניתן יהיה להוכיח חסמים תחתונים, ולהתבסס על כך כדי לתקוף מודלים כלליים יותר, הוא זה של תוכניות מתפצלות (Branching Programs; לפעמים גם קוראים להן “דיאגרמות החלטה בינארית” - Binary Decision Diagrams). גם כאן, לא אכנס לתיאור מדויק של המודל, אבל הוא פשוט בצורה מחרידה - ניתן לחשוב על הגרסה שלו שרלוונטית לנו בתור חישוב שיכול להימצא באחד מכמה מצבי זכרון שונים, ובכל צעד עובר למצב זכרון חדש על בסיס מצב הזכרון הקיים וערכו של ביט אחד ויחיד מן הקלט. זה הכל. את העסק אפשר לתאר בעזרת גרף שבנוי משכבות; הסיבוכיות שלו נמדדת באמצעות אורך הגרף (אורך המסלול הארוך ביותר בגרף - לרוב אומרים “עומק” הגרף אולם כאן לטעמי “אורך” מתאים יותר) שמודד את אורך החישוב במודל הזה; ורוחב הגרף, שמודד את מספר הצמתים המקסימלי בשכבה אחת של הגרף - זהו מדד לכמות מצבי הזכרון המקסימליים שהתוכנית תזדקק להם.

להוכיח חסמים תחתונים גם על המודל הזה, זה קשה, קשה להחריד - אני רואה שאתם כבר מזהים תבנית כלשהי בתורת הסיבוכיות. מה כן אפשר לעשות? להשית מגבלות נוספות על המודל ולהוכיח חסמים תחתונים על המודל המוגבל. המגבלה הטבעית ביותר שקופצת לראש היא הגבלה או של האורך או של הרוחב - הרעיון הוא להראות שאם מנסים להקטין את האחד, השני חייב לגדול משמעותית. בפרט, מגבלה אחת נראתה קטלנית לחלוטין - הגבלה של הרוחב להיות קבוע באורכו ולא משנה כמה גדול הקלט (אני קצת מרמה כאן - לקלטים מאורכים שונים מותאמות תוכניות מתפצלות שונות; הנקודה היא שהרוחב של כולן חייב להיות זהה). השערה הועלתה שעבור רוחב קבוע שכזה, גם חישוב של פונקציות פשוטות יחסית שקיימים מעגלים יעילים שמחשבים אותן ידרוש גרף באורך “לא יעיל” (לא פולינומי). התקווה הלכה והתממשה כאשר הצליחו להוכיח שאכן, עבור רוחב קבוע יש חסם תחתון על אורך הגרף - לפעמים האורך חייב להיות יותר מאשר לינארי (כלומר, הוא לא תמיד לכל היותר \( O\left(n\right) \) כאשר \( n \) הוא אורך הקלט). זה רק צעד ראשון, כי התקווה הייתה להוכיח שהאורך חייב להיות לא פולינומי (כלומר, לא \( O\left(n^{2}\right) \), לא \( O\left(n^{3}\right) \) וגם לא \( O\left(n^{1000}\right) \)), אבל זו נראתה כמו התחלה מבטיחה. ואז בא ברינגטון.

משפט ברינגטון אומר שכל פונקציה שניתן לחשב על ידי מעגלים בוליאניים יעילים (שוב, אני מרמה פה - פורמלית, הוא מדבר על המחלקה \( \mbox{NC}^{1} \) שאתאר בפירוט בפוסט המתאים) ניתן לחישוב על ידי תוכניות מתפצלות מאורך פולינומי ורוחב 5. כלומר, אפשר “תמיד” לוותר על רוחב גדול - 5 זה כל מה שצריך. וכפי שקורה בדרך כלל במשפטים עם ניסוח מוזר שכה, המספר 5 אינו מקרי כלל; עבור 4 ומטה זה לא עובד, והסיבה לכך היא שחבורת התמורות \( S_{5} \) היא עשירה ומעניינת מספיק כדי שתקרה בה תופעה מסויימת שלא מתרחשת ב-\( S_{4} \) (הדבר מזכיר מאוד את האופן שבו משוואות ממעלה חמישית ומעלה אינן ניתנות לפתרון כללי באמצעות רדיקלים - שוב, בגלל ש-\( S_{5} \) עשירה מספיק כדי שתקרה בה תופעה כלשהי שלא מתרחשת בחבורות הקטנות יותר). הבניה עצמה משתמשת באופן מחוכם ויפהפה בתמורות; היא מסוג הדברים שעליהם אני חושב בו זמנית גם “אלוהים, כמה זה פשוט”, גם “אלוהים, איך לעזאזל הוא חשב על זה?” ו”אלוהים אדירים!” באופן כללי.

NL=coNL:

בואו נדבר על \( \mbox{NP} \): זהו אוסף של בעיות הכרעה, כשבעיית הכרעה היא משהו שמחפשים עבורו תשובת “כן/לא”. למשל, “האם המספר הזה פריק?” או “האם יש מסלול שעובר בכל הערים במפה הזו מבלי לבקר באף עיר פעמיים?”. לבעיות שב-\( \mbox{NP} \) תכונה חשובה אחת נוספת - אם התשובה היא “כן”, אפשר להוכיח זאת באופן כזה שההוכחה תינתן לבדיקה ביעילות (המספר פריק? ההוכחה תהיה הפירוק; יש מסלול שעובר בכל הערים? ההוכחה תהיה המסלול עצמו. כדי להבין למה זה לא טריוויאלי תמיד, חשבו איך אפשר להוכיח באופן יעיל לבדיקה שמספר הוא ראשוני…).

\( \mbox{coNP} \), לעומת זאת, הוא אוסף בעיות הכרעה שבו דווקא תשובת “לא” היא זו שקלה להוכחה. כדי להוכיח שמספר הוא לא ראשוני, אפשר לתת כהוכחה לכך את הפירוק שלו לגורמים. כפי שבוודאי שמתם לב, מה שעשיתי פה הוא פשוט לקחת בעיה שכבר ראינו שהיא ב-\( \mbox{NP} \) (“האם מספר הוא פריק?”) ולהחליף אותה בבעיה ה”משלימה” שלה (“האם מספר הוא לא פריק?”). זה לא במקרה - הגדרה חלופית ל-\( \mbox{coNP} \) היא כאוסף כל המשלימות של בעיות מ-\( \mbox{NP} \).

שאלה פתוחה מרכזית במדעי המחשב היא האם \( \mbox{NP=coNP} \). זה אחד מהדברים שאותם \( \mbox{P=NP} \) יוכיח מייד, אבל הכיוון ההפוך אינו נכון; ייתכן ש-\( \mbox{P\ensuremath{\ne}NP} \) ועדיין \( \mbox{NP=coNP} \), כך שזו טענה “סבירה קצת יותר” מאשר \( \mbox{P=NP} \). עם זאת, היא עדיין נחשבת לבלתי סבירה בעליל ויש תחומים בסיבוכיות ש(אני קצת מגזים עכשיו) עצם קיומם מתבסס על ההנחה ש-\( \mbox{NP\ensuremath{\ne}coNP} \) (למשל Proof Complexity שעוסק בשאלה כמה מסובכת צריכה להיות הוכחת “כן” לטענה ב-\( \mbox{coNP} \)).

יש משהו טבעי ונכון בהנחה ש-\( \mbox{NP}\ne\mbox{coNP} \). בואו ניקח כדוגמה את בעיית המסלול ההמילטוני (“יש מסלול שעובר בכל הערים”). אם קיים מסלול, קל להוכיח זאת על ידי הצגה שלו. אבל אם אין מסלול, האם יש הוכחה פשוטה כלשהי לכך? איך מוכיחים שמשהו הוא בלתי אפשרי? הרי זה אותו קושי שתיארתי קודם שקיים באופן כללי אצל מדעני המחשב בבואם להוכיח חסמים תחתונים! לתת חסם עליון לבעיה יחסית קל, כי אפשר לתת פתרון עבורה והוא משרה חסם עליון; אבל חסם תחתון צריך איכשהו להקיף כל אפשרות שהיא. כך גם הוכחה שאין מעגל המילטוני - היא צריכה איכשהו לטפל “בכל האפשרויות” ולהראות שאף אחת מהן לא עובדת. זה נראה כמו קושי שונה מהותית מאשר סתם לתת דוגמה למסלול וללכת הביתה.

התחושה הזו עוברת כמו שהיא גם לסיבוכיות זכרון. המחלקות המקבילות ל-\( \mbox{NP} \) ו-\( \mbox{coNP} \) בכל הנוגע לסיבוכיות זכרון יעילה (כלומר, לוגריתמית בגודל הקלט; סיבוכיות זכרון פולינומית בגודל הקלט זה הרבה יותר מדי) מסומנות ב-\( \mbox{NL} \) ו-\( \mbox{coNL} \), כך שאתם כבר מבינים לאן אני חותר - בראשית שנות השמונים הוכיחו שני חוקרים, באופן בלתי תלוי, ש-\( \mbox{NL=coNL} \), להפתעתה הגדולה של קהילת הסיבוכיות. יותר מאשר ההוכחה הזו אומרת משהו על שאלת \( \mbox{NP=coNP} \), היא אומרת משהו על האופן שבו העולם של סיבוכיות הזכרון שונה מאוד באופיו מזה של סיבוכיות הזמן; ההבדל המרכזי הוא שזכרון ניתן למחזר, וזמן לא - וזה גורם לבעיות להתנהג באופן שונה ולא צפוי ומרתק.

IP=PSPACE:

כבר אמרתי בפוסט הזה שאפשר לחשוב על \( \mbox{NP} \) בתור מחלקת בעיות ההכרעה כך שקל להוכיח את נכונות תשובת “כן” עבורן. הוכחה, במקרה הזה, היא פשוט מחרוזת תווים כלשהי שאלגוריתם הבדיקה של נכונות הטענה מסוגל להיעזר בה כדי להשתכנע שהטענה נכונה. זו כבר הכללה כלשהי של מושג ההוכחה שמוכר במתמטיקה (וקל לראות שמושג זה הוא אכן מקרה פרטי של מה שאני מדבר עליו כאן) - ההכללה הבאה מגיעה כאשר מרשים להוכחה להיות אינטראקטיבית: יש לנו “מוודא” ו”מוכיח”, והם מקיימים דיאלוג שבו המוכיח מנסה לשכנע את המוודא בכך שטענה כלשהי היא נכונה. זו הכללה מובהקת של \( \mbox{NP} \), שכן אחד מהדברים שהמוכיח יכול לעשות הוא פשוט לתת למוודא הוכחת-\( \mbox{NP} \) ולהגיד לו “קרא ותגיד מה דעתך”, אבל המוכיח יכול גם לענות לשאלות חדשות שהמוודא שואל אותו בתגובה לדברים שהוא אומר; והוא יכול גם להגיב ל”אתגרים” שהמוודא יכול להציב בפניו. בקיצור, במובהק יש לנו כאן משהו חזק יותר מ-\( \mbox{NP} \).

או שלא? מסתבר שאם דורשים שכל הדיאלוג יתבצע בפרק זמן שעדיין מאפשר לו להיחשב “יעיל”, אין שום הבדל בין מה שאפשר להוכיח אינטראקטיבית ובין \( \mbox{NP} \), מהנימוק הפשוט שהוכחת ה-\( \mbox{NP} \) יכולה לכלול מראש את כל הדיאלוג הצפוי בין המוודא והמוכיח, כל עוד הדיאלוג הזה הוא דטרמיניסטי באופיו. לכן קריטי להכניס לדיון מימד הסתברותי כלשהו, ולאפשר למוודא לטעות לפעמים, אבל בהסתברות זניחה. כאשר מרשים את זה, מתברר שאפשר פתאום להוכיח עוד דברים שלא ידוע אם הם שייכים ל-\( \mbox{NP} \) או לא. מצד שני, לא היה נראה שאפשר להוכיח הרבה יותר; בפרט, שני החיזוקים השונים של מושג ההוכחה (אינטראקטיביות מחד ואקראיות מאידך) היו כאלו שכל אחד בנפרד לא מחזק אותנו יותר מדי, והיו ראיות נוספות לכך שכנראה מערכות הוכחה אינטראקטיביות שכאלו לא פותרות “הרבה” בעיות מעניינות שלא ידוע כבר כעת שהן ב-\( \mbox{NP} \), ולכן ההשערה הייתה שביחס ל”מחלקת העל” של תורת הסיבוכיות - המחלקה \( \mbox{PSPACE} \), של בעיות שניתן לפתור בזכרון פולינומי, מחלקה גדולה להחריד שמכילה את רוב מחלקות הסיבוכיות הסטנדרטיות האחרות, אבל אנחנו עדיין לא יודעים שהיא שונה מ-\( \mbox{P} \) - ההשערה הייתה שביחס למחלקה זו, מחלקת הדברים שיש להם הוכחה אינטראקטיבית, \( \mbox{IP} \), היא קטנה, ואולי קטנה בהרבה.

ואז התגלה שהן שוות - \( \mbox{IP=PSPACE} \). זה אומר שהכוח של הוכחות אינטראקטיביות הוא גדול בהרבה ממה שניתן היה לשער - ולכן גם עושה את התחום הזה למעניין יותר. וכרגיל, גם ההוכחה עצמה משתמשת ברעיונות מתוחכמים ויפים; היא מהווה דוגמה אלגנטית שחביבה עלי מאוד להוכחה ש”יוצאת מהמסגרת”. אבל בואו לא נקדים את המאוחר…

האלגוריתם של שור:

הנחת העבודה הבסיסית של מדעי המחשב היא שהמודל של מכונת טיורינג מתאר נכונה את “מה שאפשר לחשב”. ההנחה הזו מכונה “התזה של צ’רץ’ וטיורינג”, ולמרות שאין ולא תהיה לה הוכחה (כי היא מנסה לומר משהו כללי מדי) עד היום לא קיבלנו שום רמז לכך שהיא אינה נכונה - כל מודל חישובי שחזק יותר ממכונת טיורינג הוא גם כזה שלא מוכרת שום דרך לממש אותו בפועל (וכרגיל, אולי כדאי להיות קצת זהירים עם הטענה הזו אבל כאן לא המקום להיכנס להסתייגויות).

לעומת זאת כשמדברים לא על השאלה מה אפשר לעשות בכלל אלא מה אפשר לעשות מהר, המשחק משתנה למדי. ייתכן שהמודל המסורבל של מכונת טיורינג הוא חלש מדי מכדי לתפוס כל חישוב יעיל? ובכן, זו אחת הסיבות מדוע מזהים את המושג של “חישוב יעיל” עם “חישוב בזמן פולינומי”; הפולינומיות היא דרישה לא כבדה יותר מדי, ולא קשה לראות שאם משהו יכול להתבצע בזמן פולינומי על ידי מחשב רגיל, גם מכונת טיורינג יכולה לעשותו בזמן פולינומי. אם כן, זה הוביל לניסוח גרסת-סיבוכיות-זמן של התזה של צ’רץ’ וטיורינג - “הגרסה החזקה” של התזה. הגרסה הזו טוענת שכל מה שניתן לחשב ביעילות, ניתן לחשב ביעילות בעזרת מכונת טיורינג. התזה הזו - אולי הנחת העבודה הבסיסית ביותר של העוסקים בתורת הסיבוכיות - חטפה זבנג לפרצוף כשב-1994 הוכיח פיטר שור שניתן לפתור את בעיית הפירוק לגורמים בעזרת מחשב קוונטי.

מחשב קוונטי (רעיון שהועלה כבר בשנות השבעים, בפרט על ידי ריצ’רד פיינמן) הוא מחשב שמשתמש באפקטים קוונטים לצורך החישוב שלו. זאת להבדיל ממחשב “קלאסי” שבו החישובים אינם שונים מכאלו שאדם מבצע עם נייר ועט (אין זה אומר שלא צריך לדעת את תורת הקוונטים כדי להיות מסוגלים לבנות פיזית מחשב קלאסי - רק שאפקטים קוונטיים נותרים בו ברמת המיקרו ואינם מורגשים במה שהמחשב עושה ישירות עם אינפורמציה). הרעיון הבסיסי הוא לאחסן מידע באופן כזה שהוא יהיה בסופרפוזיציה של מצבים אפשריים רבים שונים (כלומר, יהיה איכשהו בכולם “בו זמנית”). הקושי שבעניין הוא שלמידע כזה קשה לבצע מניפולציות (אפילו פעולת AND בסיסית לא ניתנת לביצוע כמות שהיא וצריך להתחכם), וקשה לגשת אליו באופן ישיר - הדרך היחידה לדעת מה תוכן המידע הוא לקרוא אותו, מה שיגרום לסופרפוזיציה “לקרוס”. למרות זאת, גם לאחר שקלול הקשיים הללו, מחשבים קוונטיים נראים מבטיחים ובעלי פוטנציאל גדול. קצת קשה להסביר כאן עד הסוף למה - ההבדלים בין מחשב קוונטי וסתם מחשב הסתברותי הם עדינים יותר משנדמה במבט ראשון - אבל בדיוק בשביל זה יש לנו את האלגוריתם של שור, כדי להבהיר שזה אכן, ככל הנראה, המצב.

בעיית הפירוק לגורמים (ואפילו בעיה פשוטה יותר - בהינתן מספר פריק, למצוא מספר גדול מ-1 וקטן ממנו שמחלק אותו) מעסיקה את האנושות כבר אלפי שנים, כולל את המוחות המתמטיים הגדולים ביותר אי פעם. בשנים האחרונות הומצאו אלגוריתמים קלאסיים חזקים ומתוחכמים ביותר, שמתבססים על מתמטיקה מאוד לא טריוויאלית, ופותרים את הבעיה - אך למרבה הצער, אפילו הם עדיין לא יעלים מספיק כדי להיקרא “יעילים” על פי ההגדרה הסטנדרטית של תורת הסיבוכיות. לעומת זאת, האלגוריתם של שור, שמשתמש בכמה רעיונות מבריקים למדי ובחישוב קוונטי, הוא כן יעיל לפי אותה הגדרה. אם תחושת הבטן של עולם הסיבוכיות נכונה ופירוק לגורמים היא אכן דוגמה לבעיה שאין לה פתרון “קלאסי” יעיל, אז האלגוריתם של שור הוא ההוכחה לכך שחישוב קוונטי הוא חזק יותר (בכל הנוגע לסיבוכיות זמן ריצה) מאשר חישוב קלאסי - ובפרט, שסימולציה של תהליכים קוונטיים באמצעות חישובים “קלאסיים” דורשת זמן לא יעיל. כלומר, זה אומר משהו יותר חזק מאשר סתם “אפשר לפרק לגורמים”: זה אומר משהו על היכולת שלנו לתאר את המציאות באמצעות מחשב קלאסי!

כמובן, לאלגוריתם גם השלכות הרסניות למדי על העולם הפרקטי אם ימומש בפועל, מכיוון ששיטות ההצפנה הפומביות הקיימות מתבססות ברובן על פירוק לגורמים (אך לא כולן; וכמובן, דגש על “פומביות” - הצפנות סימטריות לא קשורות לפירוק לגורמים) או על בעיות קרובות ברוחן שחישוב קוונטי מחסל, מחשב קוונטי מתפקד ייאלץ הרבה טכנולוגיות להיזרק לפח. אלא שכרגע בפועל מחשב קוונטי רחוק מלהיבנות - מדובר באתגר הנדסי משמעותי, שעשוי להחביא בתוכו עוד בעיות שטרם חזינו. כך שבינתיים האלגוריתם של שור נותר על הנייר - אך גם שם הוא מרתק מספיק בפני עצמו.

אם כן, אלו הן ארבע הבעיות. בפוסטים עתידיים אנסה לכסות אותן באופן פחות או יותר מלא. האם זה ניתן לביצוע בזמן פולינומי? ימים יגידו.