הפרדוקס של בנך-טרסקי (חלק א')

פרדוקס בנך-טרסקי הוא אולי הדרך הטובה ביותר להמחיש להדיוטות כמה מוזרה המתמטיקה. בפשטות, הפרדוקס אומר את הדבר הבא: ניתן לקחת כדור, לחתוך אותו ל-5 חתיכות, להזיז אותן טיפה (ולסובב, ולשקף וכאלה) ולבנות מהן שני כדורים באותו הנפח של הכדור המקורי.

רגע, מה?

ברוכים הבאים למתמטיקה, העולם שבו קורים דברים מוזרים. מן הסתם אחרי תיאור הפרדוקס צריכה לבוא הסתייגות כלשהי שבאה להסביר למה זה לא יכול לקרות “בעולם האמיתי”, ולרוב נשלפת בשלב הזה החשודה המיידית - אקסיומת הבחירה הידועה לשמצה. מהי אקסיומת הבחירה? אסביר זאת בהמשך (וגם הסברתי זאת בעבר), אבל לדעתי האישית התפקיד שהיא ממלאת בכל העניין הזה הוא שולי יחסית והיא אינה הגורם המרכזי לפרדוקסליות. ה”פרדוקסליות” של הפרדוקס איננה כה מפתיעה כפי שהיא נדמית ממבט ראשון, וכפי שאמרתי - היא צצה ועולה במתמטיקה כל הזמן. מה שמוזר בבנך-טרסקי הוא לא הקונספט של “לקחת אובייקט ולשכפל אותו”, אלא העובדה שאותו אובייקט הוא כדור ושהשכפול מתבצע על ידי חיתוך למספר סופי של פלחים וביצוע הזזות וסיבובים וכדומה. כלומר, השכפול נדמה “פשוט” מדי - וכמובן שיש לזה מחיר, והמחיר הוא שאותם חמישה פלחים הם די מסובכים (וכאן אקסיומת הבחירה נכנסת לעניין).

בואו נתחיל בקטן. איפה במתמטיקה אפשר למצוא שכפול דומה לבנך-טרסקי שלא יהיה לנו כה מוזר? המספרים הטבעיים, \( \mathbb{N} \), הם דוגמה יפה. הבה נפצל את \( \mathbb{N} \) לשתי קבוצות - קבוצת הזוגיים, שאסמן ב-\( \left\{ 2,4,6,\dots\right\} \), וקבוצת האי זוגיים, שאותה אסמן ב-\( \left\{ 1,3,5,\dots\right\} \). עכשיו בואו נתעלל בהן באופן הבא: כל איבר בקבוצת הזוגיים נחלק ב-2, ולכל איבר בקבוצת האי זוגיים נחבר 1 ואז נחלק ב-2. בשני המקרים נקבל את הקבוצה \( \left\{ 1,2,3,4,\dots\right\} \), שהיא פשוט \( \mathbb{N} \) עצמה. אז מה קרה פה? לקחנו את \( \mathbb{N} \), פירקנו אותה לשתי קבוצות זרות, הפעלנו על כל קבוצה מניפולציות כלשהן שלא מוסיפות איברים חדשים לקבוצה, וקיבלנו שני עותקים של \( \mathbb{N} \). בצורה ציורית אפשר לתאר את העסק כך: \( \mathbb{N}=A\uplus B \) (הסימון הזה בא לציין איחוד זר - זה אומר ש-\( \mathbb{N} \) מורכב בדיוק משתי הקבוצות \( A,B \) ושאין להן איברים משותפים), וכמו כן \( \mathbb{N}=\frac{A}{2} \) ו-\( \mathbb{N}=\frac{B+1}{2} \) (זה לא סימון סטנדרטי אבל אתם מבינים את הכוונה).

למי מכם שזה מוזר להם - ברכותי, ברוכים הבאים למתמטיקה, לכו וקראו את הפוסט על המלון של הילברט ואז באמת יהיה לכם מוזר. אבל לכל היתר, שכבר רגילים לעסק הזה, יש לי שאלה קטנה - מה ההבדל המהותי בין זה ובין בנך-טרסקי? אני מודה שהבדל מהותי אני לא רואה. בכל זאת, הבדל משמעותי אחד הוא שבנך-טרסקי הוא פרדוקס גאומטרי - הוא מתעסק ביצור גאומטרי פשוט, כדור, ובפעולות שלכאורה משמרות את הנפח של הכדור ולכן לא יכולות לגרום להכפלה שלו. אבל מה המשותף לבנך-טרסקי ולמה שהראיתי כרגע? מה בעצם ההגדרה הכללית?

ובכן, נאמר שקבוצה \( X \) היא פרדוקסלית (ביחס לסט פעולות מסויים) אם אפשר לפרק את \( X \) לחלקים - \( A_{1},A_{2},\dots,A_{n} \) ו-\( B_{1},B_{2},\dots,B_{m} \), כך שכל החלקים זרים - אין לאף חלק איברים משותפים עם איברים אחרים - ואפשר להפעיל פעולות מסויימות (מתוך הסט המדובר) על כל אחת מסדרות החלקים בנפרד, כך שה-\( A_{i} \)-ים, לאחר שביצענו עליהם את הפעולות, יתנו לנו את \( X \) המקורית, וכך גם ה-\( B_{i} \)-ים. הדרישה שכל החלקים יהיו זרים היא קריטית, כמובן, אחרת היינו בוחרים \( A=B=X \), ואז מה עשינו? אין שום דבר מפתיע בשכפול שכל מה שעושים בו הוא לספור את אותו הדבר פעמיים.

למי שהדוגמה של הטבעיים לא עשתה עליו רושם, בואו נעבור לדבר על משהו הרבה יותר מהותי שגם בו צצה פרדוקסליות דומה: חבורות. בניגוד לדוגמת הצעצוע הקודמת, הדוגמה הנוכחית היא חשובה ביותר, כי על בסיס מה שקורה בה נבנה גם פרדוקס בנך-טרסקי עצמו.

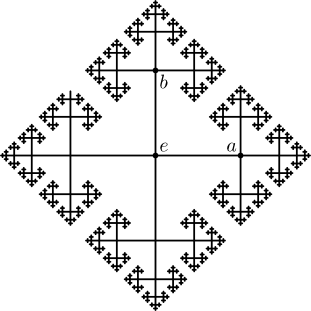
לא אחזור כאן על ההגדרה של חבורה, אלא אתאר מייד את החבורה שמעניינת אותנו - החבורה החופשית עם שני יוצרים \( a,b \). זו קבוצה שכל איבר בה הוא סדרה של תווים מבין ארבעת הבאים: \( \left\{ a,b,a^{-1},b^{-1}\right\} \). הכלל הוא ש-\( a \) ו-\( a^{-1} \) “מצמצמים” זה את זה - אם שניהם נכתבים בסמיכות הם נמחקים מהמילה. כנ”ל לגבי \( b,b^{-1} \). כלומר, \( aba^{-1}b^{-1} \) זו מילה חוקית בחבורה, אבל המילה \( abb^{-1}a \) היא בעצם דרך מסורבלת לכתוב את \( aa \). בנוסף, יש מילה בת 0 תווים - המילה הריקה - שאסמן ב-\( e \). אם יש לנו שתי מילים אפשר לשרשר אותן: למשל, השרשור של \( aa \) ושל \( bbb \) הוא \( aabbb \), והשרשור של \( ab \) ו-\( b^{-1}a \) הוא \( abb^{-1}a \), כלומר \( aa \).

יש הצגה גרפית יפה לחבורה הזו:

אפשר לחשוב על החבורה הזו כעל “פתית שלג” שמחולק לארבע ענפים עיקריים - הענף של המילים שמתחילות ב-\( a \), אלו שמתחילות ב-\( b \), אלו שמתחילות ב-\( a^{-1} \) ואלו שמתחילות ב-\( b^{-1} \). באמצע יש את האיבר הגלמוד \( e \). בואו נסמן את החבורה כולה ב-\( F \) (מלשון Free), ואת קבוצת “האיברים שמתחילים ב-\( a \)” ב-\( F\left(a\right) \) (ובדומה, \( F\left(b\right) \), \( F\left(a^{-1}\right) \) ו-\( F\left(b^{-1}\right) \)). עכשיו מגיע הקסם: מהי \( a\cdot F\left(a^{-1}\right) \), כלומר הקבוצה שמתקבלת כאשר לוקחים את \( F\left(a^{-1}\right) \) וכופלים את כל האיברים שבה מצד שמאל ב-\( a \) (דהיינו, משרשרים את \( a \) משמאל להם)? לא קשה להשתכנע שזו קבוצת כל האיברים ב-\( F \) שאינם מתחילים ב-\( a \), כי מה שקורה הוא שה-\( a \) שכפלנו בו משמאל מבטל את ה-\( a^{-1} \) שבו התחילה המילה; ואם המילה התחילה ב-\( a^{-1} \) אז האות הבאה יכולה להיות כל אות למעט \( a \) (אחרת שתי האותיות הראשונות היו מבטלות זו את זו). המסקנה היא ש-\( F=F\left(a\right)\cup aF\left(a^{-1}\right) \). באותו אופן, \( F=F\left(b\right)\cup bF\left(b^{-1}\right) \). מה קרה כאן? לקחנו את \( F \), ופירקנו אותה לחמישה חלקים: \( F=F\left(a\right)\cup F\left(b\right)\cup F\left(a^{-1}\right)\cup F\left(b^{-1}\right)\cup\left\{ e\right\} \). זו חלוקה לקבוצות זרות, כמובן. את החלק של \( \left\{ e\right\} \) הגלמוד זרקנו לפח. את היתר חילקנו לשני זוגות. עכשיו עשינו להטוט כלשהו עם כל אחד מהזוגות - לקחנו קבוצה אחת, הפעלנו עליה מניפולציה כלשהי (כפל ב-\( a \) או כפל ב-\( b \)), איחדנו עם הקבוצה השניה וקיבלנו מחדש את \( F \) המקורית.

למה בעצם זה כל כך חשוב? ובכן, חבורות הן לא סתם אובייקטים שלא קשורים לכלום. לעתים קרובות מאוד, ובפרט בדיון הנוכחי, חבורות צצות כאובייקט שפועל על אובייקטים מתמטיים אחרים. אנחנו מזהים אוסף של פעולות שמבצעים על אובייקט, ואז שמים לב לכך שלאותו אוסף יש מבנה של חבורה - אפשר “להכפיל” שני איברים ממנו בצורה בעלת משמעות (לרוב על ידי הרכבה של הפעולות - הפעלה של אחת מהן ולאחר מכן השניה). הרעיון המרכזי הוא שאם יש לנו חבורה שהיא עצמה פרדוקסלית ופועלת על אובייקט מסויים, אז ייתכן שניתן יהיה “להרים” את הפרדוקסליות של החבורה אל פרדוקסליות של האובייקט שעליו היא פועלת (אך צריך להניח עוד דבר או שניים - ארחיב על כך בהמשך).

במקרה של בנך טרסקי, החבורה הרלוונטית היא חבורת האיזומטריות של המרחב. איזומטריה היא העתקה ששומרת על מרחקים; איזומטריה שמופעלת על קבוצה משמרת את “המבנה הפנימי” של הקבוצה. איזומטריה היא בדיוק מה שדיברתי עליו קודם כשדיברתי על “הזזות, סיבובים, שיקופים”. כדי להבהיר איך העסק רלוונטי אלינו אתחיל בתיאור של פרדוקס דומה לבנך-טרסקי: פרדוקס סירפינקי-מזורקביץ’. ההבדלים העיקריים בינו ובין בנך-טרסקי: הוא מתרחש במישור, לא במרחב; הוא לא מתבסס על החבורה החופשית עם שני יוצרים אלא על משהו פשוט טיפה יותר; הקבוצה שבה הוא מתעלל היא לא יפה כמו כדור; והוא לא דורש את אקסיומת הבחירה. למעשה, הפירוק הפרדוקסלי שהוא מציג הוא קונסטרוקטיבי למדי. בנוסף, הפרדוקס הזה קודם היסטורית לבנך-טרסקי.

הפרדוקס מתעסק בקבוצה במישור, \( \mathbb{R}^{2} \), ולכן החבורה שמעורבת בסיפור, שאסמן ב-\( G \), היא חבורת האיזומטריות של המישור. עוד מעט אראה איך אפשר למצוא שני איברים \( \tau,\rho\in G \) שמקיימים את התכונה הבאה: קיים \( x\in\mathbb{R}^{2} \) (למעשה, הוא יהיה \( \left(0,0\right) \)) כך שכל שתי מילים ב-\( \tau,\rho \) (כלומר, מילים שמכילות רק את שני הסימנים הללו; לא את \( \tau^{-1} \) ו-\( \rho^{-1} \)) שהאחת מתחילה ב-\( \tau \) והשניה מתחילה ב-\( \rho \) מעבירות את \( x \) לאיברים שונים כשהן מופעלות עליו. במילים אחרות, אם יש סדרת פעולות של \( \tau \) ו-\( \rho \) שמפעילים על \( x \), אז סדרה שמסתיימת ב-\( \tau \) תניב פעולה שונה בהכרח מסדרה שמסתיימת ב-\( \rho \) (כשמפעילים מילה כלשהי על \( x \), קודם כל פועל על \( x \) מה שנמצא בסוף המילה; אלו עניינים טכניים-הגדרתיים לא קריטיים).

אם נמצא שני איברים שכאלו, כמעט מייד אפשר למצוא תת-קבוצה פרדוקסלית של \( \mathbb{R}^{2} \). בואו נסמן ב-\( E \) את אוסף כל האיברים ב-\( \mathbb{R}^{2} \) שמגיעים אליהם באמצעות כפל במילה שמורכבת מ-\( \tau \) ו-\( \rho \). עכשיו, ממה שאמרתי קודם נובע שלכל שתי מילים שכאלו \( w_{1},w_{2} \), מתקיים ש-\( \tau w_{1}\left(x\right)\ne\rho w_{2}\left(x\right) \). מכאן שהקבוצות \( \tau\left(E\right) \) ו-\( \rho\left(E\right) \) הן זרות. למה? ובכן, איך נראה איבר בקבוצה \( \tau\left(E\right) \)? הוא נראה כמו הפעלה של \( \tau \) על איבר מ-\( E \). ואיך נראה איבר ב-\( E \)? הוא נראה כמו הפעלה של מילה \( w \) כלשהי על \( x \), כלומר מה שסימנו ב-\( w\left(x\right) \). מכאן שהאיבר נראה בסך הכל כמו \( \tau\left(w\left(x\right)\right) \), אבל פעולת הכפל בחבורה שלנו היא בדיוק הרכבת האיזומטריות, כלומר \( \tau\left(w\left(x\right)\right)=\tau w\left(x\right) \).

אם כן, פירקנו את \( E \) לשתי קבוצות זרות, \( \rho\left(E\right) \) ו-\( \tau\left(E\right) \) (\( x \) המסכן נותר בחוץ). עכשיו כל מה שנותר לשים לב אליו הוא ש-\( \tau^{-1}\left(\tau\left(E\right)\right)=E \) וגם \( \rho^{-1}\left(\rho\left(E\right)\right)=E \). כלומר, אפשר לקחת את \( E \), לפרק אותו לשתי תת-קבוצות זרות, להפעיל על כל אחת מהן איזומטריה ולקבל את \( E \) המקורית. אז למה על בנך-טרסקי כולם מדברים ועל הפרדוקס הזה לא?

ובכן, \( E \) היא קבוצה “לא מעניינת” - לא ברור איך היא נראית והיא בוודאי לא משהו פשוט כמו כדור והיא מכילה רק מספר בן מניה של נקודות. התחמנות שלנו בפרדוקס הזה יותר מדי גלויה לעין, ו-\( E \) היא יותר מדי מלאכותית מכדי שיהיה לפרדוקס עוקץ של ממש במקרה הזה. אם לתת נימוק קצת יותר מתמטי, המידה של \( E \) היא אפס (מה זו מידה אפס? דיברתי על זה קצת כאן) כי היא בת מניה; אז זה שהצלחנו לשכפל את \( E \) לא נראה בעייתי כי בסך הכל הראינו ש-\( 2\cdot0=0 \). אם נעשה את אותו הדבר לקבוצה בעלת מידה גדולה מאפס, אז זה יתחיל להיות מוזר. אלא שלרוע המזל זה בלתי אפשרי במישור - ניתן להוכיח שכל קבוצה ב-\( \mathbb{R}^{2} \) בעלת פנים לא ריק (כלומר, שקיימת נקודה בקבוצה ש”מוכלת עמוק בתוכה” - יש לה סביבה שכולה בתוך הקבוצה) אינה יכולה להיות פרדוקסלית.

טוב, בואו נחזור אל הוכחת הפרדוקס. מה שנשאר לי לעשות הוא לתאר שתי איזומטריות של המישור \( \tau,\rho \) כך ש-\( \tau w_{1}\left(0\right)\ne\rho w_{2}\left(0\right) \) לכל \( w_{1},w_{2} \). כאן צריך לגלוש, מה לעשות, לגאומטריה ולדברים טכניים, ולכן שמרתי את זה לסוף. עם זאת, אל תוותרו כל כך מהר! ההוכחה גם נחמדה, גם מכילה רעיונות מעניינים, והיא גם קונסטרוקטיבית לגמרי.

דרך מאוד נוחה מבחינה טכנית לדבר על \( \mathbb{R}^{2} \) וטרנספורמציות עליו היא באמצעות המספרים המרוכבים, \( \mathbb{C} \). המספר המרוכב \( a+bi \) מתאים לקוארדינטה \( \left(a,b\right) \), והיתרון שבדיבור על מרוכבים הוא שקל לתאר איזומטריות באמצעות פעולות אריתמטיות במרוכבים. בואו נבחר מספר מרוכב \( u \) שנמצא על מעגל היחידה, ולכן התיאור שלו בהצגה הקוטבית של המרוכבים הוא \( u=e^{i\theta} \) עבור זווית \( \theta \) לבחירתנו. נבחר את \( \theta \) כך ש-\( u \) יהיה מספר טרנסנדנטלי, כלומר לא יהיה אף פולינום במקדמים רציונליים שמאפס אותו (אפשר להראות שקיים כזה משיקולי ספירה; יש מספר לא בר מניה של \( \theta \)-ות שאפשר לבחור אבל רק מספר בן מניה של מספרים אלגבריים). עכשיו בואו נגדיר \( \tau\left(z\right)=z+1 \) - זוהי איזומטריה של הזזה - ו-\( \rho\left(z\right)=uz \) - זוהי איזומטריה של סיבוב.

בואו ניקח שתי מילים \( w_{1},w_{2} \) כך ש-\( w_{1} \) מתחילה ב-\( \tau \) ו-\( w_{2} \) מתחילה ב-\( \rho \). את \( w_{1} \) אפשר לכתוב באופן המבהיל הבא: \( w_{1}=\tau^{a_{1}}\rho^{a_{2}}\tau^{a_{3}}\rho^{a_{4}}\dots\tau^{a_{t}} \) - זוהי פשוט מילה ב-\( \tau,\rho \) וה-\( a_{1},a_{2},\dots \) מציינים כמה \( \tau \)-ים רצופים יש בהתחלה, ואז כמה \( \rho \) רצופים יש עד ה-\( \tau \) הבא וכן הלאה. שימו לב שאני מניח כאן באופן מובלע שהמילה גם נגמרת ב-\( \tau \). זאת מכיוון שסוף המילה הוא גם הפעולה הראשונה שמופעלת כשמפעילים את המילה על איבר כלשהו, והאיבר שעליו אנחנו הולכים לפעול כאן הוא \( 0 \), ו-\( \rho\left(0\right)=0 \) ולכן מופעים של \( \rho \) בסוף המילה יהיו מיותרים.

אז איך נראה \( w_{1}\left(0\right) \)? ובכן, תעשו את החשבון… תקבלו ש-\( w_{1}\left(0\right)=a_{1}+a_{3}u^{a_{2}}+a_{5}u^{a_{2}+a_{4}}+\dots+a_{t}u^{a_{2}+a_{4}+\dots+a_{t-1}} \). לא יפה, אבל לא נורא (מי שבאמת בוער לו להוכיח את זה - קדימה, באינדוקציה).

מה שמעניין ביצור הזה הוא שבסופו של דבר, הוא פולינום ב-\( u \). באותו אופן מראים גם ש-\( w_{2}\left(0\right) \) הוא פולינום ב-\( u \), אבל כזה שהמקדם החופשי שלו הוא אפס, כי הפעולה האחרונה ש-\( w_{2} \) מבצע היא \( \rho \), שמתוארת על ידי כפל ב-\( u \). זה מבדיל את הפולינום הזה מ-\( w_{1}\left(0\right) \) שהמקדם החופשי שלו הוא בהכרח לא אפס (כי \( a_{1}\ne0 \); אחרת \( w_{1} \) הייתה מתחילה ב-\( \rho \)). לכן \( w_{1}\left(0\right)-w_{2}\left(0\right) \) הוא פולינום במקדמים שלמים ב-\( u \) שאינו פולינום האפס, ולכן הוא אינו יכול להיות שווה אפס, כי בחרנו את \( u \) להיות טרנסנדנטי. לכן \( w_{1}\left(0\right)\ne w_{2}\left(0\right) \), כפי שרצינו.

איפה אקסיומת הבחירה פה? בשום מקום. האיזומטריות \( \tau,\rho \) הוצגו באופן מפורש, ולכן גם \( E \) נתונה באופן מפורש: היא אוסף הפולינומים ב-\( u \) עם מקדמים טבעיים (למה לא שליליים? נסו להבהיר זאת לעצמכם), והחלוקה של \( E \) גם היא מפורשת - מפרידים לפולינומים עם מקדם חופשי 0, ועם מקדם חופשי שונה מאפס. בנימה האופטימית הזו סיימנו עם סירפינקי-מזורקביץ’. בפוסט הבא אציג פרדוקס אחר, פרדוקס האוסדורף, או בשמו היותר מדויק - פרדוקס כמעט-בנך-טרסקי. הרעיונות המרכזיים של בנך-טרסקי נמצאים כבר בו ומה שהולך שם מעניין לטעמי יותר מהתיקון שיידרש אחר כך כדי להפוך את האוסדורף לבנך-טרסקי של ממש.