מערכות הוכחה אינטראקטיביות - דוגמאות

בפוסט הקודם הצגתי את המושג של מערכת הוכחה אינטראקטיבית ועכשיו הייתי רוצה לתת כמה דוגמאות. לרוע המזל, מציאת דוגמאות קונקרטיות היא לא עניין פשוט כל כך. הסיבה לכך היא זו: ראשית, לכל בעיה ששייכת למחלקה \( \mbox{NP} \) יש מערכת הוכחה אינטראקטיבית טריוויאלית - המוכיח פשוט שולח את ההוכחה הכתובה שלו והבודק בודק אותה. זהו, לא צריך שום אינטראקציה. זה מבטל את הצורך במערכת הוכחה אינטראקטיבית עבור בעיות ב-\( \mbox{NP} \), ולכן מחסל את מרבית הדוגמאות הטבעיות לבעיות שאנחנו מכירים.

באופן טבעי אנחנו מפנים את מבטנו אל המחלקה \( \mbox{coNP} \), של הבעיות ה”משלימות” לבעיות ב-\( \mbox{NP} \). אם ב-\( \mbox{NP} \) יש את השפה “הגרפים שניתנים לצביעה ב-3 צבעים”, הרי שב-\( \mbox{coNP} \) יש את השפה “הגרפים שאינם ניתנים לצביעה ב-3 צבעים”. רק מה? רוב הבעיות שאנו מכירים ב-\( \mbox{coNP} \) הן או קלות (כלומר, ב-\( \mbox{P} \)) או ממש קשות - מה שנקרא “\( \mbox{coNP} \)-שלמות”. פירוש הדבר הוא שאם פתרנו בעיה אחת מהן, פתרנו את כל \( \mbox{coNP} \). עבורנו זה אומר שאם נמצא מערכת הוכחה אינטראקטיבית עבור בעיה כלשהי שהיא \( \mbox{coNP} \) שלמה, הדבר נותן לנו מערכת הוכחה אינטראקטיבית עבור כל שפה ב-\( \mbox{coNP} \). אני באמת הולך להראות מערכת הוכחה שכזו, כחלק מההוכחה ש-\( \mbox{IP=PSPACE} \); אבל זו כבר מערכת מסובכת למדי. האם קיימות מערכות פשוטות עבור שפות שהן \( \mbox{coNP} \)-שלמות? זו שאלה טובה והתשובה עליה כנראה שלילית אם אנחנו מזהים “פשטות” עם “מספר סיבובים קבוע”. קיימת הוכחה שאם יש מערכת הוכחה אינטראקטיבית בעלת מספר סיבובים קבוע עבור שפה שהיא \( \mbox{coNP} \)-שלמה, אז “דברים רעים קורים” (“ההיררכייה הפולינומית קורסת לרמה השניה”). ומערכת הוכחה עבור שפות שהן מחוץ ל-\( \mbox{coNP} \) ו-\( \mbox{NP} \)? גם זה כבר קשה ולא צפוי שנוכל לתת דוגמה פשוטה יותר מהדוגמה-שהיא-כבר-הוכחה של \( \mbox{IP=PSPACE} \).

אז המקום שבו אנחנו מחפשים בעיות שיש להן מערכת הוכחה אינטראקטיבית פשוטה ונחמדה ומתאימה לדוגמאות הוא רק בבעיות ב-\( \mbox{coNP} \) שאינן ידועות להיות לא ב-\( \mbox{P} \) ולא ב-\( \mbox{NP} \) ולא \( \mbox{coNP} \) שלמות; וכאלו בעיות, מה לעשות, אנחנו לא מכירים כל כך הרבה. ובכל זאת יש אחת פשוטה ויפה, ולכן כזו שמוצגת תמיד כדוגמא - איזומורפיזם של גרפים.

גרף הוא אחד מהמושגים הבסיסיים ביותר במדעי המחשב והצגתי אותו כאן כבר מספרים פעמים. הוא מורכב מקבוצה של צמתים \( V \), ומקשתות, שהן זוגות של צמתים: \( E\subseteq V\times V \). כל זוג צמתים \( u,v \) הוא או מחובר בקשת או שלא. זה הכל; אבל המושג הפשוט הזה ממדל אינספור דברים.

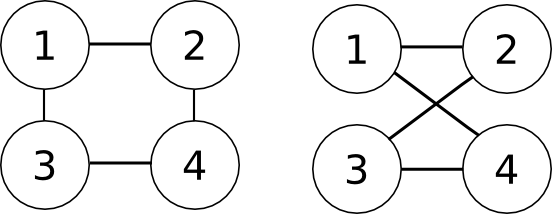
שני גרפים הם איזומורפיים אם הם זהים עד כדי הסימון שאנחנו נותנים לצמתים. אצלנו תמיד נסמן את הצמתים במספרים טבעיים, כלומר \( V=\left\{ 1,2,3,\dots,n\right\} \), ואז שני גרפים \( G_{1}=\left(V_{1},E_{1}\right) \) ו-\( G_{2}=\left(V_{2},E_{2}\right) \) הם איזומורפיים אם קיימת תמורה \( \sigma \) של הקבוצה \( \left\{ 1,\dots,n\right\} \) (תמורה היא סידור מחדש של אברי הקבוצה - פונקציה חד-חד ערכית ועל מהקבוצה לעצמה) כך ש-\( \left(u,v\right)\in E_{1} \) אם ורק אם \( \left(\sigma\left(u\right),\sigma\left(v\right)\right)\in E_{2} \). במילים: שני צמתים בגרף \( G_{1} \) מחוברים בקשת אם ורק אם שני הצמתים ב-\( G_{2} \) שאליהם \( \sigma \) מעבירה אותם גם הם מחוברים בקשת. כרגיל, תמונה אחת שווה אלף מילים:

כאן יש שני גרפים. בשניהם \( V=\left\{ 1,2,3,4\right\} \), אבל בראשון \( E_{1}=\left\{ \left(1,2\right),\left(1,3\right),\left(2,4\right),\left(3,4\right)\right\} \) ובשני \( E_{2}=\left\{ \left(1,2\right),\left(1,4\right),\left(2,3\right),\left(3,4\right)\right\} \). הגרפים הללו “נראים” שונה, אבל הם איזומורפיים: \( \sigma\left(1\right)=1,\sigma\left(2\right)=2,\sigma\left(3\right)=4,\sigma\left(4\right)=3 \), ששווה ערך להחלפת צמתים 3 ו-4 (דמיינו שאתם עושים זאת לגרף הראשון בלי “לקרוע” את הקשתות) הוא האיזומורפיזם המתאים.

הבה ונגדיר שפה: \( \mbox{GI}=\left\{ \left(G_{1},G_{2}\right)|G_{1}\cong G_{2}\right\} \) - שפת כל זוגות הגרפים שאיזומורפיים זה לזה. מה אפשר להגיד על השפה הזו? בבירור \( \mbox{GI}\in\mbox{NP} \) - אם יש לנו זוג גרפים איזומורפיים, אז הוכחה לכך היא פשוט \( \sigma \) שמהווה איזומורפיזם; בהינתן \( \sigma \) כזו לא קשה לבדוק את התנאי על הקשתות. האם \( \mbox{GI}\in\mbox{P} \)? זוהי שאלה פתוחה. הייחוד של \( \mbox{GI} \) היא בכך שמאוד לא סביר שהיא \( \mbox{NP} \)-שלמה - יש הוכחה לכך שאם \( \mbox{GI} \) היא \( \mbox{NP} \)-שלמה אז “דברים רעים קורים” (שוב, ההיררכייה הפולינומית קורסת). הרבה יותר סביר שיתגלה ש-\( \mbox{GI}\in\mbox{P} \), אבל לעת עתה, למרות שלפני כמה שנים היה נדמה לרגע שנמצאה לכך הוכחה - זו עדיין שאלה פתוחה.

אבל \( \mbox{GI\ensuremath{\in}NP} \), אז איך היא רלוונטית לדיון בכלל? ובכן, היא לא, אבל השפה המשלימה שלה כן: \( \mbox{GNI} \), שפת כל זוגות הגרפים שאינם איזומורפיים, היא אמנם ב-\( \mbox{coNP} \) אך איננו חושבים שהיא \( \mbox{coNP} \)-שלמה (אם היא הייתה כזו אז \( \mbox{GI} \) הייתה \( \mbox{NP} \)-שלמה) וגם איננו יודעים אם היא ב-\( \mbox{P} \). זה הופך אותה לדוגמה המושלמת עבורנו. אם כן, איך תעבוד מערכת הוכחה אינטראקטיבית לשפה זו? איך להוכיח ששני גרפים אינם איזומורפיים?

כאן מאוד לא סביר שמשהו שהמוכיח יגיד ואינו תלוי כלל במוודא יעזור. יש פה את אותו קושי שהזכרתי כבר כאשר דיברתי על משפט אימרמן - הקושי של להוכיח שמשהו לא קורה. אני צריך איכשהו לשכנע את המוודא שכל \( \sigma \) שהוא ינסה לא יהיה איזומורפיזם טוב; איך אפשר לעשות את זה? נסו לחשוב על הבעיה רגע כדי לקבל מושג על הקושי שלה.

הפתרון הוא משהו ששונה מאוד באופיו מהוכחות שאנחנו מכירים, ולכן אולי קשה אינטואיטיבית לעיכול. מה שהמוודא יעשה הוא להציב “אתגר” למוכיח - שאלה כלשהי, שהמוכיח יכול לענות עליה אם \( G_{1} \) אינו איזומורפי ל-\( G_{2} \), אבל אם הם איזומורפיים אין למוכיח שום דרך לענות עליה, והוא יצטרך “לנחש” מה המוודא רוצה לשמוע אם הוא מנסה לרמות אותו.

התעלול של המוודא פשוט. בתחילת הדיאלוג, הוא מטיל מטבע בחשאי לעצמו - בחשאי, כלומר באופן שבו המוכיח אינו יודע מה המוודא קיבל בהטלת המטבע. על פי הטלת המטבע המוודא בוחר אחד משני הגרפים - או \( G_{1} \) או \( G_{2} \). כעת המוודא מגריל - שוב, בחשאי - פרמוטציה \( \sigma \), ומפעיל אותה על צמתי הגרף שהוא בחר. התוצאה היא גרף חדש, \( G_{3} \), שאיזומורפי אל… אל מי, בעצם? ברור ש-\( G_{3} \) איזומורפי לגרף שהמוודא בחר, אבל אם \( G_{1}\cong G_{2} \), אז \( G_{3} \) איזומורפי לשני הגרפים גם יחד.

כעת המוודא שואל את המוכיח שאלה פשוטה - מה הגרף שבחרתי בהגרלה? אם \( G_{1} \) אינו איזומורפי ל-\( G_{2} \), אז \( G_{3} \) איזומורפי בדיוק לאחד משני הגרפים הללו. המוכיח הוא בעל כוח חישובי בלתי מוגבל ולכן הוא יכול לבדוק למי משניהם \( G_{3} \) איזומורפי ולענות בהתאם. הוא תמיד יענה נכון, ולכן המוודא יקבל. לעומת זאת, אם \( G_{1}\cong G_{2} \) אז \( G_{3} \) איזומורפי לשניהם, ולכן המוכיח לא מקבל שום אינפורמציה על הגרף שבו המוודא בחר; ומכיוון שהמוודא בחר את הגרף שלו בהסתברות חצי-חצי, אז בכלל לא משנה איך המוכיח בוחר מה לענות לו, המוכיח יצליח לקלוע לבחירה של המוודא רק בהסתברות \( \frac{1}{2} \). כלומר, יש למוודא הסתברות של \( \frac{1}{2} \) לטעות.

כדי להקטין את ההסתברות לטעות, המוודא יכול לשחק את המשחק הזה כמה סיבובים שמתחשק לו. אם הוא משחק \( k \) סיבובים עם המוכיח, ההסתברות שהמוכיח יצליח לעבוד עליו בכל \( k \) הסיבובים היא \( \frac{1}{2^{k}} \) - והדבר הזה שואף מהר מאוד לאפס, בלי להגדיל משמעותית את זמן החישוב של המוודא (פורמלית - יש לנו הקטנה אקספוננציאלית של הטעות במחיר הגדלה פולינומית של זמן הריצה). בקיצור, קיבלנו מערכת הוכחה אינטראקטיבית בדיוק כפי שרצינו - שלמות מלאה, נאותות בהסתברות טובה כרצוננו, וזמן ריצה פולינומי.

מערכת ההוכחה שלנו התבססה בצורה חזקה למדי על כך שהמוודא יכול להטיל מטבעות בצורה חשאית - זה נותן לו יתרון כלשהו על המוכיח. באופן כללי אכן נדבוק בהנחה הזו, אך תוצאה מפתיעה למדי מראה שעבור חלק מהבעיות, ובפרט עבור \( \mbox{GNI} \) היא איננה הכרחית - יש מערכת הוכחה אינטראקטיבית ל-\( \mbox{GNI} \) שבה כל ההגרלות שמבצע המוודא גלויות למוכיח. מערכת ההוכחה הזו מחוכמת בהרבה ממה שהצגתי כאן ולא אציג אותה כעת; זה בהחלט נושא מעניין לפוסט נפרד.

מערכת הוכחה מאוד דומה באופיה לבעיה אחרת שגם היא ב-\( \mbox{coNP} \) אך איננו יודעים אם היא ב-\( \mbox{P} \) קשורה לבעיית שארית ריבועית. בהינתן מספר \( n \), אומרים ש-\( a \) הוא שארית ריבועית מודולו \( n \) אם קיים פתרון למשוואה \( x^{2}\equiv a\left(\mbox{mod n}\right) \). במילים אחרות, קיים \( x \) כלשהו שכאשר מעלים אותו בריבוע ומחלקים ב-\( n \), השארית המתקבלת שווה לשארית החלוקה של \( a \) ב-\( n \). בדרך כלל מסתפקים בדיון הזה במספרים שהם בין \( 0 \) ו-\( n-1 \).

אם \( n \) הוא ראשוני, קיימות דרכים יעילות לבדוק האם \( a \) הוא שארית ריבועית מודולו \( n \). לעומת זאת אם \( n \) אינו ראשוני, האלגוריתמים המוכרים כיום לבדיקה האם \( a \) הוא שארית ריבועית מודולו \( n \) מסתמכים על ידיעת הפירוק לגורמים של \( n \) - ואם הוא לא ידוע מראש, אנחנו לא מכירים כיום דרך יעילה למצוא אותו. מכאן שגם בדיקה האם מספר הוא שארית ריבועית היא קשה. מה שכן יודעים לחשב ביעילות הוא משהו שנקרא “סימן יעקובי” של \( a \) שיכול להיות 1 או \( -1 \); אם סימן יעקובי הוא \( -1 \)אז בודאות \( a \) אינו שארית ריבועית, אך אם הוא \( 1 \) ייתכן ש-\( a \) הוא שארית ריבועית וייתכן שלא. מכאן והלאה כל המספרים שאדבר עליהם יהיו כאלו שסימן יעקובי שלהם הוא 1.

כעת, נניח שהמוכיח רוצה להוכיח למוודא ש-\( a \) כלשהו, שסימן יעקובי שלו הוא 1, איננו שארית ריבועית. אז מערכת הוכחה תתנהל כך: המוודא יגריל מספר כלשהו \( x \) בין \( 0 \) ל-\( n-1 \),יגריל ביט \( b\in\left\{ 0,1\right\} \), ישלח למוכיח את \( a^{b}x^{2} \) וישאל אותו מהו הביט \( b \). איך המוכיח יכול לענות על כך?

ובכן, נניח ש-\( a \) אינו שארית ריבועית. אז \( a^{0}x^{2}=x^{2} \) הוא בוודאי שארית ריבועית; ואפשר להוכיח ש-\( a^{1}x^{2} \) איננו שארית ריבועית (מכיוון ששארית ריבועית כפול משהו שאינו שארית ריבועית, אינו שארית ריבועית). לכן המוכיח (הכל יכול מבחינה חישובית) רק צריך לבדוק אם מה ששלחו לו הוא שארית ריבועית או לא, ולענות 0 או 1 בהתאם. לעומת זאת, אם \( a \) הוא כן שארית ריבועית, אז גם \( x^{2} \) וגם \( ax^{2} \) הם שאריות ריבועיות, ומכיוון ש-\( x \) נבחר באקראי, גם \( x^{2} \) וגם \( ax^{2} \) שניהם שאריות ריבועיות אקראיות כלשהן, ולכן למוכיח לא יהיה מושג מה לענות. אני מניח שהדמיון למערכת ההוכחה של איזומורפיזם הגרפים ברור.

עכשיו אני לא יכול להתאפק ורוצה לעבור לדון בסוג מיוחד של הוכחות אינטראקטיביות - הוכחות באפס ידע. את המושג הזכרתי כבר בראשית ימי הבלוג (לינק), אבל עכשיו זו הזדמנות פז להציג עוד כמה דוגמאות. נתחיל מאיזומורפיזם גרפים - השפה \( \mbox{GI} \), של זוגות גרפים שהם כן איזומורפיים. האם יש דרך שבה המוכיח יוכיח למוודא ש-\( G_{1}\cong G_{2} \)? ובכן, כמובן, הוא יכול פשוט לתת לו את פונקציית האיזומורפיזם, \( \sigma \); אבל האם יש דרך שבה הוא יכול להוכיח זאת למוודא מבלי לגלות לו כלום? כלומר, שהמידע היחיד שהמוודא יסיק מתהליך ההוכחה הוא שאכן \( G_{1}\cong G_{2} \)?

התשובה חיובית, והפתרון פשוט ואלגנטי ביותר. הוא מעין היפוך להוכחה של \( \mbox{GNI} \). המוכיח יגריל פרמוטציה כלשהי \( \pi \), יבחר באקראי אחד משני הגרפים \( G_{1},G_{2} \), יפעיל את הפרמוטציה עליו ויקבל גרף \( G_{3} \), וישלח אותו למוודא. המוודא יגריל מספר \( b \) - או 1, או 2, וישלח אותו למוכיח. המוכיח ישלח לו בחזרה פרמוטציה שהופכת את \( G_{b} \) ל-\( G_{3} \). האם אתם רואים מדוע זו מערכת הוכחה אינטראקטיבית?

אולי אתם תוהים לעצמכם - רגע, מה אפס ידע כאן? הרי המוודא לומד משהו מהפרוטוקול - המוכיח נותן לו איזומורפיזם בין \( G_{b} \) ובין גרף חדש, \( G_{3} \). זה נכון, כמובן, אבל הנקודה היא שהידע הזה הוא משהו שהמוודא היה יכול לייצר בעצמו. מה כבר המוודא קיבל? איזומורפיזם בין אחד מהגרפים המקוריים ובין גרף אקראי כלשהו. גם המוודא יכל לייצר את זה בצורה פשוטה - להגריל \( \pi \), להפעיל אותה על אחד מהגרפים, ולקבל כתוצאה גרף חדש, שנבחר באקראי בין הגרפים שאיזומורפיים ל-\( G_{1},G_{2} \). זו המשמעות של אפס-ידע - המוודא לא לומד שום אינפורמציה שהוא לא יכל לייצר בעצמו. יש לכל זה גם הגדרה מתמטית מדויקת, כמובן, והצגתי את הרעיון שמאחוריה בעבר, אבל לא אחזור עליה כעת.

אוקיי, ומה על מערכות ההוכחה שכבר הצגתי, זו עבור \( \mbox{GNI} \) וזו עבור \( \mbox{QNR} \)? הן בהחלט נראות כמו הוכחות אפס-ידע; כל מה שהמוכיח מוסר למוודא זה ביט יחיד שאומר למוודא את מה שהוא כבר יודע מראש - מה הייתה הבחירה האקראית שלו. אם כן, גם אלו הוכחות אפס-ידע, כן? ממש, ממש לא.

מה הבעיה? שהמוודא יכול לרמות. על פי הפרוטקול של \( \mbox{GNI} \) המוודא צריך לבחור גרף מבין \( G_{!},G_{2} \), להפעיל עליו פרמוטציה כלשהי ולשלוח למוכיח. אבל בואו נניח שיש למוודא גרף \( G_{3} \) שלו עצמו אין מושג למי משני הגרפים הוא איזומורפי אבל הוא יודע שהוא איזומורפי לאחד מהם. איך סיטואציה כזו התרחשה בכלל? לא חשוב - העיקר שהיא עשויה להתרחש. כעת, המוודא יעבוד על המוכיח ובמקום לפעול על פי הפרוטוקול הוא ישלח את \( G_{3} \) למוכיח, והמוכיח יעשה בשבילו את העבודה ויגיד לו לאיזה משני הגרפים \( G_{3} \) איזומורפי. הנה - המוודא למד מידע חדש שלא היה ידוע לו קודם.

לא ארחיב יותר מכך כרגע על העניינים הללו כי זה ראוי לפוסט נפרד שעוסק בהוכחות אפס ידע; רק אעיר שניתן לפתור את הבעיה ולהציג מערכות אפס-ידע טובות גם עבור \( \mbox{GNI} \) ו-\( \mbox{QNR} \). לבינתיים נשכח מהוכחות אפס ידע - בפוסט הבא אתאר את \( \mbox{PSPACE} \) ולאחר מכן אעבור להוכחה ש-\( \mbox{IP=}\mbox{PSPACE} \).