גבישים כמו-מחזוריים וריצופים כן-מחזוריים
בשעה טובה פרופ’ דני שכטמן מהטכניון זכה בפרס נובל על גילוי הגבישים הכמו-מחזוריים, וזו הזדמנות טובה להסביר קצת את ההיבט המתמטי של העניין. במובן מסויים המתמטיקה היא הטיפוס הרע בסיפור הזה: אם לוותר בכוונה על הדיוק למען הרומנטיקה, שכטמן גילה חומר בטבע שמפר את חוקי המתמטיקה. בפועל, כמובן, זה לא בדיוק מה ששכטמן גילה, אבל היחס העוין לשכטמן בשנים הראשונות שלאחר פרסום התגלית אכן היה כאילו הוא טען שאחד ועוד אחד שווה שלוש.
את הסיפור המרתק של שכטמן כבר סיפר “הארץ” לפני כחצי שנה בערך, הרבה לפני מהומת פרס הנובל הנוכחית (אם כי זה שנים רבות שהגילוי של שכטמן כבר הפך לעובדה בלתי מעורערת, וכבר שנים רבות שפרס הנובל היה צפוי). בקצרה, שכטמן עסק בחקר גבישים, ויום אחד ראה דרך המיקרוסקופ שלו תמונה לא סבירה בעליל - גביש בעל סימטריה מחומשת (מה זה? ובכן, אסביר בקרוב, זו מטרת הפוסט). שכטמן מייד הבין שמשהו מאוד מוזר קורה פה, כי אחד מהחוקים הבסיסיים הידועים לכל מי שעוסק בגבישים, זה שהופיע חיש קל בכל ספר לימוד בנושא, היה שמבחינה מתמטית גביש בעל סימטריה מחומשת לא יכול בכלל להתקיים. המסקנה, כמובן, לא הייתה שמשהו מקולקל במתמטיקה, אלא שמשהו מקולקל בקריסטלוגרפיה: שההגדרה של “גביש” לא הייתה מקיפה דיה. כיום זו אכן המסקנה מהתגלית של שכטמן, וההגדרה עצמה (הגדרה שעומדת בבסיס תחום מדעי שלם) עודכנה בהתאם. הסיפור הוא דווקא דוגמה נפלאה של הדרך שבה המתמטיקה עוזרת למדע - אלמלא התוצאה המתמטית לפיה סימטריה מחומשת אינה אפשרית, לא הייתה סיבה להניח שהחומר ששכטמן בחן הוא שונה מהותית מגבישים “רגילים”.
גביש “רגיל” הוא חומר שבו הסדר הפנימי של האטומים חוזר על עצמו: יש תבנית בסיסית פשוטה, והאטומים בתוך הגביש חוזרים על התבנית הזו באופן מסודר ואחיד שממלא את המרחב כולו. גבישים הם תלת ממדיים, אבל כדי להבין את הסיפור אפשר להסתפק במקרה הדו ממדי, ובו יש לנו המחשות ויזואליות למה שמדובר עליו - “טפטים”. כאן תמונה אחת באמת שווה אלף מילים:
מה שיש לנו כאן הוא תמונה שחוזרת על עצמה שוב ושוב ושוב. כשאנחנו רואים כזה דבר, המילה “סימטריה” כנראה קופצת לנו לראש מייד, אבל מה זה בעצם אומר? מבחינה מתמטית פורמלית, סימטריה של אובייקט היא פעולה כלשהי שניתן לבצע על האובייקט שאחריה הוא נראה כאילו לא בוצע בו שום שינוי. כשאנחנו מדברים על אובייקטים גאומטריים כמו טפטים או גבישים, לרוב אנחנו מגבילים את עצמנו מראש לדיבורים על סימטריות שהן איזומטריות - אם נחשוב על האובייקט כמורכב מנקודות, אז הפעולות שמותר לבצע עליו הן כאלו שבסופן המרחק בין כל זוג נקודות זהה למרחק שהיה ביניהן בהתחלה.
במקום להציג הגדרה יותר מפורשת פשוט אגיד מה זה אומר בפועל - כשמתעסקים עם צורות מישוריות, האיזומטריות היחידות הן הזזה, שיקוף וסיבוב. בואו נשכח משיקופים שלא יהיו כל כך רלוונטיים לצורך הדיון ונדבר רק על הזזות וסיבובים, שאותם אפשר לתאר בדרך אינטואיטיבית למדי. חשבו שאתם עומדים על רצפה שעליה מופיע הציור שהבאתי קודם. אז “הזזה” פירושה שפשוט תלכו מהמיקום הנוכחי שלכם כמה צעדים בכיוון כלשהו; ו”סיבוב” פירושו שפשוט תסתובבו במקומכם (המקום שבו אתם עומדים באותו הרגע הוא ציר הסיבוב). חשבו שהרצפה נמשכת עד לאינסוף בכל הכיוונים באותו האופן. ברור שאם תלכו צעד קטן מאוד או תסתובבו רק טיפה במקום, התמונה שאתם רואים תשתנה מעט; אבל, למשל, אם תסתובבו סיבוב של 90 מעלות בעיניים עצומות, כשתפקחו את העיניים לא תראו שום הבדל בין מה שאתה רואים כעת ומה שראיתם לפני שעצמתן אותן, וזאת למרות שבבירור ביצעתם תזוזה מסויימת. זוהי סימטריה.
צורות בעלות סימטריה לסיבובים לא חסרות. נתחיל מהמעגל, שהוא מושלם מהבחינה הזו - כל סיבוב, בכל זווית שהיא, שצירו הוא מרכז המעגל מותיר את המעגל ללא שינוי. לכן המעגל הוא סימטרי עבור כל סיבוב סביב מרכז המעגל. עוד צורות סימטריות הן המצולעים המשוכללים - מצולע משוכלל הוא מצולע שאורכי כל צלעותיו וכל זוויותיו שוות (למשל - משולש שווה צלעות, ריבוע, משושה משוכלל וכו’ וכו’). לא קשה לראות שמצולע משוכלל עם \( n \) צלעות הוא סימטרי ביחס לסיבוב בזווית של \( \frac{360}{n} \) מעלות (למשל: ריבוע סימטרי ביחס לסיבוב בזווית של 90 מעלות). הדוגמה הזו תשמש אותי בטרמינולוגיה בהמשך: “סימטריה ריבועית” היא סימטריה ביחס לסיבוב ב-90 מעלות, כמו במקרה של הריבוע; ולכן “סימטריה מחומשת” תהיה עבור סיבוב בזווית של \( \frac{360}{5}=72 \) מעלות, סיבוב שהוא סימטרי עבור המחומש. כעת ברור מה שכטמן ראה: משהו שנראה כמו גביש אבל הפגין סימטריה ביחס לסיבוב בזווית של 72 מעלות (למעשה, הוא הפגין סימטריה ביחס לסיבוב ב-36 מעלות, כלומר כזו שמתאימה למצולע משוכלל עם 10 צלעות, אבל אני מעדיף לשמור את העניינים פשוטים).
בואו נעבור לדבר על צורות בעלות סימטריה להזזה. כאן האינטואיציה היומיומית שלנו כבר קצת פחות רלוונטית, כי על פי ההגדרה היבשה צורות סימטריות להזזה חייבות להיות אינסופיות, שהרי אם הצורה הייתה סופית והיינו מזיזים אותה בכיוון כלשהו בעיניים עצומות, היינו שמים לב לשינוי כשהיינו פוקחים עיניים - הצורה כבר לא הייתה מונחת באותו מקום! לכן סימטריה להזזה בכיוון מסויים פירושו שהצורה היא אינסופית בכיוון הזה (ובכיוון ההפוך לו בדיוק) ומורכבת מעותקים של איזו יחידה בסיסית שכאשר מזיזים אותה בכיוון של הסימטריה ובכמות הדרושה, מכסה בדיוק יחידה בסיסית אחרת. בעולם האמיתי אין דברים כאלו, כמובן, כי צורות הן סופיות; אבל אם אותה תבנית חוזרת על עצמה מספיק פעמים גם בתוך צורה סופית אנחנו מבינים את הקטע ומסוגלים לדמיין את הצורה האינסופית, שבעצם נראית בדיוק כמו הצורה הסופית שלנו, רק שיש יותר ממנה.
אם יש לצורה סימטריה להזזה בכיוון אחד זה נחמד, אבל אם יש לה סימטריה להזזה בשני כיוונים שונים בלתי תלויים (שאינם מנוגדים) זה בכלל נפלא - במקרה זה הצורה חייבת לכסות את המישור כולו (להבדיל מסימטריה בכיוון אחד שבו הצורה יכולה להיות רצועה צרה שנמשכת עד אינסוף רק בכיוון של ההזה והכיוון המנוגד). אם כן, יש לנו תבנית בסיסית כלשהי שחוזרת על עצמה ומכסה את כל המישור - נשמע מוכר? זו בדיוק ההגדרה ל”גביש” שהזכרתי בתחילת הפוסט (שם זה היה על אובייקטים תלת ממדיים אבל הרעיון הוא אותו רעיון). אפשר גם ללכת בכיוון ההפוך - מכיוון שכל גביש בנוי מתבנית שחוזרת על עצמה באופן שמכסה את המישור/מרחב והחזרות עצמן הן מחזוריות (כלומר, כל פעם באותם מרחקים), יש לגביש תמיד סימטריה להזזה בשני כיוונים/שלושה כיוונים (שוב, תלוי אם אנחנו מדברים על המישור או המרחב).
וכעת שואלים את עצמם המתמטיקאים - נניח שיש לנו קבוצת סימטריות של טפט כלשהו, ואנחנו יודעים שיש שם סימטריה להזזה בשני כיוונים; אילו עוד סימטריות עשויות להיות שם? ובכן, לפעמים הכל יכול להיות שם - חשבו על טפט שהוא כולו שחור. כל הזזה או סיבוב יהיו סימטריות שלו, אבל זה בבירור לא מה שאנחנו רוצים. אנחנו רוצים לדבר על סימטריות של אובייקט בדיד, כזה שאפשר לחשוב עליו בתור אינסוף עותקים של יחידה בסיסית כלשהי שהיא עצמה כבר לא סימטרית להזזה.
זה מוביל להגדרה הבאה - קבוצת סימטריות שהסימטריות שלה להזזה נוצרות על ידי שתי הזזות בלתי תלויות נקראת חבורה קריסטלוגרפית מישורית; ואם זו קבוצת סימטריות של גביש בתלת מימד שהסימטריות שלה להזזה נוצרות על ידי שלוש הזזות בלתי תלויות היא נקראת חבורה קריסטלוגרפית מרחבית. ויש עוד שמות - למשל, Wallpaper group עבור חבורה מישורית וסתם Space group עבור חבורה מרחבית, וכדומה. המילה “חבורה” מציינת שקבוצת הסימטריות היא גם בעלת מבנה מסויים - אפשר תמיד להרכיב שתי סימטריות ולקבל סימטריה אחרת (הרכבת סימטריות פירושה הפעלה של אחת הסימטריות ואז הפעלה של השניה - למשל, הזזה בכיוון אחד ואז בכיוון אחר היא עצמה הזזה בכיוון שלישי שהוא תערובות של שניהם, ואם שתי ההזזות שבוצעו הותירו את הצורה ללא שינוי גם ההזזה המעורבת תותיר את הצורה ללא שינוי).
האתגר הראשוני של הקריסטלוגרפיה, אם כן, הוא למיין חבורות קריסטלוגרפיות. להבין אילו חבורות קריסטלוגרפיות יכולות בכלל להתקיים. בכל הנוגע לחבורות קריסטלוגרפיות מישוריות, התשובה היא שקיימות בדיוק 17 חבורות שכאלו ויש; חבורות קריסטלוגרפיות מרחביות יש הרבה יותר - 230 (אפשר גם לדבר על חבורות קריסטלוגרפיות במימדים גבוהים יותר ואז המספר שלהן הולך וגדל). המיון של החבורות הללו הוא בעיה מעניינת מאוד בתורת החבורות, אבל אני לא צריך לדבר עליו כאן; די לי לדבר על המשפט שמופיע בתחילת המיון, “משפט האיסור הקריסטלוגרפי” (Crystallographic restriction theorem), שהוא הצעד הראשון בדרך להבנה מי כן ומי לא יכול להיות חבורה קריסטלוגרפית.
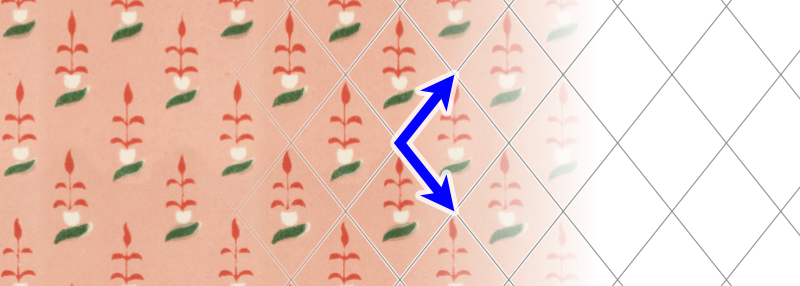
אמרנו כבר שהדרישה הבסיסית מחבורה קריסטלוגרפית מישורית היא שתכיל הזזות בשני כיוונים בלתי תלויים. הסוג האחר של סימטריות שיכול להיכנס לחבורות קריסטלוגרפיות מישוריות הוא סימטריה לסיבובים. כדי להבין את ההבדל, הנה תמונה של טפט שיש לו סימטריה להזזות אך לא לסיבובים:
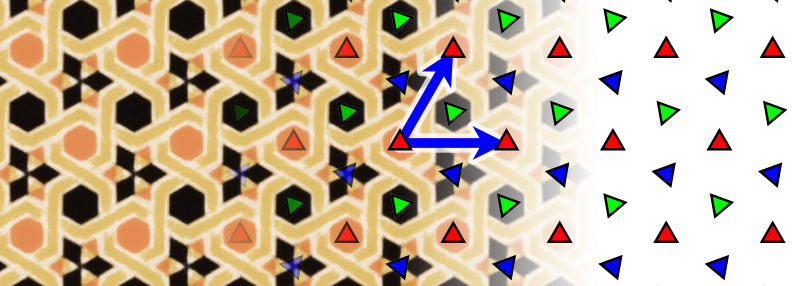
החצים מראים את ההזות כאן. הנה דוגמה לטפט שיש לו גם סימטריה להזזות וגם סימטריה ל-3-סיבובים, כלומר סיבובים של שליש מעגל, כלומר של 120 מעלות, כלומר של משולש שווה צלעות:
כאן המשולשים מופיעים על צירי הסיבוב.
והנה דוגמה שבה יש (בין היתר) סימטריה ל-4-סיבובים, כלומר של 90 מעלות:
ועכשיו אפשר לדבר על המשפט הכללי: בחבורה קריסטלוגרפית סוגי הסיבובים היחידים שיכולים להופיע הם עבור 2,3,4,6-סיבובים (כלומר: 180,120,90 ו-60 מעלות). סיבובים בזוויות אחרות פשוט לא יכולים לתת סימטריה עבור אובייקט שכבר יש לו סימטריה להזזה בשני כיוונים שונים. זה בדיוק המשפט שהגביש של שכטמן הפר.
אם נסתכל על התמונה שבה שכטמן מדבר עם ראש הממשלה, כנראה שזה בדיוק מה שהוא מסביר לו:
ההוכחה של המשפט הולכת בערך כך: אם קבוצת הסימטריות להזזה שלנו נוצרת על ידי שתי סימטריות הזזה בלתי תלויות, נובע מכך שקיימת הזזה “קצרה ביותר” שמזיזה למרחק גדול מאפס. בלי להוכיח זאת פורמלית, לא קשה להבין את ההגיון - אם לכל מרחק, קטן ככל שיהיה, הייתה לנו סימטריה להזזה שלא עוברת יותר מאת המרחק הזה, אז הצורה שלנו הייתה פשוט נראית אותו הדבר בכל מקום (פורמלית זה נובע מהדרישה שהאובייקט שלנו יהיה בדיד). עכשיו, אם מכניסים לתמונה גם סימטריות של סיבוב, אז אפשר לבנות סימטריות הזזה חדשות על ידי כך שלוקחים את ההזזה הקצרה ביותר ומפעילים יחד עם הפעלת סיבובים, ופתאום מקבלים הזזה קצרה עוד יותר. אני מעדיף להתחמק עכשיו מניסוח מדויק של המשפט כי הפוסט הזה הוא בעיקרו לא פורמלי, והוכחה מדויקת של המשפט דורשת הכנסה של מושגים נוספים.
מה שאני רוצה לדבר עליו עכשיו הוא השאלה המציקה הברורה שעולה כבר מראשית הדיון - איך מה ששכטמן גילה מסתדר עם המתמטיקה? המתמטיקה, כאמור, אומרת חד משמעית שלגביש לא יכולה להיות סימטריה מחומשת. איך שכטמן גילה גביש בעל סימטריה מחומשת?
התשובה היא ששכטמן גילה משהו שנראה כמו גביש, אך מפר את ההנחה היסודית ביותר של הקריסטלוגרפים - שלגביש יש סימטריה להזזות. כבר ראינו שסימטריה להזזות היא דרך שונה לומר “הצורה חוזרת על עצמה באופן מחזורי”. שכטמן גילה חומר שחוזר על עצמו באופן לא מחזורי. למה הכוונה? שוב, עדיף לחשוב על ריצוף של המישור. עד כה חשבנו על “ריצוף” בתור צורה מסויימת (“אריח”) שחוזרת על עצמה שוב ושוב באופן שבו המישור מכוסה על ידיה; אבל אפשר לדבר על ריצוף גם עם מספר גדול יותר של אריחים. עדיין, האינטואיציה הראשונית היא לחשוב שכל ריצוף, גם עם מספר גדול של אריחים, חייב להיות בעל מחזוריות כלשהי (ולכן בעל סימטריה להזזות). אלא שכבר בשנות השישים הוכיחו שזה לא כך.
זה מתקשר לבעיה מעניינת בתורת החישוביות שהזכרתי בבלוג בעבר - בעיית הריצוף של וואנג. וואנג שקד ומצא אלגוריתם שבהינתן קבוצת אריחים קובע האם אפשר לרצף את המישור בעזרתה או לא. לרוע המזל, האלגוריתם שלו התבסס על ההנחה לפיה ריצוף חייב להיות מחזורי (כלומר, האלגוריתם שלו למעשה עונה על השאלה “האם קבוצת האריחים הזו מסוגלת לרצף את המישור באופן מחזורי?”). זמן מה לאחר מכן הצליח מתמטיקאי בשם רוברט ברגר להראות שבעזרת אריחי וואנג אפשר לבצע סימולציה של חישובים כלליים (לבקיאים בטרמינולוגיה: הוא סימלץ מכונת טיורינג), באופן כזה שתשובה לשאלה “האם קבוצת האריחים הזו והזו מרצפת את המישור?” זהה לתשובה לשאלה “האם תוכנית המחשב הזו והזו עוצרת?” והשאלה השניה היא בלתי כריעה מבחינה חישובית; אין דרך חישובית להכריע עבור כל תוכנית מחשב האם היא עוצרת או לא; כל שיטה שתציעו בהכרח תיכשל על חלק מהקלטים (“תיכשל” אין פירושו בהכרח “תענה לא נכון”; ייתכן שהשיטה פשוט לא תחזיר תשובה).
מה שמובלע בהוכחה של ברגר היא העובדה שקבוצות האריחים שהוא בונה חייבות לרצף את המישור באופן לא מחזורי (כי עבור ריצוף מחזורי האלגוריתם של וואנג עובד). לרוע המזל, קבוצת האריחים שלו הייתה ענקית - 20,000 אריחים נדרשו כדי לממש אפילו תוכניות מחשב פשוטות. זמן מה אחריו רפאל רובינסון הציג הוכחה משופרת שבה היו רק בערך 100 אריחים שמרצפים את המישור באופן לא מחזורי, אבל גם 100 זה המון. מי שחיסל את הבעיה באופן מוחלט היה המתמטיקאי והפיזיקאי רוג’ר פנרוז, שמצא קבוצה של שני אריחים, שכל ריצוף של המישור על ידם אינו יכול להיות מחזורי. האריחים הללו מכונים אריחי פנרוז על שמו (למען האמת, פנרוז גילה כמה קבוצות שכאלו אבל נעזוב את זה). למען ההגינות יש לציין שברגר ורובינסון התעסקו עם אריחי וואנג, שהם מוגבלים יותר באופיים מאשר אריחי פנרוז.
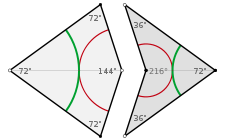
הנה תמונה של אריחי פנרוז:
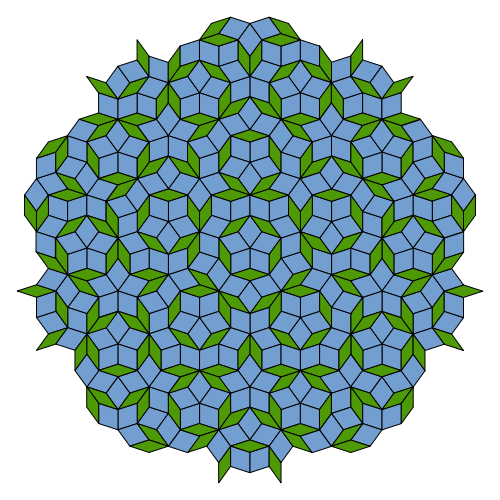
והנה (חלק מ-) ריצוף על ידי האריחים הללו:
בתמונה הזו אפשר לראות די בבירור סימטריה מחומשת סביב המרכז; באופן מעניין למדי, זו הסימטריה המחומשת היחידה (לא קשה להוכיח שאכן יכולה להיות רק אחת כזו), אם כי כשמסתכלים רק על איזורים קטנים של הריצוף יש בהם סימטריה סיבובית “מקומית”.
אם כן, מבחינה מתמטית ריצוף בעל סימטריה מחומשת הוא דבר לגיטימי בהחלט; הדבר היחיד שמתחייב הוא שלריצוף כזה לא תהיה סימטריה להזזות. כך גם עבור הגביש של שכטמן: הוא פשוט לא יכול להיות מחזורי. זה מפר את ההנחה הבסיסית ביותר של הקריסטלוגרפיה, ולכן מעביר את הויכוח מתחום המתמטיקה לתחום הקריסטלוגרפיה עצמה: האם שכטמן אכן גילה סוג חדש של גביש (“כמו-מחזורי”) שמפר את הנחות היסוד של התחום (בדומה לגילוי חלקיק שנע מהר ממהירות האור), או שהוא פשוט לא יודע לבצע ניסויים? עם הענקת פרס הנובל לשכטמן, אני מקווה שהתשובה כעת ברורה גם לפקפקנים האחרונים.
נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: