חוק המספרים הגדולים עושה אותך כזה קטן

הפנו אותי אל מאמר מתוך “דה-מרקר” שבתורו נלקח, לא פחות, מה”ניו-יורק טיימס”. המאמר מתהדר בכותרת “סיבה לדאגה לאפל? “חוק המספרים הגדולים יוביל לנפילתה”” ובכותרת המשנה “החוק שהוכיח מתמטיקאי שווייצי בן המאה ה-17 עשוי לבשר על כך שגורלה של אפל יהיה זהה לזה של חברות ענק קודמות” - וזה, מה נאמר, כמו דם במים בשביל כריש.

בואו נתחיל מהטקסט. הוא נפתח בלספר כי אפל היא החברה הגדולה ביותר בעולם כיום ואז מביא נתונים שמראים שאפל מרוויחה בוחטות ונמצאת בעליה מתמדת. ואז מגיע הפאנץ’:

אך כאן גם טמונה בדיוק הבעיה של אפל: החברה הפכה לכל כך גדולה כך שחוק המספרים הגדולים החל לפעול נגדה. חוק המספרים הגדולים, שאותו הוכיח המתמטיקאי השווייצי בן המאה ה-17 יעקב ברנולי, קובע כי כל משתנה ילך ויתקרב לממוצע ככל שמדגם התוצאות גדול יותר. במקרה של חברות גדולות, משמעות החוק היא כי ככל שחברות הולכות וגדלות, צפויה האטה בצמיחה החדה ברווחיהן ובעלייה החדה במחיר מניותיהן.

מה כן נכון: קיים משפט מתמטי בשם “חוק המספרים הגדולים”. מקרה פרטי בסיסי של חוק המספרים הגדולים אכן הוכח על ידי יעקב ברנולי במאה ה-17 ובכך זיכה את ברנולי, ובצדק, בתואר של אחד ממייסדי תורת ההסתברות. כל השאר שגוי - גם ניסוח המשפט (טוב, זה לא מפתיע) וגם כל הסקת המסקנות ממנו. כמובן, ייתכן מאוד שקיימת תופעה שבה ככל שחברות הולכות וגדלות צפויה האטה בצמיחתן; אבל קשר לחוק המספרים הגדולים - נייט.

הפסקה הבאה קצת שופכת אור על זה:

האנליסט רוברט סירה מחברת אוורקור פרטנרס, המכסה את מניית אפל, אמר השבוע כי חוק המספרים הגדולים כפי שהוא חל על אפל "מהווה מקור לדאגה כבר שנים. עם זאת, בשנתיים האחרונות נרשמה, למעשה, האצה בצמיחת הכנסות החברה, אבל זה לא יכול להימשך לנצח. אם הולכים קדימה עם התחזיות מספיק רחוק, כדי להמשיך לצמוח באותו הקצב תצטרך אפל למכור אייפון לכל גבר, אשה, ילד, בעלי חיים ואבן על פני כדור הארץ".

שימו לב שאותו רוברט סירה לא הזכיר את חוק המספרים הגדולים אפילו ברמז. במקום זה הוא נותן נימוק סביר לכך שהאטה בצמיחה של אפל היא בלתי נמנעת - השוק שלה קטן דווקא בגלל שהיא מצליחה למכור כל כך הרבה. לי אישית זה מעלה בראש משוואות דיפרנציאליות ואת מודל טורף-נטרף ואפילו שמעתי לא מזמן הרצאה יפה של פרופ’ דניאל הרשקוביץ (שכרגע מחלטר כשר המדע) שנתנה את שוק הפלאפונים בדיוק כדוגמה לעניינים הללו. מה שזה לא מזכיר לי זה את חוק המספרים הגדולים.

אבל!

חוק המספרים הגדולים של ברנולי כבר חזה, כך נדמה, את נפילתן של חברות אחרות שהחזיקו בתואר החברה הגדולה בעולם במונחי שווי שוק. שווי השוק של סיסקו זינק ל-557 מיליארד דולר - יותר משווי השוק הנוכחי של אפל - בשיאה של בועת ההייטק בחודש מארס 2000. כיום, שווי השוק של סיסקו הוא כ-100 מיליארד דולר, ומחיר מנייתה נמוך בכמעט 80% מהשיא אליו הגיע במארס 2000. שווי השוק של חברות אחרות שהחזיקו בבכורה, דוגמת ג'נרל אלקטריק, מיקרוסופט ואקסון מוביל, נמוך אף הוא כעת משהיה בתקופה בה החזיקו בבכורה.

ובכן: היו חברות שהיו הגדולות ביותר. עכשיו, מטבע הדברים, הן כבר לא. מסקנה: חוק המספרים הגדולים חזה את זה. איכשהו.

וזה מופיע בניו-יורק טיימס? באמת?

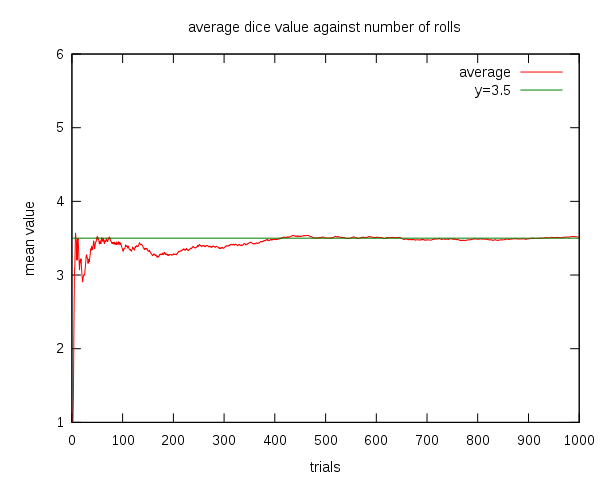
טוב, בואו נדבר על “מה כן” במקום על “מה לא” כל הזמן. בניסוח הכי לא פורמלי שאני יכול לתת, מה שחוק המספרים הגדולים כן אומר הוא שאם תטילו קוביה הרבה מאוד פעמים ותנהלו רישום של התוצאה הממוצעת שקיבלתם (כלומר, תחלקו את סכום התוצאות שהיו עד כה במספר ההטלות שהיו עד כה), אז ככל שמספר ההטלות יגדל, כך הממוצע שרשום אצלכם יתקרב לממוצע התיאורטי שאפשר לחזות רק מתוך היכרות עם הקוביה: לממוצע התיאורטי הזה יש שם מתמטי - תוחלת. מה שחוק המספרים הגדולים אומר הוא בעצם שמושג התוחלת עובד. בדוגמה הקונקרטית של קוביה, אותו ממוצע תיאורטי צפוי הוא \( 3.5 \) (ואסביר עוד מעט בדיוק למה), ואכן אם תכתבו תוכנית מחשב שמטילה לה קוביות וירטואליות ומבצעת את חישוב הממוצע תראו - בודאות! אני מבטיח! - שהממוצע הזה הולך ומתקבע לו בסביבת \( 3.5 \) ככל שהחישוב מתמשך. בויקיפדיה האנגלית אפילו יש להם גרף יפה שמתאר בדיוק את זה.

כמובן, חוק המספרים הגדולים לא מדבר רק על הטלות קוביה. “הטלת קוביה” כאן היא מטאפורה לכל ניסוי הסתברותי שיש לו כמה תוצאות מספריות אפשריות. לדבר כזה קוראים משתנה מקרי. אפרט עוד קצת בהמשך.

למה זה לא קשור לאפל? ובכן, קודם כל יש את הבעיה הכללית של החלת מודלים מתמטיים על המציאות המבולגנת שלנו: חוק המספרים הגדולים דורש שניקח את הממוצע של חזרה שוב ושוב על אותה הגרלה של אותו משתנה מקרי. לא ברור מהי אותה הטלת קוביה במקרה של חברות - האם לכל חברה יש בדיוק אותם סיכויי הצלחה? וכשמדברים ספציפית על אפל, האם אפל עצמה מטילה קוביה כל יום? חודש? שנה? והאם מותו של סטיב ג’ובס לא שינה את הקוביה שהיא מטילה? האם גם הוא שוקלל פנימה איכשהו? כמו שאתם רואים, אין לנו ברירה אלא לנטוש את המודל המתמטי הפשוט והיפה. מה שאנחנו עדיין יכולים לקוות לו הוא שהמודל המתמטי הפשוט הוא קירוב טוב למה שקורה במציאות, אבל זה מאלץ אותנו להיות זהירים שבעתיים בהסקת המסקנות שלנו מהמודל. אל תסיקו ממה שאמרתי שמודלים סטטיסטיים הם לא שימושיים בעולם האמיתי - ברור שהם שימושיים. אבל להפעיל מודל סטטיסטי בפיזיקה על קבוצה גדולה של חלקיקים שכל אחד מהם זהה לאחרים ולכן אפשר לחשוב עליהם במובן מסויים בתור הטלה שוב ושוב של אותה הקוביה - או אפילו לנתח את הרווחים שיהיו לקזינו משולחן רולטה - שונה מאוד מאשר להפעיל אותה על שוק החברות העולמי.

אבל, זו אפילו לא הבעיה האמיתית עם השימוש בחוק כאן, אלא רק משנה הזהירות שצריך תמיד לנקוט בו. הבעיה האמיתית היא שהחוק מדבר על ממוצע, והמאמר מנסה להסיק ממנו מידע על מקרה בודד.

למרבה הצער, המאמר לא ממש מסביר על מה הוא מפעיל את חוק המספרים הגדולים, ולכן יש שתי אפשרויות שנראות לי טבעיות באותה מידה: או שהוא מפעיל את החוק על השוק כולו, או שהוא מפעיל אותו על אפל ספציפית. נתחיל דווקא מהמקרה השני, שבו אני מניח שהכוונה היא שאפל מטילה קוביה שוב ושוב. חוק המספרים הגדולים אכן אומר שממוצע ההטלות של אפל אכן ישאף לתוחלת; אבל מהי התוחלת הזו? האם אנחנו בכלל יודעים שהיא סופית? האם לא ייתכן שהיא כן משתנה עם הזמן? ויותר מכך - מכיוון שאנחנו מתעניינים רק בממוצע ההטלות, האם לא ייתכן שמדי פעם יתקבלו הטלות גרועות ממש, שיאזנו את ההטלות החיוביות? המאמר מנסה איכשהו להסיק שההטלות של אפל יהפכו להיות קרובות לממוצע - כלומר, שהחל משלב מסויים, כל הטלת קוביה תהיה 3 או 4 כי אלו הערכים שקרובים ל-\( 3.5 \). זה ממש לא נכון.

ונניח שמדובר כאן על השוק כולו. כאן המצב הוא עוד יותר גרוע. אמנם, יותר סביר להניח במקרה זה שיש איזו “תוחלת שוק” סבירה וקבועה, אבל למה שדווקא אפל תשאף אליה? כל עוד יש מספיק חברות כושלות אחרות שמאזנות את הממוצע, אפל יכולה לנסוק כמה שרק מתחשק לה. במילים אחרות, כל עוד אנחנו מקבלים 1 מספיק פעמים בקוביה אין בעיה שנקבל גם 6 - עדיין נקבל ממוצע \( 3.5 \).

אני רק רוצה להבהיר - מה שהמאמר מדבר עליו בפועל - האטה בצמיחה של אפל - הוא כנראה משהו שיקרה בפועל, ומשהו מאוד סביר, וגם נתנו לו הסבר סביר בגוף המאמר. אני רק מתקומם על הנסיון לדחוף פנימה באופן בלתי קשור בעליל משפט מתמטי יפהפה. בעצם, כנראה שמה שהכי מפריע לי כאן הוא הנסיון של הכותב לשכנע בצדקתו על ידי שליפת כוח עליון - המתמטיקה - שרוב הקוראים לא יעזו להתווכח איתו. פוי.

לסיום אני רוצה לומר מה המשפט כן אומר, באופן מדויק. לא אוכיח אותו כאן כי ההוכחה לא בהכרח קצרה (תלוי איזו גרסה של המשפט מוכיחים) ובכל מקרה דורשת קצת עבודת הכנה. אבל לנסח אפשר.

ובכן, מבחינה מתמטית יש לנו ברקע של ניסוי הסתברותי תמיד משהו שנקרא מרחב מדגם. על מרחב המדגם הזה מוגדרים משתנים מקריים. ההגדרה של כל אלו לא טריוויאלית באופן כללי, אבל במקרה הפשוט שבו המשתנה המקרי יכול לקבל רק אחד מבין מספר סופי של ערכים, אפשר לתמצת את הסיטואציה לכך: אם \( X \) הוא משתנה מקרי, נסמן ב-\( \mbox{P}\left[X=a\right] \) את ההסתברות (מספר בין 0 ל-1) ש-\( X \) יקבל את הערך \( a \) בהגרלה שאנחנו מבצעים, ומתקיים \( \sum\mbox{P}\left[X=a\right]=1 \), כשהסכום נלקח על אותם \( a \)-ים שיש ל-\( X \) הסתברות חיובית לקבל. כעת נגדיר את התוחלת של \( X \) להיות הממוצע המשוקלל של הערכים שלו - משוקלל בהסתברויות שהם יתקבלו. כלומר, \( \mbox{E}\left[X\right]=\sum a\cdot\mbox{P}\left[X=a\right] \). עבור קוביה הערכים האפשריים הם המספרים מ-1 עד 6 וההסתברות לכל אחד מהם היא \( \frac{1}{6} \) ולכן \( \mbox{E}\left[X\right]=\frac{1+2+3+4+5+6}{6}=\frac{21}{6}=3.5 \), כמובטח.

כעת בואו נניח שיש לנו לא משתנה מקרי אחד אלא סדרה אינסופית שלהם: \( X_{1},X_{2},X_{3},\dots \). עוד נניח שכולם מתפלגים באותו האופן, ושהם בלתי תלויים אחד בשני (כל אחד מייצג הטלה שונה של אותה הקוביה). בפרט, יש לכולם את אותה תוחלת שנהוג לסמן ב-\( \mbox{E}\left[X_{i}\right]=\mu \) עכשיו נגדיר מהם משתנים חדשים שמייצגים את “הממוצע של כל המשתנים עד כאן”, כלומר \( \overline{X}_{n}=\frac{\sum_{i=1}^{n}X_{i}}{n} \). מה שחוק המספרים הגדולים אומר הוא שהסדרה \( \overline{X}_{n} \) מתכנסת ל-\( \mu \). בחשבון אינפיניטסימלי יש לנו מושג מדויק שמתאר התכנסות של סדרות לערכים - מושג הגבול, אבל כאן הסיטואציה קצת יותר בעייתית כי \( \overline{X}_{n} \) היא סדרה של משתנים מקריים; זה אומר שהיא לא סתם סדרה של ערכים קבועים, אלא מייצגת התפלגות כלשהי על סדרות כאלו. לכן צריך גם לתת הגדרות של התכנסות שמביאות את זה בחשבון. יש כמה הגדרות שונות שאפשר לתת, ואנחנו מתפצלים לשתי גרסאות שונות של חוק המספרים הגדולים עבור שתי הגדרות שונות להתכנסות - החוק החלש של המספרים הגדולים, והחוק החזק של המספרים הגדולים. הם נקראים כך כי ניתן להסיק את החוק החלש מתוך החוק החזק, אבל כאמור - שניהם מטפלים בשני סוגי התכנסות שונים.

החוק החלש מטפל במה שנקרא “התכנסות בהסתברות”. לא אציג את המושג הכללי אלא רק את משמעותו בהקשר של חוק המספרים הגדולים: לכל \( \varepsilon>0 \) מתקיים ש-\( \lim_{n\to\infty}\mbox{P}\left[\left|\overline{X}_{n}-\mu\right|<\varepsilon\right]=1 \). מה זה אומר? לכל \( n \) טבעי, נשאל את עצמנו “מה הסיכוי שאם אני מסתכל על הממוצע של \( n \) המשתנים הראשונים, הוא יהיה קרוב לתוחלת עד כדי \( \varepsilon \)?”. הסיכוי הזה לא יהיה 1, חלילה; תמיד יש איזה שהוא סיכוי לחריגה אלא במקרים פשוטים ביותר. אבל, ככל שנגדיל את \( n \), כך גם הסיכוי ילך ויתקרב ל-1 במובן הסטנדרטי של שאיפה לגבול.

החוק החזק מטפל במה שנקרא “התכנסות כמעט בודאות”. הניסוח כאן יותר פשוט , בלי אפסילונים: \( \mbox{P}\left[\lim_{n\to\infty}\overline{X}_{n}=\mu\right]=1 \). במילים אחרות, אם אני מגריל סדרת ממוצעים כלשהי ומסתכל על הגבול של אותה סדרת ממוצעים, הגבול הזה יהיה \( \mu \) כמעט בכל המקרים (הסתברות 1 לא תמיד אומרת “בכל המקרים בודאות”, אבל גם זו פינה אפלה שאני לא אכנס אליה כעת). שימו לב להבדל - בחוק החלש הגבול היה על סדרת ההסתברויות, וכאן הגבול הוא של סדרת המשתנים עצמה. זה החוק החזק שאנו חושבים עליו כשאנו אומרים שמושג התוחלת “עובד” - זה אומר שלמעט אולי בכמה מקרים חריגים וזניחים, סדרת הממוצעים שואפת לתוחלת, נקודה.

יעקב ברנולי, למיטב ידיעתי, הוכיח רק את המשפט החלש, וגם זה רק למקרה פרטי של משתנים שמקבלים או 0 או 1 (משתני ברנולי). גם זה היה הישג אדיר בתקופתו, בהתחשב בכך שתורת ההסתברות עוד לא הייתה קיימת וכך גם התשתית שבה משתמשים כדי להוכיח את המשפטים כיום; את הגרסה הכללית ביותר (המשפט החזק, ועבור משתנים מקריים כלשהם) הוכיח מתמטיקאי רוסי - קינצ’ין - רק במאה ה-20. למי מגיע הקרדיט על גרירת החוק לענייני כלכלה אני לא יודע, ואולי טוב שכך.