(קצת על) הגאומטריה של מרחבי מכפלה פנימית

בפוסט הקודם על אלגברה לינארית הצגנו את מושג המכפלה הפנימית וכמה מושגים נלווים, אבל לא דיברנו על מה שלדעתי הוא הדבר העיקרי פה - האופן שבו מכפלה פנימית משרה על מרחבים וקטורים גאומטריה, במובן זה שאם יש לנו מכפלה פנימית על מרחב יש לנו מושגים של אורך וזווית ודברים שנובעים מהם.

נתחיל עם היצור שהגדרתי בפוסט הקודם כחלק אגבי מתהליך גרם-שמידט: נורמה. כזכור, אם \( x\in V \) אז הגדרתי \( \|x\|=\sqrt{\left\langle x,x\right\rangle } \), בהתבסס על כך ש-\( \left\langle x,x\right\rangle \) הוא מספר ממשי חיובי (והפונקציה \( \sqrt{} \), כתמיד, מחזירה את השורש החיובי). הנורמה מקיימת שלוש תכונות שמאפיינות כל כך טוב את מושג ה”אורך” שאפשר לראות אותה כהכללה טבעית שלו:

1. \( \|x\|\ge0 \) ו-\( \|x\|=0 \) אם ורק אם \( x=0 \).
2. \( \|\lambda x\|=\left|\lambda\right|\|x\| \) לכל סקלר \( \lambda\in\mathbb{F} \)
3. \( \|x+y\|\le\|x\|+\|y\| \) ("אי שוויון המשולש").

תכונה 1 היא פשוט דרישה 4 בהגדרת מכפלה פנימית.

תכונה 2 נובעת מתכונות 2 ו-3 של מכפלה פנימית: \( \|\lambda x\|^{2}=\left\langle \lambda x,\lambda x\right\rangle =\lambda\overline{\lambda}\left\langle x,x\right\rangle =\left|\lambda\right|^{2}\|x\|^{2} \) ולכן על ידי הוצאת שורש נקבל את התכונה.

תכונה 3 לעומת זאת היא מעניינת ולא מיידית. השם “אי שוויון המשולש” נובע מכך שבמשולש, סכום אורכי כל שתי צלעות הוא תמיד גדול מאורך הצלע השלישית. עוד מעט נראה שהתכונה הזו היא המהותית ביותר כאשר אנחנו רוצים לדבר על מרחק, שכן היא מונעת סיטואציה אבסורדית שבה מרחק בין שתי נקודות גדול מהמרחק בין שתיהן לאיזו נקודה בצד (ולכן יותר מהיר ללכת לא מהנקודה הראשונה לשניה אלא לעבור קודם בנקודה הצדדית). את תכונה 3 אי אפשר להרוויח “סתם” - נשתמש בטענת עזר שהיא חשובה ביותר בזכות עצמה.

ראשית, בואו ננסה להוכיח את הטענה פשוט מההגדרות:

\( \|x+y\|^{2}=\left\langle x+y,x+y\right\rangle =\left\langle x,x\right\rangle +\left\langle x,y\right\rangle +\left\langle y,x\right\rangle +\left\langle y,y\right\rangle \)

\( =\|x\|^{2}+\left\langle x,y\right\rangle +\overline{\left\langle x,y\right\rangle }+\|y\|^{2}=\|x\|^{2}+2\mbox{Re}\left\langle x,y\right\rangle +\|y\|^{2} \)

המממפף. כאן אנחנו נתקעים, כי לא ברור לנו מה לעשות עם ה-\( 2\mbox{Re}\left\langle x,y\right\rangle \) שתקוע לנו כאן. אנחנו רוצים להבין משהו על טיב הקשר שבין \( \left\langle x,y\right\rangle \) ו-\( \|x\|,\|y\| \). לצורך כך, בואו ניזכר במכפלות סקלריות: הגדרנו מכפלה סקלרית ב-\( \mathbb{R}^{2} \) בתור מכפלת האורכים של וקטורים בקוסינוס הזווית ביניהם. במילים אחרות, המכפלה הסקלרית הייתה לכל היותר מכפלת האורכים של הוקטורים; לרוב היא “התקזזה” קצת בגלל שהוקטורים לא הצביעו לאותו הכיוון. את התחושה האינטואיטיבית הזו אפשר לתרגם לאי-שוויון קונקרטי:

\( \left|\left\langle x,y\right\rangle \right|\le\|x\|\|y\| \)

לאי השוויון הזה קוראים אי שוויון קושי-שוורץ, והוא אחד מאותם משפטים מתמטיים שבהם אני נתקל בכל מקום (לעתים קרובות בניסוח למקרה פרטי עבור מכפלה פנימית ספציפית, ואז הוא נראה מסורבל יותר וקשה יותר להבנה). קשה להפריז בחשיבות שלו, אבל למרבה המזל ההוכחה שלו אינו קשה במיוחד. לפני שנוכיח אותו בואו נראה איך הוא מסיים עם אי-שוויון המשולש: \( 2\mbox{Re}\left\langle x,y\right\rangle \le2\left|\left\langle x,y\right\rangle \right|\le2\|x\|\|y\| \) ולכן:

\( \|x+y\|^{2}\le\|x\|^{2}+2\|x\|\|y\|+\|y\|^{2}=\left(\|x\|+\|y\|\right)^{2} \)

ועל ידי הוצאת שורש משני האגפים מקבלים את אי-שוויון המשולש.

יופי, אז איך מוכיחים את קושי-שוורץ? גם כאן כדאי לזכור את מה שהלך עם מכפלה סקלרית. בדוגמה שנתתי, עם עבודה של כוח על גוף, לקחנו את הוקטור שתיאר את העבודה ופירקנו אותו לשני רכיבים - אחד בכיוון תנועת הגוף, והשני בניצב לכיוון הזה. המכפלה הסקלרית של הרכיב הראשון עם הכיוון הייתה בדיוק מכפלה של שני גדלי הוקטורים; המכפלה הסלקרית של הרכיב השני עם הכיוון הייתה 0 (כי הם ניצבים). זה גם מה שנעשה כאן, ונשתמש בדיוק באותם רעיונות שבהם השתמשנו בתהליך גרם-שמידט. ראשית ניקח את \( x \) וננרמל אותו - נגדיר \( a=\frac{x}{\|x\|} \) (כאן עלינו להניח ש-\( x\ne0 \) אבל אם \( x=0 \) אז \( \left\langle x,y\right\rangle =0=\|0\|\|y\| \) ואי השוויון טריוויאלי). כעת נגדיר \( b=y-\left\langle y,a\right\rangle a \) . כלומר, \( b \) הוא בדיוק מה שנשאר מ-\( y \) אחרי שמחסרים ההטלה של \( y \) על וקטור היחידה \( a \) שנמצא באותו כיוון כמו \( x \). בפרט, \( \left\langle b,a\right\rangle =0 \)

כעת:

\( 0\le\|b\|^{2}=\left\langle b,b\right\rangle =\left\langle b,y-\left\langle y,a\right\rangle a\right\rangle \)

\( =\left\langle b,y\right\rangle -\left\langle b,\left\langle y,a\right\rangle a\right\rangle =\left\langle b,y\right\rangle \)

\( =\left\langle y-\left\langle y,a\right\rangle a,y\right\rangle =\left\langle y,y\right\rangle -\left\langle y,a\right\rangle \left\langle a,y\right\rangle \)

\( =\|y\|^{2}-\frac{\left\langle y,x\right\rangle \left\langle x,y\right\rangle }{\|x\|^{2}}=\|y\|^{2}-\frac{\left|\left\langle x,y\right\rangle \right|^{2}}{\|x\|^{2}} \)

העברת אגפים, כפל, הוצאת שורש וקיבלנו \( \left|\left\langle x,y\right\rangle \right|\le\|x\|\|y\| \). החישוב שלמעלה נראה טיפה טכני אבל הוא מיידי למדי, והעיקר פה הוא הרעיון שהצגתי קודם.

בואו ננצל את ההזדמנות הזו ונציג רעיון שלא אשתמש בו בהמשך אבל שווה לשים אליו לב: מכיוון ש-\( \left|\left\langle x,y\right\rangle \right|\le\|x\|\|y\| \) הרי ש-\( 0\le\frac{\left|\left\langle x,y\right\rangle \right|}{\|x\|\|y\|}\le1 \) תמיד ולכן אפשר לדבר על \( \mbox{arccos}\left(\frac{\left|\left\langle x,y\right\rangle \right|}{\|x\|\|y\|}\right) \) - הביטוי הזה ייתן לנו לנו זווית בין 0 ל-90 מעלות, שבמובן מסויים ניתן לחשוב עליה בתור הזווית בין \( x \) ו-\( y \). בפרט, אם \( \left\langle x,y\right\rangle =0 \) אז הזווית היא בת 90 מעלות, בהתאם לרעיון שלנו של “וקטורים אורתוגונליים הם מאונכים”. אבל כאמור, אני לא הולך להגיד על זה יותר שום דבר.

כעת, צריך להיזהר ולא לתת את הרושם השגוי שנורמות צצות רק בהקשרים של מכפלה פנימית. כל פונקציה \( V\to\mathbb{R} \) עבור מרחב וקטורי \( V \) שמקיימת את תכונות 1-3 היא נורמה (אפשר לדבר על נורמות גם בהקשרים שאינם של מרחבים וקטוריים, אבל צריך לתקן את התכונות בהתאם - בפרט תכונה 2), ולא כל נורמה מתקבלת ממכפלה פנימית. כלומר, ייתכן שנגדיר נורמה על מרחב \( V \) כך שפשוט אין מכפלה פנימית על \( V \) שנותנת את הנורמה הזו. איך אפשר להוכיח דבר כזה? או, טוב ששאלתם. בואו נראה שלוש נורמות שונות על \( \mathbb{R}^{2} \) - שלוש מה”פופולריות” ביותר:

1. הנורמה האוקלידית הרגילה: \( \|\left(x,y\right)\|_{2}=\sqrt{x^{2}+y^{2}} \)
2. נורמת "נהגי המוניות": \( \|\left(x,y\right)\|_{1}=\left|x\right|+\left|y\right| \)
3. נורמת הסופרמום: \( \|\left(x,y\right)\|_{\infty}=\mbox{max}\left\{ \left|x\right|,\left|y\right|\right\} \)

לא אוכיח שאלו נורמות אבל די קל לראות את זה (בפרט שתי התכונות הראשונות הן מיידיות). הסימונים הדומים עבור הנורמות הללו אינם מקריים: באופן כללי, לכל מספר ממשי \( p\ge1 \) אפשר להגדיר נורמה על ידי \( \|\left(x,y\right)\|_{p}=\left(\left|x\right|^{p}+\left|y\right|^{p}\right)^{\frac{1}{p}} \) מה שמכליל לנו את שתי הנורמות הראשונות, והשלישית מתקבלת כאשר \( p\to\infty \) (במובן שלא אכנס אליו כרגע).

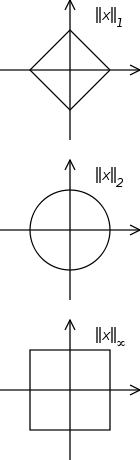
ההמחשה הטובה ביותר לאופי של הנורמות הללו, לטעמי, היא הציור של “מעגל היחידה” בכל אחד מהן - אוסף כל הנקודות שהמרחק שלהן מהראשית הוא 1, כלומר הוקטור שמתחיל בראשית ונגמר בהן הוא מנורמה 1:

למי שהאיור הזה נראה לו מופרך לגמרי - נסו זאת בעצמכם! נסו לחשוב כיצד לצייר את מעגלי היחידה עבור שתי הנורמות ה”חדשות”. זה קל באופן מפתיע ואחרי זה המעגלים הללו לא ייראו מוזר כל כך.

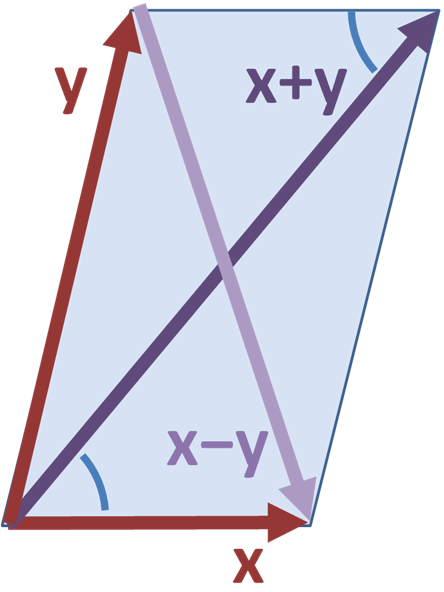
כעת אני רוצה לטעון שיש תכונה שכל נורמה שמושרית ממכפלה פנימית חייבת לקיים - תכונה שהיא גאומטרית במהותה: כלל המקבילית. נניח שיש לנו שני וקטורים, \( a,b \). אפשר לחשוב עליהם כעל שתי צלעות של מקבילית. לא קשה לראות שהאלכסונים של אותה מקבילית יהיו \( a+b \) ו-\( a-b \):

כעת, כלל המקבילית הוא מין הכללה של משפט פיתגורס: סכום ריבועי אורכי כל צלעות המקבילית שווה לסכום ריבועי אורכי האלכסונים. בלשון נורמות:

\( 2\|a\|^{2}+2\|b\|^{2}=\|a+b\|^{2}+\|a-b\|^{2} \)

למה הכללה של פיתגורס? כי אם \( a,b \) מאונכים זה לזה המקבילית היא מלבן, והאלכסונים בה שווים, ולכן על ידי חלוקה ב-2 מקבלים בדיוק \( \|a\|^{2}+\|b\|^{2}=\|a+b\|^{2} \); אבל היופי בכלל המקבילית הוא שהוא נכון תמיד, בכל מקבילית.

איך מוכיחים את זה? אפשר עם גאומטריה אוקלידית, אבל אני רוצה לתת כאן הוכחה שתעבוד בכל מרחב מכפלה פנימית שהוא. ובכן, בואו פשוט ננסה לעבוד עם ההגדרה:

\( \|a+b\|^{2}+\|a-b\|^{2}=\left\langle a+b,a+b\right\rangle +\left\langle a-b,a-b\right\rangle \)

\( =\left(\left\langle a,a\right\rangle +\left\langle a,b\right\rangle +\left\langle b,a\right\rangle +\left\langle b,b\right\rangle \right)+\left(\left\langle a,a\right\rangle -\left\langle a,b\right\rangle -\left\langle b,a\right\rangle +\left\langle b,b\right\rangle \right) \)

\( =2\left\langle a,a\right\rangle +2\left\langle b,b\right\rangle =2\|a\|^{2}+2\|b\|^{2} \)

וואו. זה היה… קל. די מפתיע איך דרך ההצגה הזו של נורמות ומכפלות פנימיות הופכת דברים מסויימים לטריוויאליים.

ובכן, בואו נראה מה מעוללת נורמת הסופרמום בהקשר של כלל המקבילית, עם הוקטורים \( a=\left(1,0\right) \) ו-\( b=\left(0,1\right) \):

\( 2\|\left(1,0\right)\|_{\infty}^{2}+2\|\left(0,1\right)\|_{\infty}^{2}=2+2=4 \)

\( \|\left(1,1\right)\|_{\infty}^{2}+\|\left(1,-1\right)\|_{\infty}^{2}=1+1=2 \)

אופס! כלל המקבילית לא מתקיים! לכן אנו רואים, מייד, שנורמת הסופרמום לא נתקבלה ממכפלה פנימית.

ומה על נורמת נהגי המוניות? ובכן, \( \left(1,0\right),\left(0,1\right) \) דווקא לא יגרמו צרות, אבל:

\( 2\|\left(2,0\right)\|_{1}^{2}+2\|\left(0,2\right)\|_{1}^{2}=8+8=16 \)

\( \|\left(2,2\right)\|_{1}^{2}+\|\left(2,-2\right)\|_{1}^{2}=16+16=32 \)

ולכן גם נורמת נהגי המוניות לא מתקבלת ממכפלה פנימית. מצאנו קריטריון פשוט ונחמד לבדוק מתי נורמה לא מושרית ממכפלה פנימית, אבל מסתבר שהקריטריון עוד יותר חזק מכך: אם נורמה כלשהי כן מקיימת את כלל המקבילית, אז היא כן מושרית ממכפלה פנימית, ואפילו אפשר לייצג את המכפלה הפנימית בעזרת הנורמה. בואו נניח לרגע שאנחנו מעל \( \mathbb{R} \) ושיש לנו נורמה \( \|\cdot\| \) שמקיימת את כלל המקבילית, ונשחק ב”נדמה לי” שהנורמה אכן הושרתה על ידי מכפלה פנימית, כלומר \( \|x\|^{2}=\left\langle x,x\right\rangle \). כפי שכבר ראינו, \( \|a+b\|^{2}=\|a\|^{2}+\left\langle a,b\right\rangle +\left\langle b,a\right\rangle +\|b\|^{2} \), ואם אנחנו מעל \( \mathbb{R} \) אז \( \left\langle a,b\right\rangle =\left\langle b,a\right\rangle \), ולכן קיבלנו:

\( \left\langle a,b\right\rangle =\frac{\|a+b\|^{2}-\|a\|^{2}-\|b\|^{2}}{2} \)

כלומר, עלה בידינו להביע את המכפלה הפנימית של שני איברים שרירותיים באמצעות הנורמה בלבד.

את הביטוי למעלה אפשר לשנות קצת כדי לקבל משהו יותר סימטרי. אם נחזור על התעלול ונפתח את \( \|a-b\|^{2} \) נקבל בסוף \( \left\langle a,b\right\rangle =\frac{\|a\|^{2}+\|b\|^{2}-\|a-b\|^{2}}{2} \). מחיבור שני הביטויים ל-\( \left\langle a,b\right\rangle \) וחלוקה ב-2 נקבל:

\( \left\langle a,b\right\rangle =\frac{\|a+b\|^{2}-\|a-b\|^{2}}{4} \)

זהות זו נקראת זהות הפולריזציה.

אם אנחנו מעל \( \mathbb{C} \) אותו תעלול יעבוד אבל הנוסחה תהיה מסובכת יותר בגלל שכבר לא מתקיים ש-\( \left\langle a,b\right\rangle =\left\langle b,a\right\rangle \):

\( \left\langle a,b\right\rangle =\frac{\|x+y\|^{2}-\|x-y\|^{2}+i\|x+iy\|^{2}-i\|x-iy\|^{2}}{4} \)

עכשיו אפשר לחזור ביתר שאת לדיון הגאומטרי. הסכמנו כבר (אני מקווה) שנורמה מייצגת “אורך”. אם \( u,v \) הם שני איברים במרחב \( V \) אז \( u-v \) הוא הוקטור המחבר ביניהן (ו-\( v-u \) הוא אותו וקטור, בכיוון ההפוך). כלומר, \( \|u-v\| \) הוא אורך הוקטור שמחבר את \( u \) עם \( v \), דהיינו המרחק בין \( u \) ו-\( v \). בלשון יותר פורמלית, כל נורמה משרה מטריקה - מטריקה היא הכללה של מושג המרחק כשם שנורמה היא הכללה של מושג האורך, אבל מטריקה היא מושג כללי יותר (אפשר להגדיר מטריקות גם על מרחבים שאינם וקטוריים ומרחבים שאין כל משמעות לדיבורים על נורמה בהם). לא אציג עכשיו את התורה של מרחבים מטריים; נסתפק בתחושה האינטואיטיבית ש-\( \|u-v\| \) אכן מייצג מרחק ונראה מה עושים עם זה כאן.

אולי מוכרת לכם תוצאה מגאומטריה ב-\( \mathbb{R}^{2} \): אם נתון לנו ישר ונקודה מחוצה לו, אז מרחק הנקודה מהישר הוא אורך האנך מהנקודה לישר - כש”אנך” הוא קו שמועבר בין הנקודה אל עבר נקודה כלשהי על הישר, כך שהזווית שהוא יוצר עם הישר היא בת 90 מעלות. מה זה אומר שאורך האנך הוא ה”מרחק” של הנקודה מהישר? שאורכו הוא המרחק הקטן ביותר של הנקודה מכל נקודה על הישר.

אפשר לדבר על אותה סיטואציה גם במרחב מכפלה פנימית כללי (במקרה שלנו, סוף-ממדי. אנחנו תמיד מדברים על מרחבים סוף ממדיים בכל הסיפור הזה). אצלנו את מקום הנקודה תופס וקטור \( u \), ואת מקום הישר תופס תת-מרחב \( W\subseteq V \). וכעת הטענה היא: \( \min\left\{ \|u-w\||w\in W\right\} \) קיים ומתקבל בנקודה יחידה \( w_{0}\in W \). כדי להבין למה לא טריוויאלי שמינימום על קבוצת מספרים יהיה תמיד קיים, הביטו בקבוצה \( \left\{ 1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\dots\right\} \) שבבירור אין לה מינימום - האיברים בקבוצה “הולכים ומתקרבים” לאפס, אבל אפס אינו איבר בקבוצה (אפס הוא כן מה שנקרא האינפימום של הקבוצה, אבל לא על זה מדברים פה).

המקרה הדו-ממדי הפשוט נותן לנו אינטואיציה חזקה מאוד לגבי מה שצריך לעשות כאן: אנחנו מצפים שאם \( w_{0} \) קיימת, אז הוקטור \( u-w_{0} \) יהיה מאונך ל”ישר” \( W \), כלומר שיהיה אורתוגונלי לכל וקטור בתת-המרחב \( W \), כלומר שיתקיים \( \left\langle u-w_{0},w\right\rangle =0 \) לכל \( w\in W \). הבה ונתחיל מלהראות שאכן קיים \( w_{0}\in W \) כך ש-\( u-w_{0} \) אורתוגונלי לכל \( W \).

מכיוון ש-\( V \) ממימד סופי כך גם \( W \) ולכן קיים ל-\( W \) בסיס אורתונורמלי (גרם-שמידט…) \( \left\{ e_{1},\dots,e_{k}\right\} \). כמו שכבר ראינו כשהתעסקנו עם גרם-שמידט, \( \sum\left\langle u,e_{i}\right\rangle e_{i} \) הוא בדיוק הרכיב של \( u \) שחי “בתוך” \( W \) - ההטלה של \( u \) על \( W \). וכפי שראינו, \( u-\sum\left\langle u,e_{i}\right\rangle e_{i} \) יהיה אורתוגונלי לכל אחד מוקטורי הבסיס \( e_{i} \) ולכן אורתוגונלי לכל \( W \). כלומר, נגדיר \( w_{0}=\sum\left\langle u,e_{i}\right\rangle e_{i} \). אולי עכשיו קצת יותר ברור למה נכון לחשוב עליו כעל “הטלה” - הפיסות מתחילות להתחבר.

מה שהולך לקרות עכשיו תקף גם במרחבים שאינם סוף-ממדיים, בעצם: אני הולך להראות שאם \( u-w_{0} \)אורתוגונלי לכל \( W \) (כאשר \( w_{0} \) וקטור כלשהו ב-\( W \) ולא משנה איך הגעתי אליו - העיקר שתתקיים תכונת האורתוגונליות) אז \( \|u-w_{0}\| \) אכן מינימלי. לצורך כך בואו ניקח \( w\in W \) כלשהו השונה מ-\( w_{0} \), וננסה להעריך את \( \|u-w\| \) תוך שימוש באחד התעלולים הכי סטנדרטיים באנליזה (וברגע שהתחלנו לדבר על נורמות, בין אם נרצה ובין אם לאו, אנחנו מתחילים להתעסק באנליזה) - להוסיף ולהחסיר את אותו איבר:

\( \|u-w\|^{2}=\|u-w_{0}+w_{0}-w\|^{2}=\|u-w_{0}\|^{2}+2\mbox{Re}\left\langle u-w_{0},w_{0}-w\right\rangle +\|w_{0}-w\|^{2} \)

רק מה, \( w_{0}-w\in W \) כי אנו מחסירים זה מזה שני איברים ב-\( W \), ולכן המכפלה הפנימית באמצע היא 0, ולכן קיבלנו ש-\( \|u-w\|^{2} \) שווה ל-\( \|u-w_{0}\|^{2} \) ועוד משהו חיובי, שהרי \( w_{0}\ne w \) ולכן \( \|w_{0}-w\|^{2} \) חייב להיות חיובי. סוף הסיפור - הראינו שאם \( u-w_{0} \) אורתוגונלי ל-\( W \) אז \( w_{0} \) הוא “הקירוב הטוב ביותר” ל-\( u \) ב-\( W \). אפשר להראות גם ההפך - שאם \( w_{0} \) הוא הקירוב הטוב ביותר אז \( u-w_{0} \) אורתוגונלי ל-\( W \); ההוכחה קצת יותר טכנית ולכן אתחמק ממנה.

צריך עדיין להראות שאם \( w_{0} \) המהולל קיים הוא גם יחיד. כדי לחשוב על סיטואציה שבה קירוב טוב ביותר הוא לא יחיד, חשבו על קבוצה בצורת פרסה, ונקודה שנמצאת בדיוק באמצע הרווח שבין שני צדדי הפרסה. אלא שפרסה איננה תת-מימד ולכן לא רלוונטית למשפט שלנו (למעשה, אפשר לחזק את המשפט שלנו ולדרוש ש-\( W \) תהיה רק קבוצה קמורה, אבל נעזוב את זה). ההוכחה כאן קצרה להפתיע, בהינתן ההוכחה של מה שחמקתי מלהוכיח פסקה קודם: אם שני וקטורים הם קירובים-טובים-ביותר, אז \( u \) פחות כל אחד מהם אורתוגונלי לכל \( W \), ופשוט לא ייתכן שזה יתקיים עבור שני וקטורים שונים, כי שימו לב להוכחה שבה הראיתי שוקטור אורתוגונלי נותן את הקירוב הטוב ביותר - לכל וקטור אחר ב-\( W \), קיבלנו ש-\( \|u-w\|>\|u-w_{0}\| \).

התוצאה הזו היא יפה בפני עצמה, אבל עדיין חסר העוקץ. לצורך כך, הבה ונוסיף הגדרה אחת אחרונה למשחק: אם \( W \) הוא תת-מרחב של \( V \), נסמן ב-\( W^{\perp} \) את המשלים האורתוגונלי שלו - המשמעות של השם תכף תתברר, אבל בינתיים נסתפק בהגדרה היבשה של “כל הוקטורים ב-\( V \) שאורתוגונליים לכל הוקטורים ב-\( W \)”, כלומר \( W^{\perp}=\left\{ v\in V|\forall w\in W:\left\langle v,w\right\rangle =0\right\} \).

הבה ונסמן ב-\( E \) את הפונקציה שבהינתן וקטור \( u \) מחזירה את ההיטל שלו ב-\( W \). זוהי טרנספורמציה לינארית, כפי שניתן לראות מהמשוואה שהגדירה את \( w_{0} \) ותכונות הלינאריות של מכפלה פנימית. יותר מכך, זוהי הטלה במובן שהגדרתי לפני אי-אילו פוסטים, כלומר מתקיים \( E^{2}=E \) כי \( E\left(w\right)=w \) לכל \( w\in W \) (למה? זה באמת לא קשה). אם אתם זוכרים במעורפל, בשעתו השתמשנו בהטלות כדי לפרק את המרחב כולו לסכום ישר של תתי-המרחבים שעליהם ההטלות, ובכן, מטילות. גם כאן אני טוען שמתקיים \( V=W\oplus W^{\perp} \), לכל \( W \). איך נראה את זה?

ניקח \( v\in V \) כלשהו. אז \( Ev\in W \) על פי ההגדרה. מכאן שאפשר לכתוב \( v=Ev+\left(v-Ev\right) \), וכפי שאמרתי קודם (אבל חמקתי מלהוכיח), \( v-Ev\in W^{\perp} \). צריך גם לראות ש-\( W\cap W^{\perp}=\left\{ 0\right\} \), מה שנובע מייד מכך שאם \( w\in W\cap W^{\perp} \) אז \( \left\langle w,w\right\rangle =0 \) (כי \( w\in W \) ו-\( w\in W^{\perp} \) אורתוגונליים).

מה שאתם צריכים עכשיו להעלות בדמיון שלכם זה את \( \mathbb{R}^{2} \) עם מערכת הצירים הרגילה - ציר \( x \) וציר \( y \) הם התת-מרחבים האורתוגונליים שנפרשים על ידי הוקטורים האורתונורמליים \( \left(1,0\right),\left(0,1\right) \) וההטלות על הצירים הללו הן ההטלות ה”רגילות” שאנו מכירים. הנה שוב קיבלנו הכללה של הגאומטריה המוכרת לנו.

טוב, מספיק להשתעשע, בפוסט הבא בנושא נעבור לאקשן האמיתי - מה קורה במפגש הענקים בין הטרנספורמציות הלינאריות והמכפלות הפנימיות.