מראה מראה שעל הקיר, למה את מבדילה בין ציר וציר?

הכירו את ונוס החתולה (אמיתית לגמרי, זה לא פוטושופ):

כמו הלהיט הנוכחי Tard the Grumpy Cat (גגלו!) כך גם ונוס הפכה ללהיט אינטרנט אדיר אפילו ביחס לחתולה (חתולים הם שליטי האינטרנט הבלתי מעורערים) בשל הפנים המחולקות באופן מושלם שלה: צד ימין שלהן שחור, וצד שמאל כתום. בהתחלה רציתי לעשות את הפוסט הנוכחי עם דו-פרצוף של באטמן; אחרי מבט במספר תמונות הגעתי למסקנה שחתולה מגניבה עדיפה על הזוועה הדו-פרצופית הקומיקסית. אבל לאיזו מטרה גייסתי את ונוס?

ובכן, נניח שונוס תתבונן במראה. הנה התמונה שהיא תראה:

כלומר, ונוס תראה במראה חתולה שונה מהונוס שאנחנו מכירים; היא תראה חתולה שצד שמאל של פניה שחור, ואילו צד ימין הוא הכתום. עד כאן אין שום דבר מוזר בעניין - כולנו כנראה נתקלנו אי-אז במראה ולמדנו על התופעה שבה היא הופכת דברים. אבל הנה שאלה שייתכן שחלקכם לא נתקלו בה עד כה: למה המראה הופכת את צד ימין ושמאל של ונוס, אבל לא הופכת אותה גם למעלה-למטה? במילים אחרות, למה התמונה של ונוס היא לא כזו?

יש כאן חוסר סימטריה מוזר בין ימין-שמאל ולמעלה-למטה. הוא בא לידי ביטוי, למשל, באופן שבו יצרתי את התמונה של “ונוס בראי” - בעורך התמונות שלי בחרתי באופציה “Flip horizontally’’, הפעלתי אותה, וחסל. למה האופציה של “Flip vertically” לא נדרשה כאן? איך הראי יודע “להבדיל” בין ימין-שמאל ובין למעלה-למטה?

התשובה הקצרה היא: המראה לא יודעת לבצע שום הבדלה שכזו, והתחושה שלנו שהמראה מבצעת הבדלה היא שגויה, ונובעת מכך שאפשר לחשוב על מה שהמראה עושה בשלוש דרכים שונות (לפחות): אחת שנותנת “עדיפות” להיפוך מאוזן; אחת שנותנת “עדיפות” להיפוך מאונך, ואחת - שהיא כנראה הדרך הנכונה לחשוב על מה שהמראה מבצעת - שנותנת עדיפות להיפוך בציר השלישי ששמו טרם הוזכר כאן.

מכיוון שזה בלוג מתמטי, אני מתכוון בסופו של דבר להכניס לתמונה נוסחאות ומשוואות ולהוכיח בצורה מדויקת שאכן אין כאן שום בעיה, אבל לפני כן אני רוצה לתת הסבר מילולי לא מדויק לתופעה הזו.

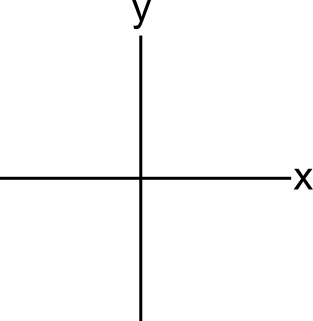
ראשית כל, המושג המרכזי בפוסט הזה הולך להיות שיקוף. שיקוף הוא תמיד ביחס לציר מסוים, אז בואו ניזכר איך נראית מערכת צירים:

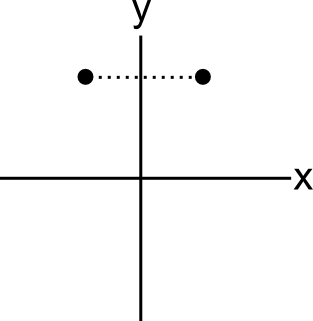
ציר ה-\( x \) הוא הציר האופקי, וציר ה-\( y \) הוא הציר האנכי. שיקוף ביחס לציר פירושו לקחת כל נקודה בצד אחד של הציר, למתוח קו מאונך ממנה אל הציר, להמשיך אותו מצדו השני של הציר באותו אורך, ואז להחליף בין שתי נקודות הקצה. זה נראה כך:

מה שקראתי לו קודם “היפוך מאוזן” הוא בעצם דרך אחרת לומר “שיקוף של התמונה ביחס לציר \( y \) כאשר התמונה משמאל לציר והוא נוגע בקצה הימני שלה”. ככה זה נראה (הציר הוא הקו השחור באמצע):

שימו לב שאפשר גם את האפשרות האחרת, “שיקוף של התמונה ביחס לציר \( y \) כאשר התמונה מימין לציר והוא נוגע בקצה השמאלי שלה”:

אפשר היה גם לשקף ביחס לציר \( y \) שעובר באמצע התמונה ואז במקום לקבל שני עותקים היינו פשוט מקבלים את התמונה במהופך.

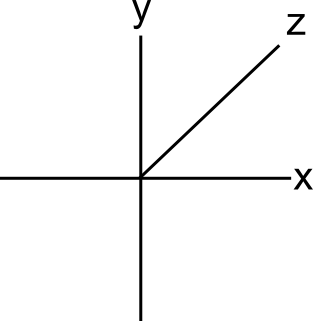
בשלב הזה אני מקווה שאתם כבר מתחילים לקבל תחושה שמה שקורה במראה הוא לא בדיוק שיקוף ביחס לציר \( y \), למרות שכך יצרתי את התמונה של “מה ונוס רואה במראה”. הסיבה לכך היא ששיקוף ביחס לציר \( y \) היה אמור ליצור את הדמות שבמראה ליד ונוס עצמה, ולא מול ונוס. אבל כשאני מדבר על “מול” אני מכניס לתמונה את השחקן שעד כה לא דיברתי עליו - המימד השלישי, ציר \( z \).

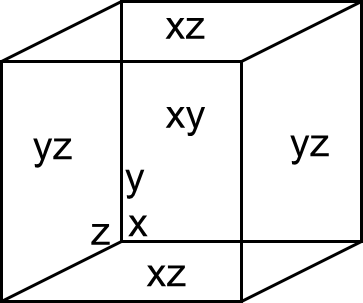
אם ציר \( x \) הוא “ימינה/שמאלה” וציר \( y \) הוא “למעלה/למטה” אז ציר \( z \) הוא “קדימה/אחורה”. בתלת מימד שיקופים הם כבר לא ביחס לציר, הם ביחס למישור. אפשר לחשוב על מישור כעל קיר: נניח שאתם בחדר ובוהים בקיר. הקיר שמולכם עולה למעלה ויורד למטה, והולך ימינה ושמאלה, ולכן הוא דוגמה למישור שמורכב מהצירים \( xy \); לעומת זאת, הקיר שמימינכם עולה מעלה ויורד למטה, אבל הולך “קדימה” ו”אחורה” (מנקודת מבטכם) ולכן הוא מישור שמורכב מהצירים \( yz \); ואילו התקרה הולכת קדימה ואחורה וימינה ושמאלה אבל לא למעלה-מטה, ולכן היא מישור שמורכב מהצירים \( xz \). הנה קוביה שבה מסומנים המישורים הללו בבירור (ה-xy הוא על הקיר הקדמי/אחורי):

אם כן, כשאנו מתבוננים בראי שעומד מולנו, אנחנו מתבוננים בשיקוף שלנו ביחס למישור \( xy \). מה שקריטי להבין כעת - זו כנראה הנקודה המרכזית בפוסט - הוא שהשיקוף הזה לא הופך את ימין ושמאל! קל מאוד לראות את זה - אם תניפו את היד שבצד ימין שלכם, אז הדמות שבראי תניף את היד שבצד ימין של הראי. אם הראי היה הופך בין ימין ושמאל, היינו מצפים לראות את מה שקורה בצד ימין שלכם משתנה דווקא בצד שמאל של הראי.

אבל רגע, אם זה כל כך פשוט, איך אני מסביר את מה שקורה לונוס? הרי בבירור החתולה מתהפכת כשמשקפים אותה בראי! החלק השחור בפנים שלה עובר מצד ימין לצד שמאל. אם עכשיו החתולה ונוס-שבראי תצא ממנו, היא תהיה שונה מונוס באופן מובחן. אז מה קורה כאן? עכשיו אנחנו מגיעים לחלק המבלבל ביותר של הפוסט: התשובה היא שברגע שמבצעים למישהו שיקוף ביחס למישור כלשהו - וזה לא משנה אם השיקוף הוא ביחס למישור \( xy \), או ביחס למישור \( xz \) או ביחס למישור \( yz \) - אותו מישהו הופך ל”דמות מראה”. דמות מראה היא בעלת התכונה שאם נגרום לה להיות זהה לדמות המקורית בשניים מתוך שלושה הצירים האפשריים, היא תהיה הפוכה ממנו בציר השלישי. זה נכון באותה מידה לכל הצירים; הבעיה שגורמת לנו לחשוב שיש פה “שבירת סימטריה” היא שהאינטואיציה שלנו מכשילה אותנו וגורמת לנו לחשוב רק על מקרה אחד מבין השלושה בתור “היפוך”.

לא מסכימים? מצוין, אז בואו נשחק את המשחק הבא: נניח שונוס התבוננה בראי ופתאום בדרך קסם אכן הבבואה שלה הוחלפה בחיה בשר ודם, “סונו” שמה. אתם טוענים בפני שונוס וסונו הן לא אותה חיה. אני דורש שתוכיחו. אתם אומרים “החלק השחור של הפנים שלהם בצד הלא נכון!” לכך אני עונה ב”למה? כרגע החלק השחור של הפנים של ונוס הוא בצד ימין שלי (אני עומד מאחורי ונוס, אבל הרי אני זוכר איפה החלק השחור של הפנים שלה) וגם החלק השחור של הפנים של סונו הוא בצד ימין שלי”.

אוקיי, ההתחכמות הזו בוודאי מרגיזה אתכם. מן הסתם אם ונוס היא עם הגב אלי ואילו סונו היא עם הפנים אלי אז למרות שהן הפוכות, החלק השחור של הפנים שלהן יהיה באותו הצד. כדי להראות לי שאני טועה ואלו שתי חיות שונות, אתם לוקחים את ונוס ומעמידים אותה ליד סונו, כשהיא עם הפנים אלי. עכשיו, כשאני רואה את שתיהן זו ליד זו, ברור לי שהן שונות. האם הסיפור נגמר?

מה שקרה למעלה, בחטף, היה שבאופן מובלע לחלוטין שהסתמך על האינטואיציה הטבעית שלכם, ביצעתי העדפה של ציר \( y \) על פני שאר הצירים. למה אני מתכוון? בואו נחשוב לרגע מה כלל התהליך של “לוקחים את ונוס ומעמידים אותה ליד סונו, כשהיא עם הפנים אלי”. ראשית כל היינו צריכים לסובב את ונוס - קודם היא הייתה בגבה אלי, ואחרי הסיבוב היא תהיה עם הפנים אלי. אחר כך מזיזים אותה קצת כדי שתהיה ליד סונו, אבל זה פחות חשוב. מה שחשוב הוא הסיבוב. סיבובים הם תמיד סביב ציר כלשהו; כאן הסיבוב הוא סביב ציר \( y \). זה אומר שלכל נקודה על גבי ונוס השתנו קואורדינטות ה-\( x \) וה-\( z \) שלה, אבל קואורדינטת ה-\( y \) נותרה ללא שינוי. למי שקשה לו לראות את זה, ניסוי: שבו בקרוסלה והסתובבו. המושגים של “קדימה/אחורה/ימינה/שמאלה” יתחרבשו לכם - מי שלפני רגע עמד מולכם (לא בקרוסלה אלא מולה) עוד שניה יהיה מצד ימין שלכם, ואחר כך מאחוריכם וכן הלאה. מה לא משתנה? מה שהיה מעליכם נשאר כל הזמן מעליכם, ומה שמתחתיכם נשאר כל הזמן מתחתכם.

נחזור לסיטואציה שבה ונוס עומדת מול סונו. אפשר לעשות עם ונוס משהו שונה לגמרי - לסובב אותה לא סביב ציר \( y \) אלא סביב ציר \( x \). במילים אחרות, אתם באים אל ונוס מאחורה, תופסים אותה בזנב ומרימים למעלה. ונוס האומללה מתהפכת - עכשיו הפנים שלה פונות אליכם, הראש שלה הפוך, הרגליים הקדמיות מתחת לאחוריות, והרגליים האחוריות הן הדבר הגבוה ביותר בה. עכשיו אתם הולכים ושמים את ונוס מעל סונו וצועקים “רואה? רואה שהן שונות?”. לכך אני משיב ב”למה? החלק השחור של הפנים שלהן הוא עדיין בצד ימין עבור שתיהן!”

אתם משתתקים לרגע, חושבים, ואז צועקים עלי בחזרה “נכון! אבל ונוס הפוכה וסונו לא הפוכה!”

לזה אני רוצה להשיב שזה בגלל שאתם מחזיקים את ונוס הפוך, אבל משטרת צער בעלי החיים מגיעה ועוצרת את כולנו. לעולם, לעולם, לעולם אל תעשו את הניסוי הזה בבית! עם זאת, בהחלט אפשר לחזור עליו עם בובה.

בחרתי לתאר בצורה כל כך מזעזעת את מה שקורה כשאנחנו מסובבים סביב ציר \( x \) ולא סביב ציר \( y \) לא מתוך רצון להתעלל בבעלי חיים אלא כדי להבהיר לנו למה האינטואיציה שלנו מקשה עלינו להתייחס לאפשרות הזו כשיטה לגיטימית ל”הוכחה” שונוס שונה מסונו. עם זאת, מבחינה מתמטית עשינו את אותו דבר. סובבנו את ונוס סביב אחד משני הצירים \( x \) או \( y \) ואז הזזנו את ונוס לאותו מקום כמו סונו והראינו שלא מקבלים את אותו דבר. במקרה הראשון זה כי צד ימין של ונוס היה צד שמאל של סונו; במקרה השני זה כי צד ה”למעלה” של ונוס היה שווה לצד ה”למטה” של סונו. כדי להשלים את התמונה צריך להבין שכבר המצב ההתחלתי הוא מצב של קלקול דומה: במקרה ההתחלתי, צד ה”קדימה” של ונוס (כלומר, החלק של ונוס שיותר רחוק מאיתנו, אם אנחנו עומדים מאחוריה) הוא צד ה”אחורה” של סונו (כלומר, החלק של סונו שיותר קרוב אלינו). אלו בדיוק שלוש הסיטואציות האפשריות: בכל אחת מהן שניים משלושת הצירים בסדר, אבל הציר השלישי “הפוך”.

כשאנחנו רואים את הדמות שלנו במראה, לא מפריע לנו שהדמות במראה הפוכה בציר \( z \) - כלומר, שאנחנו רואים את הפנים של עצמנו במקום את הגב. תחת זאת, כשאנו חושבים מדוע הדמות בראי שונה מאיתנו, אנחנו מדמיינים את התרחיש שבו הדמות הזו מסתובבת סביב ציר \( y \) ואז ההבדלים בינינו ברורים. אנחנו לא מדמיינים את התרחיש שבו היא מסתובבת סביב ציר \( x \) (“מתהפכת”) ככל הנראה כי הוא לא נראה טבעי לנו - בעולם שלנו, עם כוח הכבידה, אנשים הפוכים זה לא משהו שקורה. כתוצאה מכך אנחנו מקבלים תחושה שה”בעיה” עם הדמות ההפוכה היא רק עם החלפה בין צד ימין ושמאל - אבל כאמור, הבעיה היא עם כל שלושת הצירים, במובן זה שאם שניים מהם הם בסדר אז השלישי הפוך, ושאפשר “לתקן” היפוך של ציר באמצעות סיבוב - אבל זה בהכרח יגרום להיפוך בציר אחר. מעניין איך הייתה האינטואיציה שלנו מתנהגת אם היינו רגילים לחיים בחלל, שבהם “למעלה” ו”למטה” הם כיוונים לגיטימיים בדיוק כמו “ימינה” ו”שמאלה”.

בתגובות לפוסט ציין מישהו שאינטואיטיבית, הבעיה של חלק מהאנשים עם עניין המראה הזה היא “למה יד ימין שלי נמצאת מול יד שמאל של הדמות במראה אבל הראש שלי לא מול הרגליים”. הבעייתיות בניסוח הזה היא ש”יד ימין” ו”יש שמאל” הם מושגים יחסיים, בעוד ש”ראש” ו”רגליים” לא. “יד ימין” היא “היד שנמצאת בצד ימין של הגוף”, בעוד ש”ראש” הוא “הדבר הזה שנראה כמו ראש” ולא “הדבר הזה שנמצא למעלה”. אם מישהו עומד מולנו, אז מה שהוא קורא לו “יד ימין” ייראה לנו בכלל כאילו הוא נמצא בצד השמאלי של הראיה שלנו, אבל מכיוון שאנחנו מודעים לכך שהוא עומד מולנו אנחנו נסובב אותו בראש סביב ציר y ונבין שהיד הזו נמצאת בצד ימין של הגוף שלו.

חשבו שניה על בובה שמקדימה ומאחורה נראית אותו דבר בדיוק - אצלה אין דרך להבין, בהינתן יד, האם זו יד שמאל או ימין, כי אנחנו לא מסוגלים להבין האם הבובה פונה אלינו או שהיא ב”גבה” אלינו. לעומת זאת, עדיין נוכל לזהות את הראש שלה גם אם היא תהיה הפוכה, בגלל חוסר הסימטריה של הגוף. זה מוביל לכך שאנחנו מזהים את הדמות שמתקבלת אחרי סיבוב בציר \( y \) כדמות לגיטימית-אך-מוזרה (כי הצד השחור של הפנים עבר לשמאל), אבל אנחנו לא מוכנים לקבל את הדמות שמתקבלת אחרי סיבוב בציר \( x \), שהוא לגיטימי באותה מידה מבחינה מתמטית, כדמות “אמיתית” (כי הראש שלה למטה! מי שמע על כך שהאיבר שנראה כמו ראש נמצא בצד התחתון ולא העליון?). אני אומר את כל זה כי המענה לציטוט שלעיל הוא “במראה אנחנו רואים את הראש שלנו מול האיבר שיימצא בצד התחתון של הדמות אם נסובב אותה כך שבשאר הצירים היא תהיה בסדר - כך שאם מבחינתו “רגליים” הם מה שנמצא תמיד בצד התחתון של הדמות, זה דווקא נכון לומר שהראש שלנו נמצא מול הרגליים של הדמות”.

כדי להשלים את התמונה רק נציין שאפשר גם להגיע למצב שבו כל הצירים “מקולקלים”. נניח שונוס וסונו עומדות זו מול זו כמו קודם, וכעת אנו מסובבים את ונוס דווקא בציר \( z \) - זה משול לכך שנחזיק אותה ונסובב אותה כך שגבה אלינו כל הזמן, אבל בסוף הסיבוב היא עם הראש כלפי מטה שוב. התוצאה היא שכעת ונוס “מקולקלת” גם בציר \( z \) (שבו היא הייתה מקולקלת מלכתחילה), גם בציר \( y \) (הרי היא הפוכה!) וגם בציר \( x \) (כי כעת הצד השחור שלה הוא בשמאל, בעוד שאצל סונו הוא בימין).

נקודה אחת שאולי עוד נותרה פתוחה היא זו - הרי כשיצרתי את התמונה של סונו בהתחלה, השתמשתי ב”היפוך מאוזן”; זו הייתה ההצדקה העיקרית שהבאתי לתחושת “חוסר הסימטריה”. איך זה נפתר? ובכן, התשובה היא שמלכתחילה רימיתי אתכם: התמונה הראשונה בפוסט, זו של ונוס, לא באמת מייצגת את “ונוס מסתכלת במראה” אלא את “ונוס מסתכלת עליכם”. כלומר, זו ונוס אחרי סיבוב סביב ציר \( y \) . מה שעשיתי היא לקחת את הסיבוב הזה ו”לחבר” אליו שיקוף ביחס למישור \( yz \) , שהוא שקול מבחינה מתמטית (כפי שתכף אפשר יהיה לראות פורמלית) לשיקוף ביחס למישור \( xz \)  של ונוס המקורית.

אני מקווה שהצלחתי לעזור לכם להבין מה הולך כאן (אני הבנתי עד הסוף את העניין רק כשכתבתי את הפוסט; זו בעצם הייתה מטרתו מלכתחילה).למי שעדיין צריך אישושים, בואו נדבר טיפה על העניין מבחינה מתמטית קצת יותר פורמלית. אנחנו בעצם עוסקים כאן בשני סוגי פעולות - פונקציות - על המרחב \( \mathbb{R}^{3} \): שיקופים ביחס למישורים מסויימים, וסיבובים ביחס לצירים מסויימים.

מכיוון ש-\( \mathbb{R}^{3} \) הוא מרחב וקטורי עם הבסיס \( \left\{ \left(1,0,0\right),\left(0,1,0\right),\left(0,0,1\right)\right\} \), הדרך הנוחה להבין איך מתנהגים סיבובים ושיקופים היא דרך הפעולה שלהם על אברי הבסיס. למשל, סיבוב ב-180 מעלות ביחס לציר \( x \): הוא משאיר את \( \left(1,0,0\right) \) במקום (כי זה וקטור שנמצא על ציר \( x \) עצמו), אבל את \( \left(0,1,0\right) \) הוא שולח ל-\( \left(0,-1,0\right) \) ואת \( \left(0,0,1\right) \) הוא שולח ל-\( \left(0,0,-1\right) \). מכאן קל להסיק (בגלל הלינאריות של הסיבוב) שאת הוקטור הכללי \( \left(a,b,c\right) \) הוא שולח ל-\( \left(a,-b,-c\right) \). בדומה אפשר להבין איך יתנהגו סיבובים סביב ציר \( y \) ו-\( z \).

עכשיו בואו נעבור לשיקוף ביחס למישור \( xy \). וקטורים שנמצאים במישור הזה - כלומר \( \left(1,0,0\right) \) ו-\( \left(0,1,0\right) \) - יישארו באותו המישור. מי שישתנה הוא רק \( \left(0,0,1\right) \) שיעבור ל-\( \left(0,0,-1\right) \). לכן שיקוף ביחס למישור \( xy \) מעביר את \( \left(a,b,c\right) \) ל-\( \left(a,b,-c\right) \).

כעת אפשר להבין איך נראית הרכבה של שתי פעולות בזו אחר זו: למשל, אם קודם כל משקפים ביחס למישור \( xy \) ואחר כך מסובבים ביחס לציר \( y \), אז כל נקודה תעבור את הטרנספורמציה הבאה:

\( \left(a,b,c\right)\mapsto\left(a,b,-c\right)\mapsto\left(-a,b,c\right) \)

כאן אנחנו רואים שאחרי הפעולות הללו, בכל הנוגע לצירים \( y,z \) התמונה תיראה זהה למקור; ההבדל יהיה בציר \( x \), כלומר ב”ימינה-שמאלה”, כלומר בדיוק הבעיה של הפנים השחורות שעברו מימין לשמאל.

עכשיו, די ברור שהדבר היחיד שמאפיין כל אחת מהטרנספורמציות שדיברתי עליהן הוא לאילו קואורדינטות הן נותנות מינוסים ולאילו לא. לכן, כדי לפשוט לעצמנו את החיים, אפשר לזהות כל טרנספורמציה עם וקטור בינארי באורך 3, כש-1 מסמל “נותן מינוס לקואורדינטה הזו” ו-0 מסמל “לא נותן מינוס”. למשל, שיקוף ביחס למישור \( xy \) הוא \( \left(0,0,1\right) \) ואילו סיבוב ביחס לציר \( z \) הוא \( \left(1,1,0\right) \). כעת לא קשה לראות שחיבור נקודתי של הוקטורים הללו מודולו \( 2 \) מתאים בדיוק לפעולת ההרכבה של הטרנספורמציות. במילים אחרות, החבורה החיבורית \( \mathbb{Z}_{2}^{3} \) איזומורפית לחבורת הטרנספורמציות שנוצרת על ידי שיקופים וסיבובים ביחס לצירים.

המצב ההתחלתי, ונוס, הוא \( \left(0,0,0\right) \). אחרי הפעלת שיקוף ביחס למישור \( xy \) נקבל את \( \left(0,0,1\right) \) - “סונו”. הטענה “סונו שונה מונוס” אצלנו היא בעצם הטענה “לא משנה כמה נסובב את סונו, בלי לשקף אותה לא נקבל בחזרה את ונוס”. זו טענה שטריוויאלי להוכיח בהינתן הייצוג של \( \mathbb{Z}_{2}^{3} \) לטרנספורמציות: הפעולה של סיבוב שקולה לחיבור וקטור עם שני 1-ים ו-0 אחד לוקטור הנוכחי שלנו. כעת יש שלוש אפשרויות בסיטואציה כזו: או ששני ה-1-ים מתחברים עם 1-ים והופכים את שניהם ל-0; או ששניהם מתחברים עם 0-ים והופכים אותם ל-1-ים; או שאחד מהם מתחבר עם 1 והופך אותו ל-0, והשני מתחבר עם 0 והופך אותו לאחד. בכל שלושת המקרים, הזוגיות של מספר~ה-1-ים בוקטור נשמרת. מכיוון שב-\( \left(0,0,0\right) \) יש מספר זוגי של 1-ים וב-\( \left(0,0,1\right) \) יש מספר אי זוגי, סיימנו; אין דרך לעבור מ-\( \left(0,0,1\right) \) אל \( \left(0,0,0\right) \) באמצעות סיבובים בלבד. זו הוכחה פשוטה ביותר עם רעיון שחביב עלי מאוד, עד כדי כך שהופיע כבר בפוסט הראשון בבלוג - אינוריאנטות.

המסקנה היא שסונו שונה מונוס, אבל לא באופן שמוטה “לטובת” ציר \( x \) - על ידי הפעלות של סיבובים אפשר להגיע מ-\( \left(0,0,1\right) \) לכל אחד מהוקטורים \( \left(1,0,0\right),\left(0,1,0\right),\left(1,1,1\right) \) (כל הוקטורים עם מספר אי זוגי של 1-ים) ולכן כל הצירים “מקולקלים במידה שווה” - ובפרט אפשר גם להגיע למצב \( \left(1,1,1\right) \) שבו שלושת הצירים מקולקלים בו זמנית (אבל לא למצב שבו שני צירים מקולקלים ואחד לא - במצב כזה מספר ה-1-ים הוא זוגי, ובפרט אפשר על ידי סיבוב אחד להגיע אל ונוס).

מה למדנו מכל זה? ובכן, דבר אחד בטוח - מכיוון שונוס היא חצי שחורה וחצי ג’ינג’ית, הרי שלחתולה לבנה באמת לא היה קשר לכל מהומת המראות הזו.