הקסם שבריבועי קסם

בואו נתחיל עם צפיה בקסם המרהיב שבסרטון בלינק הבא:

למי שלא יכול או לא רוצה לראות וידאו (למרות שכדאי, מכיוון שנתעמק בפרטיו אחר כך), מה שקורה פה הוא הדבר הבא: לקוסם יש חבילה של קלפים (לא קלפי משחק) עם מספרים שונים ומשונים עליהם - לא רק מספרים בין 2 ל-13 כמו בחפיסת קלפי משחק רגילים אלא גם מספרים כמו 42. הוא נותן למשתתף חלק מהקלפים, מבקש ממנו לפרוש אותם כשפניהם כלפי מטה ולבחור אחד מהם באופן שבו הקוסם והצופים רואים את גבו של הקלף שנבחר אבל לא מה מספרו. לאחר מכן הקוסם לוקח את יתר הקלפים ובונה מחלקם ארבע ערימות של ארבעה קלפים כל אחד. ואז מתברר שמספרי הקלפים בכל אחת מהערימות מסתכמים למספר 42, ולאחר שהקוסם פורס את הערימות ויוצר מהקלפים ריבוע של \( 4\times4 \) מסתבר שגם כל שורה וכל עמודה וכל אלכסון מסתכמים גם הם ל-42 - במילים אחרות, הקוסם בנה ריבוע קסם מסדר \( 4\times4 \) עבור המספר 42. כמובן, מספר הקלף שהמשתתף בחר הוא 42. לאחר מכן הקוסם מראה שעל גבם של חלק מהקלפים שמרכיבים את ריבוע הקסם כתוב (בשלבים) “אתה הולך לבחור 42”. תענוג לצפיה.

התהיה הראשונה היא למה מבין כל הקלפים המשתתף בחר דווקא בזה שמספרו 42 (שהוא, כידוע, כוכב “המדריך לטרמפיסט בגלקסיה” של דגלאס אדמאס). על השאלה הזו לא אוכל לענות בפוסט, אבל אני מקווה שאוכל להסביר איך הקסם התבצע. אני עצמי ידעתי רק איך לבנות ריבוע קסם מסדר \( 4\times4 \) שמסתכם למספר נתון (וזו המטרה ה”מתמטית” של הפוסט); הקרדיט על ניתוח האופן שבו הקסם מתבצע שייך לגלעד דיאמנט מהבלוג המצוין “חשיבה חדה”, ואת הדיון המעניין של קהילת הבלוג על הקסם אפשר לראות בקבוצה של הבלוג בפייסבוק.

מן הסתם אני עומד לגלות איך הקסם מתבצע, אז לאלו מכם שלא אוהבים להבין איך קסמים מתבצעים אני ממליץ להיזהר בהמשך קריאת הפוסט, כי אני אחרב לכם את הקסם לחלוטין. אבל זה יהיה רק בסוף הפוסט, עם כותרת מתאימה; אתחיל עם העניין המתמטי ה”כללי” - איך בכלל בונים ריבוע קסם \( 4\times4 \)?

על ריבועי קסם באופן כללי

באופן כללי, ריבוע קסם הוא ריבוע של \( n\times n \) משבצות שבתוכו כתובים מספרים (לעתים קרובות המספרים \( 1,2,3,\dots,n^{2} \) אבל לא חובה) כך שכל שורה וכל עמודה מסתכמת לאותו מספר, ואם עוד דברים (כמו האלכסונים) מסתכמים לאותו מספר על אחת כמה וכמה טוב. הנה דוגמה לריבוע קסם \( 3\times3 \), שעד סוף הפוסט כולנו נבין איך לבנות:

\( \left[\begin{array}{ccc}2 & 7 & 6\\9 & 5 & 1\\4 & 3 & 8\end{array}\right] \)

והנה ריבוע הקסם של הקוסם בסרט:

\( \left[\begin{array}{cccc}8 & 11 & 22 & 1\\21 & 2 & 7 & 12\\3 & 24 & 9 & 6\\10 & 5 & 4 & 23\end{array}\right] \)

עזבו את השאלה איך הקוסם בכלל ידע שהמשתתף הולך לבחור 42. נניח שבאים אליכם ואומרים לכם שאתם צריכים לבנות ריבוע שבו כל שורה, כל עמודה, כל אלכסון וכל רבע מסתכמים ל-42 - איך בכלל תעשו את זה? ואם המספר לא היה 42 אלא, נאמר, 53, האם עדיין אפשר היה לעשות את זה? אפשר לחשוב על זה בתור חידה: הפסיקו לרגע את קריאת הפוסט, הסתכלו על הריבוע של הקוסם שלמעלה ונסו לחשוב איך אפשר להסיק ממנו שיטה כללית לבניית ריבוע בעל אותן תכונות מרהיבות עבור כל סכום שהוא מספר דו ספרתי, ובעצם עבור כל מספר שהוא גדול או שווה ל-10.

ובכן, משהו שקופץ מהר מאוד לעין הוא שרוב המספרים בריבוע שלעיל הם קטנים יחסית, אבל יש כמה מספרים גדולים. עד כמה גדולים? עשרים ומשהו. בחינה יותר קפדנית מראה שיש בדיוק ארבעה מספרים שהם מהגודל הזה, ושמספריהם הם רצופים: 21,22,23,24. כעת אני שם לב לעוד משהו שעבורי בולט מאוד פשוט כי כבר נתקלתי בדברים דומים בעבר, אבל אולי למי שעוד אין לו נסיון לא יהיה בולט מספיק: שארבעת המספרים הללו היו פזורים בתוך הריבוע באופן שמתאר פרמוטציה. למה אני מתכוון? לכך שכל מספר שכזה היה היחיד מבין הארבעה הן בשורה שלו והן בעמודה שלו. איך זה קשור לפרמוטציות?

ובכן, פרמוטציה של המספרים מ-\( 1 \) ועד \( n \) היא פשוט ערבוב כלשהו של המספרים הללו. למשל, פרמוטציה לדוגמה של המספרים מ-1 עד 4 היא \( 3,1,2,4 \). תיאור מילולי של הפרמוטציה הזו יהיה “האיבר הראשון בפרמוטציה הוא 3, השני הוא 1; השלישי הוא 2; הרביעי הוא 4”.

פרמוטציות אפשר לתאר באמצעות מטריצות, שבהקשר שלנו הן בסך הכל שם אחר לטבלאות עם מספרים בתוכן. הנה מטריצה שמתארת את הפרמוטציה שכרגע הזכרתי:

\( \left[\begin{array}{cccc}0 & 0 & 1 & 0\\1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 0 & 1\end{array}\right] \)

מה קורה פה? עברו על המטריצה הזו שורה שורה ובדקו מהו מספר העמודה שבה יש 1. בשורה הראשונה זוהי עמודה 3; בשניה זוהי 1; בשלישית זוהי 2; ברביעית זוהי 4. הנה הפרמוטציה!

המטריצה הזו היא יותר מאשר “סתם” דרך כתיבה משונה למשהו שכתבתי באופן פשוט יותר: אם כופלים אותה בוקטור \( \left(1,2,3,4\right) \) מקבלים:

\( \left[\begin{array}{cccc}0 & 0 & 1 & 0\\1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}1\\2\\3\\4\end{array}\right]=\left[\begin{array}{c}3\\1\\2\\4\end{array}\right] \)

כלומר, מבחינה אלגברית, המטריצה הזו מתארת את הטרנספורמציה הלינארית שמבצעת את הפרמוטציה בפועל. אין צורך להבין את זה כדי להבין את המשך הפוסט, אבל זה קישור שלא רציתי לוותר עליו.

עכשיו, איך כל זה קשור לריבוע של הקוסם שלנו? פשוט מאוד: המיקומים של מספרי ה”עשרים ומשהו” הם בדיוק המיקומים של ה-1-ים במטריצה שלעיל. אפשר לכתוב זאת כך:

\( \left[\begin{array}{cccc}0 & 0 & 22 & 0\\21 & 0 & 0 & 0\\0 & 24 & 0 & 0\\0 & 0 & 0 & 23\end{array}\right] \)

אחרי שמבינים את זה, קל יותר לנחש מה ההמשך. אם הקוסם לקח רביעיה אחת של מספרים, 21,22,23,24 ופיזר אותה בתוך משבצות בריבוע שמהוות פרמוטציה, אולי הוא עשה את זה עם עוד רביעיות? אז כדאי לחפש מספרים בריבוע שערכיהם סמוכים. המספר הגדול ביותר בריבוע מלבד אלו של העשרים ומשהו הוא \( 12 \), אז אפשר לנחש שהרביעיה הבאה היא \( 9,10,11,12 \), ואכן, הם מפוזרים במקומות הבאים בריבוע:

\( \left[\begin{array}{cccc}0 & 11 & 0 & 0\\0 & 0 & 0 & 12\\0 & 0 & 9 & 0\\10 & 0 & 0 & 0\end{array}\right] \)

עכשיו כבר ברור שיהיו עוד שתי רביעיות, אחת של \( 5,6,7,8 \) ואחת של \( 1,2,3,4 \). בסופו של דבר נקבל “פירוק” של הריבוע לסכום של ארבעה ריבועים:

\( \left[\begin{array}{cccc}0 & 0 & 22 & 0\\21 & 0 & 0 & 0\\0 & 24 & 0 & 0\\0 & 0 & 0 & 23\end{array}\right]+\left[\begin{array}{cccc}0 & 11 & 0 & 0\\0 & 0 & 0 & 12\\0 & 0 & 9 & 0\\10 & 0 & 0 & 0\end{array}\right]+\left[\begin{array}{cccc}8 & 0 & 0 & 0\\0 & 0 & 7 & 0\\0 & 0 & 0 & 6\\0 & 5 & 0 & 0\end{array}\right]+\left[\begin{array}{cccc}0 & 0 & 0 & 1\\0 & 2 & 0 & 0\\3 & 0 & 0 & 0\\0 & 0 & 4 & 0\end{array}\right] \)

למה כדאי להסתכל על הריבוע של בתור הפירוק הזה? מהטעם הפשוט שאם ניקח את אחד מהריבועים, ונוסיף או נחסיר רק למספרים שבו מספר קבוע כלשהו, אז בבירור סכום כל העמודות והשורות בריבוע הקסם ישתנה בדיוק במספר הקבוע הזה. במילים אחרות, אם אחליף את הריבוע

\( \left[\begin{array}{cccc}0 & 0 & 22 & 0\\21 & 0 & 0 & 0\\0 & 24 & 0 & 0\\0 & 0 & 0 & 23\end{array}\right] \)

בריבוע שבו החסרתי 20 מכל מספר, כלומר

\( \left[\begin{array}{cccc}0 & 0 & 2 & 0\\1 & 0 & 0 & 0\\0 & 4 & 0 & 0\\0 & 0 & 0 & 3\end{array}\right] \)

אקבל שסכום כל שורה ועמודה ואלכסון ורבע בריבוע הקסם החדש הוא 22.

כעת, לכל אחד מארבעת הריבועים בפירוק, המספרים בתוך כל ריבוע צריכים להיות שונים (כרגע זו עדיין תחושה בלבד; אסביר בקרוב למה זה הכרחי) אבל אין בעיה שאותו מספר יופיע ביותר מריבוע אחד. לכן, אם אני רוצה לקבל את הריבוע הפשוט ביותר שמציית לחוקיות של הריבוע של הקוסם, אני פשוט אחליף את המספרים בכל אחד מארבעת הריבועים בפירוק במספרים 1 עד 4 - כמובן, לפי סדר הגדלים שמופיע בכל ריבוע. התוצאה היא הפירוק הבא:

\( \left[\begin{array}{cccc}0 & 0 & 2 & 0\\1 & 0 & 0 & 0\\0 & 4 & 0 & 0\\0 & 0 & 0 & 3\end{array}\right]+\left[\begin{array}{cccc}0 & 3 & 0 & 0\\0 & 0 & 0 & 4\\0 & 0 & 1 & 0\\2 & 0 & 0 & 0\end{array}\right]+\left[\begin{array}{cccc}4 & 0 & 0 & 0\\0 & 0 & 3 & 0\\0 & 0 & 0 & 2\\0 & 1 & 0 & 0\end{array}\right]+\left[\begin{array}{cccc}0 & 0 & 0 & 1\\0 & 2 & 0 & 0\\3 & 0 & 0 & 0\\0 & 0 & 4 & 0\end{array}\right] \)

והסכום של כל אלו נותן לי את הריבוע:

\( \left[\begin{array}{cccc}4 & 3 & 2 & 1\\1 & 2 & 3 & 4\\3 & 4 & 1 & 2\\2 & 1 & 4 & 3\end{array}\right] \)

קל לראות שהריבוע הזה הוא פתרון שאפשר לתת במקרה שבו צריך למצוא ריבוע קסם שמסתכם ל-10: זהו סכום השורות, העמודות, האלכסונים, הרבעים ועוד כהנה וכהנה דברים (הפינות, למשל). אם כן, כבר ברורה שיטה שבה אפשר לייצר ריבוע קסם למספר כלשהו שגדול או שווה ל-10; רק צריך לזכור את הריבוע שכתבתי זה עתה ואת הפירוק שלו לסכום של ארבע פרמוטציות, ואז אפשר לבחור פרמוטציה מבין הארבע ולהוסיף לכל איבריה מספר כלשהו. אם אבחר פרמוטציה ואוסיף לה, נאמר, 7, אקבל ריבוע קסם שבו השורות-עמודות-אלכסונים-רבעים מסתכמים כולם ל-17. נסו זאת! כמובן שאפשר להשיג את אותו האפקט גם בדרך אחרת: להוסיף 4 לאחת הפרמוטציות ולהוסיף 3 לאחרת.

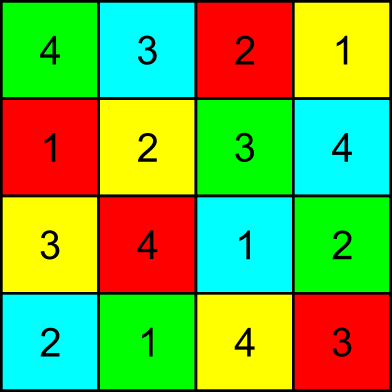
בואו נעבור עכשיו להבין למה זה עובד, וחשוב מכך - לאילו מושגים כלליים במתמטיקה זה מתקשר. לצורך כך, הנה דרך נוחה יותר להתבונן על הריבוע הבסיסי כשרואים בעיניים את הפירוק שלו לארבע פרמוטציות:

כאן צבעתי כל רביעייה בצבע שונה, ועכשיו אפשר לראות בעיניים את התכונות של הריבוע:

לכל משבצת יש צבע מבין 4 צבעים אפשריים ויש בתוכה מספר בין 1 ל-4.
בכל שורה ובכל עמודה כל המספרים שונים.
בכל שורה ובכל עמודה כל הצבעים שונים.
כל שילוב אפשרי של צבע ומספר מופיע בדיוק פעם אחת.

תכונת ה”בכל שורה ובכל עמודה כל המספרים שונים” כנראה מוכרת לרובכם: במשחק סודוקו אלו שתיים משלוש הדרישות על לוח סודוקו חוקי (השלישית היא דרישה על תת-ריבועים שלא רלוונטית כאן). עם זאת, המושג הזה של ריבוע בגודל \( n\times n \) של מספרים מתוך קבוצה בת \( n \) איברים כך שבכל שורה ובכל עמודה מספר שונה של מספרים הוא עתיק בהרבה משגעון הסודוקו; במתמטיקה קוראים לריבוע שכזה ריבוע לטיני והחוקר הידוע ביותר של ריבועים לטיניים (אם כי היו גם לפניו) היה המתמטיקאי לאונרד אוילר בן המאה ה-18.

הנה דוגמה פשוטה לאופן שבו אפשר לבנות ריבוע לטיני, נאמר מסדר \( 3\times3 \) עם המספרים \( 1,2,3 \): השורה הראשונה תהיה \( 1,2,3 \). השורה השניה תהיה \( 2,3,1 \) שהיא מה שמתקבל כאשר “מזיזים שמאלה” את אברי הסדרה \( 1,2,3 \) ואת המספר השמאלי ביותר בה מעבירים לצד הימני ביותר. להזזה כזו קוראים “הזזה ציקלית” (ציקלי מלשון מעגלי; חשבו ש-\( 1,2,3 \) היו מסודרים במעגל ואז היינו מזיזים את כולם שמאלה). השורה השלישית תהיה הזזה ציקלית של השורה השניה, כלומר \( 3,1,2 \). נקבל:

\( \left[\begin{array}{ccc}1 & 2 & 3\\2 & 3 & 1\\3 & 1 & 2\end{array}\right] \)

נסו להוכיח לעצמכם ששיטת הבניה שלי אכן עובדת תמיד. זה לא קשה.

בבירור כל ריבוע לטיני הוא גם ריבוע קסם, במובן זה שסכום כל השורות וכל העמודות בו הוא זהה, ושווה לסכום קבוצת המספרים שמופיעים בריבוע. למשל, בריבוע שבניתי הסכום יהיה \( 1+2+3=6 \). מדוע זה עובד? ובכן, בכל שורה ובכל עמודה בריבוע הלטיני כל האיברים שונים זה מזה ולכן הם בדיוק כל \( n \) המספרים שבכלל יכולים להופיע בריבוע הלטיני ולכן סכום כל שורה וכל עמודה שווה לסכומם.

נניח שאני רוצה שסכום השורות והעמודות בריבוע שבניתי למעלה לא יהיה 6 אלא מספר אחר, נאמר 77, מה אעשה? ובכן, פתרון אחד הוא להחליף כל מופע של 1 ב-72:

\( \left[\begin{array}{ccc}72 & 2 & 3\\2 & 3 & 72\\3 & 72 & 2\end{array}\right] \)

שכנעו את עצמכם שזה אכן יעבוד באופן כללי. מכיוון שזה כל כך קל, ריבוע קסם שבו רק סכומי השורות והעמודות הם זהים הוא “לא מעניין” וכדאי לדרוש עוד אילוצים. אפשר לדרוש, למשל, שגם סכומי האלכסונים יהיו שווים לסכומי השורות והעמודות, ונדבר על כך אחר כך; אבל לבינתיים אני רוצה לדרוש פשוט שכל אברי הריבוע יהיו שונים זה מזה. ברור שזה מחסל את שיטת הבניה הנוכחית שלי שבה מתחילים מריבוע שאותם שלוש מספרים מופיעים בו שלוש פעמים שונות וכדי לשנות את ערך הסכום שלו פשוט בוחרים אחד מהמספרים הללו ומגדילים אותו בערך קבוע. כדי להתמודד עם האילוץ החדש הזה אצטרך קצת יותר מאשר “סתם” ריבוע לטיני.

בואו נחזור שניה אל הריבוע של הקוסם. אם נסתכל רק על הצבעים בו, נראה שגם מהבחינה הזו מדובר בריבוע לטיני; אמנם, אלו צבעים ולא מספרים, אבל מה ההבדל? אם נרצה, נוכל להתאים מספר לכל צבע. הדבר החשוב הוא שבכל שורה ובכל עמודה מופיעים כל צבע בדיוק פעם אחת. לכן הריבוע של הקוסם הוא בעצם שני ריבועים לטיניים ש”מונחים אחד על השני”. תכונה 4 אומרת לנו מה הקשר ביניהם: כל זוג של מספר וצבע מופיע בדיוק פעם אחת. זו לא תכונה טריוויאלית; אם אקח את הריבוע הלטיני

\( \left[\begin{array}{ccc}1 & 2 & 3\\2 & 3 & 1\\3 & 1 & 2\end{array}\right] \)

ובמקום להשתמש במספרים אתאר אותו בצבעים, אקבל שצבע אחד מופיע רק עם 1, צבע אחר רק עם 2 וכן הלאה. מכאן שאנחנו צריכים לקחת שני ריבועים לטיניים שונים שאיכשהו מתנהגים יפה אחד עם השני כדי לקבל ריבוע שדומה לזה של הקוסם. לזוג ריבועים כזה קוראים ריבועים לטיניים אורתוגונליים. עכשיו אני יכול גם להסביר למה בכלל קוראים לריבועים הללו “ריבועים לטיניים”; במקור אוילר לא השתמש במספרים וצבעים כדי לתאר את תוכן הריבועים, אלא באותיות יווניות ולטיניות (יווניות בריבוע אחד, לטיניות בריבוע אחר, כדי להימנע מבלבול). לזוג ריבועים אורתוגונליים קראו גם ריבוע יווני-לטיני (הוא נכתב על ידי כך שבמקום שני ריבועים שונים, בכל משבצת בריבוע יהיה הזוג של האות היוונית והאות הלטינית שמתאימות לאותה משבצת). עם הזמן שיטת הסימון של אוילר נשכחה וגם ה”יווני” נשכח ונותר הלטיני.

ההיסטוריה של ריבועים לטיניים מעניינת למדי. קל להראות שאין זוג ריבועים לטיניים אורתוגונליים מסדר \( 2\times2 \) ואפשר בקלות רבה למצוא זוג מסדר \( 3\times3 \) (תכף נראה איך); במאה ה-18 נתגלו גם זוגות עבור \( 4\times4 \), ואז בא לאונרד אוילר ומצא בניות של זוגות ריבועים לטיניים אורתוגונליים עבור כל גודל \( n\times n \) כאשר \( n \) הוא אי זוגי או מתחלק ב-4. זו הייתה קפיצת דרך מרהיבה, אבל היא עדיין הותירה פתוחה את השאלה מה קורה כאשר \( n \) הוא מספר זוגי אשר משאיר שארית 2 בחלוקה ב-4. המספרים הראשונים מסוג זה הם 2 ו-6: אוילר ידע שאין פתרון עבור 2 ולא עלה בידו למצוא פתרון עבור 6 (אבל גם לא הוכחה שאין פתרון כזה), והוא העלה את ההשערה שבאופן כללי אין פתרון עבור \( n \) שמשאיר שארית 2 בחלוקה ב-4.

רק בשנת 1901 הוכח שאוילר צדק בכך שחשב שאין פתרון עבור 6, אבל 1959 הוכח כי עבור כל \( n\ne2,6 \) אכן קיים פתרון! לי אין מושג איך בונים את הפתרונות הללו, אבל אולי אקדיש לכך פוסטים בעתיד אם הבניה פשוטה דיו להצגה כאן.

טוב, אז איך זוג ריבועים לטיניים אורתוגונליים עוזרים לנו כאן? בואו נמשיך לחשוב על זוג כזה בתור ריבוע אחד, עם מספרים וצבעים, כאשר המספרים הם בין 1 ל-\( n \). עכשיו אני רוצה להפוך את הריבוע הזה לריבוע קסם “קלאסי”, כזה שבו המספרים הם \( 1,2,\dots,n^{2} \) וסכום כל השורות והעמודות זהה. מה עושים? ראשית כל שמים לב לאבחנה הבאה: אם ניקח את כל המשבצות שצבועות בצבע מסויים ונוסיף לכולן את אותו המספר \( a \), סכום השורות והעמודות לא ישתנה. למה? כי בכל שורה מופיעה בדיוק משבצת אחת עם הצבע הזה, ולכן לסכום של כל שורה יתווסף בדיוק \( a \) ולא יותר מכך, וכך גם עם העמודות.

על כן, דרך הפעולה שלי היא כזו: אני אבחר צבע ואותיר את המספרים \( 1,2,\dots,n \) שלו ללא שינוי. אחר כך אני אבחר צבע אחר ואוסיף לכל מספר בו \( n \) וכך אקבל את המספרים \( n+1,n+2,\dots,2n \). אחר כך אלך אל הצבע הבא ואוסיף למספרים שלו \( 3n \) וכן הלאה.

ה”בעיה” בתעלול הזה היא שכדי לבנות ריבוע קסם קודם כל צריך למצוא זוג ריבועים לטיניים אורתוגונליים, וזה יכול להיות קשה למדי (ועבור \( n=6 \) זה פשוט בלתי אפשרי, אבל בהחלט קיימים ריבועי קסם מגודל \( 6\times6 \); יש עוד דרכים לבנות ריבועי קסם שאינן משתמשות בריבועים לטיניים אורתוגונליים). עם זאת, אמרתי שעבור \( n=3 \) כולנו נדע לעשות את זה בסוף הפוסט, אז בואו נעשה את זה - כפי שאמרתי, עם ניסוי וטעיה.

נתחיל עם ריבוע לטיני בודד מסדר \( 3\times3 \) מתבקש לבחור בתור השורה הראשונה את 1,2,3. בשביל השורה השניה אני יכול לבחור או את 2,3,1 או את 3,1,2; הראשון מביניהם נחמד יותר (הוא פשוט “הזזה ציקלית” של 1,2,3) ולכן נבחר אותו, ועכשיו השורה האחרונה נקבעת בצורה יחידה (פשוט תסתכלו בכל עמודה ותראו מה המספר שטרם הופיע. נקבל:

\( \left[\begin{array}{ccc}1 & 2 & 3\\2 & 3 & 1\\3 & 1 & 2\end{array}\right] \)

עכשיו בואו נבנה ריבוע לטיני נוסף ונקווה שהוא יצא אורתוגונלי לריבוע שבנינו זה עתה. אשתמש, באופן הולם למדי, באותיות הלטיניות \( a,b,c \) כדי לתאר את איבריו. השורה הראשונה תהיה אם כן \( a,b,c \). מה תהיה השורה השניה? אפשר \( b,c,a \) אבל אז זה יהיה אותו הדבר כמו הריבוע שכבר בנינו ואין סיכוי שהם יהיו אורתוגונליים (כי אז, למשל, \( a \) ו-1 תמיד יופיעו יחד). אז בואו נבחר את האפשרות האחרת: \( c,a,b \). נקבל:

\( \left[\begin{array}{ccc}a & b & c\\c & a & b\\b & c & a\end{array}\right] \)

ועכשיו כשנשלב את שני הריבועים שבנינו יחד נקבל:

\( \left[\begin{array}{ccc}\left(1,a\right) & \left(2,b\right) & \left(3,c\right)\\\left(2,c\right) & \left(3,a\right) & \left(1,b\right)\\\left(3,b\right) & \left(1,c\right) & \left(2,a\right)\end{array}\right] \)

כלומר, לשמחתנו הרבה אכן קיבלנו זוג ריבועים אורתוגונליים! כאן ממש נדחפנו לפתרון הזה - לא היה לנו שום חופש בחירה.

עכשיו, איך נבנה ריבוע קסם מהדבר הזה? ובכן, את המספרים שהם שכנים של \( a \) נותיר כמות שהם; את המספרים שהם שכנים של \( b \) נגדיל ב-3, ואת המספרים שהם שכנים של \( c \) נגדיל ב-6. נקבל:

\( \left[\begin{array}{ccc}1 & 5 & 9\\8 & 3 & 4\\6 & 7 & 2\end{array}\right] \)

קיבלנו ריבוע של המספרים מ-1 עד 9 כאשר כל שורה וכל עמודה מסתכמת ל-15, אך לא האלכסונים. מה עשיתי לא נכון? אם תסתכלו על האלכסונים בריבוע האורתוגונלי שלמעלה, תראו שהם לא “נחמדים” - באחד מהם מופיע 3 בכל המשבצות, ובשני מופיע \( a \) בכל המשבצות. במקרה של האלכסון \( \left(3,c\right),\left(3,a\right),\left(3,b\right) \) זה אומר שהסכום שלו יהיה 9 (הסכום של שלושת ה-3-ים) ועוד הערכים שאני נותן ל-\( a,b,c \) שהם במקרה שלנו \( 0,3,6 \), כלומר הסכום הכולל יהיה 18 - לא מוצלח.

אז בואו נכתוב את הריבוע האורתוגונלי כמו שאוילר התכוון - עם אותיות לטיניות ויווניות ובלי מספרים כלל:

\( \left[\begin{array}{ccc}\left(\alpha,a\right) & \left(\beta,b\right) & \left(\gamma,c\right)\\\left(\beta,c\right) & \left(\gamma,a\right) & \left(\alpha,b\right)\\\left(\gamma,b\right) & \left(\alpha,c\right) & \left(\beta,a\right)\end{array}\right] \)

וכעת, כדי לקבל ריבוע קסם מהיצור הזה אנחנו צריכים לבחור ערכים מספריים לכל אות יוונית ולכל אות לטינית, ואז לכל משבצת בריבוע לחבר את המספרים שבחרו לאות היוונית והלטינית שמופיעות במשבצת. אנחנו יודעים שאוטומטית, הסכום של כל שורה ושל כל עמודה יהיה שווה ל-\( \left(a+b+c\right)+\left(\alpha+\beta+\gamma\right) \) ולכן כל שנותר לנו לדאוג לו הוא האלכסונים. הסכום של אחד האלכסונים הוא \( 3\gamma+\left(a+b+c\right) \) והסכום של האלכסון השני הוא \( 3a+\left(\alpha+\beta+\gamma\right) \). מה עוד מגביל אותנו? אם אנחנו רוצים שכל המספרים יהיו שונים זה מזה ושכולם יהיו בטווח מ-1 עד 9, אנחנו חייבים לבחור עבור \( a,b,c \) את הערכים 1,2,3 (לא בהכרח בהתאמה) ועבור \( \alpha,\beta,\gamma \) את הערכים \( 0,3,6 \) (לא בהכרח בהתאמה). כמובן, אפשר היה להגיד שדווקא האותיות הלטיניות צריכות לקבל 0,3,6 והיווניות 1,2,3 אבל זה לא היה משנה כלום.

אם האותיות היווניות קיבלו 0,3,6 אז \( \alpha+\beta+\gamma=9 \) ולכן כדי שיתקיים \( \left(\alpha+\beta+\gamma\right)=15 \)\( 3a+ \) בהכרח חייב להתקיים \( a=2 \). בדומה, אם האותיות הלטיניות קיבלו את 1,2,3 אז \( \left(a+b+c\right)=9 \) אז \( 3\gamma+\left(a+b+c\right)=15 \) גורר ש-\( \gamma=3 \). את שאר המספרים אפשר לבחור בחופשיות (תחת המגבלות שכבר מצאנו). בואו נבחר \( \alpha=0,\beta=6,b=1,c=3 \) ונקבל את הריבוע הבא:

\( \left[\begin{array}{ccc}2 & 7 & 6\\9 & 5 & 1\\4 & 3 & 8\end{array}\right] \)

וקיבלנו בדיוק את מה שרצינו - ריבוע קסם מסדר \( 3\times3 \) עם המספרים מ-1 עד 9 שבו כל השורות, העמודות והאלכסונים מסתכמים ל-15. כפי שאפשר לראות, בסופו של דבר לא נדרש הרבה יותר מהגיון בריא בסיסי כדי למצוא את הריבוע הזה, וגם ילדים יכולים לעשות זאת (וכנראה עם הרבה פחות קשקושים מסביב ממני).

איך מוצאים את הריבועים האורתוגונליים מסדר \( 4\times4 \) שהם הבסיס לקסם שבו פתחתי את הפוסט? טוב… ובכן… זו שאלה טובה. קסם?

איך הקסם עבד?

עכשיו, אחרי שהבנו לעומק את הרעיון המתמטי שמאחורי ריבועי קסם, בואו נדבר על איך הקוסם ביצע את הקסם בפועל, ואיך כל אחד מאיתנו יכול (תיאורטית) לעשות את אותו הדבר. נתחיל עם ציון המובן מאליו - התכונה העיקרית שנדרשת מקוסם טוב היא היכולת לבצע את הקסם במהירות ותוך הסחת דעת הצופה מהמתרחש, והקוסם בסרטון עושה זאת היטב - בצפיה ראשונה קיבלתי את הרושם השגוי לחלוטין שהוא מערבב את חפיסת הקלפים שלו (מה שהיה מקלקל את כל הקסם) והוא מבצע את השלבים מהר מספיק כדי שאי אפשר יהיה אפילו לנסות להבין מה מתרחש. רק שבימינו אפשר לעצור סרטוני וידאו ולהחזיר אותם אחורה כרצוננו וזה מקל מאוד על פענוח התעלול.

הנחה בסיסית שלי היא שהקוסם יודע בדיוק מה מספר הקלף שהמשתתף בחר למרות שאנחנו לא רואים את הקלף הזה בשום שלב. קרוב לודאי שצדם האחורי של הקלפים שמהם המשתתף יכל לבחור מסומן בדרך כלשהי - מספיק סימון זעיר שאינו בולט לעין אבל הקוסם יודע להבחין בו. זה תעלול קוסמים נפוץ מאוד ובוודאי שאינו העיקר כאן. אז ברגע שבו המשתתף בחר קלף, הקוסם ידע בודאות מהו. עדיין, איך ייתכן שהקוסם קיבל ריבוע קסם יפה כל כך מיתר הקלפים?

את התעלול הקוסם מתחיל כשהחבילה מונחת לידו, כשהיא כבר מסודרת באופן שנוח לקוסם. אף אחד לא מערבב אותה בשום שלב, וזה כמובן קריטי לחלוטין. בתחילת הקסם הקוסם מסיר מראש החבילה מספר קלפים עד שהוא מגיע לקלף 8 (כפי שכבר ראינו, 8 הוא מספר קטן מכדי להופיע בתור סכום של ריבוע קסם). אפשר להניח בשקט שהקלפים מעל 8 הם קלפים ספציפיים שהחבילה מהונדסת כדי שהתעלול יעבוד עבורם. אליו מספרים יש שם? 26 (פעמיים), 42, 22 (פעמיים), 34, 30, 50. כולם מספרים שאפשר לבנות ריבוע קסם עבורם (עבור 22 ו-30 הסיטואציה טיפה בעייתית כי בריבוע הקסם שיתקבל יהיו מספרים שמופיעים יותר מפעם אחת - אני משער שלקוסם אין בעיה עם זה).

אם נקפוץ קדימה לשלב שבו הקוסם מתחיל ליצור את ערימות הקלפים שירכיבו את ריבוע הקסם (1:22) נראה שהוא בונה ארבע ערימות באופן הדרגתי: בהתחלה מניח 8,7,9,10 (בסדר הזה), אחר כך מניח 11,1,6,3, אחר כך 2,12,4,5, ואז… הויסה, רגע. בואו ניזכר בפירוק לארבע פרמוטציות של ריבוע הקסם של הקוסם:

ברור לגמרי שהקלפים הונדסו כך שבכל שלב של החילוק יונח קלף אחד בדיוק עבור כל רבע. למשל, הקלפים שהונחו ראשונים בכל שלב היו 8,11,2, שנמצאים ברבע השמאלי-עליון של הפרמוטציות - מלבד זו השמאלית ביותר שטרם הופיעה. אם עבור הפרמוטציה השמאלית ביותר היינו בוחרים את המספרים 1,2,3,4 היינו מקבלים שסכום כל שורה-טור-אלכסון-רבע הוא 22, המספר הראשון שהיה עשוי להיבחר על ידי המשתתף; כך שאפשר להניח בשקט ש-12 הקלפים שחולקו בשלב הזה הם חלק קבוע מסידור החפיסה שאינו תלוי בבחירה של המשתתף.

מה כן משתנה? ארבעת הקלפים הבאים, שהם כמובן 21,22,23,24. מרגע שהם הונחו, כל שנותר לקוסם לעשות הוא לסדר את ריבוע הקסם בצורה נכונה (זה כמובן דורש שינון כלשהו) והופה! ריבוע הקסם התקבל. צריך גם להסביר איך קרה שעל גב הקלפים כתוב שהמשתתף הולך לבחור 42. ובכן, מה שכתוב על רוב הקלפים הוא חסר חשיבות כי הוא אינו תלוי במספר; הדבר היחיד שחשוב הוא הקלף האחרון, בפינה הימנית-תחתונה, שעליו כתוב “42”. הקלף הזה הוא הקלף שמספרו 23, כלומר לא אחד מ-12 הקלפים ה”גנריים” אלא קלף שמתאים לפרמוטציה השמאלית ביותר, שנקבעת ספציפית על פי המספר שהמשתתף בחר.

אם כן, החבילה של הקוסם כוללת 12 קלפים גנריים, עוד 4 קלפים “ספציפיים לבחירה” מתחתיהם, ומתחת לאלו כל יתר הקלפים שלהם הקוסם לא נזקק לצורך המשך התעלול. השאלה היחידה שנותרה היא איך יצא שמתחת ל-12 הקלפים הגנריים יש בדיוק את ארבעת הקלפים שמתאימים לבחירה של המשתתף? הרי הקוסם לא יכל לחזות אותה מראש! התשובה היא פשוטה: הקוסם מניח אותם שם מול העיניים שלנו, בלי בושה ובלי למצמץ, ואנחנו כמובן לא שמים לב. בסרטון אפשר לראות את זה החל מ-1:06: הקוסם בוחר מראש החפיסה את 12 הקלפים הגנריים, שם אותם בצד, עובר על יתר הקלפים עד שהוא מגיע אל הקלף הראשון מבין 4 הקלפים ה”ספציפיים”, מניח אותם בראש החבילה שהוא סרק ושם עליהם את 12 הקלפים הגנריים שהיו בצד. וכל זה - פעולות מאוד מדויקות שהן הדבר הקריטי ביותר פה - נעשה בנונשלנטיות גמורה שגורמת לנו להרגיש שזה הדבר הכי טבעי בעולם.

אם כן, כעת גם אתם יודעים איך למצוא ריבועי קסם באופן כללי ובפרט איך לבצע את הקסם הספציפי שראינו. למרות שאני יכול להבין את אלו שהידע הזה מוציא להם את כל ההנאה מהקסם, אני דווקא חושב שבמקרה הספציפי הזה, הוא מהנה הרבה יותר כאשר ברור איך הוא מתבצע.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: