העתקות מביוס והספירה של רימן

אני ממשיך את סדרת הפוסטים שלי על אנליזה מרוכבת, והפעם אני רוצה להציג מחלקה חשובה של פונקציות מרוכבות - העתקות מביוס, שהן פונקציות מרוכבות מהצורה \( f\left(z\right)=\frac{az+b}{cz+d} \) כאשר \( a,b,c,d\in\mathbb{C} \) המקיימים את התנאי הנוסף \( ad-bc\ne0 \) שנבין בהמשך מה משמעותו. כדי להבין למה אלו העתקות מעניינות, בואו נראה שלושה סוגים של העתקות כאלו: \( f\left(z\right)=az \) (“ניפוח” - באנגלית Dilation), \( f\left(z\right)=z+b \) (“הזזה” - Translation באנגלית) ו-\( f\left(z\right)=\frac{1}{z} \) (“היפוך” - Inversion באנגלית). אלו שלוש פונקציות פשוטות שברור שהולכות לעניין אותנו אם אנחנו הולכים לחקור פונקציות מרוכבות; ולכן סביר להניח שגם מה שאפשר להרכיב באמצעותן יעניין אותנו. האבחנה הראשונה שלנו היא שכל העתקת מביוס ניתנת לתיאור באמצעות הרכבה של שלושה סוגי הפונקציות הללו. למה?

ובכן, קודם כל בואו ניקח העתקת מביוס שבה \( c=0 \), כלומר היא מהצורה \( f\left(z\right)=\frac{a}{d}z+\frac{b}{d} \) (לא ייתכן ש-\( d=0 \) כי אז היינו מקבלים \( ac-bd=0 \)). זו בבירור הרכבה של ניפוח והזזה: \( f\left(z\right)=g\left(h\left(z\right)\right) \) כאשר \( h\left(z\right)=\frac{a}{d}z \) ו-\( g\left(z\right)=z+\frac{b}{d} \).

עכשיו, אם \( c\ne0 \), איך אפשר להגיע ל-\( \frac{az+b}{cz+d} \) באמצעות הרכבות של ניפוחים, הזזות והיפוכים? זה סוג של משחק שבו כדאי לחשוב על מה שאנחנו “נאלצים” לעשות. ברור שבלי היפוך לא נוכל להגיע למצב שבו יש \( z \) בתוך המכנה אז נהיה חייבים להשתמש בהיפוך מתישהו, אבל אחרי ש-\( z \) עבר למכנה, איך נוכל לגרום לו להיכנס שוב למונה? זה דווקא קל יחסית, הסתכלו בשוויון הבא: \( \frac{1}{z}+a=\frac{1+az}{z} \). כלומר, הזזה תוכל “להחזיר” לנו את \( z \) למונה אם הוא נמצא כרגע רק במכנה. אבל צריך יהיה להנדס את הפרמטרים היטב כדי שהכל יעבוד. הדרך הטובה ביותר לראות איך צריך להנדס אותם היא להתחיל מהסוף, ואני רוצה להראות את זה במפורש כי לרוב הספרים שמוכיחים את המשפט הזה פשוט שולפים את הפתרון מהכובע כמו קסם (Gamelin אפילו מתייחס לזה ישירות ואומר “Now we conjure up by magic the identity…”) וזו אמנם שיטת עבודה לגיטימית בספרי לימוד אבל אני רוצה כאן שנצא עם קצת יותר אינטואיציה והבנה איך לטפל בבעיות כאלו באופן כללי.

כדאי לנסות ולעבוד עם דוגמאות פשוטות כדי לקבל רעיון איך להתקדם מכאן.

אז הסכמנו כבר (?) שהצעד האחרון שלנו יהיה חיבור, כדי להחזיר את \( z \) למונה. אז אם אחריו התוצאה הייתה \( \frac{az+b}{cz+d} \), מה היא הייתה לפניו? אנחנו רוצים לקבל משהו שמכיל את \( az \) על ידי הכפלה ב-\( \left(cz+d\right) \). אז נצטרך לכפול ב-\( \frac{a}{c} \), מה שייתן לנו \( az+\frac{ad}{c} \). המחובר הימני הוא שארית שלא טובה לנו, אבל לפחות אין בה \( z \) ואפשר מראש לחסר אותה ממה שהיה במונה, כלומר אפשר לכתוב:

\( \frac{az+b}{cz+d}=\frac{b-\frac{ad}{c}}{cz+d}+\frac{a}{c} \)

אם נחשב את הערך של המונה, נקבל שהוא \( \frac{bc-ad}{c} \). אפשר כעת לכפול מונה ומכנה ב-\( c \), ולקבל:

\( \frac{az+b}{cz+d}=\frac{bc-ad}{c\left(cz+d\right)}+\frac{a}{c} \)

וזה כבר ממש טוב לנו! כי אפשר כעת לכתוב \( \frac{bc-ad}{c\left(cz+d\right)}=\frac{bc-ad}{c}\cdot\frac{1}{cz+d} \) ולמוכפל הימני ברור לנו איך להגיע על ידי שילוב של שלוש העתקות מביוס. למעשה, עם התחכמות נוספת אני אצטרך רק שתיים: \( \frac{bc-ad}{c}\cdot\frac{1}{cz+d}=\frac{bc-ad}{c^{2}}\cdot\frac{1}{z+\frac{d}{c}} \).

ועכשיו סיימנו: נגדיר

\( g_{1}\left(z\right)=z+\frac{d}{c} \)

\( g_{2}\left(z\right)=\frac{bc-ad}{c^{2}}z \)

\( g_{3}\left(z\right)=\frac{1}{z} \)

\( g_{4}\left(z\right)=z+\frac{a}{c} \)

וקיבלנו \( g_{4}\left(g_{3}\left(g_{2}\left(g_{1}\left(z\right)\right)\right)\right)=\frac{az+b}{cz+d} \).

יפה. אז ראינו שכל העתקת מביוס מורכבת מהזזות, ניפוחים והיפוכים. האם גם ההפך נכון, כלומר כל הרכבה של הזזות, ניפוחים והיפוכים היא העתקת מביוס? לא בדיוק, כי \( g\left(z\right)=az \) כאשר \( a=0 \) היא לא העתקת מביוס כי אינה מקיימת את התנאי \( ad-bc=0 \). אבל פרט לכך, קל לראות ש-\( g\left(z\right)=az \) כאשר \( a\ne0 \), ו-\( g\left(z\right)=z+b \) ו-\( g\left(z\right)=\frac{1}{z} \) כולן העתקות מביוס (אולי טיפה מבלבל לראות שב-\( z+b \) הערך של \( d \) הוא 1 ולא 0), וקצת יותר חישובים יראו שהפעלה של אחת מהפונקציות הללו על העתקת מביוס מחזירה העתקת מביוס. אם ננסה לברר מה בעצם התנאי \( ad-bc\ne0 \) מבטיח, נוכל לבדוק דוגמאות שבהן דווקא \( ad-bc=0 \). נסו לעשות זאת - תגלו שאיכשהו המונה והמכנה תמיד מתבטלים ואתם נשארים עם פונקציה קבועה ביד. זה לא מקרה: אם נגזור את \( \frac{az+b}{cz+d} \) תוך שימוש בכללי הגזירה הרגילים עבור פולינומים ועבור מנה של פונקציות (ההוכחה של כללי הגזירה הללו במקרה המרוכב זהה להוכחה שלהן במקרה הממשי) נקבל:

\( \left(\frac{az+b}{cz+d}\right)^{\prime}=\frac{1}{\left(cz+d\right)^{2}}\left(a\left(cz+d\right)-\left(az+b\right)c\right)=\frac{ad-bc}{\left(cz+d\right)^{2}} \)

כך שאם \( ad-bc=0 \) הנגזרת היא 0 בכל מקום ולכן הפונקציה קבועה. אז יש לנו הסבר חדש מהן העתקות מביוס: אלו ההעתקות הלינאריות השבריות (העתקות שהן המנה של שתי פונקציות לינאריות) שאינן קבועות.

עכשיו אפשר לשים לב למשהו נוסף: הרכבה של שתי העתקות מביוס היא בעצמה העתקת מביוס. למה? כי אפשר לקחת כל העתקה כזו ולפרק אותה למרכיביה, שהם ניפוחים (עם מקדם שונה מ-0), הזזות והיפוכים, ואז נקבל שהרכבת שתי ההעתקות גם היא הרכבה של ניפוחים הזזות והיפוכים ולכן היא העתקת מביוס. אפשר גם לנקוט בגישה הטכנית ופשוט לחשב את הנוסחה שנותנת לנו הרכבה של העתקות:

נניח ש-\( f\left(z\right)=\frac{az+b}{cz+d} \) ו-\( g\left(z\right)=\frac{\alpha z+\beta}{\gamma z+\delta} \). מהי ההרכבה \( g\left(f\left(z\right)\right) \)? ובכן,

\( \frac{\alpha\frac{az+b}{cz+d}+\beta}{\gamma\frac{az+b}{cz+d}+\delta}=\frac{\alpha az+\alpha b+\beta cz+\beta d}{\gamma az+\gamma b+\delta cz+\delta d}=\frac{\left(\alpha a+\beta c\right)z+\left(\alpha b+\beta d\right)}{\left(\gamma a+\delta c\right)z+\left(\gamma b+\delta d\right)} \)

וזה, חברים, נראה פשוט זוועה. חייבת להיות דרך טובה יותר לחשוב על זה, נכון? ובכן, יש! מטריצות!

\( \left(\begin{array}{cc}\alpha & \beta\\\gamma & \delta\end{array}\right)\left(\begin{array}{cc}a & b\\c & d\end{array}\right)=\left(\begin{array}{cc}\alpha a+\beta c & \alpha b+\beta d\\\gamma a+\delta c & \gamma b+\delta d\end{array}\right) \)

מה שאנחנו רואים כאן בעצם הוא שאם נקודד את המקדמים של העתקת מביוס בתוך מטריצה, אז כפל המטריצות של שתי העתקות מביוס יתן לנו את המקדמים של העתקת מביוס המורכבת מהן. עכשיו, התנאי \( ad-bc\ne0 \) על המקדמים של העתקת מביוס הוא בעצם התנאי \( \det\left(\begin{array}{cc}a & b\\c & d\end{array}\right)\ne0 \) - ואנחנו יודעים שהדטרמיננטה של מטריצה שונה מאפס אם ורק אם המטריצה הפיכה. כלומר, המטריצה שמייצגת כל העתקת מביוס היא הפיכה, ולכן (בגלל מה שכבר ראינו על הרכבת העתקות) כל העתקת מביוס היא הפיכה, ולמעשה אנחנו רואים יותר מכך - אנחנו רואים שיש הומומורפיזם מחבורת המטריצות ההפיכות מסדר \( 2 \) מעל \( \mathbb{C} \) אל העתקות המביוס, מה שאומר שלהעתקות המביוס יש מבנה של חבורה. רק שימו לב לכך שזה הומומורפיזם אבל לא איזומורפיזם, כי כמה מטריצות שונות עשויות לתאר את אותה העתקה. למשל, \( \left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right) \) ו-\( \left(\begin{array}{cc}2 & 0\\0 & 2\end{array}\right) \) מתארות שתיהן את ההעתקה \( f\left(z\right)=z \). באופן כללי כל שתי מטריצות שנבדלות זו מזו על ידי כפל בקבוע מתארות את אותה העתקת מביוס.

אגב, האנלוגיה למטריצות עוזרת לנו גם למצוא את ההעתקה ההפוכה של \( \frac{az+b}{cz+d} \): להפוך מטריצה מסדר 2 זה קל ואפשר לעשות את זה, למשל, בעזרת כלל קרמר. מקבלים שההופכית של \( \left(\begin{array}{cc}a & b\\c & d\end{array}\right) \) היא \( \frac{1}{ad-bc}\left(\begin{array}{cc}d & -b\\-c & a\end{array}\right) \). עכשיו, המטריצה \( \frac{1}{ad-bc}\left(\begin{array}{cc}d & -b\\-c & a\end{array}\right) \) מתארת את אותה העתקה בדיוק כמו \( \left(\begin{array}{cc}d & -b\\-c & a\end{array}\right) \) כי הן נבדלות עד כדי כפל בקבוע, ולכן קיבלנו שהעתקת המביוס ההופכית של \( \frac{az+b}{cz+d} \) היא פשוט \( \frac{dz-b}{-cz+a} \).

כל הדיון עד כה היה נחמד מאוד, אבל איך בעצם הוא קשור לאנליזה מרוכבת? מה עשינו עד כה שאי אפשר היה לעשות גם במספרים ממשיים? שום דבר, אם איני טועה. לכן עכשיו אני רוצה להכניס לתמונה את ההיבט הגאומטרי של העתקות מביוס - מה הן עושות למישור המרוכב - והשלב הראשון יהיה להציג משהו שעשוי להיראות לכם מאוד, מאוד מוזר: את המישור המרוכב המורחב.

הבעיה היא פשוטה. בואו נתבונן בהעתקה \( f\left(z\right)=\frac{1}{z} \). זו העתקת מביוס פשוטה ונחמדה, אבל היא “מתפוצצת” ב-\( z=0 \) ולא מוגדרת שם. זה לא טוב לנו. גם לא טוב לנו שכל העתקה מהצורה \( \frac{az+b}{cz+d} \) תהיה לא מוגדרת בנקודה מסויימת - \( -\frac{d}{c} \). היה לנו הרבה יותר טוב אם היינו יכולים להתייחס לפונקציות הללו כמוגדרות בכל מקום - זה יאפשר תיאור הרבה יותר “נקי” שלהן ושל מה שהן עושות. אז מה עושים?

התשובה היא שלוקחים את המישור המרוכב \( \mathbb{C} \) ומוסיפים לו נקודה אחת נוספת, שנקרא לה “אינסוף” ונסמן אותה ב-\( \infty \). נסמן את התוצאה של ההרחבה ב-\( \mathbb{C}^{*}=\mathbb{C}\cup\left\{ \infty\right\} \). עכשיו נוכל להגדיר את ההגדרות הבאות: אם \( f \) היא העתקת מביוס כך ש-\( c=0 \), נגדיר \( f\left(\infty\right)=\infty \). אם לעומת זאת \( c\ne0 \) אז נגדיר \( f\left(\frac{-d}{c}\right)=\infty \), ו-\( f\left(\infty\right)=\lim_{z\to\infty}f\left(z\right)=\frac{a}{c} \). עם ההגדרות הללו, נקבל שכל העתקת מביוס מוגדרת על כל המישור המורחב, ואף יותר מכך - היא הפיכה בו, ולכן היא העתקה חח”ע ועל מהמישור המורחב לעצמו.

למי שלא ראה את זה בעבר, מה שעשיתי כרגע בוודאי נראה כמו רמאות.

אני אנסה לתת שתי הצדקות - אחת “אנליטית” והשניה “גיאומטרית” למה שעשיתי. ראשית האנליטית. מה שעשינו כאן הוא מקרה פרטי של מה שנקרא בטופולוגיה קבוצתית קומפקטיפיקציה על ידי נקודה אחת. לוקחים מרחב טופולוגי - כלומר, מרחב שבו יש משמעות כלשהי ל”קבוצות פתוחות” שמאפשרת להגדיר גבולות ועניינים - ומוסיפים לו נקודה אחת (שנהוג באמת תמיד לסמן ב-\( \infty \)) תוך עדכון הטופולוגיה של המרחב בהתאם כדי שהמרחב שנקבל כתוצאה יהיה קומפקטי. מבלי להיכנס כרגע להגדרה של קומפקטיות - שיש כבר בבלוג - בהקשר שלנו אפשר לחשוב על הכללה של מושג ה”סביבה” כדי שגבולות של “שאיפה לנקודה” וגבולות של “שאיפה לאינסוף” ייראו אותו הדבר. בואו נפרק שניה את הגדרת הגבול כדי להבין את זה.

כרגע כשאנחנו אומרים \( \lim_{z\to z_{0}}f\left(z\right)=w \) אנחנו אומרים שלכל \( \varepsilon>0 \) קיימת \( \delta>0 \) כך שאם \( \left|z-z_{0}\right|<\delta \) אז \( \left|f\left(z\right)-w\right|<\varepsilon \). עכשיו, אוסף הנקודות \( z \) כך ש-\( \left|z-z_{0}\right|<\delta \) נקרא כדור פתוח מרדיוס \( \delta \) סביב \( z_{0} \), ובדומה יש לנו כדור פתוח מרדיוס \( \varepsilon \) סביב \( z_{0} \). אז את \( \lim_{z\to z_{0}}f\left(z\right)=w \) ניתן להבין גם כ”לכל כדור פתוח \( B_{1} \) סביב \( w \) קיים כדור פתוח \( B_{2} \) סביב \( z_{0} \) כך שהתמונה של \( B_{2} \) מוכלת ב-\( B_{1} \)”. וגם את זה אפשר לקחת צעד אחד קדימה, להגדרה הכללית שלפיה \( \lim_{z\to z_{0}}f\left(z\right)=w \) פירושו ש”לכל קבוצה פתוחה \( U \) שמכילה את \( w \) קיימת קבוצה פתוחה \( V \) שמכילה את \( z_{0} \) כך ש-\( f\left(V\right)\subseteq U \)” (בהקשר שלנו קבוצה פתוחה היא קבוצה שלכל נקודה \( z \) בה קיים כדור פתוח שמכיל את \( z \) ומוכל בקבוצה).

עכשיו, קומפקטיפיקציה על ידי נקודה אחת של מרחב גוררת גם הרחבה של אוסף הקבוצות הפתוחות בו - פורמלית, אם הוספנו את \( \infty \) למרחב, אז נוסיף לטופולוגיה שלו (אוסף הקבוצות הפתוחות במרחב) את כל הקבוצות \( V \) שמכילות את \( \infty \) כך שהמשלימות שלהן הן קבוצות סגורות וקומפקטיות במרחב המקורי. עכשיו אפשר יהיה להגדיר שאיפה לאינסוף בדיוק באותו האופן כמו שאיפה לכל נקודה אחרת: למשל, \( \lim_{z\to z_{0}}f\left(z\right)=\infty \) פירושו “לכל קבוצה פתוחה \( U \) שמכילה את \( \infty \) קיימת קבוצה פתוחה \( V \) שמכילה את \( z_{0} \) כך ש-\( f\left(V\right)\subseteq U \)” (ואפשר להגדיר גם גבולות כמו \( \lim_{z\to\infty}f\left(z\right)=w \) באופן דומה). לא קשה להראות שעם ההגדרות שהצגתי, כל קבוצה פתוחה שמכילה את \( \infty \) בפרט מוכלת בקבוצה מהצורה \( \left\{ z\in\mathbb{C}\ |\ \left|z\right|>N\right\} \) עבור \( N\in\mathbb{N} \) כלשהו, ולכן כשמתעסקים עם גבולות מספיק להתעסק עם קבוצות מהצורה הזו, וזה מתלכד עם האופן ה”רגיל” שבו אנחנו מגדירים גבולות שמערבים אינסוף.

אתן דוגמה פשוטה: נתבונן ב-\( f\left(z\right)=\frac{1}{z} \) ונוכיח את נכונות הגבול \( \lim_{z\to0}\frac{1}{z}=\infty \). לצורך כך יהא \( N>0 \) ונרצה למצוא \( \delta \) כך שאם \( \left|z-0\right|<\delta \) אז \( \left|f\left(z\right)\right|>N \). בבירור \( \delta=\frac{1}{N} \) עושה זאת, כי אם \( \left|z\right|<\frac{1}{N} \) אז \( \left|f\left(z\right)\right|=\frac{1}{\left|z\right|}>N \). הבנתם את הרעיון, אני מקווה. השורה התחתונה היא שההבדל בין גבול “רגיל” ובין גבול של “שאיפה לאינסוף” הוא מלאכותי במידת מה, וכשעושים קומפקטיפיקציה וחושבים על הכל בלשון של קבוצות פתוחות ההבדלים נעלמים.

כל זה אולי מפיס את הדעת מבחינה פורמלית, אבל מה למען השם המשמעות הגאומטרית של \( \mathbb{C}^{*} \) הזה? למרבה המזל, יש משמעות גאומטרית פשוטה ויפה מאוד: כדור. ליתר דיוק, ספירה (ספירה היא המעטפת של כדור; “כדור” מתייחס גם למה שבפנים) שנקראת “הספירה של רימן”.

כדי להבין איך זה עובד, בואו נחשוב שניה על הצרור האייקוני על מקל של חסרי בית וטיילים בקומיקסים. איך הוא נוצר? לוקחים בד ריבועי כלשהו, אוספים את הקצוות שלו יחד וקושרים אותם למקל, ומקבלים צורה כדורית. הספירה של רימן מתקבלת באותו האופן: אנחנו לוקחים את הקצוות של המישור המרוכב, מרימים אותן, מדביקים אותן יחד ומקבלים משהו דמוי כדור - ומכיוון שבמתמטיקה מדויקת עסיקנן, מקבלים משהו שהוא בדיוק כדור. כמובן, ייתכן שתגידו עכשיו שמשהו ממה שאמרתי לא הגיוני כי למישור המרוכב אין קצוות, ואתם כמובן צודקים, אבל מכיוון שבמתמטיקה עסיקנן, למה שזה יעצור אותנו?

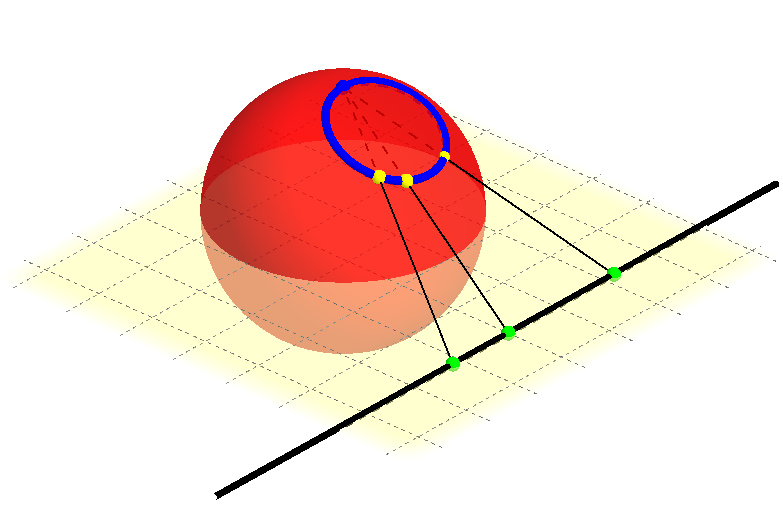
פורמלית, הרעיון הוא כזה: בואו נסתכל על המישור המרוכב, ואז נחשוב עליו כמשהו שחי בעולם תלת-ממדי, כאשר המישור המרוכב עצמו הוא בגובה 0. עכשיו נסתכל על כדור היחידה בעולם התלת-ממדי הזה, כלומר כדור שמרכזו ב-\( \left(0,0,0\right) \) ורדיוסו 1. הנקודה הגבוהה ביותר בכדור הזה - “הקוטב הצפוני” שלו - היא \( \left(0,0,1\right) \). עכשיו, לכל נקודה על הכדור ששונה מהקוטב הצפוני, נמתח את הקו הישר היחיד שמחבר אותה עם הקוטב הצפוני, נאריך אותו ככל שיידרש עד שיחתוך את המישור המרוכב. מכיוון שכל נקודה על הכדור פרט לקוטב הצפוני היא בעלת גובה נמוך יותר מהקוטב, הישר שמחבר את שתי הנקודות הללו יהיה בעל שיפוע שונה מאפס ביחס לציר \( z \) (ציר ה”גובה”) ולכן הישר באמת יחתוך את המישור המרוכב פעם אחת. כעת נזהה את נקודת החיתוך הזו עם הנקודה על הספירה. אפשר לעשות גם ההפך - לקחת נקודה כלשהי במישור המרוכב, לחבר אותה עם הקוטב הצפוני, לראות איפה הישר חותך את הספירה ולזהות את הנקודה במישור המרוכב עם נקודת החיתוך הזו. הנה תמונה שממחישה את זה - כאן הקוטב הוא הנקודה הכחולה, הנקודה במישור היא הנקודה הירוקה, והנקודה המתאימה על הספירה היא הנקודה הצהובה:

שימו לב, אגב, לכך שלא תמיד הנקודה שבה הישר חותך את הספירה נמצאת בין הנקודה על המישור והקוטב; לפעמים דווקא הנקודה שעל המישור היא בין הקוטב והנקודה המתאימה על הספירה.

אם זה נשמע לכם יותר מדי באוויר, בואו נעשה חישוב שיפיס קצת את הדעת ויאפשר לנו לעבור מקואורדינטות של המישור המרוכב לקואורדינטות של הספירה של רימן, ולהפך. אם ניזכר בגאומטריה אנליטית, בהינתן שתי נקודות \( a,b \) אפשר לתאר את הישר שמחבר אותן באמצעות צירוף לינארי מהצורה הבאה: \( at+\left(1-t\right)b \) כאשר \( -\infty\le t\le\infty \) (כאשר \( 0\le t\le1 \) אנחנו מקבלים בדיוק את הנקודות שבין \( a,b \)). בואו ניקח את אחת הנקודות להיות \( \left(0,0,1\right) \) ואת השניה להיות \( \left(X,Y,Z\right) \) (כך ש-\( X^{2}+Y^{2}+Z^{2}=1 \) - זה המשמעות של להיות על ספירת היחידה) ונתבונן במשוואה \( \left(x,y,0\right)=t\left(X,Y,Z\right)+\left(1-t\right)\left(0,0,1\right) \) - האם יש למשוואה הזו פתרון? ובכן, משוואה כזו למעשה מקפלת בתוכה שלוש משוואות, אחת לכל קואורדינטה:

\( x=tX \)

\( y=tY \)

\( 0=tZ+1-t \)

מהמשוואה השלישית אפשר לחלץ את \( t \): \( t=\frac{1}{1-Z} \). בשל כך נקבל בשתי המשוואות הראשונות:

\( x=\frac{X}{1-Z} \)

\( y=\frac{Y}{1-Z} \)

וזה נותן לנו התאמה בכיוון אחד: \( \left(X,Y,Z\right)\mapsto\frac{X}{1-Z}+i\frac{Y}{1-Z} \) (שימו לב שבהכרח \( Z<1 \) בגלל ש-\( X^{2}+Y^{2}+Z^{2}=1 \) וההנחה שלנו ש-\( \left(X,Y,Z\right)\ne\left(0,0,1\right) \)).

מה נעשה בכיוון השני - כלומר, בהינתן \( z=x+iy \) איך נמצא את הנקודה על הספירה שמתאימה לו? שוב, יש לנו את שתי המשוואות הבאות:

\( x=\frac{X}{1-Z} \)

\( y=\frac{Y}{1-Z} \)

אבל הן לא מספיקות כדי לקבוע ביחידות את \( \left(X,Y,Z\right) \) בהינתן \( x,y \) (כי אלו שתי משוואות ויש לנו שלושה נעלמים). לכן אנחנו צריכים להשתמש במשוואה הנוספת שיש לנו - \( X^{2}+Y^{2}+Z^{2}=1 \). כעת, אנחנו יודעים ש-\( x=tX \) וש-\( y=tY \) וש-\( tZ=t-1 \) ולכן יהיה משתלם להכניס למשוואה הזו את \( t \), אבל מכיוון שכל המשתנים בריבוע כדאי שגם \( t \) יהיה בריבוע. אז נכפול את המשוואה ב-\( t^{2} \) ונקבל:

\( t^{2}=\left(tX\right)^{2}+\left(tY\right)^{2}+\left(tZ\right)^{2}=x^{2}+y^{2}+\left(t-1\right)^{2} \)

ולכן \( t^{2}=\left|z\right|^{2}+t^{2}-2t+1 \)

ולכן \( t=\frac{\left|z\right|^{2}+1}{2} \)

מה שמניב לנו את הפתרון:

\( X=\frac{2x}{\left|z\right|^{2}+1} \)

\( Y=\frac{2y}{\left|z\right|^{2}+1} \)

\( Z=\frac{\left|z\right|^{2}-1}{\left|z\right|^{2}+1} \)

ועכשיו קיבלנו את ההתאמה בכיוון השני: \( x+iy\mapsto\left(\frac{2x}{\left|z\right|^{2}+1},\frac{2y}{\left|z\right|^{2}+1},\frac{\left|z\right|^{2}-1}{\left|z\right|^{2}+1}\right) \). שתי ההתאמות קלות למדי לחישוב, ועכשיו אפשר לחשוב באופן טבעי על המישור המורחב בתור מה שקורה על פני הספירה, שהקוטב הצפוני הוא פשוט הנקודה \( \infty \). כאן העובדה ש-\( \infty \) היא נקודה ככל הנקודות היא ברורה במיוחד: בפרט, אין הבדל עקרוני בינה ובין 0, שהוא הקוטב הדרומי. אפשר אפילו לראות בעיניים איך נראה “עיגול” סביב \( \infty \) - זה פשוט עיגול על הספירה, שמתורגם לעיגול רגיל במישור, כפי שאפשר לראות בתמונה:

עם זאת, האינטואיציה שהספירה נותנת לנו לא נגמרת כאן - היא מאפשרת לנו לחשוב על קווים ישרים בתור מעגלים: אם נצייר קו ישר במישור ונבדוק לאן הוא עובר על הספירה, נראה שהוא עובר בדיוק למעגל שעובר דרך הקוטב הצפוני, כלומר “עובר דרך אינסוף ויוצא חזרה מהצד השני”. יש כאן לא מעט הגיון - ישר נקבע על ידי שתי נקודות ומעגל על ידי שלוש; לכן אפשר לחשוב על ישר בתור מעגל שהנקודה השלישית שקובעת אותו היא \( \infty \). זה דבר שמאוד חביב עלי בנושא הזה - האופן שבו אמירות אבסורדיות כמו זו מקבלות משמעות קונקרטית, פשוטה והגיונית.

המטרה של הספירה של רימן היא לשכנע אתכם בכך שהיצור הזה, \( \mathbb{C}^{*}=\mathbb{C}\cup\left\{ \infty\right\} \) הוא “חוקי” מבחינה מתמטית; בפועל מכאן ואילך אני פשוט אשתמש בחופשיות ב-\( \infty \) כשזה יהיה רלוונטי וכולנו נבין למה הכוונה.

רק הערת סיום קטנה: שימו לב שנראה שבעצם עשינו כאן את הלא יעשה והגדרנו \( \frac{1}{0}=\infty \) (וגם \( \frac{1}{\infty}=0 \)). אבל זה לא באמת נכון. לכתוב \( \frac{1}{0}=\infty \) זה לומר שמתקיים השוויון \( 0\cdot\infty=1 \), ואף אחד לא טוען שזה קורה. למעשה, בכלל לא הגדרנו כללי אלגברה עבור \( \infty \) (למשל חוק הפילוג) וגם לא נעשה את זה. כל מה שעשינו היה להרחיב את ההגדרה של העתקות מביוס בצורה מסויימת (או לחילופין, אם להיות ממש פורמליים, בהינתן העתקת מביוס על \( \mathbb{C} \) הגדרנו העתקה על \( \mathbb{C}^{*} \) שמזדהה איתה על כל נקודה ב-\( \mathbb{C} \) שבה היא מוגדרת). זו המחשה יפה של נקודה שאני מנסה להעביר תמיד ביחס לעניין החלוקה באפס: אפשר תמיד להגדיר חלוקה באפס בכל אופן שמתחשק לנו; רק צריך להבין מה אנחנו משיגים בזה ומה ההשלכות של זה. בהקשר הנוכחי שלנו, ההגדרה היא נוחה למדי ואנחנו לא מאבדים שום דבר (כי כאמור, \( \infty \) לא הולך לציית לכללי האלגברה וזה לא מפריע לנו).

בואו נחזור עכשיו לאקשן של העתקות מביוס. לפני רגע הזכרתי שמעגל נקבע על ידי שלוש נקודות שעליו; ליתר דיוק, בהינתן שלוש נקודות (שאינן שלושתן על קו ישר כלשהו) קיים מעגל שעובר דרך שלושתן והוא יחיד. האינטואיציה לכך היא שמעגל נקבע על ידי שלושה פרמטרים - קואורדינטות \( x,y \) של המרכז, והרדיוס. בדומה ישר נקבע על ידי שתי נקודות, בהתאם לכך שיש לו שני פרמטרים (שיפוע ונקודת חיתוך עם ציר \( y \)). זו אינטואיציה שהיא נפנוף ידיים פרוע וכמעט שקרי, כמובן, אבל היא טובה בשביל הדבר הבא שאני רוצה לטעון - שגם העתקת מביוס נקבעת באופן יחיד על ידי ערכיה על שלוש נקודות (עם דרישה כלשהי של “שונות זו מזו” עליהן), ושלכל בחירת ערכים שכזו קיימת העתקת מביוס מתאימה. למה שלוש נקודות, אם להעתקת מביוס יש ארבעה ערכים שמגדירים אותה? כי כבר ראינו שאחד מהם הוא “מיותר” - זה התבטא בכך שהמטריצה שמאפיינת את העתקת המביוס היא יחידה רק עד כדי כפל בסקלר.

הטענה המדויקת היא זו: בהינתן שתי שלשות של נקודות, כך שהנקודות בכל שלשה שונות זו מזו, \( z_{1},z_{2},z_{3}\in\mathbb{C}^{*} \) ו-\( w_{1},w_{2},w_{3}\in\mathbb{C}^{*} \) קיימת העתקת מביוס יחידה \( f \) כך ש-\( f\left(z_{i}\right)=w_{i} \) עבור \( 1\le i\le3 \).

בואו קודם כל נוכיח שקיימת העתקה כזו. ראשית, נעשה לעצמנו חיים קלים - אין צורך להוכיח את הטענה בכלל עבור \( w_{1},w_{2},w_{3} \) כלליים, אלא עבור שלושה ערכים קונקרטיים שיהיו נוחים לנו ככל האפשר - נאמר, \( 0,1,\infty \). למה? כי אם נצליח למצוא \( g \) שמקיימת \( g\left(z_{1}\right)=0,g\left(z_{1}\right)=1,g\left(z_{2}\right)=\infty \) , וגם נצליח למצוא \( h \) שמקיימת \( h\left(w_{1}\right)=0,h\left(w_{2}\right)=1,h\left(w_{3}\right)=\infty \) אז אפשר יהיה להגדיר \( f \) שמקיימת \( f\left(z_{i}\right)=w_{i} \) בצורה הבאה: \( f=h^{-1}g \). הוכיחו לעצמכם שזה עובד. הנה לכם תעלול סטנדרטי ונפוץ במתמטיקה.

עכשיו, למצוא העתקה שמעבירה ל-\( 0,1,\infty \) זה יחסית קל כי אין לנו הרבה בחירה. קודם כל, העתקת מביוס פשוטה במיוחד שמעבירה את \( z_{1} \) ל-\( 0 \) היא \( f\left(z\right)=z-z_{1} \); בדומה, העתקת מביוס פשוטה במיוחד שמעבירה את \( z_{3} \) ל-\( \infty \) היא \( f\left(z\right)=\frac{1}{z-z_{3}} \). הכפל של שתיהן עדיין עובד: \( f\left(z\right)=\frac{z-z_{1}}{z-z_{3}} \) היא העתקה שמעבירה את \( z_{1} \) ל-0 ואת \( z_{3} \) ל-\( \infty \). שימו לב כמה קריטי פה ש-\( z_{1} \) ו-\( z_{3} \) יהיו שונים זה מזה, מן הסתם.

כעת, מה קורה כשמציבים \( z_{2} \) ב-\( f \)? מקבלים \( f\left(z_{2}\right)=\frac{z_{2}-z_{1}}{z_{2}-z_{3}} \) וזה לא ממש 1, אבל אפשר לקבל 1 על ידי כפל בהופכי של הביטוי הזה. לכן \( f \) הסופית שמקיימת את התכונה הנדרשת שלנו היא \( f\left(z\right)=\frac{z-z_{1}}{z-z_{3}}\frac{z_{2}-z_{3}}{z_{2}-z_{1}} \). קצת מזכיר את אינטרפולציית לגראנז’ (שמתוארת כאן לקראת הסוף).

טוב ויפה, אבל לא לגמרי נכון. אנחנו רגילים לחשוב על \( z_{1},z_{2},z_{3} \) בתור מספרים “רגילים”, אבל אחד מהם עשוי להיות \( \infty \), ואי אפשר לעשות חשבון עם \( \infty \) אז כל הנוסחאות הנחמדות שלמעלה לא עובדות. למרבה המזל, התיקון הוא פשוט בכל אחד מהמקרים - לוקחים את הגבול המתאים של הנוסחה כשהמשתנה הרלוונטי שואף לאינסוף כדי לקבל נוסחה מתוקנת שעובדת. הנה דוגמה. נניח ש-\( z_{1}=\infty \). אז ניקח את \( \frac{z-z_{1}}{z-z_{3}}\frac{z_{2}-z_{3}}{z_{2}-z_{1}} \) ונחשב את הגבול \( \lim_{z_{1}\to\infty}\frac{z-z_{1}}{z-z_{3}}\frac{z_{2}-z_{3}}{z_{2}-z_{1}} \) כאשר יתר הערכים הם פרמטרים קבועים (כולל \( z \), שהוא בדרך כלל המשתנה שלנו). האופן שבו מחשבים גבולות כאלו הוא עם תעלול סטנדרטי - מחלקים מונה ומכנה ב-\( z_{1} \), מצמצמים מה שאפשר ומחליפים את כל הקבועים-חלקי-\( z_{1} \) ב-0. במקרה שלנו נקבל \( \frac{z/z_{1}-1}{z-z_{3}}\frac{z_{2}-z_{3}}{z_{2}/z_{1}-1} \) ואחרי השאפה לאינסוף: \( f\left(z\right)=\frac{-1}{z-z_{3}}\frac{z_{2}-z_{3}}{-1}=\frac{z_{2}-z_{3}}{z-z_{3}} \). קל לבדוק שהפונקציה הזו עושה בדיוק את מה שאנחנו רוצים. בדרך דומה מטפלים במקרים שבהם \( z_{2} \) או \( z_{3} \) הם \( \infty \).

עכשיו, איך מוכיחים יחידות, כלומר שקיימת רק העתקת מביוס אחת שמעתיקה את \( z_{1},z_{2},z_{3} \) ל-\( w_{1},w_{2},w_{3} \)? כמקודם, מנסים לפשוט את העניין להדגמה של יחידות של העתקה מאוד ספציפית - במקרה שלנו, זו שמעבירה את \( 0,1,\infty \) לעצמן. כדי לראות שההעתקה הזו היא יחידה, בואו נשים לב ראשית לכך ש-\( f\left(\infty\right)=\infty \) ולכן בהכרח \( f \) היא מהצורה \( f\left(z\right)=az+b \) (כלומר, \( f \) היא מהצורה \( \frac{az+b}{cz+1} \) כך ש-\( c=0 \), כי אם \( c\ne0 \) הערך של ההעתקה ב-\( \infty \) היה, כזכור, \( \frac{a}{c} \)). כעת, \( f\left(0\right)=0 \) ולכן \( b=0 \), ו-\( f\left(1\right)=1 \) ולכן \( a=1 \) - ההעתקה היא פשוט \( f\left(z\right)=z \) ואין לנו שום חופש בחירה.

איך זה עוזר לנו באופן כללי? בואו ניקח \( g,h \) ששתיהן מקיימות \( g\left(z_{i}\right)=w_{i} \) ו-\( h\left(z_{i}\right)=w_{i} \), וניקח העתקה חדשה \( k \) כך ש-\( k\left(z_{1}\right)=0,k\left(z_{2}\right)=1,k\left(z_{3}\right)=\infty \). עכשיו נרצה לבנות בעזרתן העתקה שמעבירה את 0 ל-0, את 1 ל-1 ואת \( \infty \) ל-\( \infty \). איך? ובכן, למשל, את 0 נעביר ל-\( z_{1} \), את \( z_{1} \) נעביר ל-\( g\left(z_{1}\right) \) כלומר אל \( w_{1} \), ואז נחזיר אותו ל-\( z_{1} \) עם \( h^{-1} \), ואז נחזיר אותו ל-0 עם \( k^{-1} \). פשוט! במילים אחרות, אנחנו בונים את \( f\left(z\right)=k^{-1}\left(h^{-1}\left(g\left(k\left(z\right)\right)\right)\right) \). עכשיו בואו נחשוב על כל הסיפור הזה במונחים של הרכבת פונקציות: קיבלנו שפונקציית הזהות שווה ל-\( k^{-1}h^{-1}gk \), ולכן אחרי העברת אגפים נקבל \( hk=gk \). כשמדובר על פונקציות הפיכות, אפשר “לצמצם” אותן מאגפי המשוואה, ונקבל \( h=g \), כנדרש.

לסיום אני רוצה לציין, בלי להוכיח, עוד תכונה אחת של העתקות מביוס, שמסייעת להבין מה הן עושות, גיאומטרית: הן מעבירות מעגלים (מוכללים, כלומר מעגלים ב-\( \mathbb{C}^{*} \) - ולכן אני מדבר כאן גם על ישרים) למעגלים. מכיוון שהרכבה של שתי פונקציות שמעבירות מעגלים למעגלים גם כן מעבירה מעגלים למעגלים, ומכיוון שראינו שכל העתקת מביוס היא הרכבה של הזזות, ניפוחים והיפוכים, מספיק להראות שהזזות משמרות מעגלים - אבל זה די ברור, לא? - ושניפוחים משמרים מעגלים - אבל זה די ברור, לא? - ושההיפוך \( f\left(z\right)=\frac{1}{z} \) משמר מעגלים, שזה קצת פחות ברור אם לא מדובר על מעגלים נחמדים סביב הראשית. מכיוון שכאן ההוכחה היא קצת טכנית - פשוט לוקחים משוואת מעגל עבור משתנה \( z \), מסיקים ממנה משוואה עבור \( \frac{1}{z} \), מזיזים קצת דברים מצד לצד ואז אומרים “היי, תראו! קיבלנו שוב משוואת מעגל!” אני אוותר עליה כאן.

שימו לב רק לדואליות הנחמדה שממחישה יפה למה היה כדאי לעבור לדבר על \( \mathbb{C}^{*} \) ועל מעגלים מוכללים: ההיפוך \( \frac{1}{z} \) מעביר כל מעגל שעובר דרך 0 - קואורדינטה תמימה לכאורה - לישר, דהיינו למעגל שעובר דרך \( \infty \); ובאופן דואלי הוא מעביר כל מעגל מוכלל שעובר דרך \( \infty \) למעגל שעובר דרך 0. ומה קורה למעגל מוכלל שעובר גם דרך 0 וגם דרך \( \infty \)? ובכן, אני ממליץ לכם לא להתעצל, לחשב ולראות בעצמכם.