אוטומטים אי דטרמיניסטיים ושאר מריעין בישין

בפוסט הקודם הצגתי את המושג של אוטומט סופי דטרמיניסטי והגדרתי אותו בצורה פורמלית. בשביל מתמטיקאים, הגדרה פורמלית היא סדין אדום. מייד מתעוררות שאלות - למה להגדיר כך ולא אחרת? האם כל ההנחות שהשתמשנו בהן נחוצות? מה קורה אם משנים קצת את כללי המשחק? אם מקלים על הנחות מסויימות? וכן הלאה. ובכן, בואו ננסה לחשוב על ההנחות שלנו ועל אילו מהן אפשר לוותר.

הנחה אחת הייתה שאני מראש מדבר רק על פתרון בעיות “כן/לא”. לא ניגע בה, למרות שאפשר. הנחה אחרת הייתה שהגודל של קלטים ופלטים הוא סופי. גם בה לא ניגע, למרות שאפשר. ההנחות הללו משנות לנו את סוג הבעיות שאנחנו רוצים לעסוק בהן, ולכן שינוי שלהן יעביר אותנו לדיבור על דברים שאינם קשורים ישירות לנושא של שפות רגולריות.

הנחה אחרת הייתה הנחת הסופיות של האוטומט - קבוצת המצבים שלו יכולה להיות גדולה, אבל היא חייבת להיות סופית. זו הנחה שהיא בבירור הכרחית - זה תרגיל נחמד להוכיח שאם אנחנו מרשים לקבוצת המצבים להיות אינסופית, אז ה”אוטומט” המתקבל יכול לקבל כל שפה שהיא. אבל אי אפשר לממש אותו בפועל או אפילו לתת לו תיאור מפורש סופי (למשל, אלגוריתם שמחשב את הפונקציה \( \delta\left(q,\sigma\right) \) של האוטומט), אז מה הטעם.

עוד הנחה הייתה שהאוטומט קורא את הקלט שלו רק בכיוון אחד - כלומר, אנחנו הולכים על הקלט משמאל לימין, וברגע שקראנו אות מהקלט היא אבודה לנצח ולא נוכל לחזור אליה. זו הנחה מאוד כבדה ולא טריוויאלית ונראה שיהיה קשה מאוד להצדיק אותה. אני הולך להצדיק אותה בעתיד על ידי האבחנה שמודל שבו אפשר לעשות את זה הוא שקול בכוחו החישובי למודל הפשוט שלנו, אבל זה ידרוש עוד כלי מרכזי (משפט נרוד) שטרם הצגתי, ולכן לא ניגע בהנחה הזו כרגע.

אבל היו שתי הנחות שהרבה פחות קל להצדיק ואנחנו הולכים להעיף אותן לכל הרוחות הפעם: ראשית, שהאוטומט פועל בצורה מוזרה שבה הוא קורא אות אחת מהקלט בכל צעד חישוב שלו. למה שלא נאפשר לו לעשות צעדי חישוב “על ריק”? ובכן, אנחנו הולכים להרשות לו. אבל עצרו רגע ותחשבו על זה - תראו שאם זה כל מה שאנחנו משנים במודל שלנו, לא הרווחנו כמעט שום דבר - המודל החדש שנקבל יהיה אפילו יותר מסורבל מהמודל הנוכחי, כי צעד חישוב “על ריק” כזה בעצם לא עושה כלום. אתם תתחילו להגיד לעצמכם “נו, אם אתה רוצה לעבור אל \( p \) על ריק, למה לא הלכת לשם מלכתחילה?”. אז בפני עצמה ההנחה שאנחנו קוראים אות בכל צעד חישוב היא סבירה. אלא אם האוטומט יהיה מסוגל לבחור בין קריאת אות קלט ובין ביצוע צעד חישוב על ריק.

אלא שכרגע המודל שלנו הוא דטרמיניסטי, מה שאומר שיש לו פונקציית מעברים. בואו ניזכר מה זה אומר, פונקציה: פונקציה \( f:A\to B \) מתאימה לכל איבר ב-\( A \) איבר אחד ויחיד ב-\( B \). זה אומר שאין לנו “בחירה” בין שני פלטים אפשריים של הפונקציה בהינתן קלט מסויים, וגם אין לנו את האפשרות להגיד “לא רוצים להוציא פלט, מה תעשו לנו”. באוטומט, ה-\( A \) של פונקציית המעברים הוא אוסף כל הזוגות של מצב ואות קלט, ואילו \( B \) הוא המצבים. מה שאנחנו רוצים לעשות הוא לזרוק לפח את הדרישה שפונקציית המעברים \( \delta:Q\times\Sigma\to\Sigma \) היא פונקציה - כלומר, בהינתן הזוג של המצב הנוכחי ואות הקלט הנוכחית, אנחנו רוצים להרשות לאוטומט כמה אפשרויות בחירה - כמה מצבים שונים שהוא יכול לעבור אליהם. או אפילו להרשות לו לא לעבור לשום מצב בכלל אלא “להיתקע”, מה שיסיים את החישוב מייד בלי לקבל את מילת הקלט. אוטומט כזה נקרא אי דטרמיניסטי (שימו לב שאני עדיין לא מרשה מעברים “על ריק”; אל זה נגיע אחר כך).

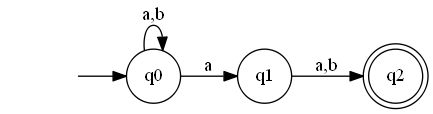
כשמציירים את האוטומט בתור גרף, קל להדגים אי דטרמיניזם - בסך הכל מדובר על מצבים שמהם לא יוצא חץ עבור אות מסויימת, או שיוצא יותר מחץ אחד עבור אות מסויימת:

אבל איך מתארים אוטומט כזה בצורה פורמלית? דרך אחת היא להגיד שאין לנו יותר פונקציית מעברים אלא יחס מעברים - אוסף של שלשות מהצורה \( \left(q,\sigma,p\right) \) שבא לומר שהאוטומט יכול, אם הוא במצב \( q \) וקורא \( \sigma \), לעבור למצב \( p \) (מבחינה פורמלית פונקציה היא פשוט מקרה פרטי של יחס, עם דרישות נוספות שמבטיחות שלכל קלט יהיה פלט אחד ויחיד). עם זאת, אני מעדיף דווקא לנקוט בגישה השניה, שאומרת שעדיין יכולה להיות לנו פונקציית מעברים, אם רק נשנה את הטווח שלה. דרך הפתרון שאני מציג כאן היא די סטנדרטית כאשר רוצים להגדיר פונקציות “רב ערכיות” בצורה פורמלית.

מה שאני אומר הוא שהפונקציה שלי, לכל קלט של \( \left(q,\sigma\right) \), תחזיר קבוצה - את קבוצת המצבים שאפשר לעבור אליהם כשהאוטומט במצב \( q \) וקורא \( \sigma \). הקבוצה הזו יכולה להכיל איבר בודד (קבוצה כזו נקראת “סינגלטון”) כמו שקורה באוטומט דטרמיניסטי; יכולה להיות ריקה; ויכולה להכיל שניים או יותר מצבים. כך שההגדרה הזו תופסת בו זמנית את הרעיון של “היתקעות” ושל “בחירה בין אפשרויות” מבלי להשליך לפח את האפשרות של דטרמיניזם. כלומר, הרחבנו את המודל של אוטומט סופי דטרמיניסטי; עם קצת שינויים סינטקטיים, אפשר לחשוב על כל אוטומט דטרמיניסטי כמקרה פרטי של אוטומט אי דטרמיניסטי. פורמלית כותבים את פונקציית המעברים כך: \( \delta:Q\times\Sigma\to2^{Q} \) (הסימון \( 2^{Q} \) פירושו “כל-תתי הקבוצות של \( Q \)”; קרוב לודאי שהוא נראה מוזר ושרירותי עבור מי שלא מכיר את תורת הקבוצות, אבל סמכו עלי שיש בו הגיון יפה).

התיאור הפורמלי של האוטומט שבציור, אם כן, הוא זה: \( Q=\left\{ q_{0},q_{1},q_{2}\right\} \) ו-\( F=\left\{ q_{2}\right\} \) ופונקציית המעברים הבאה:

\( \delta\left(q_{0},a\right)=\left\{ q_{0},q_{1}\right\} ,\delta\left(q_{0},b\right)=\left\{ q_{0}\right\} \)

\( \delta\left(q_{1},\sigma\right)=\left\{ q_{2}\right\} \)

\( \delta\left(q_{2},\sigma\right)=\emptyset \)

מה שעדיין חסר לי הוא הסבר של מה זה אומר שאוטומט אי דטרמיניסטי כזה רץ על מילה, ומתי הוא מקבל אותה. המושג של ריצה נותר זהה - ריצה של אוטומט על מילה \( w \) היא סדרה של מצבים שכל אחד מהם מתקבל מקודמו על ידי פונקציית המעברים, בהתאם לקלט שהאוטומט קורא. אם קודם אמרנו ש-\( p \) נובע מ-\( q \) כאשר האוטומט קורא \( \sigma \) אם התקיים \( \delta\left(q,\sigma\right)=p \), עכשיו אנחנו אומרים את זה אם מתקיים \( p\in\delta\left(q,\sigma\right) \), כלומר אם \( p \) הוא אחד המצבים שהאוטומט עשוי לעבור אליהם.

זה אומר שלאוטומט אי דטרמיניסטי יכולות להיות הרבה ריצות שונות על אותה מילת קלט. חלק מהריצות הללו עשויות להסתיים במצב מקבל וחלק לא - כלומר, האוטומט לכאורה “מקבל ודוחה בו זמנית” את המילה. מכאן שכשאנחנו באים לענות על השאלה האם \( w\in L\left(A\right) \), אנחנו בעצם שואלים שאלה על מה קורה בכל הריצות של \( A \) על \( w \). תשובה סבירה אחת היא שנאמר ש-\( A \) מקבלת את \( w \) רק אם כל ריצה של \( A \) על \( w \) מסתיימת בקבלה, אבל אז נקבל מודל חדש שלא נוח לעבוד איתו (כי מה עוזר לנו שיש הרבה מסלולי חישוב אפשריים אם אנחנו צריכים לעבוד כדי להבטיח שבכולם האוטומט יקבל את המילים הנכונות?). לכן אנחנו מעדיפים את ההגדרה השניה: \( w\in L\left(A\right) \) אם קיים מסלול חישוב כלשהו של \( A \) על \( w \) שהוא מקבל. אפילו אם יש מיליארד מסלולי חישוב דוחים, ורק אחד שמקבל - המילה עדיין תהיה בשפה של האוטומט.

בואו נסתכל לרגע באוטומט שציירתי למעלה. מה הוא מקבל? אפשר לראות שבהתחלה הוא יכול לקרוא אותיות באופן חופשי ולהישאר במצב ההתחלתי, וכך זה יכול להימשך לנצח בעיקרון (ואז האוטומט לא יגיע למצב מקבל אף פעם). אלא שהוא יכול גם לעבור ל-\( q_{1} \) אחרי קריאה של \( a \). אם הוא יעשה את זה, בצעד הבא הוא יעבור ל-\( q_{2} \), ואז הוא “ייתקע” כי אין לו לאן ללכת. אז מתי הוא יקבל? רק אם שני צעדי החישוב האחרונים שלו (המעבר ל-\( q_{1} \) ואחריו המעבר ל-\( q_{2} \)) הם בדיוק הצעדים שבהם קוראים את שתי האותיות האחרונות במילה. צעד החישוב האחרון מתבצע תמיד, בלי תלות בשאלה מה האות האחרונה במילה, אבל הצעד שלפניו יכול להתבצע רק אם האות היא \( a \). המסקנה: האוטומט מקבל בדיוק את המילים שבהן \( a \) היא האות הלפני-אחרונה.

העניין הזה, ש-\( A \) מקבל מילה אם ורק אם קיים ל-\( A \) מסלול חישוב מקבל על המילה, יכול להיות מבלבל למדי. זה הופך את \( A \) למשהו לא מציאותי; כדי לדעת אם הוא מקבל מילה, אי אפשר סתם “להריץ אותו ולראות מה קורה”, כי אם ההרצה תסתיים בדחייה של המילה, זה עדיין לא אומר שהאוטומט לא מקבל את המילה - אולי יש מסלול חישוב אחר שבו הוא כן יקבל אותה. דרך נחמדה לתת אינטואיציה היא לחשוב על \( A \) כאילו הוא מצויד ב”מטבע קסם” - בכל פעם שבה הוא צריך לבצע בחירה אי דטרמיניסטית בין כמה אפשרויות הוא מטיל את המטבע, והמטבע יגריל את האפשרות “הטובה ביותר” במובן זה שאם יש ל-\( A \) מסלול חישוב מקבל כלשהו על המילה, מטבע הקסם יוודא ש-\( A \) ילך במסלול החישוב הזה (או, אם יש כמה, באחד מהם).

זה קצת מזכיר חישוב הסתברותי, אבל זה לא - אנחנו לא דורשים ש-\( A \) תקבל בהסתברות גבוהה או משהו דומה; אין לנו חישובי הסתברויות בכלל. ייתכן שזה גם מזכיר חישוב קוונטי - כאילו \( A \) נמצאת בסופרפוזיציה של הרבה ריצות אפשריות - אבל אם עקבתם אחרי סדרת הפוסטים שלי על חישוב קוונטי (או, יותר סביר, סתם מכירים חישוב קוונטי וכנראה יותר טוב ממני) אתם יודעים שחישוב קוונטי לא ממש עובד ככה ושאנחנו מתעלמים מההיבטים המורכבים שלו (איך לגלות את התוצאה, למשל). אז אני מעדיף לא ללכת יותר מדי לכיוון של אינטואיציות ולקוות שההגדרה המדויקת מספיק טובה כדי להבין מה הולך פה.

פורמלית, אנחנו רוצים להגדיר הרחבה של \( \delta \), \( \hat{\delta}:Q\times\Sigma^{*}\to2^{Q} \), באופן דומה לאיך שעשינו את זה עם אוטומט דטרמיניסטי - באינדוקציה. אז נגדיר \( \hat{\delta}\left(q,\varepsilon\right)=\left\{ q\right\} \) ו-\( \hat{\delta}\left(q,w\sigma\right)=\bigcup_{p\in\hat{\delta}\left(q,w\right)}\delta\left(p,\sigma\right) \). במילים - קבוצת המצבים שאליהם ניתן להגיע מ-\( q \) על ידי קריאת \( w\sigma \) היא קבוצת המצבים שאליהם ניתן להגיע על ידי קריאת \( \sigma \) מתוך אחד מהמצבים שאליהם ניתן להגיע מ-\( q \) על ידי קריאת \( w \). מכיוון ש-\( \hat{\delta} \) מקבלת מצב יחיד ופולטת קבוצה של מצבים כבר אי אפשר להרכיב אותה על עצמה ובשל כך יש את האיחוד הזה בחוץ. אפשר גם להתחכם מבחינת הסימון ולהגדיר \( \hat{\delta}:2^{Q}\times\Sigma^{*}\to2^{Q} \) באופן הבא: \( \hat{\delta}\left(\left\{ q\right\} ,w\right) \) יהיה שווה ל-\( \hat{\delta}\left(q,w\right) \) שכבר הגדרנו, ועבור קבוצות \( P\subseteq Q \) כלליות נגדיר \( \hat{\delta}\left(P,w\right)=\bigcup_{p\in P}\hat{\delta}\left(p,w\right) \) (כאן הכתיב של \( \hat{\delta}\left(p,w\right) \) הוא בעצם דרך מקוצרת לכתוב \( \hat{\delta}\left(\left\{ p\right\} ,w\right) \) - ל”רמאות” כזו יש אפילו שם מקובל - Abuse of Notation. עכשיו אפשר לכתוב \( \hat{\delta}\left(q,w\sigma\right)=\hat{\delta}\left(\hat{\delta}\left(q,w\right),\sigma\right) \) מבלי שתהיה עם זה בעיה.

עכשיו מתעוררות שתי שאלות, שקשורות אחת לשניה בקשר הדוק. הראשונה - נניח שנותנים לנו אוטומט אי דטרמיניסטי \( A \) ומילה \( w \) ושואלים אותנו אם \( w\in L\left(A\right) \) - מה אנחנו עושים? אנחנו כבר יודעים שאי אפשר סתם להריץ את \( A \) על \( w \) ולבחור שרירותית בחירות אי דטרמיניסטיות כי אם הריצה לא תסתיים בקבלה זה לא אומר לנו עדיין כלום. השאלה השניה - האם המודל האי דטרמיניסטי שקול בכוחו למודל הדטרמיניסטי? דהיינו, האם בהינתן \( A \) אי דטרמיניסטי קיים אוטומט \( A^{\prime} \) דטרמיניסטי כך ש-\( L\left(A\right)=L\left(A^{\prime}\right) \)?

השאלה הראשונה בעצם מבקשת מאיתנו למצוא אלגוריתם כלשהו להכרעת שאלת השייכות של מילה לשפה של אוטומט אי דטרמיניסטי; השאלה השניה מבקשת את אותו דבר בדיוק אבל תוך הדרישה הנוספת שכמות הזכרון שהאלגוריתם הזה צריך תהיה חסומה. כמו כן, תשובה לשאלה הראשונה אפשר לתת בנפנוף ידיים, אבל תשובה לשאלה השניה אתן על ידי בניה מפורשת ומדויקת.

פתרון כוח גס לשאלה הראשונה זה קל. בהינתן מילה \( w \) מאורך \( m \), יש רק מספר סופי של מסלולי חישוב אפשריים של \( A \) על \( w \). הנה חסם טיפשי: אם דרגת היציאה המקסימלית של צומת ב-\( A \) היא \( k \), אז יש לכל היותר \( k^{m} \) מסלולי חישוב אפשריים (למה?) אז אפשר לעבור על כולם. אבל סיבוכיות הזכרון של האלגוריתם הזה ככל הנראה תהיה גבוהה, כי צריך לזכור איכשהו באילו מסלולים כבר עברנו. זה לא אלגוריתם שנוח לממש בפועל במחשב. ודאי יש דרך קלה יותר. עצרו רגע וחשבו מהי.

ועכשיו, במקום לגלות לכם את הפתרון, אני הולך לעצור לרגע ולפתור בעיה שהיא לכאורה שונה לגמרי, אבל כמובן שתתקשר למה שאנחנו רוצים לעשות. הבעיה היא זו: נתונות לנו שתי שפות רגולריות \( L_{1},L_{2} \); אנחנו רוצים להוכיח שגם החיתוך שלהן, \( L_{1}\cap L_{2} \), שפת כל המילים שנמצאות גם ב-\( L_{1} \) וגם ב-\( L_{2} \) - היא שפה רגולרית. כלומר, אם \( A_{1}=\left(\Sigma,Q_{1},q_{0}^{1},\delta_{1},F_{1}\right) \) ו-\( A_{2}=\left(\Sigma,Q_{2},q_{0}^{2},\delta_{2},F_{2}\right) \) הם אוטומטים עבור השפות, אנחנו רוצים לבנות מהם אוטומט \( A=\left(\Sigma,Q,q_{0},\delta,F\right) \) כך ש-\( L\left(A\right)=L_{1}\cap L_{2} \).

אלגוריתם נאיבי שעושה דבר כזה יפעל כך: בהינתן \( w \), קודם כל יריץ את \( A_{1} \) על \( w \), ואם \( A_{1} \) קיבלה, יריץ את \( A_{2} \) על \( w \) ויענה כמוה. הבעיה היא שאנחנו רוצים לבנות אוטומט עבור שפת החיתוך, ואוטומט לא יכול לבצע שתי הרצות בזו-אחר-זו של אותה מילה, בגלל הגישה המוגבלת שיש לו למילה - הוא יכול לקרוא אותה רק פעם אחת. לכן הפתרון הוא שהאוטומט יבצע סימולציה של \( A_{1},A_{2} \) בו זמנית. בכל רגע נתון, המצב של האוטומט שלנו יהיה זוג \( \left(p,q\right) \) שאומר “הסימולציה של \( A_{1} \) נמצאת כרגע במצב \( p \) והסימולציה של \( A_{2} \) נמצאת כרגע במצב \( q \)”. כל אות שאנחנו קוראים מהקלט תגרום לנו לקדם את שני המצבים בזוג בו זמנית, בהתאם למעברים באוטומטים שלהם.

פורמלית, ההגדרה של \( A \) היא זו: \( Q=Q_{1}\times Q_{2} \), \( F=F_{1}\times F_{2} \) (כי מצב מקבל הוא זוג \( \left(p,q\right) \) שבו שני המצבים הם מקבלים, כל אחד באוטומט שלו), \( q_{0}=\left(q_{0}^{1},q_{0}^{2}\right) \), ופונקציית המעברים מוגדרת לכל \( p\in Q_{1},q\in Q_{2},\sigma\in\Sigma \) באופן הבא: \( \delta\left(\left(p,q\right),\sigma\right)=\left(\delta_{1}\left(p,\sigma\right),\delta_{2}\left(q,\sigma\right)\right) \). לא קשה להוכיח באינדוקציה שהבניה הזו אכן עובדת ו-\( A \) מקבל את שפת החיתוך. האוטומט הזה נקרא אוטומט מכפלה כי קבוצת המצבים שלו היא מכפלה של קבוצות המצבים של האוטומטים שאנחנו מסמלצים.

נחזור כעת אל סילוק האי-דטרמיניזם שלנו. כאן אנחנו רוצים לעשות משהו דומה - לבצע סימולציה של כמה חישובים במקביל. כל החישובים הולכים להתבצע על אותו אוטומט, ולכן נשאלת השאלה - מה מבדיל חישובים שונים זה מזה? ובכן, כמובן, הבחירות האי דטרמיניסטיות שבוצעו במהלך החישוב, שאומרות שה”היסטוריה” של החישוב - כל המצבים שהיינו בהם עד כה, עד וכולל המצב הנוכחי - תהיה שונה בין חישובים שונים. וכאן מגיע הפאנץ’: לא אכפת לנו מההיסטוריה. הדבר היחיד שמעניין אותנו בחישוב כלשהו הוא איפה אנחנו נמצאים כרגע. שני חישובים אי דטרמיניסטיים שונים, שאחרי קריאת כך-וכך אותיות הגיעו שניהם לאותו מצב, הם מבחינתנו מרגע זה והלאה אותו דבר בדיוק - זה שהם הגיעו לאותו מצב בשתי דרכים שונות לא משפיע בשום צורה על מה שיקרה מכאן והלאה. למי מכם שמכיר שרשראות מרקוב, זו בדיוק תכונת “חוסר הזכרון” של שרשראות מרקוב.

אם \( \left|Q\right|=n \), המשמעות היא שאנחנו צריכים בכל עת לתחזק עד \( n \) “ריצות במקביל” של האוטומט. בפועל מה שנעשה יהיה פשוט יותר - הסימולציה שלנו תתבצע על ידי כך שנזכור בכל שלב את קבוצת המצבים שבהם האוטומט שאנחנו מסמלצים נמצא בלפחות אחד ממסלולי החישוב שלו. אלגוריתמית, אפשר לחשוב על זה בתור מערך באורך \( n \) של ערכים בוליאניים (“כן/לא”) שאנחנו מעדכנים בכל צעד. זה כל הזכרון שנזדקק לו, ומכיוון שהוא לא תלוי בגודל מילת הקלט \( w \) זהו זכרון חסום. כאשר נבנה אוטומט דטרמיניסטי עבור האלגוריתם הזה, האוטומט יכיל מצב אחד לכל סדרת ערכים אפשרית של המערך - דהיינו, יהיו לו \( 2^{n} \) מצבים. זה מספר קבוע וסופי, אבל הוא אקספוננציאלי במספר המצבים של האוטומט שאנחנו מסמלצים. מסתבר שזה בלתי נמנע - לכל \( n \) טבעי אפשר למצוא שפה שיש אוטומט אי-דטרמיניסטי עם \( O\left(n\right) \) מצבים עבורה, אבל כל אוטומט סופי דטרמיניסטי עבורה יהיה עם \( \Omega\left(2^{n}\right) \) מצבים. השפות הללו הן הכללה של השפה שנתתי בתור דוגמה - עבור \( n \), זו תהיה השפה של כל המילים הבינאריות שיש בהן 1 בדיוק \( n \) צעדים מהסוף. כמובן, עוד לא הסברתי איך מוכיחים שכל אוטומט סופי דטרמיניסטי עבור השפה יהיה בעל לפחות כך-וכך מצבים; זה משהו שיינתן לנו על ידי משפט נרוד שכבר הזכרתי בפוסט.

נעבור לבניה הפורמלית. נניח ש-\( A_{ND}=\left(\Sigma,Q_{ND},q_{0}^{ND},\delta_{ND},F_{ND}\right) \) הוא אוטומט אי דטרמיניסטי כלשהו, אז נבנה אוטומט דטרמיניסטי \( A_{D}=\left(\Sigma,Q_{D},q_{0}^{D},\delta_{D},F_{D}\right) \) כך ש-\( L\left(A_{ND}\right)=L\left(A_{D}\right) \).

הבסיס של הבניה הוא זה: \( Q_{D}=2^{Q_{ND}} \). כלומר, כל מצב של האוטומט הדטרמיניסטי הוא, מבחינה פורמלית, קבוצה - קבוצה של מצבים מתוך \( Q_{ND} \). זה די מבלבל, כי התרגלנו אולי לחשוב על מצבים של אוטומט בתור מין “אטומים” - אובייקטים שאנחנו מסמנים ב-\( q_{t} \) ואין להם מבנה מתמטי מורכב יותר. אבל מבחינה פורמלית, זה לא הכרחי; כל מה שאנחנו דורשים על אוטומט הוא שקבוצת המצבים שלו תהיה קבוצה סופית כלשהי, והאיברים של אותה קבוצה יכולים להיות כל דבר - מספרים טבעיים, מחרוזות, סימבולים, או אפילו קבוצות. בבניה הנוכחית, נוח לנו שהאיברים הללו יהיו קבוצות. מכאן מגיע שם הבניה: האוטומט \( A_{D} \) שבנינו נקרא אוטומט חזקה, כי קבוצת המצבים שלו היא קבוצת החזקה של קבוצת המצבים של האוטומט \( A_{ND} \).

כעת, \( q_{0}^{D}=\left\{ q_{0}^{ND}\right\} \). כלומר, המצב ההתחלתי של האוטומט הדטרמיניסטי הוא קבוצה (הרי אמרנו שכל מצב של האוטומט הוא קבוצה…) שהאיבר היחיד שלה הוא המצב ההתחלתי של האוטומט האי-דטרמיניסטי. כלומר, הסימולציה שלנו מתחילה עם חישוב יחיד, שמתחיל ב-\( q_{0}^{ND} \). למעשה, אפשר היה להרחיב עוד קצת את המודל האי-דטרמיניסטי ולהרשות כמה מצבים התחלתיים שונים, ואז הסימולציה הייתה מתחילה עם קבוצת כל המצבים הללו וזה היה כל ההבדל.

כמו כן, \( F_{D}=\left\{ P\subseteq Q_{ND}\ |\ P\cap F_{ND}\ne\emptyset\right\} \), כלומר המצבים המקבלים שלנו הם אלו שבהם לפחות אחת מהסימולציות נמצאת באותו הרגע במצב מקבל.

נשאר רק לתאר את פונקציית המעברים, לכל \( P\in Q_{D} \) ו-\( \sigma\in\Sigma \): \( \delta_{D}\left(P,\sigma\right)=\hat{\delta}_{ND}\left(P,\sigma\right) \). דהיינו, האוטומט הדטרמיניסטי הולך מהמצב \( P \) שלנו על ידי קריאת \( \sigma \) אל קבוצת כל המצבים באוטומט האי דטרמיניסטי שניתן להגיע אליהם בצעד אחד ממצב כלשהו ב-\( P \) על ידי קריאת \( \sigma \). מתבקש. קל להוכיח שמתקיים \( \hat{\delta}_{D}\left(P,w\right)=\hat{\delta}_{ND}\left(P,w\right) \) לכל מילה \( w \) ומכאן הוכחת השקילות של שני האוטומטים כבר נובעת מאליה.

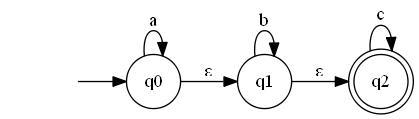
זה מסיים את הטיפול במודל האי דטרמיניסטי, אבל עדיין לא סיימנו - אני עדיין צריך לטפל בהקלה השניה על כללי המשחק ולהסתכל על המודל שבו אפשר לבצע מעבר בין מצבים בלי לקרוא אות. למעבר כזה אני אקרא “מעבר-\( \varepsilon \)”. ונתחיל בדוגמא לאוטומט שמשתמש במעברים כאלו:

האוטומט הזה מקבל את כל המילים שבנויות מרצף של 0 או יותר \( a \)-ים, אחריו רצף של 0 או יותר \( b \)-ים ואחריו רצף של 0 או יותר \( c \)-ים. בהמשך נראה איך ייראה אוטומט בלי מעברי-\( \varepsilon \) שעושה את זה ועד כמה מעברי ה-\( \varepsilon \) מפשטים את דרך ההצגה שלנו, אבל בינתיים אני ממליץ לכם לנסות ולבנות אוטומט כזה (אי דטרמיניסטי!) בעצמכם ולראות כמה אתם מסתבכים כדי שתוכלו להעריך את הפשטות היחסית של האוטומט הזה. מה שהוא עושה הוא זה: כל עוד יש \( a \)-ים לקרוא, קורא אותם. אחר כך קופץ למצב הבא על ידי מעבר \( \varepsilon \), קורא שם \( b \)-ים כל עוד יש, ואז קופץ למצב האחרון וקורא שם \( c \)-ים כל עוד יש, עד (בתקווה) סוף המילה. כמובן, שימו לב שאני מייחס לאוטומט מעין חוכמה שאין לו (לדעת מתי ה-\( a \)-ים “נגמרו”) - בפועל מה שקורה הוא שיש לאוטומט המון מסלולי חישוב אפשריים שרובם פשוט “נתקעים” (למשל, אם האות הראשונה במילה היא \( a \) אבל האוטומט בחר לבצע את מסע ה-\( \varepsilon \) אל \( q_{1} \) במקום לקרוא אותה) ואני פשוט מתאר את הריצה המקבלת. שימו לב איך אני נעזר בכך שהאוטומט הוא אי-דטרמיניסטי, ולא “רק” יכול לבצע מסעי-\( \varepsilon \).

אתם כבר יודעים מה סדר הפעולות כשמציעים מודל מורחב שכזה. ראשית, תוהים איך להגדיר אותו פורמלית; שנית, תוהים איך להגדיר פורמלית “ריצה” במודל ומה זה אומר שהמודל “מקבל” מילה; ולבסוף, תוהים איך להוכיח שהוא שקול למודל פשוט יותר.

ובכן, ההגדרה פורמלית זהה לגמרי לזו של אוטומט אי דטרמיניסטי רגיל, פרט להגדרת פונקציית המעברים - \( \delta:Q\times\left(\Sigma\cup\left\{ \varepsilon\right\} \right)\to2^{Q} \). כלומר, “הרחבנו” את הא”ב \( \Sigma \) על ידי הוספת הסימבול \( \varepsilon \) ו-\( \delta\left(q,\varepsilon\right) \) מחזיר את כל המצבים שאליהם ניתן להגיע מ-\( q \) על ידי מסע-\( \varepsilon \) יחיד. לרוע המזל, לסימבול \( \varepsilon \) כבר יש משמעות מאוד קונקרטית עבורנו - המילה הריקה. Hilarity ensues.

כדי להבין את הבעיה, בואו ננסה להגדיר את פונקציית המעברים המורחבת \( \hat{\delta} \), שתתאר מה האוטומט עושה על מילים. כרגיל, מתחילים בלהגדיר אותה על המילה הריקה. עבור אוטומט אי דטרמיניסטי רגיל הגדרנו \( \hat{\delta}\left(q,\varepsilon\right)=\left\{ q\right\} \); אבל מה נגדיר עבור אוטומט עם מסעי-\( \varepsilon \)? ובכן, העובדה שאנחנו משתמשים באותו סימון כדי לתאר מסע-\( \varepsilon \) וגם את המילה הריקה נותנת לנו אינטואיציה חזקה שצריך להגדיר \( \hat{\delta}\left(q,\varepsilon\right)=\delta\left(q,\varepsilon\right) \). אבל זה לגמרי לא נכון! הנקודה הזו מבלבלת אנשים למוות. ממשלות כבר נפלו בגללה. טיסות חלל התרסקו, וקת’ולהו התעורר (אבל כשהוא ניסה להבין את הבעיה הוא גם נרדם שוב). בואו ננסה להבין מה הולך כאן.

כדי לעשות סדר בבלאגן, אני רוצה לשנות לרגע את השם של מסעי-\( \varepsilon \) ולקרוא להם מסעי-\( \spadesuit \). כלומר, אני מגדיר את פונקציית המעברים \( \delta:Q\times\left(\Sigma\cup\left\{ \spadesuit\right\} \right)\to2^{Q} \), ועכשיו אני רוצה להסביר לכם למה השוויון \( \hat{\delta}\left(q,\varepsilon\right)=\delta\left(q,\spadesuit\right) \) הוא לא נכון (קחו שניה כדי לוודא שאתם מבינים למה לא הפכתי את ה-\( \varepsilon \) באגף שמאל ל-\( \spadesuit \)). הסיבה פשוטה: \( \delta\left(q,\spadesuit\right) \) היא קבוצת כל המצבים שאפשר להגיע אליה מ-\( q \) על ידי ביצוע של מסע-\( \spadesuit \) אחד בדיוק בזמן ש-\( \hat{\delta}\left(q,\varepsilon\right) \) היא קבוצת כל המצבים שאפשר להגיע אליהם על ידי ביצוע של 0 או יותר מסעים שלא קוראים אות. באוטומט שבאיור מתקיים ש-\( \delta\left(q_{0},\spadesuit\right)=\left\{ q_{1}\right\} \) אבל \( \hat{\delta}\left(q_{0},\varepsilon\right)=\left\{ q_{0},q_{1},q_{2}\right\} \).

עכשיו, נניח לרגע שפתרנו איכשהו את הבעיה של ההגדרה של \( \hat{\delta} \) עבור \( \varepsilon \). מה יקרה כשננסה להמשיך את ההגדרה האינדוקטיבית, כלומר להגדיר את \( \hat{\delta}\left(q,w\sigma\right) \)? צריך להכניס לתמונה איכשהו את מסעי-\( \varepsilon \). האינטואיציה הראשונה (שלי, לפחות) היא להרשות ל-\( \sigma \) להיות לא רק איבר של \( \Sigma \) אלא גם \( \varepsilon \), המילה הריקה, ולהגדיר באותו האופן בדיוק גם במקרה הזה: \( \hat{\delta}\left(q,w\sigma\right)=\delta\left(\hat{\delta}\left(q,w\right),\sigma\right) \). אבל בואו נציב שניה \( \sigma=\varepsilon \) - אנחנו מקבלים את המשוואה \( \hat{\delta}\left(q,w\right)=\delta\left(\hat{\delta}\left(q,w\right),\varepsilon\right) \) שמגדירה את \( \hat{\delta}\left(q,w\right) \) באמצעות \( \hat{\delta}\left(q,w\right) \) - הגדרה מעגלית. ברור שמשהו כאן לא עובד כל כך טוב וצריך איכשהו לתקן ועדיף מבלי להתייחס אל \( \sigma \) בתור משהו שיכול לייצג גם את \( \varepsilon \). כלומר - צריך להתייחס למעברי-\( \varepsilon \) בצורה שונה מיתר המעברים.

זו הסיבה שבגללה אני לא אוהב את השימוש הכפול בסימבול \( \varepsilon \) כדי לתאר גם את המילה הריקה, וגם את המעברים שאינם קוראים אות. אבל אין מה לעשות - זה הסימון המקובל בספרות ובפרט בספרי הלימוד הרלוונטיים לטעמי (זה של הופקרופט ואולמן; זה של סיפסר; וזה של האוניברסיטה הפתוחה בישראל). לכן גם אני אשתמש בו, אבל בזהירות.

אז איך נגדיר את \( \hat{\delta}\left(q,\varepsilon\right) \)? ובכן, אנחנו צריכים כתיב פורמלי עבור “כל המצבים שישיגים מ-\( q \) על ידי 0 או יותר מסעי-\( \varepsilon \)”. נסמן את הקבוצה הזו ב-\( \mbox{Cl}^{\varepsilon}\left(q\right) \) - סגור-\( \varepsilon \) של \( q \) (Cl הוא קיצור של Closure - סגור, שמבוטא בחולם). לטעמי הדרך הנחמדה ביותר להגדיר את הקבוצה הזו היא בתור הקבוצה הקטנה ביותר של מצבים שמכילה את \( q \) וסגורה ביחס למעברי \( \varepsilon \). פורמלית, \( q\in\mbox{Cl}^{\varepsilon}\left(q\right) \) וכמו כן אם \( p\in\mbox{Cl}^{\varepsilon}\left(q\right) \) ו-\( p^{\prime}\in\delta\left(p,\varepsilon\right) \) אז גם \( p^{\prime}\in\mbox{Cl}^{\varepsilon}\left(q\right) \).

כעת נגדיר:

\( \hat{\delta}\left(q,\varepsilon\right)=\mbox{Cl}^{\varepsilon}\left(q\right) \)

\( \hat{\delta}\left(q,w\sigma\right)=\mbox{Cl}^{\varepsilon}\left(\delta\left(\hat{\delta}\left(q,w\right),\sigma\right)\right) \)

גם כאן אני מניח באופן מובלע ש-\( \delta \) מוגדרת על קבוצות של מצבים ולא רק על מצבים בודדים.

מה שההגדרה שלי בעצם אומרת היא זו: ראשית, כל עוד לא קראתם אף אות, המצבים שישיגים מ-\( q \) הם בדיוק אלו שניתן להגיע אליהם על ידי 0 או יותר מסעי-\( \varepsilon \) מ-\( q \). כעת, המצבים שישיגים מ-\( q \) על ידי קריאת \( w\sigma \) (כאשר \( \sigma\in\Sigma \)) הם בדיוק המצבים שניתן להגיע אליהם מאחד המצבים ב-\( \hat{\delta}\left(q,w\right) \) על ידי כך שקודם כל מבצעים מסע תוך קריאת \( \sigma \) ולאחר מכן מבצעים כמה מסעי-\( \varepsilon \) שרוצים.

זה מסיים את שלב ההגדרות - וקצת מדכא לראות כמה מתוסבכת ההגדרה של רעיון יחסית פשוט כמו מסעי-\( \varepsilon \). נשאר להוכיח שאוטומט אי דטרמיניסטי עם מסעי-\( \varepsilon \) שקול לאוטומט אי דטרמיניסטי בלי מסעים כאלו - להראות איך אפשר “לסלק” מסעי \( \varepsilon \). מספיק לעבור למודל אי דטרמיניסטי בלי מסעי-\( \varepsilon \) כדי להוכיח שקילות למודל הדטרמיניסטי הרגיל, כי כבר ראינו שהמודל האי-דטרמיניסטי שקול למודל הדטרמיניסטי. בסילוק אי-דטרמיניזם ניפחנו אקספוננציאלית את מספר המצבים; בסילוק מסעי-\( \varepsilon \) מספר המצבים כלל לא ישתנה, רק נוסיף עוד קשתות לגרף של האוטומט.

הרעיון הוא פשוט: אנחנו רוצים להגדיר את \( \delta\left(q,\sigma\right) \) עבור האוטומט בלי מסעי-\( \varepsilon \), בצורה ש”תסמלץ” את מה שהאוטומט עם מסעי ה-\( \varepsilon \) יכול לעשות. זה אומר ש-\( \delta\left(q,\sigma\right) \) תכלול את כל המצבים שאפשר להגיע אליהם מ-\( q \) באופן הבא: ביצוע של 0 או יותר מסעי-\( \varepsilon \) מ-\( q \); ביצוע צעד תוך קריאת \( \sigma \); ביצוע 0 או יותר מסעי-\( \varepsilon \) מהמצב שאליו הגענו. למרבה המזל, יש לנו כבר כעת דרך קומפקטית מאוד לכתוב את כל המהומה הזו: \( \hat{\delta} \)! ההגדרה של \( \hat{\delta} \) עבור אוטומט עם מסעי \( \varepsilon \) הייתה מסובכת, אבל עכשיו אפשר להשתמש בה בצורה חופשית ולקבל בניה מאוד פשוטה.

פורמלית, נניח ש-\( A_{EM}=\left(\Sigma,Q,q_{0},\delta_{EM},F_{EM}\right) \) הוא אוטומט עם מסעי-\( \varepsilon \). אז נבנה אוטומט בלי מסעים כאלו, \( A_{ND}=\left(\Sigma,Q,q_{0},\delta_{ND},F_{ND}\right) \) שקול. קבוצת המצבים והמצב ההתחלתי של שניהם יהיו זהים, ולב הבניה טמון בהגדרת פונקציית המעברים, שהיא פשוטה כל כך לניסוח פורמלי שזה מרגיש כמו רמאות:

\( \delta_{ND}\left(q,\sigma\right)=\hat{\delta}_{EM}\left(q,\sigma\right) \)

נשאר רק לטפל במצבים המקבלים. מן הסתם נרצה שכל מצב מקבל של \( A_{EM} \) יהיה מצב מקבל של \( A_{ND} \), אבל למרבה הצער - זה לא מספיק. יש לנו מקרה קצה מעצבן שצריך לטפל בו - המילה הריקה. כי מה קורה? הבניה שלנו של פונקציית המעברים מבטיחה שהאוטומטים יתנהגו בצורה מאוד דומה - שיתקיים \( \hat{\delta}_{ND}\left(q,w\right)=\hat{\delta}_{EM}\left(q,w\right) \) כמעט לכל מילה. אבל עבור \( w=\varepsilon \) השוויון הזה פשוט לא נכון. למה? כי באוטומט עם מסעי-\( \varepsilon \), אפשר להגיע לקבוצה לא קטנה של מצבים תוך קריאת המילה הריקה - \( \mbox{Cl}^{\varepsilon}\left(q_{0}\right) \), אם להיות פורמליים - אבל באוטומט בלי מסעי \( \varepsilon \) המצב היחיד שאפשר להגיע אליו בלי לקרוא אף אות הוא \( q_{0} \).

אם \( \varepsilon\notin L\left(A_{EM}\right) \) כל זה לא רלוונטי. אבל אם \( \varepsilon\in L\left(A_{EM}\right) \) אז אין לנו ברירה; אנחנו חייבים שיתקיים \( q_{0}\in F_{ND} \) אחרת פשוט לא יתקיים \( \varepsilon\in L\left(A_{ND}\right) \). מכאן אנחנו מקבלים את ההגדרה הבאה:

\( F_{ND}=\begin{cases}F_{EM} & \varepsilon\notin L\left(A_{EM}\right)\\F_{EM}\cup\left\{ q_{0}\right\} & \varepsilon\in L\left(A_{EM}\right)\end{cases} \)

השאלה היא האם ה”תיקון” הזה לא עשוי לקלקל לנו איכשהו את יתר השפה שהאוטומט מקבל. קל לראות שזה לא יכול לקרות, והנה הסבר בנפנוף ידיים: הדבר היחיד שיכול להשתבש הוא שבמקרה בו \( \varepsilon\in L\left(A_{EM}\right) \) תהיה מילה לא ריקה \( w \) כך ש-\( w\notin L\left(A_{EM}\right) \) אבל \( q_{0}\in\hat{\delta}_{ND}\left(q_{0},w\right) \) . עצרו רגע להסביר לעצמכם למה זה המקרה הבעייתי היחיד.

אני רוצה לשכנע אתכם שזה לא יכול לקרות. ספציפית, שאם \( q_{0}\in\hat{\delta}_{ND}\left(q_{0},w\right) \) אז \( w\in L\left(A_{EM}\right) \). ההסבר פשוט מאוד: מכיוון ש-\( q_{0}\in\hat{\delta}_{ND}\left(q_{0},w\right) \), הרי ש-\( q_{0}\in\hat{\delta}_{EM}\left(q_{0},w\right) \), כלומר באוטומט עם מסעי ה-\( \varepsilon \) אפשר להגיע אל \( q_{0} \) על ידי קריאת \( w \). כעת, מכיוון ש-\( \varepsilon\in L\left(A_{EM}\right) \) המשמעות של זה היא שבאותו אוטומט, קיימת סדרה של מסעי-\( \varepsilon \) שמובילה מ-\( q_{0} \) אל מצב מקבל כלשהו. לכן כדי לקבל את \( w \) באוטומט הזה קודם כל נקרא אותו בצורה שמעבירה אותנו ל-\( q_{0} \) בסוף הקריאה של אותיות \( w \), ואז מבצעת עוד סדרה של מסעי-\( \varepsilon \) אל מצב מקבל.

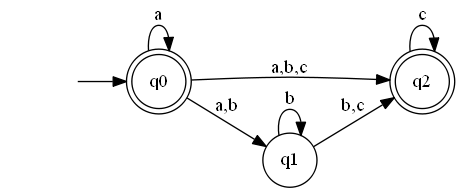
זה מסיים את ההוכחה, והחל מהפוסט הבא נוכל להשתמש בחופשיות באוטומטים אי-דטרמיניסטיים עם מסעי-\( \varepsilon \) כדי לעשות דברים. רק תרגול אחד לסיום - נסו לקחת את האוטומט שמצויר לעיל ולסלק לו את מסעי ה-\( \varepsilon \). הנה מה שאמור להתקבל: