אוטומטים ושפות רגולריות - מבוא
אני רוצה לפתוח כאן בסדרת פוסטים על נושא שיש לי היכרות אישית טובה איתו אבל בבלוג נגעתי בו רק בחטף - תורת השפות הפורמליות, וספציפית אוטומטים. אני אשכח מפוסטים קודמים שאולי נגעו בנושאים הללו (כמו זה) וקרוב לודאי שאחזור על עצמי קצת בהתחלה, אבל אחר כך אציג דברים חדשים ובתקווה מגניבים.
אז על מה אנחנו הולכים לדבר? תורת האוטומטים היא תחום במדעי המחשב התיאורטיים, וזה אומר (בצורה פשטנית מאוד, כמובן) שמה שאנחנו מתעניינים בו פה הוא סוג של מודל חישובי: מודל שהוא מתמטי-פורמלי ומנסה לתפוס סוג מסויים של הדבר החמקמק הזה שאנחנו קוראים לו “חישוב”. השאלות הנפוצות כשעוסקים במודל חישובי כלשהו הן: מה מאפיין את הבעיות שהמודל יודע לפתור? איך ניתן לבנות בעיות חדשות שהמודל יודע לפתור מתוך בעיות קיימות? האם יש בעיות שהמודל אינו יודע לפתור, ואיך מוכיחים את זה עבורן? איך המודל הזה ביחס למודלים אחרים - חזק יותר או חלש יותר או שונה מהותית מבחינת הבעיות שהוא יודע להתמודד איתן?
יש כמה דרכים שונות לתאר את מה שמנסים להשיג עם המודל של אוטומט, אבל הדרך החביבה עלי היא זו: אוטומט הוא מודל שמנסה לתאר חישובים בזכרון חסום. וכאן צריך להסביר מה הכוונה ב”זכרון חסום”. כל מי שכתב קוד בחיים יודע שחלק עיקרי מרוב שפות התכנות הוא משתנים, שיכולים להחזיק מידע כלשהו. המשתנים הללו מאוחסנים ב”זכרון” של המחשב, וכל אלגוריתם דורש, אם כך, כמות כלשהי של זכרון במהלך הריצה שלו. המילה “חסום” כאן אומרת שכמות הזכרון הכוללת שהאלגוריתם יזדקק לה אינה תלויה בגודל הקלט שהוא מקבל. פורמלית, נהוג לדבר על “כמה זכרון אתה צריך כפונקציה של גודל הקלט שקיבלת” ו”זכרון חסום” הוא בעצם דרך לומר “הפונקציה שמתארת את כמות הזכרון כפונקציה של גודל הקלט היא חסומה”.
בואו נראה דוגמה פשוטה במיוחד. נתונה הבעיה הבאה: הקלט שלנו הוא מחרוזת של ביטים, כלומר משהו שנראה ככה: 01001010. סדרה של אפסים ואחדים. השאלה שעלינו לענות עליה: האם מספר ה-1-ים בקלט הוא זוגי או אי זוגי?
הנה קוד נאיבי שפותר את הבעיה (עונה True עבור מספר זוגי של 1-ים ו-False עבור מספר אי זוגי):
count = 0
while (c = read_next_char):
if c == 1:
count += 1
if count % 2 == 0:
return true
return falseבקוד הזה אנחנו סופרים את מספר ה-1-ים במחרוזת, ובסוף בודקים אם הוא זוגי או לא ועונים בהתאם. נשאלת השאלה - בכמה זכרון אנחנו משתמשים כאן?
וכאן יש הבדל אדיר בין מה שקורה בעולם האמיתי ומה שקורה בעולם התיאורטי של מדעי המחשב. בעולם האמיתי המשתנה count שהגדרתי בקוד דורש כמות זכרון קבועה שתלויה בהגדרות שרלוונטיות לשפת התכנות שלי ולמחשב שעליו מקמפלים אותה, אבל היא תהיה, נאמר, בת 32 ביטים. לא יותר. לכן לכאורה האלגוריתם שלי פועל בזכרון חסום; אלא שלמשתנה הזה יש ערך מקסימלי שאם עוברים אותו המשתנה יתאפס (או שערכו יהפוך לשלילי, תלוי בפרטים נוספים שלא אכנס אליהם כאן) והאלגוריתם עלול להיכשל (למעשה, בגלל שבחרתי דוגמה כל כך נאיבית, האלגוריתם עדיין יעבוד, אבל כבר עבור בדיקה של חלוקה ב-3 זה לא היה נכון).
הפתרון? לא להשתמש במשתנה חסום שכזה… יש שפות תכנות, כדוגמת Ruby ו-Python, שבהן משתנים כאלו אכן לא יכולים להגיע לחריגה (ייצוג פנימי חכם מטפל בכך) אבל הם אכן צורכים יותר ויותר זכרון ככל שמאחסנים בהם ערכים גדולים יותר. אבל בעולם התיאורטי הפרטים הללו לא מעניינים אותנו בכלל. אנחנו מניחים מראש ש-count יכול להחזיק כל מספר טבעי, אבל ה”מחיר” לכך הוא שגודל הייצוג שלו תלוי בערך של המספר שהוא מחזיק: אם הוא מחזיק את המספר \( n \), אז כמות הזכרון שהוא צורך היא \( O\left(\lg n\right) \). מכאן שהאלגוריתם שהצגתי לא פועל בזכרון חסום.
האם אפשר לתקן את האלגוריתם כך שישתמש בזכרון חסום? כמובן. אנחנו רק רוצים לדעת את הזוגיות של count, לא את ערכו האמיתי. מספיק לשם כך ביט בודד:
count = 0
while (c = read_next_char):
if c == 1:
count = (count + 1) % 2
if count % 2 == 0:
return true
return falseקיבלנו קוד שהוא תיאור חוקי לגמרי של אלגוריתם שפועל בזכרון חסום. אבל הקוד הזה הוא ייצוג מסורבל למדי מבחינה מתמטית - הוא כולל כל מני פעולות אריתמטיות, ולולאות, ופיצולים (if) והשוואות וכדומה. האמת היא שאנחנו לא בהכרח צריכים את כל המידע הזה. אנחנו מחפשים דרך לבצע לו אבסטרקציה - להיפטר מהחלקים הלא רלוונטיים ולהישאר עם המהות של האלגוריתם.
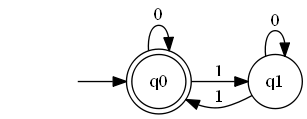
אם חושבים על זה קצת, רואים שהאלגוריתם יכול להיות באחד משני “מצבים” אפשריים - או ש-count שווה 0, או שהוא שווה 1. מה שקורה בכל צעד של האלגוריתם תלוי בתו הבא מהקלט שקראנו: אם קראנו 0 המצב שלנו לא משתנה; ואם קראנו 1 אנחנו עוברים מהמצב שלנו למצב השני. אנחנו מתחילים במצב של 0, והפלט שלנו אמור להיות “כן” רק אם גם סיימנו במצב של 0. את כל המידע הזה אפשר לקודד באיור באופן הבא:
מה שנכלל באיור הזה הוא מצבים, שהם עיגולים, ונתתי להם את השמות \( q_{0},q_{1} \). יש מעברים בין מצבים שמתוארים על ידי חצים (“אי שינוי מצב” מתואר על ידי מעבר ממצב לעצמו) כשעל החצים יש את סימון התו מהקלט שקראנו וגרם למעבר הזה. את \( q_{0} \) סימנו בשני עיגולים כדי לומר שזה מצב מקבל, כזה שאם האלגוריתם מסיים את ריצתו בו אז התשובה של האלגוריתם היא “כן”, וכמו כן יש חץ משום מקום שנכנס לתוך \( q_{0} \) כדי לתאר שזה המצב ההתחלתי שבו האלגוריתם מתחיל את ריצתו.
האיור הזה הוא בדיוק דוגמה לאוטומט, וכולל את כל מרכיביו של האוטומט: מצבים, מעברים, מצבים מקבלים ומצב התחלתי. אתן הגדרה מדויקת יותר בהמשך, אחרי שנפתח עוד קצת את האינטואיציה.
לבינתיים, בואו נדבר על סוג הבעיות שאנחנו הולכים לנסות ולפתור בכלל. הרבה מאוד ממה שאלגוריתמים עושים אפשר לתאר בתור חישוב פונקציה מסויימת - יש קלט סופי, האלגוריתם עושה איתו מהומות, ובסוף מוציא פלט סופי. זה לא נכון לכל האלגוריתמים; יש אלגוריתמים שמעצם טבעם מיועדים לרוץ לנצח (למשל, מערכת ההפעלה שלכם היא תוכנה שלא אמורה לסיים את ריצתה אף פעם) ואפשר לשאול שאלות בסגנון “האם בכלל ייתכן שבמהלך הריצה הנצחית הזו יקרה כך-וכך?”. אלו אחלה שאלות ויש אוטומט שמתאר אלגוריתמים נצחיים שכאלו ואגיע אליו בעתיד, אבל לעת עתה אני רוצה לדבר רק על אלגוריתמים שהופכים קלט סופי לפלט סופי.
מהו הקלט? קלט לאלגוריתמים יכול להיות מידע מכל הסוגים והמינים: גרף שאנחנו רוצים למצוא לו עץ פורש; נוסחה לוגית שאנחנו מחפשים לה השמה מספקת; סרטון וידאו שאנחנו רוצים להמיר לפורמט אחר, וכן הלאה וכן הלאה. אלא שאנחנו רוצים לבצע אבסטרקציה, ולכן נלך אל הגורם המשותף המינימלי לכל האובייקטים הללו - במחשב, כולם מיוצגים על ידי סדרה סופית (“מחרוזת”) של ביטים. אז בואו נדבר רק על סדרות סופיות של ביטים!
למעשה, סדרות סופיות של ביטים זה לא כל כך נוח לנו. הרבה פעמים נרצה לתאר מחרוזות עם יותר משני סימבולים כי ככה יותר קל להבין מה קורה פה. אמנם, כל מחרוזת עם יותר משני סימבולים אפשר לקודד בעזרת מחרוזת עם שני סימבולים בלי להגדיל אותה יותר מדי, אבל יהיה לנו יותר נוח פשוט להרשות למחרוזות להיות מעל אוסף סופי כלשהו של סימנים. לכל אוסף כזה קוראים אלפבית ונסמן אלפבתים באות \( \Sigma \) לרוב. למשל, \( \Sigma=\left\{ 0,1\right\} \) הוא דוגמה לאלפבית שדיברנו עליו עד כה, אבל גם \( \Sigma=\left\{ 0\right\} \) הוא אלפבית לגיטימי, וגם \( \Sigma=\left\{ a,b,c\right\} \) וכדומה. כמובן שגם אפשר לקחת כאלפבית את כל האלפבית הלטיני או העברי, או את כל הסימבולים שבהם משתמשים בסינית, אבל זה כבר יהיה לרוב יותר מדי עבורנו.
אם כן, הקלטים שלנו הן סדרות סופיות של מחרוזות מתוך א”ב סופי \( \Sigma \) - אומרים על זה שהקלט הוא מילה מעל \( \Sigma \). ומה עושים עם הקלט הזה? בדרך כלל מוציאים פלט, שגם הוא מילה מעל אלפבית כלשהו (לאו דווקא \( \Sigma \)). לעתה עתה, כדי לשמור על פשטות, נתעסק במקרה הפשוט ביותר של הוצאת פלט - פלט של ביט בודד. כן או לא. כמו בדוגמה שכבר נתתי. בגישה הזו, כל בעיה שאנחנו רוצים לפתור ניתנת לתיאור בצורה הבאה: נתונה קבוצה \( L \) כלשהי של מילים, ונתונה מילה \( w \); צריך לקבוע אם \( w\in L \). לקבוצה \( L \) כזו קוראים שפה. למשל, בדוגמה שכבר נתתי השפה הייתה \( L=\left\{ w\in\left\{ 0,1\right\} ^{*}|\#_{1}\left(w\right)\equiv_{2}0\right\} \). כאן אני מכניס כמה סימונים חדשים לתמונה. למשל, אם \( \Sigma \) היא אלפבית כלשהו אז \( \Sigma^{*} \) היא קבוצת כל המילים מעל \( \Sigma \) (בהמשך נבין למה הסימון הזה) ויש לי גם סימון עבור “מספר ה-1-ים במילה \( w \)”.
אם כן, המטרה שלנו ברורה: בהינתן שפה \( L \) מעל אלפבית \( \Sigma \) למצוא אלגוריתם שמכריע לכל \( w\in\Sigma^{*} \) האם \( w\in L \) ועושה את זה בזכרון \( O\left(1\right) \). יש רק עוד נקודה עדינה אחת שצריך לדבר עליה - אופן הגישה של האלגוריתם הזה לקלט. הקלט הרי נמצא במקום כלשהו בזכרון; האם אפשר לכתוב למקום הזה? לא, כי אז האלגוריתם יוכל “לרמות” ולהשתמש ב-\( O\left(n\right) \) זכרון (גם לזה יש מודל מעניין אבל נעזוב את זה כרגע). אז הקלט נמצא באיזור בזכרון שהוא “לקריאה בלבד”. אבל איך האלגוריתם יכול לגשת לאיזור הזה? בדרך כלל זכרונות של מחשב מספקים לנו גישה אקראית - בלי להיכנס לעומק הקורה, זה אומר שאם אנחנו רוצים לגשת לביט ה-17 בקלט, אנחנו פשוט עושים את זה מבלי שנצטרך לעבור קודם בכל הביטים עד לביט ה-17. אבל די ברור שאם אנחנו רוצים לשמור על \( O\left(1\right) \) זכרון אפשר לשכוח מהגישה האקראית הזו לזכרון. כדי לכתוב מספר תא כללי בקלט שאורכו \( n \) נצטרך באופן כללי \( O\left(\lg n\right) \) ביטים - זכרון לא קבוע. לכן אנחנו נוקטים בגישה של קריאה סדרתית של הקלט, כפי שעשינו בדוגמה - בכל צעד חישוב האלגוריתם קורא את האות הבאה מהקלט ופועל על פיה (עוד נקודה טריקית - אלגוריתם שרץ במחשב אמיתי כנראה יקבל אוטומטית גישה אקראית לקלט, כך שההגבלה שלנו נראית קצת מלאכותית, לכן חשוב לזכור שאנחנו מנסים לבצע אבסטרקציה לפרטי המימוש הללו).
ייתכן מאוד שאתם צועקים עכשיו “אבל חכה רגע! הסכמנו לגישה סדרתית, אבל למה שזה יגיד שבכל צעד חישוב קוראים את האות הבאה מהקלט? מה אם רוצים לבצע חישוב בלי לקרוא כלום? ומה עם לחזור אחורה בקלט במקום ללכת קדימה?”. שתי ההשגות הללו לגיטימיות, אבל מה שנחמד פה הוא ששתיהן לא משנות כלום. אני אשכנע אתכם בעתיד שהוספת שתי היכולות הללו לא מוסיפה למודל שלנו כוח חישובי ולכן מספיק לדבר על המודל הפשוט יותר שבכל צעד קורא את האות הבאה (ובגלל שהוא פשוט יותר, יהיה קל יותר לנתח אותו).
אם כן, בואו נסכם את המרכיבים שלנו - אלגוריתם שפועל בזכרון קבוע, וקורא את הקלט אות אות בכל צעד. ממה אלגוריתם כזה מורכב? בעקרון, משני חלקים: יש לו קוד ויש לו משתנים. בין המשתנים הללו בפרט יש אחד שאומר “באיזה מקום בקוד אנחנו נמצאים כרגע” (במחשב משתנה כזה נקרא לרוב PC, מלשון Program Counter. קפיצה כלשהי בתוכנית (למשל, אחרי פקודת if) היא בעצם השמה של ערך כלשהו למשתנה הזה. מה שהאלגוריתם עושה בכל רגע נתון תלוי בדיוק בשני פרטי מידע, אם כן: ראשית, אות הקלט שהוא קיבל כרגע; ושנית, תוכן כל המשתנים שלו. התוכן של PC בוודאי, כי הוא אומר מה הפקודה הבאה שנבצע; אבל לעתים קרובות תוכן של עוד תא גם משפיע, כי משתמשים בו בתוך חישוב או השוואה או משהו. הפעולה שהאלגוריתם מבצע בצעד הזה כוללת רק דבר אחד: שינוי של חלק מהמשתנים (כמעט תמיד לפחות PC משתנה וגדל ב-1).
התוכן של כל המשתנים של האלגוריתם ברגע נתון הוא מעיין “תמונת מצב” של ריצת האלגוריתם, או בקיצור - מצב. האלגוריתם ניתן לתיאור בתור סדרה של מצבים, שכל אחד נובע מקודמו ומאות הקלט שנקראה באותו רגע. המצב שבו האלגוריתם מתחיל (התוכן ההתחלתי של המשתנים) הוא המצב ההתחלתי, ומצב שבו האלגוריתם אומר במפורש “כן” הוא מצב מקבל. כדי לעשות לנו את החיים קצת יותר פשוטים, כשאנו עוברים לאבסטרקציה שלנו אנחנו מרשים לכל מצב להיות מצב מקבל.
ועכשיו לנקודה החשובה מכל. יש לנו מספר סופי של משתנים באלגוריתם, וכמות הזכרון שכל משתנה כזה יכול להשתמש בה היא סופית ואינה תלויה בקלט. גם PC הוא כזה, כי גודל הקוד של האלגוריתם לא תלוי בקלט (סדר העניינים הוא זה: קודם נתונה \( L \); אחר כך בונים את האלגוריתם על פי \( L \) ולבסוף מריצים אותו על מילה \( w \) כלשהי). מכאן עולה שיש רק מספר סופי של מצבים שבהם האלגוריתם יכול להיות. האבסטרקציה המרכזית שנעשה תהיה לשכוח מכך שיש משתנים וקוד ופשוט לדבר על קבוצה סופית כלשהי של “מצבים”, שיהיו בסך הכל סימבולים. לרוב נסמן אותה באות \( Q \) ואת האיברים שלה ב-\( q_{0},q_{1},q_{2},\dots \) וכדומה.
בהינתן \( Q \) כזו, המצב ההתחלתי של האלגוריתם הוא בסך הכל איבר כלשהו של \( Q \) - לרוב בוחרים את \( q_{0} \) לתפקיד. המצבים המקבלים הם תת-קבוצה \( F\subseteq Q \). נשאר רק לתאר את ה”לוגיקה” של האלגוריתם - האופן שבו אנחנו עוברים בין מצבים. אמרנו כבר שבכל צעד חישוב המצב הבא נקבע על בסיס המצב הקיים ואות הקלט הנוכחית שנקראה, אז אפשר לדבר פשוט על פונקציה \( \delta:Q\times\Sigma\to Q \) שלכל זוג של מצב ואות קלט אומרת מה המצב שאליו נעבור.
אלו כל המרכיבים של המודל התיאורטי שלנו. אוטומט הוא חמישייה שכוללת את כולם: \( A=\left(\Sigma,Q,q_{0},\delta,F\right) \). זה המודל שאני ארצה להתעסק בו. כבר בשלב הזה מעניין להשוות אותו למודל הסטנדרטי עבור חישוב כללי - מכונת טיורינג. המודלים דומים מאוד, ולא במקרה; טיורינג הציע את המודל שלו הרבה לפני שהתחילו לדבר על אוטומטים, וקרוב לודאי שכאשר התחילו לדבר על המקרה המצומצם יותר של אוטומט אימצו את דרך החשיבה והסימונים של טיורינג, אבל נפטרו ממה שמיותר.
מה שמבדיל מכונת טיורינג מאוטומט הוא הזכרון - לאלגוריתם כללי יש זכרון לא חסום, דהיינו בכל רגע נתון הוא משתמש רק בכמות סופית של זכרון, אבל אם יש צורך הוא תמיד יכול לבקש עוד. לצורך כך, טיורינג חושב על הקלט כנתון על סרט שמחולק לתאים, ותחת שנקרא את הקלט תו-תו, יש למכונת טיורינג ראש קורא וכותב שיכול לנוע על הסרט צעד אחד בכל פעם. כדי להבטיח שהזכרון לא יהיה חסום, הסרט הוא אינסופי בכיוון אחד. פרט לכך ההגדרות זהות - יש קבוצת מצבים סופית (במקרה של טיורינג אפשר לחשוב עליה “רק” כמייצגת את ה-PC ותו לא), פונקציית מעברים (שבנוסף למצב החדש אליו עוברים מתארת גם מה הראש כותב על הסרט ואיזה צעד הוא מבצע - על הפונקציה הזו צריך לחשוב בתור תיאור התוכנית שהמכונה מבצעת), מצב התחלתי ומצבים מקבלים (וגם אלפבית אחד לקלט ואלפבית שמכיל אותו עבור הסימבולים שיכולים להיות על הסרט, כולל סימבול מיוחד לתא ריק). די יפה שתוספות לא מורכבות כל כך מקפיצות את האוטומט למעמד של מודל חישוב כללי; אבל הן גם גורמות לניתוח של מה שהוא עושה להיות מורכב פי כמה וכמה.
כדי שהתיאור הפורמלי שלנו של אוטומט יהיה שלם, צריך לתאר לא רק את האוטומט עצמו אלא גם מה זה אומר, פורמלית, שהאוטומט “רץ” על מילה. ריצה היא בסך הכל סדרת מצבים שהראשון שבהם הוא המצב ההתחלתי של האוטומט וכל מצב מתקבל מקודמו על ידי קריאת אות מהקלט ועל פי פונקציית המעברים. אם \( w=\sigma_{1}\sigma_{2}\dots\sigma_{n} \) היא מילה בת \( n \) אותיות, אז ריצה על המילה הזו תהיה סדרה \( p^{0},p^{1},\dots,p^{n} \) של מצבים שמקיימת \( p^{0}=q_{0} \) ולכל \( 0<i\le n \) מתקיים \( p^{i}=\delta\left(p^{i-1},\sigma_{i}\right) \). לבסוף, \( w \) מתקבלת על ידי האוטומט אם ורק אם \( p^{n}\in F \).
כדי לפשט בסימונים ובכתיבה, מה שנוח לעשות הוא לקחת את פונקציית המעברים של האוטומט ולהרחיב אותה למילים. דהיינו, במקום לדבר על \( \delta:Q\times\Sigma\to Q \) מדברים על פונקציה \( \delta:Q\times\Sigma^{*}\to Q \) שאומרת לאן האוטומט מגיע בריצה שלו על כל מילה אפשרית. מה שקריטי להבין כאן הוא שהפונקציה מוגדרת על כל זוג של מצב ומילה, אבל רק ההגדרה שלה על מצב ואות היא חלק מההגדרה של האוטומט; כל השאר נובע מההגדרה הזו באופן חד-ערכי (לפעמים מסמנים את הפונקציה המורחבת ב-\( \hat{\delta} \) או משהו דומה כדי שההבדל בין שתי הפונקציות יהיה ברור).
קל לתאר את \( \delta \) המורחבת הזו באופן אינדוקטיבי. ראשית, נסמן ב-\( \varepsilon \) את המחרוזת הריקה - מחרוזת ללא תווים (אני מקווה שאין לאף אחד כאן בעיה עם המושג הזה - הרי הוא קיים גם בשפות תכנות סטנדרטיות). אז ברור ש-\( \delta\left(q,\varepsilon\right)=q \) כי אם עוד לא קראנו כלום אנחנו נשארים במצב שהתחלנו בו. כמו כן, אם \( w \) היא מילה כלשהי ו-\( \sigma \) היא אות כלשהי, אז מתקיים \( \delta\left(q,w\sigma\right)=\delta\left(\delta\left(q,w\right),\sigma\right) \), כלומר המצב שאליו מגיעים מ-\( q \) על ידי קריאת \( w\sigma \). הוא המצב שאליו מגיעים על ידי כך שקודם כל קוראים את \( w \), מגיעים למצב כלשהו, ואז בו קוראים את \( \sigma \) ומבצעים מעבר אחד נוסף. למעשה, אם רוצים להיות ממש פורמליים אז מגדירים את פונקציית המעברים המורחבת על ידי שתי המשוואות הללו (עבור \( \varepsilon \) ועבור \( w\sigma \)) - זו המחשה להגדרה אינדוקטיבית של פונקציה.
כדי לוודא שהבנו, הנה הוכחה טכנית של טענה קצת יותר כללית על פונקציית המעברים: \( \delta\left(q,w_{1}w_{2}\right)=\delta\left(\delta\left(q,w_{1}\right),w_{2}\right) \) כאשר \( w_{1},w_{2} \) מילים כלשהן (מה שראינו - או הגדרנו - קודם הוא שזה נכון עבור \( w_{2} \) שהיא אות). הוכחה של טענה כמו זו היא באינדוקציה על האורך של \( w_{2} \), כשמקרה הבסיס (\( \left|w_{2}\right|=0 \) ולכן \( w_{2}=\varepsilon \)) טריוויאלי. עבור הצעד, מפרקים \( w_{2}=w\sigma \) ומניחים שהטענה כבר נכונה עבור \( w_{1}w \), ואז מקבלים את שרשרת המעברים הבאה:
\( \delta\left(q,w_{1}w\sigma\right)=\delta\left(\delta\left(q,w_{1}w\right),\sigma\right)= \)
\( \delta\left(\delta\left(\delta\left(q,w_{1}\right),w\right),\sigma\right)=\delta\left(\delta\left(q,w_{1}\right),w\sigma\right)=\delta\left(\delta\left(q,w_{1}\right),w_{2}\right) \)
עכשיו אפשר סוף סוף לתת את ההגדרה האחרונה שלנו - מה השפה שהאוטומט מזהה, או כפי שיותר נהוג לומר - מקבל. אם \( A=\left(\Sigma,Q,q_{0},\delta,F\right) \) הוא אוטומט, אז נגדיר \( L\left(A\right)=\left\{ w\in\Sigma^{*}|\delta\left(q_{0},w\right)\in F\right\} \). שפה שמתקבלת על ידי אוטומט סופי דטרמיניסטי כלשהו נקראת שפה רגולרית.
לסיום הפוסט הזה, וכדי לראות שהפשטות של המודל מקילה עלינו להוכיח דברים, בואו ניתן דוגמה קונקרטית לשפה שאפשר להוכיח שאינה רגולרית (למי שמכיר קצת תורת הקבוצות ברור שיהיו כאלו - יש מספר בן מניה של אוטומטים אבל מספר לא בן מניה של שפות). השפה היא \( L=\left\{ a^{n}b^{n}|n\ge0\right\} \) עבור הא”ב \( \left\{ a,b\right\} \). למי שלא מבין מה כתוב פה - חזקה של אות היא בסך הכל חזרה שוב ושוב על אותה אות, כלומר השפה הזו היא שפת כל המחרוזות שכוללות רצף של a-ים ואחריו רצף של b-ים כשאורך שני הרצפים זהה. מה האינטואיציה שמאחורי הקושי של השפה? ובכן, אלגוריתם נאיבי עבורה עובר אות-אות בקלט. כל עוד הוא קורא \( a \)-ים הוא סופר את הכמות שלהם על ידי הגדלת מונה, וכשה-\( b \)-ים מתחילים הוא מתחיל לחסר מהמונה. הוא מקבל רק אם המונה שווה 0 בסיום, ואם לא התחילו לצוץ \( a \)-ים שוב באמצע.
האלגוריתם הזה בבירור לא פועל בזכרון קבוע בגלל המונה שלנו. אבל כאן התחושה האינטואיטיבית היא שאנחנו חייבים את המונה, לא כמו בדוגמה שבה התחלנו עם הזוגיות. אלא ש”תחושות” כאלו הן חסרות משמעות מבחינה מתמטית; אנחנו חייבים לשלול את הקיום של אלגוריתם כלשהו, מתוחכם וגאוני ככל שיהיה, שמזהה את השפה הזו בסיבוכיות זכרון קבועה. איך עושים את זה?
שוב, מעניין להשוות למה שטיורינג עשה בהוכחה שלו שיש שפות שמכונת טיורינג לא יכולה לקבל. בהוכחה של טיורינג יש רעיון מקסים ומבריק לפיו מה שהמכונה תעשה הוא לקבל קלט שמתפרש בתור קידוד של מכונה, ואז כשמזינים לה את עצמה כקלט הכל מתחרבש - תעלול מקסים של הפניה עצמית שגורם לכך שהמכונה נקלעת לסיטואציה שבה כל תשובה שהיא תענה תוביל לסתירה.
זה ממש לא מה שאנחנו הולכים לעשות.
המודל של אוטומט כל כך פשוט שיהיה הרבה יותר קל להראות שאף אוטומט לא יעבוד. נניח ש-\( A \) הוא אוטומט כלשהו שמקבל כל מילה ב-\( L \) ונוכיח שהוא בהכרח מקבל גם מילה שאינה ב-\( L \), ולכן הוא אינו מקבל בדיוק את \( L \). מכיוון שזה יהיה נכון לכל אוטומט שמקבל את כל המילים ב-\( L \), זה יסיים את ההוכחה.
נסתכל על קבוצת המצבים של \( A \). היא סופית, אז בואו ניתן שם לגודל שלה: \( \left|Q\right|=n \). עכשיו, בואו נזכור שבכל צעד חישוב האוטומט קופץ למצב כלשהו. זה אומר שאחרי \( n \) צעדים, אוסף המצבים שבהם האוטומט היה הוא מגודל \( n+1 \) ולכן (עקרון שובך היונים…) היה מצב כלשהו שבו האוטומט עבר פעמיים. זה אומר שאפשר היה בפרט “לוותר” על כל הצעדים שבין לבין, מה שאומר שהאוטומט יקבל מילה שאינה בשפה. בואו ונראה את זה פורמלית.
ראשית, לכל \( 0\le k\le n \) נגדיר \( p^{k}=\delta\left(q_{0},a^{k}\right) \). מכיוון שהגדרנו \( n+1 \) מצבים, לפחות אחד ממצבי האוטומט מתקבל פעמיים באופן הזה, כלומר יש \( i<j \) כך ש-\( \delta\left(q_{0},a^{i}\right)=\delta\left(q_{0},a^{j}\right) \). כמו כן האוטומט מקבל, על פי ההנחה שלנו, כל מילה ב-\( L \), ולכן \( \delta\left(q_{0},a^{n}b^{n}\right)\in F \). עכשיו בואו תראו קסם:
\( \delta\left(q_{0},a^{n}b^{n}\right)=\delta\left(\delta\left(q_{0},a^{j}\right)a^{n-j}b^{n}\right)=\delta\left(\delta\left(q_{0},a^{i}\right)a^{n-j}b^{n}\right)=\delta\left(q_{0},a^{n-j+i}b^{n}\right) \)
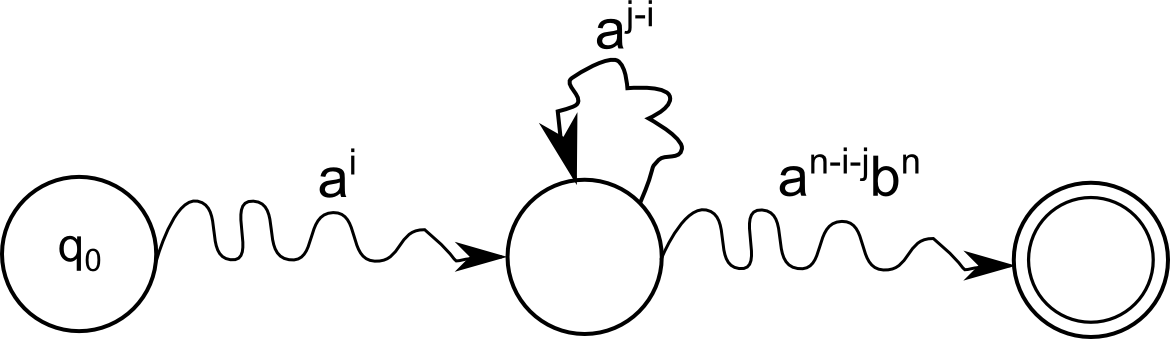
עכשיו, מכיוון ש-\( i<j \) הרי ש-\( n-j+i<n \) ולכן האוטומט קיבל מילה שאינה בשפה. סוף הסיפור. אם עדיין לא ברור למה זה עבד, הנה איור שממחיש את זה:
האיור איננו של אוטומט, אלא תיאור סכמטי של מסלול החישוב שהאוטומט מבצע על המילה הספציפית \( a^nb^n \). חץ “מזגזג” במקום חץ ישר באיור פירושו שמוסתר כאן מסלול שלם, שעובר במצבים שאני לא טורח לצייר. הכיתוב של החץ אומר מה המילה שנקראת במהלך הריצה במסלול הזה. הצומת שבמרכז הוא הצומת שבו מבקרים פעמיים. האיור הזה מסייע לטעמי מאוד להבין מה קורה כאן - בסך הכל ויתרנו על הלולאה האמצעית; החישוב עדיין אמור להסתיים באותו מצב מקבל למרות שהוא קרא פחות \( a \)-ים ממה שהוא היה “אמור” לקרוא.
זה היה החימום. בהמשך נדבר על מודל חישוב או שניים ששקולים לאוטומט סופי דטרמיניסטי ויקלו עלינו להוכיח טענות על שפות רגולריות. יהיה אקשן.
נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: