למת הניפוח לשפות רגולריות

עד עכשיו בסדרת הפוסטים שלי על שפות רגולריות נראה לי שהצלחנו לקבל מושג לא רע לגבי מה הן: ראינו מצד אחד אפיון שלהן בתור שפות שניתנות לזיהוי על ידי מספר מודלי חישוב (אוטומטים), ומצד שני אפיון שלהן בתור קבוצה אינדוקטיבית של שפות שניתן להרכיב מתוך השפות הסופיות על ידי איחוד, שרשור וסגור-קלייני, והאפיון הזה גם נתן לנו שיטת תיאור נוחה לשפות כאלו - ביטויים רגולריים. ראינו שהן מקיימות שלל תכונות סגור נוספות. מה שלא באמת ראינו עד עכשיו הוא שיטה שתאפשר לנו לזהות מתי שפה איננה רגולרית.

להראות ששפה נתונה איננה רגולרית זה עניין מורכב. נניח שאנחנו מנסים לבנות אוטומט לשפה הזו ולא מצליחים - האם זה אומר שהשפה לא רגולרית? לאו דווקא - אולי אנחנו פשוט גרועים בבניית אוטומטים. כדי להראות שהשפה אינה רגולרית צריך להוכיח שכל בניה של אוטומט, ולא משנה כמה מתוחכם בונה האוטומטים יהיה, תיכשל. ואיך ייראה “כישלון” שכזה? ובכן, רמז אפשר למצוא בהוכחה שכן הראיתי בעבר לכך ש-\( L=\left\{ a^{n}b^{n}\ |\ n\in\mathbb{N}\right\} \) אינה רגולרית - שם הראיתי שאם אוטומט מקבל מילה ארוכה דיו ששייכת לשפה, אז הוא בהכרח “יתבלבל” ויקבל גם מילה אחרת שאינה שייכת לשפה.

את ההוכחה שהראיתי אז אפשר להכליל בקלות רבה ולקבל כלי נשק מועיל מאוד בהוכחה כללית ששפות אינן רגולריות, מבלי לטרוח ולחזור שוב ושוב על הטיעון מבוסס האוטומטים. בניסוח “נקי” בכלל לא צריך לדבר על אוטומטים. כדי לא להשאיר אתכם במתח אציג את הניסוח הזה עכשיו, אבל אזהיר מראש שהוא לא טריוויאלי להבנה אז לא לדאוג - הכל יתברר בהמשך.

אם כן, הנה למת הניפוח לשפות רגולריות: אם \( L \) אם היא שפה רגולרית אז קיים קבוע \( n\ge1 \) כך שלכל \( z\in L \) מאורך \( \left|z\right|\ge n \) קיים פירוק \( z=uvw \) המקיים ש-\( \left|uv\right|\le n \), ו-\( \left|v\right|\ge1 \) ולכל \( i\ge0 \) מתקיים \( uv^{i}w\in L \).

אני חושב שיהיה הרבה יותר קל להבין את הלמה אחרי שנראה את ההוכחה. אז בואו נתחיל. מכיוון ש-\( L \) רגולרית אז קיים אוטומט סופי דטרמיניסטי \( A \) כך ש-\( L\left(A\right)=L \). נסמן \( \left|Q\right|=n \), דהיינו הקבוע \( n \) שלנו יהיה מספר מצבי האוטומט. כעת ניקח מילה \( z\in L \) המקיימת \( \left|z\right|\ge n \). מהנתון הראשון עולה ש-\( \hat{\delta}\left(q_{0},z\right)\in F \) - קריאת המילה מביאה אותנו למצב מקבל. הנתון השני אומר שריצת \( A \) על \( z \) כוללת לפחות \( n \) צעדים. אחרי שביצענו \( k \) צעדים, האוטומט כבר ביקר ב-\( k+1 \) מצבים, לאו דווקא שונים (כי יש את המצב שבו הוא התחיל, ואחרי כל צעד הוא משנה את המצב שלו). לכן אחרי קריאת \( n \) התווים הראשונים של \( z \), מעקרון שובך היונים נקבל ש-\( A \) היה במצב כלשהו פעמיים. נסמן את המצב הזה ב-\( p \), וכעת נפרק את \( z \) לשלושה חלקים \( z=uvw \) באופן הבא: \( u \) היא תת-המילה שהביאה את האוטומט אל \( p \) בפעם הראשונה; \( v \) היא תת המילה שהביאה אותו אל \( p \) בפעם השניה; ו-\( w \) זה כל היתר.

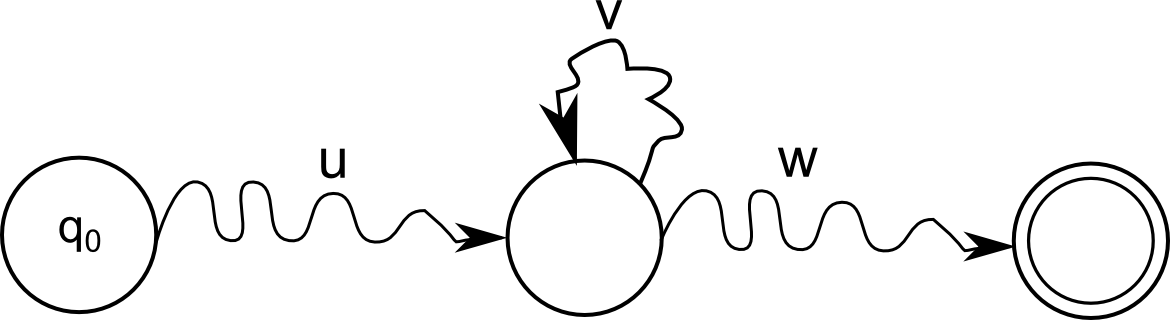
מייד ברור שאכן מתקיים \( \left|uv\right|\le n \) מהנימוק שנתתי קודם - אחרי \( n \) הצעדים הראשונים כבר היה מצב שהופיע פעמיים, ולכן כל המילה שאנחנו מספיקים לקרוא עד הפעם השניה שבה הגענו למצב הזה לא ארוכה מ-\( n \). גם ברור ש-\( \left|v\right|\ge1 \) כי אחרת היינו מקבלים ש”הפעם הראשונה” ו”הפעם השניה” שבה האוטומט מבקר ב-\( p \) הן אותה פעם, בסתירה לכך שזה מצב שאנחנו רואים פעמיים. נשאר רק להוכיח שהדבר הזה עם ה-\( uv^{i}w \) מתקיים. זה פשוט למדי אחרי שמסכמים את מה שאנחנו כבר יודעים באיור הזה, שהוא וריאציה על האיור מהפוסט הראשון עם \( \left\{ a^{n}b^{n}\ |\ n\in\mathbb{N}\right\} \):

מה שקורה פה הוא פשוט שלא משנה כמה פעמים נחזור על הלולאה באמצע או נוותר עליה בכלל - בסוף עדיין נגיע למצב מקבל. כמובן, הוכחה באמצעות איור אינה לגיטימית, אז הנה הפורמליזם למי שזה באמת חשוב לו:

\( \hat{\delta}\left(q_{0},u\right)=p \)

\( \hat{\delta}\left(p,v\right)=p \)

\( \hat{\delta}\left(p,w\right)\in F \)

טריוויאלי להוכיח ש-\( \hat{\delta}\left(p,v^{i}\right)=p \) לכל \( i\ge0 \) (באינדוקציה, כמובן), ומכאן זה סתם משחק בסימבולים:

\( \hat{\delta}\left(q_{0},uv^{i}w\right)=\hat{\delta}\left(\hat{\delta}\left(\hat{\delta}\left(q_{0},u\right),v^{i}\right),w\right)=\hat{\delta}\left(\hat{\delta}\left(p,v^{i}\right),w\right)=\hat{\delta}\left(p,w\right)\in F \)

ועל כן \( uv^{i}w\in L\left(A\right)=L \). הוכחה קלה ופשוטה ואלגנטית ויפה מאוד.

אבל איך זה עוזר לנו להוכיח ששפה היא לא רגולרית?

אפשר לחשוב על הלמה בתור סוג של משחק לשני שחקנים, אליס ובוב. המשחק מתנהל עבור שפה מסויימת \( L \) שבוב טוען שאינה רגולרית ואליס מנסה להקשות עליו את החיים (אני בכוונה לא כותב “ואליס טוענת שהיא כן רגולרית” כי כלל לא ניתן לטעון את זה, ואני אחזור לנקודה הזו בפירוט בהמשך). המשחק מתנהל כך: ראשית כל אליס אומרת מספר טבעי \( n \) כלשהו. עכשיו בוב מגיב למהלך של אליס בכך שהוא מספק מילה \( z\in L \) שמקיימת \( \left|z\right|\ge n \) (שימו לב שהמהלכים הללו אינם בלתי תלויים - המילה שבוב נותן תלויה ב-\( n \) שאליס אמרה). כעת אליס מציעה פירוק \( z=uvw \) כלשהו, ולכך בוב משיב עם מספר טבעי \( i\ge0 \). ואז בודקים מה קורה. אם \( uv^{i}w\in L \) אז אליס ניצחה, ואחרת בוב ניצח.

הטענה שלי היא שאם \( L \) היא שפה רגולרית אז אליס תמיד יכולה להבטיח את הנצחון שלה במשחק אם תשחק היטב. את הטענה הזו ניתן לנסח באופן שקול, שלילי באופיו: אם אליס אינה יכולה להבטיח את הנצחון שלה במשחק, אז \( L \) בודאות אינה רגולרית. כלומר, כשאנחנו באים להראות ששפה אינה רגולרית אנחנו בעד בוב ואנחנו צריכים להסביר איך הוא יוכל להביס את אליס. לשם כך, בואו ננסח מחדש את הלמה בגרסה ה”שלילית” שלה (שהיא שקולה לוגית לגרסה שנתתי):

עבור שפה \( L \) כלשהי, אם לכל קבוע \( n\ge1 \) קיימת מילה \( z\in L \) עם \( \left|z\right|\ge n \) כך שלכל פירוק \( z=uvw \) המקיים \( \left|uv\right|\le n \) ו-\( \left|v\right|\ge1 \)קיים \( i\ge0 \) כך ש-\( uv^{i}w\notin L \) - אם זה קורה, אז \( L \) אינה רגולרית.

בואו נשחק את המשחק עבור \( L=\left\{ a^{n}b^{n}\ |\ n\in\mathbb{N}\right\} \) הישנה והטובה. את המשחק מתחילה אליס, בכך שהיא זורקת קבוע \( n \) כלשהו לחלל האוויר. אני לא מניח שום דבר על \( n \) פרט לכך שזה מספר טבעי חיובי. עכשיו אני צריך להסביר איך בוב יכול להגיב ל-\( n \) הזה של אליס בצורה שעדיין תאפשר לו לנצח במשחק. למרבה המזל, במשחק על השפה \( L \) שלנו קל לתת תשובה כללית, שאמנם תלויה ב-\( n \) אבל מתאימה לתבנית פשוטה - בוב פשוט יגיד את המילה \( z=a^{n}b^{n} \). בוודאי שמתקיים \( \left|z\right|\ge n \) (למעשה, \( \left|z\right|=2n \); אין שום בעיה עם כך שהאורך של \( z \) גדול מ-\( n \) ובקרוב נראה שזה אפילו מועיל מאוד) ובוודאי שמתקיים \( z\in L \).

עכשיו אליס מגיבה בפירוק כלשהו של \( z \): \( z=uvw \). כמקודם, אנחנו לא יכולים להניח שום דבר על הפירוק, פרט לכך שהוא מציית לתנאי הלמה. אבל אלו תנאים לא טריוויאליים: ראשית, \( \left|v\right|\ge1 \), אבל שנית וחשוב בהרבה מכך, \( \left|uv\right|\le n \). התנאי הקטן הזה הוא שמאפשר לבוב להביס את אליס - בלעדיו, לא הייתה לו תקווה לנצח במשחק, כפי שאראה עוד רגע. כדי להבין למה הוא כל כך מועיל, בואו נראה את המשמעות שלו - המשמעות היא ש-\( uv \) נמצאת כולה בחצי הראשון של \( a^{n}b^{n} \); כלומר, \( uv \) כוללים רק \( a \)-ים. לכן אפשר לסמן \( u=a^{k},v=a^{t} \) עם הנתון \( t\ge1 \), ולכן. וכעת מגיע מהלך הניצחון של בוב: הוא יבחר \( i=0 \) ונקבל ש-\( uv^{i}w=uv^{0}w=uw=a^{n-t}b^{n} \) (למה \( n-t \)? כי הורדנו מ-\( a^{n} \) בדיוק את ה-\( a \)-ים שהיו שייכים ל-\( v \), וכאלו יש \( t \)). מכיוון ש-\( t\ge1 \) הרי ש-\( n-t\ne n \), ולכן \( a^{n-t}b^{n}\notin L \), ובוב ניצח. הוכחנו שהשפה לא רגולרית.

עכשיו, מה היה קורה אם אליס לא הייתה מוגבלת על ידי האילוץ \( \left|uv\right|\le n \)? היא תמיד הייתה מנצחת במשחק עם המהלך המבריק הבא: לא משנה איזו מילה \( z=a^{n}b^{n} \) בוב זרק לחלל האוויר, היא תבחר את הפירוק \( u=a^{n-1},v=ab,w=b^{n-1} \). קל לראות ש-\( uv^{i}w=a^{n-1+i}b^{n-1+i}\in L \) תמיד. לכן למת הניפוח בלי \( \left|uv\right|\le n \) הייתה חסרת ערך כבר נגד שפה פשוטה כמו \( L \). חשוב לי להדגיש את הנקודה הזו כי האילוץ \( \left|uv\right|\le n \) נראה קצת מלאכותי כשקוראים לראשונה את תיאור הלמה - לא ברור למה מתעקשים להתעסק איתו, כשיותר “טבעי” פשוט לא לדבר עליו. אז זו הסיבה - בלעדיו הלמה לא שימושית. כמובן, אני מניח שדי ברור לנו שהאילוץ הזה הוא לא הדבר הכי חזק שיכלנו לדרוש ואפשר להכליל אותו עוד קצת - נדבר על זה בסוף, אחרי שנראה דברים שעליהם הלמה כושלת.

בואו נראה עכשיו עוד שימוש של הלמה, הפעם עבור \( L=\left\{ ww\ |\ w\in\Sigma^{*}\right\} \) (כאשר \( \left|\Sigma\right|\ge2 \) - למשל, \( \Sigma=\left\{ a,b\right\} \)). כמקודם, אליס נותנת \( n \) ובוב נותן מילה. מפתה אולי לתת את המילה \( a^{n}b^{n} \) שבה השתמשנו קודם, אבל \( a^{n}b^{n}\notin L \) כי היא לא בנויה מחזרה על אותה תת-מילה פעמיים. אז אפשר פשוט להכפיל אותה: נגדיר \( z=a^{n}b^{n}a^{n}b^{n} \). עכשיו, כמו קודם, כל פירוק שאליס תיתן יהיה בהכרח מהצורה \( u=a^{k},v=a^{t} \) ולכן עבור \( i=0 \) נקבל ש-\( uv^{i}w=uw=a^{n-t}b^{n}a^{n}b^{n} \). צריך עכשיו לתת עוד נימוק קצר שמסביר למה לא קיימת \( w \) כך ש-\( ww=a^{n-t}b^{n}a^{n}b^{n} \), אבל זה די ברור (יש בדיוק אפשרות אחת ל-\( w \) כזו - שאורכה הוא בדיוק \( \frac{4n-t}{2} \), וקל לראות שהיא לא תעבוד).

בינתיים אולי מתקבל הרושם שכל הקטע הזה עם \( i \) מיותר ושתמיד אפשר לבחור \( i=0 \). אז בואו נסתכל על דוגמה נחמדה יותר וכנראה שגם מעניינת יותר. הפעם \( \Sigma=\left\{ a\right\} \) ולכן אפשר לחשוב על כל שפה בתור אוסף של מספרים טבעיים בייצוג אונרי. בואו נסתכל על שפת כל הראשוניים: \( L=\left\{ a^{p}\ |\ p\mbox{ is prime}\right\} \). איך נפיל אותה?

אליס נותנת \( n \). בוב, בתגובה, נותן \( z=a^{p} \) כאשר \( p \) ראשוני המקיים \( p\ge n \). כבר יש לנו טענה עם תחכום מתמטי לא טריוויאלי - איך אנחנו יודעים שראשוני כזה קיים? התשובה היא שקימים אינסוף ראשוניים. ההוכחה הסטנדרטית (של אוקלידס) לטענה הזו היא פשוטה - נניח שיש מספר סופי של ראשוניים, אז נכפול את כולם ונחבר 1 לתוצאה, והנה קיבלנו מספר שאינו מתחלק על ידי אף אחד מהראשוניים הללו אבל חייב להיות ראשוני כלשהו שמחלק אותו, או שהוא בעצמו יהיה ראשוני. יש עוד הוכחות משעשעות - הנה אחת עם אנליזה, והנה אחת עם טופולוגיה.

אליס, בתגובה, נותנת פירוק \( z=uvw \). מכיוון ש-\( z \) מורכבת כולה מ-\( a \)-ים, אפשר לתאר את הפירוק הזה בתור \( u=a^{k},v=a^{t},w=a^{p-\left(k+t\right)} \), כאשר \( k+t\le n \) ו-\( t\ge1 \). וכעת עולה השאלה - איזה \( i \) כדאי לבוב לבחור?

מה שאנחנו רוצים לעשות הוא לבחור \( i \) כזה שעבורו \( uv^{i}w\notin L \). כעת, \( uv^{i}w=a^{k}a^{it}a^{p-\left(k+t\right)}=a^{p+\left(i-1\right)t} \). לכן אנחנו רוצים לבחור \( i \) שעבורו \( p+\left(i-1\right)t \) בודאות אינו ראשוני. אם נבחר \( i=0 \) זה לא יבטיח זאת; למשל, אם \( p=17 \) ו-\( t=4 \) אז \( p+\left(0-1\right)t=13 \) וגם \( 13 \) ראשוני.

אז מה עושים? פשוט מאוד: בוחרים \( i=p+1 \) ומקבלים ש-\( p+\left(i-1\right)t=p+pt=p\left(t+1\right) \), וזה בבירור לא מספר ראשוני כי הוא שווה למכפלה של \( p \) ושל \( t+1 \) שהוא לפחות 2.

נראה לי שאלו מספיק דוגמאות כדי שנבין את הרעיון הכללי ועד כמה הלמה הזו נוחה. עכשיו בואו נעבור לחדשות המצערות - היא לא תמיד עובדת. דהיינו, היא לא משפט של “אם ורק אם” - ייתכנו שפות לא רגולריות שעדיין מקיימות את תנאי הלמה - כלומר, שאליס מנצחת במשחק עליהן. בואו נראה איך אפשר לבנות כזו.

נתחיל משפה שאנחנו כבר יודעים שהיא קשה - נאמר, שפת הראשוניים \( L \). אם אנחנו רוצים “לנטרל” את למת הניפוח, נוכל לתקוע בהתחלה של מילים איזור שנראה כמו שפה רגולרית, ורק אחרי האיזור הזה יגיע החלק הלא רגולרי. אז נעשה את התעלול הבא: נסתכל על השפה \( b^{*}L \), כלומר כל המילים שמתחילות ברצף מאורך כלשהו של \( b \)-ים ואז \( a \) בחזקת מספר ראשוני. כעת, אם בוב נותן לנו מילה מהצורה \( z=bz^{\prime} \), ולא משנה בכלל איך \( z^{\prime} \) נראה, אליס תמיד תוכל לבחור \( u=\varepsilon,v=b,w=z^{\prime} \) ונקבל ש-\( uv^{i}w \) שייך לשפה החדשה שלנו.

למה זה עדיין לא עובד? כי בוב יכול לתת לנו מילה שלא מתחילה ב-\( b \) בכלל. לכן נשתמש בעוד תעלול: “נטביע” את \( L \) בתוך \( a^{*} \). כלומר, השפה שאני בונה היא השפה \( a^{*}\cup b^{*}L \). כעת, אם בוב יתן בתור \( z \) מילה כלשהי שכוללת רק \( a \)-ים, אז לא משנה בכלל איזה פירוק נבחר עבורה - עדיין נקבל משהו ששייך ל-\( a^{*} \) לכל \( i \) שבוב יבחר. ניצחון קל של אליס.

השפה הזו עדיין נותרת לא רגולרית, כמובן, למרות המניפוליצות שעשינו לה, כי המרכיב ה”קשה” שלה נותר בצורה שאפשר לשחזר אותו: \( L=h\left(\left(a^{*}\cup b^{*}L\right)\cap b\Sigma^{*}\right) \) כאשר \( h \) הוא הומומורפיזם המקיים \( h\left(b\right)=\varepsilon \) ו-\( h\left(a\right)=a \). זו סיבה עיקרית למה הגרסה של הלמה כפי שהצגתי אותה היא מספיקה לרוב הצרכים שלנו, במקום הגרסה הכללית יותר שאציג עוד מעט - בגלל שכדי להוכיח ששפה אינה רגולרית לא חייבים להשתמש עליה בלמה; מספיק להעביר אותה באמצעות תכונות סגור לשפה שכן פגיעה ללמה (ואפילו אם השפה המקורית פגיעה ללמה בעצמה, לפעמים יותר קל לטפל בשפה שמתקבלת ממנה אחרי הפעלת כמה תכונות סגור). הנשק העיקרי שלנו בהתמודדות עם שפות הוא תכונות סגור, כי הן מאפשרות לנו לפשט אותן במאמץ כמעט אפסי, וזה ניכר כאן.

בואו נעבור לדבר עכשיו על הגרסה הכללית של הלמה. הצבעתי על כך שהאילוץ \( \left|uv\right|\le n \) הוא האילוץ הקריטי כדי שהלמה תהיה שימושית. עכשיו, כדאי לשים לב לכך שבמובן מסויים האילוץ הזה הוא עדיין די חלש. אם נתבונן על ההוכחה של הלמה, היינו יכולים לעשות תעלול דומה עבור סוף המילה ולא תחילתה. כלומר, במקום \( \left|uv\right|\le n \) היינו מקבלים את התנאי \( \left|vw\right|\le n \). זה היה מחסל, למשל, את השפה \( a^{*}\cup b^{*}L \). אבל זה כמובן לא הסוף - אפשר לבנות שפה חדשה, שתהיה חסינה גם לגרסה הזו של הלמה - \( a^{*}\cup b^{*}Lc^{*} \). כאן ריפדנו גם את ההתחלה וגם את הסוף של \( L \) בג’יבריש שמונע מהלמה - שמתמקדת בקצוות - לתפוס את החלק האמצעי ה”לא רגולרי”.

אז איך מתמודדים עם זה? אם חושבים קצת על ההוכחה של הלמה ברור שהדבר היחיד שמעניין אותנו הוא שיש שלב כלשהו בריצת האוטומט שבו הוא מבצע לפחות \( n \) צעדים. אלו לא חייבים להיות \( n \) הצעדים הראשונים או האחרונים. די בבירור אפשר לנסח את הלמה בתור: לכל \( z\in L \) כך ש-\( \left|z\right|\ge n \) קיים פירוק \( z=uvwxy \) כך ש-\( \left|vw\right|\le n \) או \( \left|wx\right|\le n \) ו-\( \left|w\right|\ge1 \) ו-\( uvw^{i}xy\in L \) לכל \( i\ge0 \). כאן \( u \) זה החלק של תחילת המילה שעליו אנחנו רוצים לדלג לפני שאנחנו מתחילים לספור \( n \) צעדים, אם סופרים מההתחלה לסוף; ו-\( y \) זה החלק בסוף שעליו אנחנו רוצים לדלג אם סופרים מהסוף להתחלה.

אבל הניסוח הזה לא טוב לנו בכלל, כי צריך לזכור שוב מה המטרה שלנו עם הלמה - להוכיח ששפות הן לא רגולריות. אם אנחנו נותנים יותר גמישות בבחירת פירוקים, אנחנו עוזרים דווקא לאליס, ולא לבוב. למשל, את המילה \( a^{n}b^{n} \) בדוגמה הראשונה שלי אליס תוכל עכשיו לפרק בתור \( u=a^{n-1},v=\varepsilon,w=ab,x=\varepsilon,u=b^{n-1} \), ואז בוב אכל אותה. כלומר, הניסוח ה”כללי” של הלמה הוא שימושי פחות. ועם זאת ברור שצריכה להיות דרך להכליל את הלמה כדי שתוכל לתפוס דווקא יותר מקרים. אז מה עושים?

התשובה היא שעושים משהו טיפה מחוכם. במקום לתת לאליס לבחור את \( u,v \) נותנים לבוב לבחור אותם, כבר כשהוא נותן את המילה \( z \). הביטו בניסוח הבא:

אם \( L \) רגולרית אז קיים \( n\ge1 \) כך שלכל מילה \( z \) ופירוק שלה \( z=uvw \), קיים פירוק \( v=xy \) כך ש-\( \left|xy\right|\le n \) ו-\( \left|y\right|\ge1 \) ו-\( uxy^{i}w\in L \) לכל \( i\ge0 \).

זה גם כן לא הניסוח הכי כללי, כי אפשר גם להחליף את תפקידי \( x,y \) כך ש-\( x \) יהיה זה שמנפחים, אבל נעזוב את זה. אני חושב שהרעיון הכללי כבר ברור. לרוע המזל, גם בניסוח הכללי ביותר למת הניפוח היא עדיין לא משפט של “אם ורק אם” - יש שפות לא רגולריות שמקיימות את תנאי הלמה. עוד יותר לרוע המזל אני לא מכיר אף דוגמה פשוטה, כך שלא אציג כאן דוגמאות.

לסיום, טיזר: הנושא של למת הניפוח מביא אותנו באופן טבעי אל משפט שכן נותן אפיון של “אם ורק אם” לשפות הרגולריות - ועושה את זה בעזרת כלים חדשים ולא צפויים, שנותנים תובנה יפה ביותר לגבי “מה בעצם הולך שם” ומה המשמעות הפורמלית של זה ששפה לא רגולרית היא כזו שדורשת “זכרון לא חסום”, ומה האוטומט המינימלי עבור שפה נתונה. המשפט הזה נקרא משפט מייהיל-נרוד והוא יהיה נושא הפוסט הבא.