התעלומה המסתורית של הנער המבריק, יחס הזהב והנוסחה השגויה במוזיאון

העיתונים - גם אתר Nrg, אבל גם אתרים לא ישראליים - מספרים סיפור יפה. נער בן 15 (יהודי, טורחים לציין ב-Nrg, איך לא) מבקר במוזיאון המדע בבוסטון. מגיע לתערוכה על מתמטיקה, ומזהה שם משוואה שנראית לו - הצעיר המבריק - לא נכונה. הוא מודיע למוזיאון, ובכך מתקן שגיאה בת 35 שנים. נפלא! צעיר מבריק! עתיד מבטיח! כל הכבוד!

האמת העגומה היא שהסיפור הזה לא נכון. הנער בן ה-15 אכן ביקר במוזיאון וראה משהו שנראה לו כמו שגיאה והודיע על כך, והמוזיאון גם אמר שיתקן, אבל חיש קל התברר שבעצם לא הייתה פה שום שגיאה. פשוט, כפי שקורה לפעמים במתמטיקה, יש יותר מדרך אחת להציג דברים. הנער הכיר את אחת הדרכים, המוזיאון הציג דרך אחרת (מקובלת פחות, יש לציין), ומכאן והלאה התקשורת השתוללה.

אני לא הולך לדבר על הנער מכאן ואילך, כי אני לא רוצה להעביר עליו ביקורת, בטח כשאני לא יודע מה בדיוק הוא אמר; לי נראה שהוא דווקא יוצא טוב מכל הסיפור. הוא גם התעניין, גם בדק שמה שהוא מכיר אכן שונה ממה שנכתב במוצג במוזיאון, וגם התריע. אחלה! בגילו בכלל לא הכרתי את המושגים הרלוונטיים. אז הוא לא הבין שהטעות אינה באמת טעות, אז מה? זה לא מתפקידו לדעת את זה; אם כבר, המוזיאון יצא מוזר מאוד בכך שמיהר להגיד שיתקן את הטעות, והעיתונים יצאו עצלנים מאוד, כרגיל.

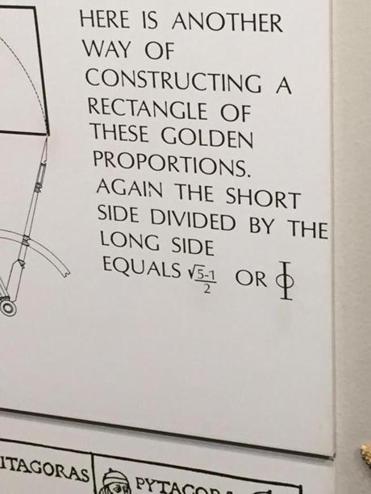
בואו נראה תמונה של המוצג, כפי שהנער צילם אותה:

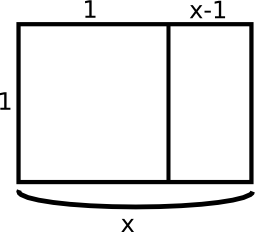
כפי שאפשר להבין, התמונה עוסקת בקבוע מתמטי מפורסם ואהוב מאוד: יחס הזהב. מעולם לא כתבתי פוסט על יחס הזהב וגם כעת איני חש צורך לעשות את זה, כי לדעתי זה יחס שזוכה ליותר מדי תשומת לב ומנסים למצוא אותו יותר מדי במקומות שלא לגמרי קשורים. עם זאת, הוא צץ במתמטיקה במספר הקשרים נחמדים, ולכן יצא לי כבר לכתוב פוסטים על נושאים שבהם הוא הופיע: למשל זה, זה וזה. כיאה למספר שמופיע במקומות שונים רבים, יש כמה דרכים שונות להגדיר אותו. הנה אחת שמשתמשת במוצג שבתערוכה: מלבן זהב (Golden Rectangle). הרעיון במלבן זהב הוא פשוט ויפה: זה מלבן שאם מפרקים אותו לריבוע ומלבן נוסף, המלבן החדש שקיבלנו הוא בעל אותן פרופורציות כמו המלבן שממנו התחלנו (כלומר, היחס בין הצלע הארוכה והקצרה במלבן החדש שווה לזה של המלבן הישן). מהן הפרופורציות הללו? ובכן, זה תרגיל חשבוני קל. נסמן את הצלע הארוכה של המלבן ב-\( x \) ואת הצלע הקצרה שלו ב-1, כך שהיחס שאנחנו מחפשים הוא בדיוק \( x \); אז הריבוע שאנחנו גוזרים מהמלבן הוא בעל אורך צלע 1, ולכן המלבן החדש שנקבל יהיה בעל צלעות מאורך \( 1 \) (הארוכה) ו-\( x-1 \) (הקצרה). אם הפרופורציות שוות, אז קיבלנו את המשוואה \( \frac{x}{1}=\frac{1}{x-1} \), שממנה מקבלים את המשוואה הריבועית \( x^{2}-x-1=0 \) (בניסוח קצת יותר נוח, \( x^{2}=x+1 \)).

את המשוואה הזו אפשר לפתור עם נוסחת השורשים, ומקבלים את הפתרונות \( \frac{1\pm\sqrt{5}}{2} \). מכיוון ש-\( \sqrt{5} \) הוא גדול מ-1, פתרון אחד יוצא שלילי ופתרון אחר יוצא חיובי. הפתרון החיובי מסומן ב-\( \phi \) (האות היוונית פי קטנה), והוא שווה ל-\( 1.6180\dots \), כאשר שלוש הנקודות פירושן שהמספר ממשיך מכאן הלאה; אין להמשך חוקיות ברורה כי זה מספר אי רציונלי ולכן לא ניתן להצגה מחזורית (אבל יש לו הצגה מחזורית פשוטה במיוחד בתור שבר משולב; לא נדבר על זה כאן).

אם כן, \( \phi=\frac{1+\sqrt{5}}{2} \). מה ראה הנער במוזיאון? מוצג שכנראה מנסה להדגים איך ניתן לבנות מלבן זהב בעזרת סרגל ומחוגה. קשה לראות את הטכניקה עצמה בתמונה. הנה הסבר שנלקח מויקיפדיה העברית:

[caption id=”attachment_3280” align=”aligncenter” width=”475”]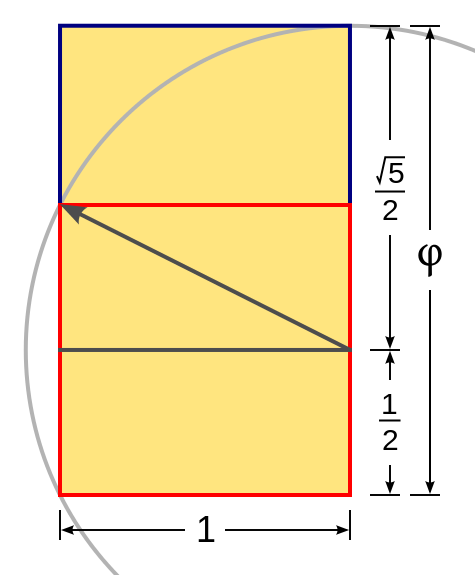 בנייה של מלבן זהב:
1. בנה ריבוע שצלעו יחידה.(מודגש באדום)
2. חצה אותו לשני מלבנים.
3. השתמש באלכסון של אחד המלבנים כרדיוס לבניית מלבן הזהב[/caption]

הנער ראה שבכיתוב במוזיאון כותבים \( \frac{\sqrt{5}-1}{2} \) בתור \( \Phi \), וקפצה לו נורת אזהרה לראש כי מה זה המינוס הזה, הרי יחס הזהב הוא \( \frac{\sqrt{5}+1}{2} \). גם אני נוהג לחפש טעויות כשאני מסתכל על מוצגים מתמטיים במוזיאון (כי נושא טוב לבלוג!) ויכול להבין מה עבר לו בראש. הפספוס שלו הוא הטקסט הקצת מוזר שכתוב במוצג: היחס בין הצלע הקצרה של המלבן והארוכה הוא \( \frac{\sqrt{5}-1}{2} \).

נזכיר: יחס הזהב הוא היחס בין הצלע הארוכה והקצרה, לא הקצרה והארוכה. אם יש לי צלע מאורך 6 וצלע מאורך 3, אז היחס בין הארוכה והקצרה הוא 2, בזמן שהיחס בין הקצרה והארוכה הוא \( \frac{1}{2} \). דהיינו, המספר שהם כתבו במוצג הוא לא \( \phi \) אלא \( \frac{1}{\phi} \). אלא שחישוב קצר יראה לכם שבאמת מתקיים \( \frac{1}{\phi}=\frac{\sqrt{5}-1}{2} \): פשוט תכפלו את \( \phi \) ב-\( \frac{\sqrt{5}-1}{2} \) ותקבלו \( \frac{5-1}{4} \). בקיצור, אין טעות בכיתוב.

אבל רגע, מה עם הסימן \( \Phi \)? יש לכל הפחות טעות בסימן, לא? ובכן, כך גם אני חשבתי הבוקר כשראיתי את הידיעה, אבל מסתבר שטעיתי - הסימון \( \Phi \) הוא דווקא סימון מקובל עבור \( \frac{1}{\phi} \), לפחות אצל וולפרם (לא בדקתי את הרפרנסים שלו). שימו לב להבדל: \( \phi \) היא אות קטנה, בעוד \( \Phi \) היא אות גדולה (זו אותה האות ביוונית - פי, phi). אז אפילו בסימון הזה הכיתוב צודק.

אני לא מתלונן, כמובן; כל דבר שמעלה את המתמטיקה לכותרות זה אחלה. עדיין, יש שני דברים שמעצבנים אותי בדיווח הזה. ראשית, הוא תורם לסטריאוטיפ של “רק גאונים יכולים להתעסק במתמטיקה”, כי הנה, הייתה טעות במוזיאון במשך עשרות שנים שחיכתה שיבוא הגאון (ונער הוא תמיד גאון יותר מוצלח ממבוגר; ויהודי, אז בכלל) שיגלה אותה. סתם אנשים לא יכולים להבין (וכמובן, כמעט בשום מקום לא מראים מה הייתה הטעות בכלל). הדבר השני שמעצבן אותי הוא הניסוחים המקושקשים לגמרי שכתב Nrg הרשה לעצמו להשתמש בהם (בכתבות לא מהארץ שקראתי על הנושא הניסוחים היו טובים בהרבה):

במשך 35 שנים עמדו מבקרים במוזיאון המדע בבוסטון מול התערוכה "מתמטיקה – עולם של מספרים, ומעבר לכך" וניסו לפתור את המשוואות המתמטיות שהציגה התערוכה. מרביתם נתקלו בקשיים רבים, עד שהגיע תלמיד התיכון היהודי ג'וזף רוזנפלד בן ה-15 וגילה כי אחת המשוואות לא ניתנת לפיתרון פשוט משום שהיא מכילה טעות.

איזה משוואה הייתה כאן לפתור? שום דבר! מה לא ניתן לפתרון כאן? שום דבר! אז למה, הו למה, כתב Nrg נחמד, למה אתה חייב להמציא דברים לא קשורים? אתה הרי מבין שאתה לא מבין על מה מדובר, ולא טרחת לברר פרטים מעבר למה שפורסם במקומות אחרים, אז בחייך, אל תתחיל להמציא שטויות. בקצב הזה עוד נגיע למסקנה שבעיתונות כותבים דברים לא נכונים.