משפט ארבעת הצבעים (חלק א')

הסיפור של משפט ארבעת הצבעים כולל את כל מה שסיפור מתמטי טוב צריך לכלול: בעיה מתמטית שהיא פשוטה להחריד לניסוח, ונראית פשוטה באופן מתעתע; סיפור נחמד על האופן שבו התגלתה; הוכחה שצצה יחסית מהר, אבל אחרי למעלה מעשור התגלה שהיא שגויה; מאה שנים נוספות שנדרשו עד למציאת פתרון נכון; והעובדה שהפתרונות שיש כיום הם לא מספקים ברמה זו או אחרת, כך שעדיין יש תקווה למשהו טוב יותר - ושלל הוכחות “קצרות ופשוטות” ושגויות לחלוטין שעדיין מופרחות לאוויר מדי פעם. בקיצור, כל החומרים שהפכו את המשפט האחרון של פרמה לסיפור כל כך מוצלח. אז למה בעצם לא כתבתי על זה עד היום?

ובכן, עם המשפט האחרון של פרמה, המצב שלי קל: אני יכול להודות ללא חשש בכך שאני לא מבין כלום מההוכחה שלו, שנחשבת למסובכת מאוד (אבל נכונה) ומסתמכת על מתמטיקה עמוקה ביותר, אבל במשפט ארבעת הצבעים זה לא המצב - ההוכחה מבוססת על רעיונות פשוטים יחסית אבל היא עדיין מפחידה מאוד, מסיבות שאסביר בהמשך. כך יצא שפשוט התרחקתי מהמשפט הזה כמו מאש ולא הרגשתי שאני מסוגל לכתוב עליו לפני שאאזור אומץ ואקרא קצת יותר.

ובכן, קראתי. כמובן, לא קראתי מספיק כדי שאוכל להסביר את ההוכחות בצורה מלאה, אבל אני מקווה שעד שאסיים פה נבין לא רע את הבעיה והאופן שבו נפתרה. בואו נתחיל עם פוסט של סקירה היסטורית ונתקדם משם.

את משפט ארבעת הצבעים קל מאוד לנסח: בהינתן מפה, אפשר לצבוע כל מדינה בה באחד מבין ארבעה צבעים, כך שאין שתי מדינות עם גבול משותף שהן באותו הצבע. הניסוח הזה לא מדויק בכלל, אפילו שגוי, אבל בתור תיאור ראשוני זה מספיק טוב. מי שרוצים ניסוח פורמלי מדויק יכולים לקבל אחד פשוט כמעט באותה המידה, במחיר שימוש בכמה מושגים מתמטיים בסיסיים: כל גרף מישורי הוא 4-צביע. כבר בניסוחים הללו אנחנו רואים שאפשר לדבר על המשפט הזה בשתי צורות שונות: אפשר לדבר על “מפות” ואפשר לדבר על “גרפים” ושתי דרכי ההתבוננות הללו מועילות.

בואו נתבונן במפה של ארצות הברית, שנבחרה בגלל הצורה הנחמדה שבה היא מתחלקת למדינות, וריבוי המדינות שבה (והיא כנראה לא תהיה ידידותית מספיק לעיוורי צבעים ועמכם הסליחה):

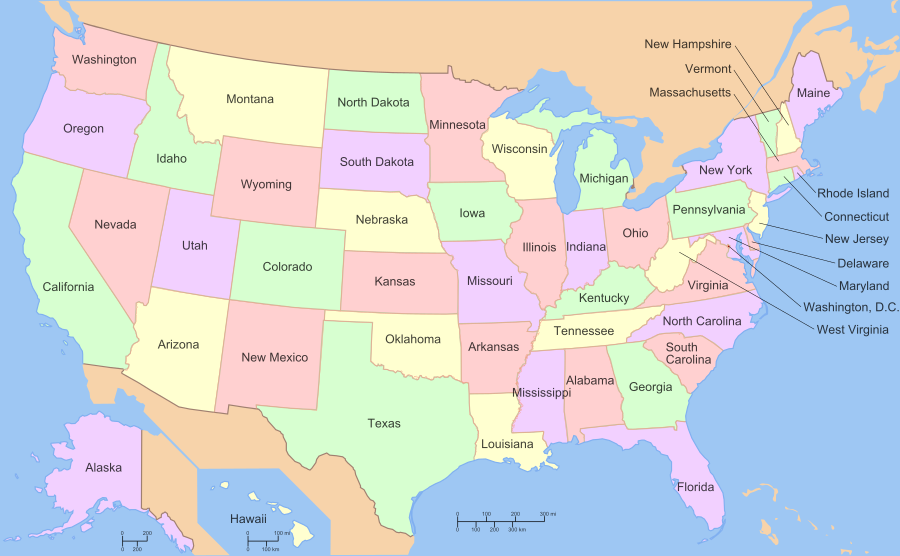
המדינות של ארצות הברית במפה הזו נצבעו בארבעה צבעים: סגול (אורגון), ירוק (קליפורניה), צהוב (אריזונה) ואדום (נבדה - בואו נניח שזה אדום). חוץ מזה יש גם כחול בשביל הים וחום בשביל קנדה ומקסיקו, אבל בואו לא נחשיב את זה כחלק מהתמונה. ה”חוק” שמאחורי הצביעה הזו הוא ששתי מדינות עם גבול משותף לא יהיו צבועות באותו הצבע, פשוט כי אז יהיה יותר קשה להבדיל ביניהן. אפשר כמובן גם לצבוע את המפה עם יותר צבעים:

וככה היא אולי נראית יותר יפה, אבל אם אנחנו רוצים להיות חסכוניים, אנחנו שואלים כמה צבעים אנחנו חייבים כדי לשמר את עניין ה”אין שתי מדינות שכנות עם אותו צבע”. האם יכלנו לצבוע את מפת ארה”ב עם שלושה צבעים בלבד? ובכן, לא. בואו נסתכל לצורך כך על החוף המערבי. קליפורניה ונבדה הן מדינות שכנות ולכן חייבות להיות צבועות בצבעים שונים, למשל ירוק ואדום כמו בתמונה. כעת, אריזונה היא שכנה משותפת של קליפורניה ונבדה ולכן לא יכולה להיות צבועה בצבעים שלהן, לכן היא צריכה להיות צבועה בצבע חדש, למשל צהוב כמו בתמונה. האם אפשר להסתפק בירוק, אדום וצהוב, ולא לצבוע אף מדינה בסגול?

בתמונה יוטה נצבעה בסגול, אבל היא לא שכנה של קליפורניה כך שבעצם אפשר לצבוע אותה בירוק (אבל לא בצהוב או אדום כי היא שכנה של נבדה ואריזונה). זה מכריח את איידהו להיות צבועה בצהוב (שכנה של יוטה שהפכנו לירוקה, ונבדה האדומה), אבל אז אנחנו נתקעים באורגון: אורגון היא שכנה של שלוש מדינות שכולן נצבעו בצבעים שונים מתוך הכרח: קליפורניה, נבדה ואיידהו. היא חייבת להיות צבועה בצבע רביעי.

המשחק הנחמד הזה מלמד אותנו את השיעור הראשון על ענייני הצביעה הללו. הנה יש לנו מצב שבו שלושה צבעים לא מספיקים למרות שבשום מקום אין ארבע מדינות שכולן שכנות זו של זו. הנה “מפה” מלאכותית שבה יש ארבע מדינות שכולן שכנות:

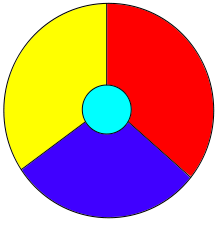
מבט אחד בתמונה הזו מבהיר שחייבים ארבעה צבעים לפחות עבור מפות מסויימות, אבל זה לא מבהיר שהצורך הזה עלול לבוא אלינו בצורה ערמומית שכזו; כלומר, שהדוגמאות הנגדיות יהיו מתוחכמות ולאו דווקא יכילו את מה שנראה כמו המכשול המובן מאליו של המשפט. זה לקח שאנשים שונים ומשונים שניסו להוכיח את המשפט למדו על בשרם (או חמור מכך, לא למדו אותו למרות שהיו צריכים).

מה שהמשפט מבטיח לנו הוא שלא משנה כמה ערמומיים נהיה אם ננסה לבנות מפות שהן מאתגרות לצביעה בכוונה - לא נוכל לבנות מפה שחייבים לפחות חמישה צבעים עבורה. תמיד די בארבעה.

עכשיו, משהבנו מה בעצם אומר המשפט, בואו נדבר קצת על ההיסטוריה שלו. אולי אפשר לחשוב שהעניין הזה של ארבעת הצבעים יהיה ידוע כבר אלפי שנים, כי אנשים מתעסקים עם מפות כבר אלפי שנים, אבל בואו נודה באמת - לאף אחד לא אכפת ממספר הצבעים הקטן ביותר שנדרש כדי לצבוע מפות. לא קורה כלום אם מפה נצבעת בחמישה צבעים במקום בארבעה. כך שהמשפט הוא מלכתחילה קוריוז אינטלקטואלי, וככזה האדם הראשון שידוע לנו שהמציא אותו היה צעיר בן 21 בשם פרנסיס גאתרי, סטודנט למתמטיקה שלימים הפך גם לפרופסור למתמטיקה, שישב וצבע לו את מפת המחוזות של אנגליה (למה? למה אנשים צובעים את מפת המחוזות של אנגליה?)

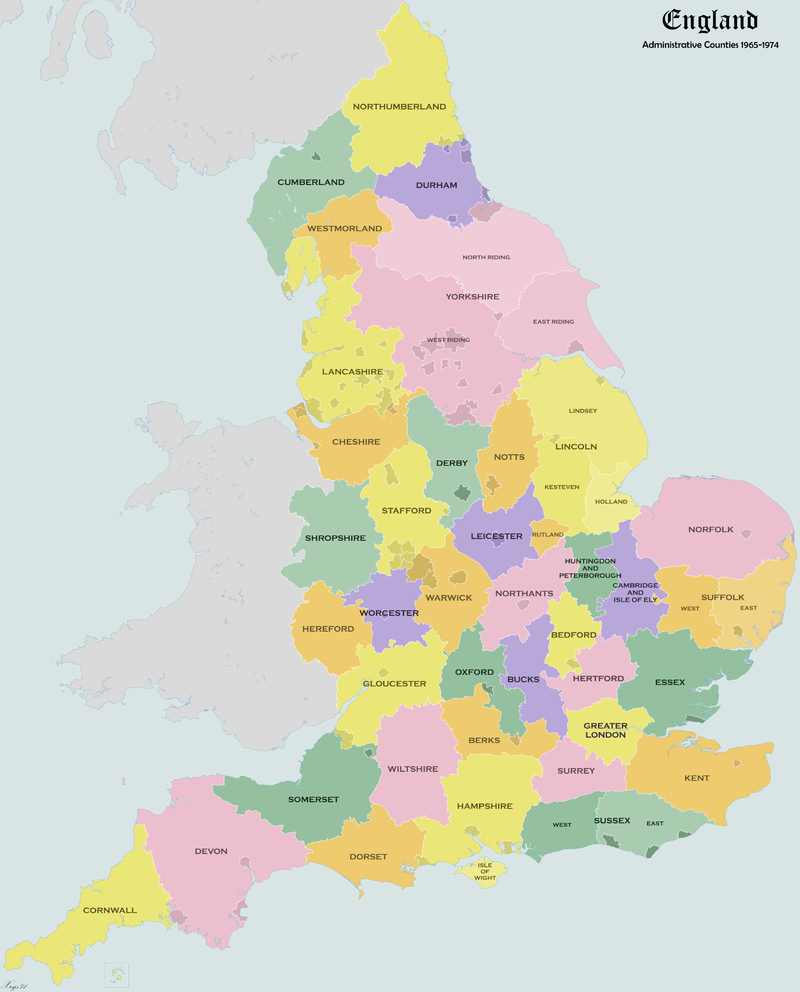
לא לגמרי ברור אם לגאתרי הייתה הוכחה כלשהי בראש או שהוא סתם ניחש שהמשפט אמור להתקיים. הוא סיפר עליו לאחיו, שהיה אז סטודנט של המתמטיקאי אוגסטוס דה-מורגן, והאח בא אל דה-מורגן אחרי השיעור ושאל אותו על המשפט הזה - האם הוא כבר ידוע, ואיך מוכיחים אותו. לדה-מורגן לא היה מושג, אבל היה לו משהו חשוב יותר - הוא התלהב מהשאלה הזו. הוא ניסה לפתור אותה, ולא הצליח; והוא סיפר עליה לכל מי שרק היה מוכן להקשיב. העדות הכתובה הראשונה לקיום הבעיה היא מכתב ששלח דה-מורגן למתמטיקאי המילטון ב-23 באוקטובר, 1852, ובו הוא תיאר את הבעיה וביקש סיוע. משעשע לראות עד כמה דה-מורגן חשב שיש פה פתרון פשוט שחומק ממנו: הוא סיים את המכתב ב-

If you retort with some very simple case which makes me out a stupid animal, I think I must do as the Sphynx did.

למרבה הצער, המילטון לא התלהב מהבעיה כמו דה-מורגן; כל התשובה שהוא טרח לתת לו הייתה

I am not likely to attempt your "quaternion of colours" very soon.

כנראה שהמילטון חשב שהשאלה הזו היא סתם שטות זניחה, וכך יצא שהוא פספס הזדמנות להיות השם החשוב ביותר שמקושר לאחת מהבעיות המפורסמות במתמטיקה.

למרות שדה-מורגן הפיץ את הבעיה בקרב עמיתיו, קשה לומר שנרשמה אצלם התלהבות גדולה או שהתחיל מחקר פעיל של הבעיה. עברו כמעט שלושים שנים מרגע שדה-מורגן שמע על הבעיה ועד שקרה איתה משהו משמעותי. דה-מורגן עצמו נפטר ב-1871 והבעיה נשכחה קצת, עד שבשנת 1878 המתמטיקאי ארתור קיילי ניסה לעורר בה קצת עניין חדש, וכנראה אז היא הגיעה לתשומת לבו של אלפרד קמפ, שהוא כנראה הגיבור המרכזי הראשון בסיפור שלנו. כמו פרמה, שהיה הדמות המרכזית בסיפור של המשפט האחרון של פרמה, כך גם קמפ היה מתמטיקאי חובב; במקצועו הוא היה עורך דין, אבל הוא פרסם מאמרים מתמטיים פה ושם, ובשנת 1879 הוא פרסם מאמר שבו הוכיח את משפט ארבעת הצבעים. על פניו נראה היה שזה מסיים את הסיפור - ההוכחה של קמפ הייתה פשוטה למדי, אם כי לא טריוויאלית, כך שנראה היה שאפשר לסגור את הסיפור בתור קוריוז מתמטי נחמד שבא על פתרונו בצורה טובה.

אבל 11 שנים לאחר מכן, ב-1890, התגלתה בהוכחה שגיאה, וזה התחיל את מחול השדים של שמונים השנים הבאות.

אני הולך להציג את ההוכחה של קמפ במלואה בהמשך, כמו גם את השגיאה; לדעתי אלו הדברים שחשוב ביותר להכיר כשמדברים על המשפט. בשביל מה לטרוח לדבר על הוכחה שגויה? ובכן, כי ההוכחה הייתה כמעט נכונה. היו בה רעיונות טובים מאוד, שהוכיחו את השימושיות שלהם בתורת הגרפים באופן כללי ובהקשר למשפט ארבעת הצבעים בפרט. היא גם מאוד משכנעת במבט ראשון, ולא קל להראות שהיא שגויה, מה שמסביר למה נדרש יותר מעשור כדי להפיל אותה. הכי חשוב: ההוכחות שנמצאו עד כה למשפט ארבעת הצבעים משתמשות בדיוק באותו רעיון מרכזי כמו ההוכחה של קמפ, וההבדל היחיד הוא בפרטים. אם נבין מה קמפ עשה, אז בכך הבנו את רוב מה שנדרש כדי לקבל את התמונה הגדולה של המשפט.

קצת אחרי קמפ, ובעקבות ההוכחה שלו, פרסם מתמטיקאי בשם פיטר טייט “הוכחה” אחרת של המשפט, שהתבססה על רעיונות שונים לגמרי. לרוע המזל, היא הייתה ממש שגויה בכל מני דרכים לא נעימות; למרות זאת היא הייתה מעניינת בפני עצמה, אבל לא אדבר עליה לעת עתה, כי היא לא רלוונטית לאופן שבו המשפט הוכח בסופו של דבר.

בשנת 1890 מצא מתמטיקאי בשם פרסי הייווד את השגיאה בהוכחה של קמפ. במאמר שפרסם הוא הציג דוגמא נגדית, שאראה בהמשך; חלק מהעניין בסיפור הוא שלמצוא דוגמא נגדית להוכחה של קמפ זה קשה (או לכל הפחות, לא טריוויאלי). הייווד כן הצביע על כך שההוכחה השגויה של קמפ מספיקה, אחרי תיקון כלשהו של הטיעון, כדי להוכיח שמספיקים חמישה צבעים כדי לצבוע כל מפה. קמפ עצמו הודה בטעותו ואמר שאינו יודע איך לתקן את ההוכחה, וגם הייווד לא ידע; קצת קשה להאשים אותם, כי גם כיום אין לנו מושג איך אפשר להוכיח את המשפט הזה בלי להשתמש בעזרים שפשוט לא היו זמינים לקמפ ולהייווד.

הבעיה לא נשכחה במאה ה-20, אבל גם לא הושגו בה התקדמויות או פריצות דרך משמעותיות. הרעיון שהוביל בסופו של דבר להוכחה היה של מתמטיקאי גרמני בשם היינריך האש; מה בדיוק היה הרעיון שלו אתאר בהמשך, אבל בבסיסו הוא המשך של הגישה של קאמפ. בשנת 1967 סטודנט בשם וולפגנג האקן ששמע הרצאה של האש בנושא התחיל להתעניין בנושא ולעבוד עליו ביחד עם האש. מה שהיה ברור כבר אז הוא שהשיטה של האש, למרות שיש בה פוטנציאל, תדרוש חישובים ידניים מזעזעים ברמת העומס שלהם (אני בכוונה לא אומר “ קושי” או “מורכבות”). האש והאקן לא הצליחו להגיע להסכמה איך בדיוק לפתח את השיטה והפסיקו את שיתוף הפעולה ב-1972, ואילו האקן המשיך בנסיונותיו עם מתמטיקאי אחרי, קנת אפל, כששניהם בטוחים שניתן להתמודד עם העומס החישובי האדיר בעזרת יצורים שכבר לא בדיוק היו חדשים באותה התקופה אבל השימוש שלהם בהוכחות במתמטיקה היה מוגבל - מחשבים.

ההוכחה של האקן ואפל מתבססת על מציאת קבוצה של יצורים שנקראים קונפיגורציות ניתנות לצמצום (תרגום שלי ל-Reducible Configurations). קונפיגורציה ניתנת לצמצום היא מעין “תת-מפה” שהיא בעלת התכונה הבאה: אם מפה כלשהי מכילה קונפיגורציה ניתנת לצמצום אז אפשר להחליף את המפה הזו במפה קטנה יותר (פחות מדינות), כך שאם המפה החדשה ניתנת לצביעה בארבעה צבעים, כך גם המפה המקורית. באופן שקול לוגית - אם המפה המקורית לא הייתה ניתנת לצביעה בארבעה צבעים (כלומר, היא הייתה דוגמא נגדית למשפט ארבעת הצבעים) אז גם המפה החדשה, הקטנה יותר, הייתה דוגמא נגדית שכזו. במילים אחרות, קונפיגורציה ניתנת לצמצום אינה יכולה להופיע בדוגמא נגדית מינימלית (מבחינת מספר הצמתים) למשפט ארבעת הצבעים.

יש הרבה קונפיגורציות ניתנות לצמצום - ההוכחה של קאמפ התבססה עליהן; למשל, “טבעת” שמורכבת משלוש מדינות שכל אחת מהן היא שכנה של האחרות היא קונפיגורציה שכזו, ונבין יותר טוב למה אחרי שנתעמק בהוכחה של קאמפ. מה שסוגר את הוכחת משפט ארבעת הצבעים הוא מציאה של קבוצת קונפיגורציות שלפחות אחת מהן חייבת להופיע בכל גרף שהוא דוגמא נגדית מינימלית למשפט ארבעת הצבעים. למה? כי כאמור, כל המהות של קונפיגורציה היא שבדוגמא נגדית מינימלית, קונפיגורציה ניתנת לצמצום אינה יכולה להופיע.

הבניה של קבוצת קונפיגורציות כזו שאכן תצליח לפתור את המשפט הייתה עניין ארוך ומתמשך של ניסוי וטעיה; בכל פעם שבה התגלתה בעיה, היה צריך לשנות קצת את הקבוצה ולראות מה קורה עכשיו. המחשב היה חלק נכבד בתהליך העבודה הזה, עד שלבסוף נמצאה קבוצה ללא תקלות שאכן מוכיחה את המשפט ב-1976 פרסמו האקן ואפל את המאמר שלהם בנושא. אז מה בעצם הבעיה?

הבעיה היא שפתרון כזה לא דרש מחשב רק כדי למצוא אותו; נדרש מחשב גם כדי לבדוק אותו, וזו בדיקת מחשב בלתי טריוויאלית בעליל.

יש תיאור פופולרי ושגוי לחלוטין של ההוכחה שהפיל גם אותי בפח בשעתו. הוא מופיע, בין היתר, בויקיפדיה העברית; מאז כתיבת הערך על משפט ארבעת הצבעים באוגוסט 2003 ועד לזמן כתיבת פוסט זה בנובמבר 2018 נאמר בערך שמה שהאקן ואפל עשו היה להראות “שכל מפה אפשרית שקולה לאחת מבין 1,936 מפות שונות” ואז “הריצו תוכנית מחשב במשך 1,200 שעות כדי להראות שכל אחת ממפות אלה ניתנת לצביעה בארבעה צבעים” (הנה קישור קבוע לגרסה הזו מ-2018 של הערך שבו הטעות מופיעה; אני מקווה שבזמן שאתם קוראים שורות אלו הטעות כבר תוקנה!). הבעיה הבסיסית בתיאור השגוי הזה היא שקל מאוד לבדוק צביעה של מפות, אם מישהו אחר כבר טרח ומצא צביעה שכזו. זו דוגמא קלאסית למה שנקרא “בעיה NP-שלמה”; בעיה שכנראה קשה למצוא לה פתרון, אבל אם מישהו אחר כבר מצא, אז לבדוק את הפתרון שלו זה טריוויאלי. אם כל מה שההוכחה הייתה כוללת הוא הוכחה ידנית של שקילות לאוסף גדול של מפות, ואז צביעה מפורשת של כל אחת מהמפות הללו, אני לא חושב שלמישהו הייתה בעיה עם ההוכחה.

אבל מכיוון שהבדיקה היא ממש לא עד כדי כך פשוטה, אנחנו ניצבים בפני שתי בעיות:

1. בעיה פרקטית: כיצד אפשר להיות משוכנעים שההוכחה נכונה ולא שנפלה טעות כלשהי בתוכנית המחשב שבודקת אותה?
2. בעיה פילוסופית: האם הוכחה שאדם לא יכול לקרוא ולהבין בעצמו עדיין יכולה להיקרא "הוכחה"?

אל הבעיה הפילוסופית אני לא רוצה להיכנס בכלל, כי הבלוג הזה מנסה באופן כללי מלהיכנס לעובי הקורה של פילוסופיה של המתמטיקה (ואני גם לא מתיימר להבין בה משהו). דעתי האישית היא שזו הוכחה סבבה מהבחינה הזו, אבל אני לא מנסה לשכנע אף אחד. אני כן מסכים שיש בפירוש הבדל עקרוני בין הוכחה כמו זו ובין הוכחות “עצומות ממדים אבל ניתנות לקריאה בידי אדם” כדוגמת ההוכחה של המשפט האחרון של פרמה או משפט המיון של חבורות פשוטות, אבל אני לא בטוח שההבדל הזה בכלל משחק לטובת ההוכחות הללו.

הבעיה הפרקטית, לעומת זאת, היא מהותית, אבל אני לא חושב שהבעיה פה היא ספציפית השימוש במחשב אלא באופן כללי הסיבוך של ההוכחות - גם הוכחת המשפט האחרון של פרמה עלולה להכיל טעות שהבודקים פספסו (ואכן, בהוכחה המקורית של וויילס הייתה טעות שוויילס עצמו לא הבחין בה ורק הבודק שם לב אליה; ועכשיו תחשבו שהבודק היה מתבלבל כמו וויילס עצמו). השאלה המהותית היא עד כמה קל לשחזר את ההוכחה; הרי מתמטיקאית טובה שקוראת הוכחה בעצם מוכיחה את המשפט מחדש בראש, תוך שהיא נעזרת בתוכן של ההוכחה שהיא קוראת (בכל הוכחה יש השמטות של פרטים, והמתמטיקאית היא מיומנת מספיק כדי להשלים את החורים בעצמה). במקרה של ההוכחה של האקן ואפל, המשמעות היא שמישהו צריך לכתוב מחדש את תוכניות המחשב שבודקות את מה שזה לא יהיה, ולהריץ אותן בעצמו, ולראות שהעסק עבד.

עשו את זה.

האם זה מספיק כדי לסמוך על ההוכחה? ואולי יש איזה באג מהותי בתוכניות? ואולי יש איזה באג משותף לכל המעבדים בכל המחשבים שהריצו את התוכניות? ואולי ואולי ואולי. כשזה מגיע למחשבים אנחנו נוטים אוטומטית להיות סקפטיים יותר.

מאז 1976 עבר קצת זמן והמחשבים קצת השתפרו. מה המצב היום? ובכן, טוב קצת יותר. ככל הידוע לי, עדיין אין שום הוכחה שלא דורשת מחשב, אבל ב-1996 נמצאה הוכחה שמתבססת על קבוצה פשוטה יותר של קונפיגורציות. זה כבר מעודד מאוד - זה מראה שאפשר להוכיח את המשפט ביותר מדרך אחת (למרות שהרעיון הבסיסי זהה) ולכן הסיכוי לטעות נראה זעום בהרבה. אבל מה שבאמת משקיט את החששות האישיים שלי היא הוכחה שנכתבה ב-2005 למערכת Coq. המערכת הזו היא מה שנקרא “proof assistant” - זו תוכנית מחשב שאפשר לכתוב בה הוכחות בלוגיקה פורמלית מסויימת, דמויית שפת תכנות, והמערכת יכולה לבדוק אוטומטית את ההוכחות. כלומר - תוכנית המחשב שבודקת את ההוכחה של משפט ארבעת הצבעים היא לא קוד מחשב שנכתב אד-הוק למטרה זו, אלא מערכת ספציפית שהושקעה עבודה רבה בתכנון שלה, בבדיקה שהיא חפה משגיאות וביסודות המתמטיים שהיא נשענת עליה. ההוכחה הזו היא כנראה גם הדוגמא ה”רצינית” ביותר שאני מכיר לשימוש במערכת כמו Coq.

אם כן, זה הסיפור של משפט ארבעת הצבעים; מעין תם-ולא-נשלם שמבחינתי הוא בהחלט סיום מספק אבל אני מבין את אלו שמתנגדים אליו. “הוכחה פשוטה למשפט ארבעת הצבעים”, כמו “הוכחה פשוטה למשפט האחרון של פרמה” תמשיך להיות גביע קדוש שאפשר לשאוף אליו וכנראה שלא נמצא לעולם (חוק כללי במתמטיקה, אבל כזה שנכון בפרט בקומבינטוריקה: הוכחות יפות הן לא משהו שמובטח לנו משמיים ולפעמים פשוט אין כאלו). בפוסט הבא ננסה להבין מה הלך בהוכחה של קאמפ ולמה היא נכשלה; הכשלון המפואר הזה יספיק כדי לתת לנו הבנה טובה מאוד של איך הוכיחו את המשפט בסופו של דבר.