משפט ארבעת הצבעים (חלק ב')

בפוסט הקודם הצגתי את בעיית ארבעת הצבעים: בהינתן מפה - כלומר, חלוקה של איזור מסויים לתתי-איזורים שלכל אחד מהם אני קורא “מדינה” - להוכיח שדי בארבעה צבעים כדי לצבוע אותה כך שלא יהיו שתי מדינות עם גבול משותף הצבועות באותו הצבע. בפוסט הזה אני אציג את ההוכחה השגויה של קאמפ למשפט הזה - הוכחה יפה עם רעיונות מוצלחים למדי שנפלה בשל נקודה עדינה שקל לפספס.

נתחיל מהבהרה קטנה לעניין “למה מפות וגרפים הן בערך אותו דבר”. אם אני אצייר עיגול קטן בתוך כל מדינה (“עיר בירה”) ואמתח קווים בין העיגולים של מדינות סמוכות (“קווי רכבת”), אני אקבל גרף מישורי; לכן הדיבורים על מפות ומדינות הן דרך אחרת לומר “כל גרף מישורי הוא 4-צביע”. הנה דוגמא לאופן שבו זה נעשה על חלק ממפת ארה”ב (כמובן, מבלי ש”ערי הבירה” יתאימו לערי הבירה האמיתיות של המדינות):

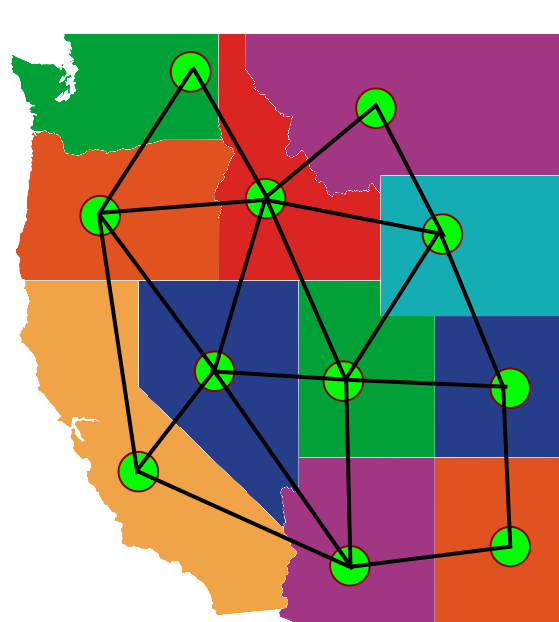
כמובן, התיאור הזה הוא פשטני מדי; מסתתרת כאן הוכחה לא טריוויאלית, אבל אני לא אכנס אליה כלל.

סיבה אחת שבגללה גרפים מישוריים מעניינים אותנו היא שהם מקיימים את נוסחת אוילר. נוסחת אוילר מקשרת את מספר הצמתים של גרף מישורי, מספר הקשתות שלו ומספר הפאות שלו. מה אלו צמתים, קשתות ופאות? צמתים הם המרכיבים הבסיסיים של הגרף - אפשר לחשוב עליהם בתור עיגולים קטנים אם רוצים. קשתות הן הקווים שמחברים זוגות של צמתים. גרף הוא מישורי אם אין שתי קשתות שדורכות זו על זו (פורמלית, גרף הוא מישורי אם אפשר לצייר אותו בצורה כזו ועדיין לשמור על התכונה של אילו צמתים מחוברים). ופאות? בגרף מישורי, פאות הם האיזורים ש”נראים כמו מדינות” - איזורים שמוקפים כולם בקשתות. בנוסף לאלו יש גם פאה אחת נוספת, ה”חיצונית”.

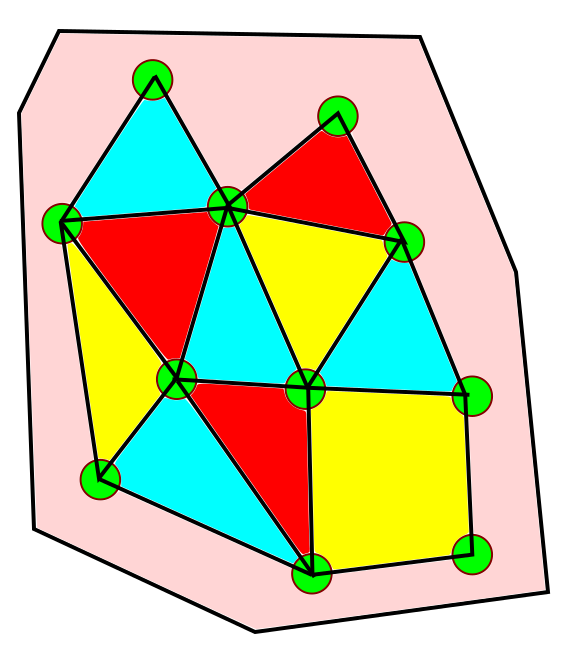
אנחנו רואים שגרף מישורי בעצם נראה כמו… מפה. כלומר, אם ניקח מפה תמימה ונבנה ממנה גרף מישורי, בעצם נקבל מפה אחרת, שנקראת הדואלית שלה. בואו נבין איך דברים משתנים במעבר הזה:

• צומת בגרף הדואלי ("עיר בירה") הייתה פאה במפה המקורית ("מדינה")
• קשת בגרף הדואלי ("קו רכבת בין ערי בירה") הייתה קשת שונה במפה המקורית ("קו גבול בין שתי מדינות סמוכות").
• פאה בגרף הדואלי ("מסלול מעגלי של רכבות") הייתה צומת במפה המקורית ("נקודת מפגש של גבולות")

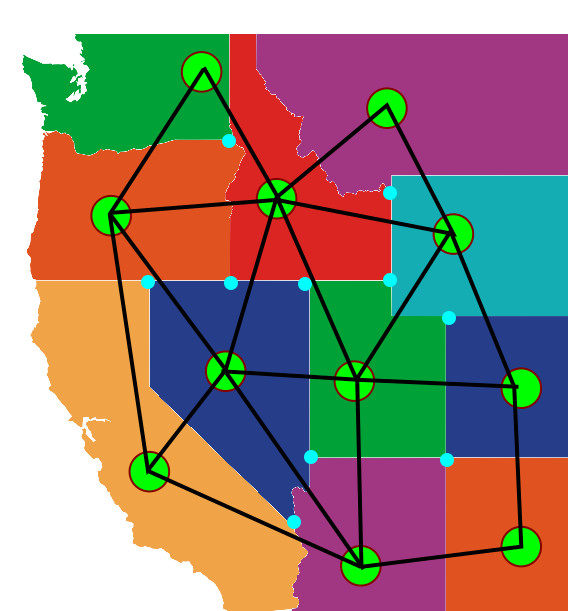
באיור, שבו הוספתי סימון עבור נקודות המפגש של שלושה גבולות ויותר, קל יחסית להבין את המעבר הזה. אם הייתה לנו מדינה בגרף המקורי, אז הצומת שמתאים לה הוא הצומת היחיד שנמצא בתוך “שטח” המדינה. עבור קשתות, כל קשת בגרף הדואלי חוצה בדיוק קשת אחת בגרף המקורי, מה שנותן את ההתאמה ביניהן. מה שאולי קצת מבלבל הוא ה”קסם” שבמסגרתו כל צומת מהגרף המקורי (מפגש של כמה גבולות) נמצאת עכשיו בתוך פאה בודדת של הגרף הדואלי, אבל העקרון ברור - אפשר לעבור במסלול מעגלי על כל המדינות שהגבול שלהן משתתף בצומת הזה.

עכשיו אפשר לחזור ולדבר על נוסחת אוילר. היא פשוטה להחריד: אם \( V \) הוא מספר הצמתים בגרף מישורי, \( E \) הוא מספר הקשתות ו-\( F \) הוא מספר הפאות שלו (כולל הפאה “החיצונית”) אז \( V-E+F=2 \). הנוסחה התמימה הזו היא כנראה הנוסחה האהובה עלי במתמטיקה, וכבר הקדשתי לה פוסט (שעוסק בפאונים ולא בגרפים מישוריים אבל זה אותו הדבר; במקור אוילר אכן הוכיח אותה לפאונים).

קאמפ משתמש בנוסחת אוילר כדי להוכיח שבכל גרף מישורי חייב להיות צומת עם לכל היותר חמישה שכנים. החלק הזה במאמר של קאמפ הוא נכון לחלוטין והטיעון לא קשה; בואו נבין אותו עד הסוף. חוץ מנוסחת אוילר אצטרך עוד כמה נוסחאות שאפשר להסיק על גרפים מישוריים די בקלות. ראשית, \( 2E\ge3F \). למה? ובכן, בואו נעבור פאה-פאה ונספור את כל הקשתות שמרכיבות כל פאה. נקרא למספר הזה \( X \). מה אני יודע על \( X \)? ראשית, מכיוון שכל פאה כוללת לפחות שלוש קשתות, הרי ש-\( X\ge3F \) (כי לכל אחת מ-\( F \) הפאות הוספנו ל-\( X \) לפחות 3). שנית, מכיוון שכל קשת שייכת בו זמנית בדיוק לשתי פאות, הרי ש-\( X=2E \) (כי ספרנו כל קשת פעמיים). קיבלנו \( 2E\ge3F \) בלי להתאמץ בכלל.

עכשיו, בואו נסמן ב-\( p_{i} \) את מספר הצמתים בגרף שיש להם \( i \) שכנים. שימו לב שמספר השכנים של צומת שווה בדיוק למספר הקשתות שמחוברות אליו, ושבשיטת הספירה הזו כל קשת נספרת פעמיים (פעם אחת לכל אחד משני הצמתים שאליהם היא מחוברת). לכן אנחנו מקבלים את הנוסחה הבאה:

\( 2E=p_{1}+2p_{2}+3p_{3}+\dots \)

הסכום באגף ימין הוא לא אינסופי כי החל ממקום מסויים \( p_{i}=0 \) לכל \( i \) ולכן הסכום נעצר שם.

עכשיו, כמה צמתים יש בגרף בסך הכל? סכום מספר הצמתים עם שכן אחד, ומספר הצמתים עם שני שכנים, וכדומה:

\( V=p_{1}+p_{2}+p_{3}+\dots \)

עכשיו ננקוט בתעלול אלגברי נחמד: נכפול את המשוואה השניה ב-6 ונחסר ממנה את הראשונה. נקבל:

\( 6V-2E=5p_{1}+4p_{2}+3p_{3}+2p_{4}+p_{5}-p_{7}-2p_{8}-\dots \)

או בסימון מקוצר:

\( 2\left(3V-E\right)=\sum_{i=1}^{\infty}\left(6-i\right)p_{i} \)

עד עכשיו לא השתמשנו בכלל בנוסחת אוילר. כעת אפשר להשתמש בה: אני מסיק ממנה ש-\( V=2+E-F \), מציב ב-\( 2\left(3V-E\right) \) ומקבל:

\( 2\left(3V-E\right)=2\left(6+3E-3F-E\right)=12+2\left(2E-3F\right) \)

מכיוון ש-\( 2E\ge3F \), הביטוי כולו הוא חיובי (הוא 12 ועוד משהו אי-שלילי). כלומר, גם הסכום \( \sum_{i=1}^{\infty}\left(6-i\right)p_{i} \) הוא חיובי. אבל יש בסכום הזה רק חמישה איברים חיוביים:

\( 5p_{1}+4p_{2}+3p_{3}+2p_{4}+p_{5} \)

המסקנה היא שלפחות אחד מה-\( p_{i} \)-ים הללו צריך להיות חיובי, והוא מתאים בדיוק לצומת עם חמישה שכנים או פחות, כפי שרצינו.

מה קאמפ עשה כאן? הוא הראה שבכל מפה צריכה להופיע תבנית מסויימת - או, כפי שאני מעדיף לקרוא לה, קונפיגורציה. במקרה הנוכחי, מדינה עם חמש שכנות או פחות. זה היה החלק הראשון של הרעיון שלו. החלק השני היה להראות שאם בגרף מישורי יש תבנית כזו, אז אפשר להקטין את הגרף (להקטין את מספר הצמתים) כך שאם הגרף לא היה 4-צביע קודם, גם אחרי ההקטנה הוא עדיין לא יהיה 4-צביע. אם זה היה עובד, זה היה מוכיח בקלות את המשפט כי בהינתן גרף “לא 4-צביע” אפשר היה פשוט להקטין אותו עוד ועוד עד לקבלת גרף כל כך קטן שהוא חייב להיות 4-צביע (למשל, אם יש בו רק 4 צמתים). דרך אחרת, טיפה יותר אלגנטית מתמטית, היא לומר ש”מבין הדוגמאות הנגדיות למשפט ארבעת הצבעים ניקח אחת שהיא מינימלית ביחס למספר הצמתים שלה”, ואז כשאפשר להקטין את מספר הצמתים ועדיין לקבל דוגמא נגדית, זו סתירה ל”מינימלית”.

בואו ננסח מחדש את התכונה הזו בצורה חיובית. מה שאני רוצה להוכיח הוא שאם בגרף יש תבנית מסויימת, אז אפשר לבחור צומת, להסיר אותה מהגרף ו”לתקן” את הגרף בהתאם כך שמקבלים גרף קטן יותר, ואז אם הגרף הזה צביע ב-4 צבעים, אפשר לחזור אל הגרף המקורי ולהשתמש בצביעה הזו כדי לבנות צביעה ב-4 צבעים של הגרף המקורי, כולל הצומת שהסרנו קודם. איך?

ובכן, יש לנו חמישה מקרים לטפל בהם, החל מצומת עם שכן אחד וכלה בצומת עם חמישה שכנים. שלושת המקרים הראשונים קלים. אם יש לנו צומת עם לכל היותר שלושה שכנים, אפשר פשוט להסיר אותו מהגרף, לצבוע את הגרף שהתקבל כתוצאה מכך, ואז לחזור אל הגרף המקורי. הצומת שהסרנו קודם הוא בעל שלושה שכנים בלבד, ויש לרשותנו ארבעה צבעים שבהם אפשר לצבוע את הגרף; פשוט נבחר עבור הצומת שנותר לנו לצבוע צבע כלשהו שאין לשכניו (מובטח שיהיה לפחות אחד כזה, במקרה שבו כל השכנים צבועים בצבעים שונים):

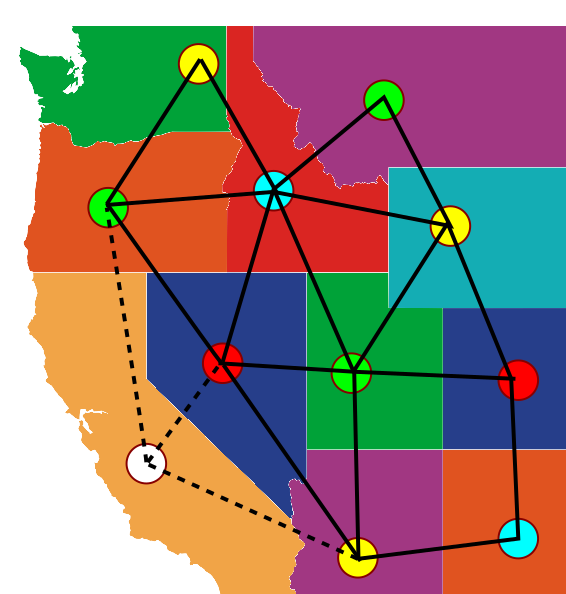
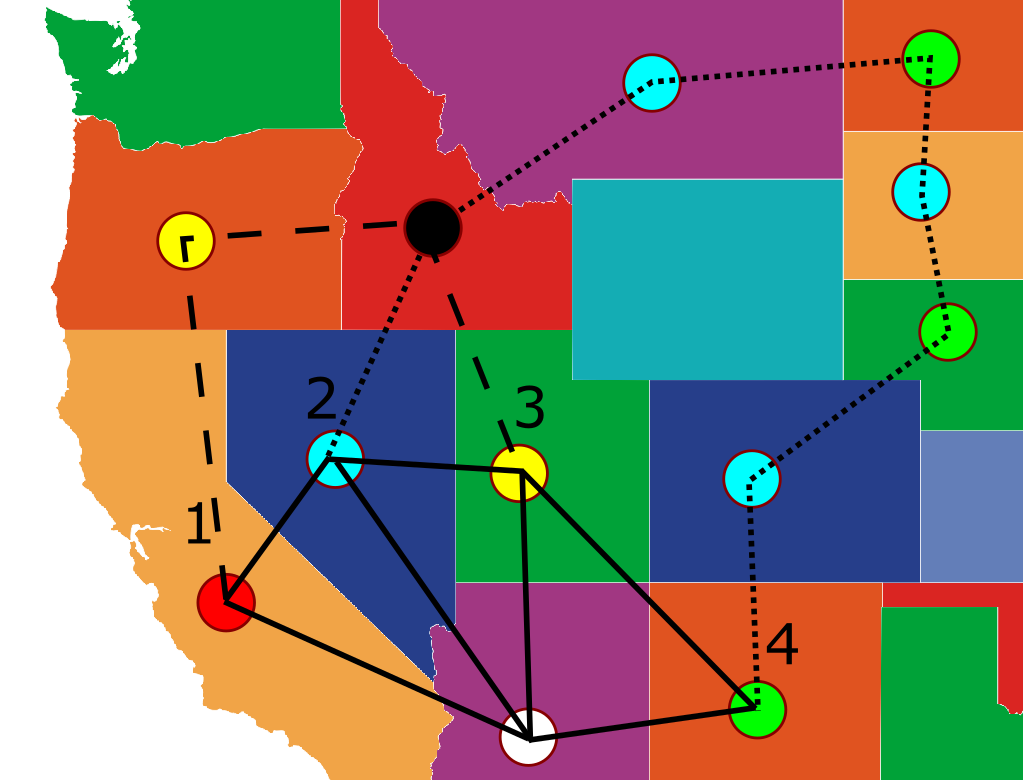
באיור הזה הסרתי את הצומת שמתאים למדינת קליפורניה ויש לו שלושה שכנים. הוא צבוע בלבן כדי לסמן שהוא טרם נצבע, והקשתות שיוצאות ממנו הן מקווקוות כדי לסמן שהן “לא חלק מהגרף”, וכעת צבעתי את יתר הגרף בארבעה צבעים. עכשיו אפשר להסתכל על קליפורניה ולראות במה נצבעו שכנותיה: בירוק, באדום ובצהוב, כך שהצבע הכחול פנוי.

בואו נעבור עכשיו למקרה של צומת עם ארבעה שכנים. נניח שכבר צבענו את יתר הגרף, אבל לרוע המזל כל השכנים של הצומת נצבעו בצבעים שונים. מה עושים עכשיו?

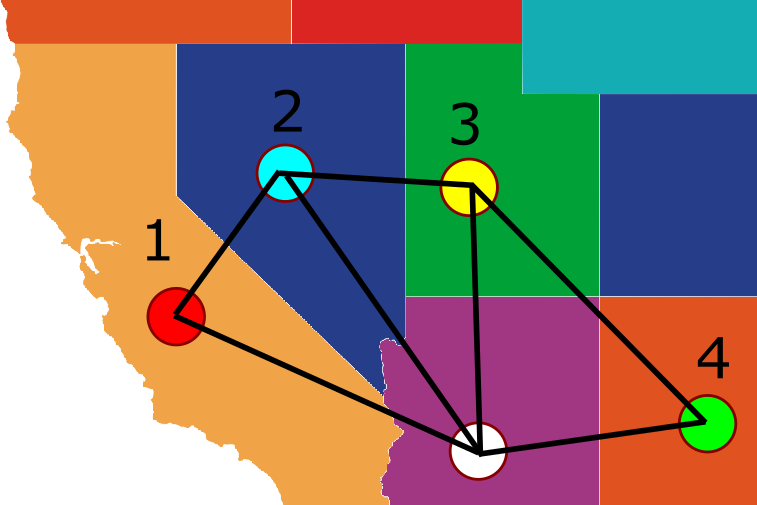
כאן קאמפ הציע את הרעיון היפה שלו. נבחר את אחד מהשכנים, נאמר את שכן מספר 1, ונחליף את הצבע שלו לצבע של שכן מס’ 3. במקרה שלנו שכן מס’ 1 הוא אדום ואילו 3 הוא צהוב, אז נצבע מחדש את שכן מס’ 1 בצהוב. בזאת “פינינו” את הצבע האדום ואפשר לצבוע בו בלב שקט את הצומת שבאמצע. רק מה, שינוי הצבע של שכן מספר 1 עלול לגרום לבעיות חדשות. מה אם לשכן מס’ 1 יש שכנים שכבר צבועים בצהוב?

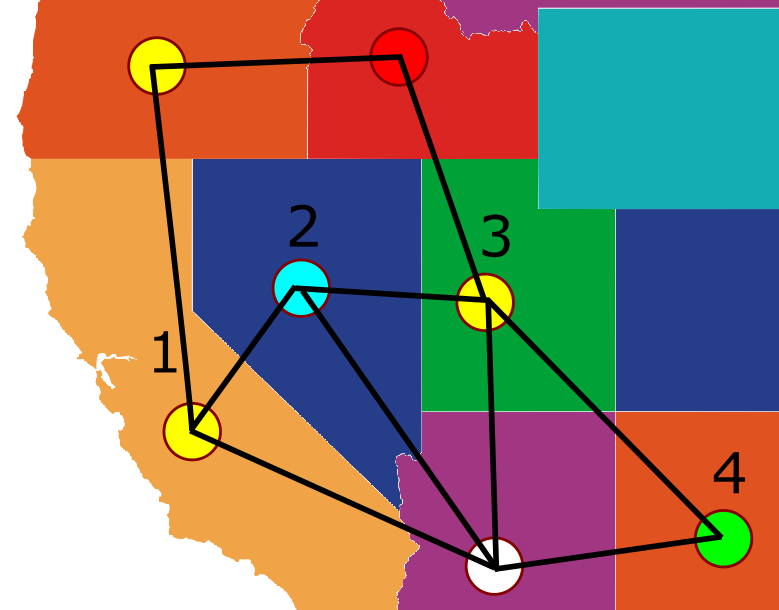
ובכן, במקרה הזה קאמפ מציע פשוט לשנות את הצבע של השכנים הללו לאדום. אבל אם יש להם שכנים אדומים? ובכן, שיוחלפו בצהובים, וכן הלאה וכן הלאה. אנחנו מקבלים מעין תגובת שרשרת לשינוי הצבע, אבל אין כאן משהו לא חוקי. במקרה הכי גרוע נקבל החלפה “מלאה” של הצבעים בגרף - כל הצמתים הצהובים יהפכו לאדומים, וכל הצמתים האדומים יהפכו לצהובים. עדיין נקבל גרף עם צביעה חוקית, אבל… אבל אם הצבע של שכן מס’ 3 יתהפך מצהוב לאדום בעצם לא הרווחנו כלום - עדיין כל השכנים של הצומת באמצע יהיו צבועים בצבעים שונים זה מזה.

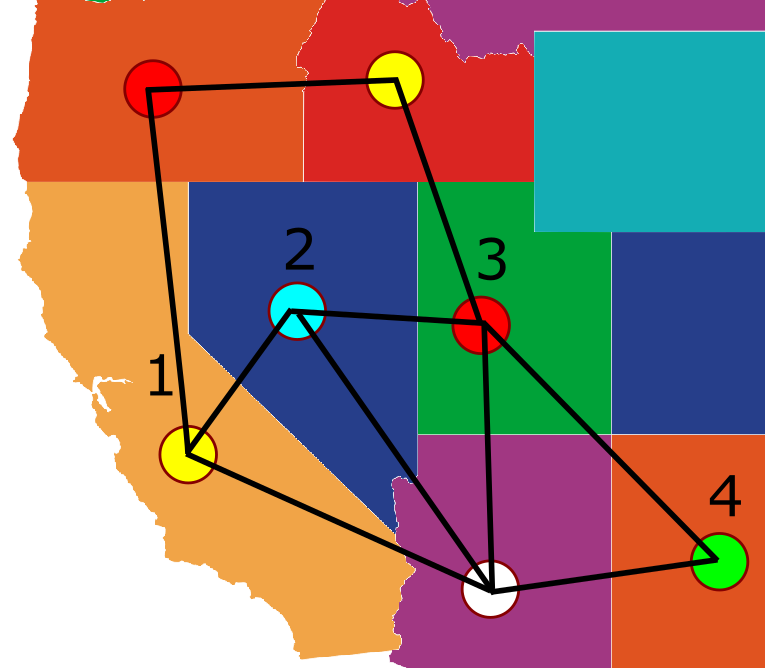
קאמפ אומר שכדי ששינוי הצבע של צומת מס’ 1 ישפיע ככה על צומת מס’ 3, חייבת להתקיים שרשרת שמובילה מצומת 1 לצומת 3 והצמתים בה צבועים לסירוגין באדום וצהוב. שרשרת מסוג זה נקראת כיום על שמו - שרשרת קאמפ. כמובן שאין מניעה לכך שבאמת תהיה כזו שרשרת וקל לבנות גרפים שבהם זה קורה. בואו נחזור לסיטואציה המקורית בגרף לדוגמא שלנו ונדגיש בה את השרשרת:

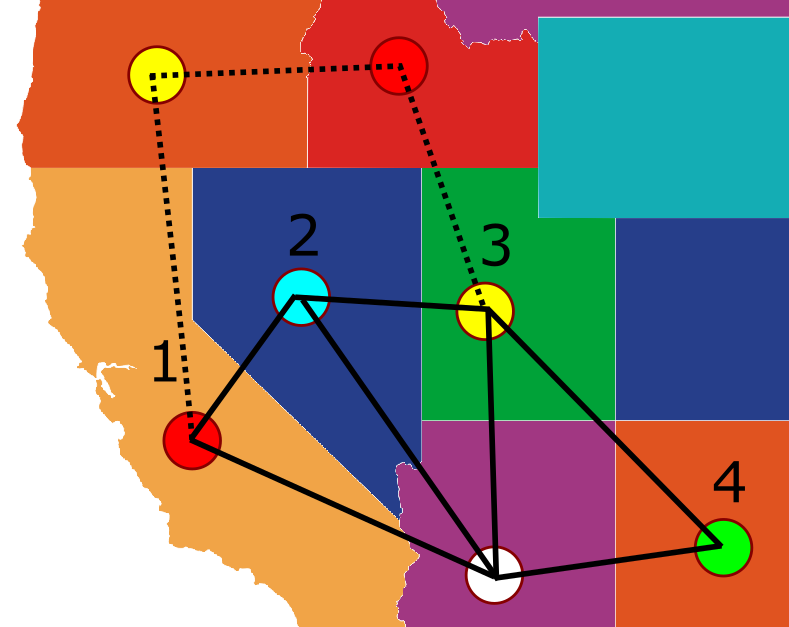
אז מה עושים?

אה-הא! בואו לא נשכח שיש לנו גם את צומת 2 וצומת 4! אפשר לעשות את תעלול החלפת הצבעים גם עבורן! וגם… וגם עבורן הוא עשוי להיכשל באותו האופן בדיוק, עם שרשרת קאמפ:

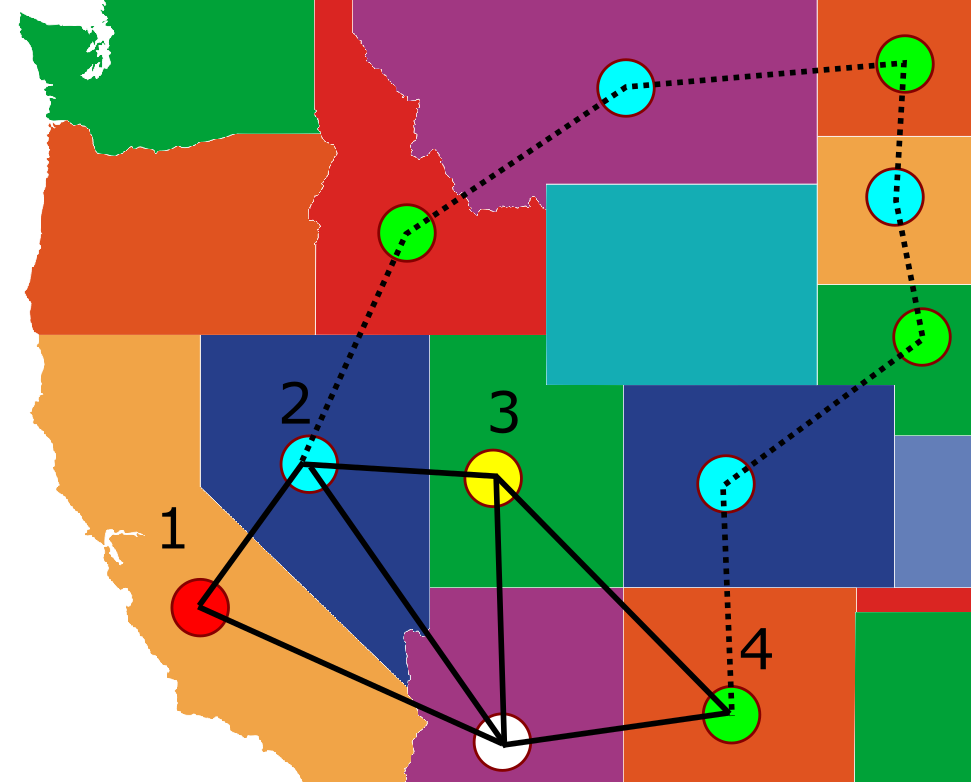
אבל כאן נכנס טיעון המחץ של קאמפ - הגרף הוא מישורי ולכן השרשרת מ-1 אל 3 והשרשרת מ-2 אל 4 בהכרח מתנגשות - כלומר, חייב להיות להן צומת משותף (אחרת יהיו קשתות מהשרשראות שחותכות זו את זו) אבל לא יכול להיות לשרשראות צומת משותף כי שרשרת אחת היא בצבעי אדום-צהוב והשניה בצבעי כחול-ירוק. זה מסיים את הטיעון הזה. אין פה שום טעות - זה עובד, ועובד נפלא. אפשר לכתוב אלגוריתם על פי השיטה שקאמפ הציע פה והוא אכן יצליח “לתקן” את הצביעה של הגרף בהתאם ולאפשר צביעה של הצומת הנוסף בצבע שלא מתנגש עם שכניו.

אז מה הבעיה? הבעיה היא שצריך לטפל גם במקרה של צומת עם חמישה שכנים. כאן קאמפ ניסה להשתמש בטיעון דומה ויצא לו משהו מאוד משכנע, עם טעות מאוד עדינה שקשה להבחין בה במבט ראשון - אבל תנסו!

אם לצומת יש חמישה שכנים, אז בצביעה של הגרף בלי הצומת הזה, בהכרח יש צבע אחד לפחות שמופיע פעמיים. כמובן, אם לא כל ארבעת הצבעים מופיעים אנחנו שוב במקרה טריוויאלי, ולכן אנחנו מניחים שכל ארבעת הצבעים מופיעים, ואחד מהם מופיע בשני צמתים שונים. עכשיו אפשר להבדיל בין שתי אפשרויות שונות. הראשונה היא שהצבע הכפול - בואו נאמר שהוא האדום - מופיע בשתי מדינות “סמוכות” אבל ללא גבול משותף:

זו סיטואציה שניתנת לטיפול כמו קודם: קודם כל ננסה להפוך את הצהוב לכחול. אם הצלחנו, מה טוב. אם לא, יש שרשרת קאמפ שמחברת את הצהוב והכחול ולכן “מבודדת” את הירוק מהאדומים. אפשר אם כן להפוך את הירוק לאדום, וסיימנו. גם פה אין טעות.

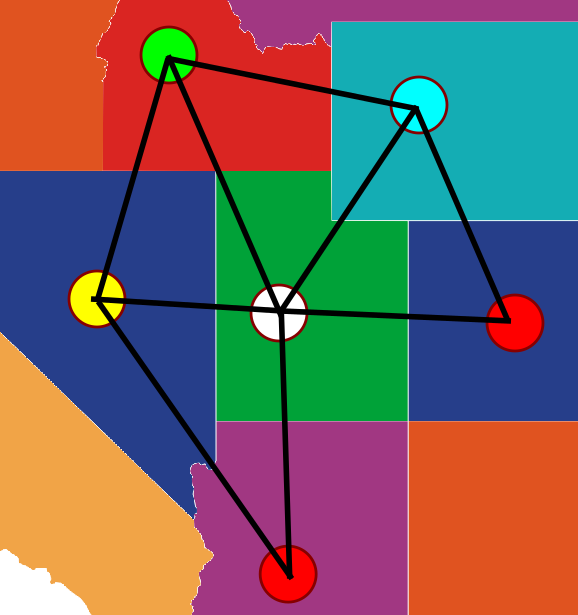
הסיטואציה המעניינת היא זו שבה שתי המדינות האדומות לא יכולות להיות “סמוכות” כי בין כל שני שכנים סמוכים של הצומת המרכזי יש קשת. הנה דוגמא לסיטואציה הזו:

כאן פשוט אי אפשר להפוך אף צומת לאדום, כי כל אחד מהצמתים הוא שכן של אדום. לכן הפתרון שעבד עבור ארבעה צמתים לא יעבוד כאן - מה שהוא לכל היותר מבטיח שהוא שנוכל לקחת את אחד מהצמתים האדומים ולשנות את הצבע שלו, אבל זה ישאיר אותנו עם צומת אדום אחר. לכן צריך כאן טיעון מתוחכם יותר, וזה מה שקאמפ עושה.

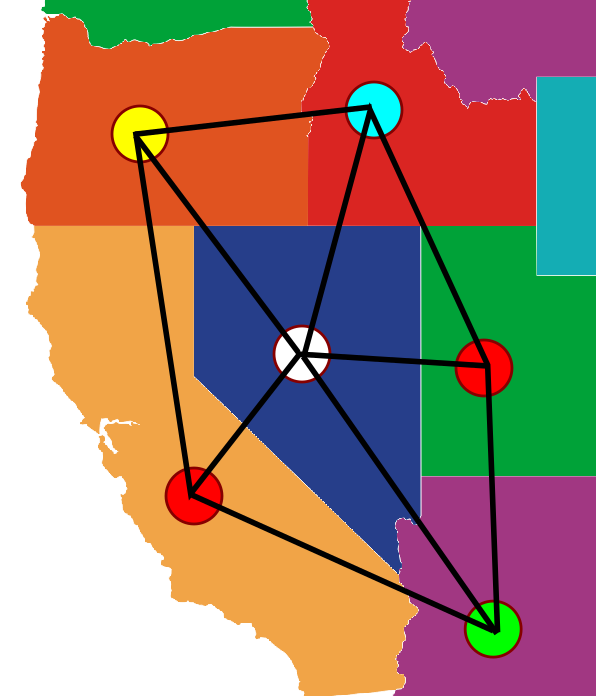
קאמפ אומר - בואו ניקח את הירוק ונבדוק אם אפשר להפוך אותו לכחול או צהוב. אם אפשר, יופי! אחרת, יש שרשרת ירוק-כחול ויש שרשרת ירוק-צהוב שמקלקלות לנו. באיור הרשיתי לעצמי לשים את שרשרת הירוק-צהוב בים - פשוט תדמיינו שהרחבתי את ארה”ב עם עוד מדינות רלוונטיות.

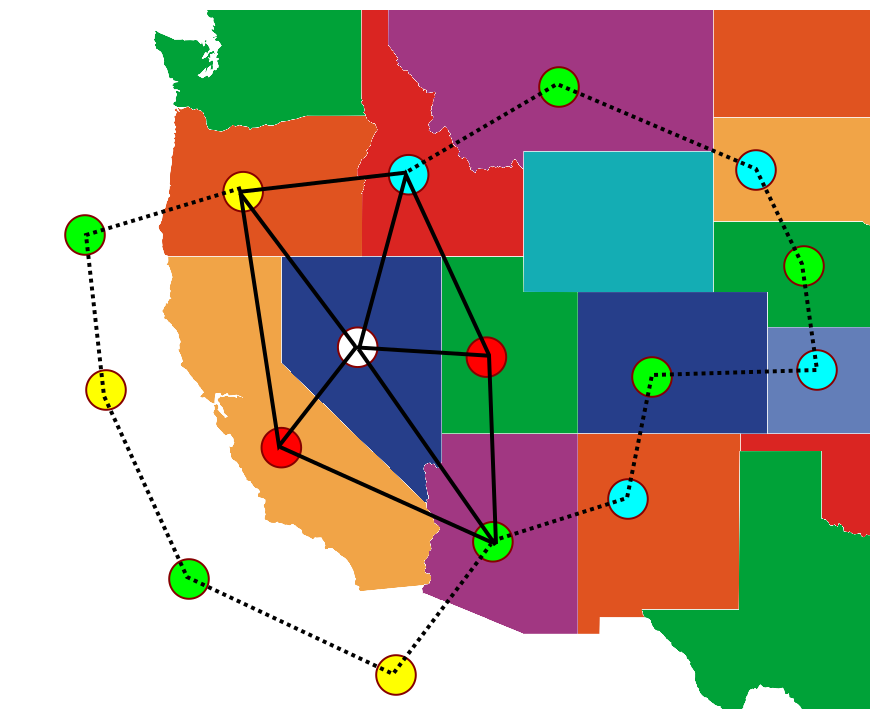
מה שקורה עכשיו הוא ששני הצמתים האדומים מוחבאים “בתוך” השרשראות - האדום השמאלי מנותק מהצומת הכחול, והאדום הימני מנותק מהצומת הצהוב (שימו לב שזה עדיין יקרה אם אם השרשרת הירוקה-צהובה לא תקיף אותו בכלל אלא תקיף את השרשרת הירוקה-כחולה; גם זה תרחיש אפשרי). פירוש הדבר הוא שאפשר לשנות את האדום הימני לצהוב ואת האדום השמאלי לכחול, ובכך להיפטר כליל מהצבע האדום ואז אפשר לצבוע בו את הצומת שבמרכז.

כאן יש טעות. אבל מהי?

הבאג בהוכחה הוא משהו שיכול להתגלות יחסית בקלות אם מממשים אלגוריתם פרקטי שמנסה לצבוע מפות באמצעות הטריק הזה ומפילים עליו המון מפות אקראיות - הטריק פשוט ייכשל מתישהו. מתי? בוודאי שאין שום סיבה שהוא ייכשל בהחלפת כחול/ירוק או בהחלפת צהוב/ירוק במקרים שבהם אין שרשראות מתאימות; לכן אם הוא נכשל בשני השלבים הללו זה מראה שהשרשראות שציירתי באיור למעלה אכן קיימות. והן אכן מנתקות את האדומים מהצהוב/כחול בהתאמה. אז מה בכל זאת ייכשל? ייכשל שלב הצביעה-מחדש של האדומים. ליתר דיוק, הצביעה-מחדש הראשונה תעבוד, אבל אז הצביעה-מחדש של האדום השני עלולה להיכשל באופן מזעזע. קשה לנו לראות את זה במבט ראשון כי האינטואיציה שלנו חושבת על שתי הצביעות-מחדש הללו בתור משהו שקורה “באותו הזמן” (או, במקרה שלי, פשוט חשבתי עליהן בתור “ברור שאפשר לעשות אותן” ואפילו לא הקדשתי מחשבה לביצוע שלהן בפועל ומה שיתרחש במהלכו).

הנה הסבר עקרוני על מה שיכול להשתבש. האיור שלמעלה מטעה כי הוא נותן תחושה ששרשראות הצהוב-ירוק והכחול-ירוק הן נפרדות לגמרי זו מזו. אבל האמת העצובה היא שהן עלולות להיות “מעורבבות” - אחת מהן יכולה לעבור דרך השניה ואז לצאת חזרה מהצד השני, כי הן יכולות לשתף צמתים ירוקים. הנה דוגמא אפשרית:

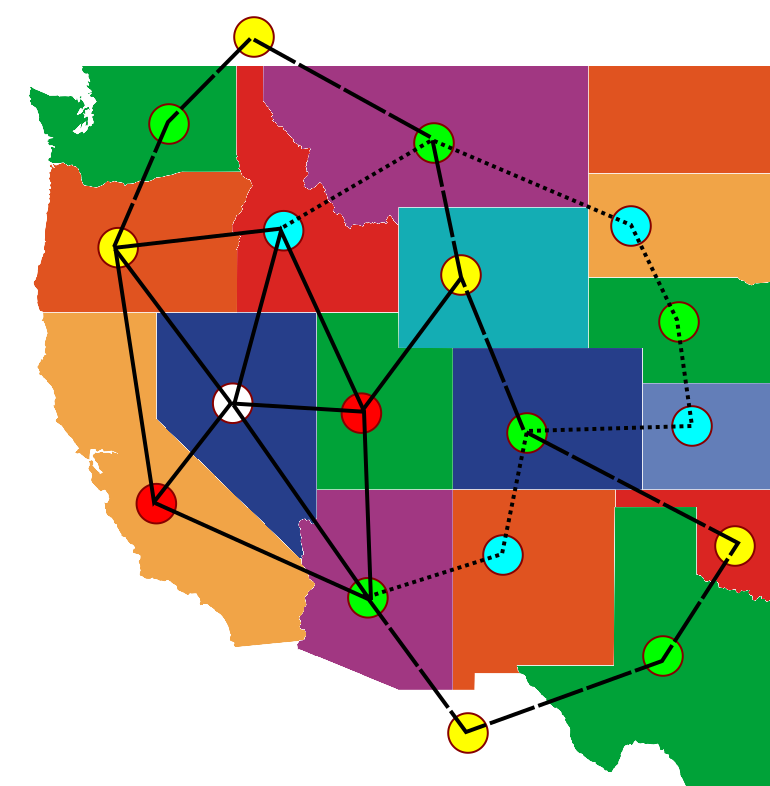
כאן הקו המקווקו העבה הוא השרשרת הצהובה-ירוקה ואילו הקו המקווקו הדק יותר הוא השרשרת הכחולה-ירוקה, ואנחנו רואים בבירור איך השרשרת הצהובה-ירוקה חותכת את השניה. ואנחנו גם רואים משהו עוד יותר גרוע בפנים - הצומת האדום הימני יותר, זה שאמור להיות מוחלף לצהוב, מחובר לאחד מהצמתים הצהובים על השרשרת הצהובה-ירוקה. זה אומר שכאשר נחליף אותו לצהוב, נשבור את השרשרת הצהובה-ירוקה - חלק ממנה יהפוך לאדום. ברגע שבו זה קרה, ההיפוך של האדום השני, זה שאמור להפוך לכחול, עשוי לגרום לכחול הנוסף שמחובר לצומת המרכזי שלנו להתהפך. כלומר, ההיפוך של האדום הראשון יצר שרשרת אדום-כחול שלא הייתה קיימת קודם.

בואו נראה את זה קורה:

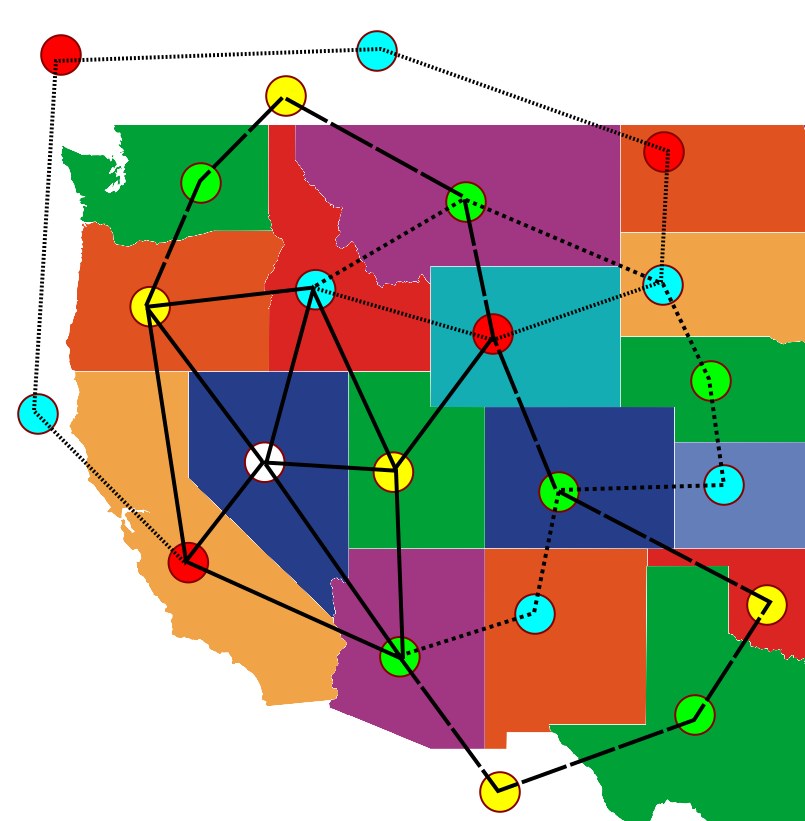
כאן הפכתי את האדום הימני לצהוב, ולכן את שכנו הצהוב לאדום. עכשיו הוספתי עוד צמתים כדי להראות כיצד יכולה להתקבל שרשרת אדום-כחול חדשה, שמנצלת את האדום החדש שזה עתה נוצר. ה”מצור” של השרשרת הצהובה-ירוקה נפרץ.

מבלבל? אוי ואבוי, בהחלט כן. אין פלא שלקחו 11 שנים לשים לב לשגיאה של קאמפ. אבל מרגע שנתגלתה השגיאה, למה בעצם להקדיש זמן ומאמץ להוכחה של קאמפ? ובכן:

1. כי היא יפה.
2. כי היא עדיין מוכיחה משפט לא טריוויאלי באפס מאמץ - שאפשר לצבוע כל מפה מישורית בחמישה צבעים, והיא גם מציעה שיטה לכך (ההוכחה לכך מטפלת במקרה של צומת עם חמישה שכנים בדיוק כמו שטיפלנו במקרה של צומת עם ארבעה שכנים - מוצאים שני זוגות שלפחות בין אחד מהם לא יכולה להיות שרשרת, ו"נפטרים" מצבע אחד בעזרתו).
3. כי הרעיונות שלה הם גם מה שהשתמשו בו בהוכחה ה"אמיתית", רק בוריאציה הרבה יותר מסובכת.

אבל הדבר הכי מעניין בהוכחה השגויה הזו הוא שבזכות השגיאה, המשפט כל כך מפורסם. אם ההוכחה של קאמפ הייתה עובדת, קרוב לודאי שמשפט ארבעת הצבעים היה נשכח שם, בתור אנקדוטה חביבה עם הוכחה לא עמוקה במיוחד. העובדה שההוכחה נפלה, ובצורה כל כך מתסכלת, ונדרשה כל כך הרבה יותר עבודה כדי להוכיח את המשפט לבסוף - זה כבר מהדהד את ה"הוכחה הנפלאה" שפייר דה פרמה טען שיש לו למשפט שלו וסביר להניח שכללה גם כן טעות עדינה שהטעתה בזמנו את פרמה. זה מה שהפך את משפט ארבעת הצבעים למפורסם כל כך.