אז מה זה מחשב קוונטי?

בשנים האחרונות מחשבים קוונטיים עולים יותר ויותר לכותרות ואני רוצה בפוסט הזה להסביר על מה מדובר בצורה שגם מי שלא מכירים את התחום בכלל יוכלו להבין. כבר יש לי סדרת פוסטים בנושא שמתחילה כאן ונכנסת לפרטים הטכניים, אבל פה אני רוצה לתת סקירה כללית יותר, וגם להתייחס יותר להיבטים הפרקטיים של הנושא. אז מה זה מחשב קוונטי ובשביל מה צריך אותו?

אם להצטמצם לפסקת מחץ אחת, אז מחשב קוונטי הוא מחשב שמתבסס על גישה לייצוג ועיבוד מידע שהיא שונה דרסטית מזו של מחשב רגיל, ומתבססת באופן ישיר על תופעות פיזיקליות שנופלות תחת המסגרת של תורת הקוונטים בפיזיקה (ומכאן השם “מחשב קוונטי”). לגישה השונה הזו יש יתרונות וחסרונות. היתרונות הם שיש דברים מסויימים שמחשב קוונטי יכול, תיאורטית, לבצע במהירות גדולה יותר במידה דרסטית (של “כמה דקות” מול “מיליוני שנים”), ולכן דה-פקטו הוא יוכל לבצע חישובים מסויימים שלא יהיה ניתן לבצע בשום דרך אחרת; והחסרונות הם שקשה משמעותית יותר לבנות ולהפעיל מחשבים כאלו, עד לרמה שבה גם כיום אנחנו לא בטוחים שנוכל לבנות מחשב קוונטי שיהיה שימושי לנו בפועל (מחשבים קוונטיים מתפקדים קיימים כך כיום, אבל הם עדיין בסיסיים ביותר ולא שימושיים לצרכים מעשיים).

לפני שנדבר על מחשב קוונטי אני רוצה לומר כמה דברים על מה שמחשב רגיל עושה. מחשבים הם יצורים מופלאים שמלווים אותנו כיום ברוב תחומי החיים ואנחנו משתמשים בהם לשלל מטרות שונות, אבל בבסיסם הם עושים משהו מאוד פשוט: מחשב מקבל קלט, מבצע עיבוד של הקלט ומחזיר פלט. הקלט והפלט הם מידע דיגיטלי: המחשב רואה אותם בסך הכל בתור סדרות של ביטים, כאשר “ביט” הוא בסך הכל משהו שיכול להיות הסימן 0 או הסימן 1. הנה דוגמא פשוטה: אנחנו מדברים אל המחשב שלנו והוא כותב את הטקסט של מה שאמרנו.

מה הלך פה? לא דיברנו ישירות אל המחשב אלא אל מיקרופון, שהוא התקן שלקח את גלי הקול שהפקנו מהפה שלנו והמיר אותם למידע דיגיטלי - לסדרה של ביטים. המחשב קיבל את הסדרה הזו וביצע עיבוד שלה - הריץ עליה מה שנקרא אלגוריתם, שהוא סדרה של פקודות שמיועדות להשיג מטרה מסויימת; במקרה הנוכחי המטרה היא לפענח את מה שאמרנו ולתרגם אותו למילים. יש אלגוריתמים רבים ושונים שמיועדים למטרה הזו וחלקם מתוחכמים למדי, אבל בסופו של דבר הפלט הוא זהה: סדרה של ביטים שמייצגת מילים. את המידע הזה המחשב העביר הלאה, אל המסך שלנו, והמסך מתרגם את המידע הדיגיטלי הזה לקרני אור שהעיניים שלנו מסוגלות לקלוט. אני לא חושב על המיקרופון ועל המסך בתור חלק מהמחשב אלא בתור עזרים חיצוניים שמשמשים ל”תיווך” בינינו ובין המחשב. המחשב עצמו הוא רק היצור שאחראי לקחת סדרה אחת של ביטים ולהמיר אותה בסדרה אחרת של ביטים.

האופן שבו מחשב עובד הוא מרתק - גם האלגוריתם המחוכם ביותר בעולם בסופו של דבר מתורגם לפעולות פשוטות להחריד שהמחשב עושה על הביטים. ברמה של “קח שני ביטים, אם שניהם 0 תחזיר 0 ואחרת תחזיר 1” (זה נקרא פעולת או לוגי). כל חישוב הוא סדרה ארוכה של הפעלות של הפעולות הפשוטות הללו, שנקראות שערים לוגיים. כמובן שאפשר לתאר את הסיטואציה בצורה יותר מורכבת אבל זה מספיק לעת עתה כדי להבין מה זה חישוב “רגיל”.

כדי להסביר מה מחשב קוונטי בעצם עושה, אני זקוק לחתולים. תודה לנועה ליברמן-פלשקס שאיירה לי את המחשב הקוונטי הראשון בעולם שנבנה באמצעות חתולים!

איור: נועה ליברמן-פלשקס

מה הולך פה? יש לנו משהו מוזר שכולל שלושה חתולים, שאתן להם שמות במקום סתם לקרוא להם א’, ב’, ג’: ארצ’יבלד, בהמות וגריזלדה (מלמעלה למטה). כרגע שלושתם נראים חייכנים ומרוצים מהחיים, אבל חכו חכו, עוד רגע המחשב יופעל ויקרה להם משהו מוזר מאוד!

איור: נועה ליברמן-פלשקס

סופרפוזיציה, או: מה הולך פה בכלל?

אם במחשב רגיל יחידת המידע הבסיסית נקראת ביט, אז במחשב קוונטי יחידת המידע הבסיסית נקראת קיוביט. להבדיל מביט שיכול להיות או 0 או 1 וזהו, קיוביט יכול להיות סופרפוזיציה של הערכים 0 ו–1. סופרפוזיציה היא התופעה הבסיסית שביסוד תורת הקוונטים, והיא מה שהופך מחשבים קוונטיים לשונים כל כך ממחשבים רגילים. לכן אנחנו צריכים להבין מה המושג הזה אומר ומה הוא לא אומר. אני מייצג בתמונה סופרפוזיציה בתור “ענן של מהומה” אבל צריך להסביר מה קורה בתוך הענן הזה.

בואו נסתכל על גריזלדה הלבנה. בתוך הענן למעלה אפשר לראות את הגרסה ה”נחמדה” שלה שראינו גם בתמונה הראשונה. מצד שני, למטה מימין יש גם גרסה “מוזרה” שלה (גריזלדה מייצגת קיוביט: אפשר לחשוב על הגרסה ה”חייכנית” בתור הערך 0 של הקיוביט, ועל הגרסה ה”מוזרה” בתור הערך 1 שלו). הסופרפוזיציה היא תערובת של שתי הגרסאות האפשריות של גריזלדה (וגם של החתולים האחרים שעוד נגיע אליהם). הסיבה לכך שאני משתמש בחתולים מלכתחילה היא הניסוי המחשבתי שנקרא החתול של שרדינגר שבו מתוארת סופרפוזיציה באמצעות חתולים, אבל שם המצבים האפשריים של החתול הם “חי” ו”מת” ואני בוודאי לא רוצה לצייר לכם חתולים מתים.

בסיטואציה “קלאסית” (המילה “קלאסית” באה לדבר על התיאור של המציאות שנותנת הפיזיקה הקלאסית, זו שלפני מכניקת הקוונטים) היינו מצפים שגריזלדה תהיה “נחמדה” או “מוזרה” אבל לא שתי האפשרויות בו זמנית. בסיטואציה קוונטית המצב מורכב יותר: גריזלדה עדיין לא בשתי האפשרויות בו זמנית אלא בתערובת כלשהי שלהן. מה זה אומר “תערובת”? זה מה שהמתמטיקאים משתמשים בביטוי “צירוף לינארי” כדי לתאר אותו. זה אומר שהתיאור המתמטי המדויק של מה שעובר על גריזלדה יכול להיראות כך:

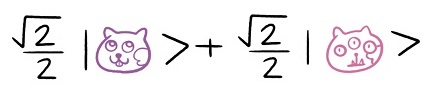
לא חייבים להבין את הסימונים עד הסוף אלא רק את העיקרון - בתמונה רואים את שני המצבים האפשריים של גריזלדה - “נחמדה” ו”מוזרה”, כשהם נמצאים בין סימון שנראה כמו \( \left|\cdot\right\rangle \) והוא מופיע כאן כי זה הסימון המקובל בפיזיקה (השם שלו הוא ket) כל אחד מהמצבים הללו מוכפל במספר \( \frac{\sqrt{2}}{2} \), שהוא המקדם של המצב. המקדמים הללו הם אלו שקובעים את ה”אופי” של הסופרפוזיציה; מספרים שונים מובילים לסופרפוזיציות שמתנהגות שונה. במקרה הנוכחי שני המספרים זהים וזה אומר ששני המצבים הם “בעלי אותו משקל” מבחינת הסופרפוזיציה, אבל באופן כללי זה ממש לא חייב להיות המצב.

יש תפיסות שגויות נפוצות לגבי מהי סופרפוזיציה, אז הנה כמה אמירות נחרצות:

• גריזלדה היא לא נחמדה ומוזרה בו זמנית. סופרפוזיציה פירושה שהיא לא זה ולא זה אלא תערובת של שני אלו.
• גריזלדה היא לא נחמדה בהסתברות כלשהי ומוזרה בהסתברות אחרת. סופרפוזיציה פירושה שהיא בתערובת של שני אלו ואין פה הסתברות (תהיה הסתברות בהמשך).
• גריזלדה היא לא נחמדה או מוזרה ופשוט חסר לנו מידע שיאפשר לדעת מה משני אלו נכון. היא באמת בתערובת של שני אלו, זה לא רק מידע חסר.

כל זה נשמע מוזר מאוד ובוודאי שלא תואם את הנסיון היומיומי שלנו עם חתולים. זה מכיוון שחתולים אכן לא מקיימים סופרפוזיציות שאנחנו שמים אליהן לב. סופרפוזיציה היא משהו שמתרחש בסדרי גודל קטנים בהרבה משל חתול; בדברים כמו אלקטרון בודד, למשל. גם בסדרי גודל כאלו סופרפוזיציה עדיין נשמעת כמו דבר מוזר מאוד, אבל קשה להתווכח עם המציאות - המציאות היא שסופרפוזיציה היא משהו שאכן קורה.

ליתר דיוק, מה שקורה בפועל הוא שאם אנחנו בונים מודל מתמטי שמנסה לתאר סיטואיציה מציאותית כלשהי, והמודל הזה נבנה בעזרת התיאור המתמטי של תורת הקוונטים, אז הניבויים שהמודל הזה יתן לנו יהיו מדוייקים בצורה יוצאת דופן. האם זה אומר שמה ש”באמת קורה שם בפועל” הוא התיאור המתמטי של תורת הקוונטים? ומה התיאור הזה בכלל אומר? מה זה \( \frac{\sqrt{2}}{2} \) “מוזרה”? כאן אנחנו נכנסים לשאלת הפרשנות של תורת הקוונטים שראויה לפוסט נפרד.

נחזור אל הסופרפוזיציה שלנו. עד כה דיברתי על סופרפוזיציה של גריזלדה ותו לא - היו שני “מצבי גריזלדה” ודיברתי על תערובת שלהם. אבל בפועל יש במהומה הזו עוד שני חתולים - ארצ’יבלד ובהמות. כמו אצל גריזלדה, גם אצלם יש שני מצבים שונים והסופרפוזיציה היא תערובת שלהם, אבל המצב הוא יותר מסובך מכך. מערכת קוונטית יכולה לקיים תכונה שנקראת שזירה שפירושה שאי אפשר לחשוב עליה כאילו היא מורכבת משתי מערכות שיושבות זו לצד זו בלי קשר ביניהן, אלא היא מורכבת מבלאגן אחד גדול. במקרה שלנו, זה אומר שאי אפשר להסתכל בנפרד על הסופרפוזיציה של ארצ’יבלד והסופרפוזיציה של בהמות והסופרפוזיציה של גריזלדה; בפועל הסופרפוזיציה מערבת את כל הצירופים האפשריים שלהם.

זו נקודה שבה האיור למעלה פשוט משקר כדי לא להוסיף יותר מדי בלאגן. באיור למעלה רואים רק גרסה אחת של כל מצב אפשרי של כל חתול. אבל בסיטואציה שכוללת שזירה, המצבים הבסיסיים שמהם המערכת מורכבת יכולים לכלול כל שלשה שבה משתתף אחד משני המצבים של החתולים. כלומר: מצב בסיס אחד הוא שלושת החתולים כשכולם “נחמדים” ומצב בסיס אחר הוא שלושת כשכולם “מוזרים” ומצב בסיס אחד הוא כשארצ’יבלד “נחמד” ואילו בהמות וגריזלדה “מוזרים” וכן הלאה - אם סופרים מגיעים לכך שישנם שמונה מצבי בסיס שונים. הנה תיאור מתמטי של העניין:

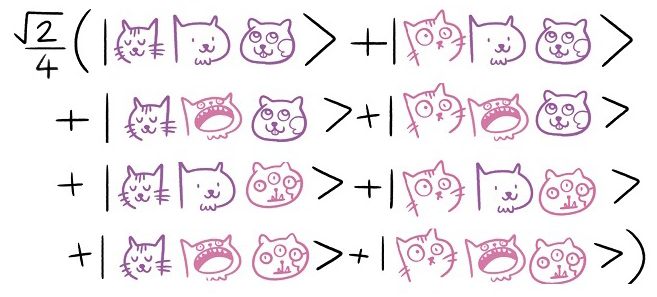
אם הייתי רוצה שהאיור של המחשב הקוונטי בפעולה יהיה מדויק, הייתי צריך לדרוש שהוא יכלול ייצוג לכל השלשות הללו, אבל אז מרוב מהומה לא היה אפשר להבין שום דבר.

עד כאן לא ברור למה סופרפוזיציה היא דבר טוב. מה בכלל עושים איתה? ובכן, בחישוב קוונטי קורים שני דברים עיקריים:

• על הסופרפוזיציה מופעלים שערים קוונטיים שגורמים לה לשינויים. אפשר לחשוב על זה בתור מקל שאנחנו דוחפים לענן וגורמים לו למהומות בפנים.
• על הסופרפוזיציה מופעלת מדידה, שגורמת לסופרפוזיציה לקרוס. קריסה כזו פירושה שאחד ממצבי הבסיס שמרכיבים את הסופרפוזיציה נבחר באופן אקראי (כשההסתברות שלו להיבחר נקבעת על פי המקדם שלו; ליתר דיוק, הערך המוחלט בריבוע של המקדם שלו) ואז הסופרפוזיציה מוחלפת במצב הבסיס הזה.

 

תדמיינו מדידה בתור תהליך שבו גורמים לענן של האיור השני להיעלם ולמחשב לחזור לסיטואציה של האיור הראשון, שבו רואים את החתולים בצורה מובחנת זה מזה; רק שבאיור הראשון כולם נחמדים ואילו מדידה בהחלט עשויה להקריס את הסופרפוזיציה למצב שבו גריזלדה מוזרה ושני האחרים נחמדים, למשל. הנקודה היא שאחרי הקריסה אנחנו יכולים לדעת לאיזה מצב קרסנו; זה השלב היחיד שבו אנחנו מפיקים מידע מהחישוב הקוונטי.

זו נקודה שבה חישוב קוונטי שונה מהותית מחישוב רגיל. בחישוב רגיל המידע שלנו מיוצג על ידי ביטים, וזהו. אין סופרפוזיציות שלהם. חישוב רגיל אפשר לעצור בכל רגע ולקרוא את ערכי הביטים שמשתתפים בחישוב. בחישוב קוונטי זה לא יכול לקרות - אין לנו דרך כלשהי לראות מה קורה “בתוך הענן” של הסופרפוזיציה; הדרך היחידה שלנו להפיק מידע היא לבצע מדידה, והיא הורסת את הסופרפוזיציה ולא מחזירה לנו את המידע המלא שייצג אותה. מה שמאפיין סופרפוזיציה הוא המקדמים של כל אברי הבסיס; מדידה בסך הכל מחזירה לנו איבר בסיס, בלי שום מידע על ערכי המקדמים.

שימו לב כיצד נפלנו מאיגרא רמא לבירא עמיקתא; לפני רגע החישוב הקוונטי שלנו היה קסום; המידע שלנו יוצג על ידי משהו מדהים שנקרא סופרפוזיציה ויכול לעשות הכל. עכשיו פתאום קרסנו לכך שאנחנו לא יכולים להפיק כמעט שום מידע מהחישוב הקוונטי - רק לקבל אברי בסיס בהסתברויות אלו ואחרות. מה שנקרא חישוב קוונטי זה בדיוק מה שיודע לנצל את המתח שבין שני הקצוות הללו כדי להפיק משהו שימושי. המטרה המרכזית שלנו בחישוב קוונטי היא לייצר הסתברות טובה לקרוס למצב מועיל. בנפנוף ידיים לא מדויק לגמרי אפשר לומר שחישוב קוונטי מנסה לגרום לתוצאות הרעות האפשריות של החישוב לבטל זו את זו, ולתוצאות הטובות לחזק זו את זו. השם הפיזיקלי של ביטולים הדדיים וחיזוקים הדדיים שכאלו הוא התאבכות, על שם התופעה הדומה והמוכרת יותר שיש בגלים.

הסברים לגבי האופן שבו משתמשים בהתאבכות כדי “לחזק פתרונות חיוביים” דורשים כבר פוסטים נפרדים שייכנסו לעובי הקורה של אלגוריתמים ספציפיים, אבל אני כן רוצה לומר את הפאנצ’ליין: כדי לבצע התאבכויות שכאלו בצורה טובה אנחנו מתבססים בצורה חזקה מאוד על כך שהמקדמים שמופיעים בתוך סופרפוזיציה יכולים להיות מספרים שליליים או אפילו מספרים מדומים (מספר מדומה הוא מספר שכאשר מעלים אותו בריבוע מקבלים מספר שלילי). אם כל המקדמים היו חייבים להיות חיוביים, לא היינו מסוגלים להשיג את האפקט המופלא הזה.

למה אני חושב שחשוב להדגיש את זה? כי זו הנקודה שבה חישוב קוונטי נפרד מחישוב הסתברותי “רגיל”. לא אכנס כאן לפרטים הפורמליים, אבל אפשר לתאר חישובים הסתברותיים בניסוח דומה לניסוח הסופרפוזיציה שנתתי קודם, אבל המקדמים יהיו חייבים להיות אי שליליים. יוצא שההבדל המהותי בין חישוב קוונטי וחישוב קלאסי טמון במורכבות של הייצוג של מידע קוונטי - מורכבות שבאה לידי ביטוי במשפט כמו “המקדמים יכולים להיות שליליים” שהוא די סתום כל עוד לא נכנסים לפרטים הטכניים. זו אחת הסיבות שבגללה קשה להסביר חישוב קוונטי על רגל אחת; הרבה תיאורים פופולריים של חישוב קוונטי מתארים אותו בתור משהו שיכול להתקיים בחישובים הסתברותיים או מקביליים “קלאסיים”.

האלגוריתם של שור וחברים, או: בשביל מה זה טוב בכלל?

כל מה שסיפרתי עד כה מראה לנו שחישוב קוונטי הוא מסובך יותר מחישוב רגיל. מסובך יותר ברמה התיאורטית, זאת אומרת - קשה יותר להבין מה הולך שם. חישוב קוונטי מסובך יותר גם ברמה הפרקטית ועל כך אדבר בהמשך - הרבה יותר קשה לבנות ולהפעיל מחשב קוונטי מאשר מחשב רגיל - ומאוד לא סביר שיום אחד נזנח את השימוש במחשבים רגילים לטובת מחשבים קוונטיים. מה כן נעשה? נשתמש במחשבים קוונטיים כדי לפתור בצורה יעילה בעיות ספציפיות.

ההיסטוריה של תחום החישוב הקוונטי היא סבוכה ואני לא אכנס לכולה כאן, אבל אחת מנקודות ההתחלה של התחום הייתה בהרצאה שהעביר ריצ’ארד פיינמן בכנס ב-MIT בשנת 1981. מבלי להיכנס לפרטים, המסר הבסיסי שלו היה זה: לבצע סימולציה של מערכות קוונטיות במחשבים זה דבר קשה, וכנראה שהקושי הזה הוא אינהרנטי ולא רק נובע מכך שעדיין לא מצאנו שיטה טובה לבצע סימולציה כזו במחשב. אם כן, אומר פיינמן, אם קשה לסמלץ את הטבע במחשב, למה שלא נשתמש בטבע עצמו לצורך החישוב הזה? למה לא לבנות מחשב שמתבסס על ייצוג מידע שנעזר באפקטים קוונטיים?

נקודת הציון הבאה בתולדות התחום שאני רוצה להזכיר הגיעה למעלה מעשור אחר כך, בשנת 1994, כשהמתמטיקאי פיטר שור הציע אלגוריתם למחשבים קוונטיים שיכול לבצע ביעילות פירוק לגורמים של מספרים. לפרק לגורמים מספר פירושו להציג אותו בתור מכפלה של מספרים קטנים יותר: למשל, את 60 אפשר לכתוב גם בתור 2 כפול 30 (ואפשר להמשיך ולפרק את 30 ולקבל בסוף ש-60 הוא 2 כפול 2 כפול 3 כפול 5).

בינינו, זה לא נראה מרשים כל כך להצליח לפרק את 60 לגורמים, אבל מה עם 49046953? אני יכול לגלות לכם שהוא שווה למכפלה של 6451 ב-7603, אבל האם הייתם יכולים לגלות זאת לבדכם, בלי אינטרנט ובלי מחשב? כמה עבודה הייתה נדרשת מכם? וזה עבור מספר שהוא מכפלה של שני מספרים בני 4 ספרות; עכשיו תחשבו מה קורה עם מספר שהוא מכפלה של שני מספרים בני 500 ספרות כל אחד. זה לא משהו שאדם יכול לעשות, וגם למחשבים אין שום סיכוי לעשות את זה ללא אלגוריתם מתוחכם.

עכשיו, יש לנו אלגוריתמים מתוחכמים לפירוק לגורמים, אפילו ממש מתוחכמים, שמתבססים על מתמטיקה מתקדמת ומרהיבה; אבל אפילו הדברים הכי מתוחכמים שיש לנו עדיין מתקשים מאוד להתמודד עם פירוק לגורמים של מכפלת מספרים בני 500 ספרות. וזה דבר טוב, כי שיטת ההצפנה של RSA, שהיא אחת משיטות ההצפנה הנפוצות והחשובות ביותר כיום, מסתמכת בדיוק על כך שפירוק לגורמים הוא קשה.

ואז הגיע פיטר שור ואמר - אם יהיה לי מחשב קוונטי מתפקד, אני יכול לפרק לגורמים מאוד מהר גם מכפלה של מספרים בני 500 ספרות. לא אכנס כאן לפירוט לגבי האיך שהוא עושה את זה; זה אלגוריתם יפהפה ולא טריוויאלי שמתבסס על מה שתיארתי קודם - “חיזוק” של ההסתברות לקבל תוצאה מועילה ו”ביטול הדדי” של תוצאות לא מועילות. מה שחשוב כאן הוא האפקט שהיה לעצם קיום האלגוריתם - החישוב הקוונטי קפץ למודעות של עולם מדעי המחשב בתור משהו שאם יתממש בפועל יוביל להשלכות לא טריויאליות.

והאם הוא התממש בפועל? ובכן, עדיין לא. אנחנו עדיין רחוקים בצורה קיצונית ממחשב קוונטי שיכול להפעיל את אלגוריתם שור על מספרים מסדרי הגודל המדוברים פה. זה בכלל לא עומד על הפרק; אבל דברים אחרים כן, למשל סימולציה של מערכות פיזיקליות (הדבר המקורי שפיינמן דיבר עליו, כזכור). גם כאן אנחנו עדיין לא שם, אבל מקווים שאנחנו נמצאים כבר מעבר לפינה.

יש עוד כמה תוצאות מעניינות ששווה להזכיר כאן. ראשית, האלגוריתם של שור לא “מוכיח” שחישוב קוונטי עדיף על פני חישוב רגיל, כי לא הצלחנו עד היום לשלול את האפשרות שקיים אלגוריתם קלאסי יעיל לפירוק לגורמים ופשוט לא הצלחנו למצוא אותו. אבל בינינו, אף אחד לא חושב שזה המצב; האתגר הוא רק איך להוכיח שאין ולא יהיה אלגוריתם קלאסי יעיל לפירוק לגורמים.

אם כן, שור לא “מוכיח” עליונות תיאורטית, אבל יש כאלו שכן. דוגמא אחת היא האלגוריתם של גרובר, שעוסק בבעיה הבאה: יש לנו רשימה לא ממוינת של פריטים ואנחנו רוצים למצוא מתוכה פריט שיש לו תכונה טובה מסויימת. איך אפשר למצוא אותו? לא קשה להשתכנע שאם ברשימה יש \( N \) פריטים אז לא משנה באיזה אלגוריתם קלאסי נשתמש, החיפוש עשוי לדרוש קריאה מפורשת של כל אחד מ-\( N \) הפריטים ברשימה. אבל מצד שני, אם הייתה לנו דרך לבצע קריאה שמערבת סופרפוזיציה של האיברים ברשימה, אז האלגוריתם של גרובר מראה כיצד אפשר להסתפק ב-\( \sqrt{N} \) קריאות. זה שיפור שפשוט לא ניתן לבצע בחישוב קלאסי, אבל מצד שני אפשר לטעון שהסיטואציה די שונה כי בחישוב קלאסי אפשר לדגום רק פריט אחד בכל פעם בעוד שבחישוב קוונטי אפשר לדגום “את כולם בבת אחת” בזכות היכולת לפעול על סופרפוזיציה.

יש דוגמאות קצת יותר חותכות לעליונות התיאורטית של מחשב קוונטי על מחשב רגיל - לא מזמן דיברתי בבלוג על מאמר של חוקרים מיבמ ואוניברסיטת מינכן שמראה יתרון של ממש של מודל מסויים של מחשב קוונטי על מודל מסויים של מחשב רגיל, בבעיה שעשויה להרגיש קצת מלאכותית ולא אכנס לפרטים שלה. השורה התחתונה היא שאין לנו ממש ספק בכך שברמה התיאורטית, מחשב קוונטי יכול להיות עדיף על מחשב רגיל בחישובים מסויימים, ולכן לכל הפחות בתור מודל תיאורטי הוא מעניין. אבל מה קורה בפועל?

על מחשבים קוונטים בכאן והעכשיו

את הדיון על חישובים התחלתי עם מחשב רגיל שמקבל קלט של 0 ו-1 ועושה עליו כל מני מניפולציות. זה טוב ויפה ברמת התיאוריה, אבל מה מחשבים עושים באמת? יש כאן בעצם שתי שאלות - הראשונה, איך הם מייצגים ביטים; השניה, איך הם מבצעים עליהם חישובים. זו שאלת המימוש של מחשבים.

מה שצריך להבין הוא שאפשר להציע הרבה מימושים שונים לאותו קונספט בדיוק של “קבלו ביטים, בצעו מניפולציות, החזירו ביטים”. אפשר, למשל, לתת לבן אדם לעשות את החישובים עם נייר ועט או עם חשבוניה. זה יהיה איטי ויסבול מהרבה טעויות, אבל זה יעבוד, וזה אכן נעשה בעבר. הסופר טרי פראצ’ט לקח את הרעיון הזה רחוק יותר - בספרי “עולם הדיסק” יש מחשב שמתבסס על חוות נמלים. למרות שזה רעיון מרהיב, אני לא מכיר דרך טובה לייצג מידע ולבצע עליו מניפולציות באמצעות נמלים.

רעיון שונה הוצע על ידי המתמטיקאי בן המאה ה-19 צ’ארלס בבאג’, שתכנן מכונה מכנית שנקראה המנוע האנליטי. המנוע האנליטי כבר היה מחשב לכל דבר ועניין, למעט הבעיה הקטנה שבנייתו מעולם לא נסתיימה. זה לא מנע מבבאג’ להיחשב למי שהמציא את המחשב הראשון, והשותפה שלו עדה לאבלייס הפכה למתכנתת הראשונה בזכות תוכנית מחשב שכתבה כדי להדגים את השימושיות של המנוע האנליטי בחישובים לא טריוויאליים (חישוב מספרי ברנולי).

להבדיל מכל אלו, מחשבים מודרניים מתבססים על חשמל. ביטים מיוצגים על ידי מתח חשמלי; בתיאור פשטני, מתח נמוך מתאר לנו 0 ומתח גבוה מתאר לנו 1, ואפשר לבצע מניפולציות של שינוי מתחים חשמליים בעזרת תעלולי אלקטרוניקה. המימוש הזה של מחשבים בעזרת חשמל הוא לא פחות ממדהים - החישובים שהוא מאפשר הם מהירים ביותר, וצריכת האנרגיה שנדרשת לשם כך היא נמוכה למדי. זה לא קרה בן רגע; המחשבים החשמליים הראשונים היו מפלצות ענק עם צריכת אנרגיה מטורפת וקצב חישוב איטי יחסית. השינוי הגדול בתחום נזקף לזכותם של מהנדסי החשמל ובפרט לזכות המצאת הטרנזיסטור, שהחליף את שפופרות הואקום שעליהם התבססו המחשבים הראשונים.

עם מחשבים קוונטיים אנחנו נמצאים כרגע בשלב שפופרות הואקום, וזה עוד בהערכה אופטימית; יש שיגידו שאנחנו בקושי בשלב הבבאג’ של התחום. יש כיום כמה גישות שונות לגמרי לשאלה “איך לייצג קיוביט”. לכל אחת יתרונות וחסרונות משלה, ואף אחת מהן לא עובדת טוב במיוחד. גישה אחת לדוגמא נקראת “יונים כלואים” - הרעיון הוא לקחת כמה אטומים, להטעין אותם במטען חשמלי (זה מה שנקרא יון), לשים אותם בתוך מיכל ואקום ו”לכלוא” אותם שם בעזרת שדות אלקטרומגנטיים ולקרר אותם באמצעות לייזרים. מרגע שהשתלטנו על אטומים אינדיבידואליים כאלו, אפשר להשתמש בתכונות שונות שלהן (למשל ספין) על מנת לייצג קיוביטים, וכדי להפעיל “שערים קוונטיים” על הדברים הללו מפגיזים אותם בשדה אלקטרומגנטי מתאים. זה נשמע מגניב בצורה שלא תאומן - וזה עובד, אבל זה עדיין לא עובד טוב כשאנחנו רוצים הרבה קיוביטים.

מימוש אחר למחשב קוונטי מתבסס על זרם על-מוליך. על-מוליכות היא תופעה של חומרים מסויימים שאחרי שמקררים אותם מספיק, ההתנגדות החשמלית שלהם יורדת לאפס. זרם חשמלי שרץ בתוך על-מוליך שכזה הוא בעל תכונות מופלאות למדי, ובין היתר אפשר לנצל אותו בתור קיוביט (את כל הזרם!). זו השיטה הנפוצה כרגע בתעשיה - המחשבים הקוונטיים של גוגל, מיקרוסופט, אינטל, יבמ ואחרים מתבססים עליה. זה עובד! אבל זה עדיין לא עובד טוב כשאנחנו רוצים הרבה קיוביטים.

הנה סדרי גודל: כיום מדברים על מחשבים של כמה עשרות קיוביטים, ברמות איכות משתנות; בשביל מימוש יעיל של האלגוריתם של שור מדברים על מיליוני קיוביטים. בקיצור, אנחנו ממש לא שם. האם בקרוב נגיע לאנשהו? האם יהיה לנו מחשב קוונטי שעושה דברים מעניינים שמחשבים רגילים לא יכולים? פעם האמנתי שזה לא יקרה בעשורים הקרובים, ועכשיו אני בהחלט פתוח לאפשרות שזה יקרה בשנים הקרובות. אבל אנחנו עדיין לא שם.

למה בעצם זה כל כך קשה? ובכן, מחשב קוונטי הוא רגיש מאוד לרעשים. “רעש” פירושו התערבות כלשהי של משהו מבחוץ על ההתנהלות התקינה של המחשב. מחשב “רגיל” גם כן מושפע ללא הרף מרעשים, אבל הוא הרבה יותר חסין להם. אם מחשב רגיל מחשיב רמת מתח של 20 בתור אפס ורמת מתח של 100 בתור אחד, ופתאום בא רעש מבחוץ ומשנה את רמת המתח מ-100 אל 70, אז המחשב עדיין יוכל לזהות אותה בתור אחד. לעומת זאת במחשב קוונטי אם בא רעש מבחוץ ומתערב בסופרפוזיציה, או מכריח אותה “להימדד”, אז החישוב אבוד. ורעשים כאלו הם בלתי נמנעים. על מנת לצמצם אותם ככל הניתן, מחשבים קוונטיים עובדים כיום בטמפרטורות נמוכות ביותר שקרובות לאפס המוחלט; זה משפר את זמן החישוב עד לרגע שבו הכל קורס ונחרב, אבל בסופו של דבר הכל קורס ונחרב, ומדובר פה על סדר גודל של שניות (מימוש כמו זה של יונים כלואים הוא יותר עמיד, אבל יש לו בעיות משל עצמו).

מה יקרה בעתיד? הייתי מביע משאלה שנעבור למחשב קוונטי מבוסס חתולים, אבל בכנות, חבל על החתולים. אלא אם אלו יהיו חתולים יוניים על-מוליכים שכלואים על ידי שדות אלקטרומגנטיים בשפופרות ואקום, כי זה פשוט נשמע מוצלח מדי מכדי לוותר על זה.