משפט הערך הממוצע של לגראנז'

ביקשו ממני לסגור את אחד החורים המציקים שיש בבלוג - לתאר את משפט הערך הממוצע של לגראנז’, שהוא אחד מהתוצאות הבסיסיות והמעניינות ביותר שמלמדים על נגזרות. כתבתי בשעתו פוסט שמתאר מהן נגזרות והוא הרקע שדרוש כדי להבין את משפט לגראנז’; אבל אל לגראנז’ עצמו לא הגעתי. אז נתחיל עם תזכורת קטנה על מה מדובר.

אנחנו מדברים על פונקציות ממשיות: פונקציות \( f:\mathbb{R}\to\mathbb{R} \). אם יש לנו מספיק מזל, הפונקציות הללו הן “נחמדות”, והקצב שבו הן משתנות ניתן גם הוא לתיאור על ידי פונקציה, שנקראת הנגזרת של \( f \). פורמלית, אנחנו מגדירים את הנגזרת של \( f \) בנקודה \( a \) בתור הערך של הגבול \( \lim_{h\to0}\frac{f\left(a+h\right)-f\left(a\right)}{h} \), במקרה שבו הוא קיים. בואו נסתכל שניה על הביטוי הזה יותר בפירוט כדי להבין מה הוא אומר: אפשר לכתוב אותו גם בתור

\( \lim_{h\to0}\frac{f\left(a+h\right)-f\left(a\right)}{\left(a+h\right)-a} \)

כלומר, אפשר לחשוב עליו בתור הערך \( \frac{f\left(b\right)-f\left(a\right)}{b-a} \) עבור נקודות \( b \) שהן “הולכות וקרבות” ל-\( a \). אבל מה זה הערך הזה? זה פשוט השינוי הממוצע בין הערך של \( f \) בנקודה \( a \) והערך שלה בנקודה \( b \). קל לראות את זה עם דוגמא יומיומית: נניח שאנחנו נוסעים מתל אביב לאילת ומודדים כמה התרחקנו מתל אביב עד כה בעזרת הפונקציה \( f \). אם בזמן \( t_{1}=1 \) (בשעות) היינו במרחק 50 ק”מ מתל אביב ובזמן \( t_{2}=4 \) היינו במרחק 290 ק”מ מתל אביב, אז המהירות הממוצעת שלנו בנסיעה הזו בין שני פרקי הזמן הללו נתונה, בקילומטר לשעה, על ידי

\( \frac{f\left(t_{2}\right)-f\left(t_{1}\right)}{t_{2}-t_{1}}=\frac{290-50}{4-1}=\frac{240}{3}=80 \)

מה המשמעות של מהירות ממוצעת שכזו? האם זה אומר שזו המהירות שבה נסענו במשך רוב הדרך? לא. ייתכן שנסענו במהירות 100 קמ”ש בשעתיים הראשונות שאחרי \( t_{1}=1 \), ואז את 40 הקילומטרים הנוספים עשינו בזחילה במהירות 40 קמ”ש בשעה האחרונה. המשמעות של המהירות הממוצעת היא זו - אם היינו נוסעים כל הדרך באותה מהירות בדיוק, בלי לשנות אותה כלל, אז היינו עוברים את אותה הדרך.

על נגזרת אפשר לחשוב בתור “ערך ממוצע רגעי”. כלומר, אנחנו מחשבים את המהירות הממוצעת שלנו לא על פני פרק זמן של שלוש שעות אלא על פני פרק זמן של דקה… לא בעצם, פרק זמן של שנייה… לא, בעצם מילישנייה… וכן הלאה. אם יש איזו מהירות מסויימת שהמהירות הממוצעת מספיק קרובה אליה, בהינתן שפרק הזמן שלנו קצר דיו (זה היה ניסוח מילולי מסורבל של מושג הגבול, \( \lim \)), אז המהירות המסויימת הזו היא הנגזרת של פונקציית המיקום שלנו באותה נקודת זמן שאנחנו לוקחים ממנה פער כל כך קצרצר. בהקשר של מהירות קוראים לזה מהירות רגעית.

כפי שאפשר להבין, מהירות רגעית שכזו היא עניין, אה, רגעי. מקומי. נקודתי. משהו שמתאר שבריר שניה אחד בהיסטוריה של הנסיעה. מה שמשפט הערך הממוצע של לגראנז’ עושה הוא להעביר אותנו מהמקומי הזה אל הגלובלי - להראות שקיימת נקודה רגעית בזמן שמה שקורה בה הוא האפיון הממוצע של מה שקורה בכל פרק הזמן הרלוונטי. זה מתאים לחוויה היומיומית שלנו: אם בהתחלה נסענו במהירות ממוצעת של 100 קמ”ש ואז ירדנו למהירות ממוצעת של 40 קמ”ש, אז היה שבריר שניה כלשהו שבו מד המהירות שלנו הראה את המהירות 80 קמ”ש, שהיא המהירות הממוצעת עבור כל הנסיעה.

אז הנה מה שלגראנז’ אומר, פורמלית: אם \( a<b \) ויש לנו פונקציה \( f:\left[a,b\right]\to\mathbb{R} \) פונקציה שרציפה בקטע הסגור \( \left[a,b\right] \) וגזירה בקטע הפתוח \( \left(a,b\right) \), אז קיימת נקודה \( c\in\left(a,b\right) \) כך ש-\( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \). בפוסט הזה נוכיח את המשפט (בהסתמך על דברים קודמים, כמובן) וניתן דוגמא או שתיים לשימושיות שלו.

ראשית, אי אפשר בלי להזכיר את האופן הגאומטרי שבו אנחנו רואים את המשפט. כשאנחנו מציירים פונקציה, אנחנו מציירים נקודות שהקואורדינטות שלהן הן מהצורה \( \left(x,f\left(x\right)\right) \) (כלומר, \( f\left(x\right) \) היא קואורדינטת ה-\( y \) של הציור). נקודות הקצה של הפונקציה הן \( \left(a,f\left(a\right)\right) \) ו-\( \left(b,f\left(b\right)\right) \). אם ניזכר איך הולכים דברים בגאומטריה אנליטית נראה שהביטוי \( \frac{f\left(b\right)-f\left(a\right)}{b-a} \) הוא שיפוע הישר שמחבר את שתי הנקודות הללו. עכשיו, מה זו נגזרת? המשמעות של נגזרת בנקודה כלשהי היא שיפוע המשיק לפונקציה בנקודה הזו. לכן לגראנז’ אומר שיש נקודה כלשהי על גרף הפונקציה ששיפוע המשיק לאותה נקודה זהה לשיפוע הישר שמחבר את שני קצוות הפונקציה. הנה איור באדיבות ויקיפדיה העברית:

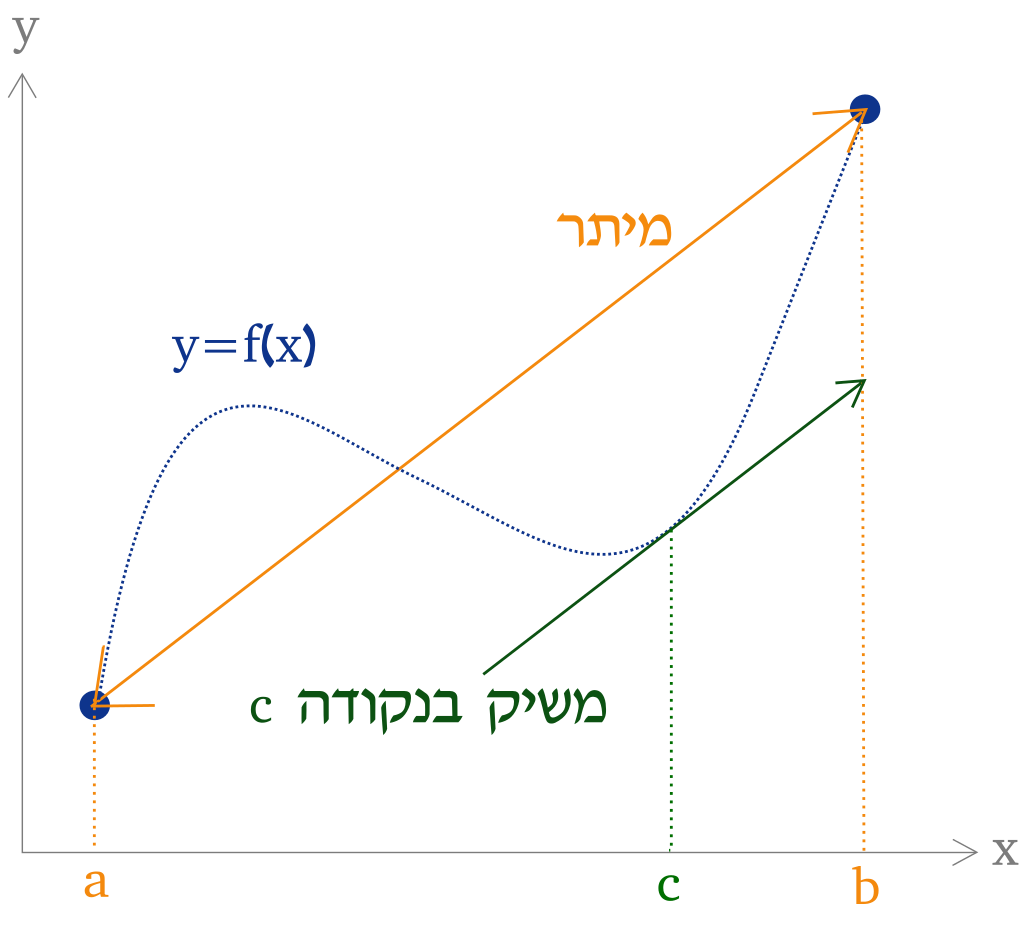
איך מוכיחים את המשפט? כאן צריך להיזהר עם האינטואיציה שלנו, שעשויה להטעות אותנו. נחזור אל דוגמת הרכב שנסע במהירות של 100 קמ”ש ואז ירד למהירות של 40 קמ”ש. האינטואיציה שלנו אומרת שבירידה מ-100 קמ”ש אל 40 קמ”ש הייתה חייבת להיות שניה שבה המהירות הייתה 80 קמ”ש, כי אנחנו חושבים על מהירות בתור משהו שמשתנה באופן רציף. יש לדבר הזה פורמליזם בחדו”א: פונקציה \( f \) היא רציפה בנקודה \( a \) אם \( \lim_{x\to a}f\left(x\right)=f\left(a\right) \) (כלומר, הערך שנראה ש-\( f \) “אמורה לקבל” ב-\( a \) הוא מה שמתקבל בפועל). אם יש לנו פונקציה רציפה, אז יש לנו עבורה משהו שנקרא משפט ערך הביניים שאומר שאם \( y \) הוא ערך כלשהו שנמצא בין \( f\left(a\right) \) ו-\( f\left(b\right) \), אז קיים \( x\in\left[a,b\right] \) כך ש-\( f\left(x\right)=y \). בפרט, מהירות של 80 קמ”ש נמצאת בין 100 קמ”ש ו-40 קמ”ש ולכן היא חייבת להתקבל מתישהו.

אז מה הבעיה? הבעיה היא שנגזרת, באופן כללי, לא חייבת להיות פונקציה רציפה. אמנם, הדוגמאות הנגדיות (של פונקציות גזירות שהנגזרת שלהן אינה רציפה) הן לא יפות במיוחד ואפשר גם להוכיח שאי רציפות של “קפיצה” ישירות מ-100 קמ”ש אל 40 קמ”ש פשוט לא יכולה להתקיים, אבל השורה התחתונה היא שאנחנו רוצים להוכיח את המשפט בלי הסתמכות על משפט ערך הביניים.

עוד נקודה שצריך לתת אליה תשומת לב היא שהתנאים של המשפט די קשיחים. ראשית, הדרישה ש-\( f \) תהיה גזירה בכל הקטע הפתוח \( \left(a,b\right) \). אחרת אפשר לקחת את דוגמת הנסיעה שלנו לאקסטרים: נדמיין שאנחנו נוסעים 100 קמ”ש ואז קופצים מיידית אל 40 קמ”ש, בלי לעבור בערכים באמצע; אז באמת לא היינו בשום מקום במהירות 80 קמ”ש כפי שמשפט לגראנז’ טוען. העניין הוא שהנקודה שבה ביצענו את הקפיצה הזו לא תהיה גזירה; הנגזרת ממש לפניה היא 100 והנגזרת ממש אחריה היא 40, ובנקודה עצמה? הנגזרת לא מוגדרת.

שנית, הדרישה הנוספת ש-\( f \) תהיה רציפה בכל \( \left[a,b\right] \) היא כמעט מובנת מאליה. היא חייבת להיות רציפה ב-\( \left(a,b\right) \) כי קל לראות שגזירות בקטע הזה גוררת רציפות בו. היא חייבת להיות רציפה בקצוות, אחרת אפשר יהיה לשנות את הערכים שלה שם באופן שרירותי לגמרי, למשל להגדיר \( f\left(a\right)=f\left(b\right)=232352 \), ואז אין סיבה שמשפט ערך הביניים יעבוד כי הוא מתבסס בצורה חזקה על הערכים בקצוות ועל כך שהם מייצגים תקינים של מה שקורה בתוך הקטע.

עכשיו אפשר לעבור להוכחה של המשפט. נתחיל עם מקרה פרטי שלו שנקרא משפט רול שבעזרתו קל להוכיח את התוצאה הכללית. משפט רול אומר שאם \( f\left(a\right)=f\left(b\right) \) אז קיימת \( c\in\left[a,b\right] \) כך ש-\( f^{\prime}\left(c\right)=0 \). אינטואיטיבית, אם נקודות ההתחלה והסיום של הטיול שלנו הן זהות, אז היה רגע שבו עמדנו במקום ולא זזנו.

זה לא משפט טריוויאלי, אבל עם ידע רלוונטי בחדו”א אפשר לתת לו הוכחה של שורה אחת, שהאינטואיציה שלה די ברורה: אם נקודות ההתחלה והסיום שלנו זהות, אז או שלא זזנו בכלל כל הזמן, או שזזנו קדימה ואז אחורה ולכן הייתה שניה שבה עברנו מלזוז קדימה אל לזוז אחורה ובה לא זזנו; או שזזנו אחורה ואז קדימה ולכן הייתה שניה שבה לא זזנו. העניין הוא שהאינטואיציה הזו שוב מניחה רציפות של הנגזרת ובפעול משפט רול מצליח לעקוף את זה (ולכן אינו טריוויאלי) בעזרת משפטים קודמים, שרק בזכותם ההוכחה היא בת שורה אחת.

בואו ניתן את השורה הזו למקרה שיש לכם את הידע הזה ואז נרחיב: מכיוון ש-\( f \) רציפה ב-\( \left[a,b\right] \) היא מקבלת בקטע הזה מקסימום ומינימום. אם הם בתוך הקטע, אז בכל אחד מהם ערך הנגזרת הוא 0 על פי משפט פרמה לנקודות קיצון; אם שניהם בקצוות הקטע אז הם שווים זה לזה ולכן הפונקציה קבועה ולכן הנגזרת שלה היא 0 בכל הקטע.

הבעיה עם להסביר את כל המלל שכתבתי למעלה היא שלא ברור כמה רחוק אני אמור ללכת. את הטענה על משפט פרמה לנקודות קיצון הוכחתי בפוסט קודם, אז אני פטור מלדבר עליה, אבל מה עם הטענה שפונקציה רציפה בקטע סגור מקבלת בו ערכי מקסימום ומינימום? הטענה הזו נקראת בחדו”א “משפט ויירשטראס” (השני; הראשון אומר שפונקציה רציפה בקטע סגור חסומה בו). אני יכול להוכיח אותה, אבל ההוכחה מתבססת על משהו יותר בסיסי שנקרא משפט בולצאנו-ויירשטראס, שבתורו נובע מהתכונות הבסיסיות של הממשיים… בקיצור, אני לא הולך ללכת בכיוון הזה ואולי אדבר על משפטי ויירשטראס בפירוט בפוסט אחר מתישהו.

דבר אחד כן קל מאוד להסביר: אם \( f \) היא פונקציה קבועה בקטע, אז הנגזרת שלה בכל נקודה בקטע היא \( 0 \) פשוט כי בביטוי \( \lim_{h\to0}\frac{f\left(a+h\right)-f\left(a\right)}{h} \) מתקיים \( f\left(a+h\right)=f\left(a\right) \) ולכן המונה הוא אפס.

עכשיו, איך עוברים מהמשפט הזה אל משפט לגראנז’? די בקלות: אם יש לנו פונקציה \( f\left(x\right) \), אפשר לדבר על הפונקציה \( g\left(x\right) \) שמודדת את המרחק של \( f\left(x\right) \) מהמיתר שמחבר את הנקודות \( \left(a,f\left(a\right)\right) \) ו-\( \left(b,f\left(b\right)\right) \). כלומר, היא מודדת כמה \( f\left(x\right) \) אינה מתאימה לממוצע בנקודה מסויימת. בנקודות הקצה המרחק הזה יהיה 0, כך שאנחנו רואים את משפט רול בפעולה.

כדי לכתוב את \( g\left(x\right) \) במפורש צריך להיזכר קודם כל בקצת גאומטריה אנליטית - איך כותבים את משוואות הקו הישר שמחבר שתי נקודות \( \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right) \)? התשובה היא שזו תהיה משוואה מהצורה \( y=mx+n \) כאשר \( m \) נקרא השיפוע של הישר ואילו \( n \) היא נקודת החיתוך של הישר עם ציר \( y \) (כמה “גבוה” הישר יהיה כשנציב \( x=0 \)). אם נציב את שתי הנקודות שידועות לנו במשוואה הזו נקבל שתי משוואות:

\( y_{1}=mx_{1}+n \)

\( y_{2}=mx_{2}+n \)

אם נחסר אחת מהשניה ונחלק, נקבל

\( m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \)

כאן אנחנו מניחים ש-\( x_{2}\ne x_{1} \) כדי שנוכל לחלק, וזה מתאים להנחה שלנו ש-\( a<b \) במשפט לגראנז’ (אם לא היינו מניחים את זה אז משפט לגרנז’ היה חסר משמעות; הוא היה אומר שקיים \( x\in\left(a,b\right) \) שמקיים כך-וכך, אבל \( \left(a,b\right) \) היה קטע ריק).

את הערך של \( n \) קל למצוא עכשיו על ידי כך שניקח את המשוואה הראשונה ונעביר אגף: \( y_{1}-mx_{1}=n \). אם נציב את זה בחזרה במשוואה הכללית \( y=mx+n \) נקבל

\( y=mx+\left(y_{1}-mx_{1}\right) \)

כלומר

\( y=m\left(x-x_{1}\right)+y_{1} \)

במקרה שלנו, שבו \( \left(x_{1},y_{1}\right)=\left(a,f\left(a\right)\right) \) ו-\( \left(x_{2},y_{2}\right)=\left(b,f\left(b\right)\right) \), משוואת המיתר תהיה

\( y=\frac{f\left(b\right)-f\left(a\right)}{b-a}\left(x-a\right)+f\left(a\right) \)

ולכן אם אנחנו רוצים ש-\( g\left(x\right) \) תתאר את ההפרש בין הערך של המיתר והפונקציה, כלומר \( f\left(x\right)-y \), נקבל:

\( g\left(x\right)=f\left(x\right)-\frac{f\left(b\right)-f\left(a\right)}{b-a}\left(x-a\right)-f\left(a\right) \)

אם נציב \( x=a \) במשוואה הזו נקבל

\( g\left(a\right)=f\left(a\right)-f\left(a\right)=0 \)

ואם נציב בה \( b \) נקבל

\( g\left(b\right)=f\left(b\right)-\left(f\left(b\right)-f\left(a\right)\right)-f\left(a\right)=0 \)

בנוסף לכך, \( g \) רציפה ב-\( \left[a,b\right] \) וגזירה ב-\( \left(a,b\right) \) בשל האופן הפשוט שבו היא מתקבלת מ-\( f\left(x\right) \) שגם כן מקיימת את התכונות הנחמדות הללו; זאת מכיוון שחיבור של פונקציות גזירות או כפל שלהן בקבוע מותיר אותן גזירות, וכמו כן פולינומים הם פונקציות גזירות.

לכן ניתן להשתמש במשפט רול על \( g \) ולקבל שיש \( c\in\left(a,b\right) \) כך ש-\( g^{\prime}\left(c\right)=0 \). כעת, מהי הנגזרת של \( g \)? קל לחשוב אותה במפורש:

\( g^{\prime}\left(x\right)=f^{\prime}\left(x\right)-\frac{f\left(b\right)-f\left(a\right)}{b-a} \)

ולכן אם \( g^{\prime}\left(c\right)=0 \) נקבל ש-

\( f^{\prime}\left(c\right)-\frac{f\left(b\right)-f\left(a\right)}{b-a}=0 \)

כלומר \( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \) שזה בדיוק מה שרצינו. האינטואיציה פה שוב פשוטה ונובעת ממה שנקרא לינאריות הנגזרת, \( \left(f+g\right)^{\prime}=f^{\prime}+g^{\prime} \): מכיוון ש-\( g \) היא ההפרש בין \( f \) ובין המיתר, אז הנגזרת של \( g \) היא ההפרש בין הנגזרת של \( f \) ובין נגזרת המיתר, שהיא פשוט השיפוע הקבוע של המיתר. לכן יש נקודה שבה ההפרש הזה מתאפס, והנגזרת של \( f \) שווה בדיוק לשיפוע המיתר.

סיימנו להוכיח את המשפט, אבל מן הסתם פוסט בנושא לא יהיה שלם בלי לראות כמה מהשימושים הפשוטים שלו. כאמור, הרעיון במשפט הזה הוא היכולת לעבור מה”מקומי” (הנגזרת) אל ה”גלובלי” (ההתנהגות של הפונקציה בכל הקטע), ובמקרי קצה פשוטים יש כמה הסקות מיידיות שניתן לבצע:

1. אם הנגזרת של \( f \) היא 0 בקטע כלשהו אז \( f \) קבועה בכל הקטע הזה (קודם ראינו את ההפך - שהנגזרת של פונקציה קבועה היא 0; עכשיו אנחנו רואים שזה קורה רק לפונקציות קבועות)
2. אם הנגזרת של \( f \) היא חיובית בקטע כלשהו אז \( f \) היא עולה ממש בכל הקטע הזה.
3. אם הנגזרת של \( f \) היא שלילית בקטע כלשהו אז \( f \) היא יורדת ממש בכל הקטע הזה.

שלושת אלו הם מה שנדרש לנו לצורך “חקירת פונקציות” כמו שלומדים בתיכון - זיהוי תחומי עליה וירידה של פונקציה. כדי לראות שזה נכון, אנחנו לוקחים שתי נקודות כלשהן בתוך הקטע, נקרא להן \( a,b \), כך ש-\( a<b \). עכשיו:

1. אם \( f \) קבועה בכל הקטע אנחנו מצפים שיתקיים \( f\left(a\right)=f\left(b\right) \)
2. אם \( f \) עולה ממש בכל הקטע אנחנו מצפים שיתקיים \( f\left(a\right)<f\left(b\right) \)
3. אם \( f \) יורדת ממש בכל הקטע אנחנו מצפים שיתקיים \( f\left(a\right)>f\left(b\right) \)

שלושת אלו אכן מתקיימים, בזכות משפט הערך הממוצע. כזכור, הוא אומר שקיימת \( c\in\left(a,b\right) \) כך ש-\( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \). אולי קצת יותר קל להרגיש מה קורה אם כופלים ב-\( b-a \) ומקבלים

\( f\left(b\right)-f\left(a\right)=f^{\prime}\left(c\right)\left(b-a\right) \)

כלומר, אנחנו יכולים לתאר את ההפרש בין \( f \) בשתי נקודות הקצה של הקטע בעזרת אורך הקטע כפול קבוע מספרי כלשהו שקשור לנגזרת של \( f \). נחזור אל שלושת המקרים שלנו:

1. אם הנגזרת של \( f \) היא 0 בכל הקטע אז \( f^{\prime}\left(c\right)=0 \) ולכן \( f\left(b\right)-f\left(a\right)=0 \), כלומר \( f\left(b\right)=f\left(a\right) \)
2. אם הנגזרת של \( f \) היא חיובית בכל הקטע אז \( f^{\prime}\left(c\right)\left(b-a\right)>0 \) ולכן \( f\left(b\right)-f\left(a\right)>0 \), כלומר \( f\left(a\right)<f\left(b\right) \)
3. אם הנגזרת של \( f \) היא שלילית בכל הקטע אז \( f^{\prime}\left(c\right)\left(b-a\right)<0 \) ולכן \( f\left(b\right)-f\left(a\right)<0 \), כלומר \( f\left(a\right)>f\left(b\right) \)

העובדה שאם הנגזרת של \( f \) היא אפס בקטע אז \( f \) היא קבועה היא הבסיס לעוד טענה מעניינת: אם הנגזרת של שתי פונקציות היא זהה, אז הן נבדלות בקבוע ותו לא. בואו נראה את זה: נניח ש-\( f^{\prime}\left(x\right)=g^{\prime}\left(x\right) \) לכל \( x \) בקטע מסויים, אז \( \left(f-g\right)^{\prime}\left(x\right)=0 \) לכל הנקודות בקטע הזה, ומכאן ש-\( f-g \) היא פונקציה קבועה: \( \left(f-g\right)\left(x\right)=c \) עבור \( c\in\mathbb{R} \) כלשהו בקטע, כלומר \( f\left(x\right)=g\left(x\right)+c \). זו אולי התוצאה הבסיסית ביותר שמכירים כשמדברים על אינטגרלים: שאם מצאנו פונקציה קדומה של משהו, אז הפונקציות הקדומות הנוספות מתקבלות ממנה על ידי חיבור קבוע כלשהו.

לסיום הפוסט אני רוצה להוכיח משפט מועיל מאין כמותו - כלל לופיטל. יש פה קוריוז היסטורי קטן: לופיטל לא גילה או הוכיח את המשפט אלא יוהאן ברנולי עשה את זה (ולופיטל, תלמידו, פרסם אותו בספר שכתב וקיבל את הקרדיט; סוג של קניה בכסף של משפט שייקרא על שמך), ואני הולך להוכיח אותו עם משהו שנקרא “משפט הערך הממוצע של קושי” שחי הרבה אחרי לופיטל וברנולי (אין לי מושג איך ברנולי הוכיח את המשפט).

כלל לופיטל הוא שיטה מועילה לחישוב גבולות שהם מנה שבה המונה והמכנה שואפים שניהם לאפס (ועם קצת עבודה אפשר להשתמש בו עבור עוד סוגי גבולות בעייתיים אבל לא אכנס לכך בפוסט הזה). פורמלית, אם \( f,g \) הן פונקציות ממשיות ו-\( a \) מספר ממשי כלשהו כך ש-\( \lim_{x\to a}f\left(x\right)=\lim_{x\to a}g\left(x\right)=0 \), ואם בנוסף לכך הגבול הבא קיים:

\( \lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \)

אז גם הגבול הבא קיים:

\( \lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)} \)

והם שווים, כלומר \( \lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)}=\lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \)

המשמעות של הכלל היא שאם יש לנו גבול קשה לחישוב, למשל \( \lim_{x\to0}\frac{\sin x}{x} \), אז אפשר לנסות לפשט אותו על ידי גזירת המונה והמכנה; אם נצליח למצוא את הגבול המתאים עבור הנגזרות, ינבע מכך הגבול המקורי. בדוגמה שלנו גזירת המונה והמכנה מניבה את

\( \lim_{x\to0}\frac{\cos x}{1}=1 \)

(יש בדוגמא שלי מעגליות מכוונת: כדי לדעת מהי הנגזרת של \( \sin \) כבר צריך להכיר את הערך של הגבול הזה; יש לי על כך פוסט כאן)

איך מוכיחים את הכלל? בשביל זה אני צריך, כאמור, הכללה של משפט הערך הממוצע של לגראנז’ שנקראת משפט הערך הממוצע של קושי. אם בלגראנז’ הרעיון הוא שקיים \( c \) עבורו מתקיים

\( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \)

אז במשפט קושי הרעיון הוא שקיים \( c \) עבורו מתקיים

\( \frac{f^{\prime}\left(c\right)}{g^{\prime}\left(c\right)}=\frac{f\left(b\right)-f\left(a\right)}{g\left(b\right)-g\left(a\right)} \)

עבור פונקציה \( g \) שמקיימת את אותם תנאים כמו של \( f \) (רציפה ב-\( \left[a,b\right] \) וגזירה ב-\( \left(a,b\right) \)) ובנוסף לכך החלוקה בה ובנגזרתה לא עושה צרות - כלומר, \( g\left(a\right)\ne g\left(b\right) \) ו-\( g^{\prime}\left(x\right)\ne0 \) לכל \( x\in\left(a,b\right) \). לגראנז’ הוא מקרה פרטי של זה עבור פונקציית הזהות \( g\left(x\right)=x \).

למען האמת, הניסוח לעיל של משפט קושי הוא קצת מעצבן; במקום שיהיה לנו משפט סימטרי ונחמד יש לנו את כל הדרישות הנוספות המעיקות על \( g \). אפשר להיפטר מהקושי הזה אם נפטרים מהחלוקה. כלומר, ניסוח “טוב יותר” של משפט קושי הוא שאם \( f,g \) רציפות על \( \left[a,b\right] \) וגזירות על \( \left(a,b\right) \) אז קיים \( c\in\left(a,b\right) \) כך ש-

\( f^{\prime}\left(c\right)\left(g\left(b\right)-g\left(a\right)\right)=g^{\prime}\left(c\right)\left(f\left(b\right)-f\left(a\right)\right) \)

איך מוכיחים את המשפט? על פניו אפשר לומר משהו כזה: נשתמש פעמיים במשפט לגראנז’ ונקבל ש-

\( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \)

\( g^{\prime}\left(c\right)=\frac{g\left(b\right)-g\left(a\right)}{b-a} \)

ועכשיו פשוט נכפול את אגף ימין של המשוואה האחת באגף שמאל של השניה, ואת אגף שמאל של השניה באגף ימין של הראשונה, ונצמצמם \( \frac{1}{b-a} \) משני האגפים. זה נשמע מאוד פשוט ואלגנטי ונחמד וזה גם שגוי מאוד בצורה שכדאי לתת עליה את הדעת כי זו טעות מאוד נפוצה במתמטיקה. רואים אותה? קחו רגע לחשוב על זה.

השגיאה היא בכך שכתבתי

\( f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \)

\( g^{\prime}\left(c\right)=\frac{g\left(b\right)-g\left(a\right)}{b-a} \)

כך שבשתי המשוואות הללו מופיע אותו ערך \( c \). זה לא מה שמשפט הערך הממוצע של לגראנז’ מבטיח! הוא מבטיח שעבור \( f \) קיים קבוע \( c_{f} \) כך ש-\( f^{\prime}\left(c_{f}\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} \), ועבור \( g \) קיים קבוע \( c_{g} \) כך ש-\( g^{\prime}\left(c_{g}\right)=\frac{g\left(b\right)-g\left(a\right)}{b-a} \), אבל שום דבר לא מבטיח לנו \( c_{f}=c_{g} \); אנחנו צריכים איכשהו להפעיל את משפט לגראנז’ סימולטנית לשתי הפונקציות הללו ביחד, ואין לנו את זה.

העניין הוא שלא צריך להסתבך עם לגראנז, בכלל, הנה הוכחה ישירה בעזרת משפט רול שוב (רואים? משפט רול יעיל! הוא בעצם מקפל בתוכו את כל החדו”א המורכב שנלמד עד לשלב הזה, ומרגע שיש לנו אותו צריך רק תעלולים פשוטים). נגדיר פונקציה

\( h\left(x\right)=f\left(x\right)\left(g\left(b\right)-g\left(a\right)\right)-g\left(x\right)\left(f\left(b\right)-f\left(a\right)\right) \)

כלומר, מאוד דומה לייצוג של המשוואה שאנחנו רוצים שתתקיים בסוף. כעת קל לראות ש-\( h \) היא רציפה ב-\( \left[a,b\right] \) וגזירה ב-\( \left(a,b\right) \) והנגזרת שלה היא

\( h^{\prime}\left(x\right)=f^{\prime}\left(x\right)\left(g\left(b\right)-g\left(a\right)\right)-g^{\prime}\left(x\right)\left(f\left(b\right)-f\left(a\right)\right) \)

וכמו כן מתקיים:

\( h\left(a\right)=f\left(a\right)\left(g\left(b\right)-g\left(a\right)\right)-g\left(a\right)\left(f\left(b\right)-f\left(a\right)\right)=f\left(a\right)g\left(b\right)-g\left(a\right)f\left(b\right) \)

\( h\left(b\right)=f\left(b\right)\left(g\left(b\right)-g\left(a\right)\right)-g\left(b\right)\left(f\left(b\right)-f\left(a\right)\right)=f\left(a\right)g\left(b\right)-g\left(a\right)f\left(b\right) \)

כלומר \( h\left(a\right)=h\left(b\right) \) ולכן ממשפט רול קיים \( c \) כך ש-\( h^{\prime}\left(c\right)=0 \), כלומר

\( f^{\prime}\left(c\right)\left(g\left(b\right)-g\left(a\right)\right)-g^{\prime}\left(c\right)\left(f\left(b\right)-f\left(a\right)\right)=0 \)

וזה מה שרצינו.

נשאר רק להוכיח את כלל לופיטל בעזרת משפט הערך הממוצע של קושי. זו הוכחה קצת פחות “נקייה” ממה שראינו עד כה, אז טוב ששמרתי אותה לסוף, אבל אין בה שום דבר נוראי; פשוט, הדרך הטובה ביותר להבין מה הולך בה היא לכתוב אותה בעצמכם. כמו מה שאני עושה כרגע. כי בחיי שאין לי שמץ של מושג מה הולך בהוכחה הזו למרות שקראתי אותה לפני רגע, אבל אני יודע שהיא פשוטה ואחרי שאכתוב אותה גם אבין אותה.

ובכן, מה יש לנו? הפונקציות \( f,g \) שמקיימות שני דברים:

1. \( \lim_{x\to a}f\left(x\right)=\lim_{x\to a}g\left(x\right)=0 \)
2. \( \lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \) קיים

הטענה השניה נותנת לנו מידע כלשהו על הנגזרות בסביבת הנקודה \( a \). באופן כללי, הטענה \( \lim_{x\to a}h\left(x\right)=L \) אומרת שלכל \( \varepsilon>0 \) קיים \( \delta>0 \) כך שלכל \( x \) עבורו \( 0<\left|x-a\right|<\delta \) מתקיים \( \left|h\left(x\right)-L\right|<\varepsilon \); בפרט, כדי שזה יתקיים, הכרחי ש-\( h\left(x\right) \) תהיה מוגדרת לכל \( x \) עבורו \( 0<\left|x-a\right|<\delta \). החריג היחיד הוא הנקודה \( a \) עצמה, שאין לנו דרישה לגבי הערך של \( h \) בה. עכשיו, אצלנו \( h\left(x\right)=\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \), כך שאנחנו יודעים שקיים \( \delta \) עבורו אם \( 0<\left|x-a\right|<\delta \) אז \( \frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \) קיים; כלומר גם \( f^{\prime}\left(x\right) \) קיימת, וגם \( g^{\prime}\left(x\right) \) קיימת ושונה מאפס.

הרעיון עכשיו הוא לקחת \( x \) כלשהו עבורו \( 0<\left|x-a\right|<\delta \) ולהפעיל את משפט הערך הממוצע של קושי על הקטע שקצוותיו הם \( a \) ו-\( x \). יש כאן שני מקרים: כאשר \( a<x \) וכאשר \( a>x \), אבל מן הסתם מה שיקרה בהם יהיה סימטרי אז נניח ש-\( a<x \). עכשיו צריך שני דברים: ש-\( f,g \) יהיו רציפות ב-\( \left[a,x\right] \), ושיהיו גזירות ב-\( \left(a,x\right) \). את הדבר השני כבר יש לנו, ואנחנו גם יודעים שהפונקציות גזירות ב-\( x \) ולכן הן רציפות שם; הקושי היחיד הוא ב-\( a \). אנחנו יודעים ש-\( \lim_{x\to a}f\left(x\right)=\lim_{x\to a}g\left(x\right)=0 \) ולכן כדי שהפונקציות הללו יהיו רציפות ב-\( a \) צריך להתקיים \( f\left(a\right)=g\left(a\right)=0 \); אבל אם זה לא מתקיים, הן לא יהיו רציפות שם. לכן נכריח את זה לקרות - נגדיר מחדש את הפונקציות הללו ב-\( a \) על ידי \( f\left(a\right)=g\left(a\right)=0 \). האם ההגדרה מחדש הזו תיצור לנו בעיות? עוד מעט נחזור לשאלה הזו כדי לראות למה אין בעיות.

עכשיו אפשר להשתמש במשפט הערך הממוצע של קושי ולקבל את הקיום של \( c\in\left(a,x\right) \) שעבורו מתקיים

\( f^{\prime}\left(c\right)\left(g\left(x\right)-g\left(a\right)\right)=g^{\prime}\left(c\right)\left(f\left(x\right)-f\left(a\right)\right) \)

ומכיוון ש-\( f\left(a\right)=g\left(a\right)=0 \) אפשר לפשט קצת ולכתוב

\( f^{\prime}\left(c\right)g\left(x\right)=g^{\prime}\left(c\right)f\left(x\right) \)

ואם נחלק, נקבל

\( \frac{f\left(x\right)}{g\left(x\right)}=\frac{f^{\prime}\left(c\right)}{g^{\prime}\left(c\right)} \)

שכבר קצת מזכיר את המבנה של כלל לופיטל. אבל רגע אחד! אם אני מחלק בדברים, צריך לוודא שהם שונים מאפס! לגבי \( g^{\prime}\left(c\right) \) כבר ראינו את זה בהתחלה. מה לגבי \( g\left(x\right) \)? ובכן, אם היה מתקיים \( g\left(x\right)=0=g\left(a\right) \) אז אפשר היה להשתמש במשפט רול כדי למצוא נקודה בין \( a \) ל-\( x \) שבה \( g^{\prime} \) שווה לאפס, וכבר ראינו שזה לא יכול לקרות.

עכשיו אפשר לסכם, עם טיעון קצת עדין שאפשר לנסח בחופזה בתור “מכיוון ש-\( c \) נמצא ב-\( \left(a,x\right) \) אז כאשר \( x \) שואף ל-\( a \) כך גם \( c \), ולכן \( \lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)} \) שווה ל-\( \lim_{c\to a}\frac{f^{\prime}\left(c\right)}{g^{\prime}\left(c\right)} \) כמבוקש”. אני ממליץ לכם לנסות להשלים את הפרטים בעצמכם כדי לקבל את תחושת ה”למה זה נכון” אבל הנה הפירוט הטכני בכל מקרה:

פתחנו עם הנתון לפיו \( \lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \) קיים; בואו ואסמן אותו \( L=\lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \). אני רוצה להוכיח שגם \( \lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)}=L \), ואני אעשה את זה לפי הספר עם הגדרת האפסילון-דלתא הסטנדרטית. יהא אם כן \( \varepsilon>0 \) כלשהו. מכיוון ש-\( L=\lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)} \) אז קיים \( \delta>0 \) כך שאם \( 0<\left|x-a\right|<\delta \) אז מתקיים \( \left|\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)}-L\right|<\varepsilon \). אני טוען שאותו \( \delta \) יוכיח ש-\( \lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)}=L \); כלומר, אני צריך להראות שאם \( 0<\left|x-a\right|<\delta \) אז \( \left|\frac{f\left(x\right)}{g\left(x\right)}-L\right|<\varepsilon \).

עכשיו, הוכחנו קודם כי על פי משפט הערך הממוצע, קיים \( c \) כך ש-\( c\in\left(a,x\right) \) (או \( c\in\left(x,a\right) \) אם \( x<a \)) כך ש-\( \frac{f\left(x\right)}{g\left(x\right)}=\frac{f^{\prime}\left(c\right)}{g^{\prime}\left(c\right)} \). מכיוון ש-\( a<c<x \) ו-\( \left|x-a\right|<\delta \) אז גם \( \left|c-a\right|<\delta \) ולכן \( \left|\frac{f^{\prime}\left(c\right)}{g^{\prime}\left(c\right)}-L\right|<\varepsilon \) ולכן \( \left|\frac{f\left(x\right)}{g\left(x\right)}-L\right|<\varepsilon \) כמבוקש, מה שמסיים את ההוכחה.

זה זמן טוב לסיים בו את הפוסט, אבל כרגיל - זה רק קצה הקרחון של השימושים במשפט הערך הממוצע, וזה פשוט ששולי הבלוג הזה צרים מלהכילם.