הונאה מעבר לגבול

בפוסט הקודם דיברתי על החשיבות הרבה של הגבול הבא: \( \lim_{x\to 0}\frac{\sin(x)}{x}=1 \). בקצרה - ממנו נובע כל החשבון האינפיניטסימלי של פונקציות טריגונומטריות. כזכור, היה עוד גבול מעצבן שהייתי צריך להתמודד איתו - \( \lim_{x\to 0}\frac{1-\cos(x)}{x} \), אך בעזרת הגבול הקודם ושימוש ברציפות של הפונקציות הטריגונומטריות (דבר שבפני עצמו צריך להוכיח אך אינו קשה עד כדי כך) לא קשה להוכיח שהוא 0 (כופלים ומחלקים ב-\( 1+\cos(x) \) ומשתמשים בכך ש-\( \sin^2(x)+\cos^2(x)=1 \)).

בוגרי אינפי אולי יתפתו להשתמש בכלל לופיטל לחישוב הגבול. אמנם, הכלל מוכיח את הגבול בקלות, אבל שימוש בו הוא רמאות גמורה; הרי כלל לופיטל מבוסס על ההנחה שאנחנו יודעים את הנגזרת של סינוס, ובשביל לדעת אותה משתמשים בגבול הזה… אם כן, צריך גישה שונה.

הגבול, כזכור, אינו נכון כשהזוויות לא נמדדות ברדיאנים. אם הן כן נמדדות ברדיאנים, מתקיים אי השוויון הבא עבור זוויות חיוביות קטנות מספיק (נניח, קטנות מ-90 מעלות): \( \sin(x)\le x\le \tan(x) \). אי השוויון הזה הוא הבסיס להוכחת הגבול. מרגע שיש לנו אותו, ההוכחה היא טריוויאלית: ראשית כל מסתכלים על \( \sin(x)\le x \), מחלקים את שני האגפים ב-\( x \) ומקבלים כי \( \frac{\sin(x)}{x}\le 1 \). כעת לוקחים את \( x\le \tan(x) \), זוכרים שעל פי הגדרה, \( \tan(x)=\frac{\sin(x)}{\cos(x)} \), מחלקים ב-\( x \), כופלים ב-\( \cos(x) \) ומקבלים \( \cos(x)\le \frac{\sin(x)}{x} \). כעת, מכיוון ש-\( \lim_{x\to 0}\cos(x)=1 \) (ההוכחה לכך אינה קשה במיוחד) מקבלים מכלל הסנדוויץ' ש-\( \lim_{x\to 0}\frac{\sin(x)}{x}=1 \) (לא צריך להתייחס לערכים שליליים של \( x \) כי \( \frac{\sin(x)}{x}=\frac{\sin(|x|)}{|x|} \)).

אם כן, הבעיה שבגבול הזה אינה קשורה לאינפי. היא קשורה לאי השוויון \( \sin(x)\le x\le\tan(x) \), שאינו קשור לאינפי דווקא, אלא מהותית לקשר שבין גודל זווית וגודל הפונקציות הטריגונומטריות שמוגדרות עליה. הדרך להוכיח את אי השוויון הזה עוברת, באופן בלתי נמנע, דרך הגאומטריה - ובפרט, דרך שרטוט שאפשר לראות כמעט בכל ספר אינפי שמכבד את עצמו:

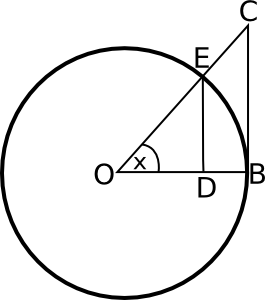
מה הולך כאן? ציירנו את מעגל היחידה (כלומר, המעגל שרדיוסו 1 - ולכן אורכי הקטעים OB ו-OE הוא 1). בתוך המעגל הזה ציירנו זווית x כלשהי, קטנה מ-90 מעלות). את הזווית מציירים באמצעות שני רדיוסים - בחרנו אחד מהם להיות מאוזן (OB), והעלינו ממנו אנך, BC (כלומר - ישר שנמצא בזווית של 90 מעלות ביחס ל-OB). את הרדיוס השני, OE, המשכנו עד שפגש את האנך BC בנקודה C. בנוסף, הורדנו מ-E אנך אל OB וסימנו את נקודת החיתוך בתור D. עד כאן - בניה גאומטרית סטנדרטית.

כעת מגיע הפאנץ’. ראשית, נביט בקשת EB (כלומר, קטע המעגל שעובר בין הנקודות E ו-B, לא הישר שאפשר למתוח בין E ו-B). הקשת הזו נשענת על זווית x שנמדדת ברדיאנים במעגל היחידה. לכן, לפי הגדרה, אורכה הוא x. יתר על כן, אפשר להראות ללא קושי רב שאורכו של ED הוא \( \sin(x) \) ואורכו של BC הוא \( \tan(x) \). לצורכי שלמות אסביר זאת כעת.

נשים לב ש-ED הוא חלק מהמשולש ישר הזווית OED. היתר של המשולש הוא OE, שאורכו 1. על פי הגדרת סינוס, \( \sin(x)=\frac{ED}{OE} \) ומכיוון שאורכו של OE הוא 1, קיבלנו ש-ED הוא אכן סינוס x. להראות ש-BC הוא הטנגנס מסובך מעט יותר. דרך אחת לראות זאת היא באמצעות דמיון משולשים - המשולש ישר זווית הגדול OBC דומה למשולש ישר הזווית הקטן יותר ODE (יש להם אותן זוויות), ולכן היחסים בין גדלי הצלעות של המשולשים שווים - כלומר, מתקיים השוויון \( \frac{BC}{ED}=\frac{OB}{OD} \). כעת מציבים במשוואה הזו את מה שכבר יודעים על האורכים - ED הוא סינוס איקס. OB הוא 1. OD הוא קוסינוס איקס (שוב - על פי הגדרה). לכן מקבלים \( BC=\frac{\sin(x)}{\cos(x)}=\tan(x) \).

עד כאן הכל נכון באופן מופתי וללא כל בעיות. החלק הבעייתי מתחיל כאן. כאן ההוכחה מתפצלת לשני כיוונים עיקריים - הוכחה מבוססת אורך, והוכחה מבוססת שטח. ההוכחה מבוססת האורך אומרת כך: “קל לראות כי ED קטן מהקשת EB והיא קטנה מ-BC” - ולכן, מכיוון שכבר חישבנו את כל האורכים הללו, מתקבל אי השוויון וסיימנו. ההוכחה מבוססת השטח אומרת “שטח המשולש OEB קטן משטח הגזרה OEB שקטן משטח המשולש OCB”. שטח המשולשים קל לחישוב על פי הנוסחה של גובה כפול צלע חלקי 2 - מקבלים ששטח OEB (שימו לב - המשולש הזה בנוי גם על הצלע EB שלא ציירתי במפורש) הוא אורך ED (סינוס איקס) כפול אורך OB (אחד) חלקי 2 - כלומר, סינוס איקס חלקי 2. בדומה, שטח OCB הוא טנגנס איקס חלקי 2. נשאר שטח הגזרה OEB. ידוע ששטח המעגל כולו הוא \( \pi \), ויש בו \( 2\pi \) רדיאנים, ולכן גזרה שנשענת על זווית x תופסת \( \frac{x}{2\pi} \) משטח המעגל - ולכן שטחה הוא \( \frac{x}{2} \), ומהשוואת השטחים מייד קיבלנו שוב את אי השוויון שלנו.

אם כן, מה הבעיה כאן? ראשית, אסייג את עצמי מראש ואגיד שאין בעיה עקרונית; שתי ההוכחות נכונות לגמרי. הבעיה שכן קיימת היא עם המילים המודגשות - ברוב ספרי הלימוד שהנחתי עליהם את ידי, הנימוק שניתן בהוכחה דומה באופיו להן. הבעיה שלי עם ה”קל לראות” היא שממש, אבל ממש, לא קל לראות - מתמטית - את הטענה הזו; אמנם, מהציור מתקבל הרושם החזק מאוד שזה נכון, אבל זה לא מוכיח כלום - אסור במתמטיקה להוכיח דברים באמצעות ציור! עם זאת, הבעיה היא רק להראות שאורך הקשת EB קטן מאורך BC; ברור שהוא גדול מ-ED שכן ED קטן מהצלע EB (שהיא היתר במשולש ישר זווית ש-ED היא אחת משוקיו), ו-EB הוא הקו הישר שמחבר בין E ו-B - והמרחק המינימלי בין שתי נקודות הוא תמיד הקו הישר ביניהן (אם אתם חושבים שאני מחפף כאן, זה בהחלט נכון, אבל לסוגייה הזו אפשר להקדיש פוסט נפרד).

הבעיה עם ה”ידוע” היא שזה בכלל לא ידוע. אמנם, כשלמדנו בתיכון סיפרו לנו - בלי הוכחה - ששטח מעגל הוא \( \pi R^2 \) (ולכן שטח מעגל היחידה הוא פאי), אבל ספר מתמטיקה רציני שמפתח דברים מאפס צריך להיזהר עם ההנחות המוקדמות שלו. אם כן, צריך לספק הוכחה לכך ששטח המעגל הוא פאי, ושההוכחה לא תסתמך בכלל על החשבון האינפינטסימלי של הפונקציות הטריגונומטריות (“הוכחה” מאוד מקובלת היא באמצעות אינטגרל בקוארדינטות קוטביות שמחשב את שטח המעגל - יש כאלו שהתרגלו כל כך להשתמש בקוארדינטות קוטביות עד שהם שוכחים שמאחוריהן מתחבא חישוב של יעקוביאן, שבתורו, מכיוון שאנו עוסקים במעגל, מצריך גזירה של פונקציות טריגונומטריות).

כאמור, רוב ספרי הלימוד שבהם נתקלתי, מתעלמים לחלוטין מנקודות אלו. אני מנחש שגם כאשר מוכיחים את הגבול הזה בהרצאות החדו”א/אינפי באוניברסיטאות, רוב המרצים מעדיפים לדלג מעל כאב הראש הזה בקלילות, ואולי מתוך תקווה שאף סטודנט לא ישים לב לבעיה. זכור לי שכשאני למדתי את הגבול הזה, המרצה נקלע למריבה ארוכה עם הסטודנטים על העניין הזה; אין לי מושג איך זה נגמר כי ממש לא הייתי בעניינים באותו הזמן.

הספר היחיד שבו נתקלתי בהוכחה רצינית ממש לשני העניינים הללו הוא Calculus I של Moise. המחבר עצמו מצהיר במבוא שמטרת הספר היא להציג את החשבון האינפיניסטימלי בצורה קצת יותר מעמיקה מספרים אחרים בנושא - אז לפחות בכל הנוגע לגבול הזה הוא מבטיח וגם מקיים. ההוכחה שמופיעה בספר היא זו מבוססת האורך; בנוסף לכך, הוא מוכיח במקום אחר בספר את נוסחת שטח המעגל מבלי להיזדקק לחשבון האינפיניטסימלי של הפונקציות הטריגונומטריות. אסתפק בלהציג כאן את הפירוט שלו להוכחה מבוססת האורך.

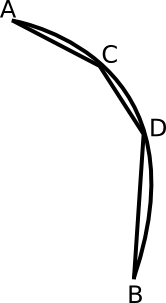
השאלה הראשונה שיש לעסוק בה היא מהו בעצם האורך של הקשת BE. בעוד שאורך של ישר הוא ברור לנו לחלוטין (אפשר לפתוח דיון גם על זה, אבל בואו נניח זאת לבינתיים…), “אורך של קשת” (ובהכללה, אורך של עקומה כלשהי) לא מוגדר בצורה פשוטה שכזו. הגישה הנפוצה להגדרתו היא זו: לוקחים קירוב של הקשת בידי קווים ישרים, וסוכמים את אורכם; אורך הקשת הוא החסם העליון של אורכי כל הקירובים שמתקבלים בצורה הזו. ב”קירוב” הכוונה היא לדבר הבא: מציירים מספר נקודות על הקשת, כשנקודת ההתחלה והסיום תמיד מופיעות, ומחברים כל שתי נקודות סמוכות בישר. כך זה נראה:

כאן הקשת היא AB, והוספנו עליה שתי נקודות נוספות, C,D, וציירנו קו שבור שעובר דרכן - כלומר, מורכב מהקווים AC, CD, DB. אורך הקו הזה הוא קירוב לאורך הקשת. מכיוון שאורך הקשת מוגדר כחסם העליון של אורכי הקירובים הפוליגונליים, הרי שקיים קירוב פוליגונלי שאורכו “קרוב כרצוננו” לאורך הקשת, בכל מידת דיוק שנבחר. זה מאפשר לנו להימנע מהוכחה ישירה שהקשת עצמה קטנה מהישר BC בשרטוט המקורי; מספיק שנראה את זה לכל קירוב פוליגונלי שלה, וזאת מהטעם הפשוט שחסם עליון של קבוצה מוגדר בתור החסם הקטן ביותר של איבריה - כלומר, חסם כזה שכל חסם אחר גדול ממנו. אם כן, מספיק להראות ש-BC הוא “חסם אחר” שכזה. כאן האינפי עוזב אותנו לחלוטין, ואנו נותרים עם טיעונים גאומטריים נטו. כאן נכנסת לעניין הבנייה הבאה:

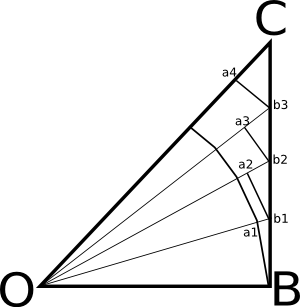מה עשיתי פה? לקחתי קירוב פוליגונלי כלשהו למעגל, והעפתי מהציור את הפרטים הלא רלוונטיים - בפרט, את המעגל עצמו. כעת העברתי מהנקודה O קווים אל BC שחותכים את הקירוב הפוליגונלי בנקודות המפגש בין הצלעות שלו. חשוב לשים לב שהדבר יוצר משולשים שווי שוקיים - כי הצלעות של כל משולש (שבסיסו הוא אחד מהקווים בקירוב הפוליגונלי) הן רדיוסים, ולכן באורך זהה. לכן גם זווית הבסיס של המשולשים הללו זהות. זה גם מה ש-Moise מצייר, וכאן הוא נכנע: הוא אומר שמשיקולים גאומטריים “פשוטים” קל לראות שכל אחד מהקטעים בקירוב הפוליגונלי קטן מהקטע ש”מתאים לו” על BC. זה אמנם נראה ברור, אבל איך מוכיחים זאת? הנה חמש האגורות שלי (כלומר, אין לי מושג אם מה שאני כותב נכון - ובפרט, אין לי מושג אם יש הוכחה פשוטה יותר):

כל קטע בקירוב הפוליגונלי (חוץ מהתחתון ביותר) העברתי מקביל “מאחוריו”, כדי שינוח על BC ובכך ייצור משולש. כך למשל המשולש התחתון ביותר הוא \( Ba_1b_1 \), המשולש הבא הוא \( b_1a_2b_2 \), וכן הלאה. המקביל לכל קטע בקירוב הפוליגונלי הוא בודאות גדול ממנו - זאת בשל דמיון משולשים (המקביל הוא בסיס למשולש שווה שוקיים בעל אורך צלע גדול יותר וזווית בסיס זהה). לכן מספיק להראות שלכל אחד מהמשולשים הללו, הצלע ש”עומדת ישר” היא הגדולה ביותר. למשל, במשולש \( b_1a_2b_2 \) צריך להראות שהצלע \( b_1b_2 \) גדולה מהצלע \( b_1a_2 \), וכן הלאה.

כאן אני שולף משפט מגאומטריה של בית ספר תיכון - במשולש, מול הזווית הגדולה ביותר מונחת הצלע הגדולה ביותר. נותר אם כן להראות שהזווית שמול הצלע ה”עומדת” היא הגדולה ביותר. אני אדגים איך אני עושה את זה למשולש \( b_1a_2b_2 \) ; זה זהה לשאר המשולשים.

ראשית, נעיף מבט במשולש \( Ob_1a_2 \). זה משולש שווה שוקיים - נסמן את זווית הבסיס שלו ב-\( x \). אם כן, מקבלים מייד שהזווית \( b_1a_2b_2 \) היא בת \( 180-x \) מעלות (משלימה של זווית ישרה). כעת נשים לב לכך שהזווית \( Ob_1b_2 \) היא בת למעלה מ-90 מעלות (למה? נביט במשולש \( OBb_2 \), שהוא ישר זווית ממש על פי הגדרה; הזווית \( Ob_2B \) משלימה את סכום הזווית בו ל-180 מעלות,. כעת, מי הזווית שמשתתפות במשולש \( Ob_1b_2 \) ומה סכומן?) ולכן הזווית \( a_2b_1b_2 \) היא בת לפחות \( 90-x \) מעלות. לזווית \( a_2b_2b_1 \) נותרו, אם כן, לכל היותר \( 180-(180-x+90-x)=2x-90 \) מעלות. הדבר האחרון שצריך לשים אליו לב הוא ש-\( x<90 \) מעלות, כי הוא זווית בסיס במשולש שווה שוקיים (אם שתי זווית הבסיס היו בנות 90 מעלות, לא היה נשאר כלום לזווית הראש). לכן \( b_1a_2b_2 \) היא בת יותר מ-180 מעלות, ואילו \( a_2b_2b_1 \) בת פחות, וזה מסיים את ההוכחה.

בררר. אין פלא שכל ספר מעדיף להגיד “גאומטריה פשוטה” מאשר להיכנס לזה. כמובן, נותר להוכיח את המשפט על “מול הזוויות הגדולות מונחות הצלעות הגדולות”. מי מתנדב?