כמה מעלות טובות לרדיאן עלינו (דבר הסנגוריה: סינוסים וקוסינוסים)

בפוסט הקודם הצגתי את יחידת המידה ה”טבעית” לזווית - הרדיאן. היחידה הוגדרה כך: קחו קטע כלשהו, סובבו אותו על ציר שנמצא על אחד מקצותיו בזווית כלשהי. חלקו את אורך הקשת שהקצה השני שלו עבר באורכו - זה גודל הזווית, ברדיאנים.

אבחנה טריויאלית אחת מכך היא שאם יש לנו את מעגל היחידה (המעגל שאורך רדיוסו 1), ואנו מסתכלים על גזרה שלו (תחום שתחום בידי שני רדיוסים), אז אורך הקשת של הגזרה הזו שווה לגודל הזווית של הגזרה. האבחנה הזו היא הבסיס לגבול הבא בחשבון אינפיניטסימלי:

\( \lim_{x\to 0}\frac{\sin(x)}{x}=1 \)

הגבול נראה תמים למדי ממבט ראשון, וגם כשלומדים אותו הוא לרוב נראה כמו דוגמה סתמית לכלל הסנדוויץ'; אבל למעשה, מדובר באחד מהגבולות החשובים ביותר באינפי, ובבסיס שעליו נשען כל האינפי של הפונקציות הטריגונומטריות.

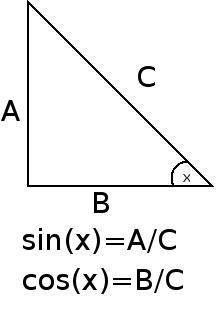
הפונקציות הטריגונומטריות הן פונקציות שמקבלות זווית כפרמטר, ומחזירות מספר ממשי. המפורסמות שבהן הן סינוס וקוסינוס, ואת האחרות (למשל טנגנס) ניתן לגזור מהן. ההגדרה ה”בסיסית” היא רק עבור זוויות בין 0 מעלות ו-90 מעלות (0 רדיאנים ו-\( \frac{\pi}{2} \) רדיאנים): מציירים משולש ישר זווית, ומגדירים סינוס של זווית בתור היחס בין השוק שמול הזווית ליתר, ואת קוסינוס בתור היחס בין השוק שליד הזווית ליתר. כבר מההגדרה הזו אפשר לקבל את כל הזהויות הטריגונומטריות ששברנו עליהן את השיניים בבית הספר; ההוכחות הן גאומטריות במהותן ואינן מסובכות עד כדי כך (הנה דוגמה להוכחה של נוסחת הסכום וההפרש).

השלב הבא הוא להגדיר את סינוס וקוסינוס לכל זווית ממשית. האינטואיציה לכך נעוצה במעגל היחידה: בגלל משפט פיתגורס, אם לוקחים רדיוס ומזיזים אותו בזווית מסויימת, כשנקודת ההתחלה היא זו שבה הוא מצביע על הכיוון החיובי של ציר x והוא נע נגד כיוון השעון, אז סינוס הזווית שהוא עבר עד כה יהיה (בתחום שבין 0 ו-90 מעלות) בדיוק קוארדינטת ה-y של קצהו; וקוסינוס הזווית יהיה קוארדינטת ה-x. אפשר להרחיב את סינוס וקוסינוס בדיוק כדי שישמרו על תכונה זו, לכל זווית אפשרית. פורמלית אפשר לעשות זאת פשוט על ידי שימוש בפונקציות שכבר הגדרנו, על ידי הבאת הערך שעליו רוצים לחשב את הפונקציה חזרה לתחום 0 עד 90 מעלות. למשל, עבור x שהוא בין 90 ל-180 מעלות, מגדירים \( \sin(x)=\sin(180^\circ-x) \) שימו לב שאגף שמאל כאן מוגדר היטב כי בו הזווית היא בין 0 ל-90 מעלות. כמובן שצריך להראות שכל הזהויות הטריגונומטריות עדיין מתקיימות (כאב ראש לא קטן…)

אם כן, סינוס וקוסינוס הן במהותן פונקציות שהגדרתן גאומטרית. בכך הן שונות למדי מפונקציות “אלגבריות” כמו פולינומים. עם זאת, שני סוגי הפונקציות נפגשים באופן בלתי נמנע כאשר מגיעים לחשבון דיפרנציאלי ואינטגרלי. כדי להדגים, אקפוץ דווקא לפיזיקה ולבעיה שמתעוררת בה באופן “טבעי” ומצריכה סינוסים וקוסינוסים לפתרונה. זו הבעיה של תנועה הרמונית פשוטה.

תנועה הרמונית פשוטה מתרחשת, למשל, בסיטואציה הבאה: מחברים גוף כלשהו לקפיץ, מותחים את הקפיץ קצת, ומשחררים. הגוף יתחיל לנוע יחד עם הקפיץ המתכווץ; יחד הם יעברו את נקודת שיווי המשקל של הקפיץ, עד לנקודה שבה הוא עובר מ”מתוח” ל”מכווץ”, ובסופו של דבר ההתנגדות שלו תגבר והגוף יתחיל לנוע חזרה לכיוון השני, וכן הלאה וכן הלאה. מהי הפונקציה שמתארת את המיקום של החפץ ביחס לנקודת שיווי המשקל של הקפיץ? מבלי להיכנס לעומק הניתוח, המסקנה הסופית היא שהמיקום (שתלוי במספר פרמטרים - הקבוע שמאפיין את המתיחות של הקפיץ; המרחק הראשוני שאליו משכו את הגוף; המסה של הגוף) כפונקציה של הזמן מקיים את המשוואה הבאה:

\( Nf(t)+f\prime\prime(t)=0 \)

כאשר N הוא פרמטר כלשהו. למשוואה כזו קוראים משוואה דיפרנציאלית. היא מערבת פונקציה ונגזרות שלה (במקרה שלנו, הנגזרת השנייה של הפונקציה; המשמעות הפיזיקלית של נגזרת שנייה של פונקצית מיקום היא פונקציית התאוצה) ופתרון למשוואה הוא פונקציה שמקיימת אותה. לצורך פשטות, נניח ש-\( N=1 \) (זה אינו הבדל מהותי) ואז יש לנו את המשוואה הפשוטה מאוד (יחסית) \( f(t)+f\prime\prime(t)=0 \), ובמילים - הפתרון הוא פונקציה שהנגזרת השנייה שלה היא בדיוק מינוס הפונקציה המקורית. האם אנחנו מכירים פונקציות כאלו? ובכן, מי שלמד אינפי בוודאי מכיר - אלו הן בדיוק סינוס וקוסינוס.

באינפי רואים זאת כאשר מוכיחים כי \( \sin\prime(x)=\cos(x) \) ו-\( \cos\prime(x)=-\sin(x) \). התכונה ה”מחזורית” הזו של הפונקציות הטריגונומטריות היא אחת מהסיבות לכך שהן ממלאות תפקיד מהותי גם בפתרון משוואות דיפרנציאליות, הרחק מהחיק החמים של הגאומטריה של מעגל היחידה ש”הולידה” אותן.

עוד תפקיד חשוב ומהותי ביותר לפונקציות הטריגונומטריות שאינו קשור (ממבט ראשון לפחות) לגאומטריה הוא זה של טורי פורייה. מכיוון שזה נושא רחב ביותר שראוי לפוסטים נפרדים, אגיד רק שהרעיון שבבסיסם של טורי פורייה הוא התגלית המפתיעה (של פורייה…) שניתן להציג פונקציות רבות מאוד (בתחום סופי מסויים) בתור סכום של סינוסים וקוסינוסים (בדומה לכך שטור טיילור מאפשר הצגה של פונקציה בתור סכום של חזקות). בשל כך, ניתן לפרק פונקציות מסובכות לרכיבים, לפעול על כל רכיב בנפרד (מה שלעתים קל יותר בשל התכונת ה”יפות” של סינוסים וקוסינוסים) ואחר כך “להרכיב מחדש” את הפונקציה לאחר השינויים. דרך פעולה זו שימושית מאוד הן במתמטיקה (למשל, בפתרון משוואות דיפרנציאליות חלקיות) והן בפיזיקה ובענפי הנדסה אחרים שאיני מבין בהם מאומה (ואולי מישהו יוכל להרחיב עליהם בתגובות). גם כאן, העובדה שההצגה הזו אפשרית בכלל נובעת בראש ובראשונה מתכונת הנגזרות ה”מחזורית” של סינוס וקוסינוס.

אלא שתכונת הנגזרות הזו כלל אינה מובנית מאליה. ברשותכם, אחטא בקצת מתמטיקה ואוכיח את תכונת הגזירה של סינוס (של קוסינוס מוכחת באופן דומה). לשם כך אין מנוס מלהזכיר את הזהות הטריגונומטרית שעליה אני מתבסס - הזהות של סכום זוויות:

\( \sin(x+y)=\sin(x)\cos(y)+\sin(y)\cos(x) \)

הנוסחה הזו, כזכור, נכונה לכל \( x,y \) ממשיים (ההוכחה שאני מכיר, כאמור, היא סתם עבודה טכנית מייגעת). כעת, נגזרת מוגדרת בתור הגבול הבא: \( f\prime(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} \). מציבים את סינוס בתור הפונקציה, משתמשים בנוסחה, ומקבלים:

\( \lim_{h\to 0}\frac{\sin(x+h)-\sin(x)}{h}=\lim_{h\to 0}\frac{\sin(x)\cos(h)+\sin(h)\cos(x)-\sin(x)}{h}= \)

\( =\lim_{h\to 0}\frac{(\cos(h)-1)}{h}\sin(x)+\lim_{h\to 0}\frac{\sin(h)}{h}\cos(x) \)

אם כן, הנגזרת של סינוס היא צירוף לינארי של סינוס וקוסינוס, כשהמקדמים הם ערכי שני הגבולות שלמעלה. מתברר שהגבול הימני הוא הגבול החשוב והמרכזי מבין השניים, ואם יש אותו, החישוב של הגבול השמאלי קל ומקבלים 0. מכאן שצריך להתמקד בגבול הימני. לכאורה, ברור שצריך להתקבל 1, כי אנחנו יודעים שהנגזרת של סינוס היא בדיוק קוסינוס (ולא “5 קוסינוס” או דבר מה דומה), אבל בפועל נראה כי הסיבה היחידה שבגללה התקבל 1 היא שאנו מודדים זוויות ברדיאנים (אגב, קיימות דרכים נוספות לחשב את הנגזרת, עם זהויות טריגונומטריות אחרות; בכל אחת מהן, מגיעים בסוף לגבול הסינוס איקס חלקי איקס הזה).

אם כן, מה ההוכחה ש-\( \lim_{x\to 0}\frac{\sin(x)}{x}=1 \)? למרבה ההפתעה (?), היא כלל וכלל אינה טריוויאלית. חמור מכך, כפי שמציגים לרוב את ההוכחה היא גאומטרית במהותה, וגובלת במה שמכונה לפעמים בלעג “הוכחה על ידי ציור”. בפוסט הבא אעסוק בהוכחה ובבעייתיות שלה, אך לעת עתה אני רוצה לחתום את עניין הרדיאנים. אם כן, נניח שהגבול אכן נכון אם אנו מבצעים את המדידה ברדיאנים. מה היה קורה, אם כך, אם היינו מבצעים אותה במעלות? במקרה זה, היה עלינו להמיר את הערך שהסינוס מקבל למעלות, כלומר לכפול ב-180 ולחלק בפאי, אבל לא לשנות את המשתנה שלמטה (כי שינינו את היחידות שסינוס מקבל, לא את היחידות של הגבול כולו…). לכן נקבל:

\( \lim_{x\to 0}\frac{\sin(x\cdot\frac{180}{\pi})}{x}=\lim_{x\to 0}\frac{180}{\pi}\frac{\sin(x\cdot\frac{180}{\pi})}{x\cdot\frac{180}{\pi}}=\frac{180}{\pi} \)

כאן אני מתעלם באלגנטיות מכך שה”יחידות” של התוצאה הן מעלות (או “1 חלקי מעלות”? מה זה חשוב) ומסתכל רק על המסקנה המספרית הפשוטה - הגבול יוצא מספר קבוע שלא נעים ולא נוח לעבוד איתו. הביטו שוב בצורה שבה חישבנו את הנגזרת של סינוס וחישבו איך הנגזרת תשתנה בהתאם.

אם כן, אנו עובדים ברדיאנים (גם) בגלל שהנגזרת של סינוס יוצאת, כאשר מודדים בהם, הכי פשוטה שרק אפשר. זה דומה לכך ש-e הוא הבסיס ל”לוגריתם הטבעי” כי רק בבסיס זה הגזירה של הלוגריתם יוצאת חפה מקבועים.

נקודה מהותית אחת לסיום: דרך ההצגה שלי את הפונקציות הטריגונומטריות הייתה בערך כזו: א) יש פונקציות שמוגדרות על זוויות בעזרת משולשים. ב) נרחיב אותן לכל מספר ממשי. ג) פתאום אנחנו מגלים שהן פותרות לנו משוואות דיפרנציאליות ועניינים וכולם שמחים. האם באמת היה צורך בשלבים א’ וב’? התשובה שלילית. למעשה, אפשר להגדיר את הפונקציות הטריגונומטריות בדרך שונה לחלוטין - ובדרך הזו, הגבול שהצגתי לעיל, כמו גם הגזירה ותכונותיה, הן טריוויאליות לגמרי. הדרך הזו היא דרך פורמלית שמבוססת על טורים אינסופיים; מה שעושים הוא פשוט להגדיר מראש את \( \sin(x) \) בתור הפונקציה הבאה:

\( \sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots \)

ובדומה מגדירים את קוסינוס על ידי:

\( \cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots \)

זוהי דוגמה למה שמכונה “טורי חזקות”, שלרוב נלמדים בקורסי אינפי בסיסיים באוניברסיטה (אך חורגים בהרבה מהחומר הבית ספרי). הטורים אמנם אינסופיים, אבל קל לראות שלא משנה איזה ערך מציבים בתור x, מהר מאוד האיבר הכללי שמוסיפים נהיה קטן מאוד (כי במונה הוא מוכפל עם עצמו n פעמים בעוד שבמכנה מוכפלים כל המספרים מ-1 עד n; בפרט, החל משלב מסויים, יוכפלו שם הרבה מאוד מספרים שגדולים מ-x), ולכן הסכום של כל אינסוף האיברים יוצא מספר סופי, לכל x - על טור כזה אומרים שהוא “מתכנס”. למעשה, ההתכנסות כאן היא חזקה למדי, ומכונה “התכנסות במידה שווה”. בלי להיכנס לפורמליסטיקה, משמעותה המעשית הרלוונטית לנו היא שכדי לגזור את הפונקציה שמוגדרת בידי הטור, מספיק לגזור את אברי הטור איבר איבר. מי שיודע לגזור פולינומים מסוגל לגזור כל איבר בטור לחוד - ודי ברור שנגזרת של סינוס תצא קוסינוס, ושנגזרת של קוסינוס תצא מינוס סינוס.

למעשה, ספרי אנליזה רבים מעדיפים את הגישה הזו להגדרת הפונקציות הטריגונומטריות, שעושה להם חיים קלים מאוד ועדיין משמרת את כל התכונות המעניינות (מנקודת מבטה של האנליזה) שלהן. כאן שאלת יחידות המדידה לא עולה בכלל ואין על מה לדאוג. מצד שני, כמו רוב הגישות שמתחילות מהתוצאה (במקרה זה, מטורי הטיילור של סינוס וקוסינוס שהוגדרו בצורה ה”מקורית”), חלק מהקסם אובד, לטעמי.