ריבוע הקסם של פרס-מרמין (או: איך תורת הקוונטים עוזרת לטלפתיה)

הפוסט הזה נולד מתוך הפוסטים על ההוכחה ש-\( \text{MIP}^{*}=\text{RE} \) אבל הוא מיועד לעמוד בפני עצמו ולכן לא אזכיר את עניין \( \text{MIP}^{*}=\text{RE} \) כאן; בפוסט בהמשך אחזור אליו ואז אתבסס על הדברים שאני רוצה להראות הפעם, שהם מגניבים ביותר בלי קשר לשום דבר אחר. מה שאני רוצה להראות הפעם הוא משחק חביב ותמים למראה שמוכיח שתורת הקוונטים מאפשרת לנו לעשות קסמים שפשוט בלתי אפשריים בלעדיה. זה ייתן לנו תירוץ טוב לפוסט נפרד שמתאר את הפורמליזם של החלק שרלוונטי לנו מתורת הקוונטים, כדי שנבין איך הקסם בכלל עובד.

בשביל פוסט האינטואיציה הזה עדיף לא להיכנס להגדרות פורמליות אלא להתחיל מתיאור של משחק, שנקרא “משחק ריבוע הקסם”. במשחק משתתפים שני שחקנים: אליס ובוב. הם לא משחקים זו נגד זה, אלא ההפך - המטרה שלהם היא לשתף פעולה כדי לנצח ביחד במשחק; הקושי הוא שהם משחקים בנפרד. הם יכולים להיפגש לפני שהמשחק מתחיל ולהחליט על אסטרטגיה משותפת, אבל אחר כך מכניסים אותם לחדרים נפרדים ומרגע זה ואילך הם לא יכולים לשלוח זה לזו שום אינפורמציה. ואז המשחק מתחיל.

המשחק משוחק על לוח משבצות \( 3\times3 \) שנראה ככה:

כל משבצת בלוח אפשר לצבוע בירוק או באדום, ואני הולך להשתמש ב-\( +1 \) כדי לסמן ירוק וב-\( -1 \) כדי לסמן אדום. למה דווקא שני אלו ולא \( 0,1 \) למשל? יש סיבה טובה שתתברר בהמשך.

עכשיו, המשחק הולך כך: אחרי שאליס נכנסת לחדר נותנים לה מספר שנבחר באקראי (בהתפלגות אחידה) בין 1 ל-3 והיא צריכה לצבוע את השורה שזה המספר שלה, כך שבשורה יהיה מספר זוגי של משבצות אדומות, כלומר משבצות עם \( -1 \) (או 0 או 2). גם בוב מקבל מספר אקראי בין 1 ל-3 והוא צריך לצבוע את העמודה שזה המספר שלה, כך שבעמודה יהיה מספר אי זוגי של משבצות אדומות. והנה האתגר: לא משנה איזה שורה ועמודה אליס ובוב קיבלו, תהיה בדיוק משבצת אחת שמשותפת לשניהם. הם צריכים לצבוע את הצביעות שלהם כך שאותה משבצת נצבעת באותו הצבע. אם הם הצליחו - הם מנצחים. אם הם נכשלו - הם מפסידים.

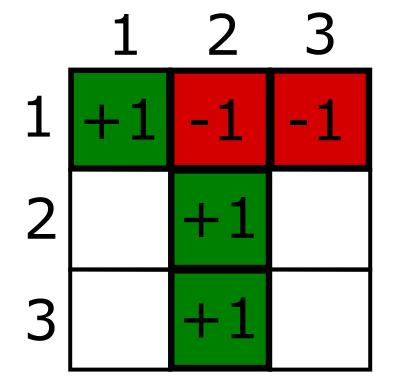
הנה דוגמא למשחק שהסתדר טוב מבחינת אליס ובוב:

מה שקרה פה הוא שאליס קיבלה את המספר 1 ובחרה לצבוע את השורה שלה כך: ירוק-אדום-אדום. בוב קיבל את המספר 2 ובחר לצבוע את העמודה שלו אדום-ירוק-ירוק. בשורה של אליס יש שני אדומים (זוגי) ובשורה של בוב יש אדום אחד (אי זוגי) ובנוסף לכך המשבצת המשותפת שלהם, \( \left(1,2\right) \), צבועה בצבע אדום בשתי הצביעות שלהם. כך שהם ניצחו.

עכשיו, למה בכלל יש פה אתגר לאליס ובוב ואי אפשר לנצח בכל פעם? אם הם יכלו לתקשר זו עם זה מן הסתם לא הייתה להם בעיה - את אותה הצביעה שהראיתי כאן הם יכלו לעשות לכל משבצת אחרת. אז חוסר היכולת לתקשר הוא בעיה, אבל מה עם זה שהם יכולים להסכים מראש על אסטרטגיה, זה לא עוזר?

על פניו אפשר היה לחשוב על התרחיש האופטימי הבא: נניח שאפשר לצבוע את הלוח בצורה כזו שכל שורה כוללת מספר זוגי של משבצות אדומות וכל עמודה כוללת מספר אי זוגי של משבצות אדומות. במקרה הזה אליס ובוב היו מסכימים מראש על צביעה מוצלחת שכזו, ובמשחק עצמו היו צובעים את השורה/עמודה שלהם בהתאם לצביעה שעליה הוסכם מראש. זה היה מבטיח שהמשבצת המשותפת שלהם תהיה צבועה באותו הצבע. אז הבעיה, כפי שודאי ניחשתם, היא שאין צביעה מוצלחת שכזו שבה בכל שורה מספר זוגי של משבצות אדומות ובכל עמודה מספר אי זוגי שלהן. הרי אם בכל שורה היה מספר זוגי של משבצות כאלו, אז מספר המשבצות האדומות הכולל בלוח היה 3 כפול מספר זוגי, כלומר מספר זוגי; ואם בכל עמודה היה מספר אי זוגי של משבצות כאלו אז מספר המשבצות האדומות הכולל בלוח היה 3 כפול מספר אי זוגי, כלומר מספר אי זוגי. אי אפשר ליישב את הסתירה הזו.

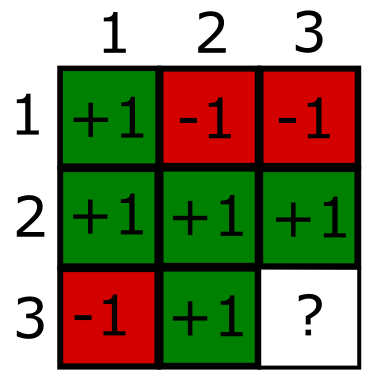
מה שכן אפשר לעשות הוא לצבוע כמעט את כל הלוח בצורה מוצלחת, כך שתהיה בעיה רק במשבצת אחת:

שורות 1-2 ועמודות 1-2 בריבוע הזה עונות על התנאים שנדרשים מהן. אם נצבע את המשבצת \( \left(3,3\right) \) באדום אז התנאי של שורה 3 יתקיים; אם נצבע אותה בירוק, אז התנאי של עמודה 3 יתקיים. אבל שני התנאים הללו לא יכולים להתקיים בו זמנית.

אל תאבדו תקווה! האיור הזה עוזר להמחיש איך אליס ובוב יכולים להסכים מראש על אסטרטגיה שתבטיח להם ניצחון במשחק ב-\( \frac{8}{9} \) מהפעמים שבהן משחקים. הם פשוט יצבעו את השורה/עמודה שקיבלו על פי מה שמופיע באיור, כאשר אם הם יצטרכו לצבוע את \( \left(3,3\right) \) הם יצבעו אותה על פי מה שטוב להם. מכיוון שהם צובעים על פי אותו הלוח, האפשרות היחידה שבה הם סותרים זו את זה היא כאשר \( \left(3,3\right) \) היא המשבצת המשותפת לשניהם. מכיוון שהשורה/עמודה שהם מקבלים נבחרת באקראי ובהתפלגות אחידה, ההסתברות שזה יקרה היא \( \frac{1}{9} \) ולכן הסתברות ההצלחה שלהם היא \( \frac{8}{9} \).

אם כן, אליס ובוב יכולים לנצח ברוב הפעמים. אבל האם הם יכולים לנצח תמיד? התשובה היא לא מהדהד. בואו נשתכנע שזה המצב. ראשית, אני מניח שאליס ובוב יכולים לפעול בצורה הסתברותית - להטיל מטבעות ולהחליט על פיהן איך לצבוע את השורה/עמודה שלהם. אבל אם אני שואל אם אליס ובוב יכולים לנצח תמיד כל ההסתברות הזו לא רלוונטית - אם הם מנצחים תמיד, הם מנצחים בפרט כשכל ההטלות שלהם יוצאות “עץ” ולכן מספיק להסתכל על מה שקורה אז.

עכשיו, בואו נסתכל על מה אליס עושה כשהיא מקבלת את הקלטים 1,2,3. היא הולכת למלא כך את כל הריבוע, בצורה שהיא חוקית ברמת השורות, ובלתי תלויה לגמרי במה שבוב עושה כי היא לא קיבלה שום מידע על מה שבוב עושה. אני טוען שהמילוי של הריבוע על ידי אליס יהיה חוקי גם ברמת העמודות. למה? כי בואו ניקח לדוגמא את עמודה מס’ 1 ונסתכל על שלוש ריצות של המשחק שבהן בוב קיבל 1 ואליס קיבלה 1,2,3 בהתאמה. בכל הפעמים הללו אליס ובוב ניצחו - כלומר, העמודה שבוב אומר כשאומרים לו 1 שווה בדיוק לעמודה מס’ 1 במילוי הטבלה שאליס ביצעה. לכן העמודה הזו חוקית (הרי בוב ממלא עמודות בצורה חוקית) וכך גם לכל הטבלה. ואמרנו כבר שאי אפשר למלא את כל הטבלה בצורה חוקית.

זה לכאורה סותם את הגולל על המשחק הזה - אליס ובוב לא יכולים לנצח בכל פעם.

אלא אם כן… נכניס את תורת הקוונטים למשחק. כי אם לאליס ובוב יהיו שני זוגות שזורים של קיוביטים, הם יוכלו לנצח בודאות, בכל פעם. תמיד. מה שמעלה את השאלה האקוטית - מה זה בכלל אומר, “שני זוגות שזורים של קיוביטים”? שהיא בעצם השאלה שכל הפוסט הזה בא לתת לה מוטיבציה. כאן אני אסתפק בתיאור עם נפנופי ידיים; בפוסט הבא יגיע הפורמליזם המתמטי, ואחר כך אפשר יהיה לחזור לריבוע הקסם ולהסביר פורמלית מה עושים בו.

קיוביט זה מושג מתמטי שאפשר לממש פיזית בכל מני דרכים שונות. האנלוגיה המתאימה היא לביטים “רגילים” של מחשב “רגיל”: במחשב רגיל אנחנו חושבים על המידע בתור 0 או 1 וקוראים ליחידת מידע בסיסית כזו “ביט”, ויש פעולות לוגיות שאנחנו יודעים להפעיל על יחידות המידע הזה שאפשר מתמטית לחשוב עליהן בתור פעולות בשדה \( \mathbb{Z}_{2} \): למשל הפעולה AND שאפשר לתאר בתור \( \text{AND}\left(x,y\right)=x\cdot y \), או הפעולה NOT שאפשר לתאר בתור \( \text{NOT}\left(x\right)=1-x \). מהפעולות הפשוטות הללו אפשר לבנות את כל האלגוריתמים שהמחשב מבצע.

כל זה הוא תיאור מתמטי של מה ביטים עושים. אבל מה קורה בפועל, בעולם האמיתי, בתוך מחשבים אמיתיים? בלי להיכנס לפרטים כי מה אני מבין בעצם, מחשבים בני זמננו משתמשים באלקטרוניקה כדי לייצג ביטים. ערך של 1 מיוצג על ידי מתח חשמלי גבוה בתוך רכיב מסויים בעוד ש-0 מיוצג על ידי מתח חשמלי נמוך, ופעולות לוגיות ממומשות על ידי מניפולציה אלקטרונית. אפשר גם לחשוב על מימושים שונים לגמרי של אותו רעיון - למשל שביט ייוצג על ידי מים: כמות גדולה של מים ברכיב כלשהו מייצגת 1, כמות קטנה מיצגת 0, ופעולות לוגיות מתבצעות על ידי שפיכה של מים בצורות שונות ומשונות.

אותו הדבר עם קיוביטים: על קיוביטים אפשר לחשוב מתמטית בתור משהו שחי בעולם טיפה יותר מורכב מאשר \( \mathbb{Z}_{2} \) אבל לא הרבה יותר מורכב. מבחינה מעשית, האופן שבו יצור כזה ממומש דורש התבססות על טכנולוגיה שמסוגלת לרתום את האספקטים המוזרים של תורת הקוונטים לשימוש שלנו - וזה אתגר גדול מאוד שעדיין מקשה מאוד על בניית מחשבים קוונטיים יעילים כיום. השיטה הפופולרית כיום היא שימוש בעל-מוליכים; יש רכיב של על מוליך שהזרם שבתוכו מתנהג בצורה קוונטית מסויימת כך שאפשר לחשוב עליו בתור ייצוג של קיוביט, והמניפולציות שאפשר לבצע בו מתרחשות על ידי שליחת פולסים אלקטרומגנטיים אליו (שליטה על התדירות של הפולס משפיעה על סוג הפעולה שמתבצעת). זה לא פוסט על מחשבים קוונטיים אז לא אכנס לעוד פרטים בסגנון, אבל מה שכן קריטי להגיד הוא שזה עובד. זה קיים כבר כיום. כשאומרים “קיוביט” לא מתכוונים לאיזה יצור דמיוני אלא למשהו שאנחנו בהחלט יודעים ליצור ולשלוט בו בשלל דרכים. הקושי הוא לעבוד עם כמות גדולה שלהם לאורך זמן (אפילו 50 זה כבר קשה, בימינו), אבל את מה שנעשה עוד רגע עם המשחק של אליס ובוב אפשר לבצע במציאות. זה קריטי להדגיש את הנקודה הזו כי אחרת נראה שמה שנעשה עם אליס ובוב הוא פשוט רמאות.

כמו שאפשר להסתכל על ביט ולבדוק מה הערך שלו, גם קיוביט אפשר למדוד כדי לקבל ערך, אבל כאן צריך להיזהר - מדידה כזו לא נותנת את הערך שהקיוביט החזיק, אלא מכריחה אותו לבחור ערך מסויים בצורה הסתברותית ולהחזיר אותו, ואחרי כן הערך של הקיוביט משתנה כדי להתאים לערך שהוא החזיר. זו כבר תופעה שלא לגמרי קיימת במחשבים קלאסיים למרות שלא קשה לממש אותה בעזרת אלגוריתם. מה שנותן לקיוביטים את הכוח הגדול שלהם בסיפור הזה הוא היכולת לשזור אותם - לקחת שני קיוביטים ולא רק קיוביט אחד ואיכשהו ליצור משניהם ביחד מצב שאי אפשר לחשוב עליו כאילו הוא מורכב משני איברים נפרדים שאין ביניהם קשר (מה שלא קיים בביטים רגילים). בפרט המשמעות של שזירה כזו היא שמדידת קיוביט אחד משפיעה על מצב הקיוביט השני. לשזירה יש עוד אפקט קסום - היא לא תלויה במרחק. אם יצרנו שני קיוביטים שזורים ואז הרחקנו אותם זה מזה מאות קילומטרים, עדיין מדידה של אחד מהם תשפיע על השני. הקסם המוזר הזה הוא מה שנקרא פרדוקס EPR למרות שזה בעצם לא פרדוקס.

זה מסביר מהיכן מגיע היתרון של אליס ובוב. לפני שהמשחק מתחיל הם חולקים זו עם זה קיוביטים שזורים. אחר כך, במהלך המשחק, אליס מודדת את הקיוביט שלה וזה משפיע על הקיוביט של בוב ולכן על התוצאה שבוב יקבל (בהנחה שאליס מודדת לפני בוב, אבל אותו דבר יקרה גם אם בוב מודד לפני אליס). אם כן, בפועל יש תיאום בין אליס ובוב; הוא פשוט נעזר במשאב קוונטי שמאפשר לאליס ובוב להיות מרוחקים זו מזה ולא להעביר אינפורמציה “קלאסית” בשום צורה.

אז איך משחק ריבוע הקסם של אליס ובוב ייפתר? כאמור, אליס ובוב חולקים שני זוגות של קיוביטים שזורים. אליס מקבלת שורה ובוב מקבל עמודה. על פי השורה שאליס קיבלה היא מבצעת שלוש מדידות שונות לכל אחד מהקיוביטים שיש ברשותה בשני הזוגות השזורים. כל מדידה של כל קיוביט שזור מחזירה \( +1 \) או \( -1 \) כך שאליס מקבלת שלושה זוגות של מספרים כשבכל זוג הערכים הם \( +1 \) או \( -1 \). היא כופלת את האיברים של כל זוג, ומקבלת את הערך שהיא צריכה למלא בתא הזה בשורה. בוב עושה את אותו הדבר. התוצאה תהיה מילוי חוקי של השורה/עמודה עבור שניהם.

כמובן, אמרתי כמעט הכל אבל לא אמרתי כלום. הרכיב הקריטי שחסר לנו פה הוא המידע איזה מדידות אליס ובוב מבצעים. זה כבר רומז שיש “כמה סוגים” שונים של מדידות קוונטיות, ולכן להבין מה זה אומר יהיה מה שננסה לעשות בפוסט הבא, שבו נצלול לתוך המתמטיקה של כל העסק הזה. אל אליס ובוב נחזור בהמשך.