אז איך פותרים אינטגרלים בתיכון?

מבוא

ביקשו ממני לכתוב פוסט על איך פותרים תרגילים עם אינטגרלים ברמת תיכון, ואני מאוד שמח לעשות את זה כי זה נושא שחביב עלי מאוד מסיבה פשוטה: לחשב אינטגרלים זה קשה. בגלל שזה קשה, פשוט אי אפשר לתת בתיכון תרגילים קשים באמת שמערבים אינטגרלים, ולכן מה שכן נותנים הוא את הדברים הפשוטים יחסית שאפשר לפתור בצורה די מסודרת אחרי שמבינים מה בעצם הולך שם, מה זה אינטגרלים ואיך ניגשים לטכניקה שלהם.

נתחיל מ”מה זה אינטגרלים”. חלק מהסיבה שבגללה אינטגרלים זה עסק מבלבל הוא שאנחנו משתמשים ב”אינטגרל” כדי לתאר שני דברים שנראים במבט ראשון שונים לגמרי, אבל אחת מהתוצאות היפות במתמטיקה (“המשפט היסודי של החשבון הדיפרנציאלי והאינטגרלי”) מראה שהם קשורים בצורה חזקה. ראשית, אינטגרלים מוצגים בתור “ההפך מנגזרת”, כלומר בתור מושג שכדי להבין אותו צריך קודם כל להבין את המושג המרכזי השני בחשבון דיפרנציאלי ואינטגרלי - הנגזרת. יש לי פוסטים על נגזרות ועל איך מחשבים אותן, כך שבפוסט הזה אניח היכרות בסיסית עם הנושא; אבל אני כן הולך להזכיר כל דבר רלוונטי לפני שאני משתמש בו.

לאינטגרל שהוא “ההפך מנגזרת” קוראים “אינטגרל לא מסויים”. יש גם מושג אחר, של “אינטגרל מסויים”, שבכלל עוסק בחישוב של שטחים, נפחים וכל מני דברים מספריים אחרים. זו, מבחינה היסטורית, הנקודה שבה מושג האינטגרל נולד, ויש לי פוסט שמסביר את מושג האינטגרל מנקודת המבט הזו. אלא שהפוסט הנוכחי הולך להיות טכני ברמת תיכון, מה שאומר שלא נצטרך לדבר הרבה על אינטגרל מסויים. ההגדרה הפורמלית שלו? דורשת טכניקה שלא נלמדת בתיכון. האינטואיציה הכללית מאחוריו? דורשת רעיונות שלא נלמדים בתיכון. מה שנשאר זה רק איך מחשבים אותו בהקשרים ספציפיים, וזה קל ונגיע לזה. החישוב הוא תמיד “תחשבו את האינטגרל הלא מסויים ואז תעשו איתו דברים”, כך שהמושג הטכני שרלוונטי לנו הוא אינטגרל לא מסויים.

פרק ראשון, שבו נספר על נגזרות ואינטגרלים של פולינומים

אם נלך לדף הנוסחאות בבגרות ונלך אל “אינטגרלים”, נראה קודם כל את הנוסחה המייאשת הבאה:

• \( \int x^{t}dx=\frac{x^{t+1}}{t+1}+C \) (\( t \) ממשי, \( t\ne-1 \))

אחרי שנבין אותה, נעבור כבר יותר מחצי מהדרך אל הבנת אינטגרלים באופן כללי. אבל כדי להבין אותה, צריך לדבר קודם כל על נגזרת. נגזרת זה משהו שעושים לפונקציות, כשאצלנו פונקציה היא משהו שמקבל קלט \( x \) ומוציא פלט שכותבים בתור איזו שהיא נוסחה שמערבת את \( x \). למשל \( 2x^{3}+5 \) זו דרך מקוצרת לכתוב את הפונקציה \( y=2x^{3}+5 \) (או \( f\left(x\right)=2x^{3}+5 \); מה שיטות הסימון של הצעירים בימינו?). הנגזרת של פונקציה אמורה לייצג את “קצב ההשתנות” שלה עבור ערכים שונים ומשונים של \( x \); זה שייך לתיאוריה שלא רלוונטית לפוסט הטכני הזה. הנקודה הרלוונטית היא שהנגזרת של פונקציה היא בעצמה פונקציה ושגזירה של פונקציה היא משהו שיש לנו דרך שיטתית מאוד לבצע.

הדברים שהכי קל לגזור הם פונקציות שנקראות פולינומים. פולינומים הם יצורים כמו \( 2x^{3}+5 \): סכום של איברים שכל איבר הוא מהצורה “מספר כלשהו כפול חזקה שלמה של \( x \)” (בדוגמא שלי \( 5 \) מוכפל בחזקה \( x^{0} \) של \( x \)). הנה הנגזרות של כמה פולינומים ממש פשוטים:

• הנגזרת של הפולינום \( 1 \) היא 0.
• הנגזרת של הפולינום \( x \) היא 1.
• הנגזרת של הפולינום \( x^{2} \) היא \( 2x \).
• הנגזרת של הפולינום \( x^{3} \) היא \( 3x^{2} \).
• הנגזרת של הפולינום \( x^{4} \) היא \( 4x^{3} \).

ונראה לי שכבר הבנו את הרעיון, לא? באופן כללי את כל אלו אפשר לתאר על ידי “הנגזרת של \( x^{t} \) היא \( tx^{t-1} \)”, וזה יהיה נכון לכל מספר ממשי \( t \), גם אם הוא לא מספר שלם בכלל (למשל, הנגזרת של \( x^{\pi} \) היא \( \pi x^{\pi-1} \)). זה זמן טוב להציג את הסימון של נגזרת - משתמשים במשהו שנקרא “תג” ובקושי אפשר לראות אותו, כי למה לא לבלבל אנשים אם אפשר. הנה איך נראית הנוסחה הכללית שראינו כשמסמנים אותה עם תג:

• \( \left(x^{t}\right)^{\prime}=tx^{t-1} \)

גם זו נוסחה שמופיעה בדף הנוסחאות, וזו נקודת המוצא שלנו. בואו נבין איך היא מתקשרת לנוסחה המוזרה עבור אינטגרלים שראינו קודם ואנחנו עדיין לא מבינים.

כזכור, אינטגרל לא מסויים הוא “ההפך מנגזרת”. אם הנגזרת של \( x^{2} \) היא \( 2x \), זה אומר שהאינטגרל הלא מסויים של \( 2x \) יהיה \( x^{2} \). באופן דומה, האינטגרל הלא מסויים של \( 3x^{2} \) יהיה \( x^{3} \) וכן הלאה. פרט לכך, כשכותבים אינטגרל לא מסויים תמיד מוסיפים לו \( +C \) בסוף. כלומר, אני כותב \( \int2xdx=x^{2}+C \) ו-\( \int3x^{2}dx=x^{3}+C \). הסיבה לכך היא שאותה נגזרת יכולה להתקבל מכמה פונקציות שונות, שההבדל ביניהן הוא חיבור של מספר קבוע. למשל, גם הנגזרת של \( x^{3}+5 \) היא \( 3x^{2} \); בהמשך גם נבין למה. מבחינה טכנית, המשמעות היא זו: בשביל למצוא אינטגרל לא מסויים של פונקציה \( f \) מספיק למצוא פונקציה \( F \) אחת כך ש-\( F^{\prime}=f \), ואז האינטגרל הלא מסויים הכללי הוא פשוט \( F+C \), כלומר כותבים \( \int fdx=F+C \).

עכשיו, לחישוב נגזרת יש שתי תכונות נחמדות מאוד שנקראות ביחד “הלינאריות של הנגזרת”. התכונה הראשונה היא ש-\( \left(f+g\right)^{\prime}=f^{\prime}+g^{\prime} \), כלומר כדי לחשב את הנגזרת של סכום שתי פונקציות מספיק לחשב את הנגזרת של כל אחת בנפרד, ורק אז לחבר; והתכונה השניה היא ש-\( \left(c\cdot f\right)^{\prime}=c\cdot f^{\prime} \) עבור מספר ממשי \( c \). כלומר, כדי לחשב את הנגזרת של “קבוע כפול פונקציה” מספיק לחשב את הנגזרת של הפונקציה, ואז לכפול בקבוע הזה.

עכשיו אפשר לחשב בקלות את הנגזרת של כל פולינום: למשל, מה הנגזרת של \( 5 \)? מכיוון ש-\( 5=5\cdot1 \) ואנחנו יודעים ש-\( \left(1\right)^{\prime}=0 \) נקבל ש-\( \left(5\right)^{\prime}=5\cdot\left(1\right)^{\prime}=5\cdot0=0 \) (“הנגזרת של כל קבוע היא אפס”). ומה הנגזרת של \( 2x^{3} \)? מכיוון שהנגזרת של \( x^{3} \) היא \( 3x^{2} \), נקבל ש-\( \left(2x^{3}\right)^{\prime}=2\left(3x^{2}\right)=6x^{2} \). ועכשיו, מה הנגזרת של \( 2x^{3}+5 \)? נשתמש בתכונה עם החיבור ונקבל ש-\( \left(2x^{3}+5\right)^{\prime}=\left(2x^{3}\right)^{\prime}+\left(5\right)^{\prime}=6x^{2}+0=6x^{2} \). הנה לנו ההסבר לעניין ה-\( +C \); באופן כללי, \( \left(f+C\right)^{\prime}=f^{\prime}+0=f^{\prime} \) ולכן כל הפונקציות מהצורה \( f+C \) עבור כל \( C \) ממשי יתנו את אותה הנגזרת.

איך זה עוזר לנו לחשב אינטגרלים?

ובכן, אם \( \left(x^{2}\right)^{\prime}=2x \), אז אפשר עכשיו לחלק ב-2 את שני האגפים ולקבל \( \left(\frac{1}{2}x^{2}\right)^{\prime}=x \). באופן דומה אפשר לטפל ב-\( x^{3} \): אם \( \left(x^{3}\right)^{\prime}=3x^{2} \) אז \( \left(\frac{1}{3}x^{3}\right)^{\prime}=x^{2} \), וכך גם לנגזרות אחרות. בואו נכתוב את זה בעזרת סימונים של אינטגרלים:

\( \int xdx=\frac{1}{2}x^{2}+C \)

\( \int x^{2}dx=\frac{1}{3}x^{3}+C \)

ומה קורה באופן כללי? ובכן, \( \left(x^{t}\right)^{\prime}=tx^{t-1} \), ולכן נקבל:

\( \int x^{t-1}dx=\frac{1}{t}x^{t}+C \)

אלא שכאן צריך להיזהר. כאשר \( t=0 \), יש לנו בביטוי הזה חלוקה באפס - זה פשוט לא עובד! המקרה הזה מגיע מהנוסחה הבאה: \( \left(x^{0}\right)^{\prime}=0\cdot x^{-1} \). במקרה הזה, אי אפשר לחלק בקבוע \( 0 \) שבו מוכפל \( x^{-1} \) ולכן לא ניתן “לחלץ” אותו - זה מקרה פרטי מיוחד שנדבר עליו בהמשך.

עכשיו, בואו ניקח את הנוסחה \( \int x^{t-1}dx=\frac{1}{t}x^{t}+C \) ונשנה אותה טיפה. בדרך כלל כשאני רוצה למצוא אינטגרל עבור משהו, זה לא עבור \( x^{t-1} \) אלא עבור \( x^{t} \) (כלומר, אני לא כותב את החזקה בתור “משהו פחות 1”). אז בואו נעשה “החלפת משתנה”: נסמן \( s=t-1 \), כלומר \( t=s+1 \), ואז נקבל את הנוסחה \( \int x^{s}dx=\frac{1}{s+1}x^{s+1}+C \). מכיוון ש-\( s \) זה סתם סימון, אפשר “לחזור” אל \( t \), ובאותה הזדמנות קצת לכווץ את אגף ימין, ולקבל

• \( \int x^{t}dx=\frac{x^{t+1}}{t+1}+C \)

זו הנוסחה שהזכרנו קודם. שימו לב מה עכשיו המקרה ה”אסור”: קודם זה היה \( t=0 \), אבל אחרי החלפת המשתנים זה עבר להיות המקרה \( t=-1 \) (קל לראות את זה - זה מה שיגרום למכנה באגף ימין להתאפס). לכן מסייגים את הנוסחה ההיא בכך ש-\( t\ne-1 \).

עכשיו אפשר להשתמש בנוסחה הזו כדי לחשב אינטגרלים קצת יותר מורכבים, כשאנחנו נעזרים בתכונה משמחת אחת: בזכות העובדה שנגזרת היא לינארית, גם אינטגרל הוא כזה. כלומר: \( \int\left(f+g\right)dx=\int fdx+\int gdx \) ו-\( \int cfdx=c\int fdx \). לכן, אם למשל אני רוצה לחשב את האינטגרל של \( 2x^{3}+5 \), אני משתמש בלינאריות ומקבל:

\( \int\left(2x^{3}+5\right)dx=2\int x^{3}dx+5\int1\cdot dx=\frac{2x^{4}}{4}+5x+C=\frac{x^{4}}{2}+5x+C \)

אפשר לעצור לסיכום ביניים קצר: אנחנו מבינים (אני מקווה!) את הנוסחה המוזרה מדף הנוסחאות, ואיך אפשר להשתמש בה כדי לחשב אינטגרל עבור כל פולינום, חוץ מהמקרה המעצבן הזה של \( x^{-1} \) שאין לנו מושג מה לעשות בו. אפשר עכשיו לעבור לדברים מתוחכמים קצת יותר.

פרק שני, שבו אנחנו עוברים לדברים מתוחכמים קצת יותר

יודעות מה? בעצם לא. אולי לא כדאי לשפוך את כל מהומת האינטגרלים הלא מסויימים על הראש בבת אחת. במקום זה, בואו נראה איך משתמשים במה שכבר יש לנו כדי לטפל באינטגרלים מסויימים, ברמה שמספיקה לפתור שאלות מהבגרות. אם כן:

פרק שני האמיתי באמת שבו אנחנו עוברים לחשב שטחים

היי, תראו, הנה שאלה אמיתית מבגרות!

בשאלה הזו מעורבות שתי פונקציות שהן פולינומים, כלומר שאנחנו כבר יודעים לטפל בהן. פונקציה אחת היא \( f\left(x\right)=x^{2}-6x+5 \), והשניה היא \( g\left(x\right)=x^{2}-10x+a \) כאשר \( a \) הוא “פרמטר” שבעצם תחילת השאלה עוסקת במציאת הערך המדויק שלו. אין פה משהו מעניין - אומרים ששתי הפונקציות הללו נחתכות בדיוק בנקודה שקואורדינטת ה-\( x \) שלה היא \( 4 \). זה אומר שאם נציב \( 4 \) בשני הפולינומים, הערך שאנחנו מקבלים אמור להיות שווה, כלומר \( f\left(x\right)=g\left(x\right) \). בואו נפשט את השוויון ובסוף נציב \( x=4 \):

\( x^{2}-6x+5=x^{2}-10x+a \) (זה \( f\left(x\right)=g\left(x\right) \))

\( 4x+5=a \) (העברתי את \( x^{2}-10x \) לאגף שמאל)

\( 4\cdot4+5=a \) (הצבתי \( x=4 \))

\( a=21 \) (זו המסקנה)

כלומר, \( g\left(x\right)=x^{2}-10x+21 \). אגב, נקודת החיתוך של שני הפולינומים היא \( \left(4,-3\right) \).

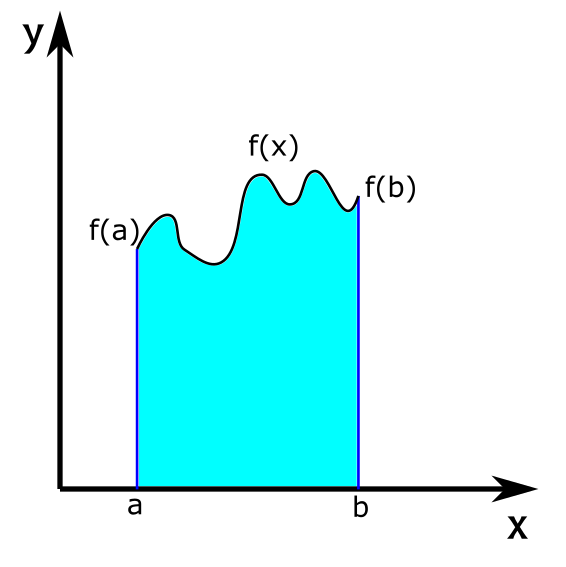
עכשיו צריך למצוא את השטח ש”מוגבל על ידי הגרפים של שתי הפונקציות”, אבל בשביל לעשות את זה קודם כל צריך להבין איך בכלל משתמשים באינטגרל כדי למצוא שטחים, ולשם כך בואו נתחיל מהמקרה הכי פשוט שמתואר באיור הבא:

כאן יש לנו פונקציה \( f\left(x\right) \) שאני מסתכל עליה אך ורק בין שתי נקודות \( a,b \). כלומר, אני מצייר את \( f\left(x\right) \) רק עבור \( a\le x\le b \). אני מותח שני קווים אנכיים, אחד בנקודה \( a \) (עד לגובה \( f\left(a\right) \)) והשני בנקודה \( b \) (עד לגובה \( f\left(b\right) \)), ואז אני צובע בתכלת את האיזור ש”כלוא” בין ארבעה קווים: שני הקווים האנכיים הללו שציירתי, ציר ה-\( x \) (הקו האופקי מ-\( \left(a,0\right) \) עד \( \left(b,0\right) \)) ולסיום, ה”קו” (ליתר דיוק, העקום) למעלה שמתאים ל-\( f \). שימו לב לכך ש-\( f\left(x\right) \) היא אי-שלילית בכל הקטע הזה.

בהינתן כל אלו, השטח שצבעתי בתכלת שווה למה שנקרא האינטגרל המסויים של \( f \) בין \( a \) ל-\( b \). הדבר הזה מסומן ב-\( \int_{a}^{b}f\left(x\right)dx \). קישרתי קודם לפוסט שלי שבו אני מסביר מה זה אינטגרל מסויים באמת (אפשר לחשוב עליו בתור סוג מתוחכם של סכום מאוד אינסופי), אבל אנחנו לא צריכים את ההגדרה הזו כדי לחשב שטחים, רק להבין איך אפשר להיעזר באינטגרל המסויים כדי לחשב אותם.

אז… איך אני מחשב את המספר \( \int_{a}^{b}f\left(x\right)dx \)? פשוט מאוד, בעזרת האינטגרל הלא מסויים. נניח ש-\( \int f\left(x\right)dx=F\left(x\right)+C \), כלומר \( F \) היא פונקציה שכאשר גוזרים אותה מקבלים את \( f \). אז מתקיים הקשר הבא, שבעיני הוא מדהים ומרהיב ואחד מהדברים הנפלאים במתמטיקה: \( \int_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right) \). כלומר, כדי לחשב את האינטגרל המסויים של \( f \) (ובדוגמא שלנו, את השטח ה”מופרע” בצבע תכלת), צריך לחשב את הערך של \( F \) בשתי נקודות בלבד, אלו של קצוות הקטע שעליו עושים אינטגרל ואז לחסר את הערך הראשון מהשני. הדבר הנפלא הזה הוא תוצאה של מה שמכונה “המשפט היסודי של החדו”א” והאינטואיציה פה היא שהאינטגרל המסוים (השטח בתכלת) מייצג בדיוק את “כמה שינוי \( F \) צריכה להשתנות החל מהנקודה \( a \) כדי להגיע לערכה בנקודה \( b \)”, אבל לא קריטי להבין את האינטואיציה הזו לצרכים הטכניים.

הכל טוב ויפה, אבל עכשיו - איך משתמשים בזה כדי לפתור את השאלה שהצגתי לעיל? שם מבקשים שטח שכלוא בין שתי עקומות, ובנוסף לכך אחד מהתנאים שהזכרתי קודם לא מתרחש - אני דרשתי מ-\( f\left(x\right) \) להיות חיובית בכל הקטע שעליו עושים אינטגרל, אבל זה לא קורה בשאלה למעלה.

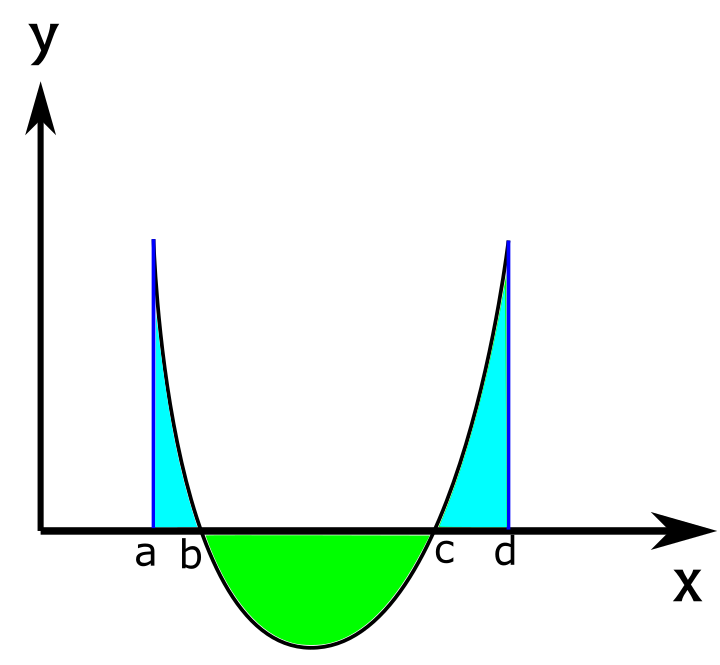
בואו נסתכל על דוגמא אחרת - פונקציה שנראית כמו פרבולה, כמו בשאלה שלעיל, כך שיש לפרבולה חלק שבו היא נמצאת מתחת לציר \( x \) (החלק בין הנקודות \( b \) ו-\( c \)):

אני מסמן בתכלת את השטח שכלוא בין הפונקציה וציר \( x \) בקטעים שבהם היא חיובית, ובירוק את השטח שכלוא בינה לבין ציר \( x \) כשהיא שלילית. כדי לחשב את השטח הירוק, אני צריך לקחת את מינוס האינטגרל של הפונקציה בקטעים הללו. כלומר, השטח הכולל של ירוק + תכלת הולך להיות סכום של שלושה אינטגרלים מסויימים:

\( \int_{a}^{b}f\left(x\right)dx-\int_{b}^{c}f\left(x\right)dx+\int_{c}^{d}f\left(x\right)dx \)

מה בעצם הרעיון פה? למה לוקחים את מינוס האינטגרל כדי לקבל את השטח הירוק? ובכן, כי האינטואיציה מאחורי אינטגרל מסויים היא לא “שטח” אלא “סכום”, וכשהפונקציה שלילית, מה שקורה הוא שסוכמים הרבה ערכים שליליים ולכן הסכום שלהם יוצא שלילי. כדי לקבל שטח מתוך אינטגרל מסויים צריך לחשב את הערך המוחלט \( \int_{a}^{b}\left|f\left(x\right)\right|dx \) והמשמעות של זה בפועל היא בדיוק מה שהצגתי - חלוקה לאיזורים חיוביים ושליליים ולקיחת מינוס האינטגרל עבור האיזורים השליליים.

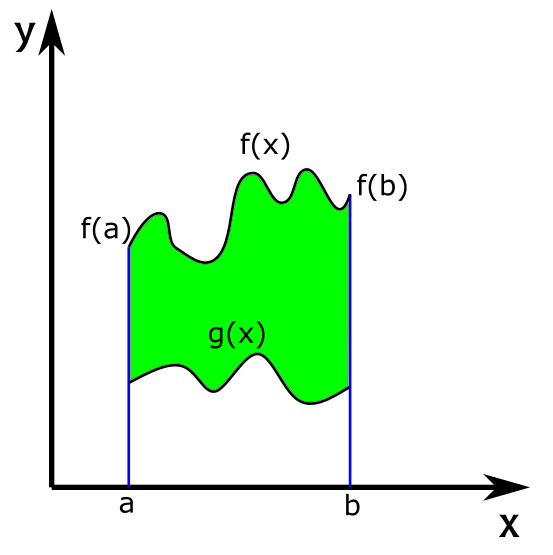
ועכשיו אפשר להגיע אל המקרה הכללי ביותר והמועיל ביותר, שמדבר על הסיטואציה שבה יש לנו שתי פונקציות ואנחנו מחשבים את השטח שכלוא בין שתיהן ובין שני קווים אנכיים. זה נראה ככה:

הסיטואציה היא זו: יש לנו שתי פונקציות \( f\left(x\right),g\left(x\right) \) כך ש-\( g\left(x\right)\le f\left(x\right) \) לכל \( a\le x\le b \). במקרה הזה אפשר להוכיח, כבר מההגדרה הבסיסית של אינטגרל מסויים (שאני לא מציג כאן…), שהשטח הירוק בתמונה שווה בדיוק ל-\( \int_{a}^{b}\left(f\left(x\right)-g\left(x\right)\right)dx \).

מה שנחמד בתוצאה הזו הוא ששתי התוצאות הקודמות שתיארתי נובעות ממנה: בשתי הדוגמאות הקודמות הפונקציה \( g\left(x\right) \) השתתפה בצורה סמויה - היא פשוט הייתה הפונקציה \( g\left(x\right)=0 \) הידועה גם בשם “ציר \( x \)”. כשחישבתי את \( \int_{a}^{b}f\left(x\right)dx \) בעצם חישבתי את \( \int_{a}^{b}\left(f\left(x\right)-0\right)dx \), ולכן חישבתי את השטח שכלוא בין \( f \) ובין \( g \), כלומר בין \( f \) ובין ציר \( x \). במקרה שבו \( f\left(x\right)\le0 \) אז חישבתי בעצם את \( \int_{a}^{b}\left(0-f\left(x\right)\right)dx \) ומכאן צץ המינוס.

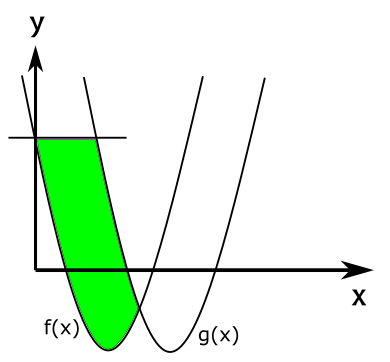
זו בעצם התורה כולה - כל היתר הוא פשוט משחק ב”אילו שטחים אנחנו רוצים לחשב”. בואו נראה את המשחק הזה עבור השאלה שאנחנו רוצים לפתור:

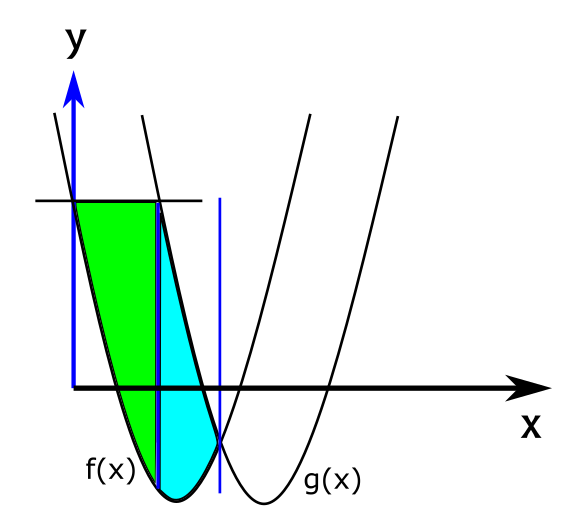
השטח הירוק שבתמונה לא מתאים לתיאורים שנתתי עד כה, בגלל הצורה המורכבת שלו. החלק התחתון שלו הוא כל הזמן הפונקציה \( f\left(x\right) \), אבל החלק העליון שלו מתחיל בתור קו אופקי, ואז פתאום הופך להיות הפונקציה \( g\left(x\right) \). אז מה שנעשה יהיה למתוח קווים אנכיים, שאסמן בצבע כחול, בכל הנקודות המעניינות - תחילת וסוף השטח הירוק, והנקודה שבה החלק העליון של השטח משתנה:

בשביל לפתור את התרגיל, נצטרך את הדברים הבאים:

• למצוא את המשוואה של הקו האופקי העליון (המשוואה היא בסך הכל \( h\left(x\right)=a \) עבור \( a \) קבוע כלשהו; האתגר הוא למצוא את \( a \)).
• למצוא את המשוואות של שלושת הקווים האנכיים הכחולים (שניים בעצם כבר מצאנו, כפי שאראה עוד רגע).
• למצוא את האינטגרלים המסויימים עבור שני השטחים - הירוק והתכלת.

בואו ניזכר מה הפונקציות \( f,g \) היו בעצם:

\( f\left(x\right)=x^{2}-6x+5 \)

\( g\left(x\right)=x^{2}-10x+21 \)

עכשיו, לישר האופקי: הוא עובר דרך הנקודה שבה \( f \) חותכת את ציר \( y \), כלומר דרך הנקודה שהגובה שלה הוא \( f\left(0\right)=0^{2}-6\cdot0+5=5 \). כלומר המשוואה של הישר הזה היא \( h\left(x\right)=5 \). זה היה קל! עכשיו, לקווים האנכיים הכחולים. הראשון הוא בעצם הקו האנכי \( x=0 \), מה שנקרא “ציר \( y \)”. השלישי עובר דרך נקודת החיתוך שמצאנו קודם - כלומר, הוא הקו \( x=4 \). נשאר רק הקו האמצעי - הקו הזה עובר דרך נקודת החיתוך של הישר האופקי \( h\left(x\right)=5 \) עם הפונקציה \( g\left(x\right) \), כלומר בנקודה \( x \) שמקיימת \( g\left(x\right)=5 \), כלומר בפתרון של המשוואה \( x^{2}-10x+21=5 \), כלומר בפתרון של המשוואה \( x^{2}-10x+16=0 \).

איך פותרים משוואה כזו? ובכן, אפשר עם נוסחת השורשים, אבל איפה הכיף פה? משהו שתמיד אפשר לעשות: לבדוק האם את המקדם החופשי, במקרה שלנו המספר 16, אפשר לכתוב בתור מכפלה של שני איברים שהסכום שלהם הוא מינוס המקדם האמצעי. במקרה שלנו, אפשר: \( 16=2\cdot8 \). אז נוקטים בתעלול הבא: מפרקים את המחובר האמצעי ומקבלים

\( x^{2}-2x-8x+16=0 \)

מוציאים גורמים משותפים ומקבלים

\( x\left(x-2\right)-8\left(x-2\right)=0 \)

ולבסוף:

\( \left(x-8\right)\left(x-2\right)=0 \)

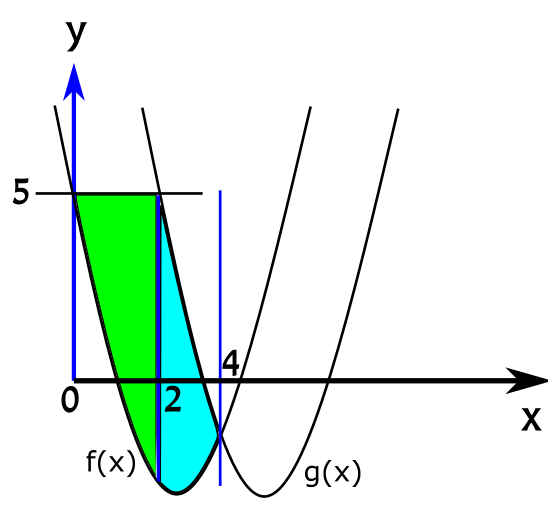
זה בעצם אומר לנו שהפתרונות הם \( x=2,8 \). אנחנו מחפשים את הפתרון הקטן יותר, שמתאים לנקודת החיתוך הראשונה, ולכן \( x=2 \) הוא מה שחיפשנו. בואו נוסיף לתמונה את כל המספרים שמצאנו:

ועכשיו - לאינטגרלים! השטח הירוק כלוא בין הפונקציה \( h\left(x\right)=5 \) והפונקציה \( f\left(x\right) \) בקטע \( 0\le x\le2 \) ולכן הוא שווה ל-

\( \int_{0}^{2}\left[5-\left(x^{2}-6x+5\right)\right]dx=\int_{0}^{2}\left(6x-x^{2}\right)dx \)

האינטגרל הלא מסויים של \( 6x-x^{2} \) הוא \( 3x^{2}-\frac{x^{3}}{3} \), מכללי האינטגרלים שכבר ראינו. אם מציבים בזה 0 מקבלים 0, ולכן הערך שאנחנו מחפשים הוא מה שקורה כשמציבים בכל זה 2:

\( 3\cdot2^{2}-\frac{2^{3}}{3}=12-\frac{8}{3}=\frac{36-8}{3}=\frac{28}{3}=9\frac{1}{3} \)

עכשיו נעבור אל שטח התכלת: זה השטח שכלוא בין \( g\left(x\right) \) (מלמעלה) ו-\( f\left(x\right) \) (מלמטה) בקטע \( 2\le x\le4 \), ולכן:

\( \int_{2}^{4}\left(g\left(x\right)-f\left(x\right)\right)dx=\int_{2}^{4}\left[\left(x^{2}-10x+21\right)-\left(x^{2}-6x+5\right)\right]dx= \)

\( =\int_{2}^{4}\left(16-4x\right)dx \)

האינטגרל הלא מסויים שלנו הפעם הוא \( 16x-2x^{2} \), וכשמציבים \( 4 \) ו-\( 2 \) ומחסרים, מקבלים:

\( \left(16\cdot4-2\cdot4^{2}\right)-\left(16\cdot2-2\cdot2^{2}\right)=64-32-32+8=8 \)

נוסיף לזה את ה-\( 9\frac{1}{3} \) שחישבנו קודם, והפתרון לתרגיל כולו הוא \( 17\frac{1}{3} \).

עצירת ביניים כדי לראות מה עשינו עד כה

ובכן, מה למדנו פה? אני מרגיש שבעצם כל מה שעשינו אי פעם מאז תחילת היקום היה לצייר שטחים בכל מני צבעים, אבל למעשה עברנו כברת דרך לא רעה להבנת “איך פותרים דברים עם אינטגרלים”. הנה תקציר:

1. ראינו שאינטגרל לא מסויים הוא "ההפך מנגזרת" ואיך בדיוק לחשב אותו עבור כל פולינום אפשרי (חוץ מ-\( x^{-1} \) המעצבן הזה).
2. ראינו שאינטגרל מסויים קשור לאינטגרל לא מסויים בעזרת הנוסחה הקסומה \( \int_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right) \)
3. ראינו שאפשר להשתמש באינטגרל מסויים כדי לחשב שטחים שכלואים בצורה נחמדה בין שתי פונקציות ושני קווים מאונכים.
4. ראינו איך אפשר לחשב שטחים שכלואים בצורות מסובכות יותר על ידי פירוק שלהם לתת-שטחים שקל יותר לחשב וחיבור בהתאם.

רוב התרגיל שפתרנו היה בכלל תרגיל של מציאת נקודות חיתוך של פונקציות עם צירים - ובמקרה הזה, הטכניקה הייתה פתרון משוואות ממעלה שניה, שהיא כלי בסיסי (וחשוב!) באופן כללי. האינטגרלים באו כמעט כלאחר יד, אבל ככה זה תמיד פה - כאמור, אינטגרלים אמיתיים זה קשה, ולכן תרגילים על אינטגרלים לרוב מתבססים על משהו קל בהרבה.

אבל עדיין, מה עוד אנחנו יכולים לומר על חישוב אינטגרלים לא מסויימים?

פרק שלישי ובו עוד כמה אינטגרלים לא מסויימים

במתמטיקה יש כמה פונקציות נפוצות שטרם הזכרתי - סינוס, קוסינוס, טנגנס אקספוננט ולוגריתם. הן כל כך נפוצות שהן מופיעות בדף הנוסחאות עבור נגזרות, אז אני אזכיר מה מקבלים מהנגזרת שלהן - וננסה להבין מזה מה אנחנו יכולים לומר על אינטגרלים.

• \( \left(\sin x\right)^{\prime}=\cos x \) מלמד אותנו ש-\( \int\cos xdx=\sin x+C \)
• \( \left(\cos x\right)^{\prime}=-\sin x \) מלמד אותנו ש-\( \int\sin xdx=-\cos x+C \)
• \( \left(\tan x\right)^{\prime}=\frac{1}{\cos^{2}x} \) מלמד אותנו ש-\( \int\frac{1}{\cos^{2}x}dx=\tan x+C \)
• \( \left(a^{x}\right)^{\prime}=a^{x}\cdot\ln a \) מלמד אותנו ש-\( \int a^{x}dx=\frac{a^{x}}{\ln a}+C \)
• \( \left(\log_{a}x\right)^{\prime}=\frac{1}{x\ln a} \) מלמד אותנו ש-\( \int\frac{1}{x}dx=\ln a\cdot\ln_{a}x+C \)

את כל אלו אנחנו מסיקים ישר מדף הנוסחאות וממה שכבר למדנו על חישוב אינטגרלים לא מסויימים. אבל אני רוצה להתעכב שניה על שני האחרונים. ראשית, מה זה \( \ln \)? זה מקרה פרטי של לוגריתם (בדיוק כתבתי פוסט על לוגריתמים!) שבו הבסיס הוא מספר מיוחד שמסומן \( e=2.7182\ldots \). נוסאות הגזירה מראות לנו בדיוק למה \( e \) הזה הוא כל כך מיוחד שטורחים לתת לו שם: מכיוון ש-\( \ln x=\log_{e}x \) אז \( \ln e=1 \) ולכן \( \left(e^{x}\right)^{\prime}=e^{x} \). כלומר, מבין כל הבסיסים האפשריים לפונקציית האקספוננט \( f\left(x\right)=a^{x} \), הבסיס \( e \) הוא היחיד שעבורו גזירה של הפונקציה לא משנה אותה. לכן האינטגרל של הפונקציה הזו הוא פשוט במיוחד: \( \int e^{x}dx=e^{x}+C \).

באופן דומה, אפשר לקחת את נוסחת הגזירה של לוגריתם, שעובדת לכל בסיס \( a>1 \), ולהשתמש בה עבור \( e \) כדי לקבל \( \left(\ln x\right)^{\prime}=\frac{1}{x} \), ולכן לקבל את האינטגרל \( \int x^{-1}dx=\ln x+C \). זה מטפל סוף כל סוף גם ב-\( x^{-1} \) שלא ידענו מה לעשות איתו עד כה; למעשה, זה טיפול כל כך טוב שלפעמים מגדירים את פונקציית הלוגריתם בעזרת האינטגרל הזה (עם עוד עניינים טכניים שלא אכנס אליהם). רק שימו לב שלוגריתם לא מוגדר בכלל עבור מספרים לא חיוביים, ולכן גם הנוסחה \( \int x^{-1}dx=\ln x+C \) לא נכונה לכל מספר אלא רק עבור \( x>0 \).

דף הנוסחאות מלמד אותנו עוד משהו על נגזרות, שנקרא כלל השרשרת אבל לא מצוין בשם הזה שם במפורש אלא נקרא “נגזרת של פונקציה מורכבת”. הוא אומר:

\( \left[f\left(u\left(x\right)\right)\right]^{\prime}=f^{\prime}\left(u\right)\cdot u^{\prime}\left(x\right) \)

ואת זה הכי קל להסביר עם דוגמא. נאמר ש-\( f\left(t\right)=\cos t \) וש-\( u\left(x\right)=x^{2}+3x \), ועכשיו אני תוקע את \( u\left(x\right) \) במקום \( t \) , כלומר אני מקבל את הפונקציה המורכבת

\( \cos\left(x^{2}+3x\right) \)

ואת הפונקציה הזו אני גוזר על פי \( x \). אז כדי לקבל את התוצאה, אני עושה שני דברים:

• גוזר את \( f\left(t\right)=\cos t \) על פי \( t \), ומקבל \( f^{\prime}\left(t\right)=-\sin t \)
• גוזר את \( u\left(x\right)=x^{2}+3x \) על פי \( x \) ומקבל \( u^{\prime}\left(x\right)=2x+3 \)

עכשיו, אני לוקח את \( f^{\prime}\left(t\right) \) שקיבלת בשלב הראשון ומציב בו את \( u\left(x\right)=x^{2}+3x \) בלי שום שינוי, כלומר אני מקבל \( -\sin\left(x^{2}+3x\right) \). את זה אני כופל ב-\( u^{\prime}\left(x\right) \) מהשלב השני, ובסך הכל אני מקבל:

\( -\sin\left(x^{2}+3x\right)\left(2x+3\right) \)

זה הרעיון מאחורי שימוש בכלל השרשרת, והמשמעות היא שאם נזהרים מספיק אפשר גם “להפוך” אותו כשעושים אינטגרל. מעשית, אם \( F^{\prime}\left(x\right)=f\left(x\right) \) ו-\( u\left(x\right) \) היא פונקציה כלשהי, אז:

\( F^{\prime}\left(u\left(x\right)\right)=f\left(u\left(x\right)\right)u^{\prime}\left(x\right) \)

כי זה כלל השרשרת בפעולה, ולכן:

\( \int f\left(u\left(x\right)\right)u^{\prime}\left(x\right)dx=F\left(u\left(x\right)\right)+C \)

זה מופיע בדף הנוסחאות, אבל להשתמש בזה בפועל - זה יכול להיות מאוד טריקי, כי כשיש ביטוי חשבוני צריך איכשהו לזהות שהוא מורכבת מנגזרת של משהו, כפול המשהו המקורי כשהוא תקוע בתוך פונקציה אחרת. זה לא קל. לכן אני מנחש שאין הרבה תרגילים שמתבססים על זה, אבל אולי אני טועה?

בדף הנוסחאות יש גם מקרה פרטי פשוט במיוחד של הסיפור הזה: כש-\( u\left(x\right)=mx+b \) (זה פשוט פולינום ממעלה ראשונה) אז \( u^{\prime}=m \) ולכן \( F^{\prime}\left(mx+b\right)=f\left(mx+b\right)\cdot m \) (זה כלל השרשרת בפעולה שוב), ולכן כשעוברים לאינטגרל, מקבלים \( \int f\left(mx+b\right)dx=\frac{1}{m}F\left(mx+b\right)+C \).

וזהו, אלו כל הנוסחאות שקשורות לאינטגרלים בדף הנוסחאות. מקווה שעכשיו הן קצת יותר ברורות ויותר קל להבין איך לחשב אינטגרלים לא מסויימים.

בעולם “האמיתי”, כאן רק מתחיל הסיפור; יש עוד המון נוסחאות של אינטגרלים בסיסיים; יש שיטות אינטגרציה נחמדות שעוזרות לפתור מקרים יותר מסובכים, כמו למשל אינטגרציה בחלקים שמבוססת על החוק עבור נגזרת של מכפלה, שלא הצגתי פה. ויש פונקציות שפשוט לא קיים להן אינטגרל לא מסויים שאפשר להציג בצורה פשוטה בעזרת פונקציות אלמנטריות. למשל הפונקציה \( e^{x^{2}} \).

פרק רביעי ובו אנו מסיימים בנימה אופטימית עם תרגיל מבגרות שכל מה שלמדנו לא עוזר בו בכלל

לסיום, אני רוצה להראות תרגיל מבגרות של השנה:

השאלה הזו היא קצת יותר מתוחכמת מהסטנדרט, אבל יש פיצוי הולם על כך - רובה מתבסס על לתת הנחיה גדולה מה בעצם לעשות. השאלה היא בעצם זו: אם \( f\left(x\right)=e^{x}\left(x-5\right) \), מהו \( \int f\left(x\right)dx \)? זו לבדה שאלה די טריקית - הרי \( e^{x}\left(x-5\right) \) היא פונקציה מסובכת - מכפלה של שתי פונקציות שלא נראית כמו אף אחת מנוסחאות האינטגרלים שאנחנו מכירים. הדבר היחיד עם מכפלה שראינו היה הנוסחה שקשורה לכלל השרשרת, אבל לא נראה שאפשר להשתמש בה כאן. אז מה עושים?

בעולם האמיתי משתמשים במה שנקרא “אינטגרציה בחלקים”, אבל זה לא אפשרי כאן. אז מה שקורה כאן הוא שנותנים לתלמידים את הפתרון על מגש של כסף; הסעיפים הראשונים בשאלה אמורים להנחות את התלמידים אל עבר הפתרון.

ראשית, למה הנגזרת של \( f \) יוצאת מה שהיא יוצאת? בשביל זה צריך להיזכר במפורש במה שקורה כשגוזרים מכפלה של פונקציות. אם \( f\left(x\right)=g\left(x\right)h\left(x\right) \) אז

\( f^{\prime}\left(x\right)=g^{\prime}\left(x\right)h\left(x\right)+g\left(x\right)h^{\prime}\left(x\right) \)

כלומר, גוזרים כל אחת מהפונקציות במכפלה בנפרד וכופלים אותה בפונקציה השניה הלא גזורה ומחברים. במקרה שלנו \( g\left(x\right)=e^{x} \) שהיא פשוטה במיוחד כי \( g^{\prime}\left(x\right)=e^{x} \) גם כן, ואילו \( h\left(x\right)=x-5 \) ולכן \( h^{\prime}\left(x\right)=1 \), ונקבל:

\( f^{\prime}\left(x\right)=e^{x}\left(x-5\right)+e^{x}\cdot1=e^{x}\left(x-5+1\right)=e^{x}\left(x-4\right) \)

שימו לב שהמספר 5 לא באמת שיחק תפקיד בנגזרות, ולכן אותו דבר קורה גם כשגוזרים שוב ושוב - בכל פעם הערך שמפחיתים מ-\( x \) הולך וקטן. התרגיל נותן במפורש את החוקיות הכללית של הנגזרת ומבקש מהתלמידים לוודא אותה.

אז מה עושים בסעיף ד’? צריך להבין שאפשר לקחת את החוקיות הזו וללכת איתה גם צעד אחד אחורה. כלומר, במקום שהמספר שמחסרים מ-\( x \) יקטן ב-1, הוא צריך לגדול ב-1. כלומר, \( F\left(x\right)=e^{x}\left(x-6\right) \). אם נגזור את \( F\left(x\right) \) נראה שזה עובד.

אבל רגע, שניה, לא סיימנו. מה שהמבחן בודק הוא שהתלמידים באמת מבינים את הרעיון של אינטגרל לא מסויים עד הסוף - בפרט, את זה שלאותה פונקציה \( f \) יש אינסוף פונקציות קדומות אפשריות. המבחן דורש בצורה מפורשת שמבין האינסוף הללו, ניתן את זו שעוברת בראשית הצירים. המשמעות היא שאנחנו צריכים למצוא \( F \) כזו שמקיימת \( F\left(0\right)=0 \).

כמובן, קל לעשות את זה: הצורה הכללית של פונקציה קדומה שכזו היא \( F\left(x\right)=e^{x}\left(x-6\right)+C \). אם נציב \( x=0 \) נקבל את המשוואה \( e^{0}\left(0-6\right)+C=0 \), כלומר \( C=6 \). לכן הפונקציה הקדומה שאנחנו מחפשים היא \( F\left(x\right)=e^{x}\left(x-6\right)+6 \), וסיימנו.

האם זה מסיים את סיפור האינטגרלים? ובכן, אני משער שיש עוד הרבה סוגי שאלות שלא לגמרי כיסיתי פה. אתן מוזמנות להפגיז איתן בתגובות ואולי אכתוב פוסט המשך.