מה בעצם הולך בטריגונומטריה בתיכון? (חלק ד' - משפט הסינוסים)

אני ממשיך בסדרת הפוסטים שלי על גאומטריה שהמטרה המוצהרת שלה היא להבין את כל הנוסחאות הטריגונומטריות שרואים בבית הספר ומה הרעיון מאחוריהן. הנה דף הנוסחאות שאני עובד איתו:

הפעם אני רוצה לדבר על אחת הנוסחאות שקשורות למשולשים ולמעגלים - משפט הסינוסים (ועל הדרך גם הנוסחה לשטח משולש שמופיעה בסוף). שום דבר לא הולך להיות קשה במיוחד אבל נצטרך להתעסק בגאומטריה (!)

זה… לא כל כך נורא, אפילו לאדם כמוני שמבועת משרטוטים גאומטריים. למעשה, מה שנראה הפעם הוא גם סוג של הסבר “למה טריגונומטריה שימושית בעצם” אם כי לא אכנס לעומק הפרטים.

ההגדרה לסינוס שראינו התבססה על משולש ישר זווית, כלומר משולש שנראה כך:

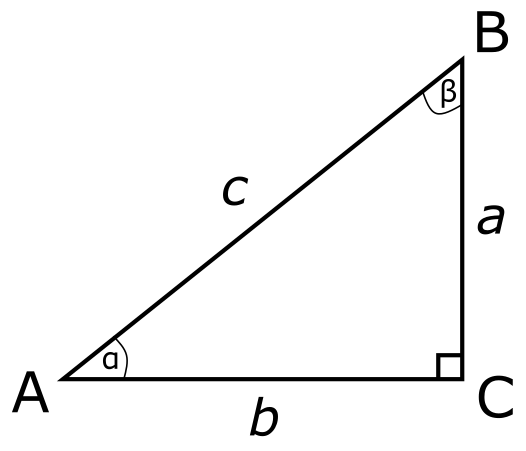
במשולש הזה, \( \sin\alpha=\frac{a}{c} \), או בניסוח אחר \( a=c\sin\alpha \). זה אמנם שימושי מאוד, אבל זה גם מעלה את השאלה מה קורה במשולש כללי, שאינו ישר זווית. למשל זה:

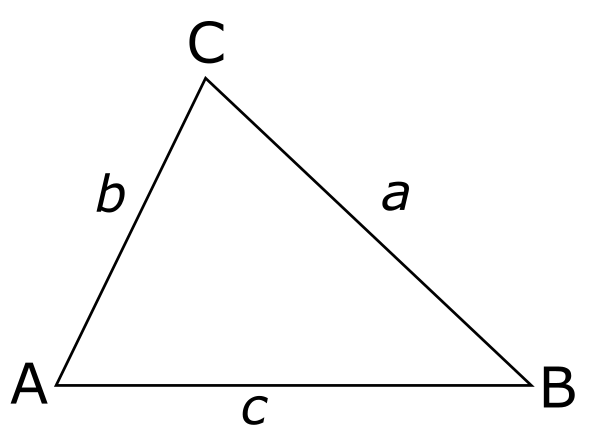
במשולש הזה אין זווית ישרה (אולי \( \angle ACB \) קצת נראית ככה כי אני מאייר גרוע, אבל היא לא), אז לא ברור איך אפשר לקשר סינוסים אליו, אבל האמת היא שבכל משולש מסתתרת זווית ישרה וכדי לחשוף אותה אני רוצה שניזכר לרגע במשהו לכאורה לא קשור - איך מחשבים שטח של משולש. הנוסחה היא \( \frac{ah}{2} \) כאשר \( a \) הוא אורך צלע ו-\( h \) הוא אורך אנך לאותה צלע. כדי להבין למה הנוסחה נכונה, מה זה אנך ומה הולך פה, בואו נדגים את זה על ידי הורדת אנך מהקודקוד \( C \) אל הצלע \( AB \):

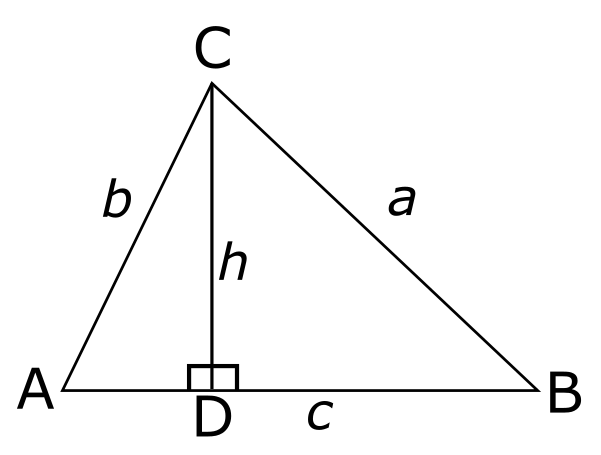
האנך הזה הוא קו ישר שמתחיל ב-\( C \) ויורד על \( AB \) ופוגש את הצלע הזו בזווית ישרה. התוצאה היא שחילקנו את המשולש התמים \( ABC \) לשני משולשים ישרי זווית: \( ACD \) ו-\( BCD \), מה שמאפשר לסינוסים לחזור בגדול. האם עבור כל משולש אפשר לעשות את הקסם הזה? כן ולא; עוד מעט אתייחס למקרה הבעייתי-שאינו-באמת-בעייתי.

ראשית, איך מגיעים מהבניה הזו אל הנוסחה לשטח של משולש? ובכן, הקסם הוא פשוט: מסתתר בתמונה הזו מלבן, וכדאי שנציג אותו במפורש:

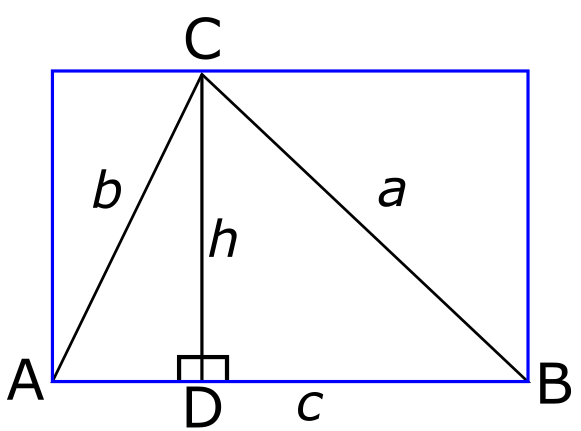
מה שטח המלבן הזה? שטח של מלבן הוא מכפלה של אורכי שתי צלעות מאונכות שלו. במקרה שלנו צלע אחת של המלבן היא \( AB \), כלומר אורכה הוא מה שסימנתי ב-\( c \); והצלעות האחרות הן מאותו אורך כמו האנך \( h \). לכן שטח המלבן הוא \( ch \). שטח המשולש הוא חצי מזה, כי אם נסתכל לרגע על המשולש \( ACD \) נראה שהוא מחלק לחצי את החלק השמאלי של המלבן - בינו ובין משולש אחר, זהה לו (או כפי שקוראים לזה בגאומטריה וקל להוכיח - חופף לו) וכך קורה גם עם המשולש \( BCD \) בחצי הימני. זה מניב את הנוסחה \( \frac{ch}{2} \) עבור השטח.

עכשיו בואו נחזיר את הטריגונומטריה למשחק, על ידי הצגת הזווית \( \angle BAC=\alpha \) במפורש:

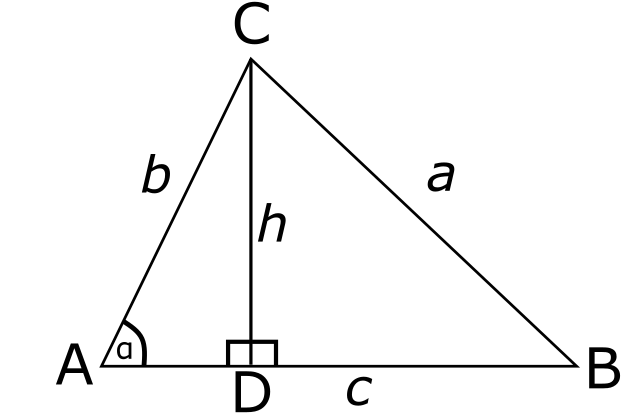
מכיוון שהמשולש \( ACD \) הוא ישר זווית והיתר שלו הוא \( b \), נקבל ש-\( h=b\sin\alpha \). אם נציב את זה בנוסחת השטח של המשולש נקבל ששטחו הוא \( \frac{bc\sin\alpha}{2} \).

הנוסחה הזו היא שרירותית בצורה מסויימת - היא מתבססת על הבחירה שלנו להסתכל דווקא על הזווית \( \alpha \) במשולש, ולהגיע ממנה איכשהו לשטח של המשולש שהוא תכונה “גלובלית”. היא בעצם אומרת - השטח של המשולש שווה למכפלת אורכי שתי צלעות כלשהן בו, כפול סינוס הזווית שכלואה ביניהן, חלקי 2. אני יכול באותה מידה לעשות את זה גם עבור יתר הבחירות של זוגות של צלעות במשולש. אני אסמן ב-\( \beta \) את הזווית שמול הצלע שאורכה \( b \) וב-\( \gamma \) את הזווית שמול הצלע שאורכה \( c \), ואקבל:

\( \frac{bc\sin\alpha}{2}=\frac{ac\sin\beta}{2}=\frac{ab\sin\gamma}{2} \)

את הביטוי הזה קל לפשט עוד קצת, על ידי זה שנכפיל את כל האגפים ב-2 ונחלק אותם ב-\( abc \). נקבל:

\( \frac{\sin\alpha}{a}=\frac{\sin\beta}{b}=\frac{\sin\gamma}{c} \)

אפשר גם לקחת את ההופכי של כל אחד מהאגפים הללו כדי לקבל

• \( \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma} \)

הנוסחה האחרונה הזו שהגעתי אליה היא מה שנקרא בדרך כלל משפט הסינוסים. הוא אומר: היחס בין אורך צלע במשולש כלשהו ובין סינוס הזווית שמול הצלע הזו הוא תמיד מספר קבוע כלשהו עבור המשולש הזה.

איזה מספר קבוע? אולי זה \( \pi \)? אולי זה \( e \)? אולי זה איזה קבוע מלהיב אחר? ובכן, למרבה הצער, לא. זה לא יכול להיות מספר אחד שקבוע לכל המשולשים, כי אם נסתכל על \( \frac{a}{\sin\alpha} \), הרי \( a \) הוא אורך צלע שיכול להיות גדול כרצוננו, ואילו \( \sin\alpha \) תמיד יהיה מספר בין מינוס 1 ובין 1. לכן \( \frac{a}{\sin\alpha} \) יהיה גודל שתלוי בגודל המשולש. מה שנחמד הוא שזה גודל שאולי לא ציפינו לו במבט ראשון: זה בדיוק הקוטר של המעגל שחוסם את המשולש, או בניסוח המקובל

• \( \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2R \)

כאשר \( R \) הוא רדיוס המעגל החוסם. זו הגרסה המלאה של משפט הסינוסים.

מה זה בכלל מעגל שחוסם משולש? אפשר להראות שלכל שלוש נקודות במישור, קיים בדיוק מעגל יחיד שעובר דרך שלושתן. המעגל שחוסם משולש הוא פשוט המעגל שעובר דרך שלושת הקודקודים של המשולש. במקרה שלנו זה נראה כך:

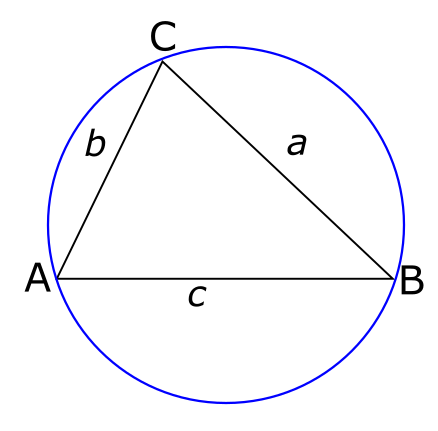
עכשיו, מה זה “רדיוס”? זה קו שמחבר את מרכז המעגל עם נקודה על המעגל. אלא שבציור למעלה בכלל לא טרחתי לסמן את מרכז המעגל. אז בואו נסמן אותו הפעם ונחבר אותו עם \( C \):

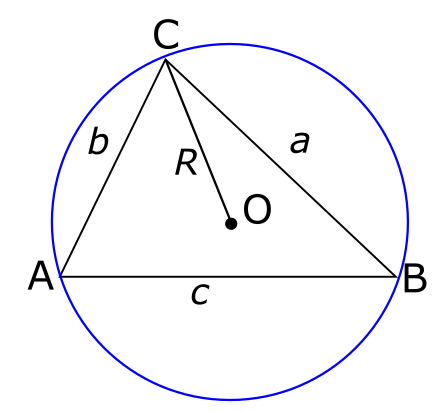
את האורך של הקו \( CO \) החדש הזה אני מסמן ב-\( R \). זה נחמד, אבל כדי שזה יהיה ממש שימושי עבורי אני צריך להמשיך את הקו \( CO \) הזה עד שיגיע גם אל הצד השני של המעגל:

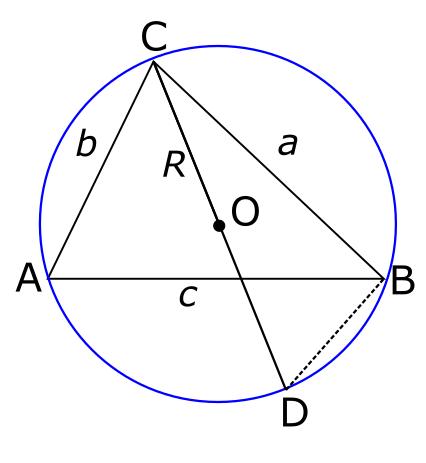
עשיתי פה שני דברים: ראשית, המשכתי את הקו הזה עד שהגיע לנקודה \( D \) בצד השני; הישר \( CD \) שהתקבל נקרא קוטר של המעגל ואורכו הוא \( 2R \). שנית, חיברתי את הנקודה \( D \) הזו בקו אל \( B \) ובכך יצרתי משולש חדש, \( BCD \). למה שאעשה דבר כזה? כי כרגיל, כדי להשתמש בטריגונומטריה אנחנו רוצים לחשוף איזה משולש ישר זווית שמתחבא פה. מה הזווית הישרה במקרה שלנו? זו הזווית \( \angle CBD \). להוכיח שהיא ישרה מתבסס על משפט בגאומטריה של מעגלים - “זווית היקפית שנשענת על קוטר היא בת \( 90^{\circ} \)”. בתרגום למה שהולך אצלנו: אם יש לנו משולש שאחת מצלעותיו היא קוטר ושתי הצלעות האחרות מחברות נקודות על המעגל, אז המשולש הוא ישר זווית והקוטר הוא היתר.

במשולש החדש הזה, \( \frac{a}{2R} \) הוא הסינוס של הזווית שמול הצלע מאורך \( a \), כלומר שמול הצלע \( BC \), כלומר הזווית \( \angle CDB \). מה הזווית הזו? ובכן, אני טוען שהיא זהה לזווית \( \angle CAB \) שקראנו לה בשעתו \( \alpha \). גם זה מתבסס על משפט שנוגע למעגלים - גם הזווית \( \angle CDB \) וגם הזווית \( \angle CAB \) הן זוויות היקפיות שנשענות על אותו מיתר, כלומר על הצלע \( BC \). זוויות היקפיות כאלו הן שוות בתנאי שהן מאותו צד של המיתר, וזה מה שקורה אצלנו.

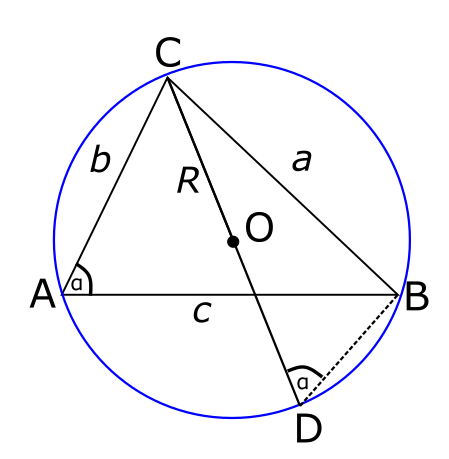
זה מסיים את ההוכחה במקרה הזה: \( \sin\alpha=\frac{\left|BC\right|}{\left|CD\right|}=\frac{a}{2R} \) ולכן \( \frac{a}{\sin\alpha}=2R \), מה שמסיים את מה שרצינו להוכיח.

מה נשאר? רק התייחסות למקרה “בעייתי” שהתעלמתי ממנו קודם. בניתוח שלי של המשולש ה”כללי” \( ABC \) הנחתי במובלע שהאנך שאני מוריד עובר בתוך המשולש, ובמשולש קהה זווית זה לא קורה. בואו נראה דוגמא:

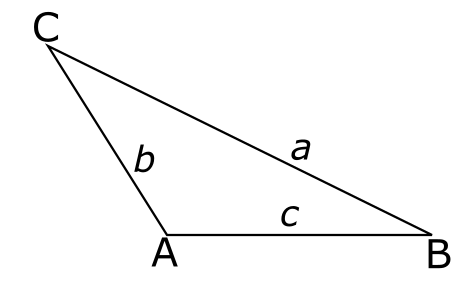
במשולש הזה אם אני אוריד אנך מ-\( A \) הוא עדיין יהיה בתוך המשולש, אבל אם אוריד אנך מ-\( C \) הוא ייפול בחוץ. ככה זה נראה:

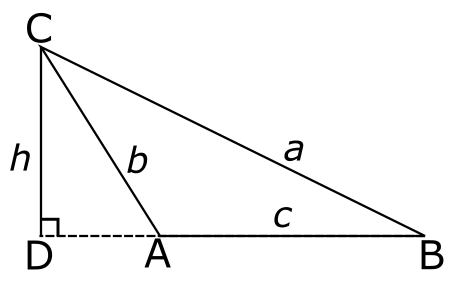
הטריק הקודם שלי לחישוב שטחת עם המלבן היפה שמתחלק לשני זוגות של משולשים חופפים, לא עובד פה. אבל מה שכן קורה הוא שפתאום צצו לנו שני משולשים ישרי זווית: \( BCD \) ו-\( ADC \). את השטח של שני המשולשים הללו קל לי לחשב: הוא \( \frac{h}{2}\cdot\left|BD\right| \) ו-\( \frac{h}{2}\cdot\left|AD\right| \), בהתאמה. מכיוון שהמשולש \( BCD \) מורכב מאיחוד המשולשים \( ACB \) (המשולש המקורי שלי) ו-\( ADC \), אני מקבל שהשטח של \( ACB \) שווה להפרש בין שטחי שני המשולשים האחרים, כלומר הוא

\( \frac{h}{2}\cdot\left|BD\right|-\frac{h}{2}\cdot\left|AD\right|=\frac{h}{2}\left(\left|BD\right|-\left|AD\right|\right) \)

ומכיוון ש-\( \left|BD\right|=\left|AD\right|+\left|AB\right| \), אני מקבל את השטח \( \frac{h}{2}\left|AB\right|=\frac{hc}{2} \), כפי שרציתי. אבל איך אני יכול לקשר את זה לסינוס של משהו? ובכן, זה טיפה טריקי אבל עדיין מאוד פשוט. בואו נסתכל על הזווית \( \angle BAC \) ששווה ל-\( \alpha \), ועל הזווית \( \angle DAC \) שמשלימה אותה ל-\( 180^{\circ} \):

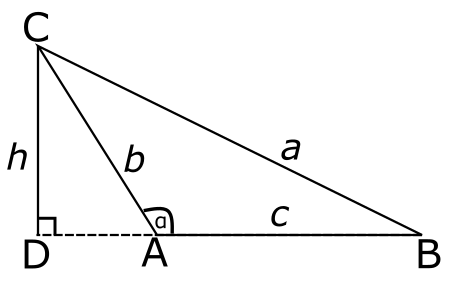
במשולש ישר הזווית \( ADC \) אפשר להשתמש בסינוסים כרגיל, ולכן נקבל ש-\( \sin\left(180^{\circ}-\alpha\right)=\frac{h}{b} \). זה משמח מאוד, כי סינוס היא פונקציה סימטרית ביחס לציר של \( 90^{\circ} \), כלומר

• \( \sin\left(180^{\circ}-\alpha\right)=\sin\alpha \)

זו משוואה שראינו כבר בפוסט הראשון על טריגונומטריה. כלומר, קיבלנו \( \sin\alpha=\frac{h}{b} \), כלומר \( h=b\sin\alpha \), ויחד עם השטח \( \frac{hc}{2} \) של המשולש נקבל את השטח \( \frac{bc\sin\alpha}{2} \) וכאן אנחנו כבר בטריטוריה המוכרת של ההוכחה מתחילת הפוסט. זה מסיים את ההוכחה גם עבור משולש קהה זווית.

לבסוף, אני רוצה לומר משהו קטן על השימושיות של משפט הסינוסים. ראשית, אני לא יודע מה השימושיות שלו בעולם האמיתי כי לא יצא לי להשתמש בו מחוץ למתמטיקה. שנית, השימושיות שלו ברורה במובן הבא: אם עבור משולש כלשהו אנחנו יודעים שתי זווית ואורך של צלע כלשהי, אנחנו יכולים להסיק מכך את אורכי כל הצלעות של המשולש. למה? מהיכרות עם שתי זוויות אנחנו מסיקים את השלישית (היא \( 180^{\circ} \) פחות שתי האחרות), ולכן אנחנו יכולים לחשב את \( \frac{\sin\alpha}{a} \) עבור הצלע שאורכה \( a \) ידוע לנו והזווית \( \alpha \) שמול הצלע הזה. עכשיו אפשר להסיק את אורכי הצלעות האחרות: למשל, \( \frac{\sin\alpha}{a}=\frac{\sin\beta}{b} \) ולכן \( b=a\cdot\frac{\sin\beta}{\sin\alpha} \).

שיטה מוכרת למדידת מרחקים שמתבססת על ידע שכזה נקראת טריאנגולציה. בשיטה הזו, אם אנחנו רוצים למדוד את המרחק עד לנקודה מסויימת, אנחנו מארגנים לעצמנו שתי נקודות תצפית עם מרחק ידוע ביניהן (ההנחה היא שנקודות התצפית קרובות יחסית ולכן קל לדעת את המרחק ביניהן ולעומת זאת הנקודה שאת המרחק אליה רוצים למדוד היא מרוחקת). כעת, בעזרת מכשיר מתאים ניתן למדוד את הזווית משתי נקודות התצפית אל הנקודה שצופים עליה, וזאת ביחס לקו הישר שמחבר את שתי נקודות התצפית. הנה איור עקום שלי להמחשה:

כאן יש לנו סירה בים, ושני נקודות תצפית בנמל שלנו, אחת על המזח הימני והשניה על המזח השמאלי. המרחק ביניהם ידוע, ולכן מדידת הזווית אל הסירה מכל אחד מהמזחים תאפשר לנו להסיק את מרחק הסירה מכל אחד מהם.כמובן, אם המזחים קרובים יחסית ההפרש בזווית יהיה קטן (התמונה שלי מאוד לא ריאליסטית) ולכן מכשירי המדידה שלנו יצטרכו להיות מדויקים יחסית כדי לקבל תוצאה שאפשר לעבוד איתה.

זה מסיים עם משפט הסינוסים; בפוסט הבא נגיע אל משפט הקוסינוסים שממש לא דומה בכלל למשפט הסינוסים, אבל גם כן מספק לנו מידע על משולשים כלליים בעזרת הפונקציות הטריגונומטריות.