אסימפטוטות, חלק א': הדברים הקלים

אחד מהנושאים המבלבלים ביותר עבורי כשלמדתי מתמטיקה בבית הספר היה אסימפטוטות של פונקציות, פשוט כי זה נושא שבבית הספר לא מלמדים את המשמעות שלו עד הסוף אלא מסתמכים על אינטואיציות… ולי היו אינטואיציות מאוד גרועות. אז בפוסט הזה אני אנסה לעשות שני דברים: ראשית, להסביר את הנושא בצורה אינטואיטיבית, עבור מי שיש לה אינטואיציות טובות משלי, ובתקווה אולי אוכל לסייע קצת לאינטואיציות הללו; ושנית, בהמשך, איפה שלא חייבים לקרוא - להיכנס להסברים הפורמליים ביותר, כדי שאפשר יהיה להרגיש שכיסינו את הנושא לגמרי.

נתחיל מהאינטואיציה.

מה זה אסימפטוטות - האינטואיציה

בהקשר של אסימפטוטות, תמונה אחת שווה אלף מילים, ואני מתנצל מראש בפני מי שלא מסתדרים עם תמונות. הנה תמונה של גרף הפונקציה \( f\left(x\right)=\frac{1}{x} \):

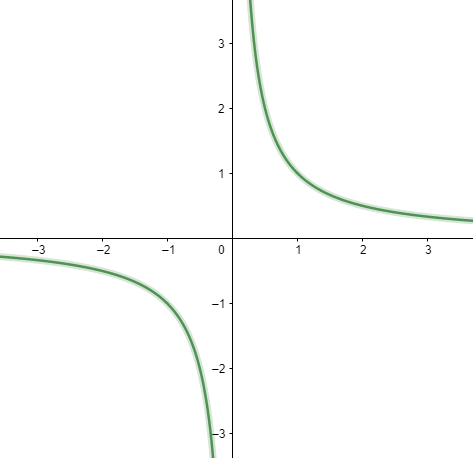
מה אנחנו בעצם רואים פה? ה”עולם” המתמטי שבו גרפים של פונקציות חיים הוא משהו שנקרא המישור, או אם רוצים להרחיב - המישור הקרטזי. אנחנו חושבים על המישור הזה בתור אוסף של נקודות, כשכל נקודה מאופיינת על ידי שתי קואורדינטות: \( \left(x,y\right) \). קואורדינטת ה-\( x \) אומרת כמה ימינה/שמאלה הנקודה נמצאת מהמרכז של המישור, וקואורדינטת ה-\( y \) אומרת כמה למעלה/למטה. הנקודה \( \left(0,0\right) \) היא ה”מרכז” של המישור - מה שנקרא ראשית הצירים. בציור ישנם שני קווים - אופקי ואנכי. הקו האופקי נקרא ציר \( x \), האנכי נקרא ציר \( y \) ונקודת המפגש ביניהם היא ראשית הצירים. על כל אחד מהצירים כתובים מספרים - כשאני לוקח נקודה כלשהי במישור, אני מותח קווים ישרים ממנה אל הצירים, ובודק מה המספרים על כל ציר - אלו הקואורדינטות של הנקודה. אני מניח שכל זה כבר ידוע, אבל לא יזיק לחזור על זה.

בנוסף לצירים, באיור יש עוד שני קווים “עקומים”. הקווים הללו הם הגרף של הפונקציה \( f\left(x\right)=\frac{1}{x} \). מה זו בעצם פונקציה? בהקשר שלנו, זה משהו שמקבל מספר ומחזיר מספר אחר. למשל, הפונקציה \( f\left(x\right)=\frac{1}{x} \) כשהיא מקבלת את המספר \( 2 \) מחזירה את המספר \( \frac{1}{2} \) וכן הלאה. הכתיב \( f\left(x\right)=\frac{1}{x} \) הוא בעצם תיאור כללי - אם המספר שהתקבל היה \( x \), המספר שיוחזר יהיה \( \frac{1}{x} \). ומה אם אני ארצה לתת ל-\( f\left(x\right) \) את הערך \( x=0 \)? זה בלתי אפשרי, כי \( \frac{1}{0} \) זה משהו לא מוגדר (ייתכן שבקהל רוצים לצעוק לי שזה אינסוף או משהו כזה; אז חכו חכו להמשך, כי עוד נראה בדיוק למה בעייתי להגיד משהו כזה, \( \frac{1}{x} \) היא הדוגמא הקלאסית לבעייתיות הזו).

הגרף של פונקציה הוא אוסף של נקודות: לכל \( x \) שהפונקציה מוגדרת עליו, אנחנו מחשבים את \( f\left(x\right) \) ואז מסתכלים על הנקודה \( \left(x,f\left(x\right)\right) \), כלומר נקודה שקואורדינטת ה-\( x \) שלה היא פשוט \( x \) וקואורדינטת ה-\( y \) היא \( f\left(x\right) \). זה נותן לנו דרך גרפית נוחה “להרגיש” איך הפונקציה מתנהגת. למשל, בגרף של \( f\left(x\right)=\frac{1}{x} \) אנחנו רואים שאם \( x>0 \) אז הפונקציה תמיד מחזירה ערכים גדולים מ-0, אבל שהערכים שהיא מחזירה הופכים לקטנים יותר ויותר ככל ש-\( x \) עצמו נהיה גדול יותר ויותר.

מה שאפשר לראות באיור הוא שככל שאנחנו הולכים ימינה יותר, הגרף של הפונקציה הולך ומתקרב אל הקו של ציר \( x \) עצמו. מה הולך לקרות בהמשך? ובכן, ככל שמציבים ערכים יותר גדולים של \( x \) בתוך \( \frac{1}{x} \) מקבלים מספרים חיוביים קטנים יותר ויותר. אם נציב \( x=10 \) נקבל \( \frac{1}{10} \) ואם נציב \( x=100 \) נקבל \( \frac{1}{100} \) וכן הלאה. האם מתישהו ממש נגיע אל ציר \( x \)? כלומר, האם הנקודה \( \left(x,0\right) \) נמצאת על גרף הפונקציה? ובכן, לא; אין פתרון למשוואה \( \frac{1}{x}=0 \), כי אם נכפול ב-\( x \) נקבל \( 1=0 \). גם לא נרד מתחת לציר \( x \), כי אם \( x>0 \) אז \( \frac{1}{x}>0 \) תמיד. אז אנחנו יודעים שלא משנה כמה ימינה נלך, לא נראה את הקו של הפונקציה חוצה את ציר \( x \). מה שהוא כן הולך לעשות הוא להתקרב אליו עוד ועוד. על התופעה הזו אנחנו אומרים שציר \( x \) הוא אסימפטוטה של \( f\left(x\right) \) כאשר \( x \) שואף לאינסוף.

הנה לנו שני מושגים לא מוגדרים: גם “אסימפטוטה” וגם “שואף לאינסוף”. ההגדרה המדויקת שלהם מסתמכת על מושג מחשבון דיפרנציאלי ואינטגרלי שנקרא גבול; אני מבטיח להציג אותו במלואו עד סוף הפוסט, אבל אנחנו עכשיו בחלק האינטואיטיבי, ואפשר כבר לגלות שבהקשר הזה “אינטואיטיבי” פירושו “אל תשתמש במושג הגבול!!!!! לא לומדים אותו בבית הספר!!!!!” אז אני זורם עם זה.

אז מה ההגדרה הלא מדויקת? אסימפטוטה של פונקציה היא קו ישר כלשהו שהפונקציה מתקרבת אליו עוד ועוד כאשר גם הקו וגם הפונקציה ממשיכים עד אינסוף. זו הגדרה טריקית כי היא מנסה לכסות יחד שני מקרים די שונים באופי שלהם, שלמרבה המזל \( f\left(x\right)=\frac{1}{x} \) היא דוגמא מושלמת כדי להדגים אותם. המקרה הראשון נקרא אסימפטוטה אופקית וזה מה שראינו עם ציר \( x \) - יש לנו קו אופקי (ציר \( x \) במקרה הנוכחי אבל אפשר גם אחרים) שהפונקציה הולכת ומתקרבת אליו ככל ש-\( x \) הולך וגדל (“הולכים ימינה”) או ככל ש-\( x \) הולך וקטן, בתור מספר שלילי (“הולכים שמאלה”).

המקרה השני נקרא אסימפטוטה אנכית הוא מה שקורה במרכז התמונה עם ציר \( y \): אם נלך שמאלה עם החלק של גרף הפונקציה שעבורו \( x>0 \), כלומר נקטין את הערכים החיוביים של \( x \) עוד ועוד, אפשר לראות שהערכים שהפונקציה מקבלת הולכים וגדלים. אם נציב \( x=1 \) נקבל \( f\left(x\right)=\frac{1}{1}=1 \) אבל אם נציב \( x=\frac{1}{2} \) נקבל \( f\left(x\right)=\frac{1}{1/2}=2 \) ואם נציב \( x=\frac{1}{100} \) נקבל \( f\left(x\right)=\frac{1}{1/100}=100 \) וכן הלאה.

בואו נסתכל על זה לרגע מנקודת מבטו של ציר \( y \). נניח שאנחנו נכנסים לצפלין ענק ומתחילים לנוע מעלה על ציר \( y \), כלומר עוברים על הנקודות מהצורה \( \left(0,y\right) \) עבור \( y>0 \) (למה צפלין? למה לא?). תוך כדי הטיסה שלנו למעלה אנחנו מדי פעם שולחים מבט ימינה, ואנחנו רואים את \( f\left(x\right) \) לצידנו. אנחנו ממשיכים לטפס למעלה, וממשיכים לשלוח מבטים, ובכל פעם שאנחנו שולחים מבט \( f\left(x\right) \) עדיין שם, רק קרובה אפילו עוד יותר. אם הטיסה הזו נמשכת לנצח בצורה הזו, אז אנחנו אסימפטוטה של \( f\left(x\right) \); אם בשלב כלשהו נעיף מבט ימינה ולא נראה את \( f\left(x\right) \), ונסתכל בבהלה שמאלה וגם לא נראה את \( f\left(x\right) \), אז הכל התקלקל - מה שראינו עד עכשיו לא יכול ללמד אותנו שאנחנו אסימפטוטה של \( f\left(x\right) \). למרות שאנחנו עדיין משאירים פתח לאפשרות שמתישהו במהלך המסע היא תחזור, והפעם אולי לתמיד.

בואו נראה עוד דוגמא שמחדדת את מה שקורה פה:

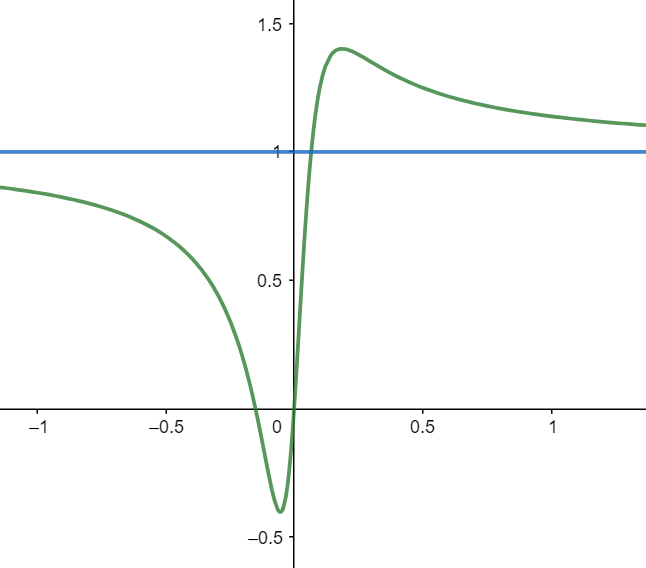
הקו המתפתל הירוק כאן הוא הפונקציה \( f\left(x\right)=\frac{100x^{2}+15x}{100x^{2}+1} \). את המספרים שבתוך הפונקציה בחרתי כדי שהיא תתנהג בצורה הנחמדה שאני רוצה; כדאי לשים לב בעיקר למכנה, שבו מופיע \( 100x^{2}+1 \), ביטוי שלא יכול להתאפס אף פעם (כי העלאה בריבוע של מספר שלילי מחזירה מספר חיובי) ולכן בניגוד אל \( \frac{1}{x} \) אין איזו קטסטרופה בראשית הצירים שמקפיצה את הפונקציה לשמיים. אז מה האסימפטוטות שלה? גם כשהולכים ימינה עד אינסוף וגם כשהולכים שמאלה, נראה שהפונקציה מתקרבת עוד ועוד אל הקו האופקי \( y=1 \) שבאיור מסומן בכחול.

עכשיו, שימו לב מה עוד רואים באיור - שבשלב מסוים, די סמוך לצד הימני של ציר \( y \), הפונקציה נוגעת בישר \( y=1 \) הזה, עוברת דרכו לצד השני, ורק בהמשך חוזרת להתקרב אליו. זה בא בניגוד לתיאור פופולרי של אסימפטוטה בתור “קו שהפונקציה מתקרבת אליו עוד ועוד אבל לא נוגעת בו”. פונקציה בהחלט יכולה לגעת באסימפטוטה שלה. מה שמעניין אותנו הוא רק מה שקורה לאורך זמן, כשהולכים עוד ועוד לאורך האסימפטוטה. כאן מנקודת המבט של \( y=1 \) היה איזה קטע בהתחלה שבו הפונקציה נגעה באסימפטוטה ואז התחילה להתרחק ממנה, אבל כל זה קרה אי שם בעבר, בהתחלה, ובסופו של דבר ההתנהגות שהתקבעה של \( f\left(x\right) \) היא זו שרואים בהמשך של הגרף - הפונקציה מתקרבת עוד ועוד אל האסימפטוטה.

לרוע המזל, גם זה לא סוף הסיפור. בואו נתבונן בגרף של הפונקציה הבאה:

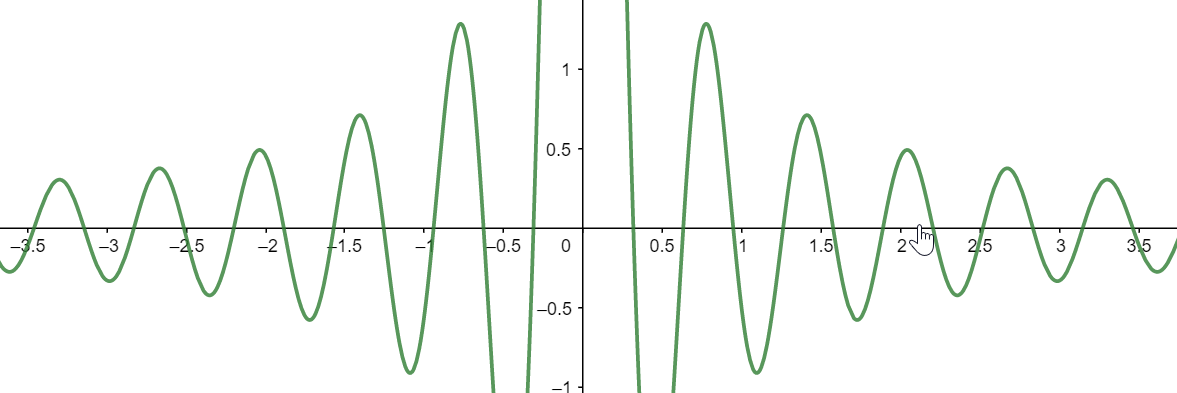
הפונקציה פה נעזרת במשהו שנקרא סינוס, \( \sin x \), שהיא פונקציה מחזורית שנעה בין 1 ל-\( -1 \). הפונקציה עצמה היא \( f\left(x\right)=\frac{\sin\left(10x\right)}{x} \) כששוב, הקבועים מהונדסים כדי שהכל יעבוד נחמד. מה הולך כאן? ראשית, אם הולכים ימינה עד אינסוף, רואים שהפונקציה חוצה שוב ושוב את ציר \( x \). זה יימשך כך לנצח, ונובע מהאופי המחזורי של סינוס. מצד שני, ה”גלים” של הפונקציה הולכים ומתמתנים עם הזמן - הפסגות והעמקים שלה יותר ויותר קרובים אל ציר \( x \), מה שנובע מ-\( \frac{1}{x} \) שמופיע בתוך הפונקציה. זה אומר שציר ה-\( x \) היא אסימפטוטה של הפונקציה, וזה למרות שהיא חוצה אותו שוב ושוב. אז צריך להיזהר עם האינטואיציות.

מהיכן מגיעה האינטואיציה ש”פונקציה לא נוגעת באסימפטוטה שלה”? ובכן, מכך שהדבר הראשון שעושים עם אסימפטוטות הוא לחשב אותן במקרים שבהם \( f\left(x\right) \) היא פונקציה פשוטה, מה שנקרא “פונקציה רציונלית”. לפונקציות רציונליות אין התנהגויות מוזרות כמו שיש לסינוס או לפונקציות שהן מסובכות אפילו יותר, וזה מצוין; התרגילים שפותרים בפועל בבית הספר כנראה יערבו אותן, ולכן טוב לפתח אינטואיציה טובה לגביהן ספציפית. רק צריך לזכור שזה באמת משהו שתקף רק לגביהן (ככה זה כל המתמטיקה: בכל תחום מנסים למצוא פונקציות “נחמדות” יחסית ולפתח אינטואיציה לגבי ההתנהגות הספציפית שלהן, למשל הפונקציות הרציפות של הטופולוגיה והטרנספורמציות הלינאריות של האלגברה הלינארית.

בואו נחזור לרגע אל \( f\left(x\right)=\frac{\sin\left(10x\right)}{x} \). ראינו שציר \( x \) הוא אסימפטוטה שלה, מה באשר לציר \( y \)? בהחלט נראה שבסביבות \( x=0 \) הפונקציה מזנקת לה לפתע לגבהים, אז האינטואיציה שלנו אומרת שיש פה אסימפטוטה; אלא שזה לא נכון. אם היינו מסתכלים על הגרף ממרחק גדול יותר, היינו רואים שהפונקציה מגיעה עד הנקודה \( \left(0,10\right) \) ואז עוברת דרכה, ובוודאי שאינה ממשיכה עד אינסוף:

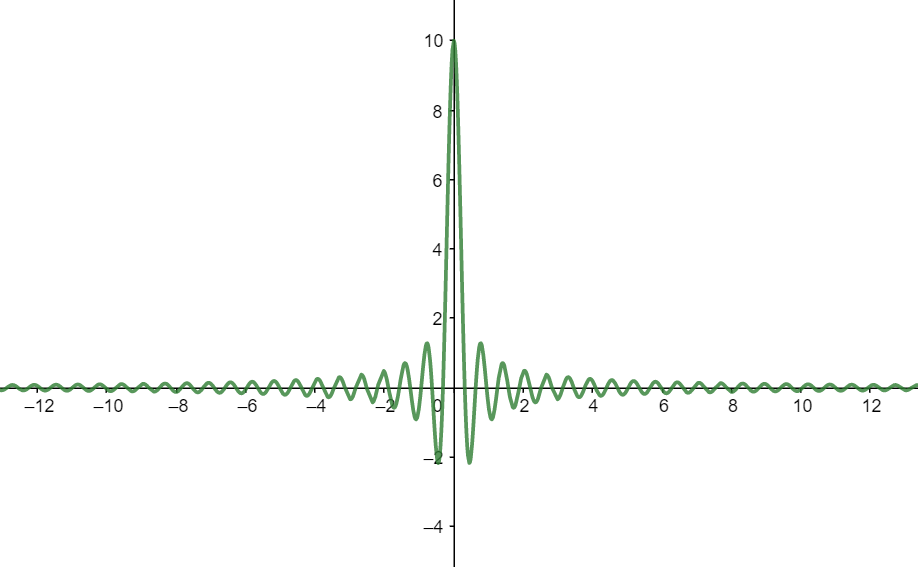
זה מוזר. זה ממש מוזר, כי זה מנוגד לכל מה שאנחנו לומדים בתור חוקים בסיסיים. הביטו ב-\( f\left(x\right)=\frac{\sin\left(10x\right)}{x} \). מה קורה אם מציבים \( x=0 \)? למי שלא מכירים את סינוס אני אגלה ש-\( \sin\left(0\right)=0 \), כך שאנחנו מקבלים \( f\left(0\right)=\frac{0}{0} \). כידוע (או שלא?) \( \frac{0}{0} \) הוא ביטוי חסר משמעות ובוודאי לא משהו שיוצא 0, אז מה הולך כאן?

התשובה היא שבאופן שבו הגדרנו את \( f\left(x\right)=\frac{\sin\left(10x\right)}{x} \), זה נכון; הפונקציה לא מוגדרת ב-\( x=0 \). זה לא אומר שיש לה אסימפטוטה כלשהי כשהיא מתקרבת ל-\( x=0 \), כי היא לא בורחת למעלה “עד אינסוף”. האינטואיציה צריכה להיות שאיכשהו, ככל שאנחנו מציבים ב-\( x \) ערכים קרובים יותר ויותר ל-0 (אבל לא את 0 עצמו!) הערך של \( \frac{\sin\left(10x\right)}{x} \) לא בורח לשום מקום, כי ה-\( \sin10x \) שבמונה (שהוא מספר קטן מאוד כש-\( x \) קרוב לאפס) מקזז איכשהו את ה-\( x \) שבמכנה (שהחלוקה בו נותנת מספר גדול מאוד כש-\( x \) קרוב לאפס).

מה שאוהבים לעשות במתמטיקה הוא להגדיר את \( f\left(x\right) \) בהתאם להתנהגות הזו, כלומר להגדיר

\( f\left(x\right)=\begin{cases} \frac{\sin\left(10x\right)}{x} & x\ne0\\ 10 & x=0 \end{cases} \)

זו הגדרה פורמלית לגמרי, והיא גם “נחמדה” במובן זה שהפונקציה \( f \) שמתקבלת היא רציפה, אבל המושג הזה לא חשוב לנו כרגע. מה שחשוב הוא רק שהמוזרויות הללו הן לא מנת חלקן של הפונקציות הרציונליות ה”נחמדות” (כמעט; יהיה משהו טיפה דומה בהמשך), אז בואו נדבר עליהן.

פולינומים ואיך שהם מסתדרים עם שאיפה לאינסוף

הנה פונקציה פשוטה: \( f\left(x\right)=1 \). הנה עוד פונקציה פשוטה: \( f\left(x\right)=x \). הנה פונקציה טיפה יותר מסובכת: \( f\left(x\right)=x^{2} \). בואו נסבך עכשיו עוד יותר: \( f\left(x\right)=2x \). ועוד יותר: \( f\left(x\right)=2x+1 \). מה משותף לכל הפונקציות הללו? כולן נקראות פולינומים. פולינומים הם משפחה של פונקציות שהן פשוטות יחסית וקל לעבוד איתן ולכן אנחנו אוהבים אותן.

מה ההגדרה הפורמלית של פולינום? זו פונקציה שלוקחת מספרים ואת \( x \) ויכולה לחבר אותם או לכפול אותם זה בזה, וזהו. אם אני לוקח את \( x \) וכופל אותו בעצמו וב-\( 3 \) אני אקבל \( 3x^{2} \). לזה אני יכול להוסיף למשל את \( 5 \) ולקבל \( 3x^{2}+5 \), וכן הלאה. באופן הכי פורמלי שבו מתארים פולינום, הוא נכתב כך:

\( f\left(x\right)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots+a_{1}x+a_{0} \)

כאשר ה-\( a_{0},\ldots,a_{n} \) הם מספרים שנקראים המקדמים של הפולינום. החזקה הכי גבוהה של \( x \) שמופיעה בפולינום עם מקדם שהוא לא 0 נקראת המעלה של הפולינום. למשל \( x^{3}-5x^{2}+3 \) הוא פולינום ממעלה 3 עם סדרת המקדמים (מהקטן לגדול) \( 3,-5,0,1 \).

פונקציות שנראות כמו קו ישר הן פולינומים; ספציפית, פולינומים ממעלה ראשונה. למשל \( f\left(x\right)=1 \) מתארת את הקו האופקי \( y=1 \). ו-\( f\left(x\right)=3x+2 \) מתארת את הקו \( 3x+2 \).

הנה איור של כמה פולינומים בפעולה: הפולינום \( 3x+2 \) שהוא הקו הישר (ירוק באיור), הפולינום \( x^{2} \) שהוא הקערה הסימטרית (כחול באיור) והפולינום \( x^{3}-5x^{2}+3 \) (אדום באיור) שנראה כמו מהומה שלמה:

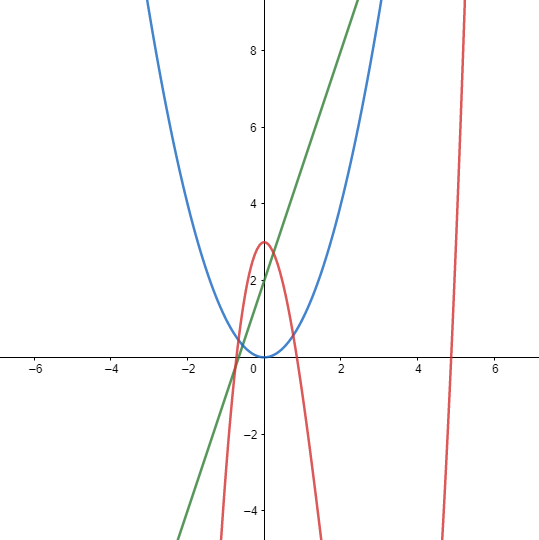
מה שמשותף לכל הפולינומים הללו הוא שבאיור הם בורחים למעלה או למטה במהירות הבזק. זה לא מקרי; זו תכונה שמשותפת לכל הפולינומים. כל פולינום שהוא, לא משנה איזה, תמיד מקבל ערכים שהולכים וגדלים עוד ועוד ככל שערכי ה-\( x \) שהוא מקבל גדלים, באופן שהוא לא חסום - כלומר, לכל גובה אפשרי, מתישהו הפולינום יגיע אל הגובה הזה, ולכן אין לו אסימפטוטה אופקית כשהולכים ימינה. לא משנה איזה קו אופקי נמתח, מתישהו הפולינום יעקוף אותו וימשיך הלאה אל האינסוף.

אלא שאני צריך לחדד את זה טיפה. אם המקדם המוביל של הפולינום (מה שמכפילים בו את החזקה הגבוהה ביותר של \( x \) בו) יהיה שלילי, יקרה ההפך. במקום שהפולינום יעלה עוד ועוד, הוא דווקא יירד עוד ועוד. הערך שהוא מקבל עדיין יילך ויגדל - בערכו המוחלט, אבל המשמעות תהיה שהערך הזה יהיה מספר שלילי שנהיה יותר ויותר קטן (יש לי קושי של ממש לקרוא ל-\( -1,000,000,000 \) “מספר קטן”, כי אמנם זה מספר די קטן, אבל בראש שלי “קטן” זו דך להגיד “קרוב לאפס”).

בכתיב חצי פורמלי אפשר לכתוב את זה כך: אם \( f\left(x\right) \) הוא פולינום עם מקדם מוביל חיובי, אז

\( f\left(x\right)\underset{x\to\infty}{\to}\infty \)

את הדבר הזה אפשר לקרוא בתור “כאשר \( x \) שואף לאינסוף, אז הפולינום \( f\left(x\right) \) שואף לאינסוף”. אני יכול לתת פה את ההסבר הקצת יותר פורמלי: הכוונה היא שלכל גובה \( M \) אפשרי, קיימת איזו שהיא נקודה, נקרא לה \( x_{0} \) כך שאם \( x>x_{0} \) נקבל \( f\left(x\right)>M \). כלומר, לכל הפחות החל מ-\( x_{0} \) ומעלה, \( f\left(x\right) \) כבר לא תיגע אף פעם ב-\( y=M \).

שימו לב ש-\( \infty \) הוא לא מספר. אי אפשר להציב בפולינום את “הערך” \( \infty \) והוא לא יודע להחזיר \( \infty \) כפלט. זה פשוט סימון שבא לתאר את ההתנהגות שנתתי לה כרגע תיאור פורמלי.

אם המקדם המוביל של \( f\left(x\right) \) שלילי, מסמנים את זה כמעט אותו דבר:

\( f\left(x\right)\underset{x\to\infty}{\to}-\infty \).

כאן המשמעות של “שואף למינוס אינסוף” היא שלכל גובה \( M \) אפשרי, בפרט כזה שהוא מספר שלילי, קיימת נקודה \( x_{0} \) כך שאם \( x>x_{0} \) נקבל \( f\left(x\right)<M \).

עכשיו, מה קורה כשאנחנו הולכים לא ימינה אלא שמאלה, כלומר כאשר הערכים של \( x \) הולכים וקטנים בתור מספרים שליליים? אני מסמן את זה בתור \( x\to-\infty \).

אם נסתכל באיור נראה שקורים שני דברים אפשריים: הפולינום \( x^{2} \) בורח למעלה גם במקרה הזה, אבל שני הפולינומים האחרים דווקא בורחים למטה. שוב, זה לא מקרי אלא משהו שמשותף לכל הפולינומים: או שהפולינום שואף לאינסוף או שהוא שואף למינוס אינסוף. על השאלה מה יקרה בפועל משפיעים שני דברים:

• האם המעלה של הפולינום (המספר \( n \) הגבוה ביותר כך ש-\( x^{n} \) מופיע בפולינום עם מקדם שונה מאפס) היא זוגית או אי זוגית.
• האם המקדם המוביל של הפולינום (המקדם של \( x^{n} \) כאשר \( n \) היא המעלה של הפולינום) הוא חיובי או שלילי.

אם המקדם המוביל הוא חיובי, אז מעלה זוגית מתבטאת בשאיפה לאינסוף, ומעלה אי זוגית מתבטאת בשאיפה למינוס אינסוף - אלו הדוגמאות שאנחנו רואים באיור. למה זה קורה? כי מספר שלילי בחזקה זוגית יוצא חיובי, אבל מספר שלילי בחזקה אי זוגית יוצא מספר שלילי. האינטואיציה היא שהגורם \( x^{n} \) כש-\( n \) הוא המעלה של הפולינום הוא בטווח הארוך הדבר הכי גדול שיש בפולינום. אפילו בפולינום כמו \( x^{3}+1000000000000x^{2} \), מתישהו יהיו ערכים גדולים מספיק שכשנציב אותם ב-\( x^{3} \) נקבל משהו גדול בהרבה מ-\( 1000000000000x^{2} \), ולכן זה מה שנותן את הטון.

אם המקדם המוביל של הפולינום הוא שלילי, המגמה מתהפכת: פולינום כזה עם מעלה זוגית ישאף למינוס אינסוף, ופולינום כזה עם מעלה אי זוגית ישאף לאינסוף, בדיוק כמו ההיפוך שקרה כאשר \( x \) שאף לאינסוף.

אז לפולינומים אין אסימפטוטות אופקיות. מה עם אסימפטוטה אנכית? באיור רואים שאין שום דבר כזה לפולינומים שציירתי, אבל אולי יש לאחרים? ובכן, לא. לאף פולינום אין אסימפטוטה אנכית. למה? כי אסימפטוטה אנכית פירושה שיש איזו נקודה קונקרטית שככל שערכי \( x \) מתקרבים אליה, ערכי הפונקציה שואפים לאינסוף או למינוס אינסוף. אבל אצל הפולינומים, לכל \( x \) אפשרי הפולינום \( f\left(x\right) \) מחזיר ערך מספרי קונקרטי, והנקודות שקרובות לאותו \( x \) מחזירות ערכים שקרובים ל-\( f\left(x\right) \) (לתכונה הזו קוראים רציפות). אז זה מסיים גם את הסיפור הזה - לפולינום אין בכלל אסימפטוטות אופקיות או אנכיות.

אם זה המצב, למה בכלל דיברתי על פולינומים עד כה? אה, כי פולינומים הם השחקן המרכזי גם בסוג הבא של פונקציה שאני רוצה לדבר עליו - סוג שבהחלט יש לו אסימפטוטות. הסוג הזה נקרא פונקציות רציונליות.

האסימפטוטות של פונקציות רציונליות

הנה כמה דוגמאות לפונקציות רציונליות:

\( \frac{1}{x},2x^{3},\frac{x}{1+x^{2}},\frac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x-5\right)\left(x-7\right)} \)

מה משותף לכל הדוגמאות? על כולן אפשר לחשוב בתור משהו מהצורה \( f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)} \) כאשר \( p\left(x\right),q\left(x\right) \) שניהם פולינומים.

למשל, עבור \( f\left(x\right)=\frac{1}{x} \) הפולינומים הם \( p\left(x\right)=1,q\left(x\right)=x \).

עבור \( f\left(x\right)=2x^{3} \) הפולינומים הם \( p\left(x\right)=2x^{3},q\left(x\right)=1 \).

עבור \( f\left(x\right)=\frac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x-5\right)\left(x-7\right)} \) הפולינומים הם \( p\left(x\right)=\left(x-2\right)\left(x-3\right),q\left(x\right)=\left(x-2\right)\left(x-5\right)\left(x-7\right) \). בואו נתעכב עוד רגע על הדוגמא המאוד חשובה הזו.

ראשית, בואו נסתכל על \( \left(x-2\right)\left(x-3\right) \). אמרתי שזה פולינום, אבל זה לא נראה כמו פולינום על פי ההגדרה שנתתי… יותר כמו מכפלה של שני פולינומים. ובכן, מכפלה כזו היא פולינום בעצמה! אם נפתח את הסוגריים נקבל \( x^{2}-5x+6 \). בעצם \( \left(x-2\right)\left(x-3\right) \) זו דרך אחרת לכתוב את אותו פולינום שהיא קצת יותר אינפורמטיבית, כי קל לראות מתוכה מה השורשים של הפולינום - מה המספרים שכשמציבים אותם בפולינום מקבלים 0 (שימו לב! זה שונה לגמרי מפונקציית השורש \( !\sqrt{x} \) השימוש באותה מילה עבור שני דברים שונים הוא מצער למדי). במקרה הזה אלו \( 2,3 \).

האם תמיד אפשר לכתוב פולינום בצורה נחמדה כזו? ובכן… זה מסובך. למשל, מה עם הפולינום \( x^{2}+1 \)? לא משנה איזה מספר ממשי נציב בו, הוא לא יתאפס. אז אין לו בכלל שורשים ואי אפשר לפרק אותו לכזו מכפלה. מצד שני, המספרים הממשיים הם לא סוף הסיפור; יש מערכת מספרים מגניבה שנקראת המספרים המרוכבים ובה יש מספר שמסומן ב-\( i \) וכן מאפס את הפולינום, ואפשר לכתוב \( x^{2}+1=\left(x-i\right)\left(x+i\right) \). אבל אני לא רוצה לדבר על מרוכבים כאן ולכן לא ניכנס לזה.

עוד עניין הוא שאם נתון לנו פולינום בצורה ה”רגילה”, זה לא אומר בכלל שיהיה לנו קל לדעת מי השורשים שלו. עבור פולינום ממעלה שניה יש כלי שנקרא נוסחת השורשים שעושה את העבודה, אבל במעלות שלישית ורביעית הנוסחאות הדומות הן מסובכות בצורה קיצונית, ואילו ממעלה חמישית ומעלה לא קיימת נוסחה בכלל באופן כללי, אז אין פתרון קסם - לפעמים אפשר, לפעמים אי אפשר.

בואו נעבור שניה אל המכנה שבדוגמא שהראיתי: \( \left(x-2\right)\left(x-5\right)\left(x-7\right) \). אם נפתח את הסוגריים ונבצע חישוב די מעיק, נקבל \( x^{3}-14x^{2}+59x-70 \). זה פולינום שנראה סתום לגמרי ממבט ראשון - אין לי דרך טובה להסביר איך למצוא את השורשים \( 2,5,7 \) שלו (אפשר לעשות סוג של ניחוש חכם, אבל נעזוב את זה). עכשיו, בואו נניח שבמקום לקבל את הפונקציה הרציונלית \( \frac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x-5\right)\left(x-7\right)} \) הייתי מקבל את הזוועה הזו:

\( \frac{x^{2}-5x+6}{x^{3}-14x^{2}+59x-70} \)

לא ממש היינו יודעים מה לעשות עם הביטוי הזה או איך לפשט אותו. לעומת זאת, אם נותנים לנו את

\( \frac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x-5\right)\left(x-7\right)} \)

אפשר לראות שה-\( x-2 \) הזה מופיע גם במונה וגם במכנה, ולכן אפשר לצמצם אותו ולקבל את הפונקציה

\( \frac{x-3}{\left(x-5\right)\left(x-7\right)}=\frac{x-3}{x^{2}-12x+35} \)

שהיא הרבה יותר פשוטה. אני מראה את הפישוט הזה כי כבר בשלב הזה חשוב להבין שאפשר לעשות את זה לפונקציות רציונליות.

אבל רגע רגע רגע… מה בעצם עשיתי? אין חוק כזה שאם מחלקים במשהו, אז הוא צריך להיות שונה מאפס? אבל \( x-2 \) עשוי להיות אפס, אם אני מציב \( x=2 \). מה קורה פה? אם אני מציב \( x=2 \) בפונקציה \( \frac{x-3}{x^{2}-12x+35} \) אני אקבל \( -\frac{1}{4-24+35}=-\frac{1}{15} \). אם לעומת זאת אני אציב \( x=2 \) בפונקציה \( \frac{x^{2}-5x+6}{x^{3}-14x^{2}+59x-70} \), אני אקבל \( \frac{0}{0} \) וכבר אמרנו שזה ביטוי בעייתי.

כדי להבין מה הולך פה, בואו נסתכל על הגרף של הפונקציה:

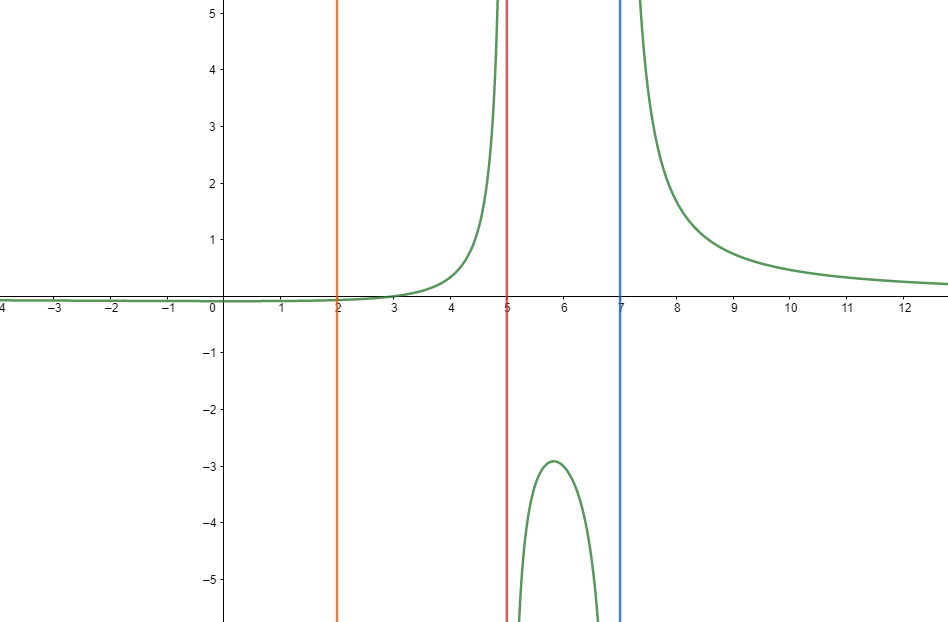
ציירתי את הפונקציה יחד עם הקווים האנכיים שעוברים דרך השורשים של המכנה: \( 2,5,7 \). אנחנו רואים שגם ב-5 וגם ב-7 יש לנו אסימפטוטות אנכיות; לעומת זאת ב-2 הפונקציה עוברת בשמחה דרך הקו האנכי כאילו כלום, ואין שום אסימפטוטה. זה מראה לנו על הבדל מהותי בין המקרים הללו: ה”בעיה” שיש בהגדרה של \( \frac{x^{2}-5x+6}{x^{3}-14x^{2}+59x-70} \) ב-\( x=2 \) נובעת מהדרך הלא טובה שבה אנחנו מייצגים את הפונקציה הזו: זה גורם לנו להגיד שהיא לא מוגדרת ב-\( x=2 \) למרות שיש דרך נחמדה להגדיר אותה שם. אם נגדיר

\( f\left(x\right)=\begin{cases} \frac{x^{2}-5x+6}{x^{3}-14x^{2}+59x-70} & x\ne2\\ -\frac{1}{15} & x=2 \end{cases} \)

נקבל פונקציה “נחמדה” מאוד (רציפה) שבמקרה או שלא במקרה מתוארת בדיוק על ידי \( \frac{x-3}{x^{2}-12x+35} \), שהיא הפונקציה שהתקבלה מצמצום ה-\( x-2 \) הסורר מהמונה והמכנה. זה המובן שבו אני מרשה לעצמי לבצע את הצמצום הזה - לעבור מפונקציה אחת לפונקציה אחרת שזהה לה כמעט לגמרי, פרט למה שנקרא נקודת אי-רציפות סליקה, שאותה אני… אה… מסלק.

כל הדיון זה היה חשוב כי זו בדיוק הדרך לזהות איפה יש לפונקציה רציונלית אסימפטוטה אנכית: כל אסימפטוטה אנכית חייבת להיות בנקודה שבה המכנה מתאפס. בנקודה כזו, יש שתי אפשרויות: או שהמונה לא יתאפס, ואז בודאות מוחלטת יש שם אסימפטוטה אנכית; או שהמונה כן מתאפס שם, ואז… זה מסובך.

ראשית, הטענה הראשונה: אם המכנה מתאפס בנקודה כלשהי, זה אומר שככל שמתקרבים לנקודה הזו, החלוקה במכנה הופכת להיות כפל במספרים הולכים וגדלים (כזכור, אם \( x=1/100 \) אז \( \frac{1}{x}=100 \)). אם בזמן הזה המונה הולך ומתקרב לאיזה ערך מספרי קבוע ששונה מאפס, שום דבר לא “ירסן” את המכנה, והתוצאה תהיה שהערכים של הפונקציה יגדלו לאינסוף או יקטנו למינוס אינסוף.

שנית, מה קורה אם גם המונה וגם המכנה מתאפסים? בואו נסתכל לרגע על הפונקציה \( \frac{x^{2}}{x^{2}} \). זו פונקציה שבה ב-\( x=0 \) המונה והמכנה מתאפסים, אבל זו בעצם הפונקציה \( f\left(x\right)=1 \) בתחפושת; בוודאי שאין לה אסימפטוטה אנכית. לעומת זאת, הפונקציה \( \frac{x}{x^{2}} \) ניתנת לצמצום דומה שיוביל אותנו אל \( \frac{1}{x} \), שהיא כן פונקציה עם אסימפטוטה אנכית. אז איך אפשר לדעת?

הנה עקרון כללי: אם פולינום \( p\left(x\right) \) מתאפס ב-\( x=a \), אז אפשר, בודאות מוחלטת, לכתוב את \( p\left(x\right) \) בתור \( p\left(x\right)=\left(x-a\right)q\left(x\right) \) כאשר \( q\left(x\right) \) הוא פולינום אחר. אז אם גם המונה וגם המכנה מתאפסים ב-\( x=a \) אפשר לחלק את המונה והמכנה ב-\( x-a \) (כמו בדוגמאות שכבר ראינו) ואז לקבל שני פולינומים חדשים, שגם עבורם אפשר לבדוק אם הם מתאפסים ב-\( x=a \) או לא.

בפועל, כמובן, אפשר לנקוט גם בדרך שונה - פשוט להציב ערכים שקרובים ל-\( x=a \) ולבדוק אם הפונקציה “מתפוצצת” או לא. אבל זו לא דרך פורמלית במיוחד להשתכנע.

עכשיו, לכל אסימפטוטה אנכית יש שני צדדים. בואו נסתכל שוב על \( \frac{1}{x} \) לרגע:

אנחנו רואים שככל ש-\( x \) מתקרב ל-0 מצד ימין, כלומר כשהערכים שלו חיוביים, אז הערכים של הפונקציה שואפים לאינסוף: מסמנים את זה לפעמים \( f\left(x\right)\underset{x\to0^{+}}{\to}\infty \). מן העבר השני, כש-\( x \) מתקרב ל-0 מצד שמאל ערכי הפונקציה שואפים למינוס אינסוף: \( f\left(x\right)\underset{x\to0^{-}}{\to}-\infty \). איך אפשר לדעת אם השאיפה תהיה לאינסוף או למינוס אינסוף? בגישה האינטואיטיבית, פשוט מציבים ערכים שקרובים לנקודת ההתפוצצות ובודקים אם התוצאה חיובית או שלילית. כן, זו היוריסטיקה בעייתית, אבל בלי להיכנס לפורמליזם רציני יותר, זה מה יש.

מה עם אסימפטוטות אופקיות? בניגוד לאסימפטוטות אנכיות, שהמספר שלהן תלוי בכמה נקודות המכנה מתאפס, לפונקציה רציונלית יכולות להיות רק שתי אסימפטוטות אופקיות: זו שמתקבלת כאשר \( x\to\infty \) וזו שמתקבלת כאשר \( x\to-\infty \). אבל איך מוצאים אותן? אפשר, כרגיל, להציב ערכים ולראות מה קורה, אבל זה לא פורמלי וגם לא נותן לנו את האסימפטוטה המדויקת ליד (כלומר, את קואורדינטת ה-\( y \) של הישר).

למרבה המזל, מה שאנחנו יודעים על פולינומים בא לעזרתנו בקלות כאן. נכון שאמרתי קודם שכאשר \( x \) שואף לאינסוף, אז חזקה גדול “מנצחת” חזקה קטנה? זה אומר שאפשר להתעלם לחלוטין מכל החזקות של הפולינומים במונה ובמכנה מלבד החזקות שהן המעלה של הפולינומים.

נחזור לשניה אל הפונקציה הרציונלית \( \frac{x^{2}-5x+6}{x^{3}-14x^{2}+59x-70} \). מה שאני אומר הוא שכאשר \( x \) שואף לאינסוף, כל החלק של ה-\( -5x+6 \) הוא זניח ביחס אל \( x^{2} \). בדומה, כל החלק של \( -14x^{2}+59x-70 \) הוא זניח ביחס אל \( x^{3} \). לכן אפשר לומר שההתנהגות של הפונקציה הזו כש-\( x \) שואף לאינסוף זהה להתנהגות של הפונקציה \( \frac{x^{2}}{x^{3}} \) כאשר \( x \) שואף לאינסוף. כלומר, זהה להתנהגות של הפונקציה \( \frac{1}{x} \) כש-\( x \) שואף לאינסוף, ואנחנו כבר יודעים שזה 0, שאליו הפונקציה שואפת “מלמעלה”. בדומה, כש-\( x \) שואף למינוס אינסוף, הפונקציה תשאף אל 0 “מלמטה”, בדיוק כמו עם \( \frac{1}{x} \).

בואו נראה עוד דוגמא, עם הפונקציה \( f\left(x\right)=\frac{100x^{2}+15x}{100x^{2}+1} \) שהראיתי קודם:

כל הדיבורים באוויר על “ההתנהגות של בלה בלה זה כמו ההתנהגות של בלו בלו” נותנים הרגשה שיש פה איזה מעשה קסמים לא ברור, אז הנה גישה קצת יותר פרקטית. בואו ניקח את הפונקציה הרציונלית הזו

\( \frac{100x^{2}+15x}{100x^{2}+1} \)

ונחלק גם את המונה וגם את המכנה ב-\( x^{2} \), שהוא המעלה של הפולינומים שנמצאים בהם. ליתר דיוק אני לא בדיוק אחלק אותם אלא אוציא אותם החוצה, ככה:

\( \frac{100x^{2}+15x}{100x^{2}+1}=\frac{x^{2}\left(100+15\frac{x}{x^{2}}\right)}{x^{2}\left(100+\frac{1}{x^{2}}\right)}=\frac{x^{2}\left(100+15\frac{1}{x}\right)}{x^{2}\left(100+\frac{1}{x^{2}}\right)} \)

אחרי שהוצאתי אותם החוצה אני מצמצם את ה-\( x^{2} \) מהמונה והמכנה. בשביל לעשות את זה אני צריך להניח ש-\( x\ne0 \), וזה בסדר; אני עושה את השינוי הזה רק כדי לבדוק את ההתנהגות של הפונקציה כשאיקס שואף ל-\( \pm\infty \). התוצאה תהיה הפונקציה \( \frac{100+15\frac{1}{x}}{100+\frac{1}{x^{2}}} \).

עכשיו, כבר ראינו ש-\( \frac{1}{x}\underset{x\to\infty}{\to}0 \), ובאופן דומה \( \frac{1}{x^{2}}\underset{x\to\infty}{\to}0 \), ולכן אני מקבל בסך הכל:

\( \frac{100+15\frac{1}{x}}{100+\frac{1}{x^{2}}}\underset{x\to\infty}{\to}=\frac{100}{100}=1 \)

זו לא הייתה הוכחה פורמלית לגמרי, אבל אני חושב שהרעיון די ברור ממנה. זו הצורה הכללית שבה “מנטרלים” את החזקות הנמוכות יותר מהמונה והמכנה; מה שנשארנו איתו בסוף היו רק המקדמים של החזקות הגבוהות ביותר.

עכשיו, העסק הזה עבד יפה בגלל שהמעלה של המונה ושל המכנה היו זהות - \( x^{2} \). מה קורה בסיטואציות אחרות? הנה שתי דוגמאות פשוטות:

ראשית ניקח את \( \frac{x^{2}+3x}{2x+7} \). נעשה את הטריק שכבר השתמשתי בו, נוציא החוצה \( x^{2} \) מהמונה ו-\( x \) מהמכנה, ונקבל

\( \frac{x^{2}+3x}{2x+7}=\frac{x^{2}\left(1+3\frac{1}{x}\right)}{x\left(2+\frac{7}{x}\right)} \)

כאן אחרי צמצום אני אקבל:

\( x\cdot\frac{1+3\frac{1}{x}}{2+\frac{7}{x}} \)

כאשר אני משאיף את \( x \) לאינסוף, הביטוי \( \frac{1+3\frac{1}{x}}{2+\frac{7}{x}} \) לבדו ישאף ל-\( \frac{1}{2} \). לעומת זאת, ה-\( x \) שבו הביטוי הזה מוכפל שואף לאינסוף. הנה תכונה שאשתמש בה בלי להוכיח כרגע אבל אני מקווה שהיא אינטואיטיבית מספיק: אם יש לנו מכפלה של שתי פונקציות שאחת שואפת לאינסוף והשניה שואפת למספר קבוע גדול מאפס, אז המכפלה שלהן שואפת לאינסוף (ואם המספר קטן מאפס אז שואפת למינוס אינסוף; ואם המספר שווה לאפס אז הרבה דברים שונים ומשונים עשויים לקרות). זה מראה לנו ש-\( \frac{x^{2}+3x}{2x+7}\to\infty \); המונה “מנצח” כי החזקה שלו גדולה יותר.

עכשיו בואו ניקח את אותה פונקציה ונחליף את המונה והמכנה. נקבל

\( \frac{2x+7}{x^{2}+3x} \)

ואחרי הוצאת גורמים וצמצום נקבל

\( \frac{1}{x}\cdot\frac{2+\frac{7}{x}}{1+3\frac{1}{x}} \)

ועכשיו יש לנו פונקציה אחת ששואפת ל-2 ומוכפלת בפונקציה אחרת (\( \frac{1}{x} \)) ששואפת לאפס והתוצאה של זה, כצפוי, שואפת לאפס (כדי שמשהו יתקלקל, צריך שמה ששואף לאפס יוכפל במשהו ששואף לאינסוף או מינוס אינסוף).

אפשר לסכם את מה שראינו פה כך - עבור כל פונקציה רציונלית \( \frac{p\left(x\right)}{q\left(x\right)} \), כשמשאיפים את \( x \) לאינסוף או למינוס אינסוף:

• אם המעלה של \( q\left(x\right) \) גדולה משל \( p\left(x\right) \), אז \( \frac{p\left(x\right)}{q\left(x\right)}\to0 \).
• אם המעלות של \( q\left(x\right),p\left(x\right) \) שוות שתיהן ל-\( n \) ו-\( \frac{p\left(x\right)}{q\left(x\right)}=\frac{a_{n}x^{n}+\ldots}{b_{n}x^{n}+\ldots} \) אז \( \frac{p\left(x\right)}{q\left(x\right)}\to\frac{a_{n}}{b_{n}} \).
• אם המעלה של \( p\left(x\right) \) גדולה מ-\( q\left(x\right) \), אז \( \frac{p\left(x\right)}{q\left(x\right)}\to\pm\infty \).

מה שמעניין אותנו, בתור ציידי אסימפטוטות, הם המקרים הראשון והשני. במקרה הראשון האסימפטוטה היא תמיד \( y=0 \) ובמקרה השני אנחנו רואים בדיוק איך לחשב את הערך של האסימפטוטה - מחלקים את המקדמים המובילים של המונה והמכנה. זה בעצם מסיים את הטיפול בפונקציות רציונליות.

סיכום ביניים קצרצר, למי שרוצים רק את השורה התחתונה

הנה מה שראינו, עבור פונקציה רציונלית כללית \( \frac{p\left(x\right)}{q\left(x\right)} \):

1. האסימפטוטות האנכיות עשויות להתקבל רק בנקודות מהצורה \( x=a \) כאשר \( a \) הוא שורש של \( q\left(x\right) \), כלומר \( q\left(a\right)=0 \). אם \( q\left(a\right)=0 \) זה עדיין לא מבטיח שיש שם אסימפטוטה אנכית; אם \( p\left(a\right)\ne0 \) אז קיום האסימפטוטה האנכית מובטח, ואחרת צריך לחלק גם את \( p\left(x\right) \) וגם את \( q\left(x\right) \) ב-\( \left(x-a\right) \) ולנסות שוב.
2. אסימפטוטות אופקיות מתקבלות אם מעלת \( q\left(x\right) \) גדולה ממעלת \( p\left(x\right) \) ואז האסימפטוטה היא \( y=0 \), או אם \( p\left(x\right),q\left(x\right) \) שניהם מאותה מעלה, ובמקרה זה האסימפטוטה תהיה \( y=\frac{a_{n}}{b_{n}} \) כאשר \( a_{n} \) המקדם המוביל של \( p\left(x\right) \) ו-\( b_{n} \) המקדם המוביל של \( q\left(x\right) \). בכל המקרים האסימפטוטה שמוצאים תקפה גם עבור \( x\to\infty \) וגם עבור \( x\to-\infty \).

בסופו של דבר כל הדיון הארוך הזה הצטמצם לשני כללים פשוטים ממש! האם לא יכלתי לתת את הכללים הללו מראש וחסל? יכלתי, אבל איפה הכיף כאן? המטרה שלי היא שנבין מאיפה הכללים הללו באים ואולי נוכל לשחזר אותם בעצמנו, במקרה הצורך.

בפוסט הבא יתחילו הצרות האמיתיות - ננסה להבין איך נראות האסימפטוטות של פונקציות מסובכות יותר (ספוילר: אי אפשר להגיד יותר מדי דברים שאינם בסיסיים ממש), ואנסה להסביר קצת יותר את הפורמליזם של מה שעשינו פה.