טומוגרפיה קוונטית: איך מגלים מה כבר יש לנו?

בפוסט הקודם שלי הצגתי את מה שקראתי לו “פורמליזם מטריצת הצפיפות” ולפני שאני ממשיך לדבר עליו - ספציפית, על השינויים שהוא יכול לעבור - אני רוצה לעצור ולהציג נושא שישתמש באופן ישיר בפורמליזם הזה והוא די מגניב בזכות עצמו: טומוגרפיית מצבים קוונטית (Quantum State Tomography).

דבר אחד שאני מקווה שהדגשתי בסדרת הפוסטים עד כה הוא שמדידה של מצב קוונטי הורסת את המצב הקוונטי. משמידה אותו. חורבן. הרס. אם הייתי במצב \( \left|+\right\rangle \) ומדדתי מדידה “רגילה”, בבסיס \( Z \) (כלומר, מדידה שמתאימה לאיברים \( \left\{ \left|0\right\rangle ,\left|1\right\rangle \right\} \)), אז זהו, אני כבר לא ב-\( \left|+\right\rangle \). אני או ב-\( \left|0\right\rangle \) או ב-\( \left|1\right\rangle \). אם הייתי במצב כללי \( \alpha\left|0\right\rangle +\beta\left|1\right\rangle \) ומדדתי בבסיס \( Z \) , אז זהו. אני או ב-\( \left|0\right\rangle \) או ב-\( \left|1\right\rangle \) וזהו. המקדמים \( \alpha,\beta \) נעלמו ואינם עוד.

גרוע מכך - מדידה אחת פשוט לא יכולה ללמד אותי מהם \( \alpha,\beta \). אם קיבלתי \( \left|0\right\rangle \) אני יכול לדעת ש-\( \alpha\ne0 \) אבל לא יותר מכך. באלגוריתמים הקוונטיים שהצגתי עד כה, כולל האלגוריתם של שור, לא התעניינו בערכים של האמפליטודות; רק ניסינו לבצע עליהם מניפולציות כדי להבטיח שבהסתברות גבוהה התוצאה הסופית תהיה כזו שעוזרת לנו.

אבל העניין הוא… שקצת שיקרתי. בהחלט אפשר לחשב את ה-\( \alpha,\beta \) הללו מתוך המצב הקוונטי, וזאת בתנאי שיש לנו מספר עותקים שלו. כמה עותקים בדיוק - את זה נראה בקרוב. עכשיו, אפשר לטעון ובצדק שאי אפשר לשכפל מצב קוונטי (יש משפט כזה! No Cloning Theorem!) ולכן אני לא יכול סתם לקחת מצב קוונטי, לשכפל אותו ואז להשתמש בשיטה הקסומה שאני הולך להציג פה. זה נכון לגמרי; אבל אם המצב הקוונטי נוצר כתוצאה של תהליך מסוים, אני יכול לחזור על התהליך הזה שוב ושוב ולקבל את אותו מצב שוב ושוב. זה מה שהרצה פרקטית של אלגוריתם במחשב קוונטי עושה גם ככה: מריצה את אותו אלגוריתם מספר פעמים גדול (נאמר, 1,000?) על המחשב ויוצרת סטטיסטיקה של תוצאות.

כמובן, אפשר לשאול ובצדק - אם אנחנו אלו שמייצרים את המצב, האם זה לא אומר שאנחנו יודעים לאיזה מצב הגענו? ובכן, לא! משתי סיבות. ראשית, כי אני לא מניח שאנחנו יודעים לחשב מה המצב גם אם יש לנו מעגל קונקרטי שמייצר אותו - אולי החישוב המלא של מה שהמעגל עושה הוא מסובך? אולי יש בתוך המעגל אלמנטים שאנחנו יכולים לשלוט עליהם אבל אנחנו לא יודעים מה הם בדיוק עושים? ושנית, באופן די דומה למה שכבר אמרתי, במעגלים קוונטיים יש בעיה של רעשים והתנהגויות לא צפויות. ייתכן שאנחנו חושבים~שאנחנו מייצרים את \( \left|+\right\rangle \) אבל עקב שגיאות במימוש של המחשב הקוונטי אנחנו תמיד מקבלים את \( \left|-\right\rangle \) - זה בהחלט משהו שהיינו רוצים להיות מסוגלים לזהות. בפועל, זה אכן שימוש מרכזי של טומוגרפיה קוונטית - בדיקה שהמחשב אכן מתנהג כפי שאנו מצפים שיתנהג, והערכה של רמת הרעש שיש בו.

אם כן, הבה ונאמר שיש לנו מצב קוונטי ואנחנו מסוגלים לשחזר שוב ושוב במדויק את התהליך שיוצר אותו. ואנחנו מודדים אותו 1,000 פעם בבסיס \( Z \) ומקבלים 483 פעם “0” ו-517 פעם “1”. מה זה אומר על המצב שבו אני נמצא? אם אני ב-\( \left|+\right\rangle =\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} \) ומודד 1,000 פעמים בהחלט ייתכן שאקבל את התפלגות התוצאות הזו, אבל גם אם אני במצב \( \sqrt{\frac{483}{1000}}\left|0\right\rangle +\sqrt{\frac{517}{1000}}\left|1\right\rangle \) זה ייתכן. כלומר, יש לנו בעיה כבר עם עצם זה שלחזור שוב ושוב על אותו ניסוי ולספור תוצאות לא נותן לנו את ההסתברויות שהובילו אליהן. אבל זו אפילו לא הבעיה המרכזית לבינתיים!

אז בואו נניח לצורך הדיון שאיכשהו המדידות שלי מושלמות ואני מצליח לגלות בצורה מדויקת את ההסתברויות לכל התוצאות, כלומר אם המצב שלי הוא \( \left|+\right\rangle \) אני מקבל את וקטור ההסתברויות \( \overline{p}=\left(\begin{array}{c} 0.5\\ 0.5 \end{array}\right) \). מה הבעיה כאן? שגם אם המצב שלי הוא \( \left|-\right\rangle \) אני אקבל את אותו וקטור הסתברויות בדיוק. מדידה בבסיס \( Z \) פשוט לא מסוגלת להבדיל בין שני המצבים הללו. אני אקבל את אותה סטטיסטיקה בדיוק. אז מה עושים?

למרבה המזל, יש עוד מדידות בעולם חוץ ממדידה בבסיס \( Z \). למשל, מדידה בבסיס \( X \), שאבריה הם \( \left\{ \left|+\right\rangle ,\left|-\right\rangle \right\} \). מדידה כזו בוודאי יכולה להפריד בין \( \left|+\right\rangle \) (שיחזיר וקטור הסתברויות \( \left(\begin{array}{c} 1\\ 0 \end{array}\right) \)) ובין \( \left|-\right\rangle \) (שיחזיר וקטור הסתברויות \( \left(\begin{array}{c} 0\\ 1 \end{array}\right) \)). אלא מה? מדידה בבסיס \( X \) לא מסוגלת להבדיל בין \( \left|0\right\rangle ,\left|1\right\rangle \) ששניהם מחזירים \( \overline{p}=\left(\begin{array}{c} 0.5\\ 0.5 \end{array}\right) \) - אותה בעיה כמו קודם.

האם צריך להתייאש? בוודאי שלא! המסקנה צריכה להיות חיובית - אולי בסיס מדידה אחד הוא לא הפתרון, אבל שילוב של מידע מכמה מדידות שונות יאפשר לשחזר את המצב בודאות. מכאן מגיע השם של השיטה שאציג - טומוגרפיה קוונטית. בעולם האמיתי, “טומוגרפיה” הוא שם של טכניקה בתחומים רבים ושונים שמאפשרת לשחזר מידע על אובייקט מורכב (חומרים, איברים בגוף וכו’) על ידי מדידה של “חתכים” שלו. כאן צריך לחשוב על מדידה בבסיס ספציפי (שנותנת הסתברויות) בתור “חתך” שכזה. אבל כמה חתכים צריך? כמה מידע צריך לשחזר?

בואו נסבך קצת יותר את הסיטואציה. מה אם התהליך שמייצר את המצב הקוונטי שלנו איננו דטרמיניסטי, למרות שהוא בעל חוקיות ברורה? למשל: התהליך קודם מייצר את המצב \( \left|+\right\rangle \), ואז התהליך עצמו מודד אותו בבסיס \( Z \) וכמובן שלא מספר לנו מה התוצאה. זה אומר שהמצב הקוונטי שאנחנו מנסים לבצע לו טומוגרפיה הוא \( \left|0\right\rangle \) בהסתברות \( \frac{1}{2} \) ו-\( \left|1\right\rangle \) בהסתברות \( \frac{1}{2} \). מדידה בבסיס \( Z \) תיתן לנו את וקטור ההסתברויות \( \left(\begin{array}{c} 0.5\\ 0.5 \end{array}\right) \) וגם מדידה בבסיס \( X \) תיתן לנו את אותו וקטור הסתברויות - סיטואציה שונה מאלו שראינו קודם, שממחישה שכשאנחנו משחזרים מצב, אנחנו לא רוצים לשחזר וקטור אלא מטריצה - את מטריצת הצפיפות שמתארת את המצב. כלומר, אם אנחנו מתעסקים עם מצב של קיוביט יחיד, אנחנו רוצים לשחזר מטריצה \( \rho=\left(\begin{array}{cc} \alpha & \beta\\ \gamma & \delta \end{array}\right) \).

עכשיו, כשדיברנו על מטריצות צפיפות ראינו ש-\( \text{tr}\rho=1 \), כלומר \( \alpha+\delta=1 \), מה שאומר שאפשר להסיק את \( \delta \) מתוך \( \alpha \). נשארו לנו שלושה פרמטרים שצריך להסיק - שלוש “דרגות חופש” של המטריצה. האינטואיציה שלנו מאלגברה לינארית אולי אומרת לנו שצריך, אם כן, מערכת של שלוש משוואות לינאריות שמערבת את \( \rho \) איכשהו, וזה במקרה הממוזל שבכלל אפשר להסיק את \( \rho \) ממערכת משוואות לינארית שכזו. זה מה שיפה כאן - בתנאים האידאליים שלנו (שבהם וקטורי ההסתברויות נתונים לנו במדויק) זה אכן כל מה שצריך, פתרון של מערכת משוואות לינארית. אבל איזו?

כזכור מהפוסט הקודם על מטריצות צפיפות, אם אני במצב \( \rho \) ואני מודד אותו עם קבוצת אופרטורי מדידה כלשהי, אז ההסתברות ש-\( M_{i} \) יעלה בגורל היא \( p\left(i\right)=\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right) \). זו אחלה משוואה בזכות עצמה, אבל אם רוצים לפשט אותה קצת, אפשר לעבור שוב ללשון של וקטורים. על מטריצה \( A \) מסדר \( n\times m \) קל מאוד לחשוב בתור וקטור מאורך \( n\cdot m \): נאמר, וקטור שמכיל קודם כל את אברי השורה הראשונה של \( A \), ואז השורה השניה וכן הלאה; או העמודה הראשונה של \( A \) ואז העמודה השניה וכן הלאה. אני אלך לפי הקונבנציה שלוקחים את השורות בזו אחר זו, אבל שתי הגישות נפוצות ואין עדיפות עקרונית לאחת מהן.

אם כן, אם אם \( A \) היא מטריצה מסדר \( n\times m \), אני אסמן ב-\( \left|\left.A\right\rangle \right\rangle \) את וקטור העמודה מאורך \( n\cdot m \) שאבריו לפי הסדר הם \( a_{11},\ldots,a_{1m},a_{21},\ldots,a_{nm} \). הנה דוגמא קונקרטית עבור מטריצת \( 2\times3 \):

\( A=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{array}\right) \)

במקרה הזה נקבל

\( \left|\left.A\right\rangle \right\rangle =\left(\begin{array}{cccccc} a_{11} & a_{12} & a_{13} & a_{21} & a_{22} & a_{23}\end{array}\right)^{T} \)

עכשיו, כמו שהגדרתי בשעתו \( \left\langle \psi\right|=\left(\left|\psi\right\rangle \right)^{\dagger} \) אני יכול להגדיר גם \( \left\langle \left\langle A\right.\right|=\left(\left|\left.A\right\rangle \right\rangle \right)^{\dagger} \), ואז אני מקבל את השוויון היפה

\( \left\langle \left\langle A\right.\right|\left|\left.B\right\rangle \right\rangle =\text{tr}\left(A^{\dagger}B\right) \)

קל לבדוק שזה אכן מתקיים:

\( \text{tr}\left(A^{\dagger}B\right)=\sum_{k=1}^{m}\left[A^{\dagger}B\right]_{kk}=\sum_{k=1}^{m}\sum_{i=1}^{n}\left[A^{\dagger}\right]_{ki}\left[B\right]_{ik}= \)

\( =\sum_{k=1}^{m}\sum_{i=1}^{n}\overline{\left[A\right]_{ik}}\left[B\right]_{ik}=\left\langle \left\langle A\right.\right|\left|\left.B\right\rangle \right\rangle \)

שימו לב שהמעבר האחרון לא כל כך מתעניין בשאלה אם האופן שבו \( A,B \) הפכו לוקטור היה לפי שורות, עמודות, או כל סדר אחר; לכן הבחירה שלי ללכת על פי שורות היא קונבנציה ולא משהו קריטי.

אגב, לא נכנסתי לפרטים הללו כאן, אבל \( \text{tr}\left(A^{\dagger}B\right) \) מגדיר לנו מכפלה פנימית על המרחב הוקטורי של המטריצות מהסדר המתאים; זו לא פעולה אקראית שצצה משום מקום. בהקשר שלנו, \( \text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right) \) זה הערך שמעניין אותנו, ואנחנו יכולים לנצל את זה ש-\( \left(M_{i}^{\dagger}M_{i}\right)^{\dagger}=M_{i}^{\dagger}M_{i} \) כדי לכתוב

\( p\left(i\right)=\left\langle \left\langle M_{i}^{\dagger}M_{i}\right.\right|\left|\left.\rho\right\rangle \right\rangle \)

למעשה, כדי לפשט עניינים, נוח לסמן \( E_{i}=M_{i}^{\dagger}M_{i} \) ולעבור לתאר מדידות עם ה-\( E_{i} \)-ים הללו, שמקיימים \( \sum E_{i}=I \) וכל \( E_{i} \) הוא מטריצה חיובית (במובן שתיארתי בפוסט הקודם: \( \left\langle \psi\right|E_{i}\left|\psi\right\rangle >0 \) לכל \( \left|\psi\right\rangle \ne0 \)). אפשר לעשות את ההפך, להתחיל מסט של אופרטורים שמקיימים את שתי התכונות הללו ולהסיק ממנו \( M_{i} \)-ים שנותנים לנו מדידה; הפורמליזם שבו עובדים עם ה-\( E_{i} \)-ים נקרא פורמליזם ה-POVM (ראשי תיבות של Positive Operator Valued Measurements), אבל אני לא נכנס לעובי הקורה הזה.

סיכום ביניים: אם יש לי מדידה עם אופרטור מתאים \( E_{i} \), אני מקבל

\( p\left(i\right)=\left\langle \left\langle E_{i}\right.\right|\left|\left.\rho\right\rangle \right\rangle \)

את הפעולה הזו אפשר לתאר בתור כפל של השורה \( \left\langle \left\langle E_{i}\right.\right| \) בעמודה \( \left|\left.\rho\right\rangle \right\rangle \), והיא מתאימה לתוצאה אפשרית אחת של מדידה אפשרית אחת של \( \rho \). אני יכול לאסוף בצורה הזו הרבה שורות, שמתאימות למדידות שונות, ולקבל מטריצה \( M \), ואז יש לי את מערכת המשוואות

\( M\left|\left.\rho\right\rangle \right\rangle =\vec{p} \)

כאשר \( \vec{p} \) הוא וקטור ההסתברויות: וקטור של סקלרים, שבו הכניסה ה-\( i \) מתאימה למדידה על פי האופרטור שרשום בשורה ה-\( i \) של \( M \).

כל זה מתוסבך נורא, אז בואו נראה דוגמא קונקרטית עבור המקרה של קיוביט בודד. כבר דיברתי על מדידה של קיוביט בבסיסים \( Z,X \) שנגזרים מאופרטורי פאולי \( X,Z \); אני אזכיר איך בדיוק הם נגזרים, ואעשה את אותו דבר בדיוק גם עבור \( Y \).

נתחיל עם \( X=\left(\begin{array}{cc} 0 & 1\\ 1 & 0 \end{array}\right) \). הרעיון הוא שבגלל שזה אופרטור הרמיטי, קיים לו פירוק ספקטרלי, כלומר שאפשר לכתוב \( X=\sum\lambda P_{\lambda}^{X} \): צירוף לינארי שהמקדמים \( \lambda \) שלו הם הערכים העצמיים השונים של \( X \) ו-\( P_{\lambda}^{X} \) הוא אופרטור ההטלה למרחב העצמי שמתאים ל-\( \lambda \). עבור \( X \) (וגם עבור \( Y,Z \)) הערכים העצמיים הם \( \pm1 \) ולכן מקבלים

\( X=1\cdot P_{1}^{X}+\left(-1\right)\cdot P_{-1}^{X} \)

בדיקה זריזה מעלה ש-

\( P_{1}^{X}=\frac{1}{2}\left(\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right),P_{-1}^{X}=\frac{1}{2}\left(\begin{array}{cc} 1 & -1\\ -1 & 1 \end{array}\right) \)

עבור \( Y=\left(\begin{array}{cc} 0 & -i\\ i & 0 \end{array}\right) \) נקבל

\( P_{1}^{Y}=\frac{1}{2}\left(\begin{array}{cc} 1 & -i\\ i & 1 \end{array}\right),P_{-1}^{Y}=\frac{1}{2}\left(\begin{array}{cc} 1 & i\\ -i & 1 \end{array}\right) \)

ועבור \( Z=\left(\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}\right) \) נקבל

\( P_{1}^{Z}=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right),P_{-1}^{Z}=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \)

ה-\( P \)-ים הללו הם ה-\( M_{i} \)-ים בשיטת הכתיב הקודמת שלי, כך שאנחנו רוצים לקבל מהם את \( E_{i}=M_{i}^{\dagger}M_{i} \), אבל מכיוון שאלו אופרטורים הרמיטיים (כלומר \( M_{i}^{\dagger}=M_{i} \)) והטלות (כלומר \( M_{i}^{2}=M_{i} \)) נקבל בדיוק את אותם אופרטורים. אז כדי לבנות את המטריצה \( M \) שדיברתי עליה צריך לעשות שני דברים: לפרוש אותם לשורה אחת ארוכה כל אחד, ולהצמיד את האיברים (כי כזכור, \( \left\langle \left\langle E_{i}\right.\right| \) מסמל את \( \left(\left|\left.E_{i}\right\rangle \right\rangle \right)^{\dagger} \)). לכן \( P_{1}^{Y} \) יהפוך אל \( \left(\begin{array}{cccc} \frac{1}{2} & -\frac{i}{2} & \frac{i}{2} & \frac{1}{2}\end{array}\right) \) אחרי השיטוח ואל \( \left(\begin{array}{cccc} \frac{1}{2} & \frac{i}{2} & -\frac{i}{2} & \frac{1}{2}\end{array}\right) \) אחרי ההצמדה. בסך הכל נקבל את המטריצה

\( M=\left(\begin{array}{cccc} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{i}{2} & -\frac{i}{2} & \frac{1}{2}\\ \frac{1}{2} & -\frac{i}{2} & \frac{i}{2} & \frac{1}{2}\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right) \)

עכשיו, הרעיון הוא כזה: יש לנו מצב קוונטי \( \rho \) שאנחנו לא יודעים מהו. אנחנו מודדים אותו בבסיסים \( X,Y,Z \) ומקבלים התפלגות של תוצאות. לכל בסיס אנחנו מקבלים שתי תוצאות, אחת לכל אחד מהערכים העצמיים (שתי התוצאות הללו מסתכמות ל-1, אז הן לא בלתי תלויות זו בזו). את התוצאות הללו אנחנו מכניסים לוקטור \( \vec{p} \), ואז אנחנו מקבלים מערכת משוואות לינארית:

\( M\left|\left.\rho\right\rangle \right\rangle =\vec{p} \)

כאן \( M,\vec{p} \) ידועים ו-\( \left|\left.\rho\right\rangle \right\rangle \) הוא הנעלם שאנחנו רוצים לשחזר. איך פותרים מערכת משוואות לינארית? בדרך כלל מחשבים את \( M^{-1} \) וכופלים בה את שני האגפים ומקבלים \( \left|\left.\rho\right\rangle \right\rangle =M^{-1}\vec{p} \), אלא שזה פשוט לא יכול לעבוד כאן, כי \( M \) גדולה מדי - היא לא מטריצה ריבועית. יש לה רק ארבע עמודות, אבל שש שורות. אפשר, כמובן, להסיר חלק מהשורות הללו, אבל אפשר גם לעשות משהו אחר.

כאמור, \( M \) היא לא מטריצה ריבועית, אבל \( M^{\dagger}M \) היא כן מטריצה ריבועית, ובתקווה היא גם הפיכה (במקרה שלנו היא אכן יוצאת הפיכה; אם היא לא יוצאת הפיכה זה אומר שבחרנו למדוד את \( \rho \) בשילוב בסיסים שהוא לא מלא טומוגרפית - אי אפשר להשתמש בו בשביל טומוגרפיה). ועכשיו תראו איזה קסם אני עושה. אני מתחיל עם \( M\left|\left.\rho\right\rangle \right\rangle =\vec{p} \), כופל את שני האגפים ב-\( M^{\dagger} \) ומקבל \( M^{\dagger}M\left|\left.\rho\right\rangle \right\rangle =M^{\dagger}\vec{p} \), ואז אני כופל בהופכית של \( M^{\dagger}M \) ומקבל:

\( \left|\left.\rho\right\rangle \right\rangle =\left(M^{\dagger}M\right)^{-1}M^{\dagger}\vec{p} \)

וכך אני מצליח לשחזר את \( \rho \) המקורית!

בואו נראה איך זה עובד בפועל. אם תחשבו, תקבלו ש-

\( M^{\dagger}M=\left(\begin{array}{cccc} 2 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 2 \end{array}\right) \)

ההופכית שלה היא

\( \left(M^{\dagger}M\right)^{-1}=\left(\begin{array}{cccc} \frac{2}{3} & 0 & 0 & -\frac{1}{3}\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ -\frac{1}{3} & 0 & 0 & \frac{2}{3} \end{array}\right) \)

ולכן מקבלים בסוף

\( \left(M^{\dagger}M\right)^{-1}M^{\dagger}=\left(\begin{array}{cccccc} \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{2}{3} & -\frac{1}{3}\\ \frac{1}{2} & -\frac{1}{2} & -\frac{i}{2} & \frac{i}{2} & 0 & 0\\ \frac{1}{2} & -\frac{1}{2} & \frac{i}{2} & -\frac{i}{2} & 0 & 0\\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & -\frac{1}{3} & \frac{2}{3} \end{array}\right) \)

זו המטריצה הקסומה שכשכופלים אותה בוקטור ההסתברויות \( \vec{p} \) שקיבלנו מהניסוי, משחזרים את המצב \( \rho \) המקורי. בואו ננסה למשל לשחזר את \( \rho \) שמתאר את הסיטואציה שבה אנחנו ב-\( \left|0\right\rangle ,\left|1\right\rangle \) בהסתברות חצי-חצי. אנחנו כבר יודעים שתוצאות המדידה בבסיס \( X \) הולכות להיות \( \left(\frac{1}{2},\frac{1}{2}\right) \) בגלל שלא משנה אם אנחנו ב-\( \left|0\right\rangle \) או ב-\( \left|1\right\rangle \), מדידה בבסיס \( X \) מתפלגת חצי-חצי עבור שני המצבים הללו. בנוסף אנחנו יודעים שגם המדידה בבסיס \( Z \) הולכת להיות \( \left(\frac{1}{2},\frac{1}{2}\right) \) מסיבה שונה: אם אנחנו ב-\( \left|0\right\rangle \) אז המדידה תחזיר בודאות \( \left|0\right\rangle \) אבל אנחנו ב-\( \left|0\right\rangle \) רק בהסתברות \( \frac{1}{2} \) מראש. מה שעוד לא דיברתי עליו הוא מה קורה במדידה בבסיס \( Y \), אבל חישוב עם הנוסחה \( p\left(i\right)=\left\langle \psi\right|E_{i}\left|\psi\right\rangle \) מראה שגם במקרה זה, לא משנה אם אנחנו ב-\( \left|0\right\rangle \) או ב-\( \left|1\right\rangle \), ההסתברות לכל תוצאה היא \( \frac{1}{2} \). לכן בסך הכל

\( \vec{p}=\left(\begin{array}{c} \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2} \end{array}\right) \)

עכשיו נחשב ונקבל

\( \left(M^{\dagger}M\right)^{-1}M^{\dagger}\vec{p}=\left(\begin{array}{c} \frac{1}{2}\\ 0\\ 0\\ \frac{1}{2} \end{array}\right) \)

וכשמשחזרים מזה את המטריצה המקורית מקבלים \( \left(\begin{array}{cc} \frac{1}{2} & 0\\ 0 & \frac{1}{2} \end{array}\right) \), כפי שציפינו.

מה אם במקום זה היינו במצב \( \left|+\right\rangle \) בהתחלה? כזכור, זה משפיע על המדידות בבסיס \( X \) שיוצאות \( \left(\begin{array}{c} 1\\ 0 \end{array}\right) \), אבל אם עושים את החישובים עבור בסיסים \( Y,Z \) עדיין מקבלים חצי חצי, כלומר וקטור ההסתברויות במקרה זה הוא

\( \left(\begin{array}{c} 1\\ 0\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2} \end{array}\right) \)

ועכשיו מקבלים:

\( \left(M^{\dagger}M\right)^{-1}M^{\dagger}\vec{p}=\left(\begin{array}{c} \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2}\\ \frac{1}{2} \end{array}\right) \)

כלומר \( \rho=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right) \) כמו שציפינו לקבל.

יפה, אז אנחנו רואים שאפשר לבצע את הקסם של שיחזור \( \rho \) מתוך מדידות, אבל איך מבצעים את המדידות הללו? כמובן, אם אנחנו אלו שמתעסקים במחשב הקוונטי ברמת המימוש (או בניסוי הקוונטי שעושים; טומוגרפיה קוונטית לא חייבת להיות של מצב במחשב קוונטי) אנחנו אולי יכולים לממש סוגים שונים של מדידות. אבל נאמר שאנחנו עובדים עם מחשב קוונטי שיודע למדוד רק בבסיס \( Z \), האם יש דרך לבצע מדידות גם בבסיסים אחרים?

ובכן, יש. בואו ניזכר במשהו שכבר הראיתי פעם-פעמיים, עבור המטריצה \( H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right) \):

\( H^{\dagger}ZH=X \)

אפשר לראות את זה על ידי חישוב מפורש. זה כמובן עובר לרמת ההטלות:

\( X=H^{\dagger}ZH=H^{\dagger}\left(P_{1}^{Z}-P_{-1}^{Z}\right)H=H^{\dagger}P_{1}^{Z}H-H^{\dagger}P_{-1}^{Z}H \)

ומכאן אפשר להסיק שלכל מצב \( \left|\psi\right\rangle \) מתקיים

\( \left\langle \psi\right|P_{\lambda}^{X}\left|\psi\right\rangle =\left\langle \psi\right|H^{\dagger}P_{1}^{Z}H\left|\psi\right\rangle =\left\langle H\psi\right|P_{1}^{Z}\left|H\psi\right\rangle \)

כלומר, אפשר להמיר מדידה בבסיס \( X \) של \( \left|\psi\right\rangle \) במדידה בבסיס \( Z \) של \( H\left|\psi\right\rangle \) - התפלגות התוצאות שנקבל תהיה זהה. זה באמת מה שעושים במחשב קוונטי - מעגל אחד שפשוט מייצר את המצב הקוונטי עבור מדידה בבסיס \( Z \), מעגל אחר שמייצר את המצב הקוונטי ואז מפעיל עליו \( H \) עבור מדידה בבסיס \( X \). ומה עם בסיס \( Y \)? ובכן, \( SXS^{\dagger}=Y \) עבור \( S=\left(\begin{array}{cc} 1 & 0\\ 0 & i \end{array}\right) \), ולכן \( \left(HS^{\dagger}\right)^{\dagger}Z\left(HS^{\dagger}\right)=Y \), ומכאן שכדי למדוד בבסיס \( Y \) קודם מפעילים על המצב \( S^{\dagger} \), אחר כך מפעילים עליו \( H \) ואז מודדים בבסיס \( Z \) כרגיל.

כל הדיון עד כה התעסק בסיטואציה של קיוביט בודד. אבל מה אם \( \rho \) הוא מצב של מערכת על \( n \) קיוביטים? נתחיל מ-\( n=2 \). במקרה הזה, אנחנו מסתכלים על כל הזוגות \( \left(P_{1},P_{2}\right) \) כאשר \( P_{i}\in\left\{ X,Y,Z\right\} \) - בסך הכל תשעה זוגות כאלו. כל זוג מגדיר לנו מעגל אחר עם מדידות אחרות. למשל, \( \left(X,Y\right) \) פירושו “למדוד את הקיוביט הראשון בבסיס \( X \) ואת השני בבסיס \( Y \)”, כששתי המדידות הללו מבוצעות בצורה שתיארתי זה עתה. מה שמתקבל הוא 4 תוצאות מדידה אפשריות: \( 00,01,10,11 \), שכל אחת נותנת לנו הסתברות אחרת ותקבל שורה משלה בוקטור \( \vec{p} \) - כלומר, זה יהיה וקטור עם 36 כניסות. עבור \( n \) כללי, אנחנו מסתכלים על כל ה-\( n \)-יות \( \left(P_{1},\ldots,P_{n}\right) \) כאשר \( P_{i}\in\left\{ X,Y,Z\right\} \). יש בסך הכל \( 3^{n} \) \( n \)-יות כאלו וכל \( n \)-יה כזו מגדירה \( 2^{n} \) תוצאות מדידה אפשריות… כפי שאפשר לראות, זה גדל אקספוננציאלית. זה אומר שבפועל, טומוגרפיה הופכת למשהו בלתי יישים בעליל עבור יותר ממספר זעיר של קיוביטים; מה שעושים בפועל הוא טומוגרפיה רק לחלק מהקיוביטים במערכת במקום לכולם.

הנה למשל מעגל טומוגרפיה על שני קיוביטים שקודם כל מייצר את המצב השזור \( \frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \) (או, אם לחדד את הפואנטה מאחורי טומוגרפיה קוונטית, קודם מנסה ליצור את המצב הזה, ומטרת הטומוגרפיה היא לראות כמה הוא הצליח בזה) ולאחר מכן מודד את הקיוביט הראשון בבסיס \( X \) ואת השני בבסיס \( Y \):

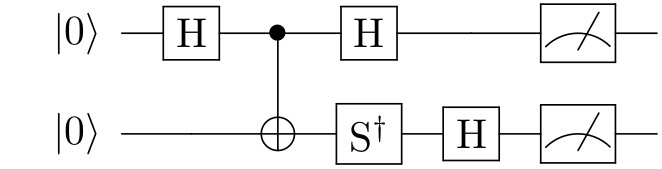
לסיום, אי אפשר לוותר על רגע ה”כל מה שאמרתי לכם עד כה היה שקר גמור” הבלתי נמנע. כלומר, לא שיקרתי בשום צורה, אבל כן הזנחתי את העניין המרכזי. אי שם בתחילת הפוסט אמרתי שבואו נניח לצורך פשטות שיש לי את הערכים המדויקים של \( \vec{p} \), שזה נחמד אבל זה לא משהו שהולך להתקבל בניסוי. בניסוי אני לא אקבל \( \frac{1}{2} \) אלא זוועה כמו \( \frac{483}{1000} \). בסיטואציה כזו, הוקטור \( \vec{p} \) שקיבלתי הוא לא מדויק; שיטת היפוך המטריצה שהצגתי לא רק שלא תחזיר את \( \rho \) הנכונה אלא רק קירוב שלה (את זה אפשר לסבול, בכל מקרה אנחנו לא מצפים לדיוק מוחלט), אבל גרוע מזה - סביר להניח שהיא תחזיר \( \rho \) שאינה מטריצת צפיפות, כלומר אינה בעלת עקבה 1 או שאינה חיובית. זו כבר בעיה משמעותית יותר - בדרך כלל אנחנו רוצים שטומוגרפיה תחזיר לנו מצב קוונטי שהוא קירוב של המצב האמיתי, לא שתחזיר לנו קירוב שאיננו אמיתי.

זה אומר שנוקטים בשיטת פתרון אחרת, שנעזרת בכלים סטנדרטיים של אופטימיזציה: מה שאנחנו רוצים הוא להביא למינימום את הביטוי

\( \|M\left|\left.\rho\right\rangle \right\rangle -\vec{p}\| \)

כאשר אברי \( \left|\left.\rho\right\rangle \right\rangle \) הם המשתנים של בעיית האופטימיזציה, והם כפופים לאילוצים נוספים שמבטיחים ש-\( \rho \) תהיה מטריצת צפיפות תקינה. חשבתי להיכנס כאן לעובי הקורה של איך עושים את זה, ואולי אעשה את זה בהמשך, אבל נראה לי שעדיף לשמור על הפוסט הזה ממוקד יחסית.

עוד בעיה שצריך להביא בחשבון היא שחישוב קוונטי הוא תהליך רועש. זה אומר שבביצוע תהליך המדידה עצמה עשויות להצטבר בעיות; וגרוע לא פחות - גם בשערי ה-\( H \) וה-\( S^{\dagger} \) שאנחנו משתמשים בהם כדי למדוד בבסיסים שונים גם כן עשויות להצטבר בעיות. מה שהיינו רוצים הוא שיטת טומוגרפיה שאיכשהו מביאה את זה בחשבון, ואמנם יש כזו (במחיר של סיבוכיות הרבה יותר גדולה של מה שהיא עושה) שנקראת Gate Set Tomography, אבל לפני שאדבר עליה צריך לחזור אל השאלה שבה סיימתי את הפוסט הקודם - איך בעצם ממדלים שינויים שיכולים להתבצע על מערכת קוונטית, וספציפית איך ממדלים רעשים?