חישוב קוונטי: פורמליזם מטריצות הצפיפות

מה זה מטריצות צפיפות ואיך מגיעים אליהן מוקטורי מצב?

בואו נדבר על סיטואציה פשוטה מאוד בחישוב קוונטי שכבר ראינו כמה פעמים בסדרת הפוסטים הזו: יש לנו את המצב הקוונטי על קיוביט בודד \( \left|+\right\rangle =\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} \) ואנחנו מודדים אותו. מה קורה? קורים שני דברים: אנחנו, המודדים, מקבלים “החוצה” ביט של מידע - או 0 או 1 - והמצב הקוונטי עובר שינוי: אם ביט המידע שקיבלנו היה \( 0 \) אז המצב הקוונטי הופך להיות \( \left|0\right\rangle \), ואם ביט המידע שקיבלנו היה 1 אז המצב הקוונטי הופך להיות \( \left|1\right\rangle \). כל אחת מהתוצאות הללו מתקבלת באותה הסתברות, כלומר \( \frac{1}{2} \).

טוב ויפה, אבל עכשיו נניח שאנחנו לא אלו שמודדים את המצב; אנחנו רואים מישהי אחרת באה ומודדת את המצב, ולא מגלה לנו מה התוצאה! מה אנחנו כן יכולים להגיד על המצב הנוכחי של הקיוביט? ובכן, בדיוק את מה שראינו לפני רגע: אנחנו יכולים לומר “בהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|0\right\rangle \) ובהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|1\right\rangle \)”.

אחד הדברים המבלבלים והקשים ביותר להבנה כשמתחילים לדבר על חישוב קוונטי (ואולי על תורת הקוונטים בפרט?) הוא להבין שלומר “הקיוביט במצב \( \left|+\right\rangle \)” זה ממש לא אותו דבר כמו לומר “בהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|0\right\rangle \) ובהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|1\right\rangle \)”. הראשון הוא כמו לומר “החתול של שרדינגר בסופרפוזיציה של רגוע ועצבני” והשני הוא כמו לומר “החתול של שרדינגר רגוע או עצבני, אנחנו פשוט לא יודעים מי מהם כי עדיין לא פתחנו את הקופסה”. עד סוף הפוסט, אולי אפילו עד האמצע שלו, כבר נראה את ה”ממש לא אותו דבר” הזה במלוא הפורמליזם המתמטי שלו - פורמליזם שעד כה טרם הצגתי, כי לא נזקקתי לו אבל אני רוצה להתחיל לדבר על דברים שמערבים אותו: פורמליזם מטריצת הצפיפות.

הרעיון במטריצת צפיפות הוא להכליל את האופן שבו אנחנו מתארים מצב של מערכת קוונטית. עד כה השתמשנו בוקטור כדי לתאר אותה: כך למשל \( \left|+\right\rangle \) הוא הוקטור \( \frac{1}{\sqrt{2}}\left(\begin{array}{c} 1\\ 1 \end{array}\right) \). בפורמליזם של מטריצות צפיפות, מה שמתאר את המצב של המערכת הקוונטית יהיה מטריצה: אם כדי לתאר מצב קוונטי על \( n \) קיוביטים נזקקנו לוקטור מאורך \( 2^{n} \), הרי שבשביל מטריצת צפיפות נזדקק למטריצה מסדר \( 2^{n}\times2^{n} \). הגודל הנוסף הזה מאפשר לנו לכלול יותר מידע מאשר קודם; הוא מאפשר לנו בדיוק לתאר בצורה קומפקטית סיטואציה של “בהסתברות כך וכך המערכת נמצאת במצב כך וכך”, עבור קבוצה של מצבים ולא רק עבור מצב בודד שאנחנו יודעים בודאות באיזה מצב הוא.

לפני שנגיע לפורמליזם, אני רוצה לחדד את הנקודה שאיתה פתחתי המצב \( \left|+\right\rangle \) הוא מצב קוונטי ספציפי, קונקרטי. אין שום הסתברות שנלווית לתיאור הזה של המערכת. ההסתברות מתחילה לשחק תפקיד רק כאשר אנחנו מודדים את המצב, לא לפני כן. קל לראות את זה אם נזכרים שיש בעולם כמה דרכים שונות למדוד מצב קוונטי; מדידה “רגילה” היא מה שקראתי לו מדידה בבסיס \( Z \), מדידה שמתוארת על ידי האיברים \( \left|0\right\rangle ,\left|1\right\rangle \) שהם התוצאות האפשריות של המדידה. אבל יש עוד מדידות, למשל מדידה בבסיס \( X \) שמתוארת על ידי האיברים \( \left|+\right\rangle ,\left|-\right\rangle \). אם אני מבצע מדידה בבסיס \( X \) של המצב \( \left|+\right\rangle \), אני אקבל את התוצאה שמתאימה ל-\( \left|+\right\rangle \) בהסתברות של 100 אחוז.

לעומת זאת, אם המצב הקוונטי שלי הוא “בהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|0\right\rangle \) ובהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|1\right\rangle \)”, מה יקרה אם אמדוד אותו בבסיס \( X \)? אם הקיוביט במצב \( \left|0\right\rangle \) אז בהסתברות \( \frac{1}{2} \) נקבל \( \left|+\right\rangle \) ובהסתברות \( \frac{1}{2} \) נקבל \( \left|-\right\rangle \); ואם הקיוביט במצב \( \left|1\right\rangle \) אז… במקרה הספציפי הזה של בסיס \( X \), יקרה בדיוק אותו דבר - כל תוצאה בהסתברות חצי (יכולים גם לקרות דברים מסובכים יותר באופן כללי).

אז כדי לחדד, אם המצב הקוונטי שלנו הוא \( \left|+\right\rangle \) אז מדידה בבסיס \( X \) תיתן בודאות מוחלטת \( \left|+\right\rangle \), אבל אם הוא “בהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|0\right\rangle \) ובהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|1\right\rangle \)” אז מדידה בסיס \( X \) תיתן \( \left|+\right\rangle \) רק בהסתברות \( \frac{1}{2} \) ואחרת היא תיתן \( \left|-\right\rangle \). זה מראה לנו ששני המצבים הללו שונים, בודאות מוחלטת. וכאמור, להבין שהם שונים זה לטעמי אחד המכשולים הגדולים בדרך להבנה של חישוב קוונטי.

לפני שנעבור לדבר על מצבים קוונטיים מסובכים שמערבים הסתברויות, בואו ניקח צעד אחורה: ניזכר בפורמליזם המתמטי הרגיל של חישוב קוונטי באמצעות וקטורים, ונראה איך אפשר לבטא את כולו גם בשפה של מטריצות. אני חושב שזה ייראה די פשוט ולא קשה להבנה; יהיה קצת קשה להבין למה אנחנו עושים את זה אבל כבר הצהרתי מה המטרה שלנו פה.

אז הנה הפורמליזם:

1. מערכת קוונטית מתוארת על ידי מרחב הילברט \( \mathcal{H} \) מעל \( \mathbb{C} \), ומצב ספציפי של המערכת הוא וקטור \( \left|\psi\right\rangle \in\mathcal{H} \) מנורמה 1.
2. בהינתן אופרטור \( U:\mathcal{H}\to\mathcal{H} \) שהוא אוניטרי, ניתן להפעיל אותו על המערכת על ידי כפל המטריצה שמייצגת את \( U \) בוקטור שמייצג את מצב המערכת ולהעביר אותה למצב חדש: \( \left|\psi^{\prime}\right\rangle =U\left|\psi\right\rangle \).
3. בהינתן קבוצת אופרטורים \( \left\{ M_{0},M_{1},\ldots,M_{t}\right\} \) שמכונים בהקשר הזה "אופרטורי מדידה", אפשר למדוד את המערכת ביחס לאופרטורים הללו ולקבל תוצאה \( i\in\left\{ 0,1,\ldots,t\right\} \) בהסתברות \( p\left(i\right) \), ואם התקבלה התוצאה הזו המערכת עוברת למצב \( \left|\psi^{i}\right\rangle \), כך ש:
   1. \( p\left(i\right)=\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \).
   2. \( \left|\psi^{i}\right\rangle =\frac{M_{i}\left|\psi\right\rangle }{\sqrt{\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle }} \).

זה לא משהו קל לעיכול במיוחד אבל אני מניח שכבר ראינו את זה קודם - ואם לא, הנה ההתחלה של ה”קודם”. בואו נראה עכשיו איך אותו דבר בדיוק מתואר עם מטריצה במקום וקטור.

ראשית, בואו ניזכר מה הסימונים שלנו אומרים. על \( \left|\psi\right\rangle \) אני חושב בתור וקטור עמודה; במקרה הפשוט שבו \( \left|\psi\right\rangle \) מייצג מערכת של קיוביט בודד, זה יהיה וקטור עמודה מסדר 2, \( \left|\psi\right\rangle =\left(\begin{array}{c} \alpha\\ \beta \end{array}\right) \). בנוסף לכך, הצגתי סימון נוסף: \( \left\langle \psi\right| \). אפשר לחשוב על \( \left\langle \psi\right| \) בתור \( \left\langle \psi\right|\triangleq\left(\left|\psi\right\rangle \right)^{\dagger} \), כלומר זה וקטור שורה \( \left\langle \psi\right|=\left(\begin{array}{cc} \overline{\alpha} & \overline{\beta}\end{array}\right) \). יש עוד דרך לחשוב על \( \left\langle \psi\right| \) בתור פונקציונל לינארי, אבל נעזוב את זה.

עכשיו, בסימון הזה, מה בעצם \( \left|\psi\right\rangle \left\langle \psi\right| \) אומר? זו מטריצה מסדר \( 2\times2 \) (ובאופן כללי, כש-\( \left|\psi\right\rangle \) הוא וקטור מסדר \( n \), זו מטריצה \( n\times n \)). כדי לראות את זה אני פשוט אכפול את הוקטורים במפורש:

\( \left|\psi\right\rangle \left\langle \psi\right|=\left(\begin{array}{c} \alpha\\ \beta \end{array}\right)\left(\begin{array}{cc} \overline{\alpha} & \overline{\beta}\end{array}\right)=\left(\begin{array}{cc} \left|\alpha\right|^{2} & \alpha\overline{\beta}\\ \overline{\alpha}\beta & \left|\beta\right|^{2} \end{array}\right) \)

זה פשוט על פי ההגדרה הרגילה של כפל מטריצות. שימו לב שאם אני כופל את שני הוקטורים הללו בסדר הפוך אני מקבל מטריצה מסדר \( 1\times1 \) שאני חושב עליה בתור סקלר:

\( \left\langle \psi\right|\left|\psi\right\rangle =\left(\begin{array}{cc} \overline{\alpha} & \overline{\beta}\end{array}\right)\left(\begin{array}{c} \alpha\\ \beta \end{array}\right)=\left|\alpha\right|^{2}+\left|\beta\right|^{2} \)

בעצם, לכפול שני וקטורים בצורה הזו, \( \left\langle \psi\right|\left|\varphi\right\rangle \), נותן לנו את המכפלה הפנימית שלהם. על אותו משקל, לפעמים קוראים ל-\( \left|\psi\right\rangle \left\langle \varphi\right| \) “מכפלה חיצונית” אבל נעזוב גם את זה. מה שמעניין, מבחינתי, זה רק איך שתרגממו את הוקטור \( \left|\psi\right\rangle \) למטריצה \( \left|\psi\right\rangle \left\langle \psi\right| \). בשביל לקצר עניינים, אני אשתמש ב-\( \rho \) בדרך כלל כדי לתאר מטריצות כאלו (כמו גם את המטריצות היותר מורכבות שנקבל בהמשך).

לפני שנסביר איך זה מסתדר עם המתמטיקה של התפתחות המערכת בזמן ושל מדידות, בואו נראה דוגמאות! קודם כל דוגמא פשוטה:

\( \left|0\right\rangle \left\langle 0\right|=\left(\begin{array}{c} 1\\ 0 \end{array}\right)\left(\begin{array}{cc} 1 & 0\end{array}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right) \)

ובאופן דומה:

\( \left|1\right\rangle \left\langle 1\right|=\left(\begin{array}{c} 0\\ 1 \end{array}\right)\left(\begin{array}{cc} 0 & 1\end{array}\right)=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \)

והנה ידידנו מתחילת הפוסט:

\( \left|+\right\rangle \left\langle +\right|=\frac{1}{\sqrt{2}}\left(\begin{array}{c} 1\\ 1 \end{array}\right)\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1\end{array}\right)=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right) \)

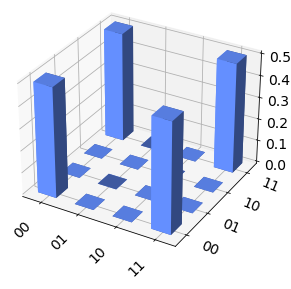
והנה דוגמא דומה עם שני קיוביטים, עם מי שנקרא “מצב בל” (אחד מהם, ליתר דיוק): \( \left|\Phi^{+}\right\rangle =\frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \):

\( \left|\Phi^{+}\right\rangle \left\langle \Phi^{+}\right|=\frac{1}{\sqrt{2}}\left(\begin{array}{c} 1\\ 0\\ 0\\ 1 \end{array}\right)\frac{1}{\sqrt{2}}\left(\begin{array}{cccc} 1 & 0 & 0 & 1\end{array}\right)=\left(\begin{array}{cccc} \frac{1}{2} & 0 & 0 & \frac{1}{2}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \frac{1}{2} & 0 & 0 & \frac{1}{2} \end{array}\right) \)

הנה איור של מטריצת הצפיפות הזו; זה האופן שבו בדרך כלל מאיירים דברים כאלו (לפעמים עם איור נוסף, למקרה שהאיברים במטריצה הם מרוכבים):

אני מקווה שאלו מספיק דוגמאות כדי לקבל תחושה ראשונית ואפשר לעבור לתיאוריה המתמטית.

אם כדי לתאר את ההתפתחות של המערכת בהתאם לאופרטור \( U \) היינו צריכים קודם לחשב מכפלה של מטריצה בוקטור, \( \left|\psi^{\prime}\right\rangle =U\left|\psi\right\rangle \), מה הנוסחה המתאימה כדי לחשב את \( \rho^{\prime} \) מתוך \( \rho \)? ובכן, אם נזכור ש-\( \left\langle \psi\right|=\left(\left|\psi\right\rangle \right)^{\dagger} \), אז נקבל ש-

\( \left\langle \psi^{\prime}\right|=\left(\left|\psi^{\prime}\right\rangle \right)^{\dagger}=\left(U\left|\psi\right\rangle \right)^{\dagger}=\left\langle \psi\right|U^{\dagger} \)

(כי ככה אלו חוקי המטריצות: \( \left(AB\right)^{\dagger}=B^{\dagger}A^{\dagger} \))

ומכאן:

\( \rho^{\prime}=\left|\psi^{\prime}\right\rangle \left\langle \psi^{\prime}\right|=U\left|\psi\right\rangle \left\langle \psi\right|U^{\dagger}=U\rho U^{\dagger} \)

הפעולה, הזו של לקחת משהו ולכפול אותו מצד אחד ב-\( U \) ומצד שני ב-\( U^{\dagger} \) נקראת הצמדה והיא מאוד נפוצה במתמטיקה (בדרך כלל אמנם בגרסה שלה שבה ה-\( U^{\dagger} \) הוא משמאל ולא מימין, אבל אין הבדל מהותי). אז בינתיים הכל נחמד - לקחנו פעולה טבעית בלשון וקטורים והחלפנו אותה בפעולה טבעית בלשון מטריצות.

עכשיו, נניח שאנחנו מודדים מצב \( \rho=\left|\psi\right\rangle \left\langle \psi\right| \), מה ההסתברות \( p\left(i\right) \) שאופרטור המדידה \( M_{i} \) יעלה בגורל? אם נלך על פי הנוסחה \( p\left(i\right)=\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \), לא ברור מה יש לנו לעשות - איכשהו ה-\( \left\langle \psi\right| \) וה-\( \left|\psi\right\rangle \) מרוחקים מאוד זה מזה ולא ברור מה אפשר לעשות איתם… אלא אם כן אני אשלוף מהשרוול פיסת קסם של אלגברה לינארית.

זוכרים איך קיבלנו \( \left|\psi\right\rangle \left\langle \psi\right|=\left(\begin{array}{cc} \left|\alpha\right|^{2} & \alpha\overline{\beta}\\ \overline{\alpha}\beta & \left|\beta\right|^{2} \end{array}\right) \) ו-\( \left\langle \psi\right|\left|\psi\right\rangle =\left|\alpha\right|^{2}+\left|\beta\right|^{2} \) וקראתי לראשון “מכפלה חיצונית” ולשני “מכפלה פנימית”? אם מסתכלים טיפה רואים שהמכפלה הפנימית מתחבאת בתוך \( \left|\psi\right\rangle \left\langle \psi\right| \): היא סכום אברי האלכסון הראשי של \( \left|\psi\right\rangle \left\langle \psi\right| \). “סכום אברי האלכסון הראשי” של מטריצה ריבועית \( A \) הוא כזה דבר שימושי במתמטיקה שיש לו שם וסימן בפני עצמו; הוא נקרא העקבה של \( A \) ומסומן \( \text{tr}\left(A\right)=\sum_{i=1}^{n}a_{ii} \), ומה שראינו עם המכפלה הפנימית והחיצונית הוא מקרה פרטי של הטענה הכללית הבאה באלגברה לינארית: אם \( A \) היא מטריצה מסדר \( 1\times n \) (“וקטור שורה”) ו-\( B \) היא מטריצה מסדר \( n\times1 \) (“וקטור עמודה”) אז

\( AB=\text{tr}\left(BA\right) \)

ההוכחה של זה היא פשוט משחק באינדקסים:

\( \text{tr}\left(BA\right)=\sum_{i=1}^{n}\left[BA\right]_{ii}=\sum_{i=1}^{n}B_{i,1}A_{1,i}=AB \)

איך זה עוזר לנו? ובכן, \( \left\langle \psi\right| \) הוא וקטור שורה ואילו \( M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \) הוא וקטור עמודה, ולכן אפשר לבצע את החלפת המקומות הזו:

\( p\left(i\right)=\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle =\text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \left\langle \psi\right|\right)=\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right) \)

וקיבלנו גם כאן ניסוח נחמד של חישוב \( p\left(i\right) \) מתוך \( \rho \) שמתבסס על מושגים מוכרים באלגברה לינארית.

אם אנחנו יודעים שהאופרטור \( M_{i} \) עלה בגורל, אנחנו יודעים שהמצב הקוונטי עבר אל \( \left|\psi^{i}\right\rangle =\frac{M_{i}\left|\psi\right\rangle }{\sqrt{\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle }} \). עם מה שכבר ראינו, אפשר לנסח את זה מחדש גם בלשון מטריצות:

\( \rho^{i}=\left|\psi^{i}\right\rangle \left\langle \psi^{i}\right|=\frac{M_{i}\left|\psi\right\rangle \left\langle \psi\right|M^{\dagger}}{\left(\sqrt{\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle }\right)^{2}}=\frac{M_{i}\rho M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)} \)

וזה משלים את הניסוח מחדש של הסיטואציות שאנחנו כבר רגילים אליהן בלשון מטריצות במקום וקטורים, שזה נחמד אבל מן הסתם זו לא הפואנטה כי עם וקטורים זה נוח יותר. עכשיו אנחנו מגיעים אל הפואנטה - האופן שבו אפשר להשתמש בלשון מטריצות כדי לתאר סיטואציה הסתברותית “קלאסית” שמערבת מצבים קוונטיים. בזה אני מתכוון לכך שיש לנו מערכת קוונטית שיכולה להיות באחד מבין המצבים הקוונטיים \( \left|\psi_{1}\right\rangle ,\left|\psi_{2}\right\rangle ,\ldots,\left|\psi_{m}\right\rangle \) אבל אנחנו לא יודעים איזה, אנחנו רק יודעים שהיא נמצאת במצב \( \left|\psi_{k}\right\rangle \) בהסתברות \( p_{k} \) שהיא מספר בין 0 ל-1: \( 0\le p_{k}\le1 \), כך ש-\( \sum_{k=1}^{m}p_{k}=1 \). והאופן הפורמלי שבו אני הולך לתאר סיטואציה כזו הוא באמצעות המטריצה

\( \rho=\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right| \)

ובמילים אחרות, אני לוקח את מטריצות הצפיפות של כל המצבים ולוקח את הממוצע המשוקלל שלהן, כשהמשקולות הן ההסתברויות של המצבים. כדאי כבר עכשיו להעיר שממטריצת הצפיפות שאני מקבל אני לא אוכל “לשחזר” את המצבים וההסתברויות שלהם; בהחלט אפשר יהיה לקבל את אותה מטריצת צפיפות מכמה סיטואציות שונות, אבל כל הסיטואציות הללו יהיו זהות מבחינת המשך ההתפתחות שלהן בזמן והתוצאות של מדידות אפשריות שלהן - כלומר, מטריצת הצפיפות היא דרך קומפקטית לשמור את המידע מבלי לאבד משהו מהותי.

בואו נבין למה שיטת הייצוג הזו באמת עובדת. נתחיל ממה קורה כשמפעילים אופרטור \( U \) על המערכת. אם, בהסתברות \( p_{k} \), המערכת שלנו הייתה במצב \( \left|\psi_{k}\right\rangle \), אז אחרי הפעלת \( U \) על המערכת אני מצפה להיות בהסתברות \( p_{k} \) במצב \( U\left|\psi_{k}\right\rangle \), כלומר אני מצפה להיות ב-

\( \rho^{\prime}=\sum_{k=1}^{m}p_{k}U\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|U^{\dagger}=U\left(\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)U^{\dagger}=U\rho U^{\dagger} \)

אז \( \rho \), גם כשהוא מייצג אוסף של מצבים קוונטיים, עדיין מתפתח כפי שציפינו על ידי הפעלת \( U \).

כעת, מה אם מנסים למדוד את \( \rho \) כשהוא מייצג אוסף? מה ההסתברות \( p\left(i\right) \) לקבל את התוצאה שמתאימה ל-\( M_{i} \)? כמובן, זה תלוי באיזה מצב המערכת נמצאת. כבר ראינו שאם היא במצב \( \left|\psi_{k}\right\rangle \), ההסתברות לקבל את \( M_{i} \) היא \( \text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right) \). לכן:

\( p\left(i|k\right)=\text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right) \)

כאן אני משתמש בנוסחה להסתברות מותנית. בואו ניזכר שניה איך זה עובד באופן כללי: אם במרחב ההסתברות שלנו יש שני מאורעות, \( A,B \), אז

\( p\left(A|B\right)=\frac{p\left(A\cap B\right)}{p\left(B\right)} \)

כאן אפשר לחשוב על מרחב ההסתברות שלנו כאילו הוא מתאר סדרה של שתי הגרלות: בהגרלה הראשונה נבחר מצב \( \left|\psi_{k}\right\rangle \) באקראי, ובהגרלה השניה, שתלויה בראשונה, נבחר אופרטור מדידה \( M_{i} \). כלומר, מרחב ההסתברות שלנו כולל זוגות \( \left(k,i\right) \) של תוצאות אפשריות, והמאורע “\( \left|\psi_{k}\right\rangle \) נבחר” הוא בעצם הקבוצה \( \left\{ \left(k,i\right)\ |\ 1\le i\le t\right\} \) (כאן \( t \) הוא מספר תוצאות המדידה האפשריות).

הסתברות מותנית מאפשרת לנו, כשאנחנו מנסים לחשב את ההסתברות של מאורע מסובך \( A \), לחלק את המרחב לפיסות נוחות לעיכול, \( B_{1},\ldots,B_{m} \) שקל לחשב את \( p\left(A|B_{k}\right) \) לכל אחת מהן, ואז לחבר את כל הפיסות הללו כדי לקבל את \( p\left(A\right) \) המקורית. זה עובד כאשר מרחב ההסתברות שלנו הוא איחוד זר של כל ה-\( B_{k} \)-ים הללו (כולם קבוצות זרות, והאיחוד שלהם נותן את כל מרחב ההסתברות). במקרה הזה מתקבל

\( p\left(A\right)=\sum_{k=1}^{m}p\left(A|B_{k}\right)p\left(B_{k}\right) \)

זה נקרא נוסחת ההסתברות השלמה וההוכחה פשוט מתבססת על כך ש-

\( \sum_{k=1}^{m}p\left(A|B_{k}\right)p\left(B_{k}\right)=\sum_{k=1}^{m}p\left(A\cap B_{k}\right)=p\left(A\cap\bigcup_{k=1}^{m}B_{k}\right)=p\left(A\right) \)

תוך שאנחנו משתמשים כאן באופן שבו הסתברות של איחוד מאורעות זרים הופכת לסכום ההסתברויות שלהם.

אם נחזור לענייננו, קיבלתי

\( p\left(i|k\right)=\text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right) \)

והמאורעות “\( \left|\psi_{k}\right\rangle \) נבחר” הם בוודאי זרים, ולכן

\( p\left(i\right)=\sum_{k=1}^{m}p\left(i|k\right)p\left(k\right)=\sum_{k=1}^{m}p_{k}\text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)= \)

\( =\text{tr}\left(M_{i}^{\dagger}M_{i}\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)=\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right) \)

כשהמעבר הלפני אחרון מתבסס על קסם אלגברה לינארית - שפונקציית העקבה \( \text{tr} \) היא לינארית בעצמה (אפשר לראות את זה מחישוב ישיר).

גם פה -הגענו אל אותה נוסחה כמו קודם, רק שעכשיו היא תקפה גם למקרה של אוסף מצבים קוונטיים.

הדבר הבא שהראיתי היה לאן עוברים אחרי מדידה אם ידוע ש-\( M_{i} \) עלה בגורל: המצב \( \left|\psi^{i}\right\rangle =\frac{M_{i}\left|\psi\right\rangle }{\sqrt{\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle }} \). אם יש לנו אוסף של מצבים קוונטיים, אני מסמן ב-\( \left|\psi_{k}^{i}\right\rangle \) את “המצב שאליו המערכת עוברת אם הייתה במצב \( \left|\psi_{k}\right\rangle \) ואז עלתה בגורל תוצאת המדידה \( M_{i} \)” (שימו לב שהמצבים הללו לא בהכרח שונים זה מזה, אבל זו לא בעיה, לא הייתה לי דרישה כזו). במילים אחרות, ההסתברות להיות ב-\( \left|\psi_{k}^{i}\right\rangle \) היא \( p\left(i,k\right) \). אבל השאלה שאני שואל כרגע היא מה ההסתברות להיות ב-\( \left|\psi_{k}^{i}\right\rangle \) אם ידוע ש-\( M_{i} \) עלה בגורל, כלומר “אם ידוע ש-\( M_{i} \) עלה בגורל, מה ההסתברות שמלכתחילה היינו במצב \( \left|\psi_{k}\right\rangle \)”, כלומר \( p\left(k|i\right) \), שהוא ההפך מ-\( p\left(i|k\right) \) שכבר חישבתי.

עכשיו, הנה טריק יעיל שנקרא “כלל בייס”: מכיוון ש-\( p\left(A|B\right)=\frac{p\left(A\cap B\right)}{p\left(B\right)} \) אפשר לכתוב \( p\left(A|B\right)p\left(B\right)=p\left(A\cap B\right) \). אבל באותה צורה ממש מקבלים

\( p\left(B|A\right)p\left(A\right)=p\left(A\cap B\right)=p\left(A|B\right)p\left(B\right) \)

ולכן:

\( p\left(A|B\right)=\frac{p\left(B|A\right)p\left(A\right)}{p\left(B\right)} \)

כלומר, זו שיטה להפוך את ההסתברות של א’ שמותנה בקיום ב’, להסתברות של ב’ שמותנה בקיום א’. בפרט, בסיטואציות כמו הנוכחית שבה אנחנו חושבים על המאורעות בתור “מה שבא קודם” ו”מה שבא אחר כך”, היא מאפשרת לעבור מהשאלה היותר אינטואיטיבית “בהינתן שקרה משהו, מה ההסתברות שינבע מכך משהו אחר בעתיד” אל השאלה הטריקית יותר “בהינתן שקרה משהו, מה ההסתברות שבעבר התרחש משהו שממנו זה נבע” (הסתברות א-פריורית אל מול הסתברות א-פוסטריורית).

עבורנו מה שמתקבל מכל זה כשאנחנו מתעסקים עם \( \rho=\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right| \) הוא

\( p\left(k|i\right)=\frac{p\left(i|k\right)p\left(k\right)}{p\left(i\right)}=p_{k}\frac{\text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)} \)

עכשיו, המטרה שלי היא להבין לאן \( \rho \) עברה אחרי המדידה בהינתן ש-\( M_{i} \) עלה בגורל; מה התפלגות המצבים החדשה, כלומר מהו

\( \rho^{i}=\sum_{k=1}^{m}p\left(k|i\right)\left|\psi_{k}^{i}\right\rangle \left\langle \psi_{k}^{i}\right| \)

בואו נפשט את הנוסחה הזו. כזכור, \( \left|\psi_{k}^{i}\right\rangle =\frac{M_{i}\left|\psi_{k}\right\rangle }{\sqrt{\left\langle \psi_{k}\right|M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle }} \) ולכן, כפי שכבר ראינו קודם,

\( \left|\psi_{k}^{i}\right\rangle \left\langle \psi_{k}^{i}\right|=\frac{M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)} \)

שימו לב שהמונה של \( p\left(k|i\right) \) והמכנה של \( \left|\psi_{k}^{i}\right\rangle \left\langle \psi_{k}^{i}\right| \) מבטלים זה את זה! בזכות זה, אם נציב את שניהם בנוסחה \( \rho^{i}=\sum_{k=1}^{m}p\left(k|i\right)\left|\psi_{k}^{i}\right\rangle \left\langle \psi_{k}^{i}\right| \), נקבל

ואם נציב את מה שכבר מצאנו בנוסחה הזו, נקבל

\( \rho^{i}=\sum_{k=1}^{m}p_{k}\frac{M_{i}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)}=\frac{M_{i}\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)}=\frac{M_{i}\rho M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)} \)

ושוב - קיבלנו את אותה נוסחה גם עבור מקבץ מצבים קוונטיים ולא מצב בודד. זה משלים את הכללת הפורמליזם של חישוב קוונטי מוקטורים שמייצגים מצב בודד, אל מטריצות צפיפות שמייצגות מקבץ של מצבים.

אבל לא סיימנו, עכשיו מגיע הקטע הכי נחמד! עד עכשיו תיארתי מה קורה עם מדידה שבה אנחנו מגרילים תוצאה ואז שואלים את עצמנו - בהינתן שקיבלנו את התוצאה \( M_{i} \), לאן עברנו? אבל עכשיו אפשר לדבר על השאלה - מה קורה אם אנחנו מבצעים מדידה ולא יודעים מה התוצאה? זה מה שאיתו פתחנו.

אינטואיטיבית, מה שקורה במקרה הזה הוא שאנחנו עוברים לסיטואציה הסתברותית קלאסית: אם בהסתברות \( p\left(i\right) \) עברנו מהמקבץ \( \rho \) אל המקבץ \( \rho^{i} \), אז עברנו אל מקבץ \( \rho^{\prime} \) שמורכב מכל המקבצים \( \rho^{i} \) הללו יחד, כשההסתברות של כל איבר במקבץ \( \rho^{i} \) מוכפלת ב-\( p\left(i\right) \) (כי עכשיו יש לנו תהליך דו-שלבי לקבלת איבר במקבץ \( \rho^{\prime} \): ראשית מגרילים \( \rho^{i} \) ואז מגרילים איבר מתוכו). כלומר

\( \rho^{\prime}=\sum_{i=1}^{t}p\left(i\right)\rho^{i} \)

אבל כבר חישבנו את \( p\left(i\right),\rho^{i} \)! נציב אותם בנוסחה ונקבל שוב ביטול הדדי נחמד:

\( \rho^{\prime}=\sum_{i=1}^{t}p\left(i\right)\rho^{i}=\sum_{i=1}^{t}\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)\frac{M_{i}\rho M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)}=\sum_{i=1}^{t}M_{i}\rho M_{i}^{\dagger} \)

זו כנראה הנוסחה הפשוטה והיפה ביותר כאן, והיא הראשונה שבאמת מהווה משהו חדש - האופן שבו מערכת קוונטית מתפתחת בזמן תחת פעולת מדידה עם תוצאות לא ידועות. בואו נראה איך זה נותן לנו את הדוגמא מתחילת הפוסט.

את הפוסט התחלנו עם המצב \( \left|+\right\rangle \), שמתורגם למטריצת הצפיפות

\( \rho=\left|+\right\rangle \left\langle +\right|\frac{1}{\sqrt{2}}\left(\begin{array}{c} 1\\ 1 \end{array}\right)\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1\end{array}\right)=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right) \)

אנחנו מודדים את \( \rho \) בבסיס \( Z \), כלומר עם אופרטורי המדידה

\( M_{0}=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right),M_{1}=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \)

לאן \( \rho \) יעבור אם אנחנו לא יודעים את תוצאת המדידה?

\( \rho^{\prime}=M_{0}\rho M_{0}^{\dagger}+M_{1}\rho M_{1}^{\dagger}= \)

\( =\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)+\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right)\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right)= \)

\( =\left(\begin{array}{cc} \frac{1}{2} & 0\\ 0 & \frac{1}{2} \end{array}\right)=\frac{1}{2}\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)+\frac{1}{2}\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right)=\frac{1}{2}\left|0\right\rangle \left\langle 0\right|+\frac{1}{2}\left|1\right\rangle \left\langle 1\right| \)

והנה, קיבלנו באופן פורמלי את “בהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|0\right\rangle \) ובהסתברות \( \frac{1}{2} \) הקיוביט במצב \( \left|1\right\rangle \)” וסגרנו מעגל עם תחילת הפוסט.

מה זה מטריצות צפיפות ואיך מגיעים אליהן בלי וקטורי מצב?

עד עכשיו הצגתי מטריצות צפיפות בתור הכללה של וקטורי מצב, אבל האם היה אפשר גם אחרת? האם בתיאוריה הייתי יכול להתחיל את התיאור של הפורמליזם המתמטי של חישוב קוונטי בלי לדבר על וקטורים בכלל, רק על מטריצות? התשובה היא “כן”, אבל צריך להיות זהירים; כשם שלא כל וקטור הוא וקטור מצב, גם לא כל מטריצה היא מטריצת צפיפות.

ראשית, זוכרים איך וקטור \( \left|\psi\right\rangle \) שהוא וקטור מצב חייב להיות מנורמה 1, כלומר לקיים \( \left\langle \psi\right|\left|\psi\right\rangle =1 \)? וזוכרים איך אפשר להחליף את הסדר בין המוכפלים אם משתמשים ב-tr? אז

\( \text{tr}\left(\left|\psi\right\rangle \left\langle \psi\right|\right)=\left\langle \psi\right|\left|\psi\right\rangle =1 \)

ועכשיו, עבור \( \rho=\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right| \) כללי:

\( \text{tr}\left(\rho\right)=\text{tr}\left(\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)=\sum_{k=1}^{m}p_{k}\text{tr}\left(\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right|\right)=\sum_{k=1}^{m}p_{k}=1 \)

כלומר, אם מטריצה \( \rho \) רוצה להיות מטריצת צפיפות, ברור שהיא חייבת לקיים \( \text{tr}\left(\rho\right)=1 \). אבל זה לא מספיק. יש עוד תכונה מהותית ש-\( \rho \) מקיימת, ונובעת מהסימטריה של \( \left|\psi\right\rangle \left\langle \psi\right| \). אבל בשביל להבין מאיפה התכונה הזו מגיעה אולי שווה לתת טיפה רקע.

באלגברה לינארית הפעולה הבסיסית שמעניינת אותנו היא טרנספורמציה לינארית, פונקציה \( T:V\to W \) שהיא לינארית, כלומר מקיימת \( T\left(u+v\right)=T\left(u\right)+T\left(v\right) \), ו-\( T\left(\lambda v\right)=\lambda T\left(v\right) \). זו תכונה כל כך יפה, שממנה נגזר שאפשר לתאר כל טרנספורמציה לינארית באמצעות הפעולה הפשוטה יחסית של כפל מטריצה בוקטור: קיימת מטריצה \( A_{T} \) כך ש-\( T\left(v\right)=A_{T}\cdot v \).

אפשר לקחת את זה לשלב הבא ולדבר על העתקה בילינארית, שהיא פונקציה \( B:V\times U\to W \) בשני משתנים שהיא לינארית בכל משתנה לחוד, כלומר

1. \( B\left(v_{1}+v_{2},u\right)=B\left(v_{1},u\right)+B\left(v_{2},u\right) \)
2. \( B\left(v,u_{1}+u_{2}\right)=B\left(v,u_{1}\right)+B\left(v,u_{2}\right) \)
3. \( B\left(\lambda v,u\right)=\lambda B\left(v,u\right) \)
4. \( B\left(v,\lambda u\right)=\lambda B\left(v,u\right) \)

במקרה שבו \( V=U \) ו-\( W=\mathbb{F} \), כלומר \( B \) מעתיקה זוגות של איברים מ-\( V \) אל איבר כלשהו בשדה ש-\( V \) חי מעליו, קוראים ל-\( B \) תבנית בילינארית, וכמו שאפשר לייצג פונקציה לינארית עם מטריצה, אפשר לייצג תבנית בילינארית עם מטריצה. ספציפית, קיימת מטריצה \( A \) כך ש-

\( B\left(v,u\right)=v^{T}Au \)

(אני מחפף פה ומניח שהוקטורים של \( V \) הם מראש וקטורי עמודה; בפועל צריך לקחת בסיס ל-\( V \) ואת וקטורי הקואורדינטות של \( v,u \) אבל נעזוב את זה).

כשאנחנו מעל \( \mathbb{F}=\mathbb{R} \), אפשר לחשוב על מכפלה פנימית בתור מקרה פרטי מעניין של תבנית בילינארית. מעל המרוכבים זה טיפה יותר מסובך - אנחנו צריכים לדבר על משהו שנקרא תבנית הרמיטית, שמקיימת את תכונות 1-3 שהראיתי קודם, אבל 4 מוחלפת ב-\( B\left(v,\lambda u\right)=\overline{\lambda}B\left(v,u\right) \), ובנוסף יש דרישה של מעין אנטי-סימטריות: \( B\left(u,v\right)=\overline{B\left(v,u\right)} \). מטריצה \( A \) מייצגת את \( B \) על ידי המשוואה הטיפה שונה

\( B\left(v,u\right)=v^{\dagger}A\overline{u} \)

אבל כדי שתבנית הרמיטית תהיה מכפלה פנימית, על כל הדברים הנחמדים שנובעים מכך, יש עוד תכונה אחת שהיא חייבת לקיים: חיוביות. לכל \( v\ne0 \) צריך להתקיים

\( B\left(v,v\right)>0 \)

עכשיו, כשאנחנו חושבים על \( B \) בתור משהו שמיוצג עם המטריצה \( A \), לאיזו דרישה על \( A \) החיוביות מתורגמת? לכך שאם \( v\ne0 \) אז יתקיים

\( v^{T}A\overline{v}>0 \)

את הדרישה הזו אני יכול לנסח בצורה יותר נחמדה עבורנו אם אחליף את \( v \) ב-\( \overline{v} \) (זה לא משנה, כי אני עובר על כל ה-\( v\ne0 \)) ואקבל

\( v^{\dagger}Av>0 \)

מטריצה \( A \) שמקיימת את התכונה הזו נקראת מטריצה חיובית (positive definite), וזו גם בדיוק התכונה שאני הולך לדרוש מ-\( \rho \) שלנו שמתיימרת לייצג מצב קוונטי, בנוסף לדרישה שכבר ראינו ש-\( \text{tr}\left(\rho\right)=1 \). בואו נבין למה זה מתקיים אם \( \rho \) הגיעה מוקטורים, כלומר היא מהצורה

\( \rho=\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right| \)

אנחנו לוקחים וקטור שונה מאפס כלשהו, \( v=\left|\varphi\right\rangle \), ומחשבים את \( v^{\dagger}\rho v \), כלומר את

\( \left\langle \varphi\right|\rho\left|\varphi\right\rangle \)

עכשיו, עבור המקרה הפשוט שבו \( \rho=\left|\psi\right\rangle \left\langle \psi\right| \) נקבל

\( \left\langle \varphi\right|\rho\left|\varphi\right\rangle =\left\langle \varphi\right|\left|\psi\right\rangle \left\langle \psi\right|\left|\varphi\right\rangle =\left|\left\langle \varphi,\psi\right\rangle \right|^{2}>0 \)

(כאשר כאן התוצאה התקבלה כי המכפלה הפנימית הרגילה מעל \( \mathbb{C} \) היא חיובית)

ומכאן להכללה עבור סכום מהצורה \( \rho=\sum_{k=1}^{m}p_{k}\left|\psi_{k}\right\rangle \left\langle \psi_{k}\right| \) הדרך טריוויאלית:

\( \left\langle \varphi\right|\rho\left|\varphi\right\rangle =\sum_{k=1}^{m}p_{k}\left|\left\langle \varphi,\psi_{k}\right\rangle \right|^{2}>0 \)

עכשיו אפשר לשכוח לחלוטין מוקטורי מצב ולנסח מחדש את עקרונות הבסיס של חישוב קוונטי בעזרת מטריצות צפיפות; אבל אני אעבור לדבר על אופרטור צפיפות, כי לדבר על מטריצה מניח במובלע בסיס (אין כזו הבדלה בשפה כשמדברים על וקטורים - המילה “וקטור” מתארת גם אובייקט כללי של מרחב וקטורי וגם את וקטור השורה שאיבריו הם אברי השדה, ולכן לא צצה הבחנה כזו קודם). מי שרגילות לאלגברה לינארית כבר יודעות שאת רוב מה שאפשר לומר על מטריצות, אפשר לומר על אופרטורים - פשוט לוקחים בסיס כלשהו ומוודאים שהמטריצה המייצגת של האופרטור בבסיס הזה מקיימת את התכונה הזו (מן הסתם זה דורש שהתכונה לא תהיה תלויה בבחירת הבסיס, ולמרבה המזל זה מה שקורה עם התכונות המעניינות באלגברה לינארית).

אם כן, בחישוב קוונטי אנחנו מתארים מערכת קוונטית מסויימת בעזרת מרחב הילברט \( \mathcal{H} \), כך שמצב המערכת בכל רגע נתון הוא אופרטור \( \rho:\mathcal{H}\to\mathcal{H} \) שמקיים

• \( \text{tr}\left(\rho\right)=1 \).
• \( \rho \) הוא אופרטור חיובי.

ואם המערכת נמצאת בהסתברות \( p_{k} \) במצב \( \rho_{k} \) אז המצב שלה הוא \( \rho=\sum_{k}p_{k}\rho_{k} \).

בהינתן אופרטור אוניטרי \( U:\mathcal{H}\to\mathcal{H} \), ניתן להפעיל אותו על המערכת כדי לשנות את מצבה:

\( \rho\mapsto U\rho U^{\dagger} \)

ובהינתן אוסף של אופרטורי מדידה \( \left\{ M_{0},\ldots,M_{t}\right\} \) מעל \( \mathcal{H} \) שהדרישה היחידה עליהם היא שיתקיים \( \sum_{i=0}^{t}M_{i}^{\dagger}M_{i}=I \), ניתן למדוד את המערכת במצב \( \rho \) ולקבל את התוצאה \( M_{i} \) בהסתברות

\( p\left(i\right)=\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right) \)

ואם התקבלה תוצאה זו, המערכת עוברת למצב

\( \rho\mapsto\frac{M_{i}\rho M_{i}^{\dagger}}{\text{tr}\left(M_{i}^{\dagger}M_{i}\rho\right)} \)

זה מסיים את ההגדרה, וכפי שראינו, תוצאה מיידית ממנה היא שאם מודדים את המערכת בעזרת \( \left\{ M_{0},\ldots,M_{t}\right\} \) אבל תוצאת המדידה אינה ידועה לנו, המערכת עוברת מבחינתנו למצב

\( \rho\mapsto\sum_{i=0}^{t}M_{i}\rho M_{i}^{\dagger} \)

ייתכן מאוד שכבר שמתם לב שאם “מודדים” את המערכת באמצעות אופרטור מדידה בודד, \( \left\{ U\right\} \), שהוא אוניטרי, השינוי של המערכת עקב ה”מדידה” הזו הוא

\( \rho\mapsto U\rho U^{\dagger} \)

כלומר, השינוי ה”רגיל”. של מצב המערכת. רק שעכשיו יש לנו קבוצה גדולה בהרבה של שינויים אפשריים, ואנחנו רוצים להבין אותה יותר טוב - למה? לא רק כי הם מייצגים מדידות, אלא גם כי הם מייצגים רעשים, שאפשר לחשוב עליהם בדיוק בתור “מדידות שלא אומרים לנו את התוצאה שלהן” ו”מדידות שמבוצעות באופן אקראי”. בשביל לתאר את הדברים הללו אנחנו כבר חייבים את הפורמליזם של מטריצת הצפיפיות, מה שמצדיק את כל הפוסט הזה. אבל מה בדיוק מאפיין את קבוצת כל השינויים האפשריים הללו ואיך מייצגים איברים שלה? על זה נדבר בפוסט הבא.