חישוב קוונטי: האלגוריתם של שור

מבוא

סדרת הפוסטים הקודמת שלי על חישוב קוונטי הסתיימה בפוסט גדול על האלגוריתם של שור. אני חושב שהגיע הזמן לתת עוד סיבוב, עם פוסט שייתן מבט רחב יותר על מה הרעיון הכללי של האלגוריתם ואיך הוא עובד, ויוותר על חלק מהפרטים הקטנים שכבר הוכחתי בפוסט המקורי ההוא. היתרון הגדול שלי עכשיו על פני הסיבוב הקודם הוא שכבר היו לי פוסטים נפרדים על התמרת פורייה הקוונטית ועל אלגוריתם הערכת פאזה, שהם הרכיבים הקוונטיים המרכזיים של האלגוריתם, והיכרות איתם מאפשרת להסתכל עליו “ממעוף הציפור”, מה שבלתי אפשרי בלעדיהם.

אז בואו נתחיל עם מעוף הציפור הזה. ראשית, הבעיה שאלגוריתם שור בא לפתור היא בעיית הפירוק לגורמים: נתון לנו מספר טבעי \( N \), ואנחנו מחפשים מספר טבעי \( 1<d<N \) כך ש-\( d \) מחלק את \( N \). למשל עבור \( N=15 \) אנחנו נשמח לקבל את \( d=3 \) או \( d=5 \). זו נראית בעיה לא גדולה כל כך במספרים קטנים, אבל כש-\( N \) הוא מספר בן מאות ספרות, אפילו האלגוריתמים המחוכמים ביותר שיש לנו כיום שאינם משתמשים במחשב קוונטי (ואלו אלגוריתמים מאוד מחוכמים, עם מתמטיקה מאוד מתקדמת) לא מסוגלים להתמודד עם הבעיה, וזה למרות שקל לנו לעשות חשבונות עם מספרים בני מאות ספרות; זו לא סתם בעיה של “המספר גדול מכדי שנעשה איתו כל דבר שהוא” - זו בעיה של סיבוכיות זמן ריצה אקספוננציאלית. מה שהאלגוריתם של שור מציע הוא פתרון מהיר של הבעיה, בזמן ריצה פולינומי (לא חייבים באמת להבין מה המילים הללו אומרות, מעבר לזה שכאן “אקספוננציאלי” זו מילה נרדפת לא מדוייקת ל”איטי” ו”פולינומי” זו מילה נרדפת לא מדוייקת ל”מהיר”). בשביל המהירות הגדולה הזו, האלגוריתם של שור משתמש במחשב קוונטי (אם כי טרם נבנה מחשב קוונטי שמסוגל להריץ את שור עבור מספרים בני מאות ספרות, וזו שאלה טובה מתי יהיה כזה).

אחרי שאמרנו את זה, צריך להבהיר שהאלגוריתם של שור, למעשה, איננו אלגוריתם לפירוק לגורמים! הוא אלגוריתם שבא לפתור בעיה אחרת, שנקראת “בעיית מציאת הסדר”, כי היכולת שלנו לפתור את בעיית מציאת הסדר נותנת לנו גם שיטה לפירוק לגורמים, אבל החלק שנעזר במציאת הסדר כדי לפרק לגורמים הוא חלק “קלאסי”, שלא מעורב בו חישוב קוונטי.

עוד נקודה שצריך להבהיר היא שהאלגוריתם של שור הוא הסתברותי - ייתכן בהחלט שנריץ אותו, לא נקבל שום דבר שיעזור לנו לפרק את \( N \) לגורמים, ונאלץ להריץ אותו שוב. ההסתברות שהוא יצליח היא טובה למדי, אבל הניתוח שנדרש כדי להראות את זה הוא לא פשוט.

ולבסוף, החלק הקוונטי של האלגוריתם של שור הוא פשוט מקרה ספציפי של אלגוריתם הערכת הפאזה, עבור \( U \) קונקרטי כלשהו שאציג בהמשך. זה מקרה מעניין יותר ממה שדיברנו עליו בפוסט הקודם, כי שם היה נתון לנו \( \left|u\right\rangle \) שהוא וקטור עצמי של \( U \), אבל באלגוריתם של שור אין לנו מושג מי הוקטורים העצמיים של \( U \); אבל באמצעות תעלול מחוכם ויפה, אנחנו הולכים להריץ את אלגוריתם הערכת הפאזה על סופרפוזיציה של הערכים העצמיים של \( U \) ואיכשהו זה יסתדר לנו.

גם אחרי שאלגוריתם הערכת הפאזה הסתיים, הפלט שלו הוא לא התוצאה הסופית של שום דבר - הוא בוודאי לא מספר שמחלק את \( N \), אבל הוא אפילו לא אותו “סדר” מסתורי שאנחנו צריכים למצוא; מה שאלגוריתם הערכת הפאזה נותן לנו הוא מספר רציונלי בין 0 ל-1 שבפני עצמו אין בו כלום; מה שאנחנו עושים (וגם זה חישוב קלאסי לגמרי) הוא ליצור בדרך מסויימת סדרה של קירובים לתוצאה הזו של הערכת הפאזה שקיבלנו. כל קירוב כזה יהיה מספר רציונלי \( \frac{s}{r} \), כשהמכנה \( r \) עשוי להיות ה”סדר” שחיפשנו. זה אומר שבהינתן התוצאה של שור, אנחנו מקבלים קבוצה של כמה וכמה מועמדים להיות ה”סדר”, ועבור כל אחד מהם צריך לבדוק אם הוא איכשהו נותן לנו פירוק לגורמים של \( N \).

זה נשמע ממש מסורבל - איפה זה ואיפה הגרסה האוטופית המדומיינת של האלגוריתם של שור, שבה אנחנו עושים איזה מעגל קוונטי חמוד, מודדים ומקבלים גורם של \( N \). אבל ככה זה בחישוב קוונטי - זה אף פעם לא פשוט כמו שעושים מזה, אבל כשמבינים את הפרטים המשוגעים זה נהיה עוד יותר יפה משזה נשמע במבט ראשון.

איך "מציאת סדר" עוזרת לפרק מספר לגורמים?

בואו ניכנס קצת יותר לפרטים של מה עושים כשרוצים למצוא גורם של \( N \). המתמטיקה שצריך להכיר פה היא זו של חשבון מודולרי, כלומר של ביצוע פעולות חיבור וכפל כשבסוף מחלקים במשהו ולוקחים את השארית. החישובים שלנו יהיו מודולו \( N \). למשל, אם \( N=15 \) ו-\( a=7 \) אז \( 7^{2} \) מודולו \( N \) הוא שארית החלוקה של 49 ב-15, כלומר 4. כותבים את זה \( 7^{2}\equiv_{N}4 \). הדבר השני שצריך להכיר הוא את הקיום של אלגוריתם יעיל שבהינתן שני מספרים \( a,b \) מחשב את ה-\( \text{gcd}\left(a,b\right) \) - המספר הגדול ביותר שמחלק את \( a \) וגם את \( b \). לא חשוב כרגע איך אלגוריתם עושה את זה (יש לי פוסט) אלא רק שאפשר לבדוק את זה ביעילות.

מה זה ה”סדר” המסתורי שהאלגוריתם של שור מחשב? זה המושג הסטנדרטי מתורת החבורות: הסדר של \( a \) מודולו \( N \) הוא המספר \( r>0 \) המינימלי שעבורו \( a^{r}\equiv_{N}1 \). מספר כזה קיים בהכרח רק \( \text{gcd}\left(a,N\right)=1 \); אבל אם \( \text{gcd}\left(a,N\right)>1 \) אז המספר \( \text{gcd}\left(a,N\right) \) (שאפשר לחשב ביעילות, כאמור) הוא מחלק לא טריוויאלי של \( N \) וסיימנו.

אז איך עובד כל התהליך? ראשית, בודקים ש-\( N \) הוא לא זוגי, כלומר פשוט מנסים לחלק אותו ב-2. אם כן - סיימנו. אחרת, בודקים ש-\( N \) הוא לא חזקה של ראשוני, כלומר \( N=p^{n} \) עבור \( n \) כלשהו. זה כבר עניין טריקי יותר, אבל יש אלגוריתם יעיל שעושה את זה ואני לא מציג אותו כי זה לא באמת קשור לאלגוריתם של שור.

בהינתן ש-\( N \) הוא לא מהצורה הזו, אנחנו עושים את הדבר הבא: מגרילים מספר \( 1<a<N \). בודקים ש-\( \text{gcd}\left(a,N\right)=1 \), כי אם הוא גדול יותר אז מצאנו מחלק של \( N \).

אחר כך אנחנו מפעילים את החלק הקוונטי של האלגוריתם של שור ומקבלים כל מני מספרים שכל אחד מהם הוא בעל פוטנציאל להיות הסדר של \( a \). לכל מספר \( r \) כזה, אם \( r \) אי זוגי מתעלמים ממנו, ואם \( r \) זוגי, אנו בודקים האם \( \text{gcd}\left(a^{\frac{r}{2}}-1,N\right)>1 \) או ש-\( \text{gcd}\left(a^{\frac{r}{2}}+1,N\right)>1 \). אם קיבלנו מספר כזה, סיימנו; מצאנו מחלק לא טריוויאלי של \( N \). אם לכל ה-\( r \)-ים שעשינו הניסוי לא הצליח, אנחנו מגרילים \( a \) אחר ומנסים שוב. זהו, זה כל האלגוריתם… למעט החלק של מציאת הסדר, שהוא כאמור העיקר.

למה כל זה עובד? כאן מגיעה הוכחה קצת מייגעת מתורת המספרים, שאני ארשה לעצמי לדלג עליה לגמרי כי כבר יש לי אותה בפוסט הקודם על האלגוריתם של שור. זה עובד, תסמכו עלי. אנחנו פה בשביל החלק הקוונטי.

איך בגדול עובד אלגוריתם מציאת הסדר?

בואו ניזכר מה עושה אלגוריתם הערכת הפאזה: הוא מניח שאנחנו יודעים לבנות מעגל עבור אופרטור \( U:\mathbb{C}^{2^{m}}\to\mathbb{C}^{2^{m}} \), ובהינתן שני רגיסטרים קוונטיים (שזה שם יפה ל”הרבה קיוביטים שאנחנו מחלקים אותם קונספטואלית לשתי קבוצות”) \( \left|0^{n}\right\rangle \left|u\right\rangle \) כך ש-\( \left|u\right\rangle \) הוא וקטור עצמי של \( U \), אנחנו מסוגלים לבצע חישוב שבסוף שלו מדידה של הרגיסטר הראשון תניב קירוב ל-\( \varphi \), שהוא מספר \( 0\le\varphi\le1 \) שמקיים \( U\left|u\right\rangle =e^{2\pi i\varphi} \).

לכן, כשאנחנו באים להשתמש באלגוריתם הזה בפועל, השאלה הראשונה שאנחנו צריכים לענות עליה היא מהו \( U \) שלנו, והשניה היא מהו \( \left|u\right\rangle \). בואו נראה איך זה יהיה אצלנו.

ראשית, בואו ניזכר איך אני משתמש בכתיב \( \left|a\right\rangle \) כאשר \( a \) הוא מספר טבעי. למשל, אם \( a=5 \) אז הייצוג הבינארי של \( a \) הוא \( 101 \), ואז הסימון \( \left|a\right\rangle \) מסמן את \( \left|101\right\rangle =\left|1\right\rangle \otimes\left|0\right\rangle \otimes\left|1\right\rangle \). צריך קצת להיזהר - אם מלכתחילה ברגיסטר שלנו משתתפים יותר קיוביטים מאשר צריך ספרות כדי לייצג את המספר, אז כל הקיוביטים ה”מיותרים” יהיו אפס. למשל, אם יש חמישה קיוביטים ואני מתבונן על המספר \( 13 \), אז \( \left|13\right\rangle =\left|01101\right\rangle \). מעכשיו בכל מה שהולך לקרות באלגוריתם של שור, אני אשתמש רק בסימון \( \left|a\right\rangle \) כש-\( a \) הוא מספר טבעי; אני לא אכתוב דברים בינאריים שם.

עכשיו אפשר לתאר את \( U \). כזכור, אלגוריתם מציאת הסדר מקבל כקלט מספר \( N \) ומספר \( a<N \) והשאלה היא מהו הסדר של \( a \) מודולו \( N \). אז האופרטור \( U \) שבו משתמשים נבנה בהתבסס על שני המספרים הללו:

\( U\left|b\right\rangle =\left|ab\text{ mod }N\right\rangle \)

כלומר, הוא בסך הכל כפל ב-\( a \) מודולו \( N \). בגלל שמעצבן לכתוב כל הזמן \( \text{mod }N \) אני הולך להשמיט אותו מעכשיו והלאה, אבל בכל פעם שבה מופיע משהו כמו \( \left|a^{2}\right\rangle \), תזכרו שאני מתכוון אל הערך של \( a^{2} \) מודולו \( N \).

עכשיו, אם אנחנו זוכרים, בהערכת פאזה צריך להיות מסוגלים לחשב לא רק את \( U \) אלא גם את \( U^{2^{t}} \) עבור ערכים הולכים וגדלים של \( t \), כלומר לחשב

\( U^{2^{t}}\left|b\right\rangle =\left|a^{2^{t}}b\text{ mod }N\right\rangle \)

אני לא הולך להסביר בפוסט הזה איך עושים את זה, כדי להישאר ממוקד. יש איזו פרדוקסליות בשאלה איך עושים את זה. מצד אחד, באופן כללי אנחנו מסוגלים לבצע חישובים “רגילים” במחשב קוונטי, מה שמזמין פוסט שעומד בפני עצמו שמסביר איך בדיוק עושים את זה. מצד שני, השאלה איך מחשבים את \( U^{2^{t}} \) בצורה אופטימלית, עם מינימום שערים, היא לא שאלה סגורה גם כיום. לכל זוג של \( a,N \) בעצם בונים מעגל אחר שמבצע את החישוב המתאים, וזו בעיה קלאסית בתחום של סינתזה של מעגלים קוונטיים - הבניה של מעגל אופטימלי מתוך התיאור האבסטרקטי יותר שלו. אז אני לא נכנס לזה בפוסט הזה כי זה מזמין סדרת פוסטים בפני עצמה. אבל אפשר לעשות את זה.

יפה, אז יש לנו את האופרטור \( U\left|b\right\rangle =\left|ab\text{ mod }N\right\rangle \). איך בדיוק הוא קשור לסדר \( r \) של \( a \) מודולו \( N \)? איך כל זה קשור ל”פאזה”? מה הולך כאן? בואו נפיל את האסימון הזה - לטעמי זה הולך להיות הרגע היפה ביותר מבין כל מה שראינו עד כה בסדרת הפוסטים הזו על חישוב קוונטי. כל כך יפה, שאני ארשה לעצמי להיות לא מדויק בניסוחים שלי - בהמשך גם זה יגיע.

בואו נסתכל לרגע על מה \( U \) עושה לכמה איברים קונקרטיים:

\( U\left|1\right\rangle =\left|a\cdot1\text{ mod }N\right\rangle =\left|a\right\rangle \)

\( U\left|a\right\rangle =\left|a\cdot a\text{ mod }N\right\rangle =\left|a^{2}\right\rangle \)

\( U\left|a^{2}\right\rangle =\left|a\cdot a^{2}\text{ mod }N\right\rangle =\left|a^{3}\right\rangle \)

אוקיי, אנחנו מבינים, על סדרת הערכים \( 1,a,a^{2},\ldots \) מה ש-\( U \) עושה הוא לקדם את האיבר הנוכחי אל האיבר הבא בסדרה. אבל מתי זה נגמר? ובכן, זה נגמר בדיוק כשמגיעים לסדר של \( a \) - לאיבר \( a^{2}\equiv_{N}1 \). במילים אחרות:

\( U\left|a^{r-1}\right\rangle =\left|a\cdot a^{r-1}\text{ mod }N\right\rangle =\left|1\right\rangle \)

ואז אנחנו חוזרים אל התחלת הסדרה (במתמטית אומרים על זה ש-\( U \) מבצע לסדרה \( 1,a,a^{2},\ldots,a^{r-1} \) הזזה ציקלית).

סבבה, איך זה נותן לנו וקטור עצמי של \( U \)? פשוט מאוד: בואו ניקח סופרפוזיציה אחידה של כל אברי הסדרה הזו, כלומר נסתכל על המצב

\( \left|u_{0}\right\rangle =\frac{\left|1\right\rangle +\left|a\right\rangle +\left|a^{2}\right\rangle +\ldots+\left|a^{r-1}\right\rangle }{\sqrt{r}}=\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\left|a^{k}\right\rangle \)

המצב הזה הוא בבירור מצב עצמי של \( U \), כלומר \( U\left|u_{0}\right\rangle =\left|u_{0}\right\rangle \); הוא מתאים לערך העצמי 1, וזה… לא עוזר לנו… בשום צורה? אלגוריתם הערכת הפאזה, אם יופעל על המצב הזה, יחזיר לנו 0. זה לא נותן לנו את \( r \); זה לא נותן לנו שום כלום. אז בשביל מה אני משגע אתכם?

אה-הא! העניין הוא שיש עוד וקטורים עצמיים! \( \left|u_{0}\right\rangle \) הוא רק האבטיפוס; הדוגמא הראשונה והפשוטה שנותנת לנו את האינטואיציה כדי להמשיך הלאה. בואו נחשוב לרגע על אותו וקטור, אבל עם מקדמים עבור האיברים:

\( \frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k}\right\rangle \)

אם אנחנו רוצים שאחרי הפעלת \( U \) נחזור לאותו מצב בדיוק כפול סקלר כלשהו, צריך להתקיים

\( U\left(\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k}\right\rangle \right)=\lambda\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k}\right\rangle \)

אבל

\( U\left(\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k}\right\rangle \right)=\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}U\left(\left|a^{k}\right\rangle \right)=\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k+1\text{ mod }r}\right\rangle \)

אם אנחנו משווים את זה אל \( \lambda\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k}\right\rangle \) אנחנו מקבלים

\( \lambda\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k}\right\rangle =\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\alpha_{k}\left|a^{k+1\text{ mod }r}\right\rangle \)

ואחרי חילוץ המקדמים, אנחנו מקבלים את המשוואות

\( \lambda\alpha_{0}=\alpha_{r-1} \)

\( \lambda\alpha_{1}=\alpha_{0} \)

\( \lambda\alpha_{2}=\alpha_{1} \)

וכן הלאה, עד שמגיעים לבסוף אל

\( \lambda\alpha_{r-1}=\alpha_{r-2} \)

אם נכפול את אגפי ימין ושמאל של כל המשוואות, נקבל

\( \lambda^{r}\prod_{k=0}^{r-1}\alpha_{k}=\prod_{k=0}^{r-1}\alpha_{k} \)

כלומר, \( \lambda^{r}=1 \). או במילים אחרות, אנחנו מסוגלים לקבל וקטור עצמי עבור כל שורש יחידה מסדר \( r \).

הצורה הכללית של שורש יחידה מסדר \( r \) היא

\( e^{\frac{2\pi i}{r}\cdot s} \)

כאשר \( 0\le s<r \).

עכשיו, עבור שורש יחידה \( e^{\frac{2\pi i}{r}\cdot s} \) קונקרטי, איך נקבל את הוקטורים העצמיים המתאימים? אפשר לקבוע שרירותית שתמיד יתקיים \( \alpha_{0}=1 \) כי ככה דברים ייצאו לנו נחמד, ואז נובע ש-

\( \alpha_{1}=\lambda^{-1}\alpha_{0}=e^{-\frac{2\pi i}{r}\cdot s} \)

ובדומה נקבל

\( \alpha_{2}=e^{-2\cdot\frac{2\pi i}{r}\cdot s} \)

ובאופן כללי, נקבל את הוקטור העצמי

\( \left|u_{s}\right\rangle =\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}e^{-k\cdot\frac{2\pi i}{r}s}\left|a^{k}\right\rangle \)

והוקטור \( \left|u_{0}\right\rangle \) שראינו קודם אכן מתקבל כאן כמקרה פרטי, כאשר \( s=0 \).

האם אלו באמת וקטורים עצמיים? אפשר לעשות שוב את החישוב, אבל כבר עשינו אותו קודם והוא יעבוד באותה צורה כל פעם. עבור \( \left|u_{s}\right\rangle \), הערך העצמי הוא שורש היחידה ה-\( r \)-י שהתאים ל-\( s \), כלומר

\( U\left|u_{s}\right\rangle =e^{\frac{2\pi i}{r}s}\left|u_{s}\right\rangle \)

ואם לחזור ללשון של אלגוריתם הערכת הפאזה, אז הפאזה \( \varphi_{s} \) של \( \left|u_{s}\right\rangle \) היא \( \varphi_{s}=\frac{s}{r} \). בפרט, אם הייתה לנו דרך להפעיל את אלגוריתם הערכת הפאזה על \( \left|u_{1}\right\rangle \) ולקבל תוצאה מדויקת, אז היינו מקבלים ליד את המספר הרציונלי \( \frac{1}{r} \). היינו מקבלים אותו בייצוג בינארי, אבל מתוך הייצוג הזה קל לחשב את \( r \) עצמו, מה שמסיים לנו את כל העבודה!

זהו, זו “נפילת האסימון” המדוברת. זה האופן שבו הסדר \( r \) עשוי לצוץ מתוך אלגוריתם הערכת פאזה. כשאני רוצה לסכם לעצמי את הפאנץ’ של האלגוריתם, אני חושב על הסדרה \( 1,a,a^{2},\ldots,a^{r-1} \) ואומר לעצמי “הזזה ציקלית. הזזה ציקלית”.

העניין הוא שזה לא מספיק. מה שתיארתי עד כה הוא אמנם נכון מבחינה רעיונית, אבל אנחנו לא באמת מסוגלים לממש את זה בפועל. נזדקק לעוד תעלול אחד אחרון. והתעלול הזה הוא כנראה הדבר הכי מגניב פה.

מה בעצם הבעיה? אם הייתי מסוגל להפעיל את אלגוריתם הערכת הפאזה על \( \left|u_{1}\right\rangle \) אכן הייתי מקבל את \( \frac{1}{r} \) (או לפחות קירוב טוב של \( \frac{1}{r} \) ועוד נחזור לחישוב המדויק). אבל אני לא יודע את \( \left|u_{1}\right\rangle \). אין לי מושג איך לבנות אותו. המקדמים שלו מקודדים איכשהו את \( e^{\frac{2\pi i}{r}} \); בשביל ליצור אותם אני כנראה אצטרך לדעת מה הוא \( r \), שהוא המספר שאותו אנחנו מחפשים! לכאורה אני במעגל ולא התקדמתי אף צעד; זה הכי כיף כשנראה שאנחנו בסיטואציה כזו כשלמעשה אנחנו במרחק צעד אחד מהפתרון.

הפתרון הוא לקחת את כל הוקטורים העצמיים \( \left|u_{s}\right\rangle \), עבור כל \( 0\le s<r \), ולהסתכל על הסופרפוזיציה של כולם ביחד, כלומר על

\( \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left|u_{s}\right\rangle \)

לכאורה לא התקדמנו בכלל - קודם היה מצב אחד שלא היה לנו מושג מהו, ועכשיו יש לנו סופרפוזיציה של הרבה מצבים כאלו; איך אנחנו אמורים לבנות אותה? התשובה היא שהיא מצב שאנחנו מכירים היטב וקל לנו מאוד לבנות - רק צריך לעשות את החישוב:

\( \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left|u_{s}\right\rangle =\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left(\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}e^{-k\cdot\frac{2\pi i}{r}s}\left|a^{k}\right\rangle \right)= \)

\( =\frac{1}{r}\sum_{k=1}^{r-1}\left(\sum_{s=0}^{r-1}e^{-k\cdot\frac{2\pi i}{r}s}\right)\left|a^{k}\right\rangle \)

עכשיו נחלץ לעזרתנו תעלול ידוע ומוכר - אם \( \omega \) הוא שורש יחידה כלשהו מסדר \( r \), אז \( 1+\omega+\omega^{2}+\ldots+\omega^{r-1}=\begin{cases} 0 & \omega\ne1\\ r & \omega=1 \end{cases} \). למה? כי אם \( \omega\ne1 \) אז הסכום משמאל הוא טור הנדסי שיוצא \( \frac{\omega^{r}-1}{\omega-1}=\frac{1-1}{\omega-1}=0 \).

במקרה שלנו, \( \omega=-k\frac{2\pi i}{r} \) - זה בהחלט שורש יחידה מסדר \( r \), והוא שווה ל-1 רק כאשר \( k=0 \). כלומר מכל הסכום הגדול נשאר רק

\( \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left|u_{s}\right\rangle =\frac{1}{r}\cdot r\left|a^{0}\right\rangle =\left|1\right\rangle \)

שימו לב: \( \left|1\right\rangle \) במקרה הזה הוא לא קיוביט בודד שערכו \( \left|1\right\rangle \), אלא כזכור, הסימון המקוצר שלי ל-\( \left|000\ldots01\right\rangle \). אבל זה בוודאי ובוודאי מצב שאנחנו יודעים לבנות - כלומר, אנחנו בהחלט יודעים לקבל את הסופרפוזיציה של כל ה-\( \left|u_{s}\right\rangle \) גם אם אנחנו לא יודעים לקבל אף אחד מהם אישית; זו גם הסיבה שבגללה כל כך עניין אותי להבין את כל ה-\( \left|u_{s}\right\rangle \) כולל \( \left|u_{0}\right\rangle \) ולא סתם התמקדתי ב-\( \left|u_{1}\right\rangle \).

בסופו של דבר, מה עושה המעגל של אלגוריתם הערכת פאזה? נקרא לו \( \text{PE} \) (קיצור של Phase Estimation). אם מריצים אותו עד השלב שלפני המדידה שבסוף, הוא מחשב את האופרטור האוניטרי

\( \text{PE}\left(\left|0^{n}\right\rangle \left|u_{s}\right\rangle \right)=\left|\tilde{\varphi}_{s}\right\rangle \left|u_{s}\right\rangle \)

כאשר \( \left|\tilde{\varphi}_{s}\right\rangle \) הוא מצב קוונטי שהמדידה שלו נותנת בהסתברות טובה קירוב טוב של \( \varphi_{s} \) - הפאזה שמתאימה ל-\( u_{s} \), כלומר \( \frac{s}{r} \). עכשיו, אם במקום לרוץ על מצב בודד, נרוץ על סופרפוזיציה שלהם, העובדה ש-\( \text{PE} \) הוא אופרטור לינארי נותנת לנו

\( \text{PE}\left(\left|0^{n}\right\rangle \left(\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left|u_{s}\right\rangle \right)\right)=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\text{PE}\left(\left|0^{n}\right\rangle \left|u_{s}\right\rangle \right)=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left|\tilde{\varphi}_{s}\right\rangle \left|u_{s}\right\rangle \)

במילים אחרות, אנחנו מקבלים ברגיסטר הראשון סופרפוזיציה אחידה של כל ה-\( \left|\tilde{\varphi}_{s}\right\rangle \)-ים, ולכן אפשר לחשוב על מדידה של הרגיסטר הראשון כאילו היא עושה שני דברים בזה אחר זה:

• מגרילה \( 0\le s<r \) באקראי ובהתפלגות אחידה.
• מודדת את \( \left|\tilde{\varphi}_{s}\right\rangle \), כלומר מקבלת ערך שבהסתברות טובה הוא קירוב טוב של \( \frac{s}{r} \).

האם כל ה-\( s \)-ים טובים עבורנו? ובכן, לא. ראינו כבר קודם שעבור \( s=0 \) אין לנו כלום - לא נוכל לחלץ את \( r \) מהערך שנקבל. ובמקרים אחרים, אם \( \text{gcd}\left(s,r\right)>1 \) אז הסיכוי שנצליח לעשות משהו טוב נפגע מאוד - \( \frac{s}{r} \) לא יהיה שבר מצומצם ולכן אם ננסה “לשחזר” את \( \frac{s}{r} \) לא נקבל את \( r \). הנה דוגמא פשוטה: נניח ש-\( r=15 \) ו-\( s=3 \). אז \( \frac{s}{r}=\frac{3}{15}=\frac{1}{5}=0.2 \); אז אפילו אם נקבל את התוצאה המדויקת \( 0.2 \) לא נוכל לשחזר מזה את \( r=15 \); המכנה שנשחזר הוא 5. בגלל הבעיה הזו, לפעמים באלגוריתם של שור כשמקבלים “מועמד ל-\( r \)” משתלם לפעול לא רק מתוך הנחה שהמועמד הזה טוב, אלא גם לנסות כמה כפולות שלו - להכפיל ב-2,3,4 וכו’ ולנסות גם עבורן. זה חישוב מהיר מאוד שלא מאט אותנו, ואם במקרה הוא מצליח ומצאנו גורם של \( N \) נדע בודאות שהצלחנו, כך שאין חיסרון של ממש להרחבה הזו.

זה סוף אלגוריתם הערכת הפאזה, כלומר סוף החלק הקוונטי של האלגוריתם; הנה איך הכל נראה בסופו של דבר.

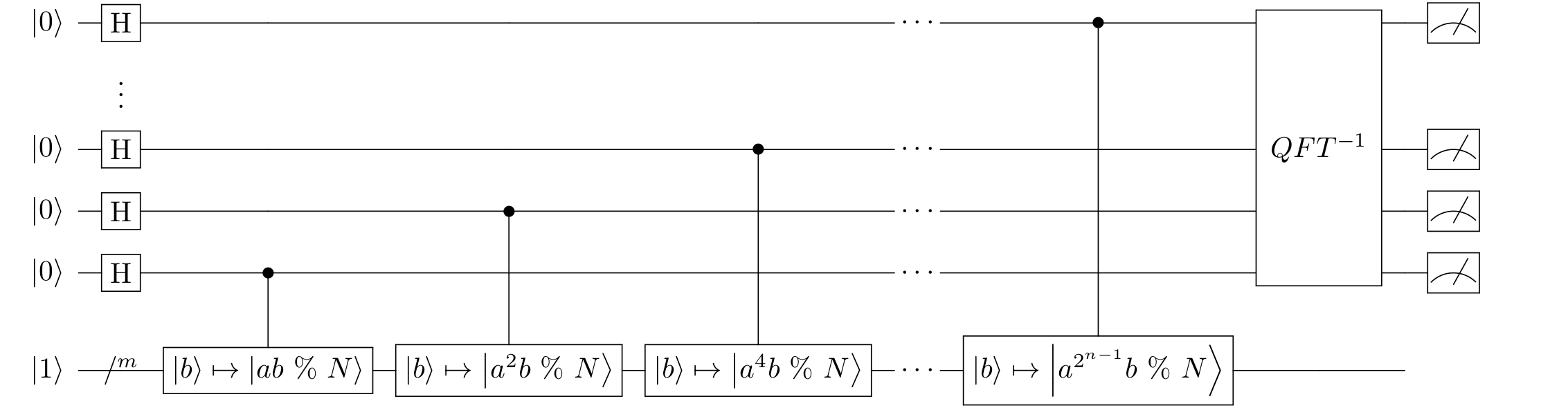
איך משחזרים את הסדר מתוך הקירוב שהערכת הפאזה נותנת לנו?

ברגע שבו אלגוריתם הערכת הפאזה מסתיים, נגמר החלק הקוונטי של האלגוריתם, אבל עדיין נשאר חלק לא טריוויאלי בעליל שצריך לבצע - השלב שבו אנחנו עוברים מהקירוב שקיבלנו לפאזה, עד שיש לנו ביד מועמד פוטנציאלי להיות הסדר, \( r \). כאן נכנס לתמונה מה שנקרא אלגוריתם השברים המשולבים, שזו פשוט דרך מפחידה להגיד “שיטה למציאת קירובים רציונלים טובים למספר שקיבלנו”.

מה זה שבר משולב? יש לי פוסט על זה אבל הוא נכנס לעומק שאני לא זקוק לו פה, ומצד שני תמיד נחמד להציג שוב נושא כל כך מגניב, בטח כשיש לו שימוש פרקטי. אז הנה מבוא על רגל אחת. נתחיל עם דוגמא קונקרטית - המספר \( \pi \) - היחס בין היקף מעגל לקוטרו - הוא אחד מהקבועים המתמטיים המפורסמים ביותר. אם ננסה לכתוב אותו בבסיס עשרוני הוא ייראה משהו כמו \( \pi=3.14159\ldots \), כשהנקודות אומרות שיש עוד ספרות בהמשך. אם נוותר על הנקודות ונסתכל על המספר \( 3.14159 \), מה שיש לנו ביד הוא קירוב רציונלי של \( \pi \) - קירוב שאפשר לכתוב אותו בתור מנה של שני מספרים שלמים, \( \frac{314159}{10000} \) (זאת להבדיל מ-\( \pi \) עצמו שיש הוכחה שאי אפשר להציג בתור מנה של שני מספרים שלמים). אני יכול גם להסתכל על קירובים שמתקבלים מלקחת פחות ספרות של \( \pi \): אני מקבל את סדרת הקירובים

\( 3,\frac{31}{10},\frac{314}{100},\frac{3141}{1000},\frac{31415}{10000} \)

האם זו סדרת קירובים טובה? הקירוב \( \frac{314}{100}=3.14 \), למשל, הוא מפורסם במיוחד: צורת הכתיב שלו, בשילוב עם שיטת כתיב התאריכים האמריקאית ויום ההולדת של אלברט איינשטיין, הולידו את יום פאי. אבל האמת היא, בינינו, שזה קירוב די גרוע לעומת קירוב אחר, \( \frac{22}{7} \), שזכה ליום פחות מפורסם משל עצמו (“יום קירוב פאי”, למרות שכאמור הוא דווקא הקירוב הטוב יותר). אם נחשב את ההפרש של כל אחד מהקירובים מפאי נקבל\( \left|\pi-3.14\right|=0.001592\dots \) ו-\( \left|\pi-\frac{22}{7}\right|=0.001264\ldots \), כלומר יש יתרון ברור ל-\( \frac{22}{7} \), למרות שלכאורה נקודת המוצא של \( \frac{314}{100} \) היא טובה הרבה יותר, כי המכנה שלו הוא מספר גדול יותר, ולכן לכאורה מאפשר למצוא מספר שקרוב לפאי ברזולוציה טובה יותר (תחשבו על סרגל שיש בו סימוני סנטימטרים לעומת סרגל שיש בו רק שבעה סימנים ברווחים אחידים בין כל מטר - מה נראה לנו כמו כלי מדויק יותר?)

אם נסתכל על הקירוב ה”טוב”, \( \frac{22}{7} \), מה מבדיל אותו מהסדרה שהראיתי קודם? בסדרה הזו, המכנה של כל השברים היה חזקה של 10: 1, 10, 100, 1000 וכו’. לעומת בקירוב \( \frac{22}{7} \) נדחף לנו ה-7 הלא קשור הזה. העניין הוא שמבחינת המתמטיקה, האהבה שלנו למספר 10 היא שרירותית; זה בגלל שהביולוגיה חננה אותנו בעשר אצבעות, לא בגלל שעשר הוא מספר מופלא לקירובים. לכן, שיטת הקירובים שאנחנו רגילים אליה מהבסיס העשרוני שלנו היא לאו דווקא אופטימלית; שברים משולבים הם אלו שנותנים לנו את הקירובים האופטימליים, במובן מאוד מדויק שאתאר עוד מעט - ובגלל שמקבלים קירובים כל כך טובים, זה מתקשר ישירות לאלגוריתם שלנו.

איך זה קשור? ובכן, עוד מעט אראה איך בעזרת שברים משולבים אפשר לקבל סדרת קירובים למספר כלשהו \( x \). הקסם המופלא בשיטה הזו הוא שאם למספר \( x \) כלשהו יש קירוב טוב (עבור משמעות של “טוב” שאתן במדויק בהמשך), אז בודאות מוחלטת הקירוב הטוב הזה יופיע בסדרת הקירובים שמקבלים מהפיתוח של \( x \) לשבר משולב.

איך זה קשור אלינו? כי בואו נחשוב רגע מה עושה שלב הערכת הפאזה: הוא מחזיר מספר \( x \) שהוא קירוב טוב של \( \frac{s}{r} \) כאשר \( r \) הוא הסדר שאנחנו מחפשים - מטרת האלגוריתם - ו-\( 0\le s<r \) הוא מספר אקראי. אבל אם \( x \) הוא קירוב טוב של \( \frac{s}{r} \) ההפך נכון באותה מידה: \( \frac{s}{r} \) הוא קירוב טוב של \( x \), ולכן הולך להופיע בפיתוח לשברים משולבים של \( x \). כזכור, בפוסט על אלגוריתם הערכת פאזה ראינו בדיוק כיצד ניתן להגדיל את ההסתברות לקבלת קירוב טוב (עוד קיוביטים), אז מה שנצטרך לעשות הוא להבין כמה טוב צריך להיות הקירוב הטוב הזה.

עוד עניין שאין לנו דרך להתמודד איתו הוא ש-\( \frac{s}{r} \) צריך להיות שבר מצומצם. אם למשל \( s=7 \) ו-\( r=63 \), אז \( \frac{s}{r}=\frac{7}{63}=\frac{1}{9} \), ואז מה שהפיתוח לשברים משולבים ייתן לנו הוא את \( \frac{1}{9} \). זה כמובן אותו מספר בדיוק כמו \( \frac{7}{63} \), אבל אנחנו מעוניינים במספר 63 שנמצא במכנה, לא ב-9. אז כדי שהאלגוריתם יצליח, ה-\( 0\le s<r \) שנבחר באקראי צריך להיות זר ל-\( r \). למרבה המזל, רוב ה-\( s \)-ים הללו אכן כאלו, אז זו לא בעיה אמיתית - אבל מי שרוצים להיות ממש זהירים יכולים, בהינתן המספר שהתקבל במכנה, לנסות גם כפולות שלו - אם היינו מנסים לקחת את ה-9 שקיבלנו במכנה, לכפול אותו ב-7 ולנסות לפרק לגורמים את \( N \) עם ה-\( 63 \) שקיבלנו, היינו מצליחים; הנסיונות הללו לא מפריעים לשום דבר ומגדילים עוד קצת את הסיכוי שנצליח, אבל כנראה שאפשר גם בלעדיהם.

אוקיי, בואו נעבור לשברים משולבים! ספציפית אל המספר \( \frac{314159}{100000} \) שהבטחתי למצוא לו סדרת קירובים טובה יותר מאשר \( 3,3.1,3.14 \) וכן הלאה. הטכניקה שבה אשתמש תיראה מוזרה במבט ראשון, אבל סמכו עלי - היא עובדת. כזכור, אי שם בבית הספר לימדו אותנו שיש משהו שנקרא “שבר מדומה” שהוא שבר שבו המונה גדול מהמכנה. שבר כזה אפשר להפריד לסכום שנקרא “מספר מעורב” של החלק השלם ועוד החלק השברי שהוא בין 0 ל-1. במקרה שלנו:

\( \frac{314159}{100000}=3+\frac{14159}{100000} \)

עכשיו אני עושה את הטריק המרכזי שלי: אני משתמש בכך שבאופן כללי, \( \frac{a}{b}=\frac{1}{\frac{b}{a}} \) כדי לכתוב

\( \frac{14159}{100000}=\frac{1}{\frac{100000}{14159}} \)

מה הולך פה? קודם היה לנו שבר “אמיתי”, שבו המונה קטן מהמכנה; עכשיו המונה והמכנה התהפכו, אז שוב קיבלנו שבר מדומה שאנחנו יכולים להפריד למספר שלם ועוד שבר. בשביל לעשות את זה, צריך לחלק את 100,000 ב-14,159; המנה שנקבל היא החלק השלם, והשארית שנקבל היא מה שנשאר על השבר: \( \frac{100000}{14159}=7+\frac{887}{14159} \).

אם שותלים את הביטוי הזה בחישוב שכבר עשינו, מקבלים

\( 3+\frac{14159}{100000}=3+\frac{1}{7+\frac{887}{14159}} \)

אפשר להמשיך עם זה ולהתעלל גם ב–\( \frac{887}{14159} \), אבל אפשר גם לקחת הפסקה לרגע ולהגיד “אוקיי, בואו נתעלם לגמרי מה-\( \frac{887}{14159} \), מה קיבלנו עכשיו?” ואז יש לנו את השבר

\( 3+\frac{1}{7}=\frac{22}{7} \)

הופה! הנה צץ לנו הקירוב המצוין לפאי שדיברתי עליו קודם! כאילו במטה קסם. ובכן, כן, זה באמת קסם, עד כמה שדברים שקורים במתמטיקה הם קסם; זה הקסם שמאפשר לנו לסיים את האלגוריתם של שור. למה זה קורה? סבלנות! עוד אוכיח את זה באופן מלא בפוסט הזה.

נחזור אל ה-\( \frac{887}{14159} \). בשלב הזה אנחנו כבר יודעים מה לעשות - לחלק את 14159 ב-887 ולראות מה המנה ומה השארית, ואז לכתוב

\( \frac{887}{14159}=\frac{1}{15+\frac{854}{887}} \)

אם נשתול את זה בביטוי המקורי נקבל משהו שהוא כבר בלתי קריא בעליל:

\( 3+\frac{1}{7+\frac{1}{15+\frac{854}{887}}} \)

בגלל שזה בלתי קריא, משתמשים לפעמים בשיטת סימון אחרת, שבה לא צריך לרדת למטה עוד ועוד:

\( 3+\frac{1}{7+}\frac{1}{15+}\frac{1}{887/854} \)

אבל אני אשתמש בשיטת סימון עוד יותר קומפקטית: הרי לא באמת צריך את כל הפלוסים וה-1 חלקי הללו, אנחנו מתעניינים רק במספרים שליד הפלוסים. אז אפשר לכתוב

\( \left[3,7,15,\frac{887}{854}\right] \)

זו צורת הכתיב הנפוצה והמקובלת. הנה הגדרה פורמלית של מה היא אומרת:

\( \left[a_{0},a_{1},\ldots a_{n}\right]=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{\cdots+\frac{1}{a_{n}}}}} \)

ועכשיו אפשר להמשיך יותר בנוחות. נחלק את 887 ב-854 ונקבל מנה 1 ושארית 33, כלומר השלב הבא הוא

\( \left[3,7,15,1,\frac{854}{33}\right] \)

בשלב הבא נחלק 854 ב-33 ונקבל מנה 25 ושארית 29, ובואו נמשיך גם לשלב הבא כי הבנו את הקטע:

\( \left[3,7,15,1,25,\frac{33}{29}\right]=\left[3,7,15,1,25,1,\frac{29}{4}\right]= \)

\( =\left[3,7,15,1,25,1,7,\frac{4}{1}\right] \)

וזה השלב האחרון, כי 4 מתחלק ב-1 ללא שארית! זו הצורה ה”סופית” של השבר המשולב:

\( \left[3,7,15,1,25,1,7,4\right] \)

כלומר, אנחנו מרגישים רגועים לומר שסיימנו כשהאיבר האחרון, הימני ביותר, הוא עצמו מספר שלם ולא שבר.

ואיך כל זה עוזר לנו בכלל? כפי שראינו קודם, כבר כש”עצרנו” את החישוב אחרי שקיבלנו את ה-7 הראשון והתעלמנו מהשארית, קיבלנו את הקירוב \( \frac{22}{7} \) המצוין. באותו אופן אפשר לעצור את הקירוב גם בשלבים מתקדמים יותר ולקבל קירובים מצויינים אחרים. למשל:

\( \left[3,7,15\right]=3+\frac{1}{7+\frac{1}{15}}=3+\frac{1}{\frac{106}{15}}=\frac{333}{106} \)

גם זה קירוב מפורסם של פאי, וכן הלאה - הבנו את הרעיון. שימו לב, אגב, שלא עבדנו עם \( \pi \) בכלל; התחלנו עם המספר \( 3.14159 \) ומצאנו סדרת קירובים אליו; בגלל שהוא קירוב לא רע של פאי, קיבלנו שסדרת הקירובים החלקיים עד כה נותנת גם את הקירובים המצויינים של \( \pi \). אם היינו מלכתחילה רוצים לחשב שבר משולב עבור \( \pi \) היינו נתקלים בשתי בעיות - החישוב קצת יותר מסובך, והשבר המשולב המתקבל צריך להיות אינסופי; כדי להתחמק מהסיבוך הזה שלא דרוש לי הסתפקתי בלתאר איך מחשבים שבר משולב עבור מספר שהוא מלכתחילה שבר - ומה שראינו הוא שהשבר המשולב שאנחנו בונים אכן נותן סדרה מצויינת של קירובים לאותו השבר. זה המקרה הרלוונטי לנו כי כזכור, אנחנו מקבלים מאלגוריתם הערכת הפאזה מספר רציונלי \( x \) שבתקווה \( \frac{s}{r} \) הוא קירוב מצויין אליו. אם \( x \) הוא מספר רציונלי, אנחנו יודעים איך לחשב לו שבר משולב ואז לקבל ממנו את סדרת הקירובים האופטימלית שהוא נותן - זה חישוב מאוד פשוט שכולל בסך הכל פעולות של חילוק עם שארית וחישובים אריתמטיים פשוטים יותר. קל לתכנת את זה והריצה של החלק הזה לוקחת שברירי שניה.

בונוס: איך מוכיחים את כל הקטע הזה של השברים המשולבים?

יופי, סיימנו עם האלגוריתם של שור ואפשר לעבור לתורת המספרים נטו! בואו נעבור לתיאור פורמלי של עניין הקירוב טוב הזה. נתחיל עם סימון: אם \( x \) הוא מספר רציונלי עם פיתוח לשבר משולב \( \left[a_{0},a_{1},\ldots,a_{n}\right] \), אני אסמן את סדרת הקירובים שמתקבלת מהפיתוח הזה בתור \( \frac{p_{0}}{q_{0}},\frac{p_{1}}{q_{1}},\frac{p_{2}}{q_{2}},\ldots,\frac{p_{n}}{q_{n}} \). כלומר, \( \frac{p_{k}}{q_{k}}=\left[a_{0},a_{1},\ldots,a_{k}\right] \).

הנה דברים שאפשר להראות אבל לא אראה הפעם: \( q_{0}<q_{1}<q_{2}<\ldots<q_{n} \), כלומר המכנה הולך וגדל ככל שמתקדמים בסדרה; \( p_{k},q_{k} \) זרים זה לזה לכל אינדקס \( k \); והקירוב \( \frac{p_{k}}{q_{k}} \) הוא טוב במובן הבא:

\( \left|x-\frac{p_{k}}{q_{k}}\right|<\frac{1}{q_{k}q_{k+1}}<\frac{1}{q_{k}^{2}} \)

כשהמעבר השני נובע מכך ש-\( q_{k}<q_{k+1} \) (עבור \( k=n \) הנוסחה לא עובדת כי אין \( q_{k+1} \) אבל ממילא בשלב הזה ההפרש הוא 0).

\( \frac{p_{k}}{q_{k}} \) הוא הקירוב הטוב ביותר במובן זה שלכל \( 1\le d\le q_{k} \) ולכל \( c \) מתקיים

\( \left|x-\frac{p_{k}}{q_{k}}\right|\le\left|x-\frac{c}{d}\right| \)

כלומר, אם מסתכלים על כל המספרים הרציונליים עם מכנה שהוא לכל היותר \( q_{k} \), לא נמצא אף אחד שהוא קירוב יותר טוב ל-\( x \) מאשר \( \frac{p_{k}}{q_{k}} \).

יפה, כל אלו הם משפטים מעניינים, אבל המשפט שמעניין אותי באמת הוא זה שמבטיח לנו שקירוב טוב בהכרח יופיע בפיתוח לשבר משולב, וסוף סוף אפשר לנסח אותו פורמלית: אם \( c,d \) זרים זה לזה, עם \( 1\le d \), ומתקיים

\( \left|x-\frac{c}{d}\right|<\frac{1}{2d^{2}} \)

אז בודאות קיים \( k \) כך ש-\( \frac{c}{d}=\frac{a_{k}}{b_{k}} \) עבור איבר \( \frac{a_{k}}{b_{k}} \) בסדרת הקירובים שמתקבלת מהפיתוח של \( x \) לשבר משולב.

איך מוכיחים את זה?

טוב, אני אצטרך שנכיר עוד כמה דברים על שברים משולבים כדי להתקדם. הדבר הראשון הוא נוסחה די משוגעת שעבור שבר משולב \( \left[a_{0},a_{1},\ldots,a_{n},a_{n+1}\right] \) נותנת לנו את \( \frac{p_{n+1}}{q_{n+1}} \) - האיבר הבא בסדרת הקירובים - אם נתונים לנו \( \frac{p_{n}}{q_{n}},\frac{p_{n-1}}{q_{n-1}} \) ו-\( a_{n+1} \). הנה הנוסחה:

\( \frac{p_{n+1}}{q_{n+1}}=\frac{a_{n+1}p_{n}+p_{n-1}}{a_{n+1}q_{n}+q_{n-1}} \)

בואו נראה את זה בפעולה עבור \( \left[3,7,15,1,25,1,7,4\right] \), השבר המשולב שכבר מצאנו עבור הקירוב לפאי. כזכור, שני הקירובים הראשונים שקיבלנו היו \( \frac{3}{1} \) ו-\( \frac{22}{7} \), והקירוב השלישי היה \( \frac{333}{106} \). לכאורה כדי לקבל את הקירוב השלישי אנחנו לא יכולים להיעזר בשני הראשונים; אנחנו חייבים לבצע את כל החישוב \( 3+\frac{1}{7+\frac{1}{15}} \); אי אפשר לקחת את \( \frac{22}{7}=3+\frac{1}{7} \) ופשוט “לשתול” את \( 15 \) בתוכו בצורה פשוטה. אבל בואו נראה מה קורה עם הנוסחה:

\( \frac{a_{2}p_{1}+p_{0}}{a_{2}q_{1}+q_{0}}=\frac{15\cdot22+3}{15\cdot7+1}=\frac{333}{106} \)

קסם! תקשיבו לי, זה פשוט קסם! אין לי שמץ של מושג איך זה קורה למרות שלדעתי כבר ראיתי כמה פעמים את ההוכחה. בואו נראה אותה שוב ביחד.

כפי שניתן לנחש, מוכיחים את הטענה באינדוקציה. המקרה הפשוט ביותר שהוא היא רלוונטית הוא \( n=1 \). במקרה הזה, השבר המשולב שלנו הוא \( \left[a_{0},a_{1},a_{2}\right] \) והפיתוחים החלקיים שלו הם

\( \frac{p_{0}}{q_{0}}=\frac{a_{0}}{1} \)

\( \frac{p_{1}}{q_{1}}=a_{0}+\frac{1}{a_{1}}=\frac{a_{0}a_{1}+1}{a_{1}} \)

מאלו אנחנו יכולים להסיק:

\( p_{0}=a_{0},q_{0}=1 \)

\( p_{1}=a_{0}a_{1}+1,q_{1}=a_{1} \)

עבור האיבר הבא החישוב קצת יותר מסובך אבל נעשה אותו במפורש:

\( \frac{p_{2}}{q_{2}}=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}}}=a_{0}+\frac{a_{2}}{a_{2}a_{1}+1}=\frac{a_{2}a_{0}a_{1}+a_{0}+a_{2}}{a_{2}a_{1}+1}= \)

\( =\frac{a_{2}\left(a_{0}a_{1}+1\right)+a_{0}}{a_{2}a_{1}+1}=\frac{a_{2}p_{1}+p_{0}}{a_{2}q_{1}+q_{0}} \)

קיבלנו את הנוסחה במקרה הזה, ועכשיו רק נשאר לסיים באינדוקציה את המקרה הכללי. כאן פשוט חייב לבוא איזה טיעון מתוחכם, כי הנוסחה הזו מפשטת לנו מאוד משהו שנראה מבעית בהתחלה. הנה ההתחכמות: במקרה הכללי, השבר המשולב שמתקבל מהאיברים הראשונים עד \( a_{n} \) הוא

\( \left[a_{0},a_{1},\ldots,a_{n}\right] \)

ועבורו יש לנו את נוסחת הנסיגה

\( \left[a_{0},a_{1},\ldots,a_{n}\right]=\frac{a_{n}p_{n-1}+p_{n-2}}{a_{n}q_{n-1}+q_{n-2}} \)

עכשיו הטיעון המתוחכם: \( p_{n-1},q_{n-1},p_{n-2},q_{n-2} \) מתקבלים מ-\( \left[a_{0},a_{1},\ldots,a_{n-1}\right] \) ומ-\( \left[a_{0},a_{1},\ldots,a_{n-2}\right] \); השברים המשולבים הללו לא תלויים באיבר האחרון, ולכן המספרים הללו יישארו זהים גם אם נשתול בתור האיבר האחרון משהו אחר, למשל את \( a_{n}+\frac{1}{a_{n+1}} \). אבל מה זה \( \left[a_{0},a_{1},\ldots,a_{n-1},a_{n}+\frac{1}{a_{n+1}}\right] \)? אם נפתח את ההגדרה, נראה שזה

\( a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{\cdots+\frac{1}{a_{n}+\frac{1}{a_{n+1}}}}}} \)

כלומר, זה פשוט המספר \( \left[a_{0},a_{1},\ldots,a_{n-1},a_{n},a_{n+1}\right]=\frac{p_{n+1}}{q_{n+1}} \), רק שעבור הצורה הקודמת אפשר להשתמש בנוסחת הנסיגה:

\( \left[a_{0},a_{1},\ldots,a_{n-1},a_{n}+\frac{1}{a_{n+1}}\right]=\frac{\left(a_{n}+\frac{1}{a_{n+1}}\right)p_{n-1}+p_{n-2}}{\left(a_{n}+\frac{1}{a_{n+1}}\right)q_{n-1}+q_{n-2}} \)

זה קצת מזוויע אבל נכפול מונה ומכנה ב-\( a_{n+1} \) ונקבל

\( \frac{\left(a_{n+1}a_{n}+1\right)p_{n-1}+a_{n+1}p_{n-2}}{\left(a_{n+1}a_{n}+1\right)q_{n-1}+a_{n+1}q_{n-2}}=\frac{a_{n+1}\left(a_{n}p_{n-1}+p_{n-2}\right)+p_{n-1}}{a_{n+1}\left(a_{n}q_{n-1}+q_{n-2}\right)+q_{n-1}}=\frac{a_{n+1}p_{n}+p_{n-1}}{a_{n+1}q_{n}+q_{n-1}} \)

וזה בדיוק הביטוי שקיווינו לקבל! זה מסיים את ההוכחה הזו.

בעזרת הנוסחה הזו אפשר לקבל נוסחה מקסימה נוספת, שמקשרת בין \( \frac{p_{n}}{q_{n}} \) ובין האיבר הקודם לו, \( \frac{p_{n-1}}{q_{n-1}} \):

\( q_{n}p_{n-1}-p_{n}q_{n-1}=\left(-1\right)^{n} \)

ההוכחה של זה היא באינדוקציה פשוטה למדי: במקרה הבסיס \( n=1 \) אנו מתבססים על כך שבפיתוח של \( \left[a_{0},a_{1},\ldots,a_{k}\right] \) מקבלים, כמו שכבר ראינו, \( \frac{p_{0}}{q_{0}}=\frac{a_{0}}{1} \) ולכן \( p_{0}=a_{0},q_{0}=1 \) וש-\( \frac{p_{1}}{q_{1}}=a_{0}+\frac{1}{a_{1}}=\frac{a_{0}a_{1}+1}{a_{1}} \), כלומר \( p_{1}=a_{0}a_{1}+1 \) ו-\( q_{1}=a_{1} \). אנו מציבים את זה בנוסחה ומקבלים

\( q_{1}p_{0}-p_{1}q_{0}=a_{1}a_{0}-\left(a_{0}a_{1}+1\right)=1 \)

זה מסיים את המקרה הזה. ובאופן כללי? אם נניח שהקשר מתקיים עבור \( n,n-1 \), בואו נוכיח אותו עבור \( n+1,n \) תוך ניצול נוסחת הנסיגה שכבר מצאנו, שהיא כזכור

\( p_{n+1}=a_{n+1}p_{n}+p_{n-1} \)

\( q_{n+1}=a_{n+1}q_{n}+q_{n-1} \)

נציב את אלו בנוסחה שאנחנו רוצים להוכיח עבורה את הטענה:

\( q_{n+1}p_{n}-p_{n+1}q_{n}=\left(a_{n+1}q_{n}+q_{n-1}\right)p_{n}-\left(a_{n+1}p_{n}+p_{n-1}\right)q_{n}= \)

\( =\left(a_{n+1}q_{n}p_{n}-a_{n+1}p_{n}q_{n}\right)+\left(q_{n-1}p_{n}-p_{n-1}q_{n}\right)= \)

\( =-\left(p_{n-1}q_{n}-q_{n-1}p_{n}\right)=-\left(-1\right)^{n}=\left(-1\right)^{n+1} \)

מה שמסיים גם את זה! עכשיו סוף סוף יש לנו את הכלים שאנחנו צריכים כדי להוכיח את הטענה המקורית שלנו: שעבור \( x \) רציונלי, אם ניקח \( \frac{c}{d} \) חיובי שמקיים

\( \left|x-\frac{c}{d}\right|<\frac{1}{2d^{2}} \)

אז \( \frac{c}{d} \) יופיע בפיתוח לשבר משולב של \( x \). נקודה אחת שצריך לשים לב אליה ולא אוכיח פורמלית היא שהפיתוח לשבר משולב שבו כל האיברים הם שלמים הוא יחיד למעט אפשרות להתחכם קצת בשלב האחרון: אפשר להחליף את \( \left[a_{0},a_{1},\ldots,a_{n}\right] \) ב-\( \left[a_{0},a_{1},\ldots,a_{n}-1,1\right] \), כי \( a_{n}-1+\frac{1}{1}=a_{n} \). אם כן, אם אני אראה שיש ל-\( x \) פיתוח כלשהו לשבר משולב שבו \( \frac{c}{d} \) מופיע לפני הסוף, סיימנו. מצד שני, בזכות ההתחכמות שהראיתי, אפשר תמיד להניח שכשאנחנו לוקחים פיתוח של משהו לשבר משולב, אנחנו יכולים לשלוט על האם הפיתוח הוא מאורך זוגי או אי זוגי, כלומר האם \( q_{n}p_{n-1}-p_{n}q_{n-1} \) הוא 1 או דווקא \( -1 \); אני הולך להשתמש בזה בקרוב.

עכשיו אפשר לגשת סוף סוף לעניינים. מכיוון ש-\( \frac{c}{d} \) הוא עצמו מספר רציונלי, קיים לו פיתוח לשבר משולב שהאיבר האחרון שלו יסומן ב-\( \frac{p_{n}}{q_{n}} \):

\( \frac{c}{d}=\frac{p_{n}}{q_{n}}=\left[a_{0},a_{1},\ldots,a_{n}\right] \)

כאשר כאמור בהמשך אני אגיד אם \( n \) זוגי או לא, בהתאם למה שיתאים לי. הרעיון עכשיו הוא למצוא \( \lambda \) רציונלי כלשהו כך שמתקיים

\( x=\left[a_{0},a_{1},\ldots,a_{n},\lambda\right] \)

שימו לב: זה לא הפיתוח המלא של \( x \) לשברים משולבים! אבל אם \( \lambda\ge1 \) אפשר להמשיך את הפיתוח - לפתח גם את \( \lambda \) לשבר משולב ולהוסיף את זה להמשך הפיתוח. זה נשמע מבלבל, אבל זה בדיוק מה שעשינו בדוגמה של פאי שכל כך התעקשתי עליה משום מה. הגעתי לביטוי כמו

\( \left[3,7,15,1,\frac{854}{33}\right] \)

ואז פשוט המשכתי עם \( \frac{854}{33} \), בעזרת אותה טכניקה שבה מצאתי את האיברים הקודמים בסדרה. אם כן, ה-\( \lambda \) הוא ה-\( \frac{854}{33} \) שלנו כאן - אבל קודם צריך להשתכנע בכך שהוא קיים ושהוא גדול או שווה ל-1.

החלק היפה הוא שאם \( \lambda \) קיים, אנחנו יודעים בדיוק איזו נוסחה שמערבת את \( x \) הוא אמור לקיים, כי זה מה שטרחתי להוכיח קודם:

\( x=\left[a_{0},a_{1},\ldots,a_{n},\lambda\right]=\frac{\lambda p_{n}+p_{n-1}}{\lambda q_{n}+q_{n-1}} \)

אנחנו רוצים לחלץ את \( \lambda \) מפה, אז נכפול את שני האגפים ב-\( \lambda q_{n}+q_{n-1} \) ונקבל

\( \lambda q_{n}x+q_{n-1}x=\lambda p_{n}+p_{n-1} \)

נעביר אגפים ונוציא את \( \lambda \) החוצה:

\( \lambda\left(q_{n}x-p_{n}\right)=p_{n-1}-q_{n-1}x \)

ולסיום נחלק ב-\( q_{n}x-p_{n} \) ונקבל

\( \lambda=\frac{p_{n-1}-q_{n-1}x}{q_{n}x-p_{n}} \)

הביטוי הזה מוגדר תמיד, למעט במקרה שבו \( x=\frac{p_{n}}{q_{n}} \) ואז נקבל במכנה 0; אבל המקרה הזה הוא טריוויאלי, כי \( \frac{p_{n}}{q_{n}} \) הוא כזכור מה שרצינו לטעון שמופיע בפיתוח של \( x \), ולכן אם הוא עצמו \( x \) בוודאי שהוא מופיע!

אז נניח ש-\( x\ne\frac{p_{n}}{q_{n}} \). אנחנו יודעים (זו הייתה ההנחה שלנו) ש-\( \left|x-\frac{p_{n}}{q_{n}}\right|<\frac{1}{2q_{n}^{2}} \) ולכן אפשר לסמן את זה

\( x-\frac{p_{n}}{q_{n}}=\frac{\delta}{2q_{n}^{2}} \)

כאשר \( 0<\left|\delta\right|<1 \). נעביר אגף ונקבל

\( x=\frac{p_{n}}{q_{n}}+\frac{\delta}{2q_{n}^{2}} \)

עכשיו אני רוצה לקחת את זה ולהציב בתוך \( \lambda=\frac{p_{n-1}-q_{n-1}x}{q_{n}x-p_{n}} \). מכיוון שנקבל ביטוי פשוט אבל עם שלב ביניים מסובך, בואו נטפל במונה ובמכנה בנפרד. קודם כל המכנה:

\( q_{n}x-p_{n}=q_{n}\left(\frac{p_{n}}{q_{n}}+\frac{\delta}{2q_{n}^{2}}\right)-p_{n}=p_{n}+\frac{\delta}{2q_{n}}-p_{n}=\frac{\delta}{2q_{n}} \)

אוקיי, זה לא היה כל כך נורא! עכשיו המונה:

\( p_{n-1}-q_{n-1}x=p_{n-1}-\frac{p_{n}q_{n-1}}{q_{n}}-\frac{q_{n-1}\delta}{2q_{n}^{2}} \)

זה נראה מזוויע, אבל זוכרים את הנוסחה \( q_{n}p_{n-1}-p_{n}q_{n-1}=1 \)? היא מתחבאת כאן, רק צריך להעלות את ה-\( p_{n-1} \) הזה למעלה:

\( p_{n-1}-\frac{p_{n}q_{n-1}}{q_{n}}-\frac{q_{n-1}\delta}{2q_{n}^{2}}=\frac{p_{n-1}q_{n}-p_{n}q_{n-1}}{q_{n}}-\frac{q_{n-1}\delta}{2q_{n}^{2}}=\frac{\left(-1\right)^{n}}{q_{n}}-\frac{q_{n-1}\delta}{2q_{n}^{2}} \)

עכשיו, לחלק את זה ב-\( \frac{\delta}{2q_{n}} \) זה כמו לכפול את זה ב-\( \frac{2q_{n}}{\delta} \) (מותר לנו כי \( \delta\ne0 \) כי \( x\ne\frac{p_{n}}{q_{n}} \)). נקבל:

\( \lambda=\frac{2q_{n}}{\delta}\left(\frac{\left(-1\right)^{n}}{q_{n}}-\frac{q_{n-1}\delta}{2q_{n}^{2}}\right)=\left(-1\right)^{n}\frac{2}{\delta}-\frac{q_{n-1}}{q_{n}} \)

וזה יצא… ממש פשוט! עכשיו, כזכור אנחנו רוצים לקבל \( \lambda>1 \); בשביל זה אנחנו חייבים להבטיח שהביטוי \( \left(-1\right)^{n}\frac{2}{\delta} \) ייצא חיובי ולא שלילי, זה מחזיר אותנו לבחירה של \( n \) בהתחלה; אם \( \delta>0 \) אז בוחרים את \( n \) להיות זוגי ומקבלים \( \left(-1\right)^{n}=1 \), ואם \( \delta<0 \) בוחרים \( n \) אי זוגי ומקבלים \( \left(-1\right)^{n}=-1 \). בכל מקרה אנחנו לבסוף מקבלים

\( \lambda=\frac{2}{\left|\delta\right|}-\frac{q_{n-1}}{q_{n}} \)

יותר מזה, בגלל שסדרת המכנים בפיתוח לשבר משולב היא עולה, \( q_{n-1}<q_{n} \) ולכן \( \frac{q_{n-1}}{q_{n}}<1 \) ומצד שני בגלל ש-\( \left|\delta\right|<1 \) אז \( \frac{2}{\left|\delta\right|}>2 \), ואנחנו מקבלים \( \lambda>1 \), כפי שרצינו. אנחנו מפתחים אותו לשבר משולב, מקבלים \( \lambda=\left[b_{1},\ldots,b_{m}\right] \) ולבסוף מקבלים \( x=\left[a_{1},\ldots,a_{n},b_{1},\ldots,b_{m}\right] \) - פיתוח מלא של \( x \) לשבר משולב שבמהלכו מופיע \( \frac{a}{b}=\frac{p_{n}}{q_{n}} \), כפי שרצינו. זה מסיים את ההוכחה!

דברי סיכום ופרידה

ובכן, מה היה לנו הפעם? איך זה היה שונה מהפוסט הקודם שלי על האלגוריתם של שור? האלגוריתם מחולק קונספטואלית לשלושה חלקים; החלק הראשון, של הרדוקציה מבעיית הפירוק לגורמים אל בעיית הפרת הסדר, הוא חלק שהרחבתי עליו מאוד בפוסט ההוא והפעם לא נגעתי בו כי אין לי משהו נוסף לומר, אבל בשני החלקים האחרים הרחבתי לא מעט. ראשית, הצגתי באופן מפורש את שור בתור מקרה פרטי של אלגוריתם הערכת פאזה, שזה משהו שבכלל לא ניסיתי לעשות בפוסט הקודם (בואו לא נדבר על השאלה המביכה עד כמה הבנתי את זה בעצמי). שנית, הפעם התעמקתי קצת יותר במשפט הספציפי שקשור לשברים משולבים שמבטיח לנו שעם קצת מזל, ה-\( \frac{s}{r} \) שאנחנו מחפשים יצוץ מתוך תוצאת אלגוריתם הערכת הפאזה. זה דרש גלישה נוספת לתורת המספרים במקום לחישוב קוונטי, אבל הנושא של שברים משולבים הוא כל כך כיפי שלא יכלתי להתאפק.

לאן הולכים מכאן? בסדרת הפוסטים הקודמת שלי, שור היה המטרה הסופית; אבל בסדרה הנוכחית, אני מקווה שעכשיו משהוצאנו את זה מהדרך, אפשר להראות כל מני דברים לא קשורים בעליל אבל מגניבים לא פחות.