התמרת פורייה הקוונטית

מה זה בכלל ובשביל מה זה טוב?

בסדרת הפוסטים הקודמת שלי על חישוב קוונטי, מטרת העל שלי הייתה הגעה אל האלגוריתם של שור, לפירוק מהיר של מספרים לגורמים. בגלל ההשלכות המהותיות שיהיו לאלגוריתם הזה אם ימומש בפועל בצורה אמינה, הוא הפך להיות “הגביע הקדוש” של הצגה פופולרית של חישוב קוונטי - הפואנטה שמנסים להגיע אליה. וזה גרם לי קצת לרוץ על מה שקורה בדרך אליו, ובפרט דחסתי בהתחלה של הפוסט עליו את הכלי המרכזי שעליו הוא מסתמך - התמרת פורייה המהירה. לכלי הזה מגיע פוסט משל עצמו, ועכשיו סוף סוף אתקן את המעוות.

“התמרת פורייה” היא קסם שמופיע בשלל מקומות ברחבי המתמטיקה. בגדול, הרעיון בה הוא לקחת פריט מידע כלשהו ולפרק אותו לגורמים שמאפשרים לראות דברים שחבויים לרוב מתחת לפני השטח. הדוגמא הקלאסית היא גל קול. התיאור הכללי של גל קול נותן את העוצמה שלו (“אמפליטודה”) לאורך זמן. אם ניקח את גל הקול הזה ונבצע עליו התמרת פורייה, נקבל מעין פירוק שלו לאינספור גלים פשוטים, כאלו שאפשר לתאר בעזרת סינוסים וקוסינוסים, שמתאימים לתדירויות שונות ש”מתחבאות” בתוך גל הקול. אם גל הקול הוא של להקה, אז תדירויות שונות בפירוק הפורייה יתאימו לכלי נגינה שונים - יש תדירויות שמתאימות לסולנית, וכאלו שמתאימות לגיטרה בס, וכאלו שמתאימות לקלידים; ואם נחזק או נחליש תדירויות מסויימות, אז בגל הקול המקורי נשמע טוב יותר או פחות את כלי הנגינה המתאים. זה סוג של ניתוח שאפשר לבצע באמצעות התמרת פורייה שנותן אינטואיציה גם להפעלה שלה על תחומים שונים בעליל.

בפוסט הזה אני לא אכנס לשימושים - בפוסט הבא יופיע שימוש חזק מאוד, שנקרא הערכת פאזה והוא מה שמוביל גם לאלגוריתם של שור. אני אסתפק בלהציג את ההגדרות הפורמליות ואיך עושים את זה קוונטית.

מה זו התמרת פורייה?

יש לי סדרה של פוסטים על התמרות פורייה למיניהן, אז לא אכנס כאן לתיאור רחב של כל הסוגים שלהן והקשרים ביניהם (אבל יש הרבה סוגים ויש קשרים ביניהם וזה מגניב). מה שמעניין אותנו ספציפית בפוסט הזה הוא מה שנקרא התמרת פורייה הבדידה ומוגדר כך:

אם \( N \) הוא מספר טבעי כלשהו ו-\( \left(a_{0},a_{1},\ldots,a_{N-1}\right)\in\mathbb{C}^{N} \) היא סדרה של \( N \) מספרים מרוכבים, אז התמרת פורייה הבדידה שלה היא סדרה אחרת של \( N \) מספרים מרוכבים, \( \left(b_{0},\ldots,b_{N-1}\right) \) שמקיימת

\( b_{j}=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}a_{k}e^{\frac{2\pi i}{N}jk} \)

זו נוסחה טיפה מפחידה במבט ראשון ויהיה קריטי לנו להתרגל אליה, אז בואו נדבר שניה על מה זה \( e^{\frac{2\pi i}{N}jk} \). זו בסך הכל שיטת סימון למספר מרוכב מסוים, ולא סתם מספר מרוכב אלא שורש יחידה מסדר \( N \), כלומר מספר מרוכב \( z \) שמקיים \( z^{N}=1 \). למשל, שורשי היחידה מסדר 4 הם \( \left\{ 1,-1,i,-i\right\} \). אז התמרת פורייה הבדידה היא בסך הכל “כדי לקבל את האיבר ה-\( k \) של ההתמרה, בואו נחבר את כל ה-\( a \)-ים של הסדרה המקורית כשהם מוכפלים בשורשי יחידה מסויימים ש-\( k \) מגדיר לנו”. זה הכל, וזה לא כזה נורא מבחינה קונספטואלית.

איך כל זה קשור למספר \( e \)? ובכן, אחת הנוסחאות הבסיסיות באנליזה מרוכבת היא נוסחת אוילר:

\( e^{i\theta}=\cos\theta+i\sin\theta \)

על המספר המרוכב \( \cos\theta+i\sin\theta \) אפשר לחשוב בתור נקודה במישור, עם קואורדינטות \( \left(\cos\theta,\sin\theta\right) \); אם זוכרים ש-\( \cos^{2}\theta+\sin^{2}\theta=1 \) אז רואים שהמרחק של הנקודה הזו מראשית הצירים הוא 1, כך שאפשר לחשוב על כל הנקודות מהצורה הזו בתור מעגל - מעגל היחידה. הזווית \( \theta \) היא הזווית שיוצר קו מראשית הצירים אל הנקודה הזו ביחס לכיוון החיובי של ציר \( x \).

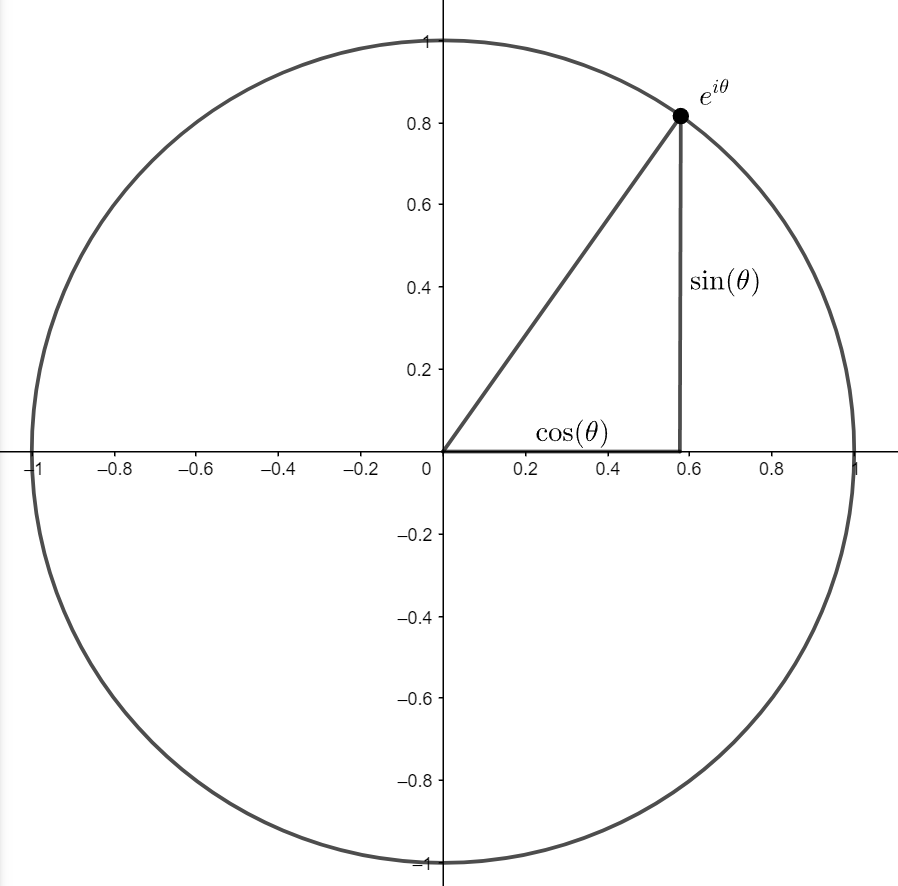
לא כזה קריטי להבין מדוע הנוסחה הזו נכונה עכשיו - מבחינתנו אפשר לחשוב עליה בתור דרך קומפקטית לכתוב מספרים מרוכבים. מה שרלוונטי לנו הוא להבין מה קורה אם מציבים \( \theta=2\pi \). במקרה הזה, אפשר לחשוב על המספר בתור מה שמקבלים כשמתחילים על הנקודה \( \left(1,0\right) \) במישור ואז מבצעים סיבוב של \( 2\pi \) מעלות סביב ראשית הצירים. כזכור, \( 2\pi \) זו הדרך להגיד ברדיאנים את מה שנקרא “360 מעלות” בשפת בני אנוש - סיבוב שלם, שמחזיר אותנו אל \( \left(1,0\right) \). שורשי היחידה הם מה שמקבלים כשלוקחים את הסיבוב השלם הזה וחותכים אותו לחתיכות מאורך שווה - למשל, שורשי היחידה מסדר 4 מתקבלים כשמחלקים את ה-360 מעלות הללו ל-4, ומקבלים סיבובים של 90 מעלות, או \( \frac{\pi}{2} \) בשפת הרדיאנים. כך למשל \( i=e^{i\frac{\pi}{2}} \).

את הביטוי המפחיד \( e^{\frac{2\pi i}{N}jk} \) אפשר להציג, אם כן, בתור דבר קצת יותר רגוע:

\( e^{\frac{2\pi i}{N}jk}=\left(e^{i\cdot\frac{2\pi}{N}k}\right)^{j} \)

כלומר, כדי לחשב את \( b_{j} \), אנחנו קודם כל לוקחים את שורשי היחידה מסדר \( N \), שהם איברים מהצורה \( e^{i\cdot\frac{2\pi}{N}\cdot k} \) עבור \( k=0,1,\ldots,N-1 \), ואז אנחנו מעלים את כולם בחזקת \( j \), כופלים ב-\( a_{n} \)-ים המתאימים ומחברים. למשל, עבור \( N=4 \):

\( b_{j}=a_{0}\cdot1^{j}+a_{1}\cdot i^{j}+a_{2}\cdot\left(-1\right)^{j}+a_{3}\cdot\left(-i\right)^{j} \)

זה יניב כל מני סכומים מורכבים יותר ופחות, כתלות בערך של \( k \). למשל עבור \( j=0 \) נקבל פשוט

\( b_{0}=\frac{1}{2}\left(a_{0}+a_{1}+a_{2}+a_{3}\right) \)

עבור \( j=1 \) כל שורשי היחידה השונים יככבו בסכום:

\( b_{1}=\frac{1}{2}\left(a_{0}+ia_{1}-a_{2}-ia_{3}\right) \)

עבור \( j=2 \) דברים הולכים להתבטל כי \( \left(-1\right)^{2}=1 \) ו-\( \left(\pm i\right)^{2}=-1 \):

\( b_{2}=\frac{1}{2}\left(a_{0}-a_{1}+a_{2}-a_{3}\right) \)

וכן הלאה - אני מקווה שהעיקרון ברור.

החישוב של ההתמרה לא נראה פה כמו עניין קשה במיוחד, והוא באמת לא קשה במיוחד אם \( N \) לא גדול. אבל אנחנו רוצים כן לטפל במקרה שבו \( N \) גדול. חישוב נאיבי של ההתמרה לוקח בערך \( O\left(N^{2}\right) \) פעולות, אבל היופי בכל הסיפור הזה הוא שקיימות שיטות מחוכמות לביצוע מהיר של התמרת פורייה הזו, שלוקחות זמן של \( O\left(N\log N\right) \). יש לי תיאור של אחת מהשיטות הללו בבלוג וזה אכן יופי של דבר. כל הדברים הללו קשורים לחישוב קלאסי, בלי מחשב קוונטי.

בחישוב קוונטי אפשר לבצע את התמרת פורייה הזו בזמן \( O\left(\log^{2}N\right) \). שימו לב להבדל: בהתמרה קלאסית, הזמן הוא \( O\left(N\log N\right) \). בקוונטית הוא \( O\left(\log^{2}N\right) \). זה שינוי עצום. אנחנו נעבוד עם המקרה שבו \( N=2^{n} \) עבור \( n \) כלשהו; במקרה הזה, \( O\left(\log^{2}N\right)=O\left(n^{2}\right) \) בזמן ש-\( O\left(N\log N\right)=O\left(n\cdot2^{n}\right) \) - אקספוננציאלי ב-\( n \) מול פולינומי ב-\( n \). זו הדגמה יפה מאוד של הכוח של חישוב קוונטי ביחס לחישוב רגיל.

אבל מה? התמרת פורייה הקוונטית היא גם המחשה מצויינת לחולשה של חישוב קוונטי אל מול חישוב רגיל. בחישוב רגיל, אנחנו מתחילים עם הסדרה \( a_{0},a_{1},\ldots,a_{N-1} \) ביד ומסיימים עם הסדרה \( b_{0},b_{1},\ldots,b_{N-1} \) ביד; לעומת זאת בחישוב קוונטי מה שיהיה לנו בסוף הוא סופרפוזיציה כלשהי של אברי הסדרה \( b_{0},b_{1},\ldots,b_{N-1} \) (ההגדרה המדויקת תכף תגיע). אנחנו לא יודעים לקרוא את ה-\( b \)-ים מתוך הסופרפוזיציה הזו; רק למדוד אותה ולקוות לטוב, או לעשות איתה עוד דברים בהמשך החישוב, ואז למדוד אותה ולקוות לטוב. ה”מידע” של התמרת הפורייה לא נגיש לנו ישירות, אלא רק דרך אפקט עקיף. כפי שנראה בהמשך, גם האפקט העקיף הזה יכול להיות חזק מאוד, בשימושים המתאימים.

איך נראית התמרת פורייה הקוונטית?

כאשר \( N=2^{n} \), התמרת פורייה הקוונטית היא אופרטור שפועל על \( n \) קיוביטים. כזכור, המצב הכללי של \( n \) קיוביטים הוא סופרפוזיציה מהצורה \( \sum_{x\in\left\{ 0,1\right\} ^{n}}\alpha_{x}\left|x\right\rangle \), כאשר ה-\( \left|x\right\rangle \)-ים הללו הם אברי הבסיס של המצב הקוונטי. בשביל התמרת פורייה אנקוט בשיטת סימון טיפ-טיפה שונה: הרי על כל \( x\in\left\{ 0,1\right\} ^{n} \) כזה אפשר לחשוב בתור ייצוג בינארי של מספר, למשל \( 110 \) הוא הייצוג הבינארי של \( 1\cdot2^{2}+1\cdot2^{1}+0\cdot2^{0}=6 \). אז במקום לדבר על המצב \( \left|110\right\rangle \) אני אדבר על המצב \( \left|6\right\rangle \). ובאופן כללי - המצבים שלי יהיו מהצורה \( \left|j\right\rangle \) כאשר \( 0\le j\le N-1 \).

שימו לב כי בשיטת הייצוג הזו, הערך של הקיוביט הראשון הוא הספרה המשמעותית ביותר ב-\( j \) והערך של הקיוביט האחרון הוא הספרה הכי פחות משמעותית; זו בחירה שרירותית, כמובן, אבל היא תשפיע על הסימונים שלנו מכאן ואילך.

כעת, כדי להגדיר אופרטור אוניטרי על \( n \) קיוביטים, מספיק להגדיר אותו על אברי הבסיס. אז הבה ונגדיר את האופרטור \( \text{QFT}_{N} \) (ראשי תיבות של Quantum Fourier Transform):

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle \)

כלומר, אם אנחנו מפעילים את \( \text{QFT}_{N} \) על סופרפוזיציה \( \sum_{j=0}^{N-1}a_{j}\left|j\right\rangle \), הפלט יהיה

\( \sum_{j=0}^{N-1}a_{j}\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle =\sum_{k=0}^{N-1}\left(\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}a_{j}e^{\frac{2\pi i}{N}jk}\right)\left|k\right\rangle = \)

\( =\sum_{k=0}^{N-1}b_{k}\left|k\right\rangle \)

כלומר, כשמפעילים את \( \text{QFT}_{N} \) על סופרפוזיציה שמקדמיה הם הסדרה \( \left(a_{0},a_{1},\ldots,a_{N-1}\right) \) מקבלים כפלט סופרפוזיציה שמקדמיה הם הסדרה \( \left(b_{0},\ldots,b_{N-1}\right) \). כלומר, במקרה הזה גם סדרת הקלט וגם סדרת הפלט נתונות בצורה מובלעת; לא בתור קלט מפורש אלא בתור מקדמים של סופרפוזיציה.

ההגדרה \( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle \) מתאימה להגדרה ה”קלאסית”, ותהיה מוכרת ונעימה למי שרגילים להתמרת פורייה הבדידה. אבל יש עוד דרך לתאר את אגף ימין פה - לא בתור סכום של \( 2^{n} \) מצבים על \( n \) קיוביטים, אלא בתור מכפלה טנזורית של \( n \) מצבים, אחד לכל קיוביט. שיטת הייצוג הנוספת הזו תהיה חדשה גם למי שמכירים את התמרת פורייה, ובמבט ראשון היא תהיה מפחידה ביותר. כל כך מפחידה, עד שגם אני, כשכתבתי בעבר דברים על התמרת פורייה הקוונטית, ניסיתי בכוח להתחמק ממנה - עד שהגעתי לשימושים בפועל בה וזה התפוצץ לי בפרצוף. האמת היא ששיטת הייצוג הזו היא גם נוחה מאוד לשימוש וגם לא כזו נוראית, אחרי שמתרגלים אליה. ומכיוון שאני לא מאמין בלשמור אתכם במתח אני אציג אותה מייד, וננסה להבין מה הולך שם ולמה זה מתאים להגדרה ה”רגילה”:

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)\frac{1}{\sqrt{N}}\bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right)= \)

\( =\frac{\left(\left|0\right\rangle +e^{2\pi i0.j_{n}}\left|1\right\rangle \right)\otimes\left(\left|0\right\rangle +e^{2\pi i0.j_{n-1}j_{n}}\left|1\right\rangle \right)\otimes\cdots\otimes\left(\left|0\right\rangle +e^{2\pi i0.j_{1}\ldots j_{n}}\left|1\right\rangle \right)}{\sqrt{N}} \)

ככל הנראה הדבר הכי קשה לעיכול בנוסחה הזו הוא מה שקורה בחזקה של \( e \), אז אני אתחיל עם זה. בואו ננסה להבין איך נראה האיבר \( e^{\frac{2\pi i}{N}jk} \) עבור \( j \) כלשהו. נתחיל עם המקרה שבו \( k=1 \). ראשית, אפשר לכתוב \( e^{\frac{2\pi i}{N}jk}=e^{2\pi i\cdot\frac{j}{N}} \), כלומר החלק שאנחנו צריכים להבין הוא את \( \frac{j}{N} \). שנית, אנחנו יודעים ש-\( 0\le j\le N-1 \), ולכן \( \frac{j}{N} \) הולך להיות שבר: מספר בין 0 ל-1. מספרים כאלו אנחנו מייצגים בדרך כלל בייצוג עשרוני, נאמר \( 0.125 \) בא לתאר את הסכום

\( 1\cdot\frac{1}{10}+2\cdot\frac{1}{100}+5\cdot\frac{1}{1000}=\frac{125}{1000}=\frac{1}{8} \)

כמו שאפשר לראות מהדוגמא, קל להבין איך ייראו הספרות של שבר כלשהו אם יש לנו הצגה שלו חלקי חזקה כלשהי של 10: מכיוון שהשבר שלנו היה מהצורה \( \frac{125}{1000} \), ידענו שהוא ייכתב בתור \( 0.125 \). אם אני מסתכל על השבר \( \frac{523}{1000} \) אני כבר יודע שהוא ייכתב בתור \( 0.523 \).

ומה קורה אם אני רוצה להציג את המספר לא בשיטה העשרונית, אלא בשיטה הבינארית? בשיטה הזו אני עדיין יכול לכתוב ספרות שהן או 0 או 1 מימין לנקודה, ולקבל סכום של חזקות שליליות של 2. אם נסתכל על מספר עם שלוש ספרות מימין לנקודה, \( 0.j_{1}j_{2}j_{3} \), הוא מייצג את

\( j_{1}\cdot\frac{1}{2^{-1}}+j_{2}+\frac{1}{2^{-2}}+j_{3}\cdot\frac{1}{2^{-3}} \)

ובאופן כללי, \( 0.j_{1}j_{2}\ldots j_{n} \) הולך לייצג את \( \sum_{r=1}^{n}j_{r}\frac{1}{2^{r}} \). וכמו במקרה העשרוני, אם יש לי מספר שברי שמראש נתון בתור “משהו חלקי חזקה של 2”, ברור לי איך ייראה הייצוג שלו: אם החזקה שבמכנה היא \( 2^{n} \), אז אני אקח ייצוג בינארי שלו בעזרת \( n \) ספרות, והן מה שיופיע מימין לנקודה. במילים אחרות, אם נתון לי \( \frac{j}{2^{n}} \), אז אני אכתוב את \( j \) בתור \( j=\sum_{r=1}^{n}j_{r}2^{n-r} \) (כלומר, כאן \( j_{1} \) היא הספרה המשמעותית ביותר, \( j_{2} \) הבאה בתור אחריה וכן הלאה; לרוב אנחנו עושים ההפך ולכן זו עשויה להיות נקודה מבלבלת). ואז אני אקבל את הייצוג הבינארי השברי

\( \frac{j}{2^{n}}=0.j_{1}j_{2}\ldots j_{n} \)

אם הנקודה הזו (שלא קשורה לקוונטים או לאלגברה לינארית, סתם לייצוג של מספרים בבסיסי ספירה שונים) ברורה לכם - ברכותי! אני מקווה שהרע ביותר כבר מאחורינו.

עכשיו, מה קורה אם אני לוקח את המספר \( \frac{j}{2^{n}}=0.j_{1}j_{2}\ldots j_{n} \) ומכפיל אותו פי 2? כמו שהכפלת ייצוג עשרוני רגיל ב-10 מזיזה את כל הספרות צעד אחד שמאלה, למשל \( 10\cdot0.125=1.25 \), אז גם בייצוג בינארי כל הספרות יזוזו צעד אחד שמאלה:

\( 2\cdot\frac{j}{2^{n}}=j_{1}.j_{2}j_{3}\ldots j_{n} \).

ובאופן כללי, אם אנחנו כופלים בחזקה כלשהי של 2, נאמר \( 2^{t} \) כאשר \( t\le n \), האפקט יהיה הזזת הספרות \( t \) צעדים שמאלה:

\( 2^{t}\cdot\frac{j}{2^{n}}=j_{1}j_{2}\ldots j_{t}.j_{t+1}\ldots j_{n} \).

אוקיי, התרגלנו קצת לצורת הכתיב הזו. עכשיו מגיע הפאנץ’. בואו נחזור שניה אל הביטוי \( e^{\frac{2\pi i}{N}jk} \) שכבר ראינו לא מעט כאן. אני יכול לכתוב אותו שוב פעם באופן קצת שונה: \( e^{2\pi i\cdot\left(k\cdot\frac{j}{N}\right)} \). כעת, מכיוון שאצלנו \( N=2^{n} \) אפשר לכתוב אותו בתור

\( e^{2\pi i\cdot\left(k\cdot\frac{j}{2^{n}}\right)} \)

ואם נניח ש-\( k \) הוא חזקה כלשהי של 2, נאמר \( k=2^{n-t} \) (למה לא \( k=2^{t} \)? כי דווקא בראשון נשתמש בהמשך), אז אפשר לכתוב

\( k\cdot\frac{j}{2^{n}}=j_{1}j_{2}\ldots j_{n-t}.j_{n-t+1}\ldots j_{n} \)

ועכשיו הפאנץ’: את כל החלק שמשמאל לנקודה הבינארית אנחנו יכולים להעלים. למה? בגלל שיש לנו אקספוננט בחזקת \( 2\pi i \) כפול משהו. בואו נראה את זה: אם יש לי מספר מהצורה \( a+b \) כך ש-\( a \) הוא מספר שלם, אז מתקיים

\( e^{2i\pi\left(a+b\right)}=e^{2i\pi a}\cdot e^{2i\pi b}=\left(e^{2i\pi}\right)^{a}\cdot e^{2i\pi b}=1\cdot e^{2i\pi b}=e^{2i\pi b} \)

כלומר, כל החלק של \( a \) נעלם, כי הוא מייצג כמות שלמה של סיבובים מלאים סביב ראשית הצירים, שלא משפיעה על התוצאה הסופית. איפה היה חשוב ש-\( a \) הוא שלם? במעבר \( e^{2i\pi a}=\left(e^{2i\pi}\right)^{a} \) שאינו נכון באופן כללי אבל כן נכון עבור שלמים.

חזרה אל המקרה שלנו, שבו יש לנו מספר בייצוג בינארי שאפשר להפריד לסכום של “מה שמשמאל לנקודה” ו”מה שמימין לנקודה”:

\( k\cdot\frac{j}{2^{n}}=j_{1}j_{2}\ldots j_{n-t}.j_{n-t+1}\ldots j_{n}=j_{1}j_{2}\ldots j_{n-t}+0.j_{n-t+1}\ldots j_{n} \)

ולכן נקבל, עבור \( k=2^{n-t} \), שמתקיים

\( e^{2\pi i\cdot\left(k\cdot\frac{j}{2^{n}}\right)}=e^{2\pi i0.j_{n-t+1}\ldots j_{n}} \)

וזה בדיוק מה שהופיע בנוסחה המוזרה של \( \text{QFT} \) שנתתי:

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)\frac{1}{\sqrt{N}}\bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

כלומר, הבנו את המשמעות של הרכיב הכי בעייתי בנוסחה; עכשיו בואו נבין למה היא נכונה ושקולה אל

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle \)

אין כאן יותר מאשר חישוב טכני. אני לא אוהב דברים שאין בהם יותר מאשר חישוב טכני. קשה לפתח ככה אינטואיציה, והרבה ספרים פשוט נותנים את החישוב הטכני וזהו. אז לפני שנעשה את החישוב הטכני, בואו נראה דוגמא קצת יותר פשוטה: הפולינום \( \left(1+x\right)\left(1+x^{2}\right)\left(1+x^{3}\right) \).

נניח שנותנים לנו את הפולינום הזה ומבקשים מאיתנו לפתוח סוגריים. זה יהיה טכני, אין ספק, אבל מה בעצם נעשה? אנחנו בעצם יוצרים 8 שלשות: כל שלשה נבנית על ידי כך שאני בוחר איבר מהסוגריים הראשונים, איבר מהשניים ואיבר מהשלישיים, וכופל את כולם. את כל 8 התוצאות שאקבל אני מחבר. עכשיו, בגלל שבכל אחד מהסוגריים אחד האיברים הוא 1, הכפלה בו לא עושה כלום, מה שדי מפשט את מה שאני מקבל:

\( 1+x+x^{2}+x^{3}+x\cdot x^{2}+x\cdot x^{3}+x^{2}\cdot x^{3}+x\cdot x^{2}+x^{3}= \)

\( =1+x+x^{2}+x^{3}+x^{3}+x^{4}+x^{5}+x^{6} \)

עכשיו אפשר לעשות את אותו דבר עם המכפלה הטנזורית שלנו:

\( \bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

כזכור, מה שיפה במכפלות טנזוריות הוא שהן משחקות יפה עם חוקי הכפל והחיבור הרגילים. אם למשל יש לי את המכפלה הפשוטה יחסית

\( \left(\left|0\right\rangle +a\left|1\right\rangle \right)\otimes\left(\left|0\right\rangle +b\left|1\right\rangle \right) \)

ואני פותח את המכפלה על פי חוקי הדיסטריביוטיביות, כמו שכבר ראינו שאפשר לעשות במהלך סדרת הפוסטים הזו, אז אני אקבל

\( \left|00\right\rangle +b\left|01\right\rangle +a\left|10\right\rangle +ab\left|11\right\rangle \)

כלומר, על ידי התבוננות בספרות של \( \left|x\right\rangle \) אני יודע אילו איברים יופיעו במקדם של האיבר הזה: אם הספרה השמאלית, המשמעותית יותר, היא 1 אז יופיע \( a \), ואם הספרה הימנית היא 1 אז יופיע \( b \), ואם שתיהן 1 אז שניהם יופיעו. אותו הדבר יקרה גם עבור הביטוי

\( \bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

כשאני אפתח אותו, אני אקבל סכום של כל האיברים מהצורה \( \left|x\right\rangle \) כך של-\( x \) יש \( n \) ספרות, והמקדמים של ה-\( \left|x\right\rangle \) הזה יהיו מכפלות של כל ה-\( e \)-ים המפלצתיים שמתאימים לכניסות של \( x \) שהן 1.

עכשיו, כשאני מרגיש שהבנו קצת יותר טוב מה הולך ב”ביטוי המפלצתי”, אני דווקא רוצה לחזור אל ההגדרה ה”רגילה” של ההתמרה:

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle \)

ובואו ננסה להגיע ממנה אל “הביטוי המפלצתי”. הדבר היחיד בהגדרה הרגילה שעדיין לא מסתדר לנו טוב הוא ה-\( k \) הזה. כזכור, הפישוט המאוד נחמד של \( e^{2\pi i\cdot\left(k\cdot\frac{j}{2^{n}}\right)} \) שעשיתי קודם שבו נפטרתי מכל הספרות משמאל לנקודה הניח ש-\( k \) הוא חזקה של 2 וזה בוודאי לא מה שקורה כשמריצים את \( k \) על כל המספרים מ-0 עד \( N-1 \). כדי להתמודד עם הבעיה הזו, אנחנו עוברים להתבונן על הייצוג הבינארי של \( k \). מכיוון ש-\( 0\le k\le N-1=2^{n}-1 \) אפשר לייצג את \( k \) בעזרת \( n \) ספרות בינאריות. נכתוב \( k=k_{1}k_{2}\ldots k_{n} \), כלומר שוב ה-\( k_{1} \) יהיה הספרה המשמעותית ביותר, מה שאומר שבייצוג בתור סכום נקבל

\( k=\sum_{t=1}^{n}2^{n-t}k_{t} \)

זוכרות שקודם מתישהו כפלתי ב-\( 2^{n-t} \) במקום ב-\( 2^{t} \) שנראה יותר טבעי? אז הנה איך \( 2^{n-t} \) צץ לו.

עכשיו אפשר להתחיל לעשות חשבון:

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle = \)

\( =\frac{1}{\sqrt{N}}\sum_{k_{1}k_{2}\ldots k_{n}=0}^{N-1}e^{\frac{2\pi i}{N}j\sum_{t=1}^{n}2^{n-t}k_{t}}\left|k_{1}\ldots k_{n}\right\rangle = \)

\( \frac{1}{\sqrt{N}}\sum_{k_{1}k_{2}\ldots k_{n}=0}^{N-1}\prod_{t=1}^{n}e^{\frac{2\pi i}{N}j2^{n-t}k_{t}}\left|k_{1}\ldots k_{n}\right\rangle = \)

כשהמעבר האחרון נובע מכך שחיבור במעריך של \( e \) הופך למכפלה, כמו בנוסחה \( e^{a+b}=e^{a}\cdot e^{b} \).

נעצור עכשיו לשניה ונסתכל על מה שהולך במעריך של ה-\( e \) הזה: אם \( k_{t}=0 \), אז \( e^{\frac{2\pi i}{N}j2^{n-t}k_{t}}=e^{0}=1 \) - המקדם נעלם כולו. אם לעומת זאת \( k_{t}=1 \) אנחנו נשארים עם \( e^{\frac{2\pi i}{N}j2^{n-t}}=e^{2\pi i\cdot0.0.j_{n-t+1}\ldots j_{n}} \) שכבר מוכרים לנו בשלב הזה. אם כן, הדבר העיקרי שאנחנו צריכים לעשות עכשיו הוא לעבור מסכום של \( N \) מכפלות של \( n \) איברים אל מכפלה הטנזורית של \( n \) איברים שכל אחד מהם הוא סכום של שניים:

\( \frac{1}{\sqrt{N}}\sum_{k_{1}k_{2}\ldots k_{n}=0}^{N-1}\prod_{t=1}^{n}e^{\frac{2\pi i}{N}j2^{n-t}k_{t}}\left|k_{1}\ldots k_{n}\right\rangle = \)

\( =\frac{1}{\sqrt{N}}\bigotimes_{t=1}^{n}\left(e^{\frac{2\pi i}{N}j2^{n-t}\cdot0}\left|0\right\rangle +e^{\frac{2\pi i}{N}j2^{n-t}\cdot1}\left|1\right\rangle \right) \)

ועל פי הפישוטים שהראיתי לפני רגע, אנחנו מקבלים

\( \frac{1}{\sqrt{N}}\bigotimes_{t=1}^{n}\left(e^{\frac{2\pi i}{N}j2^{n-t}\cdot0}\left|0\right\rangle +e^{\frac{2\pi i}{N}j2^{n-t}\cdot1}\left|1\right\rangle \right)= \)

\( =\frac{1}{\sqrt{N}}\bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

וזו בדיוק הנוסחה שרצינו. זהו, החלק הגרוע ביותר הסתיים - עכשיו אנחנו יודעים איך התמרת הפורייה הקוונטית נראית בצורה שלה שתהיה לנו שימושית יותר, וגם יהיה לנו יחסית קל להבין למה המעגל הקוונטי שתכף אתאר מחשב אותה. יש רק עוד פישוט אחד אחרון שאולי כדאי לעשות: מכיוון ש-\( N=2^{n} \) הרי שאפשר לכתוב \( \sqrt{N}=2^{\frac{n}{2}} \) ולקבל את הנוסחה

\( \frac{1}{2^{n/2}}\bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

ולפעמים אפילו כותבים

\( \bigotimes_{t=1}^{n}\frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

בתור התמרת פורייה הקוונטית. אני אישית מאוד מחבב את הצורה האחרונה, כי אחרי שמתעסקים מספיק זמן עם חישוב קוונטי כבר מתרגלים לאהוב \( \sqrt{2} \) מוזרים שנדחפים לכל מקום, וכפי שנראה עוד רגע - זו גם תהיה הצורה הכי מועילה עבורנו.

אז איך מחשבים את זה?

סיכום החלק הקודם הוא פשוט: אנחנו רוצים לממש אופרטור קוונטי בשם \( \text{QFT}_{N} \) שמקיים

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\bigotimes_{t=1}^{n}\frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

הייצוג באגף ימין, שנראה אולי מפחיד בהתחלה, מועיל מאוד להבין מה צריך לעשות, כי זה ייצוג של מצב קוונטי בצורה פשוטה מאוד, שבה המצב של כל קיוביט מתואר בנפרד. זה לא מצב שזור; כדי להבין איך מגיעים אליו מספיק להסתכל על כל קיוביט בתורו.

ראשית, בואו ניזכר בזהירות מה הקלט שלנו פה. יש למעגל \( n \) קיוביטים, והמצב שלהם הוא \( \left|j\right\rangle \), שאותו אני מתאר בתור \( \left|j_{1}j_{2}\ldots j_{n}\right\rangle \) - כל \( j_{t} \) כאן הוא או 0 או 1.

עכשיו, בואו נתחיל מהערך שאמור להגיע אל הקיוביט הראשון. כלומר, בנוסחה לעיל זה המקרה \( t=1 \) - המצב הבא:

\( \frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.j_{n}}\left|1\right\rangle \right) \)

זה מצב פשוט מאוד, אבל הוא מסווה את זה היטב עם השימוש הזה ב-\( e \). בואו נראה את זה: ל-\( j_{n} \) יש בדיוק שני ערכים אפשריים: או 0 או 1. אם \( j_{n}=0 \) אז \( e^{2\pi i0.j_{n}}=1 \) ולכן המצב הוא \( \frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} \). אם לעומת זאת \( j_{n}=1 \) אז \( 0.j_{n}=\frac{1}{2} \) (זכרו - \( 0.j_{n} \) הוא לא ייצוג עשרוני אלא ייצוג בינארי) ולכן \( e^{2\pi i0.j_{n}}=e^{\pi i}=-1 \) (סיבוב של 180 מעלות) ונקבל \( \frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}} \).

אז במילים אחרות, המצב שצריך לקבל תלוי בערך של \( j_{n} \), והוא

\( \begin{cases} \frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} & j_{n}=0\\ \frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}} & j_{n}=1 \end{cases} \)

נראה מוכר? המצב הזה הוא בדיוק התוצאה של \( H\left(\left|j_{n}\right\rangle \right) \). ככה \( H \) מוגדר. אז ברור לנו מה לעשות - כדי לקבל את הערך שאמור להגיע אל הקיוביט הראשון אנחנו רק צריכים להפעיל \( H \) על הקיוביט \( \left|j_{n}\right\rangle \), כלומר על הקיוביט האחרון. רגע רגע רגע, משהו לא מסתדר פה.

תזכרו - אם אנחנו מפעילים \( H \) על הקיוביט האחרון אנחנו משנים את הקיוביט האחרון. זה מה ששערים עושים - משנים את הקיוביט שעליו הם מופעלים. אז מה נעשה? פשוט מאוד: נפעיל את \( H \) על הקיוביט האחרון. למעשה, כל מה שיקרה מעתה ואילך הולך לייצר לנו את הפלטים בסדר הפוך ממה שרצינו בהתחלה. זה לא נורא, כי אחרי שמסיימים לייצר את המצב שרצינו רק עם סדר קיוביטים הפוך, אפשר להפעיל שערי SWAP שמחליפים את הקיוביטים.

פורמלית, שער SWAP על שני קיוביטים מוגדר כך:

\( \text{SWAP}\left(\left|00\right\rangle \right)=\left|00\right\rangle \)

\( \text{SWAP}\left(\left|01\right\rangle \right)=\left|10\right\rangle \)

\( \text{SWAP}\left(\left|10\right\rangle \right)=\left|01\right\rangle \)

\( \text{SWAP}\left(\left|11\right\rangle \right)=\left|11\right\rangle \)

אם נפעיל אותו על שני קיוביטים לא שזורים, שאחד במצב \( \alpha\left|0\right\rangle +\beta\left|1\right\rangle \) והשני במצב \( \gamma\left|0\right\rangle +\delta\left|1\right\rangle \), כלומר הם במצב המשותף

נגיע אל המצב

כלומר, זה ישיג בדיוק את האפקט שרצינו, של החלפת הקיוביטים. איך אפשר לממש \( \text{SWAP} \) שכזה? אפשר כמובן לעשות את זה כבר ברמת החומרה של המחשב הקונטי, אבל אפשר גם להשתמש בשלושה שערי \( \text{CX} \) בזה אחר זה:

\( \text{SWAP}_{1,2}=\text{CX}_{1,2}\text{CX}_{2,1}\text{CX}_{1,2} \)

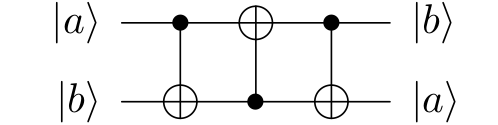
עשו את החישוב בעצמכם על ארבעת אברי הבסיס ותראו שהבניה הזו אכן עובדת. אז שערי SWAP הם לא בעיה משמעותית, ומעתה ואילך נמשיך לבנות את המעגל של התמרת הפורייה הקוונטית בלי לחשוש מכך שהוא מייצר לנו את הפלטים בסדר הפוך.

נעבור עכשיו אל המצב השני שצריך לייצר: \( \frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-1}j_{n}}\left|1\right\rangle \right) \). כאן הסיפור כבר מסתבך כי בחזקה של \( e \) מעורבות שתי ספרות של \( j \), גם \( j_{n} \) וגם \( j_{n-1} \). אם קודם פעלנו על הקיוביט \( \left|j_{n}\right\rangle \), עכשיו אנחנו רוצים לפעול על \( \left|j_{n-1}\right\rangle \), אבל מכיוון שהמצב שאנחנו צריכים להגיע אליו מערב גם את \( j_{n} \) ברור שהקיוביט \( \left|j_{n}\right\rangle \) צריך להשפיע איכשהו. ההשפעה שלו תבוא לידי ביטוי בכך שנפעיל על \( \left|j_{n-1}\right\rangle \) שער מותנה, כלומר כזה שמופעל אם \( j_{n}=1 \) ולא מופעל אם \( j_{n}=0 \). בשביל שזה יעבוד כמו שצריך, השער המותנה הזה צריך להיות מופעל לפני שאנחנו עושים את ה-\( H \) על \( \left|j_{n}\right\rangle \), אחרת נקבל סמטוחה; זכרו שכדי לייצר מצב שזור (שזה לא מה שאנחנו רוצים פה!) מפעילים \( H \) על קיוביט כלשהו ואז \( CX \) על קיוביט אחר, כך שה-\( CX \) מותנה בקיוביט שהפעלנו עליו \( H \). כלומר, מה שאני מתאר עכשיו הולך לקרות לפני הפעלת ה-\( H \) על \( \left|j_{n}\right\rangle \) (לא לדאוג! עוד מעט אראה דוגמא של המעגל השלם עבור שלושה קיוביטים ואז הכל יהיה ברור).

עכשיו, בואו ננסה להבין מה אנחנו רוצים לעשות לקיוביט \( \left|j_{n-1}\right\rangle \). אנחנו רוצים לייצר ממנו את \( \left|0\right\rangle +e^{2\pi i0.j_{n-1}j_{n}}\left|1\right\rangle \), כלומר ליצור סופרפוזיציה, כשבסופרפוזיציה הזו לא מתעסקים עם \( \left|0\right\rangle \) אבל כן מתעללים קשות במקדם של \( \left|1\right\rangle \). ראינו ש-\( H \) שמופעל על \( \left|j_{n-1}\right\rangle \) הוא בעל אפקט כזה: הוא עוזב את \( \left|0\right\rangle \) בשקט אבל כופל את המקדם של \( \left|1\right\rangle \) ב-\( e^{2\pi i\cdot0.j_{n-1}} \). עכשיו, מה עם \( j_{n} \)? ובכן, יש לנו פה את הסיטואציה הרגילה שסכום במעריך הופך למכפלה:

\( e^{2\pi i0.j_{n-1}j_{n}}=e^{2\pi i\left(0.j_{n-1}+0.0j_{n}\right)}=e^{2\pi i0.j_{n-1}}\cdot e^{2\pi i0.0j_{n}} \)

כלומר, אנחנו רוצים להפעיל על המצב הקוונטי ש-\( \left|j_{n-1}\right\rangle \) הולך אליו שער שכופל ב-1 אם \( j_{n}=0 \), אז אם \( j_{n}=1 \) אז הוא כופל ב-

\( e^{2\pi i\cdot0.01}=e^{\frac{2\pi i}{4}} \)

גם זה שער מוכר לנו: \( e^{\frac{2\pi i}{4}}=e^{\frac{\pi i}{2}}=i \), ולכן השער שרוצים לכפול בו הוא \( S \):

\( S=\left(\begin{array}{cc} 1 & 0\\ 0 & i \end{array}\right) \)

אבל ה-\( S \) הזה, שמופעל על \( \left|j_{n-1}\right\rangle \), צריך להיות מותנה ב-\( \left|j_{n}\right\rangle \). איך מייצרים שער מותנה? כבר תיארתי את זה בפוסט על שערים קוונטיים: אם רוצים ליצור גרסה מותנית של האופרטור \( U \) מסתכלים על מטריצת הבלוקים

\( \left(\begin{array}{cc} I & 0\\ 0 & U \end{array}\right) \)

כלומר, במקרה הנוכחי מפעילים את האופרטור

\( \left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & i \end{array}\right) \)

וזהו, זה משיג את האפקט שרצינו ואנו מקבלים \( \left|0\right\rangle +e^{2\pi i0.j_{n-1}j_{n}}\left|1\right\rangle \).

עוד צעד אחד וכבר נבין מה קורה באופן כללי: עכשיו אנחנו רוצים לייצר מ-\( \left|j_{n-2}\right\rangle \) את המצב \( \left|0\right\rangle +e^{2\pi i0.j_{n-2}j_{n-1}j_{n}}\left|1\right\rangle \). הרעיון כבר ברור: נפעיל \( H \) על \( \left|j_{n-2}\right\rangle \) עצמו, ונפעיל \( S \) מותנה על \( \left|j_{n-1}\right\rangle \), אבל עכשיו בשביל \( \left|j_{n}\right\rangle \) צריך שער חדש - שער שהאפקט שלו הוא להשאיר את \( \left|0\right\rangle \) ללא שינוי אבל לכפול את \( \left|1\right\rangle \) ב-\( e^{2\pi i0.00j_{n}} \), כלומר במקרה שבו \( j_{n}=0 \) לא לעשות כלום (את זה משיגים בכך שהשער יהיה מותנה ב-\( \left|j_{n}\right\rangle \)) ואם \( j_{n=1} \) אז לכפול ב-\( e^{2\pi i0.001}=e^{\frac{2\pi i}{2^{3}}} \). אמנם, גם השער הזה חשוב מספיק כדי שיהיה לו שם משל עצמו (שער T, ועוד אדבר עליו בהמשך) אבל אנחנו מנסים להבין את הרעיון הכללי ולכן לא רוצים להמשיך להשתמש בשמות פרטניים לשערים. בשלב הזה כבר ברור שאנחנו צריכים לתת סימן כללי לשערים מהצורה \( e^{\frac{2\pi i}{2^{s}}} \) עבור \( s\ge0 \). הסימון המקובל הוא

\( R_{s}=\left(\begin{array}{cc} 1 & 0\\ 0 & e^{\frac{2\pi i}{2^{s}}} \end{array}\right) \)

אם כן, \( R_{1}=Z,R_{2}=S,R_{3}=T \) ומשם והלאה אנחנו לא טורחים לתת להם שמות. אפשר לחשוב על זה גם ככה: \( R_{s+1}=\sqrt{R_{s}} \) (כשיש לנו מטריצה אלכסונית, השורש שלה הוא המטריצה שהאיברים על האלכסון שלה הם השורש של האיברים על האלכסון במטריצה המקורית; אבל “שורש” במספרים מרוכבים הוא עניין מסובך יותר מזה ולכן זו אינטואיציה בלבד).

אם כן, מה שאנחנו עושים ל-\( \left|j_{n-2}\right\rangle \) הוא שלושה דברים:

מפעילים שער \( H \) על \( \left|j_{n-2}\right\rangle \) - זה מה שמייצר את הסופרפוזיציה הראשונית של \( \left|0\right\rangle \) ו-\( \left|1\right\rangle \) ועל הדרך גם כופל את \( \left|1\right\rangle \) ב-\( -1 \) אם \( j_{n-2}=1 \) (שימו לב שאנחנו לא משתמשים פה ב-\( R_{1}=Z \)).
מפעילים על \( \left|j_{n-2}\right\rangle \) שער \( R_{2} \) שמותנה ב-\( \left|j_{n-1}\right\rangle \).
מפעילים על \( \left|j_{n-2}\right\rangle \) שער \( R_{3} \) שמותנה ב-\( \left|j_{n}\right\rangle \)

כל זה קורה לפני שאנחנו מטפלים בקיוביטים \( \left|j_{n-1}\right\rangle \) ו-\( \left|j_{n}\right\rangle \).

אם \( n=3 \), אחרי הטיפול ב-\( \left|j_{n-2}\right\rangle =\left|j_{1}\right\rangle \) בעצם סיימנו את תיאור הפעולות שאנחנו מבצעים על כל הקיוביטים במעגל. רק צריך לזכור שבסוף המעגל עושים SWAP ל-\( \left|j_{1}\right\rangle \) ול-\( \left|j_{3}\right\rangle \).

כך נראה המעגל במקרה הזה (האיקסים שמחוברים בקו בסיום מייצגים את ה-SWAP):

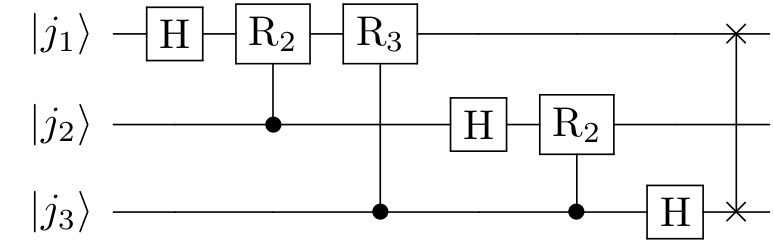
מכאן כבר די ברור מה צריך לקרות באופן כללי כשיש לנו \( n \) קיוביטים. עבור הקיוביט ה-\( t \)-י (\( 1\le t\le n \)), ראשית נפעיל עליו שער \( H \) ולאחר מכן נפעיל עליו באופן סדרתי את השערים \( R_{2},R_{3},\ldots,R_{n+1-t} \), כאשר השער \( R_{k} \) בסדרה הזו נשלט על ידי הקיוביט ה-\( k+t-1 \). בסיום סדרת השערים הזו מתבצעים SWAP-ים: לכל \( 1\le t\le n \), הקיוביט \( t \) מוחלף עם הקיוביט \( n+1-t \) (כשיש מספר אי זוגי של קיוביטים מן הסתם הקיוביט האמצעי לא יוחלף עם עצמו אלא פשוט לא נעשה לו כלום.

המעגל הזה פשוט עד להפתיע, ביחס לכל כאב הראש שעברנו עד אליו. הוא גם קטן: יש \( n \) קיוביטים ועל כל אחד מהם מופעלים \( O\left(n\right) \) שערים, כך שבסך הכל המעגל דורש \( O\left(n^{2}\right)=O\left(\log^{2}N\right) \) שערים, כמו שהבטחתי בהתחלה.

הנה איך שזה נראה באופן כללי, רק בלי שערי ה-SWAP בסוף שקצת בעייתי לצייר:

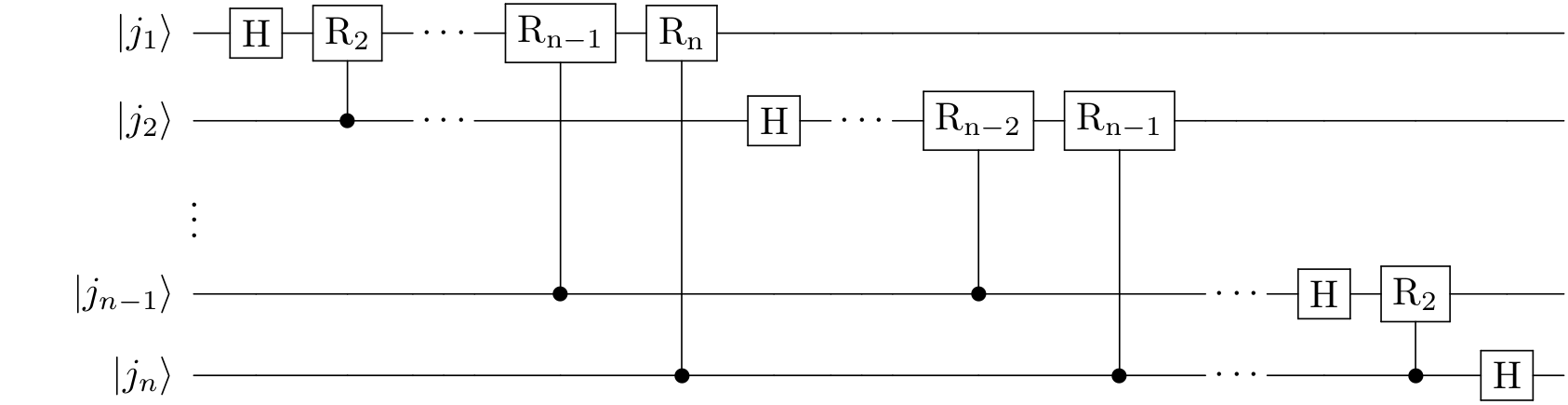
מה עדיין חסר לנו? שימוש כלשהו שיראה למה כל זה היה טוב. שימוש מרהיב כזה יהיה בפוסט הבא; לרוע המזל, השימוש אמנם משתמש בפורייה בצורה מרהיבה אבל אחרי הפוסט הבא כנראה נשאל את עצמנו בשביל מה משתמשים בשימוש הזה. ואז יגיע האלגוריתם של שור.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: