חישוב קוונטי בגישה מתמטית, חלק ד’: שערים קוונטיים

מעגלים קוונטיים

בפוסט הקודם שלי על חישוב קוונטי ראינו איך בהינתן מערכת של \( n \) קיוביטים אנחנו יכולים “לתרגם” אופרטור שפועל על קיוביט אחד לאופרטור שפועל על כל המערכת: אם האופרטור הוא למשל \( X \) שמופעל על הקיוביט הראשון, אנחנו בונים את האופרטור \( X\otimes I\otimes I\otimes\cdots\otimes I \) שפירושו “תפעיל את \( X \) על הקיוביט הראשון ועל היתר אל תעשה כלום”. אפשר כמובן גם לעשות דברים כמו \( X\otimes Z \) שפירושים “תפעיל את \( X \) על הקיוביט הראשון ואת \( Z \) על הקיוביט השני”, ודבר כזה יכול להתרחש במחשב קוונטי אמיתי על ידי כך שקודם מפעילים את \( X \) על הקיוביט הראשון (כלומר עושים \( X\otimes I \)) ואז את \( Z \) על הקיוביט השני (כלומר עושים \( I\otimes Z \)).

הסיטואציה מזכירה מאוד חישוב רגיל באמצעות מעגלים לוגיים, שבהם יש לנו כמה ביטים, ואנחנו מפעילים כל פעם פעולות כלשהן עליהם - פעולת NOT, פעולת AND וכדומה. לפעולות הללו יש שם - שערים לוגיים. לכן, בהתאם, לפעולות על קיוביטים קוראים שערים קוונטיים. בפרט כשמדברים על שער קוונטי מתכוונים לפעולה על מספר קטן של קיוביטים - אחד או שניים, בדרך כלל, אבל אין לזה הגדרה פורמלית של ממש.

עד כה כל מה שראינו היו שערים של קיוביט אחד. לא נזקקנו ליותר מזה - כאמור, גם \( X\otimes Z \) זה בעצם הפעלה של שני שערים של קיוביט בודד, בזה אחר זה. אבל ברור לחלוטין שאנחנו חייבים גם שער של שני קיוביטים. למה? כי בלי זה אין לנו איך לייצר מצב שזור, כמו \( \frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \) שראינו קודם. אופרטור כמו \( X\otimes Z \) פועל על כל קיוביט בנפרד, ולכן אם לפני ההפעלה שלו היו לנו שני קיוביטים מבודדים שלא קשורים זה לזה, אחרי ההפעלה שלו כל אחד מהקיוביטים הללו יתפתח באופן עצמאי ועדיין לא יווצר ביניהם קשר. כשם שהמצב השזור שאנחנו רוצים להגיע אליו לא ניתן לביטוי בתור \( u\otimes w \), כך גם האופרטור שאני צריך יהיה כזה שלא ניתן לביטוי בתור \( A\otimes B \).

מי שאשתמש בו הוא אופרטור על שני קיוביטים שנקרא CNOT, או CX. את ה-C צריך לקרוא בתור Controlled; הרעיון הוא שזה שער שעל קיוביט מסוים פועל או כמו הזהות (לא עושה כלום) או כמו \( X \) (והרי ראינו ש-\( X \) זה כמו פעולת NOT), כשהשאלה האם הוא יעשה משהו או לא תלויה בקיוביט אחר - קיוביט הבקרה.

הדרך להגדיר פורמלית אופרטור היא על ידי פעולתו על אברי בסיס - כאן אני עוסק באופרטור שפועל על שני קיוביטים, אז אני אגדיר אותו על ארבעת אברי הבסיס הסטנדרטי המתאימים:

\( \text{CX}\left|00\right\rangle =\left|00\right\rangle \)

\( \text{CX}\left|01\right\rangle =\left|01\right\rangle \)

\( \text{CX}\left|10\right\rangle =\left|11\right\rangle \)

\( \text{CX}\left|11\right\rangle =\left|10\right\rangle \)

כאן הבקרה היא הקיוביט הראשון (השמאלי). אם היא 0, כמו בשתי השורות הראשונות, \( \text{CX} \) לא משנה כלום; אם היא 1, \( \text{CX} \) הופך את הקיוביט השני. בכתיב מטריציוני זה נראה כך:

\( \text{CX}=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{array}\right) \)

כלומר, אפשר לחשוב על האופרטור הזה בתור מטריצת בלוקים:

\( \text{CX}=\left(\begin{array}{cc} I & 0\\ 0 & X \end{array}\right) \)

אין משהו קסום ב-\( \text{X} \) כאן, אפשר להגדיר אופרטור “נשלט” שכזה עבור כל אופרטור של קיוביט בודד, למשל אפשר להגדיר

\( \text{CZ}=\left(\begin{array}{cc} I & 0\\ 0 & Z \end{array}\right) \)

אבל בדרך כלל נזדקק רק ל-\( \text{CX} \).

שימו לב שבבירור \( \text{CX} \) לא יכול להיכתב בתור \( A\otimes B \). בשביל שזה יקרה, \( B \) צריכה להיות מטריצה שכפל בסקלר אחר יהפוך אותה ל-\( I \) וכפל בסקלר אחר יהפוך אותה ל-\( X \); אין דבר כזה.

איך \( \text{CX} \) עוזר לנו לייצר מצב שזור? קלי קלות. בואו נבצע חישוב קוונטי שכולל שני שלבים, על קלט שמאותחל ל-\( \left|00\right\rangle \):

מפעילים שער \( H \) על הקיוביט הראשון.
מפעילים שער \( \text{CX} \) על הקיוביט השני כשהוא נשלט על ידי הקיוביט הראשון.

את החישוב הזה מתארים באמצעות מעגל קוונטי שנראה כך:

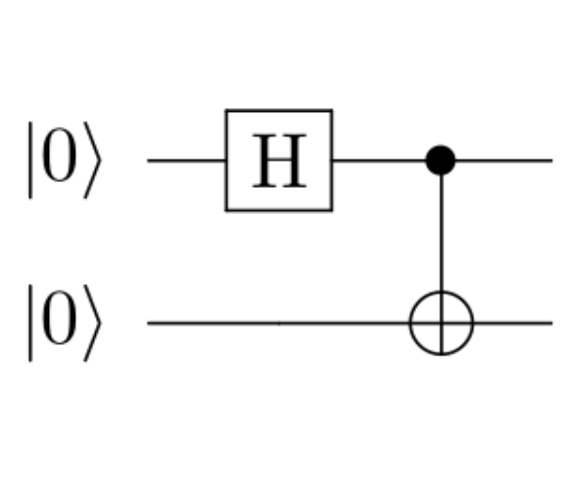
הרעיון בתיאור מעגל כזה הוא שהקיוביטים מסודרים בשורות. השורה הראשונה מתאימה לקיוביט הראשון והשניה לשני. ה-\( \left|0\right\rangle \) שמופיעים בצד שמאל הם הערכים שאליהם מאתחלים את הקיוביטים במעגל. אחר כך כיוון הקריאה הוא משמאל לימין. בהתחלה הקיוביט הראשון נכנס לשער \( H \), בזמן שהשני פשוט “זורם” בלי שיופעל עליו אף שער. אחר כך מגיע שער ה-\( \text{CX} \) שמתואר באמצעות נקודה שחורה על קיוביט הבקרה, וסימן \( \oplus \) על הקיוביט שיתהפך (כי אפשר לחשוב על הפעולה ששער CX מבצע כמו על פעולת XOR, \( \oplus \), בין שני ביטים רגילים, כשהפלט נכנס לביט השני).

בואו נבצע את החישוב הפורמלי שהמעגל מבצע:

\( H_{1}\left(\left|00\right\rangle \right)=H\left(\left|0\right\rangle \right)\left|0\right\rangle =\left(\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}}\right)\left|0\right\rangle =\frac{\left|00\right\rangle +\left|10\right\rangle }{\sqrt{2}} \)

אני מקווה שבשלב הזה כבר ברור בדיוק מה הולך בחישוב (ולהבא אני כנראה אדלג על שלבי הביניים). מי שעדיין מוטרד יכול כמובן לחשב את המטריצה של \( H_{1}=H\otimes I \), להפעיל אותה ולראות מה קורה.

הפעלת ה-\( \text{CX} \) תתבצע על פי התיאור על אברי הבסיס שנתתי למעלה:

\( \text{CX}\left(\frac{\left|00\right\rangle +\left|10\right\rangle }{\sqrt{2}}\right)=\frac{\text{CX}\left|00\right\rangle +\text{CX}\left|10\right\rangle }{\sqrt{2}}=\frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \)

והנה, באופן בלתי מפתיע ביותר, קיבלנו את \( \frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \) שהבטחתי, ועל הדרך למדנו איך מתאים שערים קוונטיים וראינו אותם בפעולה.

עכשיו, כשאולי לרגע אחד אנחנו מרגישים שהכל טוב ואפשר לנשום, בואו נסבך את הכל הרבה יותר - נתחיל לדבר על איך עובדות מדידות כשיש לנו יותר מקיוביט אחד.

מדידות, באופן כללי

בואו נזכיר איך עובדת מדידה של קיוביט יחיד: יש לנו מצב \( \alpha\left|0\right\rangle +\beta\left|1\right\rangle \). כשאנחנו מודדים אותו, אנחנו מגרילים בהסתברות \( \left|\alpha\right|^{2} \) את התוצאה 0, ומעבירים את המצב למצב \( \left|0\right\rangle \); ובהסתברות \( \left|\beta\right|^{2} \) את התוצאה 1 ומעבירים את המצב למצב \( \left|1\right\rangle \). זה היה המושג הפשטני שהצגתי עד כה - פשטני טיפה יותר מדי, כפי שנראה בהמשך.

עכשיו, אם יש לנו מצב קוונטי כללי של שני קיוביטים, \( \alpha\left|00\right\rangle +\beta\left|01\right\rangle +\gamma\left|10\right\rangle +\delta\left|11\right\rangle \), אפשר לעשות תעלול דומה. האילוץ שהמצב הוא מנורמה 1 גורר ש-\( \left|\alpha\right|^{2}+\left|\beta\right|^{2}+\left|\gamma\right|^{2}+\left|\delta\right|^{2}=1 \), כך שאפשר לחשוב על כל המספרים הללו כמגדירים הסתברות, ואז מה שיקרה במדידה הוא שנבחר את \( \left|00\right\rangle \) בהסתברות \( \left|\alpha\right|^{2} \), נחזיר 00 ונעבור למצב \( \left|00\right\rangle \), וכן הלאה. זו מדידה “של שני הקיוביטים בבת אחת”.

אבל אני רוצה לעשות משהו שונה. אני כבר יודע למדוד קיוביט בודד; מה יקרה אם יש לי מערכת של שני קיוביטים, במצב שזור אפילו, אבל אני מודד רק אחד מהקיוביטים? איך המערכת תשתנה כתוצאה מכך? התיאור המתמטי שהשתמשתי בו עד כה לא מכסה את זה.

אני יכול לנפנף בידיים. נניח שאני רוצה למדוד את \( \frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \) לפי הקיוביט הראשון. אז אני יכול לומר את הדבר הבא: המצב הזה סימטרי בין \( \left|00\right\rangle \) ובין \( \left|11\right\rangle \) ולכן ההסתברות שהמדידה של הקיוביט הראשון תיתן \( 0 \) היא \( \frac{1}{2} \) וההסתברות שהיא תיתן \( 1 \) היא \( \frac{1}{2} \). במקרה הראשון, המערכת תעבור למצב \( \left|00\right\rangle \) שהוא היחיד שבו הקיוביט הראשון הוא 0, ובמקרה השני היא תעבור למצב \( \left|11\right\rangle \). נפנוף הידיים הזה נכון אבל ממש קשה להבין ממנו מה בעצם אמור לקרות באופן כללי. זה כן מלמד אותנו כבר עכשיו על התופעה המגניבה שיש למצב \( \frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}} \): המדידה של הקיוביט הראשון משפיעה גם על הקיוביט השני. אם טרם מדדנו את הקיוביט הראשון, מדידה של הקיוביט השני יכולה להניב 0 או 1 בהסתברות חצי-חצי. אבל אם כבר מדדנו את הקיוביט הראשון, אז מדידה של הקיוביט השני תניב בודאות מוחלטת את אותה תוצאה כמו זו שהתקבלה במדידת הקיוביט הראשון. והמופלא ביותר הוא שזה קורה גם אם הקיוביט הללו מיוצגים על ידי יישויות פיזיקליות שבכלל לא סמוכות אחת לשניה; זה מה שפרדוקס EPR, שכתבתי עליו פעם פוסט, עוסק בו.

הנה עוד דרך לנפנף בידיים שאולי תיתן קצת יותר אינטואיציה: אפשר לכתוב

ואז ה”מקדם” של \( \left|0\right\rangle \) הוא \( \left(\alpha\left|0\right\rangle +\beta\left|1\right\rangle \right) \). זה לא מספר אלא וקטור, אבל אפשר לקחת לו נורמה ולקבל \( \left|\alpha\right|^{2}+\left|\beta\right|^{2} \), וזו ההסתברות לקבל 0 בקיוביט הראשון. אם זו תהיה התוצאה, אז המערכת תעבור למצב \( \left|0\right\rangle \left(\alpha\left|0\right\rangle +\beta\left|1\right\rangle \right) \) הזה, רק שהוא לא מנורמל; כדי לנרמל אותו, נחלק ב-\( \sqrt{\left|\alpha\right|^{2}+\left|\beta\right|^{2}} \) ונקבל שעברנו למצב \( \frac{\left|0\right\rangle \left(\alpha\left|0\right\rangle +\beta\left|1\right\rangle \right)}{\sqrt{\left|\alpha\right|^{2}+\left|\beta\right|^{2}}} \). אפשר, אפשר לנפנף ככה בידיים, זה באמת עובד. אבל זה מרגיש גם מסובך יחסית לנפנוף ידיים, וגם (לפחות עבורי) לא נותן תחושה שאנחנו על קרקע יציבה וממש מבינים מה אנחנו עושים.

כל זה נועד לרכך קצת את ההגדרה שאציג עכשיו - ההגדרה הכללית ביותר של מדידה שאזדקק לה, שהיא קצת כבדה מתמטית אבל פותרת אחת ולתמיד את כל חוסר הנוחות שענייני המדידה גורמים לנו. ראינו כבר שיש כל מני סוגים של מדידות - של שני הקיוביטים ביחד, של כל קיוביט בנפרד, על פי הבסיס \( \left|0\right\rangle ,\left|1\right\rangle \), על פי הבסיס \( \left|+\right\rangle ,\left|-\right\rangle \)… ההגדרה שלנו תקיף את כל המקרים הללו. שימו לב שההגדרה של מדידה בכלל לא נכנסת לשאלה איך מבצעים מדידה בפועל; זה תלוי במערכת הפיזיקלית שאיתה מממשים את הקיוביטים, וזה בדרך כלל תהליך מסובך משמעותית ממה שאני מתאר פה. כל היופי בחישוב קוונטי מבחינתי הוא ביכולת שלי לבצע אבסטרקציה לפרטים הפיזיקליים המסובכים. אז למרות שהמושג שאציג יהיה מאוד כללי, זה לא אומר שמחשב קוונטי יוכל לבצע את כל המדידות הללו - אבל את המדידה ה”פשוטה” של קיוביט יחיד על פי הבסיס \( \left|0\right\rangle ,\left|1\right\rangle \) הוא יוכל לבצע.

אם כן, נניח שיש לנו \( n \) קיוביטים, כלומר המצב הקוונטי שלנו הוא איבר של \( \mathbb{C}^{2^{n}} \). אז מדידה עם \( k \) תוצאות אפשריות מוגדרת על ידי סדרה של אופרטורי מדידה \( M_{0},M_{1},\ldots,M_{k-1} \), כך שכל \( M_{i} \) כזה הוא אופרטור \( M_{i}:\mathbb{C}^{2^{n}}\to\mathbb{C}^{2^{n}} \), והדרישה היחידה שלנו מהאופרטורים היא שיתקיים

\( \sum_{i=0}^{k-1}M_{i}^{\dagger}M_{i}=I \)

אין דרישות אחרות! האופרטורים לא חייבים להיות אוניטריים! המספר \( k \) לא חייב להיות 2, או \( 2^{n} \) או שום דבר אחר! יש לנו חופש מלא כאן!

בהינתן מצב \( \left|\psi\right\rangle \in\mathbb{C}^{2^{n}} \), ההסתברות לקבל את התוצאה ה-\( i \)-ית במדידה שלו היא

\( p\left(i\right)=\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \) (לא להיבהל! תכף אזכיר מה זה \( \left\langle \psi\right| \))

ואם התוצאה ה-\( i \) עלתה בגורל, המצב הקוונטי \( \left|\psi\right\rangle \) עובר למצב החדש

\( \frac{M\left|\psi\right\rangle }{\sqrt{\left\langle \psi\right|M^{\dagger}M\left|\psi\right\rangle }} \)

זהו, זו כל ההגדרה. עכשיו צריך

להסביר מה בשם שרדינגר הולך כאן.
להסביר למה זה תקין מבחינה מתמטית.
להסביר איך זה בעצם מכליל את כל המדידות שעליהן כבר דיברנו.

עדיף לי להתחיל מ-3: תמיד יותר קל להבין דברים כשיש לנו דוגמאות מול העיניים. נניח שאנחנו במרחב של קיוביט בודד, אז אופרטורי המדידה שלי יהיו \( M:\mathbb{C}^{2}\to\mathbb{C}^{2} \); כאלו דברים קל לייצג עם מטריצות \( 2\times2 \). המדידה “הרגילה” מוגדרת על ידי זוג המטריצות

\( M_{0}=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right) \)

\( M_{1}=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \)

המטריצות הללו מקיימות \( M_{i}^{\dagger}M_{i}=M_{i} \) ולכן באופן מיידי מקבלים \( \sum_{i=0}^{k-1}M_{i}^{\dagger}M_{i}=I \), כלומר המטריצות הללו אכן מגדירות לי מדידה חוקית על פי ההגדרה שנתתי.

עכשיו, מה קורה כאשר מודדים את המצב \( \left|\psi\right\rangle =\alpha\left|0\right\rangle +\beta\left|1\right\rangle \)? ההסתברות לקבל 0 היא \( p\left(0\right)=\left\langle \psi\right|M_{0}^{\dagger}M_{0}\left|\psi\right\rangle \). איך מחשבים את זה? ראשית, אני יכול לכתוב את \( \left|\psi\right\rangle \) בצורה פשוטה בתור וקטור: \( \left|\psi\right\rangle =\left(\begin{array}{c} \alpha\\ \beta \end{array}\right) \). עכשיו, את \( \left\langle \psi\right| \) הגדרתי אי שם בפוסט הראשון שלי בנושא: זה פשוט הצמוד ההרמיטי של \( \left|\psi\right\rangle \), כלומר זה וקטור השורה \( \left(\begin{array}{cc} \overline{\alpha} & \overline{\beta}\end{array}\right) \). כמו כן כבר ראינו ש-\( M_{0}^{\dagger}M_{0}=M_{0} \), אז הביטוי \( \left\langle \psi\right|M_{0}^{\dagger}M_{0}\left|\psi\right\rangle \) הוא בסך הכל החישוב הפשוט למדי

\( \left(\begin{array}{cc} \overline{\alpha} & \overline{\beta}\end{array}\right)\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)\left(\begin{array}{c} \alpha\\ \beta \end{array}\right)=\left(\begin{array}{cc} \overline{\alpha} & \overline{\beta}\end{array}\right)\left(\begin{array}{c} \alpha\\ 0 \end{array}\right)=\left|\alpha\right|^{2} \)

בדיוק המספר שציפינו לקבל, וגם \( \left|\beta\right|^{2} \) מתקבל בצורה דומה.

אם 0 עלה בגורל, אנחנו הולכים לעבור למצב \( M_{0}\left|\psi\right\rangle \) אחרי נירמול. המצב הזה לפני נירמול הוא \( \left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)\left(\begin{array}{c} \alpha\\ \beta \end{array}\right)=\left(\begin{array}{c} \alpha\\ 0 \end{array}\right) \). בשביל לנרמל, צריך לחשב את הנורמה של המצב. אני רוצה לטעון שהנורמה הזו היא בדיוק \( \sqrt{\left\langle \psi\right|M_{0}^{\dagger}M_{0}\left|\psi\right\rangle } \). למה? ובכן, זכרו איך נורמה של וקטור כלשהו \( v \) מוגדרת:

\( \|v\|=\sqrt{\left\langle v|v\right\rangle } \)

זכרו גם שאצלנו, אם \( \left|\psi\right\rangle ,\left|\phi\right\rangle \) הם שני וקטורים, המכפלה הפנימית שלהם שווה ל-\( \left\langle \phi\right|\left|\psi\right\rangle \). לבסוף, שימו לב שאם \( \left|\phi\right\rangle =M_{0}\left|\psi\right\rangle \) אז \( \left\langle \phi\right|=\left\langle \psi\right|M_{0}^{\dagger} \). למה? ובכן, זה מצריך לזכור משהו קטן מאלגברה לינארית: שאם \( A,B \) הן שתי מטריצות כלשהן, אז

\( \left(AB\right)^{\dagger}=B^{\dagger}A^{\dagger} \)

במקרה שלנו, שתי המטריצות הן \( M_{0}\left|\psi\right\rangle \). אם כן, בביטוי \( p\left(0\right)=\left\langle \psi\right|M_{0}^{\dagger}M_{0}\left|\psi\right\rangle \), ההסתברות היא בדיוק הנורמה של המצב \( M_{0}\left|\psi\right\rangle \) שאליו (אחרי נרמול) אנחנו רוצים להעביר את \( \left|\psi\right\rangle \), והאופרטור \( M_{0} \) בעצם אומר לנו לאן מצבים אמורים לעבור כשמודדים אותם.

השאלה שעדיין תלויה בחלל האוויר היא “למה זה עובד?”. לא לגמרי ברור מה אמור לא לעבוד כאן, אבל הרי לא דרשתי את התנאי \( \sum_{i=0}^{k-1}M_{i}^{\dagger}M_{i}=I \) סתם, הוא בא להשיג מטרה כלשהי. המטרה פשוטה: להראות שה-\( p\left(i\right) \)-ים שלי אכן מהווים הסתברות.

מה הדרישות המתמטיות מפונקציית הסתברות?

שלכל תוצאה אפשרית \( i \) יתקיים \( 0\le p\left(i\right)\le1 \)
שסכום כל ההסתברויות יהיה 1: \( \sum_{i=0}^{k-1}p\left(i\right)=1 \).

כמובן, מספיק להראות ש-\( 0\le p\left(i\right) \) ושסכום ההסתברויות יוצא 1 כדי להבטיח שיתקיים \( p\left(i\right)\le1 \) (כי אם סכום של מספרים אי-שליליים הוא 1, לא ייתכן שאחד מהאיברים בסכום גדול מ-1).

מכיוון שראינו ש-\( p\left(i\right)=\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \) הוא מכפלה פנימית, ברור ש-\( p\left(i\right)\ge0 \) - זה שמכפלה פנימית של איבר בעצמו היא אי-שלילית זו אחת מהדרישות הבסיסיות ביותר ממכפלה פנימית. נשאר רק עניין הסכום, וכאן נלחצת לעזרתנו העובדה שבאלגברה לינארית הכל לינארי, ושהביטוי \( \left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle \) אולי נראה מפחיד אבל הוא בסך הכל מכפלה של ארבע מטריצות ולכן כפוף לחוקי הלינאריות, ומתקיים

\( \sum_{i=0}^{k-1}p\left(i\right)=\sum_{i=0}^{k-1}\left\langle \psi\right|M_{i}^{\dagger}M_{i}\left|\psi\right\rangle = \)

\( =\left\langle \psi\right|\left(\sum_{i=0}^{k-1}M_{i}^{\dagger}M_{i}\right)\left|\psi\right\rangle =\left\langle \psi\right|I\left|\psi\right\rangle =\left\langle \psi|\psi\right\rangle =1 \)

כשהמעבר האחרון נובע מכך ש-\( \left|\psi\right\rangle \) הוא מנורמה 1. בסך הכל פשוט מאוד!

מדידות, באופן קצת פחות כללי

ההגדרה של מדידות שנתתי עשויה להרגיש יותר מדי כללית, ולא לגמרי ברור מאיפה סדרת ה-\( M \)-ים מגיעה. אז אני הולך לדבר עכשיו על משפחה קצת יותר מצומצמת של מדידות - כאלו שמתקבלות מאופרטור הרמיטי.

באלגברה לינארית, אופרטור \( \mathcal{H} \) הוא הרמיטי (או צמוד לעצמו) אם \( \mathcal{H}^{\dagger}=\mathcal{H} \). בהגדרה שקולה: אם \( \left\langle \mathcal{H}v,u\right\rangle =\left\langle v,\mathcal{H}u\right\rangle \) לכל \( v,u \). אופרטורים הרמיטיים הם יצורים נחמדים במיוחד. אפשר לחשוב עליהם בתוך קבוצת כל האופרטורים בערך כמו שאפשר לחשוב על הממשיים כחלק מקבוצת כל המרוכבים (למשל כל אופרטור מעל המרוכבים אפשר לכתוב כסכום \( H_{1}+iH_{2} \) של אופרטורים הרמיטיים \( H_{1},H_{2} \), קצת בדומה לכתיב \( a+bi \) של מרוכבים), אבל לא ניכנס לזה יותר מדי כאן. אבל לאופרטורים הרמיטיים יש כמה תכונות נחמדות שכן כדאי לציין:

כל הערכים העצמיים של אופרטור הרמיטים הם ממשיים. קל לראות את זה, כי אם \( \mathcal{H}v=\lambda v \) אז \( \left\langle \mathcal{H}v|v\right\rangle =\left\langle \lambda v|v\right\rangle =\|v\|^{2}\overline{\lambda} \) מחד, אבל \( \left\langle \mathcal{H}v|v\right\rangle =\left\langle v|\mathcal{H}v\right\rangle =\left\langle v,\lambda v\right\rangle =\|v\|^{2}\lambda \), ולכן \( \lambda=\overline{\lambda} \).
וקטורים עצמיים ששייכים לערכים עצמיים שונים הם אורתוגונליים, כלומר המכפלה הפנימית שלהם היא 0. הטריק שמראה את זה דומה למה שראינו קודם: אם \( v,u \) מתאימים לערכים העצמיים השונים \( \lambda,\rho \) אז \( \lambda\left\langle v|u\right\rangle =\left\langle \mathcal{H}v|u\right\rangle =\left\langle v|\mathcal{H}u\right\rangle =\rho\left\langle v|u\right\rangle \) ולכן \( \left(\lambda-\rho\right)\left\langle v|u\right\rangle =0 \) ומכיוון ש-\( \lambda\ne\rho \) זה מכריח את \( \left\langle v|u\right\rangle =0 \).

מאלו מקבלים, עם עוד קצת עבודה טכנית, שאפשר לקבל בסיס אורתונורמלי למרחב ש-\( \mathcal{H} \) פועלת עליו שכולו מורכב מוקטורים עצמיים של \( \mathcal{H} \). זה יותר מ”סתם” לכסון, בזכות העובדה שהוקטורים העצמיים הם אורתוגונליים. השורה התחתונה של זה, שהיא מה שיעניין אותנו כאן, היא שיש ל-\( \mathcal{H} \) מה שנקרא פירוק ספקטרלי - דרך להציג אותה בתור סכום

\( \mathcal{H}=\lambda_{1}P_{1}+\ldots+\lambda_{k}P_{k} \)

כאשר \( \lambda_{1},\ldots,\lambda_{k} \) הם הערכים העצמיים השונים של \( \mathcal{H} \), ו-\( P_{i} \) היא הטלה אורתוגונלית למרחב העצמי של \( \lambda_{i} \), כלומר למרחב שנפרש על ידי כל הוקטורים העצמיים של \( \mathcal{H} \) שמתאימים לערך העצמי \( \lambda_{i} \).

איך כל זה קשור למדידות? ובכן, תחשבו על \( \mathcal{H} \) בתור אופרטור שמקודד בתוכו את המידע השלם של מדידה מסוימת. הערכים \( \lambda_{1},\ldots,\lambda_{k} \) הם התוצאות האפשריות של המדידה הזו (תוצאות מספריות שמתבטאות במספרים ממשיים; תחשבו על מדידות של מהירות, מיקום וכדומה). האופרטורים \( P_{1},\ldots,P_{k} \) שמטילים למרחב העצמי המתאים הם אופרטורי המדידה שלנו, מה שקראתי לו \( M \) קודם.

אני לא ארחיב כאן יותר מדי על מה זו הטלה אורתוגונלית, אבל מה שרלוונטי לענייננו הוא שאם \( P \) היא הטלה כזו אז היא הרמיטית, כלומר \( P^{\dagger}=P \), וכמו כן \( P^{2}=P \), כך שיוצא ש-\( P^{\dagger}P=P \). לכן, כדי לראות שה-\( P \)-ים ש-\( \mathcal{H} \) נתן לנו מגדירים מדידה חוקית, מספיק להראות שמתקיים

\( \sum_{i=0}^{k-1}P_{i}=I \)

זה נובע בקלות מהמשוואה \( \mathcal{H}=\lambda_{1}P_{1}+\ldots+\lambda_{k}P_{k} \). אם מפעילים פולינום \( p \) כלשהו על המשוואה הזו, אז בזכות העובדה שוקטורים עצמיים שונים הם אורתוגונליים, שמובילה לכך ש-\( P_{i}P_{j}=0 \) לכל \( i\ne j \), מקבלים

\( p\left(\mathcal{H}\right)=p\left(\lambda_{1}\right)P_{1}+\ldots+p\left(\lambda_{k}\right)P_{k} \)

ובפרט עבור \( p=1 \) מקבלים \( P_{1}+\ldots+P_{k}=I \), שזה מה שרצינו.

כרגיל, כדאי לראות דוגמאות. אילו אופרטורים הרמיטיים אנחנו מכירים? ראינו שניים פשוטים למדי שפועלים על מרחב של קיוביט בודד:

\( Z=\left(\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}\right) \)

\( X=\left(\begin{array}{cc} 0 & 1\\ 1 & 0 \end{array}\right) \)

בשביל \( Z \) מאוד קל למצוא פירוק ספקטרלי - הוא כבר כך לכסין. והוקטורים העצמיים שלו הם פשוט \( \left(\begin{array}{c} 1\\ 0 \end{array}\right) \) ו-\( \left(\begin{array}{c} 0\\ 1 \end{array}\right) \) או בסימונים הקוונטיים שלנו, \( \left|0\right\rangle \) ו-\( \left|1\right\rangle \). שימו לב ש-\( Z \) עצמו לא מהווה מדידה! זה אופרטור אוניטרי נחמד שאפשר להשתמש בו במהלך חישוב רגיל. המדידה נכנסת לתמונה כשאנחנו לוקחים את הפירוק הספקטרלי של \( Z \), שהוא פשוט:

\( Z=\left(+1\right)\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)+\left(-1\right)\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \)

כבר ראינו את שתי המטריצות הללו קודם, בדוגמא שנתתי לאיך מדידה “רגילה” תואמת את ההגדרה באמצעות אופרטורים. עכשיו קיבלנו דרך יותר טבעית לקבל את שתיהן, וגם ראינו שבמקום להצמיד להן תגיות שהן המחרוזת “0” והמחרוזת “1” אפשר להצמיד להן את התגיות המספריות \( \pm1 \). לרוב אני אדבוק בתגיות של “0” ו-\textquotedblleft1” בכל זאת, אבל כדאי להכיר גם את הגישה השניה. לפעמים כשמדברים על “מדידה רגילה” אומרים “מדידה בבסיס \( Z \)”; עכשיו אפשר להבין מאיפה ה-\( Z \) הזה מגיע.

אם זו הייתה מדידה בבסיס \( Z \), מה זו מדידה בבסיס \( X \)? כבר ראינו בפוסט קודם שמתקיים

\( X\left|+\right\rangle =\left|+\right\rangle \)

\( X\left|-\right\rangle =-\left|-\right\rangle \)

כלומר, עבור \( X \) הוקטורים העצמיים הם \( \left|+\right\rangle ,\left|-\right\rangle \), עם הערכים העצמיים \( \pm1 \) (כמו עבור \( Z \)), ועם קצת עבודה אפשר לראות שהפירוק הספקטרלי הוא

\( X=\left(+1\right)\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)+\left(-1\right)\left(\begin{array}{cc} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{array}\right) \)

המטריצות הללו הן \( \left|+\right\rangle \left\langle +\right| \) ו-\( \left|-\right\rangle \left\langle -\right| \) אם תהיתם מהיכן הן צצו.

זוכרים את השוויון \( HZH=X \) שראינו פעם? בגלל שבפירוק הספקטרלי הכל לינארי, במקום למדוד בבסיס \( X \) אפשר לעשות את התעלול הבא: להפעיל \( H \), למדוד בבסיס \( Z \), להפעיל \( H \) שוב על המצב שהגענו אליו, וכך “לסמלץ” את המדידה בבסיס \( X \) - המצב שנגיע אליו בסוף הוא זה שהיינו מגיעים אליו אם היינו מודדים בבסיס \( X \), וגם הערך שהמדידה החזירה (\( \pm1 \)) מתאים למה שהיינו רואים אם היינו מודדים בבסיס \( X \).

מדידות, במובן המאוד פרטני שאנחנו ממש ממש צריכים כדי להמשיך

קשקשתי כל כך הרבה בפוסט הזה. האם עניתי על השאלה הבסיסית? השאלה “מה קורה אם יש לי שני קיוביטים ואני מודד רק אחד מהם?” ובכן, בתיאוריה כן, כי נתתי תשובה מאוד כללית, אבל מה קורה בפועל?

אמרתי שמדידה רגילה מתוארת על ידי הפירוק הספקטרלי של \( Z \), וסימנתי את המטריצות המתאימות ב-\( M_{0}=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right),M_{1}=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \) (שימו לב שהשתמשתי כאן בסימון המקורי ולא בזה של ההטלות). אז מדידה של הקיוביט הראשון, בלי שינוי של השני, מתוארת על ידי הפירוק הספקטרלי של \( Z\otimes I \). כלומר, המטריצות שמגדירות את המדידה הן

\( M_{0}\otimes I \)

\( M_{1}\otimes I \)

מה ש-\( M_{0} \) עושה הוא פשוט:

\( M_{0}\left|0\right\rangle =\left|0\right\rangle \)

\( M_{0}\left|1\right\rangle =0 \)

שימו לב: בשורה השניה זה לא הקיוביט \( \left|0\right\rangle \) מצד ימין. זה 0. המספר 0. וקטור האפס. כלום. נאדה, גורנישט. דבר כזה יכול להתקבל כי \( M_{0} \) הוא הטלה; הוא לא אופרטור אוניטרי ולא צריך להיות הפיך.

באופן דומה, \( \left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \) מאפס את \( \left|0\right\rangle \) ומשאיר ללא שינוי את \( \left|1\right\rangle \). זה מאפשר לנו להבין מה האופרטורים הללו עושים כשמטנזרים אותם עם \( I \): \( M_{0}\otimes I \) הולך להשאיר ללא שינוי את \( \left|00\right\rangle ,\left|01\right\rangle \) ולאפס את שני האחרים, ו-\( M_{1} \) יעשה ההפך. כלומר נקבל את האפקט הבא על מצב כללי, \( \alpha\left|00\right\rangle +\beta\left|01\right\rangle +\gamma\left|10\right\rangle +\delta\left|11\right\rangle \):

\( M_{0}\left(\alpha\left|00\right\rangle +\beta\left|01\right\rangle +\gamma\left|10\right\rangle +\delta\left|11\right\rangle \right)=\alpha\left|00\right\rangle +\beta\left|01\right\rangle \)

\( M_{1}\left(\alpha\left|00\right\rangle +\beta\left|01\right\rangle +\gamma\left|10\right\rangle +\delta\left|11\right\rangle \right)=\gamma\left|10\right\rangle +\delta\left|11\right\rangle \)

אם נחזור לתחילת הפוסט, נראה שזה מה שעשיתי כבר אז, אבל קראתי לזה נפנופי ידיים. האם עכשיו זה מרגיש יותר פורמלי? ובכן… אני מקווה.

יש נקודה נוספת שעדיין לא התייחסתי אליה והיא די מעצבנת - כדי לדעת מה ההסתברות ש-0 ייבחר, לא מספיק להפעיל את \( M_{0} \) על המצב הכללי ולקבל את \( \alpha\left|00\right\rangle +\beta\left|01\right\rangle \), צריך גם לחשב את המכפלה הפנימית של הוקטור הזה בעצמו. איך עושים את זה בקלות? ובכן, הרעיון הוא לקחת את הוקטור וקודם כל לחשב את הצמוד ההרמיטי שלו. היתרון בשיטת הסימון שלנו הוא שזה כרוך בשני דברים בלבד: להצמיד את הסקלרים, ולהפוך את הכיוון של הסוגריים:

\( \overline{\alpha}\left\langle 00\right|+\overline{\beta}\left\langle 01\right| \)

עכשיו אפשר לכפול בצורה שבה מתבצע כפל רגיל:

\( \left(\overline{\alpha}\left\langle 00\right|+\overline{\beta}\left\langle 01\right|\right)\left(\alpha\left|00\right\rangle +\beta\left|01\right\rangle \right)= \)

\( =\left|\alpha\right|^{2}\left\langle 00\right|\left|00\right\rangle +\overline{\alpha}\beta\left\langle 00\right|\left|01\right\rangle +\alpha\overline{\beta}\left\langle 01\right|\left|00\right\rangle +\left|\beta\right|^{2}\left\langle 01\right|\left|01\right\rangle \)

בבירור \( \left\langle 00\right|\left|00\right\rangle =\left\langle 01\right|\left|01\right\rangle =1 \) כי זו מכפלה פנימית של וקטור מנורמה 1 בעצמו. אבל מה זה \( \left\langle 00\right|\left|01\right\rangle \) למשל? ובכן, עד עכשיו לא ממש הסברתי איך אנחנו מגדירים מכפלה פנימית על מרחב שהוא מכפלה טנזורית, אבל אני לא חושב שמפתיע במיוחד שההגדרה המקובלת היא

\( \left\langle u_{1}\otimes w_{1}|u_{2}\otimes w_{2}\right\rangle =\left\langle u_{1}|u_{2}\right\rangle \cdot\left\langle w_{1}|w_{2}\right\rangle \)

ולכן, בסימונים שלנו:

ומכיוון ש-\( \left\langle 0\right|\left|1\right\rangle =0 \) כי אלו וקטורים אורתוגונליים, נקבל \( \left\langle 00\right|\left|01\right\rangle =0 \). וכך גם באופן כללי: אם \( x\ne y \) הם שניהם מחרוזות ב-\( \left\{ 0,1\right\} ^{n} \) אז \( \left\langle x\right|\left|y\right\rangle =0 \). לכן קיבלנו שהמכפלה הפנימית של \( \alpha\left|00\right\rangle +\beta\left|01\right\rangle \) בעצמו היא \( \left|\alpha\right|^{2}+\left|\beta\right|^{2} \), כפי שנפנפתי בידיים בתחילת הפוסט.

האם סיימנו? אני מקווה שכן! כלומר, יש לנו את כל הכלים המתמטיים שצריך כדי להתחיל להראות חישובים קוונטיים אמתיים ולהבין מה קורה בהם; את זה נתחיל בפוסט הבא.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: