חישוב קוונטי בגישה מתמטית, חלק ה': אלגוריתם דויטש-ג'וזה

מה אנחנו רוצים לפתור?

עד עכשיו בסדרת הפוסטים על חישוב קוונטי ראינו את הבסיס המתמטית שאפשר לצמצם לכמה משפטי מחץ:

• בחישוב קוונטי האובייקט שמשתנה עם הזמן הוא המצב הקוונטי של המערכת, שמיוצג בתור וקטור \( \left|\psi\right\rangle \in\mathbb{C}^{2^{n}} \).
• סוג אחד של שינוי הוא כפל המצב \( v \) במטריצה אוניטרית \( U\in\mathbb{C}^{2^{n}\times2^{n}} \), כלומר מבצעים \( \left|\psi\right\rangle \leftarrow U\left|\psi\right\rangle \).
• סוג נוסף של שינוי הוא מדידה, שבגרסה הפשוטה שלנו מוגדרת לכל קיוביט עבור שני אופרטורים \( M_{0},M_{1} \) (שתלויים בקיוביט), בחירת \( M_{0} \) בהסתברות \( \left\langle \psi\right|M_{0}\left|\psi\right\rangle \) ובחירת \( M_{1} \) בהסתברות \( \left\langle \psi\right|M_{1}\left|\psi\right\rangle \) ובהינתן ש-\( M_{i} \) עלה בגורל, הפלט שחוזר מהמדידה הוא \( i \) והיא מעבירה את המצב הקוונטי של המערכת למצב \( \left|\psi\right\rangle \leftarrow\frac{M_{i}\left|\psi\right\rangle }{\sqrt{\left\langle \psi\right|M_{i}\left|\psi\right\rangle }} \).

זה הכל. מה שמעניין פה הוא שאלו הם חישובים שלא מסובך במיוחד לתכנת גם במחשב סטנדרטי. אמנם אין לנו יכולת לשמור מספרים מרוכבים ברמת דיוק אינסופית, אבל אנחנו לא באמת צריכים את זה - הייצוגים הקיימים של מרוכבים במחשב עובדים מספיק טוב. למעשה, אין שום בעיה עקרונית לכתוב סימולטור של חישוב קוונטי שרץ במחשב רגיל, וזה אפילו תרגיל נחמד למי שרוצה ללמוד את התחום (מגלים מהר מאוד שהפעלת אופרטורים זה עסק קצת מעצבן ויש דרכי קיצור). זה גורם לאתגר הגדול של בניית מחשבים קוונטיים להיראות קצת מיותר - מה הטעם ליצור מכשיר הנדסי מסובך שהחישוב שהוא מבצע זה משהו שאפשר לעשות במחשב רגיל?

לנקודה הזו כבר התייחסתי בעבר. מכיוון שהאובייקט הספציפי שאנחנו שומרים ופועלים עליו הוא וקטור ב-\( \mathbb{C}^{2^{n}} \), כמות המידע שצריך לשמור, והזמן שלוקח לפעול עליה, גדלה אקספוננציאלית עם \( n \). עבור 50 קיוביטים, למחשבים רגילים מאוד מאתגר לסמלץ חישוב קוונטי; עבור 100 קיוביטים כבר אין על מה לדבר. נכון לכתיבת שורות אלו יש ליבמ מחשב קוונטי פעיל של 127 קיוביטים, למרות שהחישוב בו לא חף מבעיות (מתישהו אני מקווה בסדרת הפוסטים הזו להגיע לדבר על רעשים ותיקון שגיאות), וזו רק תחילת הדרך. כשיהיה חישוב קוונטי רציני, לא יהיה שום סיכוי לסמלץ אותו במחשב.

אבל זה עדיין לא עונה על השאלה האמיתית - בשביל מה זה טוב? אילו בעיות נוכל לפתור עם מחשבים קוונטיים שלא נוכל לפתור במחשב רגיל? הדוגמא הנפוצה שנזרקת לחלל באוויר בשלב הזה היא בעיית הפירוק לגורמים שהאלגוריתם הקוונטי של שור פותר ביעילות. זו דוגמא מצויינת, אבל יש בה בעיה פשוטה - זה אלגוריתם מסובך יחסית וקשה להציג אותו ישר אחרי שמבינים איך עובד חישוב קוונטי. אז בפוסט הזה אני רוצה להציג בעיה פשוטה הרבה יותר, שנפתרת על ידי אלגוריתם פשוט בצורה קיצונית, אבל כבר היא מספיקה לתת תחושה טובה למה בחישוב קוונטי יש “יותר” מאשר בחישוב קלאסי. האלגוריתם שאציג נקרא אלגוריתם דויטש-ג'וזה.

נתחיל עם להציג את הבעיה עצמה. אני מזהיר מראש שזו לא בעיה “מעניינת”. לפתור אותה לא הולך לשבור מערכות הצפנה. היא אפילו נראית די מלאכותית. היופי בבעיה הוא שקל מאוד להבין למה נסיון לפתור אותה קלאסית יהיה קשה, ואז העובדה שהיא נפתרת בקלות קוונטית מחדדת מאוד את ההבדל.

הקלט לבעיה הוא פונקציה \( f:\left\{ 0,1\right\} ^{n}\to\left\{ 0,1\right\} \), כלומר פונקציה בינארית שמקבלת קלט שהוא מחרוזת באורך \( n \) של ביטים (אפשר לחשוב עליה בתור מספר טבעי בתחום \( 0,1,\ldots,2^{n}-1 \)) ועל כל קלט כזה מחזירה 0 או 1. הפונקציה נתונה לנו בתור קופסה שחורה, כלומר משהו שאנחנו לא יכולים לראות איך המימוש שלו עובד; הדבר היחיד שאנחנו יכולים לעשות הוא לחשב את \( f \) על קלטים מסוימים. תחשבו על \( f \) כאילו מה שמחשב אותו יושב על מחשב מרוחק, וכל מה שאנחנו יכולים לעשות הוא לשלוח לו מחרוזות של \( n \) ביטים ולקבל חזרה פלט של ביט בודד.

מה שידוע לנו על \( f \) זה שהיא בדיוק אחד משני הבאים:

• \( f \) קבועה, כלומר לכל קלט \( x \) מתקיים \( f\left(x\right)=0 \), או שלכל קלט \( x \) מתקיים \( f\left(x\right)=1 \).
• \( f \) מאוזנת, כלומר בדיוק על חצי מהקלטים מתקבל 0 ועל החצי השני מתקבל 1. אם נסמן \( N=2^{n} \), זה אומר ש-\( \left|\left\{ x\in\left\{ 0,1\right\} ^{n}\ |\ f\left(x\right)=0\right\} \right|=\left|\left\{ x\in\left\{ 0,1\right\} ^{n}\ |\ f\left(x\right)=1\right\} \right|=\frac{N}{2} \).

המשימה שלנו: לקבל מה משני המקרים הללו מתקיים.

איך עושים את זה באופן קלאסי? ובכן, אם לא מערבים הסתברות בסיפור, די ברור שאנחנו חייבים \( \frac{N}{2}+1 \) קריאות ל-\( f \). למה? כי אנחנו תמיד חושבים מה יקרה במקרה הגרוע ביותר, והמקרה הגרוע ביותר הוא זה שבו אין לנו מזל - ש-\( f \) היא מאוזנת, ואיכשהו כל \( \frac{N}{2} \) ההפעלות הראשונות שלה שביצענו נפלו בדיוק על כל הערכים שעליהם \( f \) נותנת 0. בשלב הזה אנחנו עדיין לא יכולים להגיד בודאות האם \( f \) תהיה 0 על הכל, או רק על חצי. רק כשנחשב את הערך שלה על האיבר ה-\( \frac{N}{2}+1 \) נוכל להיות בטוחים: אם קיבלנו \( 0 \) אז \( f \) קבועה, ואם קיבלנו 1 אז \( f \) מאוזנת.

להראות שגם אם מערבים הסתברות עדיין נזדקק למספר גדול של שאילות זה חישוב מסובך יותר ולא אעשה אותו כרגע, כי אני לא צריך - אלגוריתם דויטש-ג’וזה הולך להשתמש בקריאה אחת בלבד לפונקציה, ולהחזיר תשובה שהיא נכונה תמיד, ב-100 אחוז מהמקרים, אפילו אם חישוב קוונטי הוא לכאורה עניין הסתברותי. איך זה יעבוד? ובכן, זה דורש מהקופסה השחורה שמחשבת את \( f \) להיות קוונטית בעצמה: במקום לחשב את \( f \) על ביט ספציפי \( x \) שנותנים, לחשב את \( f \) על סופרפוזיציה, כלומר: הקלט ש-\( f \) תקבל יהיה מצב על \( n \) קיוביטים, \( \left|\psi\right\rangle =\sum_{x\in\left\{ 0,1\right\} ^{n}}\alpha_{x}\left|x\right\rangle \) ואינטואיטיבית, הפלט יהיה

\( f\left(\sum_{x\in\left\{ 0,1\right\} ^{n}}\alpha_{x}\left|x\right\rangle \right)=\sum_{x\in\left\{ 0,1\right\} ^{n}}\alpha_{x}f\left(\left|x\right\rangle \right) \)

האינטואיציה הזו לא מלאה; בדויטש-ג’וזה נשתמש בקופסה שחורה שמתנהגת קצת שונה, ואחר כך נסביר איך עוברים מהאינטואיציה שאני מציג כאן אל הקופסה השחורה של דויטש-ג’וזה.

ייתכן מאוד שהצלחתי לאכזב אתכם עם ה”הקופסה השחורה תהיה קוונטית”. זה נשמע כאילו שיניתי פתאום את הגדרת הבעיה, ואין פלא שעם מחשב קוונטי אפשר להשיג יותר. אבל נניח שהייתי אומר מלכתחילה שהקופסה השחורה היא קוונטית, האם מחשב קלאסי היה מצליח יותר? הוא לא מסוגל לייצר סופרפוזיציה של מצבים קוונטיים, כל מה שהוא היה יכול לעשות הוא לשלוח מצבי בסיס \( \left|x\right\rangle \). זה שהקופסה השחורה היא קוונטית לא עוזר לנו בלי שיהיה לנו מחשב קוונטי שמנצל את זה. עדיין, אני לגמרי מסכים שזו לא דוגמת מחץ כמו האלגוריתם של שור, שלא נזקק לקופסאות שחורות קוונטיות שכאלו; תזכרו שמה שאני עושה כרגע הוא לא לתת דוגמת מחץ לעליונות החישוב הקוונטי, אלא לתת תחושה ראשונית של הקסם הנחמד הזה.

איך דויטש-ג'וזה עובד?

דויטש-ג’וזה הוא אלגוריתם פשוט בצורה קיצונית:

1. אתחלו מצב קוונטי אל \( \left|0^{n}\right\rangle \)
2. הפעילו \( H \) על כל הקיוביטים.
3. הפעילו את הקופסה השחורה על המצב שקיבלתם.
4. הפעילו \( H \) על המצב שקיבלתם.
5. מדדו את כל הקיוביטים במצב שקיבלתם.
6. אם קיבלתם \( 0^{n} \), אז \( f \) קבועה; אם קיבלתם משהו אחר, אז \( f \) מאוזנת.

הדבר היחיד שלא הסברתי עדיין איך הוא בדיוק עובד הוא שלב “הפעלת הקופסה השחורה”. לצורך כך אני מניח שיש לי אופרטור אוניטרי \( U_{f} \) שפועל בצורה הבאה על איבר בסיס \( \left|x\right\rangle \):

• \( U_{f}\left|x\right\rangle =\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \)

במילים אחרות: אם \( f\left(x\right)=0 \) אז \( U_{f} \) לא משנה את \( \left|x\right\rangle \) , ואם \( f\left(x\right)=1 \) אז הוא מכפיל אותו ב-\( -1 \). זה מזכיר את האופרטור \( Z \), רק כזה שפועל בבת אחת על \( n \) קיוביטים ותלוי בתכונות הספציפיות של \( f \). איך אפשר לממש אופרטור קוונטי כזה? נדבר על זה בהמשך.

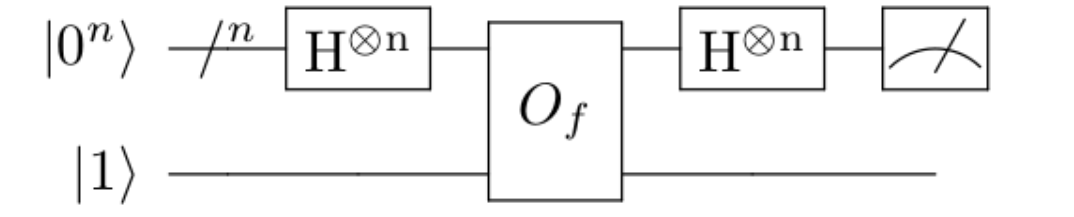
הנה איור סכמטי של האלגוריתם, במקרה של שלושה קיוביטים:

אפשר גם לצייר את זה באופן כללי ל-\( n \) קיוביטים בצורה קומפקטית:

הסימן שנראה כמו מחוג של מכשיר מדידה בצד ימין הוא, ובכן, מדידה. ה-\( H^{\otimes n} \) הוא הפעלת \( H \) על כל השערים, שתכף אתאר; אני מניח שהרעיון ברור.

כרגע אני רוצה לראות איך האלגוריתם פותר לנו את הבעיה. בסופו של דבר, להבין את האלגוריתם קם ונופל על להבין משהו כללי קצת יותר ושימושי מאוד: מה בעצם הפעלת \( H \) על כל הקיוביטים עושה.

כזכור, \( H \) הוא האופרטור שיוצר לנו סופרפוזיציה אחידה:

\( H\left|0\right\rangle =\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} \)

\( H\left|1\right\rangle =\frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}} \)

אבל זה עבור קיוביט יחיד. מה קורה כשמפעילים \( H \) על כל אחד מהקיוביטים? מקבלים את ההרכבה של \( H\otimes I\otimes\ldots\otimes I \) ו-\( I\otimes H\otimes\ldots\otimes I \) וכן הלאה - זה יוצא האופטור \( H\otimes H\otimes\ldots\otimes H \), או בסימון מקוצר, \( H^{\otimes n} \). עכשיו, אם נפעיל את האופרטור הזה על המצב ההתחלתי \( \left|0^{n}\right\rangle \) נקבל:

\( H^{\otimes n}\left|0^{n}\right\rangle =\left(H\left|0\right\rangle \right)\otimes\ldots\otimes\left(H\left|0\right\rangle \right)=\left(\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}}\right)\otimes\ldots\otimes\left(\frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}}\right) \)

מה שצריך לזכור על מכפלה טנזורית הוא האופן שבו היא מתנהגת בדומה למכפלה רגילה - אפשר להוציא החוצה סקלרים (את כל ה-\( \frac{1}{\sqrt{n}} \)), ואפשר להשתמש בדיסטריביוטיביות. יש לנו כאן מכפלה של \( n \) מחוברים מהצורה \( \left(\left|0\right\rangle +\left|1\right\rangle \right) \); זו סיטואציה שמזכירה, למשל, את הבינום של ניוטון. כשאנחנו פותחים סוגריים, אנחנו מקבלים סכום שכולל את כל המחוברים שהם מהצורה של מכפלה של \( n \) איברים שכל אחד מהם הוא או \( \left|0\right\rangle \) או \( \left|1\right\rangle \) - במילים אחרות, הסכום \( \sum_{y\in\left\{ 0,1\right\} ^{n}}\left|y\right\rangle \). לכן בסך הכל קיבלנו:

\( H^{\otimes n}\left|0^{n}\right\rangle =\frac{1}{\sqrt{2^{n}}}\sum_{y\in\left\{ 0,1\right\} ^{n}}\left|y\right\rangle \)

זה מתאים יפה לאינטואיציה שלפיה \( H \) יוצר סופרפוזיציה אחידה: כשהפעלנו אותו על כל הקיוביטים, קיבלנו סופרפוזיציה אחידה של כל \( 2^{n} \) אברי הבסיס האפשריים. שימו לב, זה כבר קסם בפני עצמו - הפעלנו רק \( n \) שערים (זה לוקח זמן קצר) וקיבלנו סופרפוזיציה של מספר אקספוננציאלי של איברים.

מה שעשינו פה הוא להבין איך \( H^{\otimes n} \) עובד על מצב בסיס אחד ספציפי: \( \left|0^{n}\right\rangle \). אבל איך הוא עובד על מצבים אחרים, כאלו שיש בהם גם 1-ים? כאן אנחנו מגיעים לנקודה הכי טכנית בפוסט, אבל גם הכי יפה שלו. כמו שתמיד כדאי כדי להבין משהו מסובך, כדאי להסתכל על דוגמא פשוטה קודם.

נניח שאני מפעיל את \( H^{\otimes3} \) על המצב \( \left|101\right\rangle \). מה אני אקבל? על פי מה שראינו קודם, נקבל

\( H^{\otimes3}\left|101\right\rangle =\frac{1}{\sqrt{2^{3}}}\left(\left|0\right\rangle -\left|1\right\rangle \right)\left(\left|0\right\rangle +\left|1\right\rangle \right)\left(\left|0\right\rangle -\left|1\right\rangle \right) \)

כשאני פותח סוגריים אני עדיין אקבל את כל האיברים מהצורה \( \left|x\right\rangle \), אבל הפעם חלקם יהיו עם מקדם מינוס. מתי? ובכן, בואו נתחיל לפתוח את הסוגריים. נניח שאני בוחר מכל אחד משלושת הסוגרים את האיבר הראשון, אני אכפיל שלושה איברים מהצורה \( \left|0\right\rangle \) ואקבל \( \left|000\right\rangle \) - בלי סימן מינוס. ולמה שיהיה סימן מינוס? על ה-\( \left|0\right\rangle \)-ים אין מינוס בכלל. כדי שיהיה מינוס, חייב להשתתף \( \left|1\right\rangle \) בסיפור הזה. למשל, אם אני אקח את האיבר השני מהסוגר הראשון, ומשני האחרים את האיבר הראשון, אני אקבל \( -\left|100\right\rangle \).

לעומת זאת, אם אני אקח את האיבר השני מהסוג השני ומשני האחרים את הראשון, אני אקבל \( \left|010\right\rangle \), בלי מינוס. למה? כי בסוגר השני, ה-\( \left|1\right\rangle \) מופיע בלי סימן מינוס. ולמה לא? כי במצב המקורי שעליו פעלנו, \( \left|101\right\rangle \), הסוגר השני מתאים לאיבר השני במחרוזת, כלומר אל 0. מכאן המסקנה היא שכדי לקבל מינוס, אני חייב לקחת את \( \left|1\right\rangle \) מתוך סוגריים ששייכים לאיבר בקלט שהיה \( \left|1\right\rangle \) בעצמו.

זה תנאי הכרחי כדי לקבל מינוס, אבל הוא לא מספיק, כי בואו נראה למשל מה שקורה כשאני לוקח את ה-\( \left|1\right\rangle \) מכל שלושת זוגות הסוגריים. אני מקבל את המכפלה

\( -\left|1\right\rangle \otimes\left|1\right\rangle \otimes\left(-\left|1\right\rangle \right)=\left|111\right\rangle \)

כלומר, הפעם קיבלתי איבר ללא מינוס כי בדיוק שני איברים במכפלה היו עם סימן מינוס. הסימן באיבר שאקבל בסוף תלוי בשאלות הבאות:

• האם מופיעים 1-ים במצב שעליו פעלנו?
• האם מופיעים 1-ים במצב שאנחנו מסתכלים עליו כרגע בפלט?
• האם יש אינדקסים שבהם מופיע 1 גם בקלט וגם בפלט?
• האם המספר של האינדקסים הללו הוא אי זוגי?

זה מאוד מסורבל לדבר על זה ככה, אבל למרבה השמחה יש כלי מתמטי פשוט מאוד שמאפשר לתאר את זה בצורה שקל לעבוד איתה: מכפלה סקלרית מודולו 2. בהינתן שני וקטורים מאותו אורך, \( x=\left(x_{1},\ldots,x_{k}\right) \) ו-\( y=\left(y_{1},\ldots,y_{k}\right) \), המכפלה הסקלרית שלהם היא \( x\cdot y=\sum_{i=1}^{k}x_{i}y_{i} \). אם \( x,y\in\left\{ 0,1\right\} ^{k} \) אז המכפלה הסקלרית שלהם תהיה מספר שלם, ואפשר לקחת אותו מודולו 2 (לחלק ב-2 ולהחזיר את השארית; 0 אם המספר זוגי ו-1 אם הוא אי זוגי).

אולי אתן אומרות “היי, זו כמו מכפלה פנימית!” וזה נכון - אפשר לחשוב על מכפלות פנימיות כאילו הן מוגדרות בעזרת סכום כזה, אבל אין למכפלה פנימית משמעות מעל \( \mathbb{Z}_{2} \) (השדה שמעליו אנחנו עובדים כרגע במובלע) אלא רק מעל \( \mathbb{R},\mathbb{C} \); כי למשל, אחת הדרישות ממכפלה פנימית היא שאם \( x\ne0 \) אז \( \left\langle x,x\right\rangle >0 \) וזה בוודאי לא מתקיים כאן (חשבו על הוקטור \( x=11 \)). אבל גם בלי להיות מכפלה פנימית, למכפלה סקלרית כזו יש תכונות אלגבריות נחמדות, למשל \( \left(x+y\right)\cdot z=x\cdot z+y\cdot z \).

בעזרת מכפלה סקלרית אפשר לנסח מאוד בקלות את המהומה שהלכה קודם:

\( H^{\otimes n}\left|x\right\rangle =\frac{1}{\sqrt{2^{n}}}\sum_{y\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{x\cdot y}\left|y\right\rangle \)

כי מה קורה כאן? המכפלה הסקלרית \( x\cdot y=\sum_{i=1}^{k}x_{i}y_{i} \) בעצם סופרת את מספר האינדקסים \( i \) שבהם גם \( x_{i}=1 \) וגם \( y_{i}=1 \), ביחד - אלו שני הדברים שהיו חייבים להתקיים סימולטנית כדי שהאינדקס \( i \) יתרום \( -1 \) למקדם של \( \left|y\right\rangle \). כשלוקחים את זה מודולו 2, מקבלים 0 אם מספר המוכפלים זוגי (ולכן המקדם הכולל יהיה 1) ו-\( 1 \) אם הוא יהיה אי זוגי (ולכן המקדם הכולל יהיה \( -1 \)). הטריק הזה של להעלות את \( -1 \) בחזקה שהיא או זוגית או אי זוגית כדי לקבל אפקט של כפל ב-1 או ב-\( -1 \) הוא נפוץ ביותר בכל חלקי המתמטיקה ומשרת אותנו גם כאן.

במקרה הפרטי שראינו בהתחלה, זה שבו \( x=0^{n} \), פשוט מתקיים \( x\cdot y=0 \) לכל \( y \), ולכן המקדם יוצא תמיד חיובי ואנחנו מקבלים את הסכום הנחמד שראינו קודם: \( H^{\otimes n}\left|0^{n}\right\rangle =\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left|x\right\rangle \).

עכשיו אפשר לחזור סוף סוף אל דויטש-ג’וזה ולהבין מה קורה בו: כל מה שנשאר לנו הוא חשבון פשוט ביותר.

ההתחלה של דויטש-ג’וזה מאפסת מצב התחלתי \( \left|0^{n}\right\rangle \) ואז מפעילה עליו \( H^{\otimes n} \), כלומר אנחנו מגיעים אל \( \frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left|x\right\rangle \). בשלב הבא מפעילים את הקופסה השחורה על המצב הזה. נזכיר מה היא עושה:

\( U_{f}\left|x\right\rangle =\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \)

ולכן נקבל

\( U_{f}\left(\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left|x\right\rangle \right)=\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}U_{f}\left(\left|x\right\rangle \right)= \)

\( =\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \)

עכשיו על כל זה אני מפעיל שוב \( H^{\otimes n} \) ומקבל סכום כפול:

\( H^{\otimes n}\left(\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \right)=\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)}H^{\otimes n}\left(\left|x\right\rangle \right)= \)

\( =\frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)}\frac{1}{\sqrt{2^{n}}}\sum_{y\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{x\cdot y}\left|y\right\rangle \)

זה סכום סופי, אז קל להפוך בו את סדר הסכימה: לכל \( y\in\left\{ 0,1\right\} ^{n} \), לקבץ את האיברים שמתאימים למקדם \( \left|y\right\rangle \):

\( =\frac{1}{2^{n}}\sum_{y\in\left\{ 0,1\right\} ^{n}}\left(\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)+x\cdot y}\right)\left|y\right\rangle \)

ה-\( \left|y\right\rangle \) השונים הם תוצאות המדידה השונות האפשריות, והמקדם שאני מחשב ילמד אותי מה ההסתברות להעלות את \( \left|y\right\rangle \) בגורל. האלגוריתם, כזכור, מכריע את ההכרעה שלו על פי השאלה האם \( \left|0^{n}\right\rangle \) עלה בגורל, אז בואו נבדוק ספציפית את המקדם של \( y=0^{n} \):

\( \frac{1}{2^{n}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)+x\cdot y}=\frac{1}{2^{n}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)} \)

עכשיו, אם \( f \) היא פונקציה קבועה, כל האיברים בסכום יהיו אותו הדבר ולכן נקבל \( \frac{1}{2^{n}}\cdot\left(\pm2^{n}\right)=\pm1 \). זה לא משנה אם המקדם חיובי או שלילי, כי כזכור - כדי לקבל את ההסתברות אנחנו לוקחים ערך מוחלט של המקדם ומעלים אותו בריבוע, ולכן בכל אחד מהמקרים הללו נקבל 1: בהסתברות של 1 בדיוק מובטח לנו שנקבל את המצב \( 0^{n} \), כמו שאמור לקרות.

אם \( f \) היא פונקציה מאוזנת, אז \( \sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)} \) הולך לכלול את אותו מספר של \( +1 \) ושל \( -1 \), וכולם יבטלו זה את זה, כך שאני אקבל 0. עזבו אתכם ממה שקורה עם שאר המקדמים של שאר האיברים במצב שהגעתי אליו - המקדם של \( 0^{n} \) הוא 0, ולכן אין לי סיכוי לקבל אותו. אני בודאות אקבל תוצאה אחרת ולכן האלגוריתם יענה נכון גם במקרה הזה. זה מסיים את ההוכחה שהוא עובד, וגם נותן לנו תחושה טובה מאיפה הגיעו ה”פונקציה קבועה או מאוזנת” הללו; נראה כאילו היה לנו כאן אלגוריתם שחיפש בעיה לפתור, אבל זה לא משנה את זה שהפתרון מרהיב ממש באלגנטיות המתמטית שלו.

אלגוריתם ברנשטיין-וזירני

אמרתי שדויטש-ג’וזה נשמע כמו אלגוריתם שמחפש בעיה לפתור, והיופי פה הוא שבעצם יש עוד בעיה שאפשר לפתור, בצורה כזו שלא זורקת הצידה את תוצאת המדידה אם היא שונה מ-\( 0^{n} \). גם הבעיה הנוספת הזו עדיין מרגישה קצת מלאכותית, אבל אולי פחות? בהקשר של הבעיה הזו, אלגוריתם דויטש-ג’וזה נקרא גם אלגוריתם ברנשטיין-וזירני למרות שזה אותו אלגוריתם בדיוק; המאמר המקורי של ברנשטיין ווזריני הוא גדול ומורכב ועוסק בהגדרות של מחלקות סיבוכיות קוונטיות והפרדה שלהן ממחלקות סיבוכיות הסתברותיות ובהקשר הזה מופיע השימוש שאני מתאר כאן; זה לא שברנשטיין-וזירני ישבו ואמרו “היי, תראו, יש עוד משמעות לדויטש-ג’וזה” וישבו לכתוב על זה מאמר.

דויטש-ג’וזה עוסק בנסיון להבין פונקציה \( f:\left\{ 0,1\right\} ^{n}\to\left\{ 0,1\right\} \) כלשהי שהיא או קבועה, או מאוזנת. ברנשטיין-וזירני עוסק בנסיון להבין פונקציה \( f:\left\{ 0,1\right\} ^{n}\to\left\{ 0,1\right\} \) שהיא לאו דווקא קבועה או מאוזנת, אבל היא לינארית, כלומר \( f\left(x+y\right)=f\left(x\right)+f\left(y\right) \) וגם \( f\left(\lambda x\right)=\lambda f\left(x\right) \) (לא כזה מרשים כי \( \lambda\in\left\{ 0,1\right\} \)), כשהחיבור והכפל בסקלר הם מעל \( \mathbb{Z}_{2}^{n} \). בואו נראה שאפשר לחשוב על הפונקציה הזו בתור מכפלה סקלרית, כלומר שקיים \( w\in\left\{ 0,1\right\} ^{n} \) כך ש-\( f\left(x\right)=w\cdot x \):

אם נגדיר \( e_{i}=\left(0,\ldots,1,\ldots,0\right) \), כלומר ה-\( 1 \) נמצא רק במקום ה-\( i \) של \( e_{i} \), אז נקבל בסיס של \( \mathbb{Z}_{2}^{n} \): אפשר להציג כל \( x\in\mathbb{Z}_{2}^{n} \) בתור \( x=\sum_{i=1}^{n}x_{i}e_{i} \). מתכונת הלינאריות של \( f \) נקבל

\( f\left(x\right)=f\left(\sum_{i=1}^{n}x_{i}e_{i}\right)=\sum_{i=1}^{n}x_{i}f\left(e_{i}\right) \)

אז פשוט נגדיר \( w_{i}=f\left(e_{i}\right) \) ונקבל שאכן, \( f\left(x\right)=w\cdot x \) לכל \( x\in\mathbb{Z}_{2}^{n} \). שימו לב שרוב הפונקציות אינן לינאריות; יש \( 2^{2^{n}} \) פונקציות מ-\( \left\{ 0,1\right\} ^{n} \) אל \( \left\{ 0,1\right\} \), אבל מכיוון שיש רק \( 2^{n} \) איברים \( w\in\left\{ 0,1\right\} ^{n} \) יש רק \( 2^{n} \) פונקציות לינאריות. מכאן שברנשטיין-וזירני מראש מטפל רק במחלקה קטנה יחסית של פונקציות, בדומה לדויטש-ג’וזה.

המשימה של ברנשטיין-וזירני היא זו: בהינתן \( f \) לינארית שכזו, למצוא את ה-\( w \) שמגדיר אותה. שימו לב: בניגוד לדויטש-ג’וזה, כאן אנחנו לא רוצים להכריע בין שתי סיטואציות אלא ממש למצוא משהו. אבל אותו אלגוריתם יעבוד:

1. אתחלו מצב קוונטי אל \( \left|0^{n}\right\rangle \)
2. הפעילו \( H \) על כל הקיוביטים.
3. הפעילו את הקופסה השחורה על המצב שקיבלתם.
4. הפעילו \( H \) על המצב שקיבלתם.
5. מדדו את כל הקיוביטים במצב שקיבלתם.
6. תוצאת המדידות \( w \) היא הערך המבוקש.

לי זה נראה כמו קסם, שפתאום נקבל את ה-\( w \) הזה, אבל האמת היא שזה די פשוט. בואו ניזכר מה מקבלים אחרי שלב 4, כי כבר ביצענו את החישוב קודם:

\( \frac{1}{2^{n}}\sum_{y\in\left\{ 0,1\right\} ^{n}}\left(\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)+x\cdot y}\right)\left|y\right\rangle \)

עכשיו, ה-\( f\left(x\right)+x\cdot y \) הזה שלמעלה נהיה פשוט יותר במקרה שלנו, כי \( f\left(x\right)=w\cdot x=x\cdot w \) ולכן נקבל

\( f\left(x\right)+x\cdot y=x\cdot w+x\cdot y=x\cdot\left(w+y\right) \)

עכשיו, במקרה שבו \( w=y \) אנחנו מקבלים \( w+y=2y=0 \) (כי זכרו, אנחנו מעל \( \mathbb{Z}_{2} \)) ולכן המקדם של \( \left|y\right\rangle =\left|w\right\rangle \) יהיה

\( \frac{1}{2^{n}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)+x\cdot y}=\frac{1}{2^{n}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{0}=\frac{1}{2^{n}}\sum_{x\in\left\{ 0,1\right\} ^{n}}1=1 \)

קסם!

בשלב הזה אני כבר ממש מוטרד. זה מרגיש כמו “קסם” במובן של אחיזת עיניים של קוסם, שגורם לנו כל הזמן להתמקד במקום אחד - במקרה זה, במקדם של ה-\( \left|y\right\rangle \) הספציפי שמעניין אותנו, ובגלל שהוא יוצא 1 אנחנו אמורים איכשהו להיות מרוצים ולהניח שכל שאר המקדמים יוצאים 0. אבל למה? ובכן, זה די קל: בואו ניקח \( y\ne w \), אז זה אומר ש-\( y+w\ne0 \) לפחות באינדקס אחד. נניח בלי הגבלת הכלליות שזה האינדקס הראשון, אז אפשר לכתוב \( y+w=1z^{\prime} \) כאשר \( z^{\prime}\in\left\{ 0,1\right\} ^{n-1} \).

עכשיו, אנחנו מסתכלים על הסכום \( \sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)+x\cdot y} \), שאחרי הפישוטים שלנו יוצא \( \sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{x\cdot1z^{\prime}} \). אני הולך לחלק את ה-\( x \)-ים לשתי קבוצות: אלו שמתחילים ב-0 ואלו שמתחילים ב-1. מן הסתם שתי הקבוצות הללו מאותו גודל, אבל שימו לב לכך שאם \( x=0x^{\prime} \) אז \( x\cdot1z^{\prime}=x^{\prime}\cdot z^{\prime} \) ואילו אם \( x=1x^{\prime} \) אז \( x\cdot1z^{\prime}=1+x^{\prime}\cdot z^{\prime} \). במילים אחרות, הזוג \( 0x^{\prime},1x^{\prime} \) יניב תוצאות שונות כשמעלים את \( -1 \) בחזקת \( x\cdot1z^{\prime} \), ולכן הסכום של שניהם יצא 0. בצורה הזו חילקנו את כל ה-\( x \)-ים שלנו לזוגות שמבטלים זה את זה, ולכן באמת נקבל 0. אני מקווה שזה משכנע גם את מי שכמוני קשה לו לקבל את זה שאם המקדם של איבר אחד יצא 1 זה אומר ששאר המקדמים הם בהכרח 0.

מה למדנו מכל זה?

כאמור, אני לא מביא את האלגוריתמים הללו בשביל להוכיח את עליונות החישוב הקוונטי על החישוב הרגיל, והטיעון המתמטי המדויק שרלוונטי לנסח בהקשר הזה הוא ארוך ומסובך למדי ואין לי כוח אליו. אני מביא אותם כדי שנרגיש מה הולך באלגוריתמים קוונטיים. באופן מאוד גס אוהבים לומר שהכוח של אלגוריתם קוונטי נובע משלושה היבטים של חישוב קוונטי:

• סופרפוזיציה
• שזירה
• התאבכות

בדויטש-ג’וזה-ברנשטיין-וזירני אין ממש שזירה (ה-\( H \)-ים בהתחלה ובסוף לא יוצרים שזירה, וגם ה-\( U \) באמצע לא חייבת ליצור שזירה). בהחלט יש סופרפוזיציה - זה מה שה-\( H \) בהתחלה עושה לנו מייד. אבל האספקט המעניין שטרם ראינו הוא שיש כאן התאבכות.

בפיזיקה, במשמעות המקורית של המילהת “התאבכות” באה לתאר סיטואציה שבה גלים שונים ש”מתנגשים” יכולים לחזק או להחליש זה את זה בנקודות ההתנגשות, בהתאם למצב הנוכחי שלהם. אפשר לחשוב על גל בתור משהו שכל הזמן עולה ויורד. אם בנקודת ההתנגשות של שני גלים, שנים בנקודה הגבוהה ביותר שלהם, הם יחזקו זה את זה ונקבל גל עוד יותר גבוה (“התאבכות בונה”) ואם הם ייפגשו בנקודה הנמוכה ביותר שלהם התוצאה תהיה עוד יותר נמוכה וגם זו תהיה התאבכות בונה. אבל אם גל אחד יהיה גבוה והשני נמוך, הם יבטלו זה את זה ונקבל איזור שבו לא רואים שום דבר (“התאבכות הורסת”). מה שיפה בדויטש-ג’וזה הוא שזה בדיוק מה שקורה גם כאן.

כשביצענו את הסופרפוזיציה הראשונית עם \( H^{\otimes n} \), אפשר לחשוב על כך כאילו לקחנו את המצב \( \left|0^{n}\right\rangle \) ופירקנו אותו לסכום של \( 2^{n} \) גלים שונים: \( \frac{1}{\sqrt{2^{n}}}\sum_{x\in\left\{ 0,1\right\} ^{n}}\left|x\right\rangle \). ברגע הזה, כל הגלים נמצאים באיזור ה”גבוה” שלהם, שבא לידי ביטוי בפאזה החיובית שלהם (הפאזה בהקשר הנוכחי היא הסימן של המקדם של \( \left|x\right\rangle \)).

אחר כך אנחנו מפעילים את \( U_{f} \), וההשפעה שלו היא פשוטה: הוא משנה את הפאזה של \( \left|x\right\rangle \)-ים מסויימים, מחיובית לשלילית. במקום שכל הגלים יהיו מסונכרנים, \( U_{f} \) פיצל את הגלים לשתי קבוצות, כל אחת עם הסינכרון שלה. לבסוף מגיע ה-\( H^{\otimes n} \) השני, ומה שהוא עושה הוא לגרום לכל הגלים להתנגש ולהסתכל מה קרה. כשהגלים “מתנגשים”, לכל \( \left|y\right\rangle \) אנחנו מקבלים בנקודת ההתנגשות את

\( \frac{1}{\sqrt{2^{n}}}\left(\sum_{x\in\left\{ 0,1\right\} ^{n}}\left(-1\right)^{f\left(x\right)+x\cdot y}\right)\left|y\right\rangle \)

בברנשטיין-וזירני, עבור רוב ערכי ה-\( \left|y\right\rangle \), ההתאבכות תהיה הורסת והם ייעלמו לגמרי. המקום היחיד שבו תהיה התאבכות בונה הוא ה-\( \left|y\right\rangle \) שאנו חפצים ביקרו. בדויטש-ג’וזה תהיה התאבכות בונה ב-\( \left|0^{n}\right\rangle \) רק אם הפונקציה קבועה, ואחרת תהיה שם התאבכות הורסת.

זו בעצם המהות של רבים מהאלגוריתמים הקוונטיים: לגרום איכשהו לחלקים השונים של הסופרפוזיציה “להתנגש” אלו באלו, כך שהחלקים הלא מועילים מתבטלים, והחלקים המועילים נשארים. בדויטש-ג’וזה, בגלל הפשטות הגדולה שלו, אנחנו יכולים לראות בדיוק מה גורם להתאבכויות הללו לעבוד - העובדה שהמקדמים של ה-\( \left|x\right\rangle \)-ים יכולים להיות שליליים. וכאן אנחנו מגיעים אל מה שהוא אולי לב-לבו של ההבדל המרכזי בין חישוב קוונטי וחישוב הסתברותי “רגיל”. ריצ’ארד פיינמן, בהרצאה מפורסמת שלו, Simulating Physics with Computers, אמר (כחלק מתיאור יותר מפורט, כמובן)

The only difference between a probabilistic classical world and the equations of the quantum world is that somehow or other it appears as if the probabilities would have to go negative.

וזה בדיוק מה שקורה פה. אם אני מבצע חישוב הסתברותי “רגיל” שבו אני מגריל מחרוזת \( x\in\left\{ 0,1\right\} ^{n} \) בהתפלגות אחידה, אפשר יהיה לחשוב על מצב החישוב שלי אחרי השלב הראשון הזה כאילו הוא ב”סופרפוזיציה” שבו ההסתברות של כל \( x \) היא בדיוק \( \frac{1}{2^{n}} \). אחר כך אני יכול לבצע חישובים שעבור \( x \)-ים שונים יובילו לאותה תוצאה, ובכך “לחזק” את ההסתברות של אותה תוצאה להתקבל. אבל האופן שבו ה”חיזוק” הזה מתבצע הוא על ידי חיבור הסתברויות, אין לי חיסור. אם לחדד: אפשר לתאר חישוב הסתברותי רגיל בתור כפל של וקטור סטוכסטי (וקטור שבו כל הכניסות בין 0 ל-1 ומסתכמות ל-1) במטריצה סטוכסטית (מטריצה שבה כל הכניסות בין 0 ל-1 וכל שורה מסתכמת ל-1). זה נותן הרבה, אבל זה פשוט לא מאפשר לנו לבצע את אותה אלגברה שאנחנו עושים בחישוב קוונטי, עם מטריצות שיש בהן גם מספרים שליליים.

עוד דרך לחשוב על זה: בחישוב הסתברותי, מה שיש לנו ביד בכל רגע נתון הוא ההסתברויות של התוצאות האפשריות. בחישוב קוונטי, מה שיש לנו ביד בכל רגע נתון הוא האמפליטודות של החישוב - אותן \( \alpha_{x} \)-ים. ה-\( \alpha_{x} \)-ים הן לא הסתברויות; הן מספרים שיכולים להיות גם שליליים וגם מרוכבים, ואת ההסתברויות אנחנו מחשבים מתוכן בעזרת שלב הביניים \( \left|\alpha_{x}\right|^{2} \). כלומר, אנחנו מסוגלים לבצע אלגברה יותר מתוחכמת, ש”מוסתרת” בסופו של דבר בידי המעבר מ-\( \alpha_{x} \) אל \( \left|\alpha_{x}\right|^{2} \). אבל כל עוד לא מדדנו, אנחנו עדיין בעולם של האלגברה המתוחכמת יותר, והיא זו שמאפשרת לנו להשיג את האפקט של ההתאבכות. חישוב קוונטי מאפשר לנו לרתום את הטבע עצמו כדי לבצע אלגברה שהיא יותר מתוחכמת מאלגברה בוליאנית.

זהו, זו הדרך הכי טובה שיש לי לתת את האינטואיציה האישית שלי לסיבה שבגללה חישוב קוונטי הוא “יותר” מחישוב רגיל. עכשיו רק נשאר לי לסגור את החוב מתחילת הפוסט לגבי הקופסאות השחורות.

אז איך מממשים קופסא שחורה קוונטית?

בתחילת הפוסט מלמלתי משהו על חישוב של \( f \) בעזרת קופסא שחורה ואז קפצתי לכך שיש לנו אופרטור \( U_{f} \) שעושה את הקסם \( U_{f}\left|x\right\rangle =\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \). אני עדיין צריך להסביר איך כזה דבר עובד.

אם תחשבו על זה רגע, עדיין בסדרת הפוסטים לא הסברתי איך מבצעים חישוב רגיל בעזרת מחשב קוונטי. אמנם, אמרתי ש-\( X \) זה כמו NOT, אבל אין לי שום פעולה שהיא כמו AND, למשל: פעולה שמחזירה 1 רק אם שני הקלטים היו 1, ואחרת מחזירה 0. ויש סיבה טובה שבגללה אין לי כזו: כי AND היא פעולה לא הפיכה אבל בחישוב קוונטי כל פעולה צריכה להיות אופרטור אוניטרי, כלומר הפיכה. אם ב-AND קיבלתי 0, אני לא יודע אם זה בגלל ששני הקלטים היו 0, או בגלל שאחד מהם היה 0 והשני 1, ואיזה מהם. אינפורמציה הלכה לאיבוד.

האם זה אומר שלא ניתן לממש פעולת AND בחישוב קוונטי? לא בדיוק. אפשר, אבל צריך יהיה לשלם מחיר כלשהו. המחיר הוא שימוש בקיוביט “זבל” שישתתף בחישוב בתור מעין משתתף זמני ואחר כך נוכל לשכוח מערכו. אני לא אכנס לפרטים הללו עכשיו אלא אציג פוסט יותר מפורט עליהם בהמשך. למה לא הראיתי את זה קודם? כי זו אחת מהבעיות הללו שכל עוד לא מרגישים שחסר לה פתרון, קצת טרחני להציג אותו.

אז נניח שיש לנו מעגל קוונטי שיודע גם לבצע חישוב רגיל. יש לו \( n \) קיוביטי קלט, וקיוביט נוסף שאנו מניחים שמאותחל ל-\( \left|0\right\rangle \) ובסוף החישוב יהיה בו הפלט, ואולי גם קיוביט עזר שלא נטרח לכתוב. כלומר, מה שיש לנו הוא מעגל שמחשב

\( O_{f}\left(\left|x\right\rangle \otimes\left|0\right\rangle \right)=\left|x\right\rangle \otimes\left|f\left(x\right)\right\rangle \)

שימו לב: כאן במכפלה הטנזורית, הרכיב השמאלי, \( \left|x\right\rangle \), הוא בעצמו מכפלה טנזורית של \( n \) קיוביטים, בעוד שהרכיב הימני הוא קיוביט בודד.

הבעיה עם ההגדרה שנתתי כרגע היא שזו עדיין לא הגדרה שלמה. הגדרתי את \( O_{f} \) לחלק מהקלטים שהם אברי בסיס, אבל לא לכולם. מה עם הקלטים מהצורה \( \left|x\right\rangle \otimes\left|1\right\rangle \)? כדי לטפל בכל המקרים, אני אגדיר

\( O_{f}\left(\left|x\right\rangle \otimes\left|b\right\rangle \right)=\left|x\right\rangle \otimes\left|f\left(x\right)\oplus b\right\rangle \)

כאן \( \oplus \) מציין חיבור מודולו 2, ולכן מה ש-\( O_{f} \) עושה הוא או להחזיר את \( f\left(x\right) \) (אם הקלט הנוסף הוא 0) או את \( \neg f\left(x\right) \) (אם הקלט הנוסף הוא 1). מה שאני רוצה להסביר עכשיו הוא איך לבנות את \( U_{f} \) שבו השתמשתי קודם מתוך \( O_{f} \) הזה. הטריק הוא חמוד ממש: במקום להפעיל את \( O_{f} \) על \( \left|x\right\rangle \otimes\left|0\right\rangle \) או על \( \left|x\right\rangle \otimes\left|1\right\rangle \), אני אפעיל אותו על \( \left|x\right\rangle \otimes\left|-\right\rangle \).

כזכור, \( \left|-\right\rangle \) הוא המצב הקוונטי שמתקבל מ-\( H\left|1\right\rangle \), כלומר \( \frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}} \). בואו נראה מה \( O_{f} \) עושה כשהוא מקבל קלט כזה, תוך התבססות על הלינאריות שלו:

\( O_{f}\left(\left|x\right\rangle \otimes\left|-\right\rangle \right)=\frac{1}{\sqrt{2}}\left[O_{f}\left(\left|x\right\rangle \otimes\left|0\right\rangle \right)-O_{f}\left(\left|x\right\rangle \otimes\left|1\right\rangle \right)\right]= \)

\( =\frac{1}{\sqrt{2}}\left[\left|x\right\rangle \left|f\left(x\right)\right\rangle -\left|x\right\rangle \left|f\left(x\right)\oplus1\right\rangle \right]= \)

\( =\left|x\right\rangle \frac{\left|f\left(x\right)\right\rangle -\left|f\left(x\right)\oplus1\right\rangle }{\sqrt{2}} \)

עכשיו, בואו נבדיל בין שני המקרים האפשריים:

• אם \( f\left(x\right)=0 \) אז מה שקיבלנו מימין ל-\( \left|x\right\rangle \) הוא את \( \frac{\left|0\right\rangle -\left|1\right\rangle }{\sqrt{2}}=\left|-\right\rangle \)
• אם \( f\left(x\right)=1 \) אז מה שקיבלנו מימין ל-\( \left|x\right\rangle \) הוא את \( \frac{\left|1\right\rangle -\left|0\right\rangle }{\sqrt{2}}=-\left|-\right\rangle \)

ובמילים אחרות, קיבלנו ש-

\( O_{f}\left(\left|x\right\rangle \left|-\right\rangle \right)=\left(-1\right)^{f\left(x\right)}\left|x\right\rangle \left|-\right\rangle \)

קיבלנו שהפעלה של \( O_{f} \) לא משנה את המצב הקוונטי כלל, חוץ מאשר על ידי כפל שלו ב-\( \left(-1\right)^{f\left(x\right)} \). לכן, אם נסתכל על האפקט רק ל-\( n \) הקיוביטים הראשונים, נקבל בדיוק את \( U_{f} \) שרצינו. זה מסיים גם את ההסבר שלי לגבי הופעת הקופסה השחורה המסתורת \( U_{f} \), אבל עדיין נשאר לי חוב של להסביר איך בכלל מבצעים חישובים רגילים בעזרת חישוב קוונטי. אל זה נגיע בעתיד. אסיים עם האיור שנותן לנו את כל דויטש-ג’וזה בעזרת \( O_{f} \) הזה, שכן גם באיור הזה אפשר להיתקל לפעמים ושווה לראות אותו, עכשיו כשאנחנו מבינים שזה אותו הדבר: