מה כל הסיפור הזה עם הערך של פאי בתנ"ך?

מבוא

אחד מהכוכבים הגדולים של המתמטיקה הוא המספר הקבוע פאי, \( \pi \), שמוגדר בתור היחס הקבוע בין היקף של מעגל לקוטר שלו. זה מספר ששווה בערך ל-\( 3.14159 \), אבל אני אומר “בערך” כי \( \pi \) הוא מה שנקרא “מספר אי רציונלי” - מספר שאם ננסה לכתוב בבסיס עשרוני נזדקק לאינסוף ספרות, בלי מחזוריות כלשהי. זה אומר שכשעובדים עם פאי משתמשים בקירוב שלו, וזה יוצר שני סוגים מעניינים של קירובים - ראשית, קירובים שהם מספיק טובים כדי לעבוד איתם בפועל, ושנית - קירובים שהם ממש טובים בשלל מובנים שונים ומשונים.

אי שם בעבר הרחוק, עוד לפני שהתחלתי ללמוד מתמטיקה בצורה מסודרת, נתקלתי ב-\( \pi \) בתוך ויכוח שכבר אז נראה לי תמוה במיוחד, בין אנטי-דתיים שמנסים לשכנע את העולם שהתנ”ך כולו הוא שטות אחת גדולה, והמתנגדים להם שמנסים לשכנע שבתנ”ך יש גאונות שמיימית ממש. כל המהומה הזו התרכזה סביב פסוק אחד בספר מלכים, שאם קוראים אותו כפשוטו נראה שהוא אומר ש-\( \pi=3 \), אבל יש קונץ מרהיב שאם משתמשים בו אפשר לטעון שהפסוק מקודד קירוב ממש טוב של פאי, את הקירוב \( \frac{333}{106}=3.14151\ldots \) שמדויק בחמש הספרות הראשונות שלו.

מאחורי הויכוח הבאמת מיותר הזה מסתתרים שני עולמות מעניינים באמת. עולם אחד הוא העולם המתמטי של קירובים לפאי ובאופן כללי קירובים לדברים, שאני הולך לנצל את הפוסט הזה כדי לתת טעימה קטנה ממנו; העולם השני הוא העולם ההלכתי שכבר דן בנושא הפסוק הזה מכל זווית אפשרית בערך ואני בהחלט לא הולך להיכנס לעובי הקורה של כל מה שהולך שם כי עבורי, שמגיע מגישה מתמטית ולא דתית, רוב העיסוק בנושא נראה כמו נסיון לענות על שאלה שאין צורך לשאול בכלל. אבל אני אנסה להבהיר מה השאלה וקצת מהרעיון הכללי של הפתרונות.

המטרה של הפוסט הזה היא לא להתנגח באף אחד (טוב, אולי חוץ מאלו שחושבים שה-\( \pi=3 \) הוא תירוץ לומר שהתנ”ך הוא שטות) אלא לראות דברים מעניינים, ובאופן די משמח הסיפור הזה נותן לנו תירוץ לראות כאלו.

בואו נתחיל להיכנס לפרטים.

חלק ראשון - מה בכלל הבעיה

מקור כל המהומה הוא פסוק כ”ג בספר מלכים א’, פרק ז’. זה פרק לא מרתק במיוחד (עבורי) שמדבר על בניית בית המקדש הראשון בידי שלמה ונכנס לפרטים טכניים למדי. אחד מהדברים שנבנו במקדש הוא מאגר מים מנחושת שנקרא “הים” והוא מתואר כך:

ויעש את הים מוצק עשר באמה משפתו עד שפתו עגל סביב וחמש באמה קומתו וקוה [וקו] שלשים באמה יסב אתו סביב

הים הוא “עגול סביב”, כלומר בקריאה הפשוטה של הפסוק אנחנו חושבים עליו בתור עיגול. המרחק “משפתו עד שפתו” הוא 10 (10 אמה, אבל כשהמדידות יהיו באמות לא אטרח לציין את זה אלא אם תהיה לי סיבה טובה) - כאן הכוונה היא ככל הנראה לקוטר, שהוא קו בעיגול שמתחיל בשפה אחת, עובר דרך מרכז העיגול ומגיע לשפה בצד השני. זה הקו הארוך ביותר בעיגול שעובר משפה אל שפה (אם לא חייבים לעבור דרך המרכז, מקבלים קווים קצרים יותר)

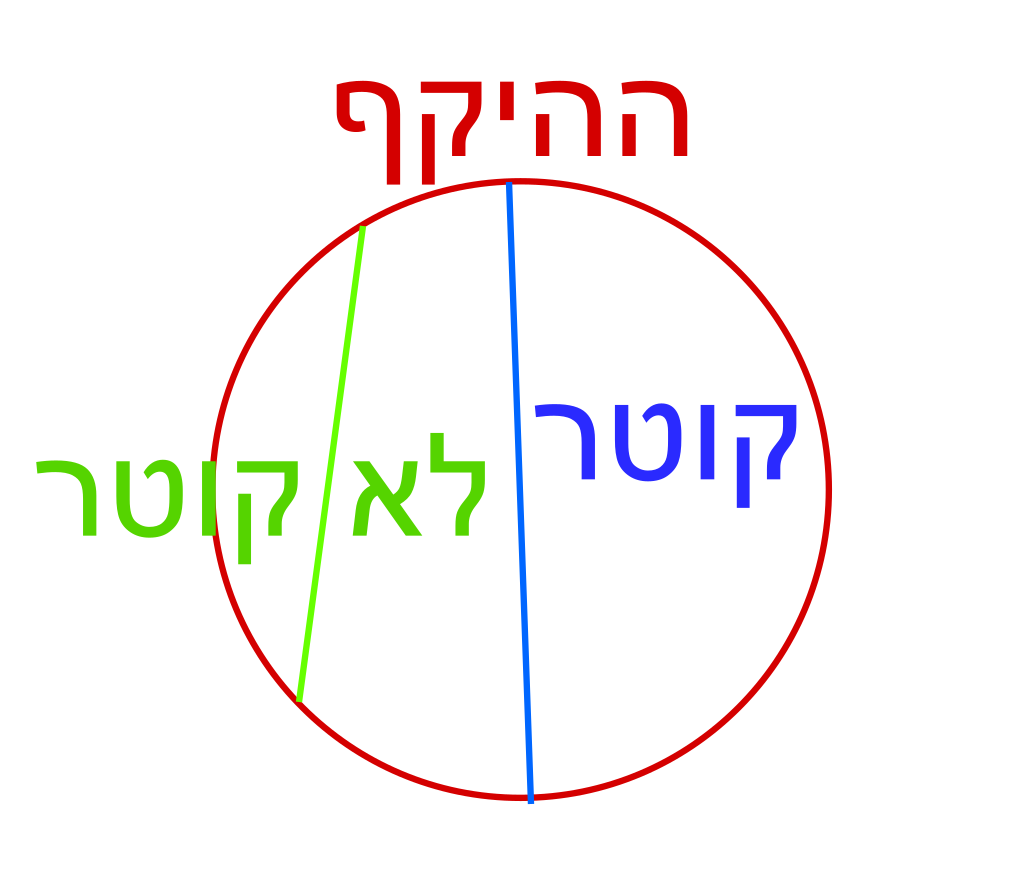
הגובה של הים הוא 5, אבל זה לא מעניין אותנו כל כך אלא ההמשך - ה”קו” (שנכתב בתור “קוה”) שסובב את העיגול - כלומר, החלק החיצוני שלו, מה שנקרא ההיקף של העיגול הוא באורך 30.

עכשיו, מה אמרנו על \( \pi \)? זה היחס בין היקף מעגל לקוטר. מה שמקבלים כשמחלקים אחד בשני. במקרה שלנו ההיקף הוא 30 והקוטר הוא 10 ולכן \( \pi=3 \) עד כאן הכל טוב, אבל הנה הצרות מתחילות, כי העניין הוא זה: בגאומטריה אוקלידית (שהיא הגאומטריה שלנו ביומיום), כל מעגל שנצייר יהיה בעל בדיוק אותו יחס בין ההיקף לקוטר שלו - זה מספר קבוע. הוא לא תלוי בעיגול ספציפי זה או אחר. ובכולם הוא יוצא משהו שהוא לא 3 אלא כאמור בערך \( 3.14159 \). לפעמים אנחנו נוהגים לכתוב \( \pi=3.14159\ldots \) עם שלוש נקודות כדי להגיד “וכאן הספרות עדיין לא נגמרות”.

אם כן, שוד ושבר, קיבלנו שהפסוק בתנ”ך לא מדויק מבחינה מתמטית! זו הנקודה שעליה שונאי התנ”ך עורכים את החגיגות שלהם, ואני חייב להודות שלא היה לי אז ועדיין אין לי היום שמץ של מושג מה הם רוצים, פשוט כי מבחינתי אין שום סיבה שהתנ”ך כן יהיה מדויק בנקודה הזו. אני חושב שבמובן מסוים חלק נכבד מהעיסוק המתמטי הוא בדיוק במתן אפשרות לנו לא להיות מדויקים כי אנחנו יודעים ש”עמוק בפנים” הכל כן בסדר ואנחנו מבינים דברים עד הסוף, אבל כדי שאפשר יהיה לעשות דברים בחיי היום יום אי אפשר להסתרבל עד אין קץ עם דיוק מוחלט, אז מזהים איך אפשר לוותר על הדיוק בלי שיגרם מכך נזק. השימושיות של המתמטיקה בתחומים כמו פיזיקה, למשל, מתבססת בדיוק על היכולת הזו.

אם, נאמר, הקוטר של העיגול אצל שלמה היה 10 ואנחנו רוצים להיות “מדויקים” אז ההיקף היה צריך להיות \( 31.4159\ldots \). אז מה התנ”ך היה צריך לעשות? לומר “וקוה שלשים ואחד ועשירית אמה”? בשביל מה זה טוב, בעצם? יודעים מה, אני מנחש שהגובה של הים אצל שלמה היה בכלל 4.96 אמה והסופר המקראי עיגל את זה ל-5. ובכלל, איך ידעו מה ההיקף? צריך למדוד. האם מכשירי המדידה היו מדויקים? אולי המודד עצמו בחר לתת קירוב?

אפשר כמובן לומר שזו לא סתם איזו באר אקראית שמישהו בנה איפה שהוא. זה בית המקדש של שלמה, הכל פה היה מחושב ומדוקדק עד הפיפס האחרון. עוד טיעון שקראתי הוא שמכיוון שכותב ספר מלכים היה (על פי המסורת, לא על פי הידע ההיסטורי שלנו) הנביא ירמיהו, הוא מחוייב לרמת דיוק גבוהה. כך במאמר של ניסן יואלי שדווקא מגיע מהגישה הפרו-דתית:

הנביא הוא נביא אמת אין אצלו “בערך”. נביא שלא דייק במשהו בנבואתו הוא נביא שקר ועונשו מיתה.

או…קיי… על זה אומרים אצלנו, That escalated quickly. עכשיו תראו, במסגרת התחקיר שלי לפוסט הזה נתקלתי גם במאמרים מנקודת מבט דתית שפחות מתרגשים מהסיפור הזה. זה באמת ויכוח פנים דתי שמשתמש בטיעונים דתיים שלא רלוונטיים עבורי. אבל מה שנחמד הוא שהתחושה שחייבים לתת הסבר מניבה רעיונות יצירתיים, למשל השערות שונות ומשונות על הצורה המדויקת של הים. הנה מאמר יפה של דוד אימבר שנכנס לפרטים ויש בו ציורים. במאמר הזה גם אפשר לראות שבעצם העניין פה הוא לא רק הפסוק שהבאתי, אלא גם מערכת אילוצים נוספת שצצה בעקבות פסוק כ”ו בהמשך הפרק:

ועביו טפח ושפתו כמעשה שפת כוס פרח שושן אלפים בת יכיל

כלומר יש לנו כאן גם מידה לעובי של הים, וגם את הקיבולת שלו. העובי הוא “טפח” והקיבולת היא “אלפים בת”. להבנתי הדלה, “אלפים בת” מתורגם אל 450 אמה מעוקבת, ואילו “טפח” בהקשר הספציפי הזה מתורגם אל שישית (או שמא חמישית?) אמה. חז”ל עסקו בזה במסכת עירובין יד ב, אבל כפי שאפשר להבין זה לא סיים את הסיפור בצורה חד משמעית. עכשיו, למרות שאני אישית בא מגישת “מי שזה לא יהיה שכתב את זה פשוט לא חש צורך להיות יותר מדויק מזה”, ההסברים שמתארים צורות אפשריות של הים הם די נחמדים בעיני. רק צריך לזכור, כמובן, שלא משנה כמה ההסבר יהיה טוב, המספרים אף פעם לא יהיו מדויקים כי זה פשוט בלתי אפשרי להיות מדויק כשפאי מעורב בנושא אבל את כל הגדלים כותבים עם מספרים טבעיים. אז אפשר לומר “אם הנביא אומר \( \pi=3 \) צריך להרוג אותו אבל אם הוא אומר \( \pi=3.14159 \) הכל טוב”, אבל אני לא כל כך מבין את ההבדל של חיים ומוות בין שני הקירובים.

העניין הוא שמעבר לכל הדיון ההלכתי יש עוד משהו, שאני קורא לו “קוריוז” או “תעלול” ואחרים יקראו לו “רמז”.

חלק שני, שבו קירוב טוב צץ באופן די מפתיע

את מה שאני אתאר עכשיו ראיתי שמייחסים בעיקר לגאון מוילנא (הגר”א) שחי במאה ה-18 ובנוסף להשכלה התורנית שלו היה גם בעל השכלה מדעית רחבה. אבל מצד שני, ראיתי גם טענות שהגר”א מעולם לא כתב את הדבר הזה והאזכור הראשון שלו הוא כנראה במאמר של הרב מתתיהו מונק מ-1962 (“שלוש בעיות הנדסיות בתנ”ך ובתלמוד”, סיני, נא. תשכ”ב). מי שזה לא יהיה שגילה את זה, אני רוצה להצדיע לו - זה באמת קוריוז חמוד ביותר ואני תוהה איך הוא שם לב אליו.

הנה הטיעון כפי שנתקלתי בו אי-אז. הבה ונחזור לפסוק מספר מלכים:

ויעש את הים מוצק עשר באמה משפתו עד שפתו עגל סביב וחמש באמה קומתו וקוה [וקו] שלשים באמה יסב אתו סביב

מה זה ה”קו” שמופיע בסוגריים? זה מה שנקרא בהקשר של התנ”ך “קרי וכתיב” שהוא חלק מהמסורה של התנ”ך. ה”כתיב” הוא ה”קוה” שמופיע בטקסט ואילו ה”קרי” הוא ה”קו” - זו הדרך שבה נהוג לקרוא את המילה (כמו כן, בדברי הימים ב’ פרק ד’ פסוק ב’ מופיע אותו הפסוק ממלכים עם הכתיב “קו”).

עכשיו, מה הערך הגימטרי של הקרי והכתיב? כלומר, כאשר נותנים ערך מספרי לאותיות על פי שיטת הספירה המקובלת בספרות עבריות? ק’ הוא 100, ו’ הוא 6 וה’ הוא 5, כך ש”קוה” שווה 111 ואילו “קו” שווה 106. והנה התעלול: בואו ניקח את הערך \( 3 \) להיקף חלקי הקוטר שאפשר להסיק מיידית מהפסוק, נכפול אותו ב-111, נחלק אותו ב-106 ונקבל

\( 3\cdot\frac{111}{106}=\frac{333}{106}=3.14151\ldots \)

וזה קירוב טוב מאוד של \( \pi \)! אבל למעשה, זה לא סתם קירוב “טוב”, זה קירוב פנטסטי של \( \pi \), כזה שאפשר לתת הצדקה מתמטית לכמה שהוא טוב. מבחינה מתמטית זה כנראה החלק הכי מעניין (עבורי) בפוסט הזה, אז בואו נסביר אותו עד הסוף (מה שכנראה גם יסייע לנו להבין שיש קירוב הרבה יותר טוב שממש קרוב אליו).

ראשית, בואו נבהיר למה בכלל צריך “לקרב” את פאי, במחיר של קצת לחזור על דברים שאמרתי קודם: מספר כמו \( \frac{333}{106} \) נקרא שבר. הוא מורכב משני מספרים שלמים שמחלקים אותם אחד בשני - זה שלמעלה נקרא המונה (333 אצלנו) וזה שלמטה נקרא המכנה (106 אצלנו). אנחנו כמובן מכירים שברים כבר מגיל צעיר למדי ורגילים לעשות איתם דברים גם בחיי היומיום. במתמטית נפוצה אנחנו קוראים להם מספרים רציונליים (כאן ה”רציו” מסמל יחס, ratio, לא “הגיון”) וזה שם קצת פחות נפוץ במציאות. מה שקצת פחות ברור בחיי היומיום הוא שלא כל המספרים הם כאלו. ואני לא מתכוון במובן של “42 הוא לא שבר” (הוא כן! למשל הוא \( \frac{42}{1} \) או \( \frac{84}{2} \) וכדומה) אלא במובן זה שיש מספרים שאי אפשר לכתוב בתור שבר. הדוגמא המפורסמת ביותר היא \( \sqrt{2} \), והצגתי הוכחה לזה כאן, אבל גם \( \pi \) הוא כזה: פשוט לא קיימים שני מספרים שלמים \( a,b \) כך ש-\( \pi=\frac{a}{b} \). לכן כל נסיון לתאר את \( \pi \) עם שבר יהיה רק קירוב, ולכן מעניין מה הקירוב הטוב ביותר עם שבר שקיים עבור פאי.

אלא שכאן הסיפור מסתבך - אפשר למצוא קירובים טובים כרצוננו. אם אני ארשה למכנה של השבר של המכנה לגדול ולגדול אני אוכל לקבל סדרה של קירובים שהולכת ומשתפרת, כך ש”השגיאה” (הערך המוחלט של ההפרש בין הקירוב ובין \( \pi \)) תקטן עוד ועוד (טכנית: לכל \( \varepsilon>0 \) יהיה קירוב שעבורו השגיאה תהיה קטנה מ-\( \varepsilon \)). הנה דוגמא לסדרה אפשרית אחת כזו: \( \frac{3}{1},\frac{31}{10},\frac{314}{100},\frac{3141}{1000},\ldots \) וכן הלאה. זו בעצם כתיבה בתור שבר של המספרים \( 3,3.1,3.14,3.141 \), כלומר בכל פעם אני מוסיף עוד ספרה אחרי הנקודה העשרונית ולכן הדיוק שלי משתפר.

העניין הוא שהקירובים הללו הם לא טובים במיוחד. בואו נסתכל למשל על הקירוב \( \frac{314}{100} \). ה”שגיאה” של הקירוב הזה היא \( \left|3.14151\ldots-3.14\right|=0.00151\ldots \), נראה לא רע! אבל עכשיו בואו נסתכל על קירוב אחר, \( \frac{22}{7}=3.1428\ldots \). אם נחשב, נקבל \( \left|\pi-\frac{22}{7}\right|=0.00126\ldots \) וזה קירוב טוב יותר מה-\( 0.00151\ldots \) שנותן \( \frac{314}{100} \). העניין הוא ש-\( \frac{22}{7} \) אמור לכאורה להיות קירוב “גס” הרבה יותר, כי מה קורה כאן? ב-\( \frac{22}{7} \) אנחנו לוקחים חלקים בגודל \( \frac{1}{7} \) ומחברים אותם זה לזה עד שאנחנו קרובים אל \( \pi \). לעומת זאת ב-\( \frac{314}{100} \) אנחנו לוקחים חלקים מגודל \( \frac{1}{100} \) ומחברים אותם זה לזה. \( \frac{1}{100} \) הוא מספר הרבה יותר קטן מ-\( \frac{1}{7} \); אפשר היה לצפות שקירוב שמתבצע בעזרת חלקים קטנים יותר יהיה מדויק יותר, אבל הנה, זה לא בהכרח המצב.

איך אפשר למצוא קירובים טובים יחסית בקלות? ובכן, זה קל אם יש לנו מחשב וקירוב מאוד טוב של פאי, למשל \( 3.1415926535897932 \). הנה שיטה פשוטה ממש לעשות את זה: לכל \( b\ge1 \) טבעי, אני רוצה למצוא את \( a \) שעבורו \( \frac{a}{b} \) הוא הקירוב הכי טוב ל-\( \pi \) מבין כל הקירובים עם מכנה \( b \). אני פשוט אבדוק ערכים שונים של \( a \), אחשב את \( \left|\frac{a}{b}-\pi\right| \) (באמצעות הקירוב של \( \pi \) שיש לי) ואקח מהם את הכי טוב. החוכמה היא לא לבדוק יותר מדי ערכים של \( a \), אז אפשר לעשות את הדבר הבא: להתחיל מ-\( a=3b \), כלומר כך ש-\( \frac{a}{b}=3 \) נותן לנו קירוב סביר של \( \pi \) מלמטה. עכשיו נתחיל להגדיל את \( a \) ב-1 בכל פעם, עד שבסוף נגיע לשלב שבו \( \frac{a}{b} \) הוא לראשונה גדול יותר מ-\( \pi \). זה אומר ש-\( \frac{a-1}{b} \) היה הקירוב הכי טוב של \( \pi \) מלמטה, ו-\( \frac{a}{b} \) הוא הקירוב הכי טוב של \( \pi \) מלמעלה שנוכל להשיג עם מכנה \( b \). נבדוק מי משניהם יותר טוב (כלומר, מקטין יותר את \( \left|\frac{a}{b}-\pi\right| \)) וניקח אותו. למשל, עבור \( b=7 \) אנחנו מתחילים מ-\( a=21 \) ועבורו מקבלים את הקירוב מלמטה \( \frac{21}{7}=3 \). הערך הבא בתור, \( \frac{22}{7}=3.1428571428\ldots \) כבר גדול יותר מ-\( \pi \), אבל זהה ל-\( \pi \) בשלוש הספרות הראשונות ולכן קירוב טוב יותר מ-\( \frac{21}{7} \), כך שקיבלנו את \( \frac{22}{7} \) בתור הקירוב הכי טוב עם מכנה \( 7 \).

אם ננסה את אותו תעלול עם \( b=8 \) צפויה לנו אכזבה. אנחנו נתחיל מ-\( \frac{24}{8}=3 \), נעלה אל \( \frac{25}{8}=3.125 \) ומשם נגיע אל \( \frac{26}{8}=3.25 \) - אלו הקירובים מלמעלה ומלמטה, ושניהם פחות טובים מ-\( \frac{22}{7} \). לכן אם אני שואל את השאלה “מה הקירוב הכי טוב ל-\( \pi \) מהצורה \( \frac{a}{b} \) כאשר \( b\le8 \)?” התשובה תהיה \( \frac{22}{7} \). בצורה הזו אני יכול להגדיר סדרה של קירובים ל-\( \pi \) שהם הכי טובים שאפשר עם מכנה שקטן או שווה למכנה שלהם. אני אקבל את הסדרה הבאה:

\( \frac{3}{1},\frac{13}{4},\frac{16}{5},\frac{19}{6},\frac{22}{7},\frac{179}{57},\frac{201}{64},\frac{223}{71},\frac{245}{78},\frac{267}{85},\frac{289}{92},\frac{311}{99},\frac{333}{106},\frac{355}{113},\frac{52163}{16604},\ldots \)

הופה, רגע, מה הולך פה? שימו לב לקפיצה האסטרונומית בין \( \frac{355}{113} \) אל \( \frac{52163}{16604} \). הקפיצה הזו מראה לנו ש-\( \frac{355}{113}=3.1415929\ldots \) הוא קירוב מדהים לחלוטין, כזה שלוקח המון, המון, המון זמן אחריו למצוא קירוב טוב ממנו. הקירוב שהגיע ממש לפניו, \( \frac{333}{106}=3.1415094\ldots \) גם הוא קירוב טוב, אבל לא באותה רמה. ב-\( \frac{355}{113} \) יש דיוק של 7 ספרות (\( 3.141592 \)) וב-\( \frac{333}{106} \) יש “רק” דיוק של 5 ספרות (\( 3.1415 \)). עדיין, אני רוצה להגן על \( \frac{333}{106} \) ולטעון שגם הוא קירוב די מיוחד, ולצורך כך אני אתאר את הדבר הכי מוזר שנשמע עליו בפוסט הזה - ובהתאם, הדבר שאני הכי אוהב פה: הייצוג של \( \pi \) בתור שבר משולב. נקדיש לזה חלק נפרד לטובת אלו שרוצים פשוט לדלג.

חלק שלישי, שבו שברים משולבים הם מגניבים

בואו נחזור לרגע לאופן שבו אני מציג את \( \pi \) בדרך כלל: \( \pi=3.141\ldots \). מה שיש לנו כאן הוא ייצוג של \( \pi \) באמצעות סדרה של ספרות שבעצם מגדירה לנו סדרה של קירובים שהולכים ומתקרבים אל \( \pi \): הסדרה \( 3,3.1,3.14 \) וכן הלאה. כל קירוב כזה בעצם מתקבל באמצעות חישוב פשוט שמשתמש בספרות: למשל, \( 3.14 \) הוא בעצם \( 3\cdot10^{0}+1\cdot10^{-1}+4\cdot10^{-2} \). כל זה טבעי ופשוט לנו (אני מקווה) אבל חשוב לי להציג את זה ככה כי אני הולך עכשיו להציג עוד שיטה שבה מייצגים את \( \pi \) באמצעות סדרה של ספרות שבעצם מגדירה לנו סדרה של קירובים שהולכים ומתקרבים אל \( \pi \) שמתקבלים באמצעות חישוב פשוט, אבל הדרך הזו תהיה מוזרה למדי למי שמעולם לא ראה אותה.

הסיבה שבגללה הדרך הזו מעניינת היא כי כל הקירובים שהיא נותנת יהיו טובים ביותר. מה זה אומר? כזכור, ראינו את סדרת הקירובים הטובים הבאה של \( \pi \):

\( \frac{3}{1},\frac{13}{4},\frac{16}{5},\frac{19}{6},\frac{22}{7},\frac{179}{57},\frac{201}{64},\frac{223}{71},\frac{245}{78},\frac{267}{85},\frac{289}{92},\frac{311}{99},\frac{333}{106},\frac{355}{113},\frac{52163}{16604},\ldots \)

אף אחד מהקירובים שמתקבל מהפיתוח העשרוני\( \pi=3.141\ldots \) לא נמנה על הסדרה הזו, חוץ מה-3 בהתחלה (בניסוח אחר: אין בסדרה הזו אף קירוב חוץ מ-3 שבו המכנה הוא חזקה של 10). לעומת זאת, בשיטה שאציג עכשיו מובטח לנו שכל קירוב שמתקבל שייך לסדרה הזו - אבל לא כולם יופיעו בה; אנחנו נראה שהקריטריון שמבטיח שקירוב יופיע בסדרה הוא שהקירוב הזה הוא “אקסטרה משובח” (אבל כן יכולים להופיע בסדרה הזו קירובים מעולים שהם קצת פחות טובים).

ובכן, זה נראה ככה:

\( \pi=3+\frac{1}{7+\frac{1}{15+\frac{1}{1+\ddots}}} \)

מה הולך פה? יש ביטוי מהצורה \( 3 \) ועוד שבר שהמונה שלו הוא 1 אבל המכנה שלו מסובך: גם המכנה הוא מהצורה “משהו ועוד 1 חלקי משהו מסובך” וכך זה ממשיך עוד ועוד עד לנצח. בגלל שקשה לכתוב את זה ככה, לרוב מסתפקים בלכתוב את סדרת הספרות שמופיעות בתוך המפלצת הזו, לא כולל ה-1-ים שבמונה. כלומר כותבים משהו כמו

\( \left[3;7,15,1,\ldots\right] \)

איפה פה סדרת הקירובים שהבטחתי? ובכן, אפשר לקחת את הסדרה של ה”הספרות” ופשוט לעצור אותה אחרי מספר צעדים סופי ולחשב מה מקבלים על פי כללי החשבון הרגילים של שברים. בואו נעשה את זה.

ראשית, אם לוקחים רק את 3, מקבלים רק את 3, שזה אחלה קירוב אבל לא כזה מעניין. מה קורה אם לוקחים את 3 ואת 7? מקבלים את הביטוי

\( 3+\frac{1}{7}=\frac{21+1}{7}=\frac{22}{7} \)

הופה! קיבלנו את \( \frac{22}{7} \) שכבר ראינו לא מעט בפוסט הזה. עכשיו שאנחנו בשוונג, בואו נעשה עוד אחד:

\( 3+\frac{1}{7+\frac{1}{15}}=3+\frac{1}{\frac{106}{15}}=3+\frac{15}{106}=\frac{333}{106} \)

הופה, תראו את מה קיבלנו עכשיו! את הקירוב מהתנ”ך! זו הסיבה שבגללה אמרתי שגם הקירוב הזה הוא די מיוחד. ואם קיבלתי אותו, קל לנחש מה הדבר הבא שנקבל - את \( \frac{355}{113} \) המהולל. אבל בואו נבצע את החישוב הפורמלי בכל זאת:

\( 3+\frac{1}{7+\frac{1}{15+\frac{1}{1}}}=3+\frac{1}{7+\frac{1}{16}}=3+\frac{1}{\frac{113}{16}}=3+\frac{16}{113}=\frac{355}{113} \)

לי אישית כל זה מרגיש כמו קסם גדול יותר ממה שקורה בתנ”ך, אבל אין כאן מקריות - שברים משולבים יכולים לשמש אותנו לתיאור כל מספר ממשי ולכל אחד מהם יתקיים אותו עיקרון - השברים המשולבים יתנו את סדרת הקירובים האופטימלית עבורו. יש לי פוסטים בנושא אז לא אכנס לעובי הקורה של ההסברים למה זה עובד. אבל כן מעניין איך בעצם מחשבים את הייצוג בעזרת שבר משולב של משהו כמו \( \pi \) ומה המשמעות המדויקת של זה שהוא נותן קירובים “טובים”. ביתר החלק אני אסביר את זה; מי שרוצים להמשיך לדבר על פאי בתנ”ך וזהו יכולים לקפוץ לחלק הבא.

אז ראשית, איך מוצאים שבר משולב עבור \( \pi \)? נתחיל מלומר שאנחנו לא יודעים את השבר המשולב במובן זה שאין לנו נוסחה כללית עבור המספרים שמופיעים בו - בדיוק כמו שקורה עם ספרות של \( \pi \) בייצוג עשרוני, מה שיש לנו הוא פשוט חישוב שהניב מספר גדול מאוד של ספרות. כלומר, בשורה התחתונה מה שידוע לנו הוא תמיד רק קירוב טוב מאוד של \( \pi \). השיטות שיש לנו למציאה של קירוב כזה של \( \pi \) מתבססות לרוב על ייצוג שלו בתור טור אינסופי, ואני לא אכנס כאן לאופן שבו מוצאים ייצוגים כאלו (אבל לגמרי הגיע הזמן לכתוב פוסטים בנושא) אלא פשוט אציג את אחד מהייצוגים השימושיים:

\( \pi=\sum_{k=0}^{\infty}\frac{2^{k+1}k!^{2}}{\left(2k+1\right)!} \)

בעזרת טור כזה אפשר לחשב קירוב מצוין של פאי, ואז להשתמש על הקירוב הזה בשיטה הכללית למציאת שבר משולב של מספר כלשהו \( x \). התוצאה תהיה שבר משולב שהספרות הראשונות בו מתאימות לשבר המשולב של פאי.

הרעיון הוא כזה: ראשית מגדירים \( x_{0}=x \). עכשיו, אנחנו רוצים למצוא ייצוג מהצורה \( x=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\ddots}} \). כלומר, הצעד הראשון שלנו הוא להפריד את \( x \) למספר שלם (ה-\( a_{0} \)) ועוד איזה חלק שהוא קטן מ-1 (כל היתר). אז מגדירים \( a_{0}=\left[x_{0}\right] \), כלומר \( a_{0} \) הוא החלק השלם של \( x_{0} \) - המספר הטבעי הגדול ביותר שקטן או שווה ל-\( x_{0} \) (במקרה של \( \pi \) מקבלים \( a_{0}=3 \)). נגדיר \( b_{0}=x_{0}-a_{0} \), ועכשיו אפשר לכתוב \( b_{0}=\frac{1}{x_{1}} \) כאשר \( x_{1} \) הוא המספר ה”חדש” שאנחנו רוצים למצוא ייצוג שלו כשבר משולב. אז נחזור על התהליך - נגדיר \( a_{1}=\left[x_{1}\right] \) ו-\( b_{1}=x_{1}-a_{1} \) ו-\( b_{1}=\frac{1}{x_{2}} \) וכן הלאה. כלומר, אנחנו עושים שלוש פעולות שונות:

• מחשבים ערך שלם של מספר.
• מקבלים את החלק השברי של המספר על ידי חיסור הערך השלם שלו ממנו.
• מקבלים את המספר הבא בתור על ידי היפוך של המספר שקיבלנו (כלומר, מחשבים את 1 חלקי המספר הזה).

שלב ההיפוך הוא החלק הבעייתי: אם מראש אנחנו עובדים עם קירוב, נאמר של \( \pi \), אז בשלב ההיפוך גם נקבל רק קירוב - אבל מספר ספרות הדיוק שלנו יקטן. זה פוסט שלם לדבר על כמה ספרות דיוק עדיין מובטחות לנו, והאמת העצובה היא שאני פשוט לא מכיר את הנושא מספיק טוב אז אדלג מעליו לגמרי כאן - אבל זו הטכניקה.

בפועל, קל מאוד לתכנת דבר כזה. הנה קוד פייתון שמבצע את החישובים הרלוונטיים:

def compute_pi(n):
    x, y, z = 2, 1, 1
    value = (x*y)/z
    for k in range(1,n+1):
        x *= 2
        y *= (k*k)
        z *= (2*k)*(2*k+1)
        value += (x*y)/z
    return value

def compute_continued_fraction(x, n):
    values = []
    for _ in range(n):
        a = int(x)
        values.append(a)
        b = x - a
        x = 1/b
    return values

להריץ אותו עם compute_continued_fraction(compute_pi(14), 4) נותן מיידית את השבר המשולב שראינו (פחות מ-14 יתן שבר משולב לא נכון כי פאי לא חושב ברמת הדיוק הנדרשת), אז אין כאן אתגר גדול במיוחד מבחינה חישובית.

עכשיו אני רוצה לצטט בלי הוכחה שתי תוצאות תיאורטיות על שברים משולבים ואיכות הקירובים שהם נותנים. נניח ש-\( x \) הוא מספר אי רציונלי כלשהו ו-\( \frac{p}{q} \) הוא שבר שמתקבל מהפיתוח של \( x \) לשבר משולב (כלומר, \( \frac{p}{q} \) מתקבל מכך שקוטעים את הפיתוח של \( x \) אחרי מספר מקומות סופי ומחשבים את התוצאה, כמו שעשינו קודם), אז לכל מספר רציונלי \( \frac{a}{b} \) שעבורו \( 1\le b\le q \) מתקיים

\( \left|x-\frac{p}{q}\right|\le\left|x-\frac{a}{b}\right| \)

כלומר, \( \frac{p}{q} \) הוא הקירוב הטוב ביותר ל-\( x \) מבין כל המספרים הרציונליים עם מכנה שהוא קטן או שווה ל-\( q \). יותר מכך, אנחנו יודעים לחסום את גודל השגיאה של הקירוב והוא הולך להיות מאוד טוב. כדי לקבל תחושה של ה”מאוד טוב” הזה, בואו קודם נראה מה קורה באופן כללי: אם \( \frac{a}{b} \) הוא הקירוב הטוב ביותר ל-\( x \) מבין כל הקירובים עם מכנה \( b \) בדיוק, אז תמיד מתקיים ש-

\( \left|x-\frac{a}{b}\right|<\frac{1}{2b} \)

(אני לא אוכיח את זה אבל זה תרגיל מצוין לחשוב למה זה קורה, זה באמת לא קשה אבל זה עושה סדר במחשבה).

לעומת זאת, אם \( \frac{a}{b} \) הוא קירוב שמתקבל משבר משולב, אז אפשר להוכיח (זה הרבה יותר קשה) שמתקיים

\( \left|x-\frac{a}{b}\right|<\frac{1}{b^{2}} \)

שימו לב להבדל העצום בין המקרים. למשל, בואו ניקח את הקירוב התנ”כי המשודרג של פאי, \( \frac{333}{106} \) ונשווה אותו אל הקירוב הטוב ביותר עם מכנה 105, \( \frac{330}{105}=3.142857\ldots \). אם נחשב את גודל השגיאה, נקבל

\( \left|\pi-\frac{330}{105}\right|=0.001264489267\ldots \)

\( \left|\pi-\frac{333}{106}\right|=0.000083219628\ldots \)

רואים איפה יש יותר אפסים אחרי הנקודה? במקרה הראשון, החסם של \( \frac{1}{2b} \) מבטיח לנו רק שגיאה שקטנה מ-

\( 0.004761904762\ldots \)

והיא אכן לא הרבה יותר קטנה ממנה; במקרה השני, החסם המשופר של \( \frac{1}{b^{2}} \) מבטיח לנו שגיאה שקטנה מ-

\( 0.000088999644\ldots \)

אפשר לחשוב על זה ככה - זה שיש לנו \( b^{2} \) במקום \( 2b \) במכנה מכפיל את מספר האפסים ברצף אחרי הנקודה שנראה בשגיאה, כלומר מכפיל את מספר ספרות הדיוק שנקבל.

לסיום, הנה המשפט האהוב עלי בהקשר הזה: אם יש לנו קירוב ממש טוב, מובטח שהוא יופיע מתוך השבר המשולב. אני אישית אוהב את המשפט הזה במיוחד בגלל שהוא צץ באופן מפתיע באלגוריתם של שור בחישוב קוונטי; האלגוריתם של שור מחפש מספר רציונלי מאוד ספציפי שהוא צריך לקבל במדויק, והוא מוצא אותו על ידי כך שהוא מוצא מספר אחר שהמספר הרציונלי שמחפשים הוא קירוב טוב מאוד שלו ואז מחפש את המספר שלו בפיתוח של המספר ההוא לשברים חלקיים.

פורמלית, אם \( \frac{a}{b} \) מקיים

\( \left|x-\frac{a}{b}\right|<\frac{1}{2b^{2}} \)

אז מובטח ש-\( \frac{a}{b} \) יופיע בסדרת השברים המשולבים. שימו לב שזה לא משפט של “אם ורק אם” כי בהחלט יכולים להופיע בסדרת השברים המשולבים גם קירובים “ממש טובים אבל פחות”, אלו שמקיימים את החסם הפחות הדוק \( \left|x-\frac{a}{b}\right|<\frac{1}{b^{2}} \). למעשה, ראינו אחד מהם - את \( \frac{333}{106} \) שעבורו מתקיים

\( \left|\pi-\frac{333}{106}\right|=0.0000832\ldots>0.0000444\ldots=\frac{1}{2\cdot106^{2}} \)

זה שונה מאשר \( \frac{22}{7} \) ו-\( \frac{355}{113} \) שמקיימים גם את החסם ההדוק יותר ולכן מובטח לנו שיופיעו:

\( \left|\pi-\frac{22}{7}\right|=0.00126\ldots<0.0102=\frac{1}{2\cdot7^{2}} \)

\( \left|\pi-\frac{355}{113}\right|=0.000000266\ldots<0.000039157\ldots=\frac{1}{2\cdot113^{2}} \)

זה מסיים את החלק המתמטי המגניב ואפשר לחזור אל שאלת מה שהולך בתנ”ך.

חלק רביעי, שבו הסיפור הזה מזכיר לי בעיקר סיפורים אחרים

למי שלא עקבו אחרי החלק המתמטי אני אסכם את מה שראינו בו: ראינו ש-\( \frac{333}{106} \) הוא קירוב מצוין של \( \pi \) עם כמה תכונות שהופכות אותו באמת למיוחד, אבל מצד שני - הוא גם קירוב משמעותית פחות מיוחד מאשר \( \frac{355}{113} \) הקרוב אליו מאוד אבל הטוב ממנו בהרבה. מכיוון שאנחנו בפוסט על קוריוז מתמטי שווה להזכיר קוריוז מתמטי נפלא אחר שקשור ל-\( \frac{355}{113} \) - ניסוי “המחט של בופון” שביצע לזאריני. זה ניסוי שאפשר לבצע בפועל עם השלכת סיכה על מחברת ובדיקה אם הסיכה נפלה על קו מסוים או לא, ואיכשהו הניסוי הזה הצליח לחשב את פאי בצורה מדויקת עד להדהים. הטריק היה שעורך הניסוי הכיר את הקירוב של \( \frac{355}{113} \) והינדס את הניסוי כך שיגיע בדיוק אל הקירוב הזה. איך מהנדסים ניסוי כזה? הסברתי את זה בפוסט הרלוונטי, אבל הרעיון הוא שאחרי כל כך-וכך השלכות יש “סיכוי” לקבל בדיוק את הקירוב הזה, ואם עוצרים את הניסוי כשהקירוב הזה התקבל התוצאה של הניסוי תהיה מדויקת להדהים בזמן שכל השלכה של סיכה אחת נוספת תקלקל לגמרי את הקירוב המופלא - ולזאריני הכיר את הקירוב והינדס את הניסוי בדיוק כך כדי שזה יקרה.

האם כאן קרה משהו דומה? כלומר, האם מי שכתב את ספר מלכים הינדס את התיקון הזה כדי לרמוז על הערך \( \frac{333}{106} \) או שמדובר על צירוף מקרים?

ובכן, לדעתי זה צירוף מקרים יפה ומרהיב כדרכם של צירופי מקרים מרהיבים, כי על צירופי המקרים הלא מרהיבים אף אחד לא מדבר ואנחנו בכלל לא שמים לב אליהם. החשיבה שלי על הקוריוז הזה היא חילונית במהותה, ואני רואה בהנחה שזה לא צירוף מקרים אלא משהו מכוון שני דברים שנראים לי כמו אנכרוניזם היסטורי:

1. אין לנו אינדיקציה היסטורית אחרת להיכרות עם קירוב טוב כל כך של פאי באותה תקופה.
2. אין לנו אינדיקציה היסטורית אחרת לקיום הגימטריה היהודית באותה תקופה.

על 2 אין לי הרבה מה להרחיב כאן - השאלה האם בתנ”ך הוצפנו מסרים בעזרת גימטריה היא רחבה הרבה יותר מהדיון הנוכחי, ולהבנתי השורה התחתונה שלו היא “זה ייתכן אבל אין לנו ראיות ישירות לכך” - כל הפרשנויות הגימטריות לדברים מהתנ”ך הוצעו בדיעבד.

בנוגע ל-1, לעומת זאת, בהחלט אפשר לדבר על שאלה מעניינת בהיסטוריה של המתמטיקה - אילו ערכים של פאי היו מוכרים בעת העתיקה? יש לנו שני מקורות מרכזיים למתמטיקה עתיקה - לוחות החרס הבבליים, והפפירוסים המצריים. אצל הבבלים ברוב המקורות \( \pi=3 \) ותו לא (כלומר - \( \pi \) לא מופיע באופן ישיר, אבל זה הערך שלו שאפשר להסיק) אבל בלוח חרס אחד שנתגלה ליד Susa ומתוארך לתקופה שבין המאות ה-19 וה-17 לפני הספירה אפשר להסיק מהכתוב את הערך \( \pi=\frac{25}{8}=3.125 \) שהוא קירוב לא רע אבל רחוק מאוד באיכותו מ-\( \frac{22}{7} \) וצריך שוב להדגיש שזה לא מספר שמופיע בלוח במפורש אלא אפשר להסיק אותו על ידי חישוב ממה שכן מופיע בלוח, שהוא היחס בין ההיקף של משושה להיקף המעגל החוסם אותו. הנה פוסט (לא שלי) בעניין.

עבור מצרים העתיקה, קירוב של פאי מופיע באחד מהאוצרות המתמטיים היקרים ביותר שיש לנו מהתקופה הזו - פפירוס רינד, שמתוארך לסביבות 1650 לפני הספירה. בעיה 41 בפפירוס עוסקת בחישוב נפח של אסם תבואה, וגם שם \( \pi \) לא מופיע בצורה מפורשת אבל אפשר להסיק מהטקסט את הקירוב \( \pi=\left(\frac{4}{3}\right)^{4}=256/81=3.16049\ldots \) שגם הוא לא קירוב מבריק במיוחד אבל מצד שני לא רע לזמנו. בשני המקורות, גם המצרי וגם הבבלי, הערך של \( \pi \) לא מוחבא בצורה ערמומית כמו בספר מלכים, שבו על פניו אין בכלל חישוב שצריך לעשות; אצלם יש חישוב ויש מספרים מדויקים שנכתבים במפורש, אבל פשוט החישוב לא עוסק ב-\( \pi \) אלא במושגים שקשורים ל-\( \pi \) ומהם ערכו של \( \pi \) מתקבל. בהקשר הזה כדאי לזכור ש-\( \pi \) עצמו הוא קבוע חצי-שרירותי, במובן זה שהיינו יכולים למשל לדבר לא על היחס בין היקף המעגל לקוטרו אלא על היחס בין היקף המעגל לרדיוסו, מה שהיה נותן לנו את הקבוע \( 2\pi=6.28318\ldots \) שבימינו אוהבים לסמן בתור \( \tau \) ואפילו לטעון שהוא קבוע יותר טוב מ-\( \pi \) (זה דיון אחר שאני מעדיף לא להיכנס אליו אף פעם אבל בטח אכתוב עליו פוסט יום אחד). בהקשר של ספר מלכים ההגדרה של “היקף חלקי הקוטר” היא הטבעית יותר כי גם ההיקף וגם הקוטר מופיעים במפורש בפסוק, אז קשה להתלונן למה הפסוק לכאורה מצפין את \( \frac{333}{106} \) ולא את \( \frac{666}{106} \) (למי שקופצים למראה ה-666 - לא, לא מצאתי בחזון יוחנן י”ג משהו עם גימטריה של 106 או 212, לא בתרגום לעברית וגם לא במקור היווני עם הגימטריה היוונית שדומה להפליא לזו שלנו).

המדידה המפורשת הראשונה של \( \pi \) שנתנה קירוב טוב היא זו של ארכימדס, בסביבות 240 לפני הספירה: הוא השתמש בשיטה מבריקה לגמרי כדי לקבל את הקירוב \( \frac{22}{7}\le\pi\le\frac{223}{71} \). שני המספרים שמופיעים בקירוב הם טובים למדי: את \( \frac{22}{7} \) ראינו בתור הקירוב האיכותי הראשון שהשבר המשולב של \( \pi \) נותן, ואת \( \frac{223}{71} \) ראינו כחלק מסדרת “הקירובים הכי טובים עבור המכנה שלהם או קטן ממנו”. שניהם פחות טובים מ-\( \frac{333}{106} \).

הקירוב הגדול הבא של פאי הגיע עם המתמטיקאי הסיני דזו צ’ונג-ג’ה בן המאה החמישית לספירה. ראשית, הוא מצא ש-\( \pi \) נמצא בין \( 3.1415926 \) ובין \( 3.1415927 \), ושנית הוא מצא את הקירוב \( \pi\approx\frac{355}{113}=3.1415929\ldots \) שאם נשים לב, הוא קצת פחות טוב מהקירובים העשרוניים הללו כי הספרה האחרונה שציינתי בו, 9, שגויה (ב-\( \pi \) הספרה הזו היא 6, מה שתואם את הקירוב של ה”ראשית”). זה החיסרון של \( \frac{355}{113} \) אבל על היתרונות שלו כבר דיברתי, ובפרט על כך שזה קירוב מאוד קומפקטי, עם מכנה בן שלוש ספרות בלבד, שמניב רמת דיוק גבוהה בהרבה מאותן שלוש ספרות - טוב הרבה יותר מ-\( \frac{333}{106} \). כלומר, זו הנקודה בהיסטוריה שבה אפשר לעצור ולהגיד שקירוב ברמה של הרמיזה בתנ”ך כבר הפך לנחלת הכלל. אלא שזה קרה במאה החמישית לספירה, בערך אלף שנים אחרי שספר מלכים נכתב, (בין אם מניחים שכתב אותו ירמיהו או מניחים שהוא נכתב בידי אנשים אחרים בגלות בבל). למעשה, לא ברור לי איפה ומתי התגלה \( \frac{333}{106} \) בתור קירוב לפאי (התורה של שברים משולבים שייכת למאה ה-18 ואני משער שבשלב הזה הקירוב כבר התגלה בדרך אחרת, אבל לא התעמקתי בזה).

לנוכח כל אלו, ההנחה הסבירה היא שבזמן כתיבת ספר מלכים, אי שם במאות החמישית-שישית-שביעית לפני הספירה, הקירוב \( \frac{333}{106} \) לפאי לא היה ידוע. אז אנחנו צריכים לבחור בין שתי אפשרויות: או שלסופר המקראי היה ידע פלאי ממש (בין אם הגיע אליו מהשמיים ובין אם חישב אותו בעצמו) והוא הצפין אותו בתורה בדרך כה מחוכמת שחז”ל פשוט פספסו ונראה שהראשון ששם לב אליה היה רב עם השכלה מתמטית מהמאה ה-20, או שמדובר על צירוף מקרים. לי אישית זה מזכיר סיפור אחר, שאני מאוד אוהב אישית: הסיפור של לוח החרס הבבלי פלימפטון 322. יש לי פוסט מפורט עליו אז לא אכנס להכל, אבל הנה הרעיון הכללי:

פלימפטון 322 הוא לוח חרס בבלי מסביבות המאה ה-18 לפני הספירה, שכתוב בתור טבלה שהאיברים המרכזיים שלה הם זוגות של מספרים ששייכים לשלשות פיתגוריות שונות ומשונות (מספיק זוג מספרים כדי להסיק את המספר השלישי בשלשה). מבחינה מתמטית מדובר על תגלית מרגשת מאוד, כי השיטה הראשונה לייצור שלשות פיתגוריות באופן סדרתי מתוארת אצל אוקלידס, כמעט 1,500 שנים אחר כך. כלומר - הלוח מרמז על רמה מתמטית מופלאה ממש שהייתה לבבלים ביחס לכל העולם מאות שנים אחריהם.

העניין הוא שהסיפור כנראה לא כזה פשוט, ואפשר לתת פרשנויות אחרות לאותם ערכים מספריים בלוח שיסבירו איך המספרים הללו נוצרו גם בלי להכיר שום שיטה לייצור שלשות פיתגוריות, פשוט כחלק מתהליך של יצירה של תרגילי אימון לפתרון משוואה ריבועית - תרגילים שידוע שהיו נפוצים אצל הבבלים. יש מאמרים מפורטים שעוסקים בגישה הזו, עם כניסה משמעותית לפרטים של הלוח ואף חשוב מכך - של לוחות אחרים בני אותה התקופה. כשקוראים על הנושא רואים כמה קל, כשמתעסקים בהיסטוריה של המתמטיקה, לייחס כוונות וידע לטקסטים מתמטיים ישנים גם אם לא היה בהם שום תוכן כזה, פשוט כי אנחנו כבר בעלי הידע הזה וחושבים על הכוונות הללו. קל לנו יותר לראות לוח עם שלשות פיתגוריות ולומר “אה-הא! מטרת הלוח הייתה להכיל שלשות פיתגוריות, ובגלל שאנחנו מכירים נוסחה לייצור שלהן אז הן בוודאי נוצרו באמצעות הנוסחה, וזה מה שמראה שהבבלים ידעו את הנוסחה!” גם אם יתר המציאות לא מסכימה עם זה.

גם כאן - אפשר לראות את התיקון הפלאי ולהגיד “אה-הא! מטרת התיקון הייתה להצפין את \( \frac{333}{106} \) בטקסט באמצעות גימטריה!” - בכך אנחנו לוקחים מושגים מודרניים יותר ומחילים אותם על הטקסט: גם מניחים שהטקסט בכלל רצה “לתקן” את הקירוב ה”שגוי” של פאי (ולהחליף אותו בקירוב אחר שגם הוא “שגוי” אבל פחות), וגם שהוא רצה לעשות את זה בדרך המאוד עקיפה שלו. כמובן, אפשר להגיד (ואומרים) “זה בסדר גמור, לא מעט מהתנ”ך הוא ככה” מה שלוקח אותנו לדיון כללי יותר על התנ”ך שאני לא רוצה לנהל פה; אבל אני אישית לא רואה צורך לנקוט בגישה הזו.

חלק חמישי ואחרון, ובו השאלה האם היה אפשר לעשות משהו טוב יותר? (כנראה שלא)

זה מסיים לומר את הדברים המעניינים שאני יודע לומר על הנושא הזה, אבל לפני שאני מסיים את הפוסט אני רוצה לדבר טיפה על השאלה המתבקשת: האם אפשר היה להצפין בתנ”ך את \( \frac{355}{113} \) במקום \( \frac{333}{106} \)? קשה לי לראות דרך לעשות את זה שלא תרגיש לנו מאולצת יותר, מטעם חשבוני די פשוט: \( 333=111\times3 \). זה אומר שאפשר להציג את הקירוב \( \frac{333}{106} \) בתור \( \frac{111}{106}\times3 \), ולכן כל מה שאנחנו צריכים הוא מילה עם ערך גימטרי 106 שאפשר להוסיף לה אות אחת ולקבל 111, מה שעבד עם “קו/קוה”. לעומת זאת ב-\( \frac{355}{113} \) אין לנו יכולת לבצע את הטריק הזה כי \( 355=5\times71 \) לא מתחלק ב-3, ולכן אם אנחנו מחפשים שני מספרים שלמים \( a,b \) כך ש-\( \frac{a}{b}\times3=\frac{355}{113} \) לא קשה לראות שהמספרים הקטנים ביותר שיתנו לנו דבר כזה הם \( a=355,b=339 \) שההפרש ביניהם הוא 16, ואין לנו דרך לעבור ממילה שערכה 339 למילה שערכה 355 על ידי שינוי של אות בודדת, כך שמלכתחילה כל מה שנעשה ירגיש מאולץ יותר.

עדיין, לפעמים יש שינוי בשתי אותיות; למשל במלכים א’ י”ב ל”ג יש לנו את “מלבד/מלבו” שבו מסירים אות ומוסיפים אות; כדי לקבל הפרש 16 על ידי פעולה כזו, אנחנו חייבים להסיר ד’ ולהוסיף כ’ (אין שתי אותיות אחרות שההפרש של הערך הגימטרי שלהן הוא 16). זה נותן לנו למשל את הזוג “שדלה/שכלה” שקופץ מגימטריה של 339 אל 355. האם זה משהו שהסופר המקראי הכל יכול היה יכול להשתמש בו בפסוק שמדבר על ים הנחושת? לא נראה לי. מצד שני, קשה לשחק את המשחק הזה עד הסוף בלי להבין מה בדיוק החופש שכן היה לסופר המקראי הכל יכול לעשות. אם היו דורשים ממנו להצפין את \( \frac{355}{113} \) במקום את \( \frac{333}{106} \) כי אסור שיהיה אצלו “בערך”, ואם ישתמש בקירוב גרוע כמו \( \frac{333}{106} \) אז הוא נביא שקר ועונשו מיתה - במקרה כזה אני חושד שהוא היה מוצא דרך טובה להשחיל את \( \frac{355}{113} \) פנימה.

מעבר לבדיחות האלו, אני חייב להודות שצירוף המקרים כאן הוא באמת מאוד יפה: המילה “קו/קוה” שעומדת במרכז הסיפור היא המילה בפסוק שמתארת את ההיקף, כלומר קשורה ישירות לעניין והכתיב הכפול “קו”/”קוה” הוא לא משהו ייחודי לפסוק הזה; ה”קוה” מופיע למשל גם בירמיהו ל”א ל”ח ובזכריה א’ ט”ז, כלומר אין בו משהו שרירותי. למרות שמדגדג לי לבדוק אם אני מצליח למצוא את \( \frac{355}{113} \) בכל מני מקומות, לא סביר שיימצא משהו כל כך יפה. אני יכול לקחת סיפורים אקראיים מפרויקט בן יהודה, להריץ עליהם סקריפט ולמצוא באותו משפט מילה של 355 ומילה של 113 (כן, נו, באמת עשיתי את זה בשביל הקטע), אבל מה זה יגיד?

כמובן, אפשר ללכת לכיוונים חופשיים עוד יותר. אם הסופר המקראי בסך הכל רוצה להצפין מספר בטקסט יש עוד דרכים לעשות את זה שלא חייבות לענות לתבנית של 1-2-3 שלמעלה. הנה אחת שמבוססת על קוריוז חמוד בפני עצמו של \( \frac{355}{113} \): בנוסף לכל מעלותיו של הקירוב הזה, כשהוא מוצג בבסיס 10 קל מאוד לזכור אותו כי אם קוראים את הספרות מלמעלה-למעלה ומשמאל-לימין מקבלים \( 113355 \). באותיות זה “אאגגהה” שהוא נטול כל משמעות, אבל זו מילה קצרה וקומפקטית שאפשר היה להכניס לפסוק!

אז מה השורה התחתונה שלי לכל הסיפור הזה? ובכן “שברים משולבים זה מגניב”. אני חושד שהמסר הזה לא הועבר מספיק כאן.