מה הקטע עם התפלגות נורמלית? (חלק א': שלוש היסטוגרמות למלכי ההתפלגות במרומם, ועקומה אחת למשול בם ולקשרם)

סדרת הפוסטים הזו נולדה משאלה קונקרטית ששאלו אותי: למה בנוסחה של התפלגות נורמלית מופיעים \( e \) ו-\( \pi \)?

הנוסחה המדוברת היא \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \) מה שנראה מבעית לגמרי במבט ראשון ולכן במקום לענות מייד לשאלה שממנה סדרת הפוסטים נולדה בואו נדבר על דברים בסיסיים יותר: מה זו בכלל התפלגות נורמלית? מה היא באה להשיג? מה הנוסחה הזו מייצגת? מה הולך בה? מה זו בכלל התפלגות? מה זו הסתברות? מהי מתמטיקה?

אוקיי, על מהי מתמטיקה לא נדבר הפעם, אבל מכיוון שהתפלגות נורמלית היא סוג של הנקודה שבה הנחל של תורת ההסתברות נשפך אל האוקיינוס של המתמטיקה, אולי צריך להתחיל בקטן ולחזור אל המקורות.

בואו נתחיל הכי בקטן, עם הדבר הבסיסי ביותר בתורת ההסתברות: הטלת מטבע. הטלת מטבע היא אחד מהאמצעים הפשוטים ביותר שבעזרתם אנחנו מכניסים אקראיות לחיים (השני הוא קוביה, שהיא טיפה יותר מסובכת). למטבע יש שני צדדים - “עץ” ו”פלי”, וכשמטילים אותו הוא נוטה ליפול על אחד מהם ולא להישאר עומד בדיוק על קו התפר. ההנחה שלנו היא שהסיכוי שלו ליפול על עץ או על פלי הוא שווה - כלומר, שאם נזרוק את המטבע המון פעמים, בערך בחצי מהן הוא ייצא עץ ובחצי מהן הוא ייצא פלי. לכזו הסתברות קוראים לפעמים “50:50” כשה-50 בא לתאר אחוזים. הרעיון באחוזים הוא שמאה אחוז זה בדיוק משהו שלם, אז חמישים אחוז זה חצי, ואכן אומרים לפעמים גם שההסתברות היא “חצי-חצי”. אפשר להפוך את הטיעון הזה לטיפה יותר מתמטי אם אומרים שעץ הוא 1 ופלי הוא 0 ואז כותבים \( p\left(0\right)=p\left(1\right)=\frac{1}{2} \) - “ההסתברות ל-0 היא חצי וגם ההסתברות ל-1 היא חצי”.

הטלה אחת זה נחמד, אבל מה נקבל אם נטיל את המטבע עשר פעמים ונספור כמה פעמים קיבלנו עץ? כאמור, אפשר היה לקוות שבדיוק ב-5 מהפעמים ייצא עץ וב-5 מהפעמים ייצא פלי, וזה באמת יכול לקרות אבל זה לא חייב לקרות. המציאות לא עובדת ככה. ייתכן שהמטבע ייפול על “עץ” בכל הפעמים, אם כי זה לא סביר, וייתכן שהוא ייפול 6 פעמים על עץ ו-4 על פלי. אז כדי לעשות סדר בבלאגן הזה ולחפש ודאות שכן קיימת, אנחנו משחקים את המשחק הזה של “בואו נטיל מטבע 10 פעמים” הרבה פעמים ובודקים מה התוצאות הכי נפוצות. למשל, אני יכול לבקש מהמחשב לשחק את המשחק הזה 10,000 פעמים, ואז לצייר את מה שנקרא היסטוגרמה - איור שבו הנתונים מוצגים בצורה שקל להבין אותם:

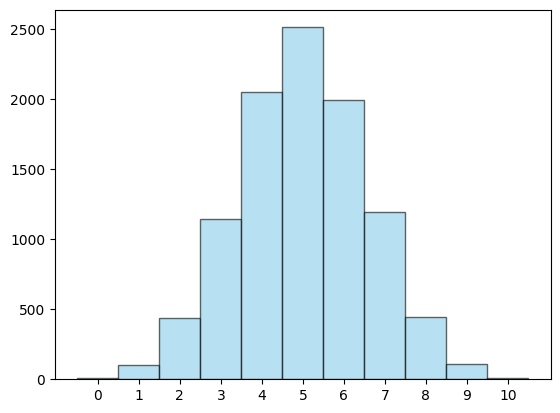
יש באיור הזה 11 פסים בגבהים שונים. כל פס מתאים למספר בין 0 ל-10: אלו בדיוק מספר הפעמים שבהן עץ יכול להתקבל כשמטילים מטבע עשר פעמים. הגובה של כל פס מתאים למספר המשחקים שבהם הוא יצא: אנחנו רואים שהעמוד של 5 הוא בערך בגובה 2,500, כלומר בערך ב-2,500 מהמשחקים (מתוך 10,000 בסך הכל) קיבלנו באמת 5 פעמים עץ. אז התוצאה 5 היא באמת הכי נפוצה, אבל היא לא לבד. רק ברבע מהמשחקים בערך קיבלנו אותה. בכלל, התמונה הזו היא די יפה. הפסים די סימטרים. אם מסתכלים טוב רואים הפרשים קטנים בגבהים בין פס 4 ו-6 למשל, אבל הם נראים די אותו דבר. הסיבה שזה עבד יפה היא שביקשתי מהמחשב לשחק 10,000 משחקים. כשאני מבקש ממנו רק 100, זה נראה ככה:

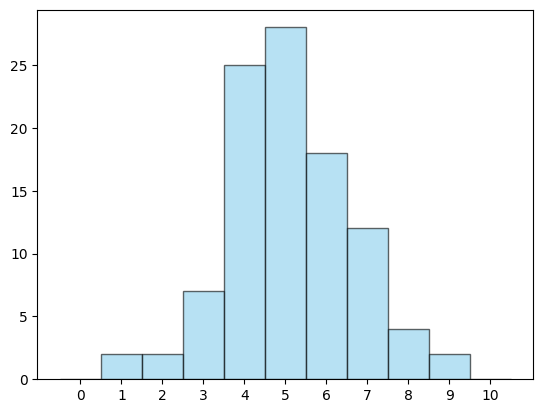
זה כבר שונה לגמרי ונראה די עקום. 4 הרבה יותר גבוה מ-6, ואילו 1 ו-2 הם בדיוק באותו הגובה. לאן נעלמה הסימטריה? ובכן, יש כאן לקח חשוב שמוכר לכל מי שמתעסק בהסתברות - ככל שחוזרים על אותו דבר יותר ויותר פעמים, כך הוא נהיה פחות מבולגן ויותר קל לראות את הסדר שמאחוריו. לכן, אם יש לי ניסוי אקראי כלשהו ואני רוצה לצייר היסטוגרמה יפה של התוצאות האפשריות שלו, כך שהגובה של הפס שמתאים לכל תוצאה גבוה יותר ככל שהיא שכיחה יותר, אני אחזור על אותו הניסוי מספר פעמים גדול - למשל 10,000 - ואבדוק מה אחוז הפעמים שבו כל תוצאה התקבלה. הנה איך ההיסטוגרמה הראשונה נראית כשאני כותב בערכים של ציר \( y \) את האחוז:

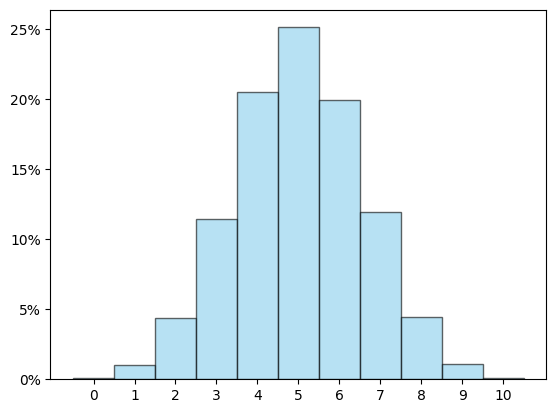
ההיסטוגרמה הזו משקפת לא רע את הניסוי “מטילים מטבע עשר פעמים וסופרים כמה פעמים קיבלנו עץ”. עכשיו בואו נדבר על ניסוי אחר: אני מנסה לזרוק כדור לסל, וזורק שוב ושוב עד שאני סוף סוף קולע. הבעיה היא שאני גרוע בהשלכת כדורים לסל ולכן מצליח לקלוע רק בהסתברות של 1 ל-10. מה שכן, אני אדם מאוד רגוע ולכן גם אם פספסתי שלושים פעמים ואני לכאורה אמור להיות מעוצבן והידיים שלי אמורות לכאוב, בפועל עדיין יש לי את אותה הסתברות בדיוק לקלוע - 1 ל-10. ועכשיו השאלה היא - מה ההסתברות שאצליח לקלוע על הפעם הראשונה? אחרי שתי פעמים? שלוש? אם מבצעים 10,000 חזרות על הניסוי ומציירים היסטוגרמה, מקבלים:

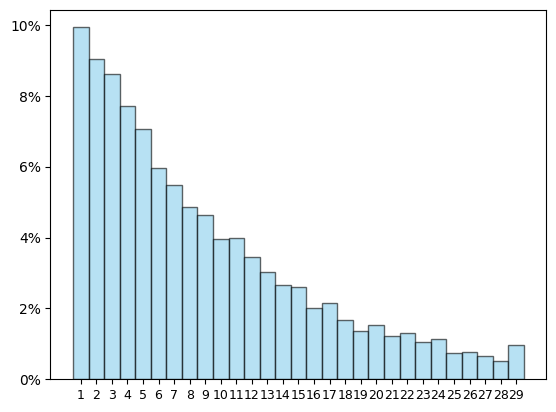
זה נראה מאוד שונה ממה שהיה קודם - ואכן, הגרף הקודם הציג משהו שנקרא התפלגות בינומית והגרף הנוכחי מציג משהו אחר שנקרא התפלגות גאומטרית. אבל בואו ותראו קסם. נניח שאני עושה את המשחק של “לזרוק לסל שוב ושוב עד הפעם הראשונה שבה אני קולע” לא רק לסל אחד, אלא למאה סלים שונים בזה אחר זה, וסופר כמה זמן בסך הכל לקח לי לקלוע לכולם. מה שהאינטואיציה הראשונית שלי אומרת לי הוא שההיסטוגרמה הזו צריכה להיות דומה להיסטוגרמה של התפלגות גאומטרית - הפס הראשון יהיה הכי גבוה כי הוא כמו סכום כל הפסים הגבוהים ב-100 ההיסטוגרמות של כל הסלים בנפרד, והפס הבא יהיה קצת פחות גבוה וכן הלאה. רק שזה לא מה שקורה. מה שקורה הוא זה:

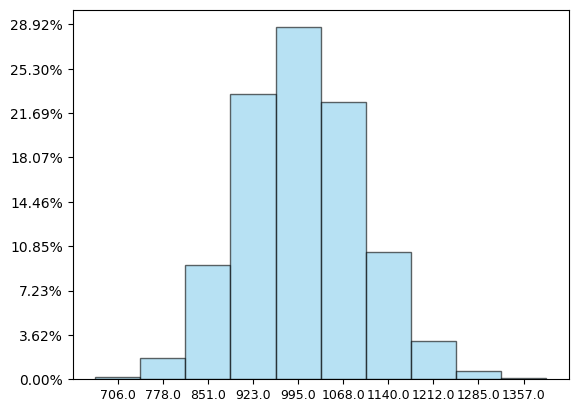
זה… קצת מזכיר את הגרף שראינו קודם, של ההתפלגות הבינומית. מה הולך כאן? המספרים שכתובים למטה נראים גבוהים מדי. הרי “1” הוא בהסתברות הכי גבוהה, ואני בסך הכל מאגד 100 היסטוגרמות ביחד. זה לא אמור לצאת קרוב אל 100? ובכן, לא. בלי להיכנס עדיין למונחים הטכניים הרלוונטיים, הערך ה”ממוצע” שאפשר לצפות לו בהתפלגות הגאומטרית של משחק הסלים שלי הוא 10. כי אמנם השטח של הפסים הראשונים נראה גדול ומרשים אבל הוא לא מה שאנחנו מודדים - ה”ממוצע” הוא סכום המכפלות של הגבהים של הפסים בערך המספרי שהם מייצגים. הגובה של הפס של 1 הוא בערך \( \frac{10}{100} \)? אנחנו כופלים אותו בערך המספרי 1. הגובה של פס 2 הוא בערך \( \frac{9}{100} \)? אנחנו כופלים אותו ב-2 ומקבלים \( \frac{18}{100} \). כך אנחנו עושים לכל ערך אפשרי - כופלים אותו בהסתברות שהוא יתקבל, סוכמים, ומגלים שדווקא ה”זנב” שבכלל לא רואים בהיסטוגרמה תורם חלקים נכבדים לממוצע. אז אם הממוצע הוא 10 למשחק, ויש 100 משחקים, לא מפתיע שהסכום הכולל הוא בסביבות 1000; ככל שמשחקים יותר משחקים כך התוצאות מסתדרות יפה סביב הממוצע.

בואו נראה עוד דוגמא. נניח שאני מטיל קוביה עם עשר פאות, כלומר מקבל תוצאה בין 1 ל-10, אבל הקוביה הזו היא לא הוגנת אלא מוטה בשלל דרכים שונות ומשונות שהופכות תוצאות מסוימות ליותר נפוצות ותוצאות אחרות לנדירות. הנה היסטוגרמה של 10,000 הטלות של הקוביה הזו:

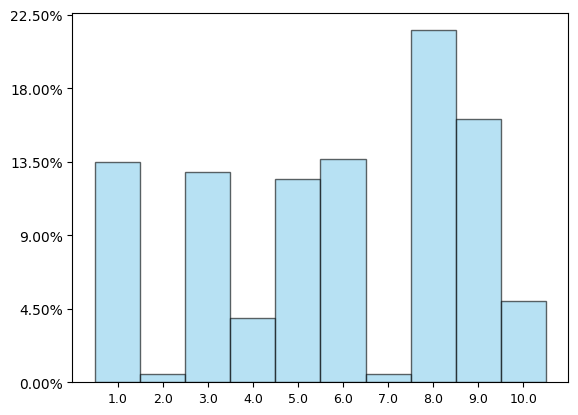
מכאן אפשר לראות ש-8 היא התוצאה הכי נפוצה ואילו 2 ו-7 בקושי מופיעות ובאופן כללי הכל פה נראה כאוטי. מאיפה ההיסטוגרמה הזו הגיעה? ובכן, פשוט הגרלתי באקראי מה יהיו המספרים שמתארים את ההסתברות שבה כל תוצאה מקבלת. אין בקוביה הזו שום דבר מיוחד או קסום בפני עצמו, זה משהו שרירותי לחלוטין.

עכשיו בואו נטיל את הקוביה הזו מאה פעמים ונחבר את התוצאות ונראה מה קיבלנו. נחזור על הניסוי הזה 10,000 פעם, ונקבל את ההיסטוגרמה:

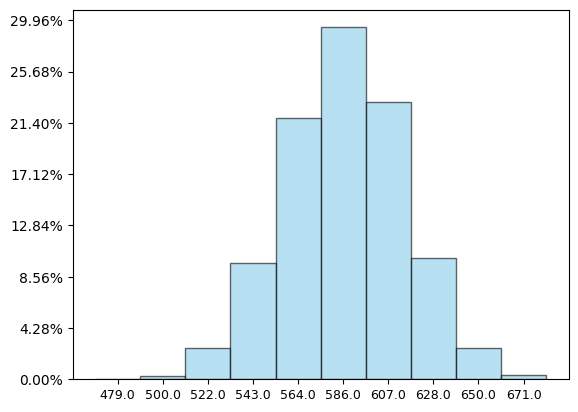
הנה זה שוב. אותו מבנה דמוי פירמידה שכבר ראינו שוב ושוב. הוא הופיע בהתפלגות בינומית; הוא הופיע בהתפלגות גאומטרית; והנה הוא מופיע גם בהתפלגות שרירותית כלשהי. בדיאגרמות של ההתפלגויות המקוריות לא בהכרח ראינו אפילו את הצל שלו, אבל אחרי שמחברים מספיק תוצאות - בום, המבנה הזה צץ.

המתמטיקאים שמו לב לתופעה הזו כבר לפני מאות שנים, והאבחנה המרכזית שלהם היא שקיימת דרך פשוטה לתאר את המבנה הזה, באמצעות משהו שנקרא התפלגות נורמלית. המילה “נורמלית” כאן מגיעה בדיוק מתוך התופעה עצמה: בגלל שהתופעה המתמטית קיימת, התפלגות נורמלית מופיעה שוב ושוב בשלל מקומות בסטטיסטיקה. למשל, הגבהים של בני האדם מתפלגים נורמלית, וגם תוצאות במבחן מתפלגות נורמלית, וכדומה. כמובן, כשאני אומר שמשהו מתפלג נורמלית אני לא מתכוון שהוא מתאים בדיוק למה שנקרא “התפלגות נורמלית” - גם הגרפים שהצגתי לא מתאימים בדיוק. הרעיון הוא שהתפלגות נורמלית היא קירוב טוב להתפלגויות הללו, ויש לנו מושג טכני מדויק שבא לתאר את ה”קירוב טוב” הזה ומשפט מרכזי בתורת ההסתברות שאומר שהקירוב הטוב הוא באמת טוב - משפט הגבול המרכזי. הניסוח של משפט הגבול המרכזי והוכחה שלו (עד כדי טענת עזר שלא אוכיח) הם המטרה של סדרת הפוסטים הזו.

לפני שנגיע להגדרות הפורמליות, בואו נראה על מה אני מדבר ב”התפלגות נורמלית” ואיך זה “קירוב”. נתחיל עם ההיסטוגרמה של ההתפלגות הבינומית שראינו בהתחלה:

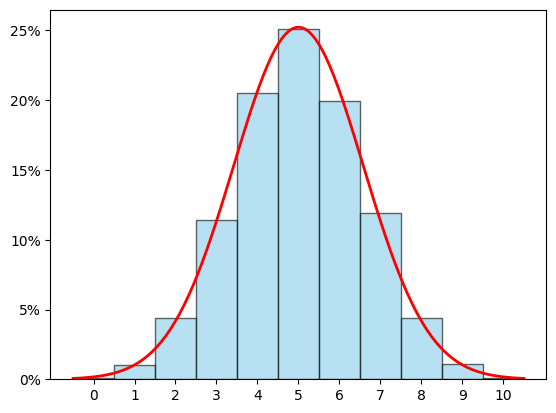
הקו האדום מייצג את ההתפלגות הנורמלית. שימו לב שאני לא מציג אותה בתור פסים כפי שהצגתי את ההתפלגות הבינומית, כי מבחינה מתמטית ההתפלגות הנורמלית היא אכן משהו קצת שונה - היא מיוצגת על ידי פונקציה ממשית רציפה, ואדבר על זה בהמשך. הרעיון הוא עדיין אותו רעיון - באיזור שבו הקו גבוה, יש הסתברות גבוהה יותר לקבל תוצאות שנמצאות באותו איזור.

עכשיו, הציור הזה נראה טוב. למעשה, הוא נראה טוב מדי. אני צריך להישבע שלא בישלתי אותו בשום צורה כי אפילו אני לא ציפיתי שזה ייצא עד כדי כך טוב בדוגמא האקראית שיצרתי. הקו האדום מצליח איכשהו לעבור דרך הפסים כך שהוא מגיע לגובה של כל פס תוך שהוא עובר כמעט בדיוק דרך נקודת האמצע שלו. עכשיו, אפשר לומר שלא ברור מה מרשים פה - הרי בסך הכל לקחתי את הפסים, מצאתי את נקודות האמצע של כל פס ואת הגובה, זרקתי את כל המידע הזה לסקריפט שלי ואמרתי לו “יאללה, תחשב עקומה” - לא? ובכן, ממש לא. הקוד שצייר את הקו האדום לא ידע כלום על הפסים וכלום על התוצאות ההסתברותיות הקונקרטיות שקיבלתי. הוא ידע רק שני מספרים שמאפיינים את ההתפלגות הבינומית הזו - התוחלת של ההסתברות וסטיית התקן שלה, ושניהם הם מספרים שלא מחושבים מתוך ההיסטוגרמה עצמה (כלומר, מתוך התוצאות הקונקרטיות שקיבלתי שמתוארות על ידי הפסים) אלא באופן תיאורטי, מתוך התכונות הבסיסיות של ההתפלגות. שני המספרים הממשיים הללו הם כל מה שצריך כדי לקבל עקומה שמקרבת בדיוק מופלא את ההתנהגות של ההתפלגות הבינומית.

בואו נראה את זה קורה עבור ההתפלגות הגאומטרית:

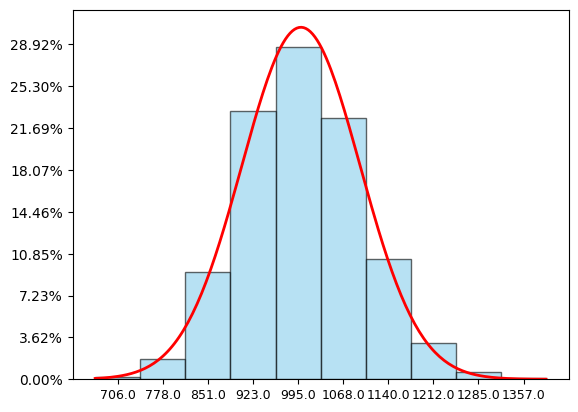
כזכור, מה שאנחנו רואים פה הוא לא גרף שמתאר איך ההתפלגות הגאומטרית נראית (היא לא דומה להתפלגות נורמלית) אלא מה קורה לה אחרי שאני לוקח 100 תוצאות שונות שלה, ומחבר. גם פה, העקומה של התפלגות נורמלית, מרגע שאני מזין לה את שני הפרמטרים המתאימים, ממדלת די במדויק את ההיסטוגרמה. כדי לחשב את שני הפרמטרים המתאימים הייתי צריך לחשב את התוחלת וסטיית התקן של ההתפלגות הגאומטרית, אבל הייתי צריך לשקלל פנימה איכשהו גם את ה-100 הזה; בהמשך כשנגיע לפרטים הטכניים נבין למה צריך לשקלל אותו פנימה, איך זה בדיוק מתבצע ולמה לכאורה קודם בהתפלגות הבינומית לא עשיתי את זה (התשובה היא שכן עשיתי את זה באופן מובלע, כי ההתפלגות הבינומית שלי היא בעצמה סכום של ניסויים פשוטים יותר של הטלות מטבע).

לסיום, הנה המקרה של ההתפלגות השרירותית לגמרי:

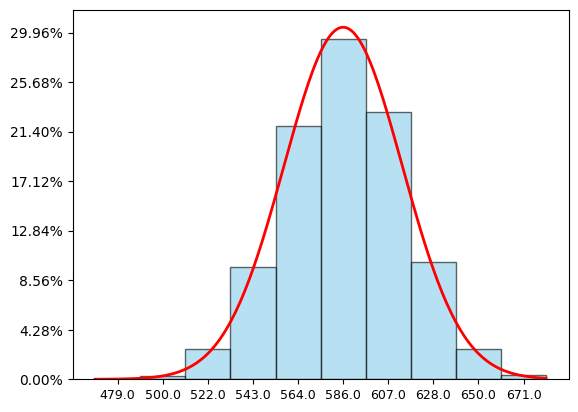
גם פה: אותה עקומה, פרמטרים שונים. לחשב את הפרמטרים מתוך מה שידוע לי על ההתפלגות השרירותית - זה היה קל, וזה גם כל מה שהיה צריך. ההתפלגות השרירותית נותנת משקל שונה לכל מספר מ-1 עד 10; כדי לייצר את העקומה הזו לא היה שום צורך לדעת מה המשקלות הללו. היה צריך לדעת רק את התוחלת, סטיית התקן ומספר התוצאת שחיברנו זו לזו (שגם פה היה 100). זה יפהפה. נראה שהטבע רוצה שיהיה סדר באי סדר; שהאקראיות תתגשם בסופו של דבר, כשאנחנו מסתכלים על סיטואציות שמורכבות מהרבה תהליכים אקראיים שכל אחד תורם את חלקו, בתור פונקציה פשוטה מאוד.

אז הבנו שיש פה איזו שהיא תופעת טבע; בפוסט הבא נעסוק בצורה שבה אנחנו מפרמלים את המודל המתמטי שמנסה לתאר את הסיטואציה הזו.