מה הקטע עם התפלגות נורמלית? (חלק ב': על שתי הסתברויות)

מבוא

בפוסט הקודם התחלתי לדבר על מה שנקרא התפלגות נורמלית ופורמלית מוגדר בתור \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \) אבל בגלל שאלו הרבה סימנים מפחידים שלא אומרים הרבה כרגע, העדפתי להסתכל על הדבר הזה:

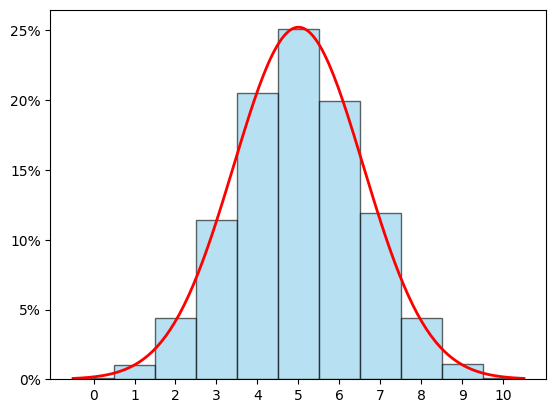
התמונה הזו מציגה את הקשר בין שתי התפלגויות שונות. אחת נקראת התפלגות בינומית ומתוארת על ידי הפסים, והשניה שמתוארת על ידי קו רציף היא ההתפלגות הנורמלית, ומה שאנחנו רואים הוא שבמובן מסוים ההתפלגות הנורמלית היא קירוב טוב של ההתפלגות הבינומית. בפוסט הזה אני רוצה שנבהיר בצורה מתמטית איך בעצם מגדירים את הנפשות הפועלות - איך מגדירים התפלגויות ומה הולך בהגדרה של התפלגות נורמלית. העניין הוא שההגדרות בתורת ההסתברות הן לא דבר פשוט ולכן הפוסט הזה כבר ייכנס למתמטיקה לא לגמרי טריוויאלית. למעשה, תמונת הפסים-מול-עקומה ממחישה את זה יפה - יש שתי דרכים שונות להגדיר התפלגויות, דרך אחת שנקראת התפלגות בדידה וכאן מתאימה לפסים, והדרך השניה שנקראת התפלגות רציפה ומתאימה לעקומה. יש המון דמיון בין שתי הגישות אבל גם הבדלים מהותיים; ויש דרך “מאחדת” להציג את שניהם בתור מקרים פרטיים של אותו דבר, אבל היא לא בהכרח הופכת את הסיטואציה לקלה יותר להבנה אז אני לא אכנס אליה כאן. בואו נתחיל מהמקרה שקצת יותר מתאים לתפיסה היומיומית שלנו של הסתברות - התפלגות בדידה.

התפלגויות בדידות

בואו נסתכל על סיטואציה הסתברותית פשוטה: הטלת קוביה הוגנת. במקרה הזה, יש שש תוצאות אפשריות להטלת הקוביה: \( X=\left\{ 1,2,3,4,5,6\right\} \). לכל תוצאה כזו אנחנו מתאימים הסתברות שהיא תקרה: \( p\left(1\right)=p\left(2\right)=\ldots=p\left(6\right)=\frac{1}{6} \). הרעיון פה הוא שהסכום של כל ההסתברויות יוצא 1, או כמו שמסמנים בקיצור, \( \sum_{i=1}^{6}p\left(i\right)=1 \). אפשר כמובן גם לדבר על קוביה לא הוגנת, למשל כזו שיש לה סיכוי של לא פחות מאשר \( \frac{1}{2} \) ליפול על 4, וכל יתר הצדדים מתחלקים שווה בשווה. במקרה הזה, מכיוון שההסתברויות צריכות להסתכם ל-1, יש לנו הסתברות של \( \frac{1}{2} \) לחלק בין חמישה צדדים של הקוביה, אז נקבל \( p\left(1\right)=\frac{1}{10} \) וכן הלאה לכל \( i \) חוץ מאשר \( p\left(4\right)=\frac{1}{2} \).

אפשר להכליל את הרעיון הזה בקלות: \( A=\left\{ a_{1},a_{2},\ldots,a_{n}\right\} \) תהיה קבוצה של \( n \) תוצאות אפשריות של הסיטואציה ההסתברותית שלנו. לכזו קבוצה קוראים מרחב המדגם (כי הסיטואציה ההסתברותית דוגמת תוצאה אחת מתוכו) ואנחנו מגדירים פונקציה \( p:A\to\left[0,1\right] \) שמתאימה לכל איבר במרחב המדגם מספר בין 0 ל-1 כך ש-\( \sum_{i=1}^{n}p\left(a_{i}\right)=1 \). ההגדרה הפשוטה הזו מספיקה להרבה מאוד סיטואציות הסתברותיות שאנחנו נתקלים בהן במציאות.

אבל ממש לא לכולן.

בפוסט הקודם דיברתי על הסיטואציה שבה אני זורק כדורסל ובגלל שאני לא באמת יודע איך לזרוק כדורסל לסל, יש לי הסתברות של \( \frac{1}{10} \) לקלוע (הייתי נדיב) והשאלה שאני שואל היא - כמה זריקות לסל יידרשו לי עד שאקלע? ובכן, ברור שיש לי הסתברות של \( \frac{1}{10} \) לקלוע בנסיון הראשון. אם פספסתי, זה קרה בהסתברות \( \frac{9}{10} \) והסיכוי שאני אצליח בנסיון השני הוא \( \frac{1}{10} \), אז אינטואיטיבית יש לי הסתברות של \( \frac{9}{10}\cdot\frac{1}{10}=\frac{9}{100} \) להצליח בזריקה השניה, וכן הלאה. טוב ויפה, אבל איך ממדלים את זה כמו שעשיתי לפני רגע, עם קבוצה \( X \) של כל התוצאות האפשריות? אני יכול לומר משהו כמו \( p\left(1\right)=\frac{1}{10} \) ו-\( p\left(2\right)=\frac{9}{100} \) וכן הלאה, אבל מספר ההטלות שיידרשו לי עד שאקלע לסל הוא לא חסום. אני לא יכול להבטיח שיידרשו לי רק 42 הטלות. אם אני אגיע אל ההטלה ה-42 זה אומר שהייתי מאוד חסר מזל עד כה, אבל ליקום לא אכפת מחוסר המזל שלי עד כה - גם בהטלה ה-42, הסיכוי שלי לקלוע יהיה רק \( \frac{1}{10} \) ולכן בהחלט ייתכן שאגיע להטלה ה-43. במילים אחרות, אם אני רוצה שיהיה לי סיכוי כלשהו למשל אפילו את הסיטואציה המאוד פשוטה הזו אני צריך ש-\( X \) תהיה קבוצה אינסופית, במקרה הזה \( A=\left\{ 1,2,3,\ldots\right\} \).

אם \( X=\left\{ a_{1},a_{2},a_{3},\ldots\right\} \) היא קבוצה אינסופית, זה יוצר לנו קושי טכני חדש. דרשתי קודם שיתקיים \( \sum_{i=1}^{n}p\left(a_{i}\right)=1 \), אבל עכשיו \( X \) היא אינסופית ולכן גם הסכום צריך להיות אינסופי: \( \sum_{i=1}^{\infty}p\left(a_{i}\right)=1 \). זה מכניס לנו לתמונה מושג חדש וממש לא טריוויאלי - סכום אינסופי, משהו שלומדים בדרך כלל בחדו”א. כל הסיפור הפך לפתע למסובך יותר: בשביל למדל סיטואציה פשוטה יחסית, אנחנו צריכים כלים מתמטיים לא לגמרי טריוויאליים.

יש עוד מושג מרכזי אחד שצריך להכיר. בואו נחזור אל ההיסטוגרמה שהבאתי בתחילת הפוסט; בפוסט הקודם סיפרתי עליה סיפור של משחק שבו אני מטיל מטבע הוגן 10 פעמים וסופר כמה פעמים נפלתי על “עץ”. אפשר למדל כאן את מרחב המדגם בתור \( A=\left\{ 0,1,\ldots,10\right\} \) אבל זה יהיה טיפה מסובך כי לא לגמרי ברור איזו הסתברות לתת לכל איבר במרחב המדגם. תחת זאת אפשר לתת מרחב מדגם שבמובן מסוים הוא פשוט יותר: \( X \) פשוט יכיל את כל התוצאות האפשריות של הטלת מטבע הוגן 10 פעמים. אם אני אסמן “עץ” בתור 1 ו”פלי” בתור 0 אני יכול לחשוב על כל תוצאה אפשרית בתור עשירייה \( b=\left(b_{1},b_{2},\ldots,b_{10}\right) \) כך ש-\( b_{i}\in\left\{ 0,1\right\} \), כלומר מרחב המדגם שלי הוא מה שמסומן ב-\( A=\left\{ 0,1\right\} ^{10} \). בגלל שלעץ ולפלי יש בדיוק אותה הסתברות \( \frac{1}{2} \) בכל הטלה, ההסתברות של כל עשירייה היא \( \frac{1}{2}\cdot\frac{1}{2}\cdots\frac{1}{2}=\frac{1}{2^{10}} \) (זו עדיין אמירה אינטואיטיבית ולא טענה פורמלית - אגיע לטענה הפורמלית עוד מעט).

עכשיו, אני יכול להגדיר פונקציה \( X:A\to\mathbb{R} \) שלכל עשירייה, סופרת כמה “עץ” יש בה, כלומר הכי פורמלית שרק אפשר, \( X\left(b\right)=\sum_{i=1}^{10}b_{i} \). זו פונקציה במובן הרגיל של תורת הקבוצות, אבל מכיוון שהיא מוגדרת על מרחב מדגם שיש עליו מבנה של אקראיות, המבנה הזה עובר גם אליה - אפשר לשאול עכשיו שאלות כמו “אם אני בוחר איבר מ-\( A \) באקראי, מה ההסתברות ש-\( X \) יחזיר עליו 3?” או בכתיב הסטנדרטי, מהו \( P\left(X=3\right) \). התשובה לזה פשוטה: כדי ש-\( X \) יקבל 3, צריך שמי שיעלה בגורל הוא אחד מאיברי מרחב המדגם שיש לו בדיוק 3 פעמים 1 ויתר הפעמים 0, אז אני סוכם את ההסתברויות של כל האיברים הללו. לכל איבר, ההסתברות שלו היא \( \frac{1}{2^{10}} \), ומספר האיברים הללו הוא בדיוק \( {10 \choose 3} \) - מספר הדרכים לבחור 3 מקומות מתוך 10 כדי לשים בהם 1 (יש לי פוסט שמסביר את זה; כאן אני מניח שאנחנו מכירים קומבינטוריקה בסיסית), אז בסך הכל נקבל \( P\left(X=3\right)={10 \choose 3}\frac{1}{2^{10}} \).

הפונקציה \( X \) שהגדרתי כאן מכונה משתנה מקרי. זה סוג האובייקטים המרכזי שאנחנו מתעסקים בו בהסתברות. היופי בשימוש במשתנים מקריים הוא שאנחנו יכולים לשמור את מרחב המדגם שלנו פשוט יחסית, ולהגדיר מעל אותו מרחב מדגם שלל משתנים מקריים שונים ומשונים, ולשאול גם שאלות יותר מורכבות מאשר סתם “איך מחשבים את זה?” אלא גם “מה הקשרים בין המשתנים המקריים השונים” וכן הלאה.

בואו נעבור למשהו כללי יותר. נניח שאני מטיל מטבע לא הוגן בדיוק \( n \) פעמים וסופר כמה פעמים קיבלתי עץ, וניקח \( 0\le k\le n \) - מה ההסתברות שקיבלתי \( k \) פעמים עץ? אפשר להגדיר משתנה מקרי \( X \) כמו קודם, ועכשיו השאלה היא מהו \( P\left(X=k\right) \). אני אסמן ב-\( p \) את ההסתברות שבהטלת המטבע מקבלים עץ וב-\( q \) את ההסתברות שמקבלים פלי (\( p+q=1 \) כי בכל הטלה יש הסתברות 1 שתתקבל אחת משתי התוצאות). אז כדי לקבל בדיוק \( k \) פעמים עץ, צריך לבחור \( k \) מתוך \( n \) ההטלות שבהן יתקבל עץ (לזה יש \( {n \choose k} \) אפשרויות) ואז באותן \( k \) הטלות ההסתברות לקבל עץ הוא \( p \) לכל הטלה, כלומר \( p^{k} \) בסך הכל, ועבור יתר ההטלות ההסתברות לקבל פלי היא \( q \) בכל הטלה, כלומר \( q^{n-k} \) בסך הכל, ולכן נקבל \( P\left(X=k\right)={n \choose k}p^{k}q^{n-k} \). משתנה מקרי שמקיים את הנוסחה הזו נקרא משתנה מקרי בינומי או פשוט התפלגות בינומית כשהמילה “בינומי” כאן מגיעה מכך שהמספרים בנוסחה מגיעים מהבינום של ניוטון (הנוסחה \( \left(p+q\right)^{n}=\sum_{k=0}^{n}{n \choose k}p^{k}q^{n-k} \)).

לא הייתי חייב לספר את כל סיפור המטבעות הזה. הייתי יכול פשוט להגדיר משתנה מקרי בינומי עם הנוסחה \( P\left(X=k\right)={n \choose k}p^{k}q^{n-k} \). להגיד “בואו ניקח \( X \) שמקיים את הנוסחה הזו ועכשיו בואו נעשה איתו דברים”. אני טרחתי וסיפרתי סיפור ובניתי מרחב מדגם \( A \) ספציפי, אבל אפשר גם לספר סיפורים אחרים ולבנות מרחבי מדגם אחרים שעדיין יניבו לנו משתנה מקרי \( X \) עם אותה התפלגות (אפילו אם בתור פונקציה, \( X \) יוגדר בצורה שונה). זו רמת אבסטרקציה שקצת צריך להתרגל אליה.

עדיין, סיפור המטבעות כן עוזר לנו להבין את \( X \) יותר טוב. הנה דוגמא: על אותו מרחב מדגם של \( A=\left\{ 0,1\right\} ^{n} \) אני יכול להגדיר עוד משתנים מקריים \( Y_{1},Y_{2},\ldots,Y_{n} \). כל משתנה מקרי מסתכל על הטלת מטבע אחת ויחידה ואומר האם בה התקבל עץ או פלי. למשל \( Y_{7} \) מקבל 1 אם בהטלה 7 יצא עץ ואחרת הוא מקבל 0. פורמלית, \( Y_{k}\left(b\right)=b_{k} \), אבל אני הולך לוותר יותר ויותר על ה”פורמלית” הזה ככל שנתקדם. משתנה מקרי כזה, שמקבל או 0 או 1, נקרא אינדיקטור, ובמקרה שלנו \( P\left(Y_{k}=1\right)=p \) ואפשר לראות שמתקיים \( X=Y_{1}+Y_{2}+\ldots+Y_{n} \), כלומר אני יכול לתאר את \( X \) בתור סכום של אינדיקטורים. כשאני אגיע לדיבורים על תוחלת זה יהיה נוח למדי לראות את \( X \) ככה.

יש עוד נקודה אחת לגבי משתנים מקריים ששווה לדבר עליה עכשיו. בואו נניח שאני שולף איבר \( b\in A \) אקראי ממרחב המדגם שלי, ועכשיו אני מסתכל על \( Y_{3}\left(b\right) \). האם זה נותן לי אינפורמציה כלשהי על הערכים של משתנים מקריים אחרים? למשל, אם \( Y_{3}\left(b\right)=1 \), בהחלט קיבלתי אינפורמציה כלשהי על \( X \): אני יודע ש-\( X\left(b\right)>0 \). זה אומר שחשיפה למידע ש-\( Y_{3}\left(b\right)=1 \) שינתה את הערכות ההסתברות שלי לגבי \( X \); אם קודם הערכתי ש-\( P\left(X=0\right)=q^{n} \), עכשיו אני מעריך ש-\( P\left(X=0|Y_{3}=1\right)=0 \) (הקו המפריד אומר “בתנאי ש-“, כלומר ההסתברות של \( X=0 \) בתנאי שמתקיים \( Y_{3}=1 \)). לעומת זאת, המידע שלי על \( Y_{5} \) לא מושפע מידע כלשהו על \( Y_{3} \) (כי הם בודקים הטלות שונות). כלומר, אפשר לכתוב באופן כללי \( P\left(Y_{5}=k|Y_{3}=t\right)=P\left(Y_{5}=k\right) \). על סיטואציה כזו, שבה יש לנו משתנים \( X,Y \) ואנחנו יודעים ש-\( P\left(X=k|Y=t\right)=P\left(X=k\right) \) אנחנו אומרים ש-\( X,Y \) הם משתנים בלתי תלויים.

עכשיו, מה ההסתברות ש-\( X=k \) וגם \( Y=t \) ביחד? אני אסמן את זה ב-\( P\left(X=k\wedge Y=t\right) \). אינטואיטיבית (ואפשר גם להוכיח את זה פורמלית) זה יהיה שווה להסתברות \( P\left(Y=t\right) \), כפול ההסתברות ש-\( X=k \) בהינתן שאנחנו כבר יודעים ש-\( Y=t \), כלומר

\( P\left(X=k\wedge Y=t\right)=P\left(Y=t\right)\cdot P\left(X=k|Y=t\right) \)

ואם ידוע ש-\( X,Y \) בלתי תלויים אפשר להציב \( P\left(X=k|Y=t\right)=P\left(X=k\right) \) ולקבל

\( P\left(X=k\wedge Y=t\right)=P\left(X=k\right)P\left(Y=t\right) \)

כלומר - עבור משתנים בלתי תלויים, ההסתברות לאירוע משותף לשניהם היא מכפלת ההסתברויות עבור כל אחד מהם בנפרד. זו ההצדקה (בנפנוף ידיים) לכך שההסתברות לקבל בדיוק \( k \) פעמים “עץ” בהטלת מטבע ספציפית היא \( p^{k}q^{n-k} \) - אחרי שבחרנו \( k \) משתנים שיקבלו “עץ” ההסתברות שכולם אכן יקבלו עץ היא \( p^{k} \), מכפלת ההסתברויות של כל אחד מהם, כי הם בלתי תלויים (ואז גם מוסיפים את \( n-k \) המשתנים האחרים שמקבלים פלי בהסתברות \( q \) לתמונה).

התפלגויות רציפות

עד עכשיו מה שראינו היה יחסית פשוט. עכשיו בואו נסבך את זה ממש. נתחיל משאלה תמימה: איך, בעצם, עם הכלים שיש לי כרגע, אני יכול להגדיר סיטואציה הסתברותית שבה אני בוחר מספר בין \( 0 \) ל-\( 1 \) באקראי, בהסתברות שווה לכל מספר?

זו כמובן לא סיטואציה מופרכת. בכל שפת תכנות שמכבדת את עצמה יש פונקציית ספרייה שמחזירה מספר בין 0 ל-1 באקראי ובהסתברות אחידה לכל תוצאה. אבל לדבר על זה במונחים של שפת תכנות זו רמאות, כי בשפת תכנות יש רק מספר סופי של מספרים בין 0 ל-1 שאנחנו בכלל טורחים לייצג, אז אנחנו פשוט במקרה פשוט של הסתברות בדידה. אבל בין 0 ל-1 אין מספר סופי של מספרים. יש למשל את \( 1 \), ואת \( \frac{1}{2} \), ואת \( \frac{1}{3} \), ואת \( \frac{1}{4} \) וכן הלאה וכן הלאה. עכשיו, מה ההסתברות שכל אחד מהמספרים הללו יתקבל? נניח ש-\( p\left(1\right)=\frac{1}{n} \) עבור \( 0\le\frac{1}{n}\le1 \) כלשהו. מכיוון שההתפלגות הזו היא אחידה, גם \( p\left(\frac{1}{2}\right)=\frac{1}{n} \) וכן הלאה, ואז אני מקבל \( p\left(1\right)+p\left(\frac{1}{2}\right)+\ldots+p\left(\frac{1}{n+1}\right)=\frac{n+1}{n}>1 \) ואופס! חרגתי מהגבול. סכום ההסתברויות על כל התוצאות האפשריות במרחב חייב להיות לכל היותר 1 וכבר עברתי את זה. המסקנה היא פשוטה: אם אני רוצה להגדיר התפלגות כלשהי על אינסוף איברים, ההתפלגות לא יכולה להיות אחידה; היא חייבת לקטון כל הזמן, אחרת סכום ההסתברות של כל התוצאות האפשריות יעבור את 1.

אז יש לנו בעיה מהותית פה, וקל להצביע על האשם בבעיה המהותית הזו: אינסוף. מושג האינסוף מסבך לנו את החיים בצורה שבה מחשבים לא מסתבכים. העניין הוא שמתמטיקאים דווקא אוהבים את האינסוף הזה - אחרי שמתרגלים אליו ומאלפים אותו, הרבה יותר קל לבצע חישובים איתו. יש תחום שלם שעוסק בזה שנקרא חדו"א. הנקודה היא שאת מה שהולך לקרות עכשיו המתמטיקאים מקבלים בשמחה ובששון כי הוא משפר להם את תורת ההסתברות, לא מסבך אותה. אבל במבט ראשון זה יהיה קצת מוזר.

הרעיון הבסיסי הוא לשנות את הגישה שלנו להסתברות. עד עכשיו הגישה הייתה “יש לנו קבוצה \( A \) ולכל איבר \( a\in A \) אנחנו מגדירים הסתברות \( p\left(a\right) \)”. עכשיו הגישה תהיה שונה - אנחנו לא נגדיר הסתברות עבור איבר בודד אלא עבור קבוצות של איברים, וההסתברות שנקבל באה לומר מה הסיכוי שנעלה בגורל איבר כלשהו מתוך הקבוצה.

בואו נבין קודם איך זה עובד עבור התפלגות אחידה בין 0 ל-1 כי אפילו במקרה הפשוט הזה אפשר לראות את הסיבוכים. ראשית, \( p\left(\left[0,1\right]\right)=1 \) על פי מה שזה עתה תיארתי - ההסתברות שאני אקבל איבר כלשהו בין 0 ל-1 היא כמובן 1, ההסתברות הכוללת האפשרית.

מה עם \( p\left(\left[0,\frac{1}{2}\right]\right) \)? אם חילקתי את הקטע שלי לשני חלקים שווים בגודלם, וההתפלגות אחידה, אני מניח שההסתברות שמספר אקראי יפול בחצי הראשון היא \( \frac{1}{2} \). אז קיבלנו \( p\left(\left[0,\frac{1}{2}\right]\right)=\frac{1}{2} \) ומאותו נימוק \( p\left(\left[\frac{1}{2},1\right]\right)=\frac{1}{2} \). ואם אני אחלק את העולם שלי לשלושה חלקים? אז מתבקש ש-\( p\left(\left[0,\frac{1}{3}\right]\right)=\frac{1}{3} \) וכן הלאה, ומכאן קצרה הדרך לטענה הכללית: \( p\left(\left[a,b\right]\right)=b-a \), לכל \( 0\le a<b\le1 \). כלומר, ההסתברות שמספר ייפול בקטע כלשהו שווה ממש לאורך שלו.

זה כמובן מעלה את השאלה מה קורה אם \( a=b \). אם ה”קטע” שלי כולל בדיוק נקודה אחת. על פי מה שאמרתי כרגע, \( p\left(\left[a,a\right]\right)=0 \), ואם חושבים על זה לרגע פשוט אין לי ברירה, זה חייב להיות ככה בדיוק מהנימוק שכבר ראינו. אבל אם ההסתברות של איבר בודד היא 0, מה הולך כאן? איך זה ייתכן שעבור איבר בודד ההסתברות היא 0 אבל עבור קבוצה של איברים היא לא, הרי ההסתברות של כל איבר בקבוצה היא 0!

אז ראשית, אנחנו לומדים מכאן ש”הסתברות 0” בהקשר הרציף שבו אנחנו נמצאים עכשיו היא בעלת משמעות שונה מאשר “הסתברות 0” בהקשר הבדיד. בהקשר הבדיד הסתברות 0 פירושה “זה אף פעם לא יקרה לעולם בחיים תשכחו מזה אין מצב” ואילו בהקשר הרציף הסתברות 0 פירושה “זה לא משהו סביר בפני עצמו אבל זה יכול לקרות”. זה לא “פרדוקס” או משהו דומה פשוט כי הסתברות רציפה היא משהו שאני ממציא כרגע. זה מבנה מתמטי שבא להקל עלינו לתאר כל מני דברים; אין איזה חוק טבע קוסמי שקובע מה המשמעות של “הסתברות 0” במבנה הזה אמורה להיות.

שנית, הקטע הזה של משהו שאינו 0 שמורכב מהרבה דברים שהם כן 0 לא אמור להיות חדש לנו, זו לא המצאה של תורת ההסתברות, אלא זו תוצאה של הגאומטריה שבחרנו לבסס את תורת ההסתברות עליה. אנחנו מגדירים את ההסתברות של קטע בתור האורך שלו, וקטע שכולל נקודה אחת הוא מאורך 0. אנחנו חיים עם זה טוב למרות שזה אומר שקטעים מאורך שגדול מ-0 מורכבים מאינסוף נקודות שהאורך של כל אחת מהן הוא כן 0, כי אנחנו לא מצפים שהאורך של קטע יהיה בסך הכל סכום האורכים של הנקודות שמרכיבות אותו אלא משהו כללי יותר. באופן דומה כשאנחנו עוברים לדו מימד אז לקו אין שטח למרות שאם ניקח ריבוע, אפשר לפרק אותו לאוסף של קווים, וכן הלאה.

בסדר, אז השלמנו נפשית עם זה שלנקודה יש הסתברות 0, והיה לנו קל לקנות את זה שבהתפלגות האחידה, ההסתברות של הקטע \( \left[a,b\right] \) היא \( b-a \). אבל מה ההסתברות של קבוצות מורכבות יותר של נקודות? אז למשל, אם ניקח את איחוד הקטעים \( \left[0,\frac{1}{3}\right]\cup\left[\frac{2}{3},1\right] \) שאורך כל אחד מהם הוא \( \frac{1}{3} \) והם זרים, נצפה שהאורך של שניהם ביחד יהיה סכום האורכים שלהם, \( \frac{1}{3}+\frac{1}{3} \). זה יוצר ציפיה כללית יותר: שאם \( A,B \) הן קבוצות זרות (או אפילו בעלות חיתוך שהוא נקודה משותפת בודדת כי פשוט אפשר להשמיט את הנקודה הזו מאחת הקבוצות) אז \( p\left(A\cup B\right)=p\left(A\right)+p\left(B\right) \). התכונה הזו נקראת אדיטיביות ואם היא מתקיימת אז אפשר להוכיח באינדוקציה שמתקיים \( p\left(\bigcup_{i=1}^{n}A_{i}\right)=\sum_{i=1}^{n}p\left(A_{i}\right) \) עבור קבוצות זרות. אבל למעשה, אנחנו רוצים אפילו יותר מכך - בגלל שאפשר לעשות לקטע \( \left[0,1\right] \) את מה שנקרא “פרדוקס הדיכוטומיה” (הפרדוקס שבו אכילס רוצה לרוץ מקצה אחד של מסלול לקצה השני אבל קודם הוא צריך לעבור את חצי הדרך ואז את חצי מה שנשאר וכן הלאה) ולקבל \( \left[0,1\right]=\left[0,\frac{1}{2}\right]\cup\left[\frac{1}{2},\frac{3}{4}\right]\cup\left[\frac{3}{4},\frac{7}{8}\right]\cup\ldots \) כך שהיינו מצפים שיתקיים \( p\left(\left[0,\frac{1}{2}\right]\cup\left[\frac{1}{2},\frac{3}{4}\right]\cup\left[\frac{3}{4},\frac{7}{8}\right]\cup\ldots\right)=1 \) וזה אכן מתקיים אם מניחים ש-

\( p\left(\left[0,\frac{1}{2}\right]\cup\left[\frac{1}{2},\frac{3}{4}\right]\cup\left[\frac{3}{4},\frac{7}{8}\right]\cup\ldots\right)=p\left(\left[0,\frac{1}{2}\right]\right)+p\left(\left[\frac{1}{2},\frac{3}{4}\right]\right)+\ldots=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots=1 \)

כשהשוויון האחרון נובע ממה שאנחנו יודעים על סכומים אינסופיים (ואנחנו יודעים אותו כי זה חלק מחדו”א). אז התכונה שאנחנו מצפים שתתקיים היא \( p\left(\bigcup_{i=1}^{\infty}A_{i}\right)=\sum_{i=1}^{\infty}p\left(A_{i}\right) \) ולדבר כזה קוראים “\( \sigma \)-אדיטיביות”.

במילים אחרות, אנחנו רוצים ש-\( p \) תהיה פונקציה על תתי-קבוצות של \( \left[0,1\right] \) שמקיימת \( \sigma \)-אדיטיביות ושלכל \( A \) יתקיים \( p\left(A\right)\ge0 \) ולא אמרתי את זה במפורש אבל מן הסתם \( p\left(\emptyset\right)=0 \) כי אפילו על קבוצה עם נקודה אחת מקבלים 0. לפונקציה \( p \) כזו יש שם: מידה. יש תחום שלם שעוסק במידות ובשימושים הנרחבים שלהן, אבל אני לא אכנס לזה בכלל כאן, רק אעיר שלוש הערות. ראשית, מ-\( p \) אנחנו דורשים עוד משהו שלא נדרש ממידות באופן כללי - ש-\( p \) על “הכל” יהיה שווה 1. למידה שמקיימת את זה קוראים מידת הסתברות. שנית, גם אם ההתפלגויות הבדידות שראינו קודם אפשר לנסח בפורמליזם של מידות. אני אוותר על זה כאן, אבל זו הדרך “לאחד” את ההתפלגויות הבדידות עם הרציפות. לבסוף, וזה החלק הקריטי, למידה יש מגבלות. בפרט, פשוט אי אפשר להגדיר מידה על כל תת-הקבוצות של \( \left[0,1\right] \) ואני נותן הוכחה לזה כאן. זה אומר שלא לכל תת-קבוצה של \( \left[0,1\right] \) תהיה הסתברות מוגדרת, אפילו תחת ההתפלגות האחידה, פשוט כי תתי-הקבוצות הללו “מסובכות מדי” (לא לבלבל את זה עם תת-הקבוצה \( \left\{ a\right\} \) שההסתברות שלה בהחלט מוגדרת, פשוט שווה לאפס).

כל זה דיבר רק על התפלגות אחידה, אבל מה קורה באופן כללי? במקרה הכללי עדיין ההסתברות של כל נקודה תהיה אפס, אבל לא כל הנקודות יהיו שוות זו לזו - יהיו נקודות שהאפס שלהן “יותר גדול”. למעשה, זה כבר קרה אם חושבים על ההתפלגות האחידה על \( \left[0,1\right] \) בתור משהו שה”עולם” שלו הוא כל הממשיים, \( \mathbb{R} \). מה שקרה הוא שלממשיים ב-\( \left[0,1\right] \) היה משקל חיובי שבא לידי ביטוי כשמאגדים מספיק מהם ביחד, בזמן שלממשיים מחוץ לקטע היה משקל אפס ולכן לא משנה כמה מהם מאגדים ביחד, לא יוצא מזה כלום. עולה השאלה - מה הכלי הטכני שיש לנו שמסוגל לשלב ככה בין האורך של קטע ובין המשקל שאנחנו נותנים לו? ויש כלי כזה, שהוא אחד מהכוכבים הנוצצים של המתמטיקה: אינטגרל.

הנה הרעיון הפורמלי: כשאנחנו באים להגדיר משתנה מקרי רציף \( X \), הוא תאופיין על ידי פונקציה \( f:\mathbb{R}\to[0,\infty( \) שנקראת פונקציית צפיפות ההסתברות כך ש-\( P\left(X\in B\right)=\int_{B}f\left(x\right)dx \) בהנחה שהאינטגרל מוגדר (ואחרת \( P\left(X\in B\right) \) פשוט לא יהיה מוגדר). ה”צפיפות” בשם הפונקציה לא תפתיע כנראה אף אחת שמכירה פיזיקה: אם יש לנו צורה \( B \) ואנחנו רוצים לחשב את המסה שלה, אנחנו מבצעים אינטגרל על \( B \) על הפונקציה שמתארת את הצפיפות של \( B \) (כמה מסה מרוכזת בכל איזור של \( B \)). זה בדיוק אותו רעיון.

הדרישה היחידה שלנו מ-\( f \) פרט לחיוביות שלה היא שההסתברות הכוללת תצא 1, כלומר שיתקיים \( \int_{-\infty}^{\infty}f\left(x\right)dx=1 \). אני מניח כאן שאנחנו בסדר עם אינטגרלים מוכללים - אבל גם אם אנחנו לא בסדר לא נורא, נראה שהחישובים הרלוונטיים הם לא סוף העולם.

עבור ההתפלגות האחידה, פונקציית הצפיפות די פשוטה:

\( f\left(x\right)=\begin{cases} 1 & x\in\left[0,1\right]\\ 0 & x\notin\left[0,1\right] \end{cases} \).

אם היינו רוצים להגדיר התפלגות אחידה על קטע גדול יותר, למשל \( \left[0,2\right] \), היינו צריכים לשנות את הפונקציה בהתאם כדי שהאינטגרל על הכל ייצא 1:

\( f\left(x\right)=\begin{cases} \frac{1}{2} & x\in\left[0,2\right]\\ 0 & x\notin\left[0,2\right] \end{cases} \)

הבנו את הרעיון? יפה, אז אפשר סוף כל סוף להגיע אל ההתפלגות שהיא הסיבה שלשמה נתכנסנו: ההתפלגות הנורמלית.

מפגש ראשון עם התפלגות נורמלית

אמרתי בתחילת הפוסט שהתפלגות נורמלית מוגדרת עם \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \) ועכשיו אנחנו סוף סוף יכולים להבין מה הולך כאן, אבל זה עדיין מסובך מדי; לעת עתה אני אסתכל על מקרה פרטי מרכזי, שממנו בעצם קל יחסית להבין את המקרה הכללי - הפונקציה \( f\left(x\right)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}} \) שמתקבלת מהצבת \( \mu=0,\sigma=1 \) בנוסחה הקודמת. ככה הפונקציה הזו נראית כשמציירים גרף שלה:

הגרף הזה מתאר רק את החלק \( \left[-3,3\right] \) כי זה החלק המעניין; מחוץ לו הפונקציה פשוט נראית ממש שטוחה. לפונקציה הזו יש שלל שמות - בפרט “עקומת הפעמון” בגלל הצורה שלה, או “גאוסיאן” על שם המתמטיקאי גאוס שעשה בה שימוש נרחב (אבל לא היה הראשון שתיאר אותה; זה היה דה-מואבר).

השאלה המנחה שלנו בכל סדרת הפוסטים הזו היא “מאיפה הפונקציה הזו הגיעה בכלל?” והתשובה שאני נותן כאן היא “ממשפט הגבול המרכזי” שאותו אני עוד צריך להראות פורמלית אבל כבר אמרתי מהו - העקומה הספציפית הזו פשוט מתארת ממש טוב את מה שקורה כשיש לנו משתנה מקרי ואנחנו מחברים הרבה עותקים בלתי תלויים של עצמו. אבל כבר בשלב הזה אני יכול להסביר מאיפה חלק מהפונקציה הגיע - למה \( \pi \) נמצא שם. התשובה הקצרה היא שהוא שם כי \( 2\pi \) הוא היקף מעגל היחידה. התשובה הקצת פחות קצרה היא שהוא שם בגלל הדרישה \( \int_{-\infty}^{\infty}f\left(x\right)dx=1 \) על פונקציות צפיפות. בואו נעבור לתשובה המלאה.

אז כאמור, אנחנו צריכים להראות שמתקיים \( \int_{-\infty}^{\infty}f\left(x\right)dx=1 \), כלומר \( \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}}dx=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx=1 \), כלומר מספיק להראות ש-\( \int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx=\sqrt{2\pi} \). עכשיו, איך בדרך כלל מחשבים אינטגרל מהצורה \( \int_{-\infty}^{\infty}f\left(x\right)dx \)? קודם כל מוצאים פונקציה קדומה, \( F\left(x\right) \) כך ש-\( F^{\prime}\left(x\right)=f\left(x\right) \). אחר כך מחשבים את האינטגרל על הגבולות הסופיים \( \int_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right) \), ולבסוף משאיפים בזהירות את \( b \) ל-\( \infty \) ואת \( a \) ל-\( -\infty \) ובודקים לאן הביטוי הולך.

זה לא מה שיקרה כאן.

לב הבעיה הוא שלפונקציה \( e^{-x^{2}} \) אין פונקציה קדומה שאפשר להציג בצורה פשוטה (“אלמנטרית”). להוכיח את זה זה סיפור בפני עצמו ואני לא אכנס לזה הפעם, אבל תשכחו מהשיטה המסורתית. לא נחשב את האינטגרל הזה בדרך המסורתית. למרבה השמחה, לא חסרות דרכים אחרות.

בואו נסמן \( I=\int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx \). במקום להוכיח \( I=\sqrt{2\pi} \), נוכיח ש-\( I^{2}=2\pi \) (ובגלל שהאינטגרל של \( I \) הוא על פונקציה חיובית, \( I \) הוא השורש החיובי של \( 2\pi \)). הרעיון הוא להפוך את \( I^{2} \), שהוא מכפלה של שני אינטגרלים במשתנה יחיד, לאינטגרל כפול באמצעות מה שנקרא משפט פוביני. בואו נתחיל מלראות איך זה בערך עובד ואז נדבר על הפרטים הטכניים שצריך לגהץ. הטריק הבסיסי הוא זה:

\( I^{2}=\left(\int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx\right)\left(\int_{-\infty}^{\infty}e^{-\frac{y^{2}}{2}}dy\right)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-\frac{\left(x^{2}+y^{2}\right)}{2}}dxdy \)

עכשיו מבצעים החלפת משתנים של האינטגרל הכפול. מגדירים

\( x=r\cos\theta \)

\( y=r\sin\theta \)

עבור \( r\in[0,\infty( \) ו-\( \theta\in\left[0,2\pi\right] \)

מה שנותן לנו:

\( x^{2}+y^{2}=r^{2}\left(\cos^{2}\theta+\sin^{2}\theta\right)=r^{2} \)

\( dxdy=rd\theta dr \)

כלומר

\( \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-\frac{\left(x^{2}+y^{2}\right)}{2}}dxdy=\int_{0}^{\infty}\left(\int_{0}^{2\pi}re^{-\frac{r^{2}}{2}}d\theta\right)dr= \)

\( =2\pi\int_{0}^{\infty}re^{-\frac{r^{2}}{2}}dr=-2\pi\left.e^{\frac{-r^{2}}{2}}\right|_{0}^{\infty}=2\pi \)

אוקיי, מה קרה פה כרגע? לי זה נראה כמו קסם בכל פעם שאני רואה את זה, אבל האמת היא שלא קרה פה שום דבר חריג - זה תרגיל מאוד סטנדרטי בחדו”א, וכפי שקורה בדרך כלל בחדו”א - להצדיק כל מעבר דורש עבודה אבל מרגע שיושב לנו למה אפשר להצדיק את כולם, העבודה היא די פשוטה. אני אתחיל דווקא מהסוף ואלך אחורה צעד-צעד כדי שנראה שהכל תקין, כי ככל שמתקרבים להתחלה כך הנניח-נזניח שלנו נהיה גדול יותר.

ראשית, האינטגרל \( \int_{0}^{\infty}re^{-\frac{r^{2}}{2}}dr \). הוא מאוד מזכיר את מה שהתחלנו ממנו, \( \int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx \), אבל יש הבדל מהותי אחד: \( e^{-\frac{r^{2}}{2}} \) מוכפל ב-\( r \), וההבדל הקטן הזה פירושו שיש פונקציה קדומה אלמנטרית לאינטגרנד. אם אנחנו גוזרים את \( e^{x} \) אנחנו מקבלים \( e^{x} \); זו התכונה הבסיסית של הפונקציה הזו (אפשר אפילו להגדיר אותה באמצעותה, הנה פוסט שעושה את זה). עכשיו, על פי כלל השרשרת, \( \left(e^{g\left(x\right)}\right)^{\prime}=g^{\prime}\left(x\right)e^{g\left(x\right)} \), ומכיוון שבמקרה שלנו \( g\left(r\right)=-\frac{r^{2}}{2} \) נקבל \( g^{\prime}\left(r\right)=-r \) כלומר \( \left(e^{-\frac{r^{2}}{2}}\right)=-re^{-\frac{r^{2}}{2}} \) ולכן הפונקציה הקדומה של \( re^{-\frac{r^{2}}{2}} \) היא \( -e^{-\frac{r^{2}}{2}} \).

מה שנשאר לנו, אם אנחנו יודעים את הפונקציה הקדומה, הוא לחשב את \( -2\pi\left.e^{\frac{-r^{2}}{2}}\right|_{0}^{\infty} \). החישוב הוא סטנדרטי לאינטגרלים מוכללים: כדי לחשב את \( \left.F\left(r\right)\right|_{0}^{\infty} \) לוקחים \( a\in[0,\infty( \) כלשהו ומחשבים את \( \lim_{a\to\infty}\left[F\left(a\right)-F\left(0\right)\right] \). במקרה שלנו, \( \lim_{a\to\infty}e^{-\frac{a^{2}}{2}}=0 \) כי \( e^{x} \) הוא פונקציה רציפה וכש-\( a\to\infty \) אז \( -\frac{a^{2}}{2}\to-\infty \) ואנחנו יודעים ש-\( \lim_{x\to-\infty}e^{x}=0 \). מצד שני, כשמציבים \( ra=0 \) ב-\( e^{\frac{-r^{2}}{2}} \) מקבלים 1, ולכן בסך הכל נשארים עם \( -2\pi\cdot0-\left(-2\pi\cdot1\right)=2\pi \). עד כאן הכל טוב.

עכשיו בואו נדבר על החלפת המשתנים שמאפשרת לנו לכתוב \( \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-\frac{\left(x^{2}+y^{2}\right)}{2}}dxdy=\int_{0}^{\infty}\left(\int_{0}^{2\pi}re^{-\frac{r^{2}}{2}}d\theta\right)dr \). כאן יש את הפער הגדול ביותר בין כמה שהפעולה הטכנית הזו היא סטנדרטית אחרי שהתרגלנו אליה, וכמה המשפט שעליה היא מבוססת הוא עמוק ומורכב. יש לי פוסט על הוכחת המשפט באופן כללי וזה… לא כל כך פשוט. אבל למרבה השמחה מה שפשוט הוא הרעיון. את הרעיון, גם במקרה הכי כללי, אפשר לתאר על ידי הנוסחה הפשוטה

\( \int_{B}f=\int_{A}\left(f\circ g\right)\left|\det Dg\right| \)

(הנוסחה הזו משמיטה את ה-\( dx \)-ים למיניהם שאנחנו משתמשים בהם כדי לעקוב אחרי משתני האינטגרציה). הרעיון פה הוא ש-\( f \) היא הפונקציה שעליה מבצעים אינטגרציה, וכדי שהמשפט יעבוד היא צריכה להיות רציפה (במקרה שלנו \( e^{-\frac{\left(x^{2}+y^{2}\right)}{2}} \) רציפה) ואילו \( g \) היא הפונקציה שמתארת את החלפת המשתנים - במקרה שלנו זו החלפה היא מאוד סטנדרטית, אולי ההחלפה הכי בסיסית שרואים בחדו”א. היא מתבססת על פונקציה \( g:\mathbb{R}^{2}\to\mathbb{R}^{2} \) שמוגדרת על ידי \( g\left(r,\theta\right)=\left(r\cos\theta,r\sin\theta\right) \). את הפונקציה הזו צריך לצמצם לתת-קבוצה \( A \), כך שעל תת-הקבוצה הזו \( g \) היא חח”ע ועל, והתמונה שלה היא בדיוק \( B \), הקבוצה שעליה אנחנו מנסים לבצע את האינטגרציה של \( f \). במקרה שלנו, \( A=\left(0,\infty\right)\times[0,2\pi( \) בזמן ש-\( B=\mathbb{R}^{2}\backslash\left\{ 0\right\} \) (אני משמיט את 0 כי איתו \( g \) כבר לא תהיה חח”ע, אבל נקודה אחת לא משפיעה על האינטגרל). על \( g \) יש דרישה חזקה יותר של רציפות - גם היא וגם ההופכית שלה צריכות להיות גזירות ברציפות, אבל לא קשה לבדוק שזה מתקיים.

הביטוי \( f\circ g \) פירושו “קודם להפעיל את \( g \) ואז את \( f \)” (כן, אני יודע שיש טקסטים שעושים בדיוק ההפך) אז במקרה שלנו אנחנו מקבלים

\( \left(f\circ g\right)\left(r,\theta\right)=e^{-\frac{\left(r\cos\theta\right)^{2}+\left(r\sin\theta\right)^{2}}{2}}=e^{-\frac{r^{2}}{2}} \)

זו “החלפת המשתנים” בפעולה (ואני מקווה שזה מבהיר למה \( g \) היא דווקא מהמשתנים ה”חדשים” ל”ישנים”; אותי זה תמיד מבלבל). מה שנשאר לעשות הוא לכפול בביטוי \( \left|\det Dg\right| \) שנקרא היעקוביאן של \( g \), שהוא הגורם שמודד כמה \( g \) “מעוותת את המרחב” ולכן משנה את תפיסת השטח שלנו. כאן \( Dg \) היא מטריצה של כל הנגזרות החלקיות של \( g \): מכיוון ש-\( g:\mathbb{R}^{2}\to\mathbb{R}^{2} \) היא פונקציה בשני משתנים יש ל-\( Dg \) שתי עמודות - בעמודה הראשונה גוזרים לפי \( r \) ובשניה לפי \( \theta \). בנוסף, מכיוון ש-\( g \) היא פונקציה עם שני רכיבים, יש ל-\( Dg \) שני שורות: בראשונה גוזרים את הרכיב \( r\cos\theta \) ובשניה את הרכיב \( r\sin\theta \). מקבלים:

\( Dg=\left[\begin{array}{cc} \cos\theta & -r\sin\theta\\ \sin\theta & r\cos\theta \end{array}\right] \)

ולכן

\( \det Dg=r\cos^{2}\theta+r\sin^{2}\theta=r\left(\cos^{2}\theta+\sin^{2}\theta\right)=r \)

ואנחנו כופלים בערך המוחלט של הביטוי הזה, כלומר עדיין כופלים ב-\( r \). כל הדבר הזה מתבטא בפועל בכלל המצחיק \( dxdy=rd\theta dr \) שהוא לא משהו פורמלי (למרות שאם באמת רוצים אפשר לפרמל את המשמעות של ה-\( dx \)-ים הללו אבל בואו לא נעשה את זה הפעם) שאומר לנו “אחרי שהחלפתם את המשתנים באינטגרנד, תחליפו גם את הסימן שמתאר לכם את משתני הסכימה אבל אל תשכחו בנוסף גם לכפול ביעקוביאן \( r \)”. מכאן והלאה האינטגרל נפתר בקלות.

מה שנשאר לי להסביר הוא את המעבר

\( \left(\int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx\right)\left(\int_{-\infty}^{\infty}e^{-\frac{y^{2}}{2}}dy\right)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-\frac{\left(x^{2}+y^{2}\right)}{2}}dxdy \)

שבו הופכים מכפלה של שני אינטגרלים חד-ממדיים לאינטגרל דו-ממדי. הכלי הבסיסי פה הוא משפט פוביני:

\( \int\int_{X\times Y}f\left(x,y\right)dxdy=\int_{X}\left(\int_{Y}f\left(x,y\right)dy\right)dx \)

כאן באגף שמאל יש לנו אינטגרל כפול, ובאגף ימין יש לנו שני אינטגרלים חד-ממדיים, אבל לא מוכפלים אלא מופעלים אחד על השני. כלומר, האינטגרל החיצוני \( \int_{X}\left(\ldots\right)dx \) מופעל על פונקציה של \( x \) שמתקבלת מכך שבוחרים ערך ל-\( x \), “מקפיאים” אותו ומחשבים את האינטגרל החד-ממדי \( \int_{Y}f_{x}\left(y\right)dy \) שמופעל על הפונקציה \( f_{x}\left(y\right) \) שמוגדרת על ידי \( f_{x}\left(y\right)=f\left(x,y\right) \). כדי שהטריק הזה יעבוד צריך שה-\( f \) שלנו תהיה רציפה (כבר ראינו שזה קורה) או שהאינטגרל לא יהיה אינטגרל רגיל אלא הגרסה המוכללת והחזקה שלו, אינטגרל לבג, אבל על זה אני לא אדבר הפעם.

במקרה הספציפי שלנו, \( f\left(x,y\right)=e^{-\frac{\left(x^{2}+y^{2}\right)}{2}}=e^{-\frac{x^{2}}{2}}\cdot e^{-\frac{y^{2}}{2}} \) כלומר אם אני מסתכל על \( f_{x}\left(y\right) \) זו פונקציה מהצורה של קבוע (שתלוי ב-\( x \)) שמוכפל ב-\( e^{-\frac{y^{2}}{2}} \). מכפלה בקבוע אפשר להוציא מחוץ לאינטגרל:

\( \int_{X}\left(\int_{Y}f\left(x,y\right)dy\right)dx=\int_{X}e^{-\frac{x^{2}}{2}}\left(\int_{Y}e^{-\frac{y^{2}}{2}}dy\right)dx \)

אבל עכשיו מה שיש באינטגרל הפנימי לא תלוי ב-\( x \) בשום צורה, כלומר הוא תמיד יוצא אותו מספר לא משנה מה הערך של \( x \), ולכן מנקודת המבט של האינטגרל החיצוני, \( \int_{Y}e^{-\frac{y^{2}}{2}}dy \) הוא קבוע שאפשר להוציא החוצה, ומקבלים

\( \int_{X}\left(\int_{Y}f\left(x,y\right)dy\right)dx=\int_{X}e^{-\frac{x^{2}}{2}}dx\int_{Y}e^{-\frac{y^{2}}{2}}dy \)

וזה מה שהשתמשתי בו בהוכחה.

יש רק בעיה קטנה אחת פה: בשביל להשתמש במשפט פוביני, אני צריך ש-\( X,Y \) יהיו קטעים סופיים. זה גורר עוד סיבוך טכני. במקום לחשב את \( I=\int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx \) אני בוחר \( a\in[0,\infty( \) ומחשב את \( I\left(a\right)=\int_{-a}^{a}e^{-\frac{x^{2}}{2}}dx \) ואז בודק מה יוצא \( \lim_{a\to\infty}I\left(a\right) \). אבל אפילו כאן מתחבא עוד סיבוך טכני! כי באינטגרל מוכלל מהצורה \( \int_{-\infty}^{\infty}f\left(x\right)dx \) זה לא תקין לבחור נקודה אחת \( a \) ולהסתכל על הגבול \( \lim_{a\to\infty}\int_{-a}^{a}f\left(x\right)dx \) כי הסימטריה שזה יוצר עלולה “למסך” תקלות. האופן שבו באמת מגדירים את הערך של אינטגרל אינסופי לשני הכיוונים שכזה הוא עם אחת משתי השיטות הבאות: או שבוחרים \( a,b \) ומסתכלים על הגבול הכפול \( \lim_{a\to\infty}\lim_{b\to\infty}\int_{a}^{b}f\left(x\right)dx \) או שמפצלים את האינטגרל לסכום של שני אינטגרלים, \( \int_{-\infty}^{\infty}f\left(x\right)dx=\int_{-\infty}^{c}f\left(x\right)dx+\int_{c}^{\infty}f\left(x\right)d\left(x\right) \).

כדי לראות למה זה קריטי, בואו ניקח \( f\left(x\right)=x \). אז למשל \( \int_{0}^{\infty}xdx=\left.\frac{x^{2}}{2}\right|_{0}^{\infty}=\infty \) ובדומה \( \int_{-\infty}^{0}xdx=-\infty \) והביטוי \( \infty-\infty \) בכלל לא מוגדר; ואם אני מסתכל על \( \int_{a}^{b}xdx=\frac{b^{2}-a^{2}}{2} \) אז הגבול הכפול \( \lim_{a\to\infty}\lim_{b\to\infty}\frac{b^{2}-a^{2}}{2} \) שוב לא יהיה מוגדר, מאותן סיבות.

באינטגרל שלנו, \( \int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx \), זו לא בעיה אמיתית כי אפשר לפרק את האינטגרל באמצע ולקבל שני חלקים שכל אחד מהם מתכנס יפה למשהו סופי (אל \( \frac{\sqrt{2\pi}}{2} \) בגלל הסימטריה) אבל אם אני חותך את האינטגרל באמצע, כל הטריקים היפים שעשיתי קודם כבר לא עובדים! הצילו! חדו”א יכול להיות מאוד אכזרי לפעמים.

למרבה המזל, יש לנו דרך קיצור כאן. יש שיטה שנקראת “הערך העיקרי של קושי” (Principal Value) שמאפשרת לתת ערך ל-\( \lim_{a\to\infty}\int_{-a}^{a}f\left(x\right)dx \), והערך הזה יוצא שווה אל \( \int_{-\infty}^{\infty}f\left(x\right)dx \) במקרים שבהם \( f\left(x\right) \) מתכנסת בערך מוחלט, כלומר אם \( \int_{-\infty}^{\infty}\left|f\left(x\right)\right|dx<\infty \). זה בהחלט המצב גם עבור \( \int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx \). ראשית, הערך המוחלט בכלל לא משפיע כאן כי \( e \) בחזקת משהו ממשי הוא תמיד חיובי; ושנית, אפשר לחסום את האינטגרל הזה בצורה די נחמדה:

\( \int_{-\infty}^{\infty}e^{-\frac{x^{2}}{2}}dx<\int_{-\infty}^{-1}-xe^{-\frac{x^{2}}{2}}dx+\int_{-1}^{1}e^{-\frac{x^{2}}{2}}dx+\int_{1}^{\infty}xe^{-\frac{x^{2}}{2}}dx \)

כי כאשר \( x \) גדול מ-1 מכפלה בו רק מגדילה את האינטגרל, וכשהוא קטן ממינוס 1 מכפלה ב-\( -x \) רק מגדילה את האינטגרל. עכשיו קיבלנו סכום של שלושה אינטגרלים שהאמצעי מביניהם הוא בוודאי סופי (כי הוא של פונקציה רציפה על קטע סגור) ואת האחרים אפשר לחשב במפורש כפי שכבר ראינו קודם, למשל \( \int_{1}^{\infty}xe^{-\frac{x^{2}}{2}}=\left.-e^{-\frac{x^{2}}{2}}\right|_{1}^{\infty}=e^{-\frac{1}{2}} \). זה מוכיח שהאינטגרל חסום ואפשר כמו שאמרתי קודם לכתוב \( I\left(a\right)=\int_{-a}^{a}e^{-\frac{x^{2}}{2}}dx \) ולבדוק מה יוצא \( \lim_{a\to\infty}I\left(a\right) \).

את \( I\left(a\right)=\int_{-a}^{a}e^{-\frac{x^{2}}{2}}dx \) אפשר לחשב כמו שראינו עם משפט פוביני, ומקבלים

\( \int_{-a}^{a}e^{-\frac{x^{2}}{2}}dx=\int_{-a}^{a}\int_{-a}^{a}e^{-\frac{\left(x^{2}+y^{2}\right)}{2}}dxdy \)

אבל עכשיו נוצר לנו סיבוך בשלב החלפת המשתנים. אנחנו עדיין משתמשים באותה החלפה בדיוק:

\( x=r\cos\theta \)

\( y=r\sin\theta \)

אבל הרעיון בהחלפת משתנים הוא כזכור לקחת אינטגרל שמוגדר על קבוצה אחת \( A \) ולהגדיר אותו על קבוצה אחרת \( B \) כך שהחלפת המשתנים מעבירה את \( B \) בדיוק אל \( A \). ואצלנו עכשיו \( A \) הוא ריבוע, \( A=\left[-a,a\right]\times\left[-a,a\right] \) בזמן שהחלפת המשתנים מוגדרת על קבוצה \( B=\left[0,t\right]\times\left[0,2\pi\right] \) (שוב, עד כדי התעלמות מהבעייתיות בנקודה 0) ומעבירה את הקבוצה הזו אל העיגול \( \left\{ \left(r\cos\theta,r\sin\theta\right)\ |\ 0\le\theta\le2\pi,0\le r\le t\right\} \) שהרדיוס שלו הוא \( t \).

אז מה עושים? שוב חוסמים! העיגול שחסום בתוך \( A \) הוא בעל רדיוס \( a \), והמעגל שחוסם את \( A \) הוא בעל רדיוס \( \sqrt{2}a \) (זה תרגיל נחמד לצייר את הריבע ולהבין למה אלו רדיוסי המעגלים), ומכיוון שהפונקציה חיובית, האינטגרל שלה על \( A \) יהיה בין האינטגרלים שלה על שני המעגלים הללו:

\( \int_{0}^{a}\left(\int_{0}^{2\pi}re^{-\frac{r^{2}}{2}}d\theta\right)dr\le I\left(a\right)\le\int_{0}^{\sqrt{2}a}\left(\int_{0}^{2\pi}re^{-\frac{r^{2}}{2}}d\theta\right)dr \)

ואת האינטגרלים הללו כבר ראינו איך לחשב. מכיוון שאין \( \infty \) מעורב שמאפס את האקספוננט, הם יוצאים פחות “נקיים”, אבל אנחנו כבר שקועים בלכלוך מכאן ועד להודעה חדשה אז למי אכפת? בסופו של חישוב האינטגרל מקבלים \( -2\pi\left.e^{\frac{-r^{2}}{2}}\right|_{0}^{t}=-2\pi\left(e^{-\frac{t^{2}}{2}}-1\right)=2\pi\left(1-e^{-\frac{t^{2}}{2}}\right) \) ורק נשאר להציב \( t=a,\sqrt{2}a \) ולקבל:

\( 2\pi\left(1-e^{-\frac{a^{2}}{2}}\right)\le I\left(a\right)\le2\pi\left(1-e^{-a^{2}}\right) \)

עכשיו אפשר להשתמש בכלל הסנדוויץ’: \( \lim_{a\to\infty}2\pi\left(1-e^{-\frac{a^{2}}{2}}\right)=2\pi\left(1-e^{-a^{2}}\right)=2\pi \) ולכן מקבלים \( \lim_{a\to\infty}I\left(a\right)=2\pi \) בצורה הכי פורמלית בעולם.

בספרי לימוד של תורת ההסתברות בדרך כלל לא יראו לכם את כל המהומה הזו; יסתפקו בהוכחה שהראיתי בהתחלה, שמדלגת מעל שלבים בצורה קלילה. עכשיו אנחנו כנראה גם מבינים למה - כי אחרי שרואים את זה צריך לנוח, ולכן אני מסיים את הפוסט כאן ולא מדלג בקלילות אל הנושא הבא - כלומר, אל השאלה מה בנוסחה הכללית \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \) התפקיד של אותם \( \sigma \) ו-\( \mu \) מזעזעים שמתחבאים בה ואיך אנחנו מקשרים את המקרה הכללי איתם אל מה שראינו כרגע.