מה הקטע עם התפלגות נורמלית? (חלק ג': על תוחלת וסטיית תקן)

מבוא

בסדרת הפוסטים הנוכחית אנחנו מנסים להבין למה ההתפלגות הנורמלית \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \) נראית כמו שהיא נראית. בפוסט הקודם הבנו מה הפונקציה הזו בכלל אומרת - זו פונקציית צפיפות ההסתברות של ההתפלגות הנורמלית, כלומר אם \( X \) הוא המשתנה המקרי שמתואר על ידי הפונקציה הזו, אז \( P\left(a\le X\le b\right)=\int_{a}^{b}\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}}dx \). בפוסט הקודם גם ראינו מאיפה ה-\( \pi \) הגיע - זה קבוע נרמול שנדרש כדי שיתקיים \( \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^{2}}{2}}=1 \). אבל מה הם ה-\( \mu \) וה-\( \sigma \) שמופיעים בנוסחה? אלו שני פרמטרים שמאפיינים לא רק את ההתפלגות הזו, אלא כל התפלגות שהיא: התוחלת \( \mu \) של ההתפלגות, וסטיית התקן \( \sigma \) שלה. באופן לא פורמלי, תוחלת של התפלגות היא הממוצע שלה, וסטיית התקן מלמדת אותנו כמה גדול הפיזור של ההתפלגות סביב הממוצע הזה. מה שמפליא הוא כמה מידע על ההתפלגות נמצא כבר בשני הערכים המספריים הללו - וההמחשה לזה היא בדיוק משפט הגבול המרכזי, שאומר שאם אנחנו יודעים את התוחלת וסטיית התקן של התפלגות, אז נדע בדיוק איך נראה מה שמתקבל מסכומים גדולים של משתנים מקריים בלתי תלויים בעלי ההתפלגות הזו.

בואו נעבור להגדרות פורמליות, ונראה איך זה בא לידי ביטוי בהתפלגות נורמלית ובהתפלגויות אחרות שראינו.

תוחלת

מה זה “ממוצע”? אם למשל יש לנו את סדרת המספרים \( 10,30,50,60,90 \) הממוצע שלה היא הסכום של כל המספרים חלקי כמה מספרים יש: \( \frac{10+30+50+60+90}{5}=\frac{240}{5}=48 \). מה המשמעות של המספר הזה, 48? אפשר לחשוב על זה כך: אם נחליף כל איבר בסדרה ב-48, נקבל סדרה \( 48,48,48,48,48 \) שסכום האיברים שלה שווה לסכום אברי הסדרה המקורית.

את הרעיון הזה אפשר להכליל קצת: אם למשל הסדרה שלנו היא \( 30,60,60 \) אז הממוצע שלה הוא \( 50 \), אבל אפשר גם “לאחד” את שני ה-60-ים ולהגיד שיש בסדרה שלנו שני איברים: האיבר \( 30 \) עם המשקל 1, והאיבר \( 60 \) עם המשקל 2. מה שאנחנו עושים הוא לסכום את האיברים כשכל אחד מוכפל במשקל שלו, ולחלק בסכום הכולל של המשקלים. אולי קל יותר להבין את זה עם נוסחה: אם יש לנו את הסדרה \( a_{1},a_{2},\ldots,a_{n} \) ואת המשקלים \( w_{1},\ldots,w_{n} \) אז הממוצע המשוקלל הוא \( \frac{\sum_{i=1}^{n}w_{i}a_{i}}{\sum_{i=1}^{n}w_{i}} \). כאשר כל המשקלים הם 1 אנחנו מקבלים את הגדרת הממוצע הקודמת.

ההגדרה של ממוצע משוקלל לא דורשת שום דבר מהמשקלים, חוץ מכך שהסכום שלהם יהיה שונה מאפס (אחרת יקרה משהו מוזר כשמנסים לחלק) אבל כמובן, ההגדרה הזו יוצאת פשוטה במיוחד אם \( 0\le w_{i}\le1 \) ובנוסף \( \sum_{i=1}^{n}w_{i} \); אנחנו מקבלים שהממוצע המשוקלל הוא פשוט \( \sum_{i=1}^{n}w_{i}a_{i} \).

איך כל זה קשור להסתברות? ובכן, הסתברות היא בדיוק המקרה שבו יש לנו איברים \( 0\le w_{i}\le1 \) שמסתכמים ל-1: אם יש לנו מרחב הסתברות ו-\( X \) הוא משתנה מקרי שמקבל מספר סופי של ערכים, נאמר הערכים \( a_{1},a_{2},\ldots,a_{n} \), אז אפשר להסתכל על הממוצע המשוקלל \( \sum_{i=1}^{n}P\left(X=a_{i}\right)\cdot a_{i} \). כלומר, אנחנו לוקחים את הממוצע המשוקלל של ה-\( a_{i} \)-ים כשהמשקולות הן בדיוק ההסתברויות ש-\( a_{i} \) יעלה בגורל. סכום כזה נקרא תוחלת ומסומן ב-\( E\left[X\right] \). אם מרחב המדגם הוא אינסופי העניינים מן הסתם מסתבכים קצת מתמטית אבל הרעיון זהה: \( \text{E}\left[X\right]=\sum_{i=1}^{\infty}P\left(X=a_{i}\right)\cdot a_{i} \) עבור מרחב מדגם אינסופי בדיד, ו-\( \text{E}\left[X\right]=\int_{-\infty}^{\infty}p\left(x\right)xdx \) עבור מרחב מדגם אינסופי רציף.

למה ממוצע משוקלל כזה הוא מעניין? אנחנו הרי מצפים שהוא ילמד אותנו משהו על המשתנה המקרי \( X \) ולא סתם יהיה הגדרה לשם הגדרה. כאן זו אחת מהסיטואציות הנדירות שבהן המתמטיקה הייתה מדע אמפירי: קודם כל התגלתה תופעה, ואחר כך הוכיחו אותה מתמטית. התופעה הייתה האבחנה שאם אנחנו חוזרים על אותו ניסוי הסתברותי מספרי שוב ושוב, הממוצע של התוצאות שלנו נוטה להיות יציב יחסית ככל שמספר הניסויים שאנחנו מבצעים גדל. בואו נראה דוגמא קונקרטית לזה עם הטלת קוביה. בימינו, למרבה השמחה, אפשר לרתום את המחשב לניסויים כאלו, אז הנה קוד פייתון קצרצר:

import random
for N in [10, 100, 1000, 10000, 100000, 1000000]:
  print(f"{N}: {sum([random.randint(1, 6) for _ in range(N)]) / N}")

מה שהקוד הזה עושה הוא להטיל קוביה מספר כלשהו של פעמים שמסומן ב-\( N \), ואז לחשב את ממוצע ההטלות. אנחנו עושים את הניסוי הזה בנפרד עבור ערכי \( N \) מ-\( 10 \) עד \( 10^{6} \), ולכל אחד מהם אנחנו מדפיסים את הממוצע. כשאני עשיתי את זה, קיבלתי:

10: 3.1
100: 3.56
1000: 3.372
10000: 3.4951
100000: 3.50129
1000000: 3.499845 

די בבירור, הממוצע מתקרב אל \( 3.5 \). זו אבחנה אמפירית; אבל אם אנחנו רוצים לדעת לאן הממוצע ישאף אנחנו לא צריכים לבצע ניסויים בפועל - אנחנו יכולים פשוט לחשב את זה, ואיכשהו מובטח שהמציאות תסתדר בהתאם לחישוב שלנו. הערך שאנחנו מחשבים הוא - הפתעה הפתעה - התוחלת של המשתנה המקרי שמתאר את הניסוי.

במקרה שלנו, \( X \) מקבל כל ערך בין 1 ל-6 בהסתברות \( \frac{1}{6} \) לכל איבר, אז על פי הגדרה \( E\left[X\right]=\frac{1+2+3+4+5+6}{6}=\frac{21}{6}=3.5 \). אין פה הפתעה, אבל מה שכן יש פה הוא חישוב פשוט למדי, שלא מצריך הטלת מיליון קוביות. והיופי פה הוא שזה עובד תמיד, לכל משתנה מקרי \( X \) שאנחנו משכפלים \( n \) עותקים זהים שלו שהם בלתי תלויים אחד בשני ומסתכלים על הממוצע של כולם (טוב, כמעט תמיד).

לתופעה הזו קוראים חוק המספרים הגדולים. יש כמה ניסוחים למשפט שאומר “מה הולך פה” והניסוח הנפוץ הוא בדרך כלל של מה שנקרא החוק החזק של המספרים הגדולים שלא אוכיח כרגע אבל כן אסביר מה הוא אומר. אנחנו מתחילים עם סדרה אינסופית של משתנים מקריים \( X_{1},X_{2},X_{3},\ldots \) שכולם מתפלגים באותו האופן (כלומר, בעלי אותה פונקצית צפיפות הסתברות) והם בלתי תלויים, במובן הבא: \( X,Y \) הם בלתי תלויים אם לכל שתי קבוצות אפשריות של תוצאות \( A,B \) מתקיים \( P\left(X\in A\wedge Y\in B\right)=P\left(X\in A\right)P\left(Y\in B\right) \); ראינו את זה טיפה בפוסט הקודם ולא אתעכב על זה הפעם.

עכשיו, מכיוון שכל המשתנים מתפלגים אותו דבר, יש להם אותה תוחלת. באופן כללי תוחלת עשויה להיות אינסופית או לא מוגדרת, אבל נניח שכאן היא מספר סופי, \( E\left[X_{i}\right]=\mu \). במקרה הזה אנחנו יכולים להסתכל על המשתנה המקרי \( \overline{X}_{n}=\frac{X_{1}+X_{2}\ldots+X_{n}}{n} \), שהוא המשתנה שמתאר את הממוצע (הרגיל, הלא משוקלל) של \( n \) התוצאות הראשונות בסדרת המשתנים המקריים. החוק החזק של המספרים הגדולים אומר שמתקיים \( \overline{X}_{n}\to\mu \) בהסתברות 1. בואו נבין טיפה יותר מה זה אומר בעצם.

ה-\( \overline{X}_{n} \)-ים שהגדרנו מתארים סדרה של משתנים שמתארת את הממוצעים ההולכים-ומשתפרים: \( \overline{X}_{1},\overline{X}_{2},\overline{X}_{3},\ldots \). אם אנחנו דוגמים איבר \( a \) כלשהו במרחב המדגם שלנו, הוא ייתן למשתנים \( X_{1},X_{2},\dots \) ערכים קונקרטיים שהם מספרים ממשיים: \( X_{1}\left(a\right),X_{2}\left(a\right),\ldots \), ולכן גם בסדרת הממוצעים נקבל ערכים קונקרטיים \( \overline{X}_{1}\left(a\right),\overline{X}_{2}\left(a\right),\ldots \); כלומר, בהינתן שאנחנו מסתכלים על איבר קונקרטי של מרחב המדגם, קיבלנו סדרה “רגילה” של מספרים ממשיים. על סדרה “רגילה” של ממשיים אפשר לשאול האם היא מקיימת את התכונה \( \lim_{n\to\infty}\overline{X}_{n}\left(a\right)=\mu \), כלומר האם לכל \( \varepsilon>0 \) קיים \( N \) כך שלכל \( n>N \) מתקיים \( \left|\overline{X}_{n}\left(a\right)-\mu\right|<\varepsilon \). לכל \( a \) במרחב המדגם שלנו התשובה לשאלה הזו היא או “כן” או “לא”. החוק החזק של המספרים הגדולים אומר שקבוצת כל ה-\( a \)-ים שעבורה התשובה היא “לא” היא ממידה אפס (זה לא אומר שזה לא יכול לקרות; זה אומר שזה זניח).

אני לא אוכיח כאן את חוק המספרים הגדולים; אני בעיקר משתמש בו כדי לתת מוטיבציה לסיבה שבגללה מושג התוחלת קופץ לנו לפרצוף ודורש שנגדיר אותו. יש עוד שימושים דומים לתוחלת, כשהפשוט שבהם הוא כנראה אי שוויון מרקוב: אם \( X \) הוא משתנה מקרי שמקבל רק ערכים אי-שליליים ו-\( a>0 \) כלשהו, אז

\( P\left(X\ge a\right)\le\frac{\text{E}\left[X\right]}{a} \)

בניסוח שקול שקצת יותר מאפשר להבין מה הקטע אפשר להכניס את התוחלת לתוך אי השוויון:

\( P\left(X\ge a\cdot\text{E}\left[X\right]\right)\le\frac{1}{a} \)

כלומר, זה נותן הערכה גסה לשאלה מה הסיכוי ש-\( X \) יהיה גדול מפי 2 התוחלת שלו (פחות מחצי), מפי 3 התוחלת שלו (פחות משליש) וכו’. זו באמת הערכה גסה, אבל לעתים קרובות היא מספיקה כדי להוכיח את מה שרוצים לעשות באותו רגע ולכן, בנוסף לפשטות שלו, אי השוויון הזה הוא כלי שימושי מאוד.

ההוכחה של אי שוויון מרקוב מצחיקה בכמה שהיא פשוטה. אני מגדיר משתנה מקרי \( I \) שהוא מה שנקרא אינדיקטור: משתנה מקרי שמקבל או 0 או 1, ולכן בעצם נותן “אינדיקציה” לכך שאירוע מסוים קרה או לא. במקרה שלנו:

\( I=\begin{cases} 1 & X\ge a\\ 0 & X<a \end{cases} \)

התוחלת של אינדיקטור, ממש על פי ההגדרה, היא ההסתברות שהאירוע שנותן 1 קרה, כלומר \( E\left[I\right]=P\left(X\ge a\right) \). עכשיו, שימו לב ש-\( I\le\frac{X}{a} \) ותאמינו לי שאפשר פשוט לקחת תוחלת לשני האגפים ולהוציא את הקבוע החוצה, ונקבל

\( P\left(X\ge a\right)=E\left[I\right]=\frac{E\left[X\right]}{a} \)

אתם כמובן לא אמורים להאמין לי שפשוט אפשר לעשות את זה, אבל אני לא אוכיח את זה הפעם. את הקטע עם “להוציא את הקבוע החוצה” אפשר להכליל - התוחלת מקיימת תכונה מועילה מאוד שנקראת לינאריות: אם \( X,Y \) הם משתנים מקריים כלשהם (שיכולים להיות גם תלויים) ו-\( \alpha,\beta \) הם קבועים מספריים, אז \( \text{E}\left[\alpha X+\beta Y\right]=\alpha\text{E}\left[X\right]+\beta\text{E}\left[Y\right] \) (ואפשר להכליל את זה לסכום סופי כלשהו של משתנים מקריים).

הראיתי את המושג האבסטרקטי של תוחלת ואיזו דוגמא מסכנה עם הטלת קוביה, אבל זה לא מספיק, בואו נראה דוגמא קונקרטית - מה שנקרא התפלגות בינומית. בהתפלגות בינומית יש לנו ניסוי בסיסי שחוזר על עצמו עם הסתברות \( p \) להצליח ו-\( q=1-p \) להיכשל בכל פעם; כבר ראינו שאם חוזרים על הניסוי \( n \) פעמים אז ההסתברות לקבל בדיוק \( k \) הצלחות היא \( p\left(X=k\right)={n \choose k}p^{k}q^{n-k} \). לכן, התוחלת של המשתנה המקרי הזה היא

\( \text{E}\left[X\right]=\sum_{k=0}^{n}k{n \choose k}p^{k}q^{n-k} \)

יש טריק מתמטי לא מסובך שמאפשר לחשב את הסכום הזה, אבל למרבה השמחה הוא עובד באופן קצת יותר כללי ויאפשר לחשב לא רק את \( \text{E}\left[X\right] \) אלא גם את \( \text{E}\left[X^{t}\right] \) לכל חזקה טבעית \( t \), וזה הולך לעזור לנו בקרוב (הערכים \( \text{E}\left[X^{t}\right] \) נקראים המומנטים של המשתנה המקרי \( X \) ויש להם חשיבות באופן כללי). הסכום במקרה הכללי יותר הזה הוא

\( \text{E}\left[X^{t}\right]=\sum_{k=0}^{n}k^{t}{n \choose k}p^{k}q^{n-k} \)

כי הדרך היחידה שבה הערך \( k^{t} \) יכול להתקבל על ידי המשתנה \( X^{t} \) היא אם הערך \( k \) יתקבל על ידי המשתנה \( X \), כלומר ההסתברות היא אותו דבר וכל מה שהשתנה הוא שמופיע בתחילת הסכום \( k^{t} \) במקום סתם \( k \).

עכשיו, קודם כל שימו לב שאם \( k=0 \) האיבר שמתאים למקרה הזה הוא פשוט אפס, כלומר אפשר לכתוב

\( \text{E}\left[X^{t}\right]=\sum_{k=1}^{n}k^{t}{n \choose k}p^{k}q^{n-k} \)

הטריק הוא עכשיו לפתוח את ההגדרה של \( {n \choose k}=\frac{n!}{k!\left(n-k\right)!} \) ולקבל

\( k{n \choose k}=k\cdot\frac{n!}{k!\left(n-k\right)!}=n\frac{k}{k!}\cdot\frac{\left(n-1\right)!}{\left(n-k\right)!}=n\frac{\left(n-1\right)!}{\left(k-1\right)!\left(n-k\right)!}=n{n-1 \choose k-1} \)

נציב את זה אצלנו ועל הדרך נוציא \( p \) אחד החוצה כדי להקטין את החזקה של \( p \) באחד:

\( \sum_{k=1}^{n}k^{t}{n \choose k}p^{k}q^{n-k}=np\sum_{k=1}^{n}k^{t-1}{n-1 \choose k-1}p^{k-1}q^{n-k} \)

עכשיו נבצע החלפת משתנה \( i=k-1 \). כלומר כש-\( k=1 \) אז \( i=0 \) ואילו כש-\( k=n \) אז \( i=n-1 \), ולכן

\( np\sum_{k=1}^{n}k^{t-1}{n-1 \choose k-1}p^{k-1}q^{n-k}=np\sum_{i=0}^{n-1}\left(i+1\right)^{t-1}{n-1 \choose i}p^{i}q^{n-i-1} \)

עכשיו בואו נסתכל על הביטוי שקיבלנו בסכום:

\( \sum_{i=0}^{n-1}\left(i+1\right)^{t-1}{n-1 \choose i}p^{i}q^{n-i-1} \)

חוץ מה-\( \left(i+1\right)^{t-1} \) בהתחלה זה נראה בדיוק כמו סכום על ההסתברויות של משתנה בינומי אחר שאסמן \( Y \), עם \( n-1 \) נסיונות ואותן הסתברויות הצלחה וכישלון \( p,q \). ה-\( \left(i+1\right)^{t-1} \) בתחילת הסכום נראה קצת מוזר אבל אם חושבים על זה, רואים שהסכום פשוט שווה אל \( \text{E}\left[\left(Y+1\right)^{t-1}\right] \). כלומר קיבלנו

\( \text{E}\left[X^{t}\right]=np\text{E}\left[\left(Y+1\right)^{t-1}\right] \)

במקרה הבסיס שבו \( t=1 \) אז \( \left(Y+1\right)^{t-1} \) הוא פשוט הקבוע 1 ולכן התוחלת שלו היא 1 ולכן קיבלנו

\( \text{E}\left[X\right]=np \)

אבל עם הנוסחה נוכל לחשב בקלות גם את \( \text{E}\left[X^{2}\right] \), למשל. כי:

\( \text{E}\left[X^{2}\right]=np\text{E}\left[Y+1\right]=np\left(\text{E}\left[Y\right]+1\right)=np\left(\left(n-1\right)p+1\right) \)

כאן למשל השתמשתי בלינאריות של התוחלת. אבל למה בעצם \( \text{E}\left[X^{2}\right] \) מעניין אותי? או, אנחנו בדיוק מגיעים אל זה.

שונות וסטיית תקן

ראינו זה עתה שאם \( X \) הוא משתנה בינומי שמתאר ספירה של הצלחות בניסוי שחוזר על עצמו \( n \) פעמים עם הסתברות הצלחה \( p \) בכל פעם, אז התוחלת שלו היא \( np \). ראינו גם שהתוחלת של התוצאה בהטלת קובייה הוגנת היא \( 3.5 \). אז אם נבחר את הפרמטרים של \( X \) להיות \( n=7,p=\frac{1}{2} \) נקבל שהתוחלת של \( X \) היא גם \( 3.5 \): התוחלת של “הטל מטבע הוגן 7 פעמים וספור כמה פעמים התקבל עץ” היא אותה תוחלת כמו של “הטל קוביה הוגנת ובדוק מה יצא”. אבל אלו בבירור ניסויים שונים למדי זה מזה - בהטלת קוביה לכל תוצאה יש אותו סיכוי, ובניסוי הבינומי אין סימטריה כזו ויש גם ערכים כמו 0 ו-7 שלא יכולים לצוץ בהטלת קוביה. עוד משחק שאני יכול לעשות הוא לשחק “הטלת מטבע” עם מטבע שהערך של צד אחד שלו הוא 0 והערך של הצד השני שלו הוא 7: גם במקרה הזה נקבל תוחלת \( 3.5 \).

אם אני לוקח את שלושת הניסויים השונים הללו ועושה עליהם את מה שעשיתי בפוסט הראשון בסדרה, כלומר מצייר את העקומה של ההתפלגות הנורמלית שמקרבת את מה שמקבלים אם חוזרים על הניסוי 100 פעמים וסוכמים את התוצאות - זה מה שאני אקבל:

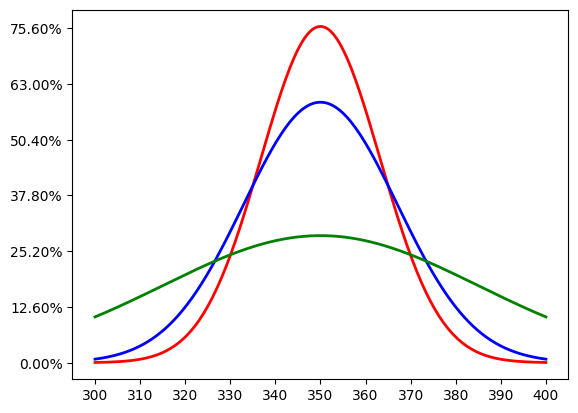
יש כאן שלוש עקומות נורמליות, שניסיתי לצבוע בצבעים שונים כדי להבדיל ביניהן (אבל אני לא בטוח אם הצבעים ייראו שונים לכל הקוראים). העקומה שמגיעה הכי גבוהה, שצבועה באדום, מתאימה למשתנה הבינומי; האמצעית, שצבועה בכחול, מתאימה למשתנה של הקוביה; והתחתונה, הירוקה, מתאימה למשתנה של המטבע עם הערכים 0 ו-7.

מה הסיבה להבדל? ככל שעקומה נורמלית היא יותר גבוהה, כך זה אומר שרוב ההסתברות שהיא מייצגת מתארת טווח קטן יחסית. המקרה הקיצוני ביותר הוא המשתנה המקרי שפשוט מחזיר \( 3.5 \) תמיד, שיתואר על ידי קו אנכי בודד בדיוק ב-\( 350 \). הסיבה שהעקומה הירוקה, הנמוכה, היא כל כך “רחבה” היא שהניסוי שהיא מתארת הוא בעל רק שני ערכים, ששניהם במרחק לא זניח מהתוחלת עצמה ולכן כל אי-אחידות בתוצאות של ההגרלה (נניח, יתרון של 9 הטלות שנתנו 7 במקום 0) “מושך” את הסכום הכולל רחוק מהממוצע הצפוי. זו האינטואיציה, אבל אנחנו רוצים את המתמטיקה הקונקרטית - מדד מספרי שיאפשר לנו לתאר עד כמה סטייה מהתוחלת היא משהו נפוץ או נדיר.

אם \( X \) הוא משתנה מקרי ו-\( \mu=\text{E}\left[X\right] \) היא התוחלת שלו, אפשר להסתכל על משתנה מקרי חדש, \( Y=X-\mu \). זה המשתנה המקרי המקורי, רק שעכשיו הוא מנורמל כך שהתוחלת שלו תהיה 0. מכיוון שמה שמעניין אותנו הוא גודל ה”סטייה מהממוצע”, והגודל הזה הוא פשוט \( \left|Y\right| \), אפשר לשאול את עצמנו מה הסטייה הממוצע מהממוצע, כלומר \( \text{E}\left[\left|Y\right|\right] \). זה אמנם מדד מתבקש למדי, אבל הוא פחות מועיל מאשר אפשר היה לקוות. פונקציית הערך המוחלט היא לא “נחמדה” מבחינה מתמטית - בפרט, היא לא גזירה ב-0. עניין אחר הוא שהיא מאותו סדר גודל כמו \( Y \) ודווקא יש עניין בכך שנעבור אל “סדר הגודל הבא”. זה מוביל אותנו להגדרה שאולי נראית פחות טבעית ממבט ראשון אבל היא שימושית בצורה בלתי נתפסת: \( \text{Var}\left(X\right)=\text{E}\left[Y^{2}\right]=\text{E}\left[\left(X-\mu\right)^{2}\right] \) כאשר Var כאן הוא קיצור של Variance, שונות. העלאה בריבוע נותנת לנו את היתרונות שרצינו: היא משמשת בתור סוג של ערך מוחלט כי \( a^{2} \) זה אותו דבר כמו \( \left|a\right|^{2} \); זה עובר לסדר הגודל השני (חשבו על העלאה בריבוע בתור העלאה של סדר הגודל; איך זה באמת חשוב, נראה אחר כך). וזו פונקציה נחמדה לעבודה מבחינה מתמטית.

דבר אחד שקל לראות הוא נוסחה אלטרנטיבית לתוחלת שמתקבלת מכך שפותחים במפורש את הביטוי, מה שאני אדגים במקרה של הסתברות בדידה:

\( \text{Var}\left(X\right)=\text{E}\left[\left(X-\mu\right)^{2}\right]=\sum_{a}p\left(X=a\right)\left(a-\mu\right)^{2}= \)

\( =\sum_{a}P\left(X=a\right)a^{2}-2\mu\sum_{a}P\left(X=a\right)a+\mu^{2}\sum_{a}P\left(X=a\right)= \)

\( =\text{E}\left[X^{2}\right]-2\mu\text{E}\left[X\right]+\mu^{2}=\text{E}\left[X^{2}\right]-2\mu^{2}+\mu^{2}=\text{E}\left[X^{2}\right]-\mu^{2}=\text{E}\left[X^{2}\right]-\text{E}\left[X\right]^{2} \)

בואו נוודא שהבנו מה הולך פה. את הביטוי המקורי פיצלתי לשלושה סכומים על פי הפתיחה של הסוגריים \( \left(a-\mu\right)^{2}=a^{2}-2a\mu+\mu^{2} \). הסכום הראשון היה \( \sum_{a}P\left(X=a\right)a^{2} \) שזו ממש ההגדרה הפורמלית של \( \text{E}\left[X^{2}\right] \). הסכום השני היה קבוע כפול \( \sum_{a}P\left(X=a\right)a \) שזו ההגדרה הפורמלית של \( \text{E}\left[X\right] \), ואחרי שהשתמשתי בכך ש-\( \text{E}\left[X\right]=\mu \) קיבלתי את הערך שרציתי.

הנוסחה \( \text{Var}\left(X\right)=\text{E}\left[X^{2}\right]-\text{E}\left[X\right]^{2} \) בהחלט נראית לי יפה ושימושית יותר מאשר \( \text{E}\left[\left(X-\mu\right)^{2}\right] \); היא מציגה את השונות בעזרת שני המומנטים הראשונים של \( X \), שיותר קל לחשב ישירות. עשיתי את זה קודם, בדוגמה למעלה, עבור התפלגות בינומית: קיבלנו ש-\( \text{E}\left[X\right]=np \) ואילו \( \text{E}\left[X^{2}\right]=np\left(\left(n-1\right)p+1\right) \), ולכן עכשיו אני אוכל לחשב בקלות את השונות של התפלגות בינומית:

\( \text{Var}\left(X\right)=np\left(\left(n-1\right)p+1\right)-\left(np\right)^{2}=np\left[\left(n-1\right)p+1-np\right]= \)

\( =np\left(np-p+1-np\right)=np\left(1-p\right)=npq \)

ובסופו של דבר קיבלנו ביטוי פשוט ואלגנטי מאוד עבור השונות. עבור המשתנה הבינומי הקונקרטי שתיארתי למעלה, של ספירת העצים ב-7 הטלות של מטבע הוגן, הפרמטרים היו \( n=7,p=q=0.5 \) ולכן התוחלת היא \( \frac{7}{2}=3.5 \) כפי שכבר ראינו, והשונות היא \( \frac{7}{4}=1.75 \).

עבור תוחלת ראיתי שמתקיימת תכונת לינאריות מועילה מאוד: \( \text{E}\left[\alpha X+\beta Y\right]=\alpha\text{E}\left[X\right]+\beta\text{E}\left[Y\right] \). עבור שונות אין לנו משהו עד כדי כך נוח, אבל עדיין יש לנו נוסחה מועילה: \( \text{Var}\left(\alpha X+\beta\right)=\alpha^{2}\text{Var}\left(X\right) \). כלומר - חיבור של קבוע לא משפיע (חיבור של משתנה מקרי אחר מסבך את הכל), והכפלה בקבוע מכילה את השונות באותו קבוע בריבוע.

עכשיו, העובדה שהשונות כוללת העלאה בריבוע היא מצד אחד חיובית מהסיבות שציינתי, ומצד שני אנחנו עדיין רוצים לקבל מדד דומה שהוא “מסדר גודל אחד פחות” ובכל זאת מתנהג נחמד. דרך פשוטה לקבל את זה היא להגדיר \( \sigma=\sqrt{\text{Var}\left(X\right)} \) - גם פונקציית השורש היא נחמדה יחסית, ומורידה את סדר הגודל. ה-\( \sigma \) הזה חשוב מספיק כדי שיקבל שם בפני עצמו: סטיית התקן של \( X \), ולעתים קרובות יותר נוח פשוט לכתוב \( \sigma^{2} \) בתור השונות של \( X \) במקום \( \text{Var}\left(X\right) \). את התוצאה שראינו לפני רגע אפשר לתאר גם בתור “אם כופלים את \( X \) ב-\( \alpha \) כופלים את סטיית התקן של \( X \) ב-\( \alpha \)”.

בואו נראה עכשיו שימוש בשונות כדי לשפר את היכולת שלנו להבין את \( X \) בעזרת מעין שדרוג של אי-שוויון מרקוב שלוקח גם את השונות בחשבון ונקרא אי-שוויון צ'בישב.

הרעיון הוא כזה. כזכור, אי-שוויון מרקוב מדבר על משתנה מקרי אי-שלילי \( X \) ועבורו, לכל \( a>0 \) , הוא נותן

\( P\left(X\ge a\right)=\frac{E\left[X\right]}{a} \)

עכשיו, אם \( X \) הוא משתנה מקרי כלשהו, לאו דווקא אי שלילי, אז בואו ניזכר ש-\( \text{Var}\left(X\right) \) הוגדרה בתור התוחלת של משתנה מקרי שהוא כן אי-שלילי: \( \sigma^{2}=\text{Var}\left(X\right)=\text{E}\left[Z\right] \) כאשר \( Z=\left(X-\mu\right)^{2} \). על ה-\( Z \) הזה אני כן יכול להשתמש באי שוויון מרקוב; בואו נראה מה קורה אם אנחנו לוקחים \( k>0 \) כלשהו ומשתמשים במרקוב עם \( a=k^{2} \):

\( P\left(Z\ge a\right)\le\frac{\text{E}\left[Z\right]}{a} \)

כלומר

\( P\left(\left(X-\mu\right)^{2}\ge k^{2}\right)\le\frac{\text{E}\left[\left(X-\mu\right)^{2}\right]}{k^{2}}=\frac{\sigma^{2}}{k^{2}} \)

עכשיו, בואו נביט על \( \left(X-\mu\right)^{2}\ge k^{2} \). הדבר הזה קורה אם ורק אם \( \left|X-\mu\right|\ge k \), ולכן ההסתברות של שני אי השוויונים זהה, כלומר אני יכול לכתוב

\( P\left(\left|X-\mu\right|\ge k\right)\le\frac{\sigma^{2}}{k^{2}} \)

זה אי-שוויון צ’בישב. כמו עם אי-שוויון מרקוב, לפעמים קל יותר להבין מה הוא אומר אם “מכניסים את סטיית התקן אל אי השוויון”, כלומר אם אני מנסח אותו על ידי

\( P\left(\left|X-\mu\right|\ge k\sigma\right)\le\frac{1}{k^{2}} \)

אם למשל נציב \( k=2 \) נקבל את הטענה הבאה: לכל משתנה מקרי \( X \), הסיכוי שהוא יקבל ערך שהמרחק שלו מהתוחלת של \( X \) הוא יותר משתי סטיות תקן הוא \( \frac{1}{4}=25\% \). לי זה מרגיש כמו טענה כללית להפתיע, כי לא משנה בכלל כמה \( X \) מורכב ומתוחכם - מרגע שחישבנו את התוחלת ואת סטיית התקן שלו, אנחנו יודעים בדיוק מה האיזור שבו 75\% מהערכים ש-\( X \) נותן הולכים ליפול. יותר מכך - בגלל שבמכנה יש \( k^{2} \) ולא \( k \), זה אומר לנו שהסיכוי של מישהו להיות במרחק של הרבה סטיות תקן צונח מהר - צונח באופן ריבוע. אם הסיכוי להיות במרחק 2 סטיות תקן היה 25\%, עבור 3 סטיות תקן הוא נופל אל \( \frac{1}{9}=11.111\ldots\% \), ועבור 4 סטיות תקן הוא כבר \( \frac{1}{16}=6.25\% \) וכשנרצה להיות במרחק 10 סטיות תקן הסיכוי כבר יהיה \( \frac{1}{100}=1\% \), וכן הלאה. ככל שסטיית התקן של \( X \) גדולה יותר כך האיזור שבו רוב הערכים שלו יכולים ליפול הוא רחב יותר, אבל אם נחלק את המרחב לאיזורים שהרוחב של כל אחד מהם הוא \( \sigma \), נדע בדיוק מה ההסתברות של איבר ליפול בכל אחד מהאיזורים הללו. זו המחשה חזקה מאוד לכוח שיש לשני מספרים בודדים \( \mu,\sigma \) לתאר את \( X \).

חזרה אל ההתפלגות הנורמלית

עכשיו כשהכרנו את המושגים של תוחלת ושונות/סטיית תקן אפשר לחזור סוף סוף אל ההתפלגות הנורמלית. הגדרתי אותה בעזרת פונקציית צפיפות ההסתברות \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \), ועכשיו אפשר לחזור למה שאמרתי בתחילת הפוסט אבל כשיש לנו את ההגדרות הרלוונטיות: ה-\( \mu \) וה-\( \sigma \) הללו הם בדיוק התוחלת וסטיית התקן של ההתפלגות הנורמלית ש-\( \mu,\sigma \) הם הפרמטרים שלה. כלומר, אנחנו מגדירים משתנה מקרי \( N\left(\mu,\sigma\right) \) על ידי פונקציית הצפיפות \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \), וכשנחשב את התוחלת וסטיית התקן שלו הנוסחאות יתנו לנו בדיוק \( \mu,\sigma \), וזה בדיוק מה שאני רוצה להראות עכשיו. דבר אחד שכדאי לשים אליו לב לפני כן הוא שאפשר להגדיר את ההתפלגות הנורמלית גם בלי להגדיר בכלל סטיית תקן: הרי \( \frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}}=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \) ולכן אם היינו למשל בוחרים לסמן את השונות שאנחנו רוצים ב-\( \tau \) אז היינו מקבלים שהתפלגות נורמלית עם תוחלת \( \mu \) ושונות \( \tau \) מתוארת על ידי \( f\left(x\right)=\frac{1}{\sqrt{2\pi\tau}}e^{-\left(x-\mu\right)^{2}/2\tau} \). הבחירה להשתמש ב-\( \sigma \) היא עניין של קונבנציה (ומן העבר השני, אנשים גם כותבים לפעמים \( \frac{1}{\sqrt{2\pi}\sigma}e^{-\left(\frac{x-\mu}{\sigma}\right)^{2}/2} \) כדי שהנוסחה תכלול רק את \( \sigma \) ולא את \( \sigma^{2} \)).

ראשית, הנה טריק מועיל כדי למצוא תוחלת ושונות של דברים. כזכור, ראינו

\( \text{E}\left[\alpha X+\beta Y\right]=\alpha\text{E}\left[X\right]+\beta\text{E}\left[Y\right] \)

\( \text{Var}\left(\alpha X+\beta\right)=\alpha^{2}\text{Var}\left(X\right) \)

אז באופן כללי, אם אנחנו רוצים למצוא תוחלת ושונות של משתנה \( X \) אבל זה קשה לנו, אפשר לנסות להגדיר משתנה “מנורמל” \( Z=\frac{X-\mu}{\sigma} \) ולקבל

\( \text{E}\left[X\right]=\sigma\text{E}\left[Z\right]+\mu \)

\( \text{Var}\left(X\right)=\sigma^{2}\text{Var}\left(Z\right) \)

אני אשתמש בזה במקרה שלנו. נניח ש-\( X \) הוא משתנה מקרי שמתפלג נורמלית עם פרמטרים \( \mu,\sigma \), כלומר \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(\frac{x-\mu}{\sigma}\right)^{2}/2} \). אם אני מגדיר את המשתנה החדש \( Z=\frac{X-\mu}{\sigma} \) אני אקבל פונקציית צפיפות הסתברות \( f\left(z\right)=\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2} \). כדי לראות את זה נשים לב לכך ש:

\( P\left(a\le Z\le b\right)=P\left(\sigma a+\mu\le X\le\sigma b+\mu\right)=\int_{\sigma a+\mu}^{\sigma b+\mu}\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(\frac{x-\mu}{\sigma}\right)^{2}/2}dx \)

ועל האינטגרל הזה אפשר לבצע את החלפת המשתנים \( z=\frac{x-\mu}{\sigma} \) שנותנת לנו \( dz=\frac{dx}{\sigma} \), כלומר מקבלים \( P\left(a\le Z\le b\right)=\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2} \).

המסקנה? אם \( X \) התפלג נורמלית עם פרמטרים \( \mu,\sigma \) אז \( Z=\frac{X-\mu}{\sigma} \) מתפלג נורמלית עם פרמטרים \( 0,1 \). עכשיו אני אוכיח ש-\( \text{E}\left[Z\right]=0 \) וש-\( \text{Var}\left(Z\right)=1 \) ואז אסיק ש-

\( \text{E}\left[X\right]=\sigma\text{E}\left[Z\right]+\mu=\mu \)

\( \text{Var}\left(X\right)=\sigma^{2}\text{Var}\left(Z\right)=\sigma^{2} \)

וזו הטענה הכללית שאני רוצה.

עכשיו, \( \text{E}\left[Z\right] \) זה קל - זה יוצא 0 בגלל שפונקציית הצפיפות \( \frac{1}{\sqrt{2\pi}}e^{-z^{2}/2} \) היא סימטרית ביחס ל-0 כי \( z^{2} \) היא פונקציה סימטרית ביחס ל-0. זה הופך את האינטגרל שמחשבים עבור התוחלת לאינטגרל של פונקציה אנטיסימטרית בגלל ההכפלה ב-\( z \). הנה משהו פורמלי קצת יותר:

\( \text{E}\left[Z\right]=\int_{-\infty}^{\infty}z\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2}=\lim_{a\to\infty}\int_{-a}^{a}z\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2}= \)

\( =\frac{1}{\sqrt{2\pi}}\lim_{a\to\infty}\left.e^{-z^{2}/2}\right|_{-a}^{a}=\frac{1}{\sqrt{2\pi}}\lim_{a\to\infty}\left(e^{-a^{2}/2}-e^{-a^{2}/2}\right)= \)

\( \frac{1}{\sqrt{2\pi}}\lim_{a\to\infty}0=0 \)

המעבר מאינטגרל אינסופי בשני הכיוונים לגבול כש-\( a \) שואף לאינסוף של אינטגרל מ-\( -a \) אל \( a \) הוא לא תקין באופן כללי אבל בפוסט הקודם כבר אמרנו שבמקרה הנוכחי זה תקין (אבל אפשר להסתדר גם אם עושים שני אינטגרלים, זה פשוט יוצא מסורבל יותר). אז זה מסיים עם התוחלת ומראה שכדי לחשב את השונות צריך פשוט לחשב את \( \text{E}\left[Z^{2}\right] \). זה יהיה טיפה יותר מסובך ויצריך טריק אינטגרציה סטנדרטי: אינטגרציה בחלקים. בואו ניזכר את הטריק הזה הולך.

עבור נגזרות, אחת מהנוסחאות החשובות ביותר היא מה יוצאת הגזירה של מכפלה של פונקציות: \( \left(uv\right)^{\prime}=u^{\prime}v+uv^{\prime} \). זו אחת מהנוסחאות הבודדות שצרובות בי עוד מהתיכון. עכשיו, אם מעבירים אגפים, מקבלים מן הסתם \( u^{\prime}v=\left(uv\right)^{\prime}-uv^{\prime} \) ואם (ועכשיו אני עובר לקצת נפנוף ידיים) לוקחים אינטגרל לשני האגפים מקבלים \( \int u^{\prime}v=uv-\int uv^{\prime} \). לכן אם קשה לנו לבצע אינטגרציה לפונקציה שלנו, אנחנו בודקים אם יש דרך נוחה לפרק אותה למכפלה של שתי פונקציות שלאחת מהן (שאנחנו קוראים לה \( u^{\prime} \)) כן קל לנו להוציא אינטגרל, את השניה (שאנחנו קוראים לה \( v \)) קל לנו לגזור, ואז אנחנו מקווים שאחרי שנוציא אינטגרל לאחת ונגזרת לשניה, המכפלה של זה תהיה משהו שקל לנו למצוא לו אינטגרל. לפעמים זה נכשל קטסטרופלית ולפעמים, כמו עכשיו, זה עובד יופי. הרי

\( \text{E}\left[Z^{2}\right]=\int_{-\infty}^{\infty}z^{2}\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2} \)

ולפני רגע, בחישוב התוחלת, ראינו שקל לנו להוציא את האינטגרל של \( u^{\prime}=z\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2} \) והאינטגרל יוצא \( u=\frac{1}{\sqrt{2\pi}}e^{-z^{2}/2} \), וכמובן שאת \( v=z \) קל לגזור ולקבל \( v^{\prime}=1 \). כמו כן \( uv \) הולך לצאת בדיוק הביטוי לתוחלת שראינו לפני רגע שהאינטגרל שלו הוא 0, ו-\( uv^{\prime} \) הולך לצאת בדיוק פונקציית הצפיפות המקורית שראינו כבר (בפוסט הקודם, ולא בקלות) שהאינטגרל שלה יוצא 1. זה מסיים (בנפנוף ידיים) את ההוכחה.

אז אם לסכם עוד סיכום ביניים: אנחנו מנסים להבין למה פונקציית הצפיפות של ההתפלגות הנורמלית נראית ככה: \( f\left(x\right)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\left(x-\mu\right)^{2}/2\sigma^{2}} \). בינתיים הבנו ש-\( \pi \) שם בתור קבוע נרמול שמגיע בבסיסו מכך ש-\( 2\pi \) הוא היקף מעגל היחידה; ואנחנו רואים עכשיו ש-\( \mu,\sigma \) שמופיעים פה מבטיחים שהתוחלת וסטיית התקן של ההתפלגות יהיו \( \mu,\sigma \); אבל עדיין לא ברור לנו הדבר העיקרי - מה הקטע עם ה-\( e \) הזה? למה הצורה של העקומה היא (עד כדי קבועים) \( e^{-x^{2}} \)? אני לא רואה איך לענות לשאלה הזו בלי להגיע אל היעד שלנו: משפט הגבול המרכזי. את זה נעשה בפוסט הבא.