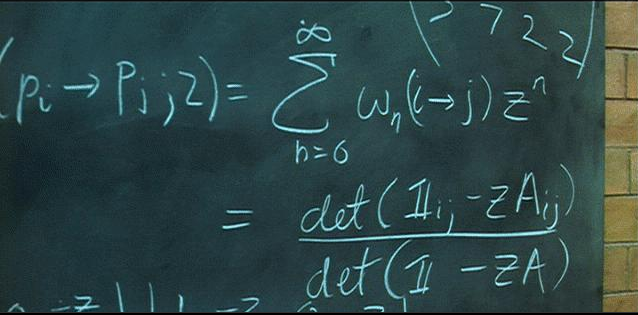בעיית וויל האנטינג

נקודת המוצא העלילתית של הסרט “סיפורו של וויל האנטינג” (וכאן אני עומד לגלות טיפה מפרטי העלילה - אבל לא משהו שלא מתגלה ממילא בעשר הדקות הראשונות של הסרט, ואיננו מהותי כל כך) היא חידה מתמטית שפרופסור ב-MIT נותן לסטודנטים בקורס מתקדם שלו, בתקווה שמישהו מהם יצליח לפתור אותה עד סוף הסמסטר ובכך יכנס להיכל התהילה. את החידה פותר כבדרך אגב דווקא השרת של הבניין, מה שחושף אותו כגאון מתמטי חבוי, וכל השאר היסטוריה. אולם מהי החידה שבחרו יוצרי הסרט לתת? מסיבות השמורות עמם, הם החליטו לאפשר לקהל לראות את החידה כתובה במלואה על הלוח, כמו גם את הפתרון. אציג את החידה, ולאחר מכן אסביר כיצד פותרים אותה.

ובכן, נתון גרף (ראו תמונה) ונשאלות עליו השאלות הבאות:

1. מצאו את מטריצת השכנויות \( A \) של הגרף \( G \).
2. מצאו את המטריצה שנותנת את מספר המסלולים מאורך 3 ב-\( G \).
3. מצאו את הפונקציה היוצרת של המסלולים מ-\( i \) אל \( j \).
4. מצאו את הפונקציה היוצרת של המסלולים מ-\( 1 \) אל \( 3 \).

כבר בניסוח שלה, השאלה מרגישה יותר כמו תרגיל סטנדרטי ולא כמו אתגר מתמטי כביר. ואכן, כפי שאראה בקרוב, מדובר בשאלה פשוטה למדי בתורת הגרפים האלגברית - מה שקצת מוזר, בהתחשב בכך שהמרצה מציג את החידה בסרט בתור “Advanced Fourier System”, בסוף שיעור שעוסק באנליזת פורייה (דהיינו, המרצה ממלמל משהו על משפט פרסבל, ששייך לאנליזת פורייה). אני סקרן לדעת איך התגלגלה השאלה הספציפית הזו לתסריט הסרט ואשמח אם מישהו שיודע זאת יספר.

הבה ונבהיר מה בעצם רוצים בשאלה הזו. ראשית, נותנים גרף \( G \) על ידי ציור. גרף מורכב (כפי שניתן לראות בציור) מאוסף של עיגולים - “הצמתים” - וקווים שמחברים חלק מהם - “הקשתות”. כך למשל בין הצומת 1 לצומת יש קשת אחת, בין 2 ו-3 יש שתי קשתות, בין 1 ו-3 אין אף קשת וכו’. מסלול בגרף מתחיל מצומת א’, ואז מבצע סדרת “צעדים”, כשכל צעד הוא מעבר מהצומת הנוכחי לצומת שמחובר לצומת הנוכחי בקשת. אם יש כמה קשתות בין שני צמתים, לרוב זה נחשב כאילו יש מספר דרכים לעבור בין שני הצמתים. כך למשל אפשר לקבל את המסלולים הבאים מצומת 1 לצומת 3 מאורך 2: ראשית הולכים מצומת 1 לצומת 2, ולאחר מכן הולכים מ-2 ל-3, אלא שיש שתי דרכים לעשות זאת כי יש שתי קשתות בין 2 ו-3. לכן יש שני מסלולים מאורך 2 מ-1 אל 3.

יש עוד שני מושגים להסביר - “מטריצה” ו”פונקציה יוצרת”, שניהם מושגים בסיסיים יחסית במתמטיקה. מטריצה, בהקשר של השאלה הזו, ניתנת לתיאור בתור טבלה של מספרים. כשמדובר על מטריצת השכנויות של גרף מדובר על מטריצה ספציפית, שמקודדת בתוכה את מספר הקשתות בין כל שני צמתים בגרף. הכלל הוא פשוט: בשורה ה-\( i \) והעמודה ה-\( j \) כתוב מספר הקשתות שמחברות את הצמתים \( i \) ו-\( j \). לכן, מבט מהיר בגרף נותן לנו את המטריצה המבוקשת:

\( A=\left(\begin{array}{cccc}0 & 1 & 0 & 1\\1 & 0 & 2 & 1\\0 & 2 & 0 & 0\\1 & 1 & 0 & 0\end{array}\right) \)

עד כאן, שום דבר מורכב. התחכום מתחיל בשאלה הבאה - מי שלא בקיא בתורת הגרפים האלגברית (או בתחומים אחרים שבהם אותם רעיונות מופיעים, כמו למשל הילוכים מקריים בדידים) יכול לתהות מה הקשר בין מטריצה ובין מספר המסלולים ומה הולך כאן. כאן נכנסת לתמונה הפעולה של כפל מטריצות. מכיוון שמושג המטריצה, והמוטיבציה להגדרת כפל המטריצות באופן שבו הוא מוגדר, ראויים שניהם לפוסט שלם, לא אכנס לכך בינתיים אלא אניח כי ההגדרות מוכרות כבר לקורא (ועם מי שטרם יודעים הסליחה). כדי לראות כיצד כפל מטריצות עוזר לנו ניאלץ לשלוף את ההגדרה הפורמלית-טכנית של הכפל. אם נכפול את \( A \) בעצמה, אז בקוארדינטה ה-\( i,j \) של המכפלה נקבל את \( \sum_{k=1}^{n}a_{ik}a_{kj} \). מה המספר הזה אומר? לכל \( k \), \( a_{ik}\cdot a_{kj} \) הוא מכפלה של מספר המסלולים מאורך 1 מ-\( i \) ל-\( k \), במספר המסלולים מאורך 1 מ-\( k \) אל \( j \). כלומר, זה מייצג את מספר הדרכים להגיע בשני צעדים מ-\( i \) אל \( j \) תוך מעבר בצומת הביניים \( k \). כשסוכמים זאת על כל הערכים האפשריים של \( k \) מקבלים את כל הדרכים לעבור מ-\( i \) אל \( j \) ב-2 צעדים.

באופן דומה אם נכפול את \( A^{2} \) ב-\( A \), הקוארדינטה ה-\( i,j \) תהיה סכום של מכפלות, כשכל מכפלה היא של מספר הדרכים להגיע מ-\( i \) אל \( k \) בשני צעדים, ומ-\( k \) אל \( j \) בצעד אחד. אני מקווה שהרעיון ברור: לכל \( m \) טבעי, הקוארדינטה ה-\( i,j \)-ית במטריצה \( A^{m} \) מייצגת את מספר המסלולים מאורך \( m \) מ-\( i \) אל \( j \) (אפילו עבור \( m=0 \) זה עובד: \( A^{0} \) היא על פי הגדרה המטריצה שבה הכניסה ה-\( i,i \) היא 1 לכל \( i \), וה-\( i,j \) היא 0 אם \( i\ne j \), וזה מתאים ל”מסלול מאורך 0” מ-\( i \) לעצמו שפשוט לא מכיל צעדים). מכאן שכדי לענות על שאלה 2 בסך הכל צריך לחשב את \( A^{3} \). זה חישוב טכני לא מעניין במיוחד ואפשר לתת לתוכנות מחשב דוגמת מטלאב לבצע אותו. מקבלים:

\( A^{3}=\left(\begin{array}{cccc}2 & 7 & 2 & 3\\7 & 2 & 12 & 7\\2 & 12 & 0 & 2\\3 & 7 & 2 & 2\end{array}\right) \)

אם משעמם לכם תוכלו לקחת את אחת מהכניסות (רצוי כזו עם מספר נמוך יחסית בתוכה) ולספור ידנית את המסלולים ולראות ששני המספרים זהים. מה שכן, שימו לב למידע המעניין יחסית שבולט מייד מהמטריצה: לא קיים מסלול באורך 3 שמתחיל ונגמר בצומת 3.

המשחק היה נהיה משעשע בהרבה אם היינו שואלים שאלות מהסגנון הבא: נניח שאנחנו יוצאים לטיול “אקראי” על הגרף, ובכל צעד אנחנו בוחרים באקראי את אחת מהקשתות שמחוברות לצומת הנוכחי שלנו. איך יראה הטיול? באילו צמתים נשהה זמן רב יחסית? וכן הלאה. זו דוגמה לסוג השאלות שניתן לשאול על שרשראות מרקוב בדידות, נושא מעניין לכשעצמו; והניתוח של התכונות הללו מתבצע בדיוק באמצעות ניתוח המטריצה \( A \) שלנו, תוך שימוש בכלים של אלגברה לינארית. אלא שזה לא הכיוון שאליו הולכת שאלת וויל האנטינג ולכן לא אמשיך לדבר על כך כרגע.

שתי השאלות הבאות הן בעצם אותו דבר - בשאלה 3 מבקשים משהו כללי, ובשאלה 4 מבקשים מקרה פרטי של המשהו הכללי שיתקבל אחרי הצבה בו. זו גם השאלה הראשונה שנראית מעט מאתגרת, אולי בעיקר כי פונקציות יוצרות הן משהו שלרוב האנשים שכבר יצא להם ללמוד אותו זכור במעומעם בתור “הדבר ההוא מקומבינטוריקה שלא באמת הבנו בשביל מה הוא טוב”. העניין הוא שכל מי שיפתח ספר רציני בקומבינטוריקה יגלה בו את הפתרון הכללי לבעיות מסוג זה.

כתבתי בשעתו פוסט על פונקציות יוצרות ולכן לא אציג אותן כאן שוב. הפוסט ההוא היה מבוא לפוסט שעסק באופן שבו מוצאים את הפונקציה היוצרת של שפה רגולרית, בעזרת האוטומט שלה - רעיון כמעט זהה לרעיון שיש כאן. אוטומט הוא סוג של גרף, וחישוב של אוטומט הוא סוג של מסלול בגרף. מכיוון שבפוסט ההוא נתתי הסברים מפורטים, בפוסט הזה ארשה לעצמי בעיקר לנפנף בידיים.

ובכן, מה שמבקשים מאיתנו הוא הצגה מפורשת לפונקציה \( f\left(x\right)=\sum_{n=0}^{\infty}b_{n}x^{n} \) כאשר \( b_{n} \) הוא מספר המסלולים מ-\( i \) אל \( j \) מאורך \( n \). אם נסמן ב-\( \left[A\right]_{ij} \) את הכניסה ה-\( i,j \) של המטריצה \( i,j \) וננפנף בידיים ממש מהר, נקבל את החישוב הבא: \( \sum_{n=0}^{\infty}b_{n}x^{n}=\sum_{n=0}^{\infty}\left[A^{n}\right]_{ij}x^{n}=\sum_{n=0}^{\infty}\left[\left(Ax\right)^{n}\right]_{ij}=\left[\sum_{n=0}^{\infty}\left(Ax\right)^{n}\right]_{ij}=\left[\frac{1}{1-Ax}\right]_{ij} \).

מה שעשיתי כאן היה להשתמש בוריאציה על הנוסחה הישנה והטובה לסכום סדרה הנדסית אינסופית מתכנסת: \( 1+x+x^{2}+\dots=\frac{1}{1-x} \). כמובן שצריך להצדיק את השימוש בה עבור מטריצות, אבל אמרתי שאנפנף בידיים.

כעת השאלה היא האם באופן כללי בהינתן מטריצה \( B \), יש נוסחה “יפה”עבור הכניסה ה-\( ij \) בהופכית שלה, כלומר \( \left[B^{-1}\right]_{ij} \)? התשובה היא שכן (אם כי “יפה” זה עניין סובייקטיבי כאן) והיא מכונה “כלל קרמר”. הכלל מסתמך על שני מושגים לא פשוטים - מטריצה מצורפת (Adjugate) ודטרמיננטה של מטריצה, ולכן עבור מי שאינו מכיר את המושגים הללו הנוסחה תיראה פשוט כמו אוסף של סימנים חסרי משמעות - אבל זה לא חשוב כל כך לבינתיים. הנקודה היא ששני היצורים הללו ניתנים לחישוב יחסית באופן פשוט. כעת, כלל קרמר אומר כי \( B^{-1}=\frac{\mbox{Adj}B}{\det B} \) (כאן אנו מחלקים מטריצה - \( \mbox{Adj}B \) - בסקלר - \( \det B \)). לכן \( \left[B^{-1}\right]_{ij}=\frac{\left[AdjB\right]_{ij}}{\det B} \). אם רוצים לפשט את הביטוי עוד יותר צריך לחפור בהגדרה של \( \mbox{Adj}B \): הכניסה ה-\( ij \) של \( \mbox{Adj}B \) מוגדרת בתור \( \left(-1\right)^{i+j}M_{ji} \), כאשר \( M_{ji} \) הוא המינור ה-\( ji \)-י של \( B \) - הדטרמיננטה של המטריצה שמתקבלת ממחיקת השורה ה-\( j \) והעמודה ה-\( i \) של \( B \). כאן כנראה וויל משתעמם ומשתמש בסימונים שאיני מכיר, כי הנוסחה הסופית שהוא כותב על הלוח היא \( \frac{\det\left(B_{ij}\right)}{\det B} \) - אני משער שכוונתו זהה לכוונה שלי (למעשה, הוא לא כותב \( B \) אלא \( I-Ax \) כמו שכתבתי קודם - ולמעשה, אפילו לא את זה, אלא \( I-zA \), שכמובן אומר את אותו הדבר בדיוק).

לסיכום, מדובר בשאלה חביבה והפתרון שלה נאה ביותר בכך שהוא מצביע על הקשר שבין תורת הגרפים ובין האלגברה הלינארית; אבל זו בהחלט לא שאלה שפרופסור למתמטיקה צריך להשתאות מכך שמישהו הצליח לפתור.

בהמשך הסרט מציב הפרופסור שאלה נוספת לתלמידיו, כזו ש”לקח לנו יותר משנתיים לפתור”. לרוע המזל, השאלה הזו לא מוצגת בסרט. כל מה שנשאר לנו הוא מה שוויל צועק על כל מה שהפרופסור זורק עליו - “זו בדיחה מזויינת”. אם הכל דומה לחידה הזו, אולי הוא לא כל כך מגזים.