רקורסיה

הבדיחה הידועה אומרת שבמילון ההגדרה של רקורסיה היא “עיין ערך רקורסיה”. אבל כנראה שזה לא מספיק טוב, כי ביקשו ממני פוסט על רקורסיות, וספציפית על רקורסיות במדעי המחשב. כך שהפוסט הזה הולך להיות עם מבוא כללי לא טכני, ואחר כך עם גלישה לפסים טכניים שיכולים להיות מאוד מעניינים עבור מי שמתעניין בדברים הללו ועוד לא מכיר.

אין הגדרה כללית למה זו בדיוק רקורסיה, אבל הרעיון הוא תמיד זהה - משהו שמתואר/מוגדר/מחושב איכשהו באמצעות עצמו. לרוב באמצעות גרסה קצת יותר פשוטה של עצמו, וכמעט תמיד עם בסיס כלשהו לתיאור/הגדרה/חישוב שהוא ישיר ולא דורש את ההפניה העצמית הזו. דוגמה נפוצה בארץ היא ההגדרה (הפשטנית במתכוון) ליהודי - “יהודי הוא מי שנולד לאם יהודיה”. כאן הבירור האם פלוני הוא יהודי מתבצע על ידי הפעלת אותו בירור על אמו של הפלוני. באיזה מובן האם היא “גרסה קצת יותר פשוטה”? התשובה היא שעץ המשפחה שלה קצר יותר. אם נמשיך ונעלה בעץ המשפחה נגיע בסופו של דבר למקרה קצה - מישהו שהיה יהודי למרות שאמו לא הייתה יהודיה - זה מקרה בסיס שלא נכלל בהגדרה הפשטנית שנתתי אבל ההכרח של הקיום שלו מובלע בה. את דוגמת עץ המשפחה אפשר לנצל לעוד רקורסיות - למשל, שני אנשים הם קרובים אם יש להם הורה משותף (זה מקרה בסיס), או אם הורה של אחד מהם הוא קרוב של הורה של השני (זו “הפעלה” של הרקורסיה).

בואו נעבור לדוגמה קלאסית מתחום המתמטיקה - סדרת פיבונאצ’י. הכלל שמגדיר את הסדרה הזו הוא שכל איבר בה שווה לסכום שני האיברים שלפניו, פרט לשני האיברים הראשונים ששניהם פשוט 1 (או לפעמים 0 ו-1 או לפעמים 1 ו-2, זה לא חשוב). זו בבירור הגדרה רקורסיבית: כל איבר בסדרה מוגדר בעזרת איברים “פשוטים” ממנו, כאשר “פשטות” כאן פירושה קרבה גדולה יותר לתחילת הסדרה. למה בעצם שזה ייחשב “פשוט יותר”? כי כדי לחשב את הערך של האיבר השישי בסדרה באמצעות הנוסחה הרקורסיבית נצטרך בסופו של דבר לחשב את ערכם של חמישה איברים אחרים, אלו שלפניו; אבל בשביל לחשב את הערך של האיבר השביעי נצטרך לחשב את ערכם של שישה איברים אחרים, וכן הלאה.

אם כן, כשאני אומר “פשוט יותר” אני לא מתכוון לפי איזה מדד אבסולוטי של פשטות, אלא לפי מעין רמת קרבה לאחד ממקרי הבסיס שבהם החישוב לא דורש הפעלה נוספת של הרקורסיה. עוד דוגמה מתמטית פשוטה היא פונקציית העצרת: !n הוא מכפלת כל המספרים הטבעיים מ-1 ועד n, כאשר מטעמי נוחות מגדירים ש-!0 שווה ל-1. זה מוביל להגדרה רקורסיבית פשוטה: \(  n!=\begin{cases} 1 & n=0\\ n\cdot\left(n-1\right)! & n>0 \end{cases} \)

כמובן, כל הדוגמאות הללו לא מספקות לנו הגדרה חד משמעית של מהי רקורסיה, וברור שיש גמישות באופן שבו אנחנו נותנים את השם הזה לדברים שונים. הביטו בשלט הבא: האם מה שמתואר בו הוא בעל אופי רקורסיבי? יש לנו כאן רחוב שנקרא על שם ישוב שנקרא על שם נביאה (שנקראה על שם בעל חיים? קרוב לודאי שלא, אבל זה משעשע יותר כך). האם זאת רקורסיה? הטהרנים יטענו שלא, כי רקורסיה תהיה רק סיטואציה של “ישוב שנקרא על שם ישוב שנקרא על שם ישוב”, אבל לדעתי אין הכרח כזה. חשבו על תהליך “בירור שם” של דבר מה - אם המשהו קרוי על שם משהו אחר, מבררים מהיכן הגיע שמו של המשהו האחר.

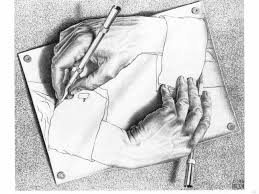
ציור הידיים של אשר, שבראש הפוסט, גם הוא סוג של דוגמה לרקורסיה, למרות שאחת מופרעת שאין לה תנאי עצירה ושרשרת ההפעלות שלה היא לולאה. זה לא משהו מציאותי במיוחד, אבל אשר מעולם לא התיימר להיות מציאותי.

דוגמה אחרת ומבדרת למדי לרקורסיה קיבלנו לפני כמה שנים בקולנוע, בסרט Inception של כריסטופר נולאן. מבלי להיכנס לפרטי עלילה מיותרים, הסרט עוסק בחלומות שמתרחשים בתוך חלומות שמתרחשים בתוך חלומות… ומה שקורה ברמה אחת עשוי להשפיע על מה שקורה ברמה אחרת. כמובן, הרעיון של סיפור שמתרחש במספר “רמות” שונות הוא נפוץ למדי בספרות, לפחות כשמדובר על שתי רמות (זה מה שמכונה “סיפור מסגרת”). ב”גדל, אשר, באך” של דגלאס הופשטטר יש שימוש בסיפור שמתרחש בכמה רמות שונות בדיוק בשביל להדגים את הרעיון של רקורסיה.

בקיצור, אנחנו מכירים רקורסיות משלל הקשרים שונים והן דבר מבדר למדי תמיד. אבל מה זה אומר במדעי המחשב, ספציפית בתכנות (כי יש מושג של “פונקציה רקורסיבית” גם במדעי המחשב התיאורטיים והמושג הזה שונה לגמרי מהמושג המקביל בתכנות)? בתכנות “פונקציה רקורסיבית” היא פונקציה שקוראת לעצמה. ובואו נסביר את המושג הזה לטובת מי שלא בעניינים. כמובן, אני לא מכיר את כל שפות התכנות בעולם וייתכן שאני לא מתאר את הדבר הכללי ביותר; אבל לשפות תכנות כמו ++C או Ruby התיאור הוא פחות או יותר מדויק.

מושג עיקרי בתכנות הוא פונקציה: פונקציה היא קטע קוד שמקבל קלטים מסויימים ועושה איתם כל מני דברים ומחזירה פלט. לפעמים אפילו אין צורך בקלט או בפלט מפורשים, והפונקציה שואבת את הקלטים שלה ממקורות אחרים (למשל, משתנים גלובליים; אבל שימוש בהם הוא פשע!) או שהיא פשוט פועלת באותה הצורה בכל פעם; ולפעמים אין צורך בפלט אלא אנחנו מריצים את הפונקציה בשביל “תופעות הלוואי” של הריצה שלה (למשל, שינוי של משתנים מסויימים שהפונקציה קיבלה כקלט, או של משתנים גלובליים - אבל משתנים גלובליים זה פשע! - או הדפסה למסך, וכדומה). מה שחשוב בפונקציה הוא שמרגע שבו כתבנו אותה, אנחנו יכולים להפעיל אותה מכל מקום - “להריץ אותה”. זה אומר שאם הקוד שלנו הגיע לשורה שבה אנחנו מריצים פונקציה, הוא שוכח באופן זמני מהאיזור בקוד שבו הוא רץ, ועובר לרוץ על איזור אחר בקוד - האיזור שבו הפונקציה שלנו כתובה. עם סיום הפונקציה הוא חוזר לאיזור המקורי שבו הוא היה.

אנלוגיה פשוטה לדבר הזה יש לנו בקריאת ספר: נניח שנתקלנו במילה לא מוכרת בספר; אנחנו עוצרים, שמים סימניה, פותחים מילון ומחפשים בו את המילה הלא מוכרת (קראנו לפונקציה “הפעל מילון” עם הקלט של המילה הלא מוכרת), קוראים את הפירוש או מתעצבים על כך שלא מצאנו פירוש, ואז סוגרים את המילון, שמים אותו בצד, חוזרים לספר שלנו ומוצאים את המקום שהיינו בו בספר בעזרת הסימניה. עכשיו, בואו נניח שהגענו בספר שלנו למילה קשה, ופתחנו את המילון, וקראנו את ההגדרה, וגם בתוך ההגדרה הייתה מילה קשה שלא הצלחנו להבין. מה עושים? שמים סימניה גם במילון, ופותחים שוב את המילון, עם חיפוש של ההגדרה הקשה, וכדומה. הבנתם את הרעיון. זו בדיוק הייתה קריאה רקורסיבית, ועכשיו יש לנו שתי סימניות להתעסק איתן.

בואו ניקח את זה צעד אחד קדימה בעזרת אנלוגיה מודרנית למדי - ויקיפדיה. להרבה אנשים מוכרת היטב התופעה שבה הם קוראים ערך בויקיפדיה, ובאמצע הקריאה נתקלים בקישור לערך מעניין אחר. ואז הם לוחצים על הקישור אליו, מתחילים לקרוא את הערך המעניין האחר, וכשהם מסיימים הם לוחצים על back כדי לחזור לערך המקורי. אבל לרוב בקריאת הערך המעניין האחר מגיעים לעוד קישור שנכנסים אליו, וכן הלאה. התוצאה היא שנוצרת “שרשרת” של ערכים ששמורה בזיכרון של הדפדפן. זה בדיוק גם מה שעשוי לקרות בתכנות - מקבלים שרשרת קריאות לפונקציות, ולכל קריאה כזו צריך לשמור את המידע של “איפה היינו”. כפי שכבר ברור, המידע הזה חייב להיות רשימה באורך לא מוגבל, כי אין לנו הגבלה עקרונית לכמות הקריאות-בתוך-קריאות שאפשר לעשות. הרשימה הזו כוללת לא רק את רשימת ה”מקומות שבהם היינו” אלא גם מידע על המשתנים המקומיים של הפונקציות - מה הערכים שהם הכילו. באנלוגיית ויקיפדיה, דמיינו שאתם לא רק לוחצים על הלינק אלא ממש פותחים אותו בטאב חדש - תקבלו סדרה של טאבים של ערכים שונים. בכל טאב שמורה הכתובת של הערך, אבל גם התוכן של הערך. לרשימה הזו, של “המידע הרלוונטי של הפונקציות, מסודר לפי סדר הקריאות להן” קוראים המחסנית.

אין צורך להיכנס יותר מדי לפרטים; כשתוכנית מחשב רצה, יש כמה איזורים עיקריים בזכרון שבהם היא משתמשת, והמחסנית היא אחד מהם. קוראים לה “המחסנית” בגלל האופי שבו מוסיפים ומורידים ממנה דברים; הכלל הוא שהפונקציה האחרונה שהתווספה למחסנית תהיה גם הראשונה שתסולק משם, אחרי שנסיים את הריצה שלה ונצא ממנה (זה לא אומר בשום פנים ואופן שאין לנו דרך לקרוא משהו שאיננו בראש המחסנית, כפי שלפעמים תופסים “מחסנית” במדעי המחשב באופן שגוי). ברקורסיה הפונקציה קוראת לעצמה, אבל ההתנהגות של המחסנית היא זהה - מבחינתה יהיו עליה הרבה עותקים של כתובת חזרה (כשכתובות החזרה יצביעו כולן לתוך הפונקציה הרקורסיבית, למעט הכתובת שנשמרה עם הקריאה הראשונה לפונקציה הרקורסיבית ומצביעה על המקום שבו קראו לה), ולכל עותק של הרקורסיה יהיו המשתנים המקומיים שלו.

אפשרי, כמובן, שיהיה סוג עקיף יותר של רקורסיה: במקום פונקציה A שקוראת לעצמה, פונקציה A שקוראת לפונקציה B שקוראת לפונקציה C שקוראת שוב ל-A - הבנתם את הרעיון. גם כזה דבר מכונה רקורסיה, אבל הוא קצת פחות נפוץ.

בואו נתחיל לראות קוד (קוד רובי, כי זו השפה שאני אוהב). הנה פונקציה רקורסיבית שמחשבת עצרת:

def factorial(n)
	return 1 if n == 0
	return n * factorial(n-1)
end

השורה הראשונה היא מקרה הבסיס - החזר 1 עבור הקלט 0; והשורה השניה היא הקריאה הרקורסיבית. ועכשיו הנה ההזדמנות לדברי כפירה - הפונקציה הרקורסיבית הזו מיותרת. הנה מימוש לא רקורסיבי:

def factorial(n)
	result = 1
	for k in 1..n do
		result *= k
	end
	return result
end

(קצת סירבלתי, אפשר לעשות את זה פשוט יותר ברובי, אבל זה לא פוסט רובי). איזה משני המימושים עדיף? חד משמעית, השני. אבל למה? הראשון הרי נראה אלגנטי יותר! ובכן, השני יקר פחות. אתם מבינים, כשמפעילים רקורסיה, מאחורי הקלעים קורים דברים - המהומות הרגילות של קריאה לפונקציה, דחיפת מידע למחסנית, וכדומה. זה לוקח זמן, וזה גוזל מקום. לכל בעיה כזו כדאי להתייחס בנפרד. מבחינת זמן, ההבדל בזמן הריצה בין שתי הגרסאות שלי עשוי להיות ממש זניח עבור הרצה בודדת של הפונקציה, אבל צריך לזכור כשכותבים קוד שלעתים קרובות אחרי שנכתב קוד, קורה האסון שאנשים אשכרה משתמשים בו. אולי כחלק מדברים אחרים שהם כותבים. ופונקציה תמימה לכאורה עשויה להיקרא מיליארדי פעמים. ובעיה “קלה” בזמן ריצה הופכת לבעיה חמורה, וכדומה. לא פעם ולא פעמיים בעבר כבר חיסלתי פונקציה רקורסיבית והמרתי אותה בפונקציה לא רקורסיבית שקולה פשוט כדי לחסוך זמן והחסכון היה משמעותי.

מקום הוא בעיה אפילו יותר רלוונטית. תחשבו שאנחנו רוצים לחשב את 1000 עצרת - אנחנו הולכים לשמור על המחסנים 1,000 עותקים של הרקורסיה. יש למחסנית כמות מקום מוגבלת. מתישהו היא תיגמר והתוכנית תקרוס, בזמן הריצה. הודעת השגיאה הרלוונטית, stack overflow, היא כל כך נפוצה ומוכרת שהיא הפכה לשמו של אתר שאלות ותשובות בנושאי תכנות סופר-פופולרי. במימוש איטרטיבי באמצעות לולאה לרוב אפשר להסתפק בכמות קבועה של מקום, בלי תלות בכמות האיטרציות שלנו (וגם כשאי אפשר, לרוב עדיין יש חסכון כלשהו). לכן כלל ברזל ברקורסיות הוא: זה אחלה להשתמש בהן, אבל תוודאו בינכם לבין עצמכם שאתם באמת צריכים את זה, או שאין שום סכנה של “התפוצצות” עם קלטים גדולים. והנה עוד דוגמה שממחישה סכנה גדולה אפילו עוד יותר - חישוב מספרי פיבונאצ’י:

def fib(n)
	return 0 if n == 0
	return 1 if n == 1
	return fib(n-1) + fib(n-2)
end

<\pre> הפונקציה הקטנה והחביבה הזו היא אסון מוחלט. היא אחד מקטעי הקוד הגרועים ביותר שניתן להציג. למה? כי היא עושה המון עבודה כפולה. כדי לחשב את מספר פיבונאצ’י עבור 5, הפונקציה קוראת רקורסיבית לחישוב של 4. כחלק מהחישוב של 4 היא מחשבת גם את 3 ו-2, וכן הלאה. אחרי שהיא סיימה היא חוזרת לחישוב של 5 עם הערך של 4, ואז קוראת לחישוב של 3. אבל כבר חישבנו את 3 קודם! המידע פשוט לא שמור בשום מקום והלך לאיבוד. ככל שמספר פיבונאצ’י שאנחנו רוצים לחשב גדל, מספר ה”חישובים הכפולים” שלנו גדל אקספוננציאלית. התוצאה היא בזבוז עצום של זמן ריצה. אל תנסו את זה בבית. אז מה עושים? כמובן, במקרה הנוכחי אפשר פשוט לתת פתרון איטרטיבי:

def fib(n)
	return 0 if n == 0
	a, b = 0, 1
	for k in 2..n do
		a, b = b, a + b
	end
	return b
end

ובמקרים מורכבים יותר, כשבכל זאת רוצים סוג של קריאה רקורסיבית? אז משתמשים במבנה נתונים שנגיש לכל הקריאות של הפונקציה (למשל, כי מעבירים מצביע אליו בכל קריאה של הפונקציה) שבו מאחסנים את המידע של תוצאות הביניים כדי שלא נחשב אותן מחדש בכל פעם. מה שנקרא “תכנון דינמי” זה בדיוק הדבר הזה. לפעמים זה אפילו לא עניין של מידע שכבר חושב, אלא סתם לדעת ש”כבר היינו כאן”. למשל, אלגוריתם סטנדרטי למציאת יציאה ממבוך הוא DFS: כשמריצים DFS על משבצת במבוך, אם היא איננה היציאה, אנחנו מריצים DFS על כל אחד מהשכנים של המשבצת. מן הסתם חייבים לסמן איכשהו שכנים שבהם כבר ביקרנו אחרת עוד יצא שנלך ימינה-שמאלה בין אותן שתי משבצות עד אינסוף (ליתר דיוק, עד שנקבל stack overflow). כשהייתי קטן ובניתי משחק של “סוגר שטחים”, זה בדיוק מה שקרה לי - כשנסגר שטח ניסיתי לצבוע את כל המשבצות שבתוכו על ידי אלגוריתם רקורסיבי שצובע משבצת ואז מטפל רקורסיבית בשכניה; ברוב חוכמתי פשוט אמרתי “צבע את המשבצת” ולא “אם המשבצת צבועה, אל תעשה כלום; אחרת…”. כמובן שקיבלתי stack overflow והייתי מאוד עצוב לראות שאפילו על כמות קטנה של משבצות הרקורסיה שלי מתה ללא סיבה.

פרט לכל אלו, יש שפות תכנות, בעיקר כאלו שבהן מסתמכים באופן מאוד חזק על רקורסיות כדוגמת Haskell, שבהן דברים מטופלים אוטומטית. למשל, מקרה ידוע לשמצה במיוחד של רקורסיה נקרא “רקורסיית זנב”. ברקורסיית זנב, הקריאה הרקורסיבית היא הדבר האחרון שמתרחש בתוך הפונקציה הרקורסיבית, והפלט של הרקורסיה הוא הפלט של ההפעלה הרקורסיבית הזו. במקרה הזה ברור שיכלנו לשחרר את המשאבים של הרקורסיה הנוכחית לפני שהפעלנו את הרקורסיה הפנימית, ובכך לחסוך מקום; אבל זה לא קורה אוטומטית בהכרח. קומפיילר חכם כן יודע לעשות דברים כאלו, וגם מתוחכמים יותר (למשל, לטפל בפונקציית העצרת שהראיתי למעלה, שבה הרקורסיה היא “כמעט רקורסיית זנב”. לא אכנס לפרטים הללו כאן.

בואו נעבור לראות כמה דוגמאות מעניינות יותר, שהן עדיין ברמת התרגיל אבל הן בכל זאת נחמדות. הדוגמא הראשונה היא משהו שהזכרתי בראשית ימי הבלוג - מגדלי האנוי. מגדלי האנוי הם משחק נחמד שבו יש לנו שלושה “מגדלים” שאפשר להשחיל עליהם טבעות בגדלים שונים. בתחילת המשחק כל הטבעות מסודרות לפי גודל על אחד המגדלים, והמטרה היא להעביר את כולן, מסודרות לפי גודל, למגדל אחר. החוקים: מותר להעביר רק טבעת אחת בפעם, ואסור לשים טבעת גדולה על טבעת שקטנה ממנה. זו הסיבה שבגללה יש שלושה מגדלים - המגדל השלישי הוא “מגדל עזר” שמסייע בהעברת הטבעות. מה שיפה כאן הוא שמספיקים שלושה מגדלים ולא משנה כמה טבעות יש.

הפתרון הרקורסיבי כאן הוא מקסים, כי הוא מציג במדויק את כוחה של החשיבה הרקורסיבית. הוא מחלק את הפתרון לשלושה שלבים: קודם כל נשים הצידה לרגע את כל הטבעות מלבד התחתונה (כלומר, נשים במגדל העזר); אחר כך נעביר את התחתונה אל מגדל היעד שלנו; ואחר כך ניקח את כל הטבעות ששמנו בצד ונעביר למגדל היעד. את הפעולה האמצעית אנחנו יודעים איך לבצע כי היא כוללת רק העברת טבעת אחת, אבל איך אנחנו יכולים להעביר את כל הטבעות “בבת אחת” ממגדל המקור אל מגדל העזר, וממגדל העזר למגדל היעד? ובכן, פשוט מאוד - נפעיל רקורסיבית את הפתרון שלנו… זה אומר שלרגע פשוט נשכח מכך שיש את הטבעת הגדולה שמסתובבת אי שם ונשחק כאילו היא לא קיימת; מכיוון שהיא הגדולה ביותר, היא לא יכולה להפריע לאחרות ולכן מבחינת ההפעלה הרקורסיבית היא באמת לא קיימת. הנה הקוד הפשוט מאוד.

def solve_hanoi(n, source_tower, aux_tower, goal_tower)
	return if n == 0
	solve_hanoi(n-1, source_tower, goal_tower, aux_tower)
	goal_tower.push source_tower.pop
	solve_hanoi(n-1, aux_tower, source_tower, goal_tower)
end

הקוד הזה הוא דוגמה לסיבה שבגללה בחרתי לכתוב דווקא ברובי - הוא כמעט פסאודו-קוד, אבל כזה שעובד ואפשר להריץ. הרעיון הוא שה”מגדלים” נתונים בתור מערכים ברובי, וככאלה הם תומכים בפעולות pop (הוצא את האיבר האחרון והחזר אותו) ו-push (דחוף לסוף המערך). כמו כן, צריך להיות מודעים לכך שמשתנים ברובי תמיד מועברים לפונקציה By Reference; כלומר, לא נוצר עותק נפרד שלהם אלא המשתנה שהפונקציה עובדת איתו הוא בדיוק אותו משתנה שמי שקרא לפונקציה עבד איתו, ולכן שינויים במשתנה שמתרחשים בתוך הפונקציה משפיעים גם מחוצה לה.

ברקורסיה הנוכחית התכונה הזו מנוצלת בצורה חכמה כדי “להחליף תפקידים” בין המגדלים השונים. בקריאה הרקורסיבית הראשונה, מי שהיה מגדל העזר הופך למגדל היעד, ומי שהיה מגדל היעד הופך למגדל העזר. בקריאה השניה החלפה דומה מתבצעת בין מגדל העזר ומגדל המקור. ה”חוכמה” של הפתרון מקופלת כולה בשרשרת החלפות התפקידים הללו שמתבצעת (נסו לעקוב אחרי האופן שבו רצה רקורסיה עבור n שווה 5 כדי לראות כמה החלפות תפקידים כאלו מתבצעות עוד לפני שמזיזים את הטבעת הראשונה). כמובן, אם תרוצו להריץ את התוכנית הזו תתאכזבו נורא כי היא לא עושה שום דבר שאתם מסוגלים לראות. אין הדפסה של המגדלים או משהו דומה. אז למי שרוצה את זה, הנה קוד יותר מלא שגם מדפיס וגם מאתחל וגם הכל:

class Hanoi
	def initialize(n)
		@source_tower = (1..n).to_a
		@aux_tower = []
		@goal_tower = []
		print_state
		solve(n, @source_tower, @aux_tower, @goal_tower)
	end
	def print_state
		puts @source_tower.inspect
		puts @aux_tower.inspect
		puts @goal_tower.inspect
		puts
	end
	def solve(n, source_tower, aux_tower, goal_tower)
			return if n == 0
			solve(n-1, source_tower, goal_tower, aux_tower)
			goal_tower.push source_tower.pop
			print_state
			solve(n-1, aux_tower, source_tower, goal_tower)
	end
end
Hanoi.new(4)

נעבור עכשיו לדוגמה אחרת - ייצור פרמוטציות. פרמוטציה של מערך היא מערך אחר שכולל את אותם איברים בדיוק, אבל בסדר שונה (לצורך העניין נניח שכל האיברים שונים זה מזה). לא קשה להראות שאם במערך יש n איברים, אז מספר הפרמוטציות שלו הוא !n, כך שפונקציה שמוציאה את כל הפרמוטציות של מערך תצטרך לעבוד קשה רק כדי לכתוב את כולן עבור ערכים גדולים של n. לכן די מתבקש להשתמש בפתרון רקורסיבי פה ממילא, כל עוד הוא לא לוקה בבזבוז משווע.

הרעיון הנאיבי הוא זה: תעברו על המערך איבר איבר. לכל איבר - הוציאו אותו מהמערך, בנו רקורסיבית את כל הפרמוטציות של המערך שנשאר, והוסיפו את האיבר שהוצאתם לכולן. הנה קוד שעושה את זה:

def permutations(a)
	n == a.length
	return [a] if n == 1
	result = []
	for i in (0...n) do
		temp_elem, temp_a = a[i], a[0...i] + a[i+1...n]
		for p in permutations(temp_a) do
			result << ([temp_elem] + p)
		end
	end
	return result
end

הקוד הזה הוא בבירור בזבזני - אנחנו יוצרים עותק חדש של המערך על כל הפעלה של הרקורסיה שאנחנו מבצעים. זה אמנם טוב לצורך הדגמת האופן שבו רקורסיה מנצלת את זה שבכל קריאה שלה היא מקבלת מקום נפרד עבור המשתנים שהיא מגדירה, אבל כאן זה מרגיש בזבזני. האם אפשר היה לעשות משהו טוב יותר? התשובה חיובית, אבל לא לגמרי קל לעלות על האלגוריתם או להבין למה הוא עובד. האלגוריתם הזה נקרא “Heap’s Algorithm” והרעיון שבו הוא שמספיק לבצע שינויים בתוך המערך שקיבלנו כקלט , וליצור עותק מהמערך רק כשאנחנו מקבלים פרמוטציה שאנחנו רוצים להוסיף לפלט הסופי. הנה איך שזה נראה בקוד:

def permutations_heap(n, a)
	return [a.dup] if n == 1
	result = []
	for i in (0...n) do
		result += permutations_heap(n-1,a)
		a[i], a[n-1] = a[n-1], a[i] if n % 2 == 0
		a[0], a[n-1] = a[n-1], a[0] if n % 2 != 0
	end
	return result
end

בואו נעבור עכשיו לדבר על סוג שונה של בעיות - בעיות הכרעה, ובעיות ספירה נלוות. בבעיות הכרעה מהסוג הנפוץ יש לנו קלט שהוא אובייקט כלשהו שאנחנו תוהים אם הוא מקיים או לא מקיים תכונה מסויימת. בבעיות ספירה גם רוצים לדעת בכמה דרכים שונות התכונה מתקיימת. הנה הדוגמה שאני הולך לפתור - הקלט הוא מערך של מספרים חיוביים ומספר “יעד” כלשהו, והשאלה היא אם אפשר לסכום חלק מאברי המערך כדי להגיע אל היעד - ושאלת ההמשך היא בכמה דרכים שונות אפשר לעשות את זה. הבעיה הזו נקראת Subset Sum וזו בעיה NP-שלמה מפורסמת, למי שהביטוי הזה אומר לו משהו. התכל’ס של מה שזה אומר הוא שלא סביר שנצליח למצוא פתרון שהוא ממש יעיל, אז יאללה, בואו נתפרע עם רקורסיה.

אלגוריתם רקורסיבי כאן כותב כמעט את עצמו. אנחנו צריכים להגיע למספר יעד כלשהו; אנחנו בוחנים את המספר הראשון במערך. או שנוסיף אותו לסכום, או שלא. עבור כל אחת משתי האפשרויות הללו אנחנו מבצעים קריאה רקורסיבית על יתר המערך; במקרה שבו הוספנו את המספר לסכום, אנחנו מפחיתים אותו מה”יעד”. העובדה שאני מניח שהמספרים הם כולם חיוביים עוזרת לי “להפסיק באמצע” בלי לבזבז זמן על חלק מהחישובים המיותרים - אם מספר היעד הפך להיות 0 פתאום, אני יודע שכבר הצלחתי ואני מסיים עם הפתרון הנוכחי (אני לא הולך להוסיף לו עוד שום דבר, מן הסתם). אם מספר היעד הופך להיות שלילי אני יודע שנכשלתי. לרקורסיה מסוג זה, שמסוגלת לזהות הצלחה או כשלון לפעמים “באמצע” ולחזור בהתאם קוראים Backtracking.

עם קצת להטוטי רובי אפשר לכתוב את הפתרון בשלוש שורות:

def subset_sum(a, n)
	return [] if n < 0 or (n > 0 and a.empty?) #empty solution set
	return [ [] ] if n == 0   #one solution - no elements
	return subset_sum(a[1..-1], n) + subset_sum(a[1..-1], n - a[0]).map{|sol| [a[0]] + sol}
end

השורה השלישית אולי נראית קצת מפחידה. אני בסך הכל אומר לקחת את כל הפתרונות לגודל n שמערבים את המערך בלי האיבר הראשון, ולהוסיף להם את כל הפתרונות שמערבים את המערך בלי האיבר הראשון, עבור הסכום n פחות האיבר הראשון, כשאני לוקח כל פתרון כזה ומוסיף לו בהתחלה את האיבר הראשון.

האם כאן אני יכול לתת פתרון איטרטיבי קצר? ובכן, לא ממש! אין לי רעיון איך לעשות פתרון שיהיה גם קצר וגם קריא וגם יעשה backtracking דומה. כמובן, תמיד אפשר לייצר סדרתית את כל המספרים מ-0 ועד 2 בחזקת גודל המערך פחות 1, להסתכל על הייצוג הבינארי שלהם ולסכום את האיברים שמתאימים למקומות שבהם כתוב 1; אבל זה כבר מסורבל למדי (אם כי פרקטי יותר, לפעמים; כאן, לא חושב) ואני לא רואה דרך נחמדה לשמר כך את תכונת ה-backtracking.

ואיך אפשר בלי פתרון מבוך. אני מניח שהמבוך נתון על ידי מערך דו ממדי שבו 0 מייצג משבצת פנויה ו-1 מייצג קיר, ושהמטרה היא להגיע אל 0,0. אני מרשה לעצמי “לקשקש” על המבוך - לכתוב 2 כדי לתאר משבצת שכרגע היא פוטנציאל למסלול היציאה, ו-3 למשבצת שכבר ויתרנו עליה. כך, אם נמצא מסלול ליציאה, הוא יהיה כתוב בתוך המבוך על ידי המשבצות שבהן כתוב 2:

def solve_maze(maze, row, col)
	return false if row < 0 or col < 0 or row >= maze.length or col >= maze.first.length or maze[row][col] != 0
	maze[row][col] = 2
	return true if row == 0 and col == 0
	neighbors = row + 1, col], [row - 1, col], [row,  col + 1], [row, col - 1
	neighbors.each{|row, col| return true if solve_maze(maze, row, col)}
	maze[row][col] = 3
	return false
end

ולמי שרוצה לראות את זה בפועל, הנה עוד קצת קוד שמאפשר לצייר מבוך ואת המסלול ליציאה שבתוכו, אם יש, ודוגמת הרצה:

def print_maze(maze)
	sym = {0 => " ", 1 => "+", 2 => ".", 3 => " "}
	maze.map{|row| row.map{|v| sym[v]}}.each{|row| puts row.join("")}
end
maze = [[0, 0, 1, 1, 1, 1, 1],
		[1, 0, 1, 1, 1, 0, 1],
		[1, 0, 1, 0, 0, 0, 1],
		[1, 0, 1, 0, 1, 0, 1],
		[1, 0, 0, 0, 1, 0, 1],
		[1, 1, 1, 1, 1, 1, 1]
	   ]

print_maze(maze)
puts
solve_maze(maze,4,5)
print_maze(maze)

ואפשר להמשיך ולתת עוד ועוד דוגמאות, אבל נראה לי שהבנו את הרעיון ואפשר לעצור כאן. למרות שאם אתם עדיין לא מרוצים, נסו לקרוא את הפוסט שלי כאן.