בסדרת הפוסטים שלי על דילוגי אותיות בתורה אמרתי פחות או יותר את כל מה שיש לי לומר על הנסיונות המוזרים לרתום את מה שנראה כמו צירופי מקרים בלתי אפשריים כדי “להוכיח” משהו שלא באמת יכולה להתקיים עבורו הוכחה. אבל זה לא אומר שלא מתחשק לי לפעמים לכתוב על נסיונות כאלו, בתנאי שהם נותנים לי תירוץ טוב לדבר על מתמטיקה אמיתית מעניינת, וזה מה שאעשה עכשיו. אמנם, את המתמטיקה הרלוונטית כבר הצגתי בעבר בבלוג, אבל זו הזדמנות לראות יישום אמיתי שלה “בשטח”.

התופעה המדהימה שאנחנו מדברים עליה כאן היא זו: לוקחים את האלפבית העברי, בוחרים צורת איות ספציפית, חריגה יחסית, לאותיות שלו, ואז משחקים את המשחק הבא: לוקחים אות, מחליפים אותה באותיות שמרכיבות את שמה, ואז מחליפים אותן באותיות שמרכיבות את שמותיהן, וכן הלאה. בכל צעד במשחק אנחנו מקבלים מחרוזת (סדרת אותיות) מאורך הולך וגדל. ה”קסם” הוא שעבור חלק מהאותיות, סדרת אורכי המחרוזות שמתקבלות תואמת בצורה מסויימת מאוד את סדרת פיבונאצ'י. מכיוון שסדרת פיבונאצ’י זוכה ליחסי ציבור מצויינים בעולם, זה כנראה אמור לומר משהו.

הפוסט הזה לא בא לנסות ולבטל את התגלית הזו או לרמוז שאתם אמורים להאמין או לא להאמין במשהו בגללה. אני רוצה לענות על כמה שאלות מעניינות יותר. ראשית, מה בדיוק קורה שם; שנית, למה בעצם זה קורה, ולבסוף איך אפשר לנתח את הסבירות שזה יקרה. אחרי שמבינים מה בדיוק קורה שם ולמה, ברמת הפרטים הטכניים, ההילה המיסטית נעלמת מעצמה (אצלי לפחות). הפוסט יהיה מורכב משלושה חלקים שפחות או יותר הולכים מהקל אל הכבד. אני מקווה שהראשון יהיה נגיש לכל הקוראים, בזמן שהשני כנראה ידרוש קצת נטייה למדעי המחשב והשלישי כבר ידרוש היכרות כלשהי עם מתמטיקה.

חלק ראשון שבו אנחנו משחקים משחקים

אם כן, בואו ונתחיל. אני נתקלתי בתופעה בסרטון הבא, אבל אין הכרח שתראו אותו, אתאר את הכל בעצמי. הדרך הפשוטה ביותר היא באמצעות דוגמה. אני מתחיל מהאות א’. את האות הזו כותבים “אלף”, אז במשחק שלנו אנחנו מחליפים אותה ב”א ל פ”. עכשיו אני מטפל בכל שלוש האותיות באופן דומה ומקבל את “א ל פ ל מ ד פ א” (שלוש האותיות הראשונות התקבלו מהא’; שלוש הבאות מהל’ ושתי האחרונות מהפ’). כך אני ממשיך עד אין קץ. עכשיו אנחנו בודקים את סדרת המספרים של מספר האותיות שיש לנו בכל שלב. בשלב הראשון יש 1; בשני יש 3, בשלישי יש 8, וכך זה מתקדם. אם תחשבו מספיק איברים מהסדרה, תגלו שהיא תואמת לגמרי את סדרת האיברים האי-זוגיים בסדרת פיבונאצ'י. בואו נציג את הסדרה הזו עבור מי שלא זוכר או מכיר: זו סדרת מספרים שהאיבר הראשון בה הוא 0 והשני הוא 1 וכל איבר אחרי שני אלו שווה לסכום של קודמיו. האיבר השלישי בסדרה הוא גם כן \( 1 \) כי \( 0+1=1 \); האיבר הרביעי בסדרה הוא 2, כי \( 1+1=2 \); האיבר שאחר כך הוא 3, אחר כך 5 וכן הלאה.

סדרת פיבונאצ’י היא דבר מעניין. היא צצה בכל מני מקומות במתמטיקה ותמיד כיף לפגוש אותה. אבל צריך להבין שזו לא סדרה קסומה באופן מיוחד, היא פשוט דוגמה פשוטה במיוחד לסדרה שמוגדרת באמצעות נוסחת נסיגה. סדרה מוגדרת באמצעות נוסחת נסיגה אם נתונים לנו כמה איברים ראשונים שלה באופן מפורש, ומכאן והלאה כל איבר ניתן לחשוב מתוך קודמיו. בואו נכניס קצת כתיב מתמטי לתמונה: \( F_{1}=0,F_{2}=1 \) הם האיברים הראשונים בסדרה, ולכל \( n\ge3 \) מתקיים \( F_{n}=F_{n-1}+F_{n-2} \).

יש סדרות פשוטות אף יותר שמוגדרות באמצעות נוסחת נסיגה. למשל, הנוסחה \( a_{1}=1 \) ו-\( a_{n}=a_{n-1} \) מגדירה את הסדרה \( 1,1,1,\dots \). באופן דומה, הנוסחה \( a_{1}=1 \) ו-\( a_{n}=2a_{n-1} \) מגדירה את הסדרה המעניינת יותר \( 1,2,4,8,16,\dots \) ובאופן כללי, אם \( q \) הוא מספר כלשהו, אז נוסחת הנסיגה \( a_{1}=1 \) ו-\( a_{n}=qa_{n-1} \) מגדירה את הסדרה \( 1,q,q^{2},q^{3},\dots \) - זה מה שנקרא סדרה הנדסית. גם נוסחת הנסיגה הזו וגם נוסחת הנסיגה של פיבונאצ’י הן מה שנקרא נוסחאות נסיגה לינאריות. זה אומר שכל איבר מתקבל באופן הבא: לוקחים חלק מהאיברים הקודמים (תמיד את אותם איברים ביחס לנוכחי, למשל “שני האיברים האחרונים” של פיבונאצ’י); כופלים אותם במספרים קבועים כלשהם; מחברים את הכל (למי שמכיר את המושג - כל איבר בסדרה הוא צירוף לינארי של מספר קבוע מקודמיו).

עכשיו, אנחנו מתעניינים כאן לא בסדרת פיבונאצ’י עצמה, אלא רק באיברים במקומות האי-זוגיים. בואו נסמן את הסדרה החדשה הזו בתור \( G_{n} \). האם אנחנו מסוגלים למצוא נוסחת נסיגה עבור \( G_{n} \)? בהחלט. נקבל ש-\( G_{n}=3G_{n-1}-G_{n-2} \). רוצים לראות את החישוב בעצמכם? אין בעיה (לא רוצים? דלגו הלאה):

אנחנו יודעים ש-\( G_{n}=F_{2n-1} \) (נסו להציב \( n=1,2,3 \) ולראות מה מקבלים אם אתם לא מאמינים), אז בואו נשתמש בנוסחת הנסיגה של \( F_{n} \):

\( G_{n}=F_{2n-1}=F_{2n-2}+F_{2n-3}=2F_{2n-3}+F_{2n-4} \)

עכשיו, \( G_{n-1}=F_{2n-3} \) אז הגענו אל \( 2G_{n-1}+F_{2n-4} \). אנחנו רוצים איכשהו להיפטר מה-\( F_{2n-4} \) המעצבן הזה. לשם כך נשים לב ש-\( G_{n-1}-G_{n-2}=F_{2n-3}-F_{2n-5}=F_{2n-4}+F_{2n-5}-F_{2n-5}=F_{2n-4} \), כפי שרצינו. לכן מגיעים לנוסחה \( G_{n}=3G_{n-1}-G_{n-2} \) המובטחת - שום דבר מרגש במיוחד עד כה.

אם כן, ראינו שגם עבור “האיברים במקומות האי-זוגיים של פיבונאצ’י” יש לנו נוסחת נסיגה לינארית (עבור האיברים במקומות הזוגיים נקבל את אותה נוסחת נסיגה, אבל עם תנאי התחלה שונים). למה אני מפיל את כל זה עליכם? כי התוצאה המתמטית הבסיסית מאחורי כל הסיפור היא זו: המשחק הזה שבו לוקחים אות ומחליפים אותה באיות שלה, וכן הלאה - אם אנחנו מסתכלים על הסדרה שהמשחק הזה מגדיר, הסדרה הזו תמיד תאופיין על ידי נוסחת נסיגה לינארית. לא משנה מאיזו אות התחלנו, ולא משנה מה האופן שבו אנחנו מאייתים את שמות האותיות. זה יהיה נכון גם באנגלית, וגם בצרפתית, וגם באלפבית מומצא וכן הלאה. נוסחת נסיגה לינארית תמיד תהיה. השאלה המעניינת היא האם זו תהיה נוסחת נסיגה פשוטה. התשובה היא שלילית; לרוב נוסחת הנסיגה תהיה יותר מסובכת - מספר האיברים “אחורה” בה יכול להיות כמספר האותיות שמשתתפות במשחק (במקרה שלנו, 22). אז בואו ננסה להבין מה גורם לנוסחה להיות פשוטה במיוחד במקרה שלנו. השורה התחתונה היא שהרבה פחות אותיות משתתפות במשחק משנדמה לנו וששמות האותיות קצרים ופשוטים יחסית, אבל עדיין לא פשוטים מדי.

בתור התחלה, בואו נראה אילו אותיות מתקבלות כשמתחלים את המשחק עם א’. מהאות א’ אנחנו מקבלים גם את ל’ ואת פ’. מ-פ’ אנחנו לא מקבלים משהו חדש - פ”א מורכבת רק מאותיות שכבר ראינו. מל’ אנחנו מקבלים את מ’ ואת ד’. מ’ לא מוסיפה לנו משהו חדש, אבל דל”ת מוסיפה לנו את ת’. ת’ מוסיפה לנו את ו’, ואילו ו’ לא מוסיפה לנו שום דבר חדש. אז סך הכל קיבלנו שבע אותיות: א ד ו ל פ מ ת (הנה לכם מסר שחבוי בא”ב העברי! מדהים, לא?). הנה האיותים שלהן שבהם משתמשים במשחק:

אל"פ
דל"ת
וא"ו
למ"ד
מ"מ
פ"א
תא"ו

זה לא האיות הסטנדרטי (בדרך כלל כותבים ו”ו ות”ו). האיות הסטנדרטי פשוט לא מניב שום דבר מעניין (מקבלים נוסחאות נסיגה מסובכות יחסית שלא מנפיקות פיבונאצ’י). האיות שבו משתמשים כאן הוא כן ככל הנראה איות לגיטימי שקיים איפה שהוא ביקום בלי קשר למשחק הזה; נחזור לנקודה הזו בהמשך. בינתיים שימו לב שכל שאר האותיות בעברית פשוט לא מעורבות במשחק הזה - הן לא רלוונטיות ואפשר לשכוח מהן. אז ה”קסם” שיש כאן, אם יש קסם, נובע רק משבע האותיות הללו.

מה שנחמד הוא שאפשר לקחת את האלפבית הזה ולפשט אותו עוד יותר ועדיין לקבל משהו שמניב בדיוק את אותה סדרה. למעשה, האלפבית הפשוט ביותר שמניב את הסדרה הזו הוא האלפבית המלאכותי הבא:

אא"פ
פ"א

אלפבית שכולל רק שתי אותיות! נסו לייצר את הסדרה שמתקבלת כאן אם אתם צריכים שכנוע שאכן מתקבל פיבונאצ’י במקומות האי זוגיים; בהמשך אוכיח לכם שזה מה שקורה בצורה שכולם יוכלו לעקוב אחריה, גם לפני התיאוריה הכללית. בואו נשחק עכשיו משחק שבו אני מדגים איך אפשר לייצר מהאלפבית הפשוט הזה את האלפבית בן 7 האותיות שלעיל, מבלי לשנות את התכונה שלפיה א’ מייצר את סדרת הפיבונאצ’י שלנו. זה כנראה יהיה השלב הקשה ביותר למעקב בחלק הזה של הפוסט, אבל למה שלא תנסו? הבונוס הוא שנלמד איך לייצר המון אלפביתים שבהם מתקיימת התכונה הפיבונאצ’ית, לא רק זה שלעיל.

התעלול הראשון שנעשה יהיה להוסיף אות חדשה שמתנהגת בדיוק כמו אות קיימת, ובכך לא משנה את הסדרה שנוצרת. נניח שאני רוצה להוסיף את האות ל’ ורוצה שהיא תתנהג בדיוק כמו א’. מה השם שאתן לה? ובכן, לא”פ הולך לעבוד. זה יהיה האלפבית החדש שלי:

אא"פ
לא"פ
פ"א

למה זה עובד? האינטואיציה היא של’ היא אות שמייצרת אותיות בצורה הבאה: היא מייצרת א’, היא מייצרת פ’, והיא מייצרת את עצמה. ומה א’ עושה? אם תחשבו על זה, היא עושה אותו דבר בדיוק: מייצרת א’, מייצרת פ’, ומייצרת את עצמה (כמובן, אולי נראה הגיוני יותר לומר שהיא מייצרת את עצמה פעמיים, אבל אז הסימטריה עם ל’ פחות ברורה).

עכשיו לתעלול הבא שלי - לשנות קצת את השם של א’:

אל"פ
לא"פ
פ"א

כאן לא השתנה שום דבר מהותי כי החלפנו מופע אחד של א’ בשם “אאפ” במופע אחד של ל’, וכבר הסכמנו שא’ ול’ הן אותו הדבר. אבל ההחלפה הזו היא חיובית מאוד מבחינתנו כי סוף סוף השם של א’ באמת נראה כמו השם שלו באלפבית הסופי שאנחנו מנסים לבנות. גם פ”א היא הצלחה. אז יש לנו בעיה רק עם ל’ המסכנה.

בואו נתחיל להוסיף אותיות. נפתח עם מ’:

אל"פ
לא"פ
פ"א
מ"מ

מ’ מייצרת רק את עצמה, פעמיים. זה יוצר סדרה שונה מאשר יצרה אא”פ בהתחלה (כי שם היה גם פ’ מעורב) או ממה שפ”א יצרה, ולכן קיבלנו פה אות חדשה שהיא לא שכפול של משהו קיים. עכשיו, נניח שהייתי מוסיף את ו’ באיות הרגיל שלה, ו”ו - הייתי מקבל שכפול של מ’. כמו כן, אם הייתי מוסיף אחר כך את ת’ באיות הרגיל שלה - ת”ו - הייתי מקבל עוד שכפול של מ’ (כי ו”ו מצייתת לחוקיות של “יוצרת את עצמה ועוד ו’ אחד” וגם ת”ו מצייתת לחוקיות של “יוצרת את עצמה ועוד ו’ אחד”). אלא ששכפולים כאלו של מ’ לא עוזרים לנו ולכן אנחנו מעדיפים את האיות האחר, עם הא’ באמצע:

אל"פ
לא"פ
פ"א
מ"מ
וא"ו
תא"ו

וממה שכבר עשינו עד עכשיו אני מקווה שברור שו’ ות’ הן שכפולים האחת של השניה - שתיהן מייצרות את אותה סדרה.

תור מי עכשיו? דל”ת. בשלב הזה אנחנו כבר משופשפים מספיק כדי לראות די בקלות שנקבל ממנה את אותה סדרה כמו וא”ו ותא”ו: אם נתחיל עם דא”ד נקבל אות שמתנהגת בדיוק כמו וא”ו (מחזירה פעמיים את עצמה ופעם אחת א’) ולכן מייצרת את אותה סדרה. עכשיו נחליף את הד’ השני בת’ השקול, ואת הא’ שבאמצע בל’ השקול:

אל"פ
לא"פ
פ"א
מ"מ
וא"ו
תא"ו
דל"ת

ברשימה הזו 1-2 הן שקולות, וגם 5-7 הן שקולות. כל האותיות הן עם השמות הנכונים שלהן למעט למ”ד. כאן מגיע הקסם היחיד: איכשהו לא”פ ולמ”ד הן שקולות למרות שהאותיות שלהן מייצגות סדרות שונות. בגלל הל’ המשותף שיש לשתיהן בהתחלה, השאלה היא קצת יותר פשוטה: למה א”פ ומ”ד הן שקולות. מכיוון שד’ שקולה לו’, יותר קל לשאול למה פ”א שקולה אל מ”ו. זה טיפה טריקי, אבל לא כל כך קשה לראות את זה. נחזור לרגע לתיאור המקורי שלנו של א’ בתור אא”פ. עכשיו, מה קורה אם לוקחים את פ”א ופותחים אותה פעם אחת? מקבלים

פ א

פ א א א פ

כלומר, ממופע אחד של פ”א קיבלנו שני מופעים של פ”א, ובנוסף לכך עוד א’ בונוס.

ומה קורה עם מ”ו? יקרה אותו דבר בדיוק: נקבל שני מופעים של מ”ו, ובנוסף לכך עוד א’ בונוס:

מ ו

מ מ ו א ו

סדר האותיות הוא שונה, אבל הסדר לא חשוב. מה שחשוב הוא שאחרי שפותחים את זה פעם אחת, מקבלים שני מ’מים, שני ו’וים, וא’ אחת. זה מסיים את המסע הארוך שהתחלנו עם הא”ב בן שתי האותיות אא”פ, פ”א. ה”קסם” של פיבונאצ’י נמצא, אם כן, כבר בא”ב הזעיר הזה - כל שאר השינויים שאני מבצע הם מהצורה של החלפה של אות אחת בשקולה לה, הוספה של אותיות חדשות עם שם פשוט, ובסוף החלפה גאונית של שתי אותיות בו זמנית. אפשר לשחק עם זה כמה שבא לכם ולבנות המוני אלפבתים מלאכותיים שיניבו כולם את סדרת פיבונאצ’י. האם יש משהו מיוחד בכך שאחד מהא”בים שנותנים אותה כך הוא אחד מהוריאנטים על כתיבת שמות אותיות בעברית? אתם תחליטו

אני עדיין חייב לכם הסבר למה האלפבית שכולל את אא”פ ואת פ”א נותן את סדרת פיבונאצ’י במקומות האי זוגיים. למרבה המזל די קל להראות את זה באופן מפורש. בואו נסמן ב-\( A\left(n\right) \) את אורך המילה שמתקבלת מאא”פ אחרי שביצענו \( n \) סיבובים של המשחק. בואו נסמן ב-\( B\left(n\right) \) את אותו הדבר עבור פ”א. אז אני יודע ש-\( A\left(0\right)=B\left(0\right)=1 \) וכמו כן יש לי את שתי המשוואות הבאות:

\( A\left(n\right)=2A\left(n-1\right)+B\left(n-1\right) \)

\( B\left(n\right)=A\left(n-1\right)+B\left(n-1\right) \)

המשוואה הראשונה אומרת: אחרי סיבוב אחד עם א’, אנחנו מחליפים אותו ב”א א פ” ועכשיו נשארו לנו רק עוד \( n-1 \) סיבובים. בסיבובים הללו ה-“א” הראשון יפתח לנו לסדרה באורך \( A\left(n-1\right) \) וכך גם (בנפרד ממנו) ה”א” השני; ואילו ה-“פ” יפתח לסדרה מאורך \( B\left(n-1\right) \). גם המשוואה השניה מחושבת באותו האופן.

כעת, שימו לב שאפשר “לפתוח עד הסוף” את המשוואה השניה על ידי הצבות חוזרות ונשנות של \( B \):

\( B\left(n\right)=A\left(n-1\right)+B\left(n-1\right)=A\left(n-1\right)+A\left(n-2\right)+B\left(n-2\right)=\dots=A\left(n-1\right)+\dots+A\left(1\right)+A\left(0\right) \)

כלומר, \( B\left(n\right) \) הוא בסך הכל סכום כל ה-\( A \)-ים עד ולא כולל \( A\left(n\right) \). אפשר להציב את זה במשוואה הראשונה ולקבל:

\( A\left(n\right)=2A\left(n-1\right)+A\left(n-2\right)+\dots+A\left(0\right) \)

שימו לב שאני הצבתי את הנוסחה ש”פתחתי עד הסוף” לא ב-\( B\left(n\right) \) אלא ב-\( B\left(n-1\right) \) ולכן הסכום התחיל מ-\( A\left(n-2\right) \).

עכשיו קחו את הנוסחה הזו והציבו במקום \( n \) את \( n-1 \) ותקבלו:

\( A\left(n-1\right)=2A\left(n-2\right)+A\left(n-3\right)+\dots+A\left(0\right) \)

מה שמעניין כאן הוא שבשתי המשוואות שקיבלתי, ה”זנב” זהה - שתיהן מהצורה “משהו ואז הסכום \( A\left(n-3\right)+A\left(n-4\right)+\dots+A\left(0\right) \)”. זה אומר שאם אני אחסר את המשוואה מהשניה כל ה”זנב” הזה יתבטל:

\( A\left(n\right)-A\left(n-1\right)=2A\left(n-1\right)+A\left(n-2\right)-2A\left(n-2\right) \)

נעביר אגפים ונפשט ונקבל:

\( A\left(n\right)=3A\left(n-1\right)-A\left(n-2\right) \)

וזו בדיוק הנוסחה לסדרת פיבונאצ’י במקומות האי זוגיים שחישבתי קודם! עכשיו אנחנו מבינים עד הסוף מאיפה היא הגיעה.

אחרי שהבנו איך זה קורה, אפשר לשאול את השאלה כמה זה נדיר - “מה ההסתברות שזה יקרה”. הבעיה היא שלא ממש ברור איך מודדים הסתברות כזו, והדרכים שנראות מתבקשות נעות בין טעויות תמימות לבין הטעיות של ממש, כמו שיש בסרטון שקישרתי אליו ומציג את העניין. לב העניין בכך שכשאני שואל “מה ההסתברות שיקרה כך וכך” אני צריך להבהיר לעצמי מה בעצם ההגרלה שמתבצעת כאן - ואפשר לחשוב על שלל הגרלות שונות ומשונות שנותנות תוצאות שונות לגמרי ולא ברור מי מהן היא ההגרלה ה”נכונה”.

הנה השאלה בצורה מסודרת: נניח שאני מגריל אלפבית כלשהו. מה ההסתברות שהסדרה שתתקבל מהאות א’ תהיה סדרת פיבונאצ’י-במקומות-האי-זוגיים? נשמע סביר? ובכן, מה זה בכלל אומר, “אלפבית כלשהו”? כמה אותיות יהיו באלפבית? 22, כמו בעברית? אולי 26 כמו באנגלית? ולמה לא 7, בעצם? הרי ראינו שה”קסם” שיש בעברית נובע משבע אותיות בלבד. וכשאני אומר “אלפבית כלשהו”, איך אני קובע מה יהיו השמות של האותיות? האם לבחור שמות שהאורך שלהם הוא מגודל שרירותי? כלומר, האם לאפשר אותיות שהשמות שלהן הם מאורך 1,000 אותיות? בעברית האותיות הרלוונטיות הן בעלות שמות מאורך 2 או 3 בלבד. אולי לבחור רק את האורכים הללו? והאם יש מגבלות נוספות על בחירת האותיות של השמות? בעברית האות הראשונה בשם של כל אות היא האות הזו עצמה (אל”ף מתחיל בא’, בי”ת מתחיל בב’ וכן הלאה). האם לדרוש את זה במפורש בהגרלה שאנחנו מבצעים?

כל השאלות הללו הן קריטיות. כאמור, הסיבה לכך שפיבונאצ’י צץ בעברית הוא שהסיטואציה היא ממש פשוטה. שיש מעט מאוד אותיות שמעורבות במשחק הזה, וכל שם של אות מתחיל באות הזו עצמה, וכדומה. אם נשנה קצת את הכללים הללו הסיכוי שנקבל סדרה פשוטה כמו פיבונאצ’י אכן יהיה אפסי; אבל איך מחליטים אילו כללים לקחת ואילו לא לקחת? כפי שאתם רואים, כל השאלות הללו לא מוגדרות היטב, ולכן כל השאלה של “מה ההסתברות שזה יקרה” היא בעייתית. עדיין, מי שלא מתחשק לו כשהוא רואה את זה לנסות כל מני הגרלות שונות ומשונות ולראות מה צץ - לא מבין אתכם. בחלק הבא נדבר על מה עושה מי שכן רוצה לבצע הגרלות שונות ומשונות.

לסיום החלק הזה אני רוצה לומר בכל זאת מילה על הסרטון שקישרתי אליו - ספציפית, אל ה”ניתוח” ההסתברותי שמתואר שם (הניתוח אינו בסרטון עצמו אלא מצורף כתגובה לסרטון בדף היוטיוב; הנה צילום מסך). הניתוח הזה הוא רמאות גמורה שהדבר הטוב היחיד שאפשר להגיד עליה הוא שייתכן שהיא נובעת מבורות במתמטיקה ולא מרצון לעבוד על הקוראים. אני לא אתעמק בו כי חבל על הזמן אבל אם מישהו רוצה לשאול שאלה קונקרטית עליו הוא מוזמן לעשות זאת בתגובות. החישוב הזה הוא דוגמה נאה במיוחד לצורך בהגדרה מסודרת של מרחב המדגם שלנו ושל המאורעות שאת ההסתברות שלהם אנחנו מודדים - כל נסיון לבצע את הפורמליזציה הזו עם מה שהוא מעולל שם פשוט לא הולך לעבוד (למשל, זה נראה שבמקום להגריל אלפבית ולראות מה קורה איתו, הוא מגריל בכל איטרציה במשחק את מה שכל אות הולכת לייצר). מה שכן מעניין שם הוא האופן שבו הוא מבצע את הסימולציה - הוא בוחר בתוך הסימולציה שמות לאותיות מאורכים שמתפלגים בדומה להתפלגות אורכי המילים בעברית באופן כללי. זה, כמובן, מאוד לא מציאותי; השמות של אותיות האלפבית העברי הן קצרות מאוד (ה-4 של גימל הוא היוצא מן הכלל באורכו). בואו נעבור לדבר עכשיו על איך מבצעים סימולציות ומה באמת הפרמטרים הסבירים לסימולציות שכאלו.

חלק שני שבו אנחנו כותבים קוד ומנפנפים בידיים

הדבר החשוב ביותר כשבאים לבצע סימולציות, כמובן, הוא למצוא דרך לחשב מהר את נוסחת הנסיגה עבור אלפבית שרירותי. כאן נכנס לתמונה ידע מתמטי לא טריוויאלי לחלוטין שעוסק בתיאוריה של כל הסיטואציה הזו - גם כדי להוכיח שבכלל תמיד מתקבלת נוסחת נסיגה, וגם כדי לדעת איך אפשר למצוא אותה. הידע הזה הוא היתרון המרכזי שיש לי על פני האדם המזדמן שנתקבל בסרטון הזה ותוהה אם מה שיש שם נכון או לא. הוא יכול לכתוב את האיברים הראשונים של מה שמתקבל מא’ בעצמו, ואולי גם לכתוב תוכנית מחשב שמייצרת אותם, אבל מתי בדיוק הוא אמור להפסיק? אחרי שהוא ניסה את 1000 האיברים הראשונים וראה שיוצא אותו דבר?

מה שאני עושה הוא לכתוב סקריפט פייתון שמקבל אלפבית כלשהו, גם שרירותי ומונפץ, ומחשב את נוסחת הנסיגה עבור כל אות שלו. למה פייתון? כי אני מתבסס על ספריה מתמטית שנקראת Sympy והיא שימושית מאוד לחישובים שאני מבצע. הנה קטע הקוד המלא שמקבל את האלפבית (בתור מילון שבו המפתחות הן אותיות והערך שמותאם לכל מפתח הוא הכתיב של האות) ומוציא את רשימת נוסחאות הנסיגה:

def gf_to_recurrence_relation(gf):
    gf = gf.simplify()
    coeffs = Poly(fraction(gf)[1],x).coeffs()
    c = (-1 / coeffs.pop())
    coeffs = [co*c for co in coeffs]
    init_vals = Poly(gf.nseries(x,0,len(coeffs))).coeffs()
    init_vals.pop()
    init_vals.reverse()
    return (coeffs, init_vals)

def find_gfs(letters, letter_names):
    n = len(letters)
    m = Matrix([[letter_names[letters[j]].count(letters[i]) for i in range(n)] for j in range(n)])
    u = Matrix([[1] for k in range(n)])
    gfs = (eye(n) - x * m)**(-1) * u
    return gfs

def find_recurrence_relations(letter_names):
    letters = letter_names.keys()
    letters.sort()
    gfs = find_gfs(letters, letter_names)
    return [(letter, gf_to_recurrence_relation(gf)) for letter,gf in zip(letters,gfs)]

מה לעזאזל קורה בקוד הזה? ובכן, את זה אסביר בחלק השלישי. אני מראה אותו כאן רק כדי שתראו עד כמה זה קל לבצע את החישוב הזה, בהינתן ידע לא נרחב בתכנות ובמתמטיקה.

הדבר הראשון שעושים, כמובן, הוא להפעיל את זה על עברית (עם האיות החריג של תא”ו ושל וא”ו) ולראות שזה עובד. הנה חלק מהתוצאות שקיבלתי:

Letter: א, Recurrence: ([-1, 3], [1, 3])
Letter: ד, Recurrence: ([2, -7, 5], [1, 3, 9])
Letter: ו, Recurrence: ([2, -7, 5], [1, 3, 9])
Letter: ל, Recurrence: ([-1, 3], [1, 3])
Letter: מ, Recurrence: ([2], [1])
Letter: פ, Recurrence: ([-1, 3], [1, 2])
Letter: ת, Recurrence: ([2, -7, 5], [1, 3, 9])

אני מציג את נוסחת הנסיגה בתור זוג של רשימות. הראשונה היא רשימת המקדמים של נוסחת הנסיגה, מהקטן לגדול; השניה היא רשימת האיברים הראשונים בסדרה שמגדירה נוסחת הנסיגה. אז עבור א’ יש לנו את הרשימה \( \left[-1,3\right] \) שמתארת את נוסחת הנסיגה \( A\left(n\right)=3A\left(n-1\right)-A\left(n-2\right) \) עם רשימת האיברים הראשונים \( \left[1,3\right] \) שמתארת את \( A\left(1\right)=1 \) ו-\( A\left(2\right)=3 \), ואכן מתקבלים פה בדיוק מספרי פיבונאצ’י במקומות האי זוגיים. עבור ה’ למשל מתקבלים אותם מקדמים של נוסחת הנסיגה אבל עם האיברים הראשונים \( \left[1,2\right] \), וזה מניב את רשימת האיברים של פיבונאצ’י במקומות הזוגיים. אין עוד משהו ממש מעניין פרט לכך עבור עברית.

עכשיו, אם עשינו את זה בעברית אפשר לעשות את זה לשפות אחרות! האם מקבלים משהו נחמד? ובכן, ניסיתי לעשות את זה עבור אנגלית, רוסית, יוונית וערבית. פיבונאצ’י לא צץ שוב. עבור רוסית, יוונית וערבית כל סדרות הנסיגה שהתקבלו היו מסובכות יחסית. באנגלית קרה בדיוק ההפך - קיבלתי סדרות מאוד פשוטות. למשל, הסדרה \( 1,2,3,\dots \) והסדרה \( 1,3,5,7,9,\dots \) וכדומה, וכמובן שגם דברים מסובכים טיפה יותר כמו \( 1,2,9,22,41,66,97,134,177,226 \) (עבור y). מה השתבש? איפה ההבדל בין זה ובין עברית? ובכן, ברוסית, יוונית וערבית שמות המילים מסובכים יותר מאשר בעברית - ארוכים יותר, ומערבים יותר אותיות. באנגלית המצב שונה בצורה דרסטית: כל חמש האותיות שמייצגות תנועה, a,e,i,o,u הן בעלות “שם” בן אות אחת - הן עצמן. זה הופך את הסדרה שלהן לסדרה הטריוויאלית \( 1,1,1,1,\dots \). שמות מרבית האותיות האחרות מבוססים על לקיחת האות והוספה של תנועה אחריה. למשל d היא dee. מכיוון ש-e מייצרת רק את עצמה, הסדרה שתתקבל מ-d היא d,dee,deeee,deeeeee וכן הלאה - קיבלנו את כל האי-זוגיים. ה”בעיה” הזו לא ייחודית לאנגלית - כל שפה עם אלפבית שמתבסס על זה הלטיני תהיה בעלת תכונה דומה (הסתכלתי למשל על צרפתית, שוודית, דנית והונגרית והגעתי למסקנה שאין טעם אפילו לנסות אותן).

האם יש שפות נוספות שכדאי לנסות לחפש בהן? אתם מוזמנים להציע כאן הצעות, ורצוי כאלו שיבואו עם מילון מתאים שאני יכול כבר להזין לסקריפט שלי.

עברו כמה שנים מאז שהפוסט פורסם עד שטרחתי להציג את השאלה הזו בפני קהל חרוץ, ומהר מאוד נתגלתה דוגמא פשוטה אף יותר מאשר בעברית: בשפה הגרמנית, איות אפשרי של A הוא AH ואיות אפשרי של H הוא HAH, ושני אלו מניבים, בהתאמה, את האיברים הזוגיים והאי-זוגיים בסדרת פיבונאצ’י (נסו!). אני מקווה שזה סוגר סופית את הדיון עם כל מי שמנסה להשתמש בתכונה המתמטית היפה הזו כדי להוכיח משהו שאינו קשור למתמטיקה, ואפשר לחזור להתמקד בכמה שמתמטית המשחק הזה נחמד.

מהניסויים הללו אפשר לשער קריטריון לגבי מה צריך להיות האיפיון של אלפבית “טוב”, כזה שפיבונאצ’י מתחבא בו. הנה הקריטריונים שחשבתי עליהם: שיהיו בו רק שבע אותיות (ליתר דיוק, שיהיו בו שבע אותיות שהשמות של כולן מורכבים רק מאותן שבע אותיות). שהשם של כל אות יהיה באורך 2 או 3. שהשם של כל אות יכלול את האות הזו עצמה. בהינתן שלושת הקריטריונים הללו, אפשר לבצע סימולציה - להגריל הרבה אלפביתים מלאכותיים, לחשב את נוסחאות הנסיגה עבורן ולראות מה קורה. סימולציה רצינית תצטרך לכלול מאות אלפי אלפבתים רציניים. אני רצתי על מדגמים קטנים בהרבה, כך שכל מה שאני כותב על הסימולציות יכול וצריך להילקח בערבון מוגבל מאוד; אני לא חושב שזה חשוב מספיק כדי להצדיק מחקר רציני יותר, אבל מי שסקרן תמיד יכול לכתוב את הקוד בעצמו.

התחלתי אם כן עם הקריטריונים שתיארתי לעיל. בניסוי הזה מה שקיבלתי הוא שבערך 10 אחוז מהאלפביתים יתנו את פיבונאצ’י במקומות האי זוגיים. שזה, לדעתי, לא רע. צריך לזכור שגם עבור עברית האיות הסטנדרטי לא עובד ונדרשו כמה “נסיונות” שונים (כלומר, כמה איותים שונים) כדי שנקבל אחד שבו התופעה צצה (עם הכתיב המוזר למראה של ת’ בתור תא”ו). כמובן שעכשיו זו שאלה מעניינת לראות איך סיכויי ההצלחה משתנים כאשר משנים את הפרמטרים השונים.

כשניסיתי להגדיל את אורך השמות האפשרי עד 10 הסקריפט לא הצליח למצוא שום פיבונאצ’י וגם קרס בשלב מסויים מרוב חישובים. לא כל כך מפתיע, וממחיש יפה איזה חיים קלים עשו לעצמם מי שבחרו לבצע רק סימולציה כזו. כשחזרתי לאורך מקסימלי 3, אבל הרשיתי גם אורך 1 (כמו באנגלית) אחוזי ההצלחה צללו ל-4.5%, כך שזו בהחלט נראית כמו תכונה שמקלקלת קצת. התעצלתי ולא טרחתי להפוך את התרחיש הזה לדומה עוד יותר למה שקורה באנגלית - שם אורך 1 שייך בלעדית לתנועות, והשמות של כמעט כל אות מורכבים בעיקר מתנועות. אין לי ספק שזה היה מוריד את הסיכוי עוד יותר.

ניסוי מתבקש אחר הוא להשאיר את אורך המילים ב-2-3, אבל להרשות לשם של אות לא להתחיל באותה האות. ציפיתי שזה יפגע בסיכויי ההצלחה, אבל לא שיערתי עד כמה - החישובים נהיו מסובכים פי כמה וכמה ואחוזי ההצלחה הפכו לאפסיים. עבור כל השפות האמיתיות שבדקתי התכונה הזו של אות שהיא הראשונה בשם שלה התקיימה ברוב האותיות; עכשיו נראה לי שהתכונה הזו ממש קריטית. האם אתם מכירים שפות שבהן זה לא מתקיים? מכל מקום ברור שסימולציה שלא דורשת את התכונה הזו במפורש היא עוד סוג של עבודה בעיניים.

ניתן להמשיך עם עוד ועוד סימולציות ואתם מוזמנים להציע כאלו בתגובות ואולי אוסיף אותן כאן בדיעבד, אבל כרגע נראה לי שמה שבאמת מעניין הוא מה לעזאזל עושה הקוד שלי ומה התיאוריה הכללית מאחורי כל העסק הזה. בואו נדבר על זה.

חלק שלישי ובו אנחנו מגיעים למתמטיקה

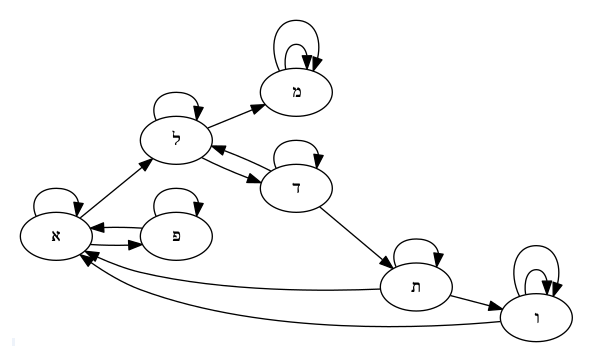
טוב, אז עכשיו בואו נפסיק עם הטיזינג ונסביר סוף סוף את המתמטיקה שהולכת פה. מה שיש לנו הוא מקרה פרטי של סיטואציה כללית שבקומבינטוריקה מתייחסים אליה בתור Transfer-matrix (זה שם שמופיע גם בשלל הקשרים אחרים; אם תחפשו אותו בויקיפדיה, למשל, בכלל לא תמצאו את הדבר הקומבינטורי שאני מתאר, שאותו אפשר למצוא למשל בפרק 4.7 ב-Enumerative Combinatorics של Stanely, חלק ראשון). קומבינטוריקה אנומרטיבית מתעסקת בספירה של איברים מסוג מסויים בהתאם לגודל \( n \) שלהם (למשל, מספר התמורות מגודל \( n \) הוא \( n! \)). מה אנחנו סופרים בסיטואציה של Transfer-matrix? הכי קל לדמיין את זה, לדעתי, הוא בתור ספירה של מסלולים בגרף. קחו גרף מכוון \( G=\left(V,E\right) \) שבו מותר שיהיו קשתות מקבילות (כלומר, יותר מקשת אחת באותו כיוון בין זוג צמתים). קחו זוג צמתים \( v,u\in V \) כלשהם ותשאלו את השאלה הבאה: מה מספר המסלולים מאורך \( n \) מ-\( v \) אל \( u \) (כאשר מסלולים שעוברים בקשתות מקבילות נספרים בנפרד)? בעיית הספירה הזו היא בדיוק בעיית Transfer-matrix, ועל כל בעיה שמטופלת עם Transfer-matrix אפשר לחשוב כבעיה כזו.

אצלנו צמתי הגרף כוללים את כל האותיות באלפבית שלנו, ויש קשת מאות \( a \) אל אות \( b \) לכל מופע של \( b \) באיות של \( a \). הנה הגרף עבור החלק הרלוונטי של השפה העברית עבורנו:

המספר שאנחנו סופרים בסופו של דבר הוא את מספר המסלולים מהאות א’ אל כל האותיות האפשריות. מה אומר מסלול מאורך 3, למשל, מהאות א’ לאות אחרת? הוא מתאר את האופן שבו האות האחרת הזו נוצרת מתוך א’ - את מי א’ גזר שאחר כך גזר אות אחרת שבסוף גזר את האות שבקצה המסלול.

איך מחשבים את זה? אני מניח שדי ברור שמאוד בזבזני לייצר את כל האותיות בפועל, כפי שעושים בסרטון כדי לעשות רושם. מה שעושים במתמטיקה הוא להשתמש באלגברה לינארית - ספציפית, כפל מטריצות. בפוסט שלי על כפל מטריצות תיארתי במדויק את האופן שבו משתמשים בכפל כזה בדיוק לצורך פתרון בעיית ספירת המסלולים הזו, כך שלא אחזור על זה כאן. הנה השורה התחתונה: אם \( A \) היא המטריצה שמייצגת את הגרף, דהיינו \( A_{ij} \) כוללת את מספר הקשתות מ-\( v_{i} \) אל \( v_{j} \), אז \( A^{n} \) מכילה את מספר המסלולים מאורך \( n \): \( \left(A^{n}\right)_{ij} \) הוא בדיוק מספר המסלולים מאורך \( n \) מ-\( i \) אל \( j \). לכן, אם אנחנו רוצים “לחלץ” מהמטריצה את מספר המסלולים מאורך \( n \) מצומת כלשהו אל כל הצמתים בגרף, נגדיר \( u=\left[\begin{array}{c}1\\1\\\vdots\\1\end{array}\right] \) ונחשב את הכפל \( A^{n}\cdot u \). התוצאה תהיה וקטור שבכניסה ה-\( i \) שלו יש את מספר המסלולים מאורך \( n \) מ-\( v_{i} \) אל כל הצמתים בגרף.

העניין הוא שהקומבינטוריקה לא עוצרת כאן. ראינו איך אפשר לחשב מספר עבור \( n \) ספציפי, אבל הקומבינטוריקה רוצה למצוא מידע על כל ה-\( n \)-ים בבת אחת. נוסחה סגורה שתלויה ב-\( n \) היא דבר אחד שאפשר לרצות, ולמעשה יש כזו; אבל היא תהיה כל כך מבורחשת שכבר נצטער שביקשנו את זה. אפשר לשאול האם יש לנו במקרה הזה נוסחת נסיגה. אני טענתי קודם שכן, תמיד יש נוסחת נסיגה; בואו נבין עכשיו למה זה כל כך ברור.

הקסם פה הוא שבהינתן מטריצה מעל שדה, יש נוסחת נסיגה עבור חזקות של המטריצה. כלומר, החל ממקום מסויים אפשר לתאר את \( A^{n} \) בתור צירוף לינארי של חזקות קטנות יותר. הנה דרך מיידית לראות את זה, שדורשת רק מעט מאוד אלגברה לינארית: אם \( A \) היא מסדר \( k\times k \) היא איבר של מרחב וקטורי ממימד \( k^{2} \) (קחו את כל המטריצות \( e_{ij} \) שיש בהן 0 בכל מקום למעט 1 בכניסה \( i,j \); זו קבוצה בלתי תלויה שפורשת את המרחב). מכאן שאם ניקח \( k^{2}+1 \) איברים במרחב הזה הם יהיו תלויים לינארית. אז בואו ניקח את \( A^{0},A^{1},A^{2},\dots,A^{k^{2}} \). קיים צירוף לינארי לא טריוויאלי \( \sum\lambda_{n}A^{n}=0 \); ניקח את החזקה הגבוהה ביותר של מטריצה שהמקדם שלה שונה מאפס, נחלק במקדם הזה את המשוואה, נעביר אגף, והופס, קיבלנו נוסחת נסיגה. מהנימוק הזה רואים שנוסחת הנסיגה תכלול לכל היותר \( k^{2} \) צעדים אחורה; אבל מתמטיקה טיפה יותר מתקדמת מראה שהמצב עוד יותר פשוט. משפט קיילי-המילטון אומר שהפולינום המינימלי שמאפס את \( A \) מחלק את הפולינום האופייני של \( A \), שלא חשוב כרגע מה הוא אבל הדרגה שלו היא \( k \); זה אומר שקיימת נוסחת נסיגה שמערבת לכל היותר \( k \) איברים אחורה. אם נחזור לעברית, אז בגרסה שבה יש לנו רק 7 אותיות, זה אומר שנוסחת הנסיגה שלנו תהיה לכל היותר בת 7 איברים אחורה. זה “שדה המשחק” שלנו מלכתחילה; אין שום סיכוי, עבור שום אלפבית שבעולם מהגודל הזה (ולא משנה כמה מסובך האיות של שמות המילים בו), שנקבל נוסחאות נסיגה מסובכות יותר, או משהו שבכלל לא ניתן לתיאור על ידי נוסחת נסיגה.

איך מוצאים את נוסחת הנסיגה בפועל? אפשר למצוא את הפולינום המינימלי של המטריצה, אבל יש דרך אחרת, שנראית פסיכית יותר והיא כנראה יעילה יותר. מה שאני הולך למצוא הוא את הפונקציה היוצרת של הסדרות הרלוונטיות; מהפונקציה היוצרת אפשר “לקרוא” את נוסחת הנסיגה. את כל זה תיארתי כבר בפוסט קודם, שבמקום לדבר על מסלולים בגרף דיבר על מילים שמתקבלות על ידי אוטומט סופי; אם חושבים על זה שניה ברור שזה אותו הדבר. החישוב שאני עושה בפועל הוא זה: לוקח את \( A \); כופל אותה בפולינום \( x \) (פולינום ממעלה 1 עם מקדם חופשי 0 ומקדם מוביל 1); מפחית את התוצאה ממטריצת היחידה \( I_{k} \); ואז מחשב את ההופכי של כל העסק הזה, כלומר את \( \left(I_{k}-xA\right)^{-1} \). כדי שתהיה משמעות לחישוב הזה צריך להבין שעברנו לעבוד בחוג המטריצות מעל שדה הפונקציות הרציונליות עם מקדמים ששייכים לשדה שמעליו היינו קודם (נאמר, הרציונליים). זה אומר שאחרי ביצוע החישוב, הכניסות של המטריצה שנקבל יהיו פונקציות רציונליות, ואז נבצע את הכפל \( \left(I_{k}-xA\right)^{-1}\cdot u \) ונקבל וקטור של פונקציות רציונליות, שאפשר להוכיח שהן הפונקציות היוצרות של הסדרות הרלוונטיות.

כאן נגמר הקסם של האלגברה הלינארית ומתחיל הקסם של ניתוח פונקציות יוצרות רציונליות, שגם אליו לא אכנס כרגע. הפאנץ’ הוא זה: עבור סדרה שמיוצגת על ידי פונקציה רציונלית, המכנה של הפונקציה הרציונלית מקודד את נוסחת הנסיגה. למשל, אצלנו עבור א’ מתקבלת הפונקציה היוצרת הבאה:

\( \frac{1}{x^{2}-3x+1} \)

מה שעושים תמיד הוא לקחת את סדרת המקדמים של הפולינום במכנה, להעיף ממנה את המקדם החופשי, לכפול הכל במינוס 1, והתוצאה שמתקבלת (כשקוראים אותה החל מהמקדם המוביל) היא סדרת המקדמים של נוסחת הנסיגה. מתמטיקה בפעולה, אנשים!

אם תסתכלו על הקוד תראו שזה גם בדיוק מה שאני עושה. כמובן, זה עדיין לא מוצא את כל המידע על נוסחת הנסיגה - צריך גם לדעת את האיברים הראשונים של הסדרה. כדי לדעת את זה, מפתחים את הפונקציה הרציונלית לטור טיילור ומוצאים את האיברים הראשונים (גם את זה הקוד שלי עושה). כאן המונה של הפונקציה בא לידי ביטוי - מונים שונים יגררו ערכי התחלה שונים. עבור פ’, למשל, הפונקציה היוצרת היא

\( \frac{1-x}{x^{2}-3x+1} \)

זה משחק נחמד, להבין איך המונה בדיוק משפיע.

זו הסיבה שבגללה כל הסיפור הזה נראה לי מגוחך מלכתחילה. אני יכול להבין את ההתלהבות של מי שלא ברור לו שאמורה להיות חוקיות כלשהי בסדרת המספרים שמופקת במשחק המוזר הזה, אבל לי היה ברור מלכתחילה שיש חוקיות של נוסחת נסיגה. היה משהו מפתיע בכך שהתקבלה נוסחת נסיגה פשוטה כל כך - שני איברים אחורה במקום 22 - אבל כפי שראינו בתחילת הפוסט, קצת בדיקה מראה בדיוק מה הגורמים שמביאים לכך (העובדה שיש רק 7 אותיות במשחק, ושיש מידה לא מעטה של סימטריה גם ביניהן, ומיעוט הקשתות באופן כללי). עבורי ההילה המיסטית נעלמה, אבל הכיף שבלדבר על דברים מגניבים במתמטיקה שמעורבים בסיפור הזה נותר.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: