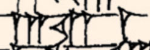המעשה המופלא בלוח המסתורי פלימפטון 322

בדיוק סיימתי פוסט על אחת מהתעלומות הגדולות במדעי המחשב - תעלומה בקושי בת עשור וקצת. נראה לי די מתאים, אם כן, לעבור לדבר על תעלומה במתמטיקה שהמקור שלה הוא בן אלפי שנים (אם כי הפולמוס סביב אותו מקור הוא בן פחות ממאה שנה) - התעלומה של לוח החרס הבבלי שנקרא “פלימפטון 322” ואפשר לראות כאן:

התעלומה הזו בדיוק עלתה שוב לכותרות ולכן זו הזדמנות פז להזכיר אותה כאן, וסוג של סגירת מעגל - את הפוסט הזה רציתי לכתוב עוד מראשית ימי הבלוג וכבר התחלתי והפסקתי אותו כמה פעמים.

מה בעצם התעלומה הגדולה? כרגיל, אני לא מאמין בלהשאיר אתכם במתח: אנחנו יודעים בדיוק מה הלוח הזה מכיל - הוא מכיל כמה טורים של מספרים שמהווים שלשות פיתגוריות (התיאור המדויק קצת יותר מסובך ואביא אותו בהמשך). ה”תעלומה” היא להבין מה המשמעות של הלוח - מה הייתה המטרה שלו, מי יצר אותו ואיך, ומה הוא מלמד אותנו על המתמטיקה הבבלית. יש שלוש פרשנויות עיקריות: אחת היא שהמטרה בלוח הייתה לרכז שלשות פיתגוריות ושהקיום שלו מעיד על כך שהבבלים שלטו בשיטה למציאת שלשות פיתגוריות; השניה היא שהמטרה של הלוח הייתה להוות טבלה טריגונומטרית ושהוא מראה שהבבלים שלטו בטריגונומטריה (העליה לכותרות היא בדיוק עקב מאמר חדש שתומך בגישה הזו וטוען שהבבלים היו פורצי דרך בתחום הזה) והשלישית היא שאין שום דבר מיוחד בלוח ושאפשר לתת הסבר בנאלי לאופן שבו הוא נוצר, שלא מעיד על רמה מתמטית מיוחדת אצל הבבלים.

מי צודק? אין לי מושג. אני מקווה שהפוסט הזה יעזור להבהיר קצת עד כמה היסטוריה של המתמטיקה, בפרט היסטוריה עתיקה של המתמטיקה, היא עסק קשה. באופן כללי בהיסטוריה יש תמיד סכנה גדולה שההיסטוריון יפרש מאורעות ומקורות היסטוריים מתוך נקודת מבט אנכרוניסטית - ניתוח מודרני שמכניס מושגים זרים ומודרניים לסיטואציות שהם לא היו בהן בכלל. במתמטיקה הסכנה הזו גדולה מאוד, מכיוון שהמתמטיקה שאנחנו מכירים כיום, ולומדים כיום באוניברסיטה, היא שונה למדי באופיה מזו שהתקיימה בעבר. לא מדובר רק על סימונים ועל הגדרות (וכמובן, על גילויים חדשים) אלא גם על דרכי התבוננות וחשיבה (למשל, מה בכלל נחשב “הוכחה” בתקופות שונות). רבים מהמשפטים המתמטיים שאנחנו לומדים כיום תחת שמותיהם של מתמטיקאים גדולים בכלל נוסחו והוכחו בצורה שונה (דוגמה טריוויאלית היא “משפט לגראנז’” בתורת החבורות - משפט בסיסי ביותר, שהוכח על ידי לגראז’ הרבה לפני שהיה קיים בכלל המושג של חבורה…). אז כשמנסים להבין טקסט מתמטי היסטורי, צריך לעבוד קשה מאוד כדי להכניס את עצמנו לעולם המושגים והלכי החשיבה של כותבי הטקסט.

בואו נתחיל.

פרק ראשון, ובו אנחנו מציגים את התיאור היבש של לוח שהיה כל כך יבש עד ששרד 4,000 שנים

השנה היא 1922. מוציא לאור אמריקאי עשיר בשם ג’ורג’ ארתור פלימפטון רוכש לוח חרס מהארכיאולוג והאספן אדגר ג’יימס בנקס (טיפוס צבעוני למדי - לא מפתיע לגלות שכנראה היווה השראה כלשהי לדמות של אינדיאנה ג’ונס). מה מקורו של הלוח? בנקס טען שמקורו בעיר הבבלית הקדומה לרסה שבמסופוטמיה (לא הצלחתי להבין אם בנקס חפר אותו במו ידיו או - סביר בהרבה - שקנה אותו ממישהו שחפר אותו באקראי) ועד כמה שאני מבין, ראיות ארכיאולוגיות אחרות תומכות בכך (דהיינו, סגנון הכתיבה תואם ממצאים אחרים שנמצאו בלרסה). פלימפטון היה אספן לא קטן של עתיקות ובערוב ימיו תרם את האוסף שלו לאוניברסיטת קולומביה. המספר הסידורי של הלוח באוסף הוא 322 ולכן הוא נקרא כיום פלימפטון 322.

לא נראה שפלימפטון או בנקס הבינו מה יש להם ביד. אני משער שהם ידעו לקרוא את המספרים שמופיעים בלוח (עוד מעט נראה כמה זה קל) אבל שהייתה חסרה להם ההבנה המתמטית עד כמה מה שנמצא שם הוא מעניין מבחינה מתמטית. בקטלוג של אוניברסיטת קולומביה הלוחית תוארה בתחילה כמכילה “עסקה מסחרית”. הקרדיט על ה”גילוי” של פלימפטון 322 ניתן לאוטו נויגבאואר. גם על נויגבאואר אפשר לכתוב פוסטים שלמים - במקור הוא היה מתמטיקאי אוסטרי שהשתייך לאוניברסיטת גטינגן כשהייתה בשיא כוחה, בשנות ה-20 וה-30 של המאה ה-20; ואז הגיעו הנאצים והרסו את הכל. נויגבאואר לא היה יהודי אך סירב לשתף עם הנאצים פעולה, הושעה ממשרתו ובסופו של דבר הסתלק לארה”ב ושם חי 50 שנים נוספות. נויגבאואר ושותפו אברהם זקס חקרו בצורה יסודית טקסטים מתמטיים בכתבי יתדות - הם פרסמו ספר שזה בדיוק שמו, ופלימפטון 322 נכלל בו, עם האבחנה עד כמה התוכן שלו מעניין, והסבר מוצע אפשרי אחד לתוכן הזה. בואו נתחיל מלדבר על התוכן הזה בלי להיכנס עדיין לפרשנויות.

הנה שוב הלוח, בתמונה שמאפשרת לראות קצת יותר טוב מה הולך בו. אל תדאגו, לא אבקש מכם לעשות את זה בפועל.

והנה ציור שבו העסק ממש ברור:

הלוח נכתב בכתב יתדות ורוב רובו כולל מספרים שנכתבו בשיטה הבבלית, אז זו הזדמנות טובה לתאר את השיטה המרהיבה הזו, שללא ספק העידה על גישה מתקדמת למתמטיקה. זו שיטה שמתבססת על בסיסי ספירה, כלומר על כך שכל “ספרה” לא מייצגת ערך מספרי קבוע אלא כזה שמוכפל בחזקה כלשהי של בסיס הספירה. במקרה הנוכחי בסיס הספירה של הבבלים היה מוזר במיוחד - לא פחות מאשר 60. למה 60? יש כמה הסברים לכך, למשל שבגלל הפירוק הנחמד לגורמים של \( 60=2\times2\times3\times5 \) הרבה שברים יצאו נחמדים בו. נחזור לנקודה הזו בהמשך. אם איני טועה בסיס 60 המדובר הוא המקור לכך שבדקה יש 60 שניות ובשעה יש 60 דקות ובמעגל יש 360 מעלות, אבל ייתכן שאני טועה, זה ממש לא תחום שאני בקיא בו.

לכאורה, בשביל לייצג מספרים בבסיס 60 צריך לא פחות מאשר 60 ספרות שונות, וזה די הרבה. מה שהבבלים עשו הוא להשתמש בשיטה משנית לייצוג מספרים: כל מספר היה אפשר לתאר באמצעות קבוצה של קווים ומשולשים. קו שווה 1 ומשולש שווה 10 וכל מספר מיוצג על ידי כך שמציירים כמה קווים וכמה משולשים סמוכים זה לזה. כך זה נראה:

כשאנחנו מצויידים בידע המרשים הזה אפשר לגשת למלאכה של תרגום החלק המספרי של הטבלה. למשל, בשורה 12 של המספרים (לא כולל שורת הפתיחה של הטבלה) ועמודה 2 נמצא הדבר הבא:

מה יש לנו כאן? אני רואה פה שתי קבוצות שונות: השמאלית ביותר כוללת שני משולשים ושבעה קווים, כלומר היא 27, ואילו הימנית כוללת 5 משולשים ועוד 9 קווים, כלומר היא 59. אני יכול לכתוב את המספר הזה בתור \( 27:59 \) ויהיה ברור לכם למה אני מתכוון. אם ארצה לכתוב את המספר הזה בבסיס 10 אני אחשב ואקבל \( 27\cdot60^{1}+59\cdot60^{0}=1,620+59=1,679 \).

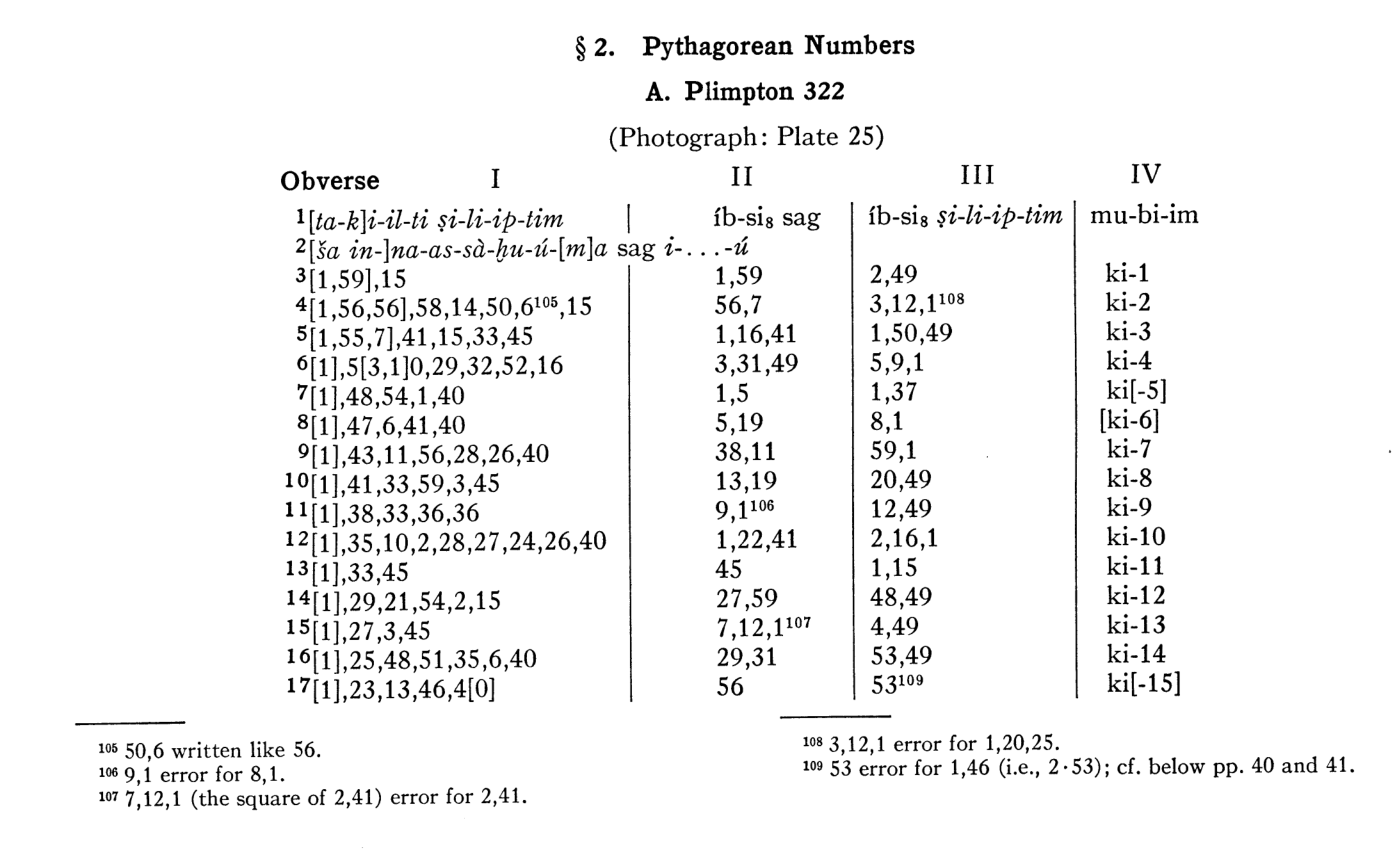
אחרי שהבנו את הרעיון הבסיסי הזה, לתרגם את יתר המספרים בלוח זה עניין טכני בלבד, ולכן אני בטוח שתשמחו אם אביא לכם פשוט את רשימת המספרים המלאה שמופיעה בלוח. אעשה את זה עוד רגע, אבל בואו נבין מה בדיוק הלוח כולל. הוא כולל ארבע עמודות ו-17 שורות, כאשר שתי השורות העליונות כוללות כותרות לעמודות ויתר השורות כוללות מספרים. בהתחלה היה נראה לי שיש חמש עמודות אבל שתי העמודות ה”נפרדות” הימניות ביותר הן למעשה עמודה אחת. הכתב הימני ביותר בעמודה הזו כולל את המספרים מ-1 עד 15 (אפילו אנחנו ההדיוטות כבר מסוגלים לראות את זה) והסימון שמשמאל למספרים הללו בכל אחת מהשורות אומר ki, שזה (אל תתפסו אותי במילה! אני רק מעביר הלאה את מה שאמרו לי!) בערך כמו לומר “כ”. כלומר, העמודה הזו משמשת רק למספור והאקשן מתרחש בעמודות האחרות.

מה שעוד אפשר לראות הוא שיש שני פגמים בולטים בטבלה - אחד בעמודה הימנית של המספרים, ושם קל לנחש מה היה אמור להיות, והשני בצד השמאלי למעלה, וגם שם נראה בהמשך שאפשר להעלות השערה סבירה ביותר מה השחזור ה”נכון”, כך שהנזק לטבלה הוא לא מהותי. הרבה יותר מהותית העובדה שנראה שהחלק השמאלי ביותר של הטבלה נשבר - כלומר, שבמקור הטבלה הייתה אמורה להימשך עוד שמאלה. אולי היו אמורות להיות עוד עמודות, ואולי היה אמור להיות כתוב עוד משהו בעמודה השמאלית ביותר. ההשערה המקובלת היא שאולי היה כתוב “1” נוסף בכל התאים בעמודה השמאלית ביותר - עוד מעט נבין למה. אני מסביר את כל אלו מראש כי עכשיו אני הולך להביא את ה”תרגום” של הטבלה ואני רוצה שנבין את מה שהולך שם. הנה התעתוק שמופיע אצל נויגבאואר. נויגבאואר מתרגם את הלוח כמות שהוא, ומציין מספר ערכים שלדעתו הם שגיאות. עוד רגע נתייחס לזה.

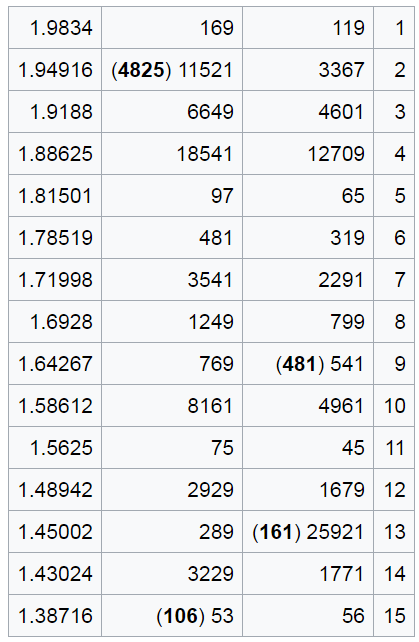
מכיוון שכל המספרים כתובים בבסיס 60 קצת קשה לנו לקרוא אותם, אז הנה ה”תרגום” שלהם לבסיס עשרוני (כאשר השגיאות שנויגבאואר מציין כבר מתוקנות, והערך המקורי מופיע בסוגריים):

העמודה הימנית היא, כאמור, מספור פשוט. העמודה השמאלית ביותר… עוד מעט נגיע אליה. בואו נדבר על שתי העמודות האמצעיות. במבט ראשון קשה לומר שיש שם משהו מעניין, אבל נויגבאואר וזקס נתנו גם מבט שני ושלישי וראו שמה שקורה שם הוא מאוד מעניין: הערכים המספריים שם מתאימים לשלשות פיתגוריות. בואו נזכיר את המושג הזה: שלשה של מספרים טבעיים \( a,b,c \) היא שלשה פיתגורית אם \( a^{2}+b^{2}=c^{2} \). השם “שלשה פיתגורית” מגיע ממשפט פיתגורס שאומר שבמשולש ישר זווית עם צלעות באורכים \( a,b,c \) (כאשר \( c \) היא הצלע הגדולה, זו שמול הזווית הישרה) מתקיים \( a^{2}+b^{2}=c^{2} \). כלומר, שלשה פיתגורית היא בעצם תיאור של אורכי הצלעות של משולש שאורך הצלעות שלו הוא מספר שלם. השלשה הפיתגורית הפשוטה ביותר היא \( 3,4,5 \); השלשות שנמצאות בפלימפטון 322 הן מסובכות יותר.

“רגע אחד”, אתם אומרים, “לא שכחת משהו? שלשה פיתגורית? אנחנו רואים פה רק שתי עמודות”. ובכן, כן: העמודות פה, שאני מסמן ב-\( s,d \), נותנות רק שניים מתוך שלושת אברי השלשה - את הצלע שמול הזווית של ה-90 מעלות (זו d) ואת הצלע הקצרה של המשולש (זו s). את הצלע השלישית, שנקרא לה \( l \), אפשר להסיק חשבונית: \( l=\sqrt{d^{2}-s^{2}} \). אם נעשה את זה עבור השורה הראשונה, למשל, שם \( s=119 \) ו-\( d=169 \) נקבל ש-\( l=120 \).

זה עובד גם עבור יתר השורות, פרט לארבע שורות: 2,9,13,15. בשורה 9, למשל, השגיאה ברורה לגמרי: במקור בעמודה של \( s \) נכתב \( 9,1 \) במקום \( 8,1 \). התפלק לו. מקרים אחרים הם קצת פחות מובהקים אבל נעזוב את זה, לפחות כרגע.

ברגע שבו אנחנו רואים את הקשר הזה בין העמודות ברור לגמרי שהלוח לא מייצג “עסקה מסחרית” או משהו דומה - זה לוח בעל משמעות מתמטית מובהקת, ולא היה ברור בכלל שהיו לבבלים את הטכניקות המתאימות לייצר אותו. במילים אחרות, זו תגלית מעניינת ביותר בפני עצמה ששופכת אור על המתמטיקה הבבלית, אבל לא לגמרי ברור עדיין איזה אור.

ומה קורה בעמודה השמאלית ביותר? גם היא כוללת נתון שאפשר לחשב משתי העמודות האמצעיות: או \( \frac{d^{2}}{l^{2}} \) או \( \frac{s^{2}}{l^{2}} \). מכיוון ש-\( l^{2}+s^{2}=d^{2} \) הרי ש-\( \frac{d^{2}}{l^{2}}=\frac{l^{2}+s^{2}}{l^{2}}=1+\frac{s^{2}}{l^{2}} \), ומכאן שההבדל בין שני המספרים \( \frac{d^{2}}{l^{2}} \) ו-\( \frac{s^{2}}{l^{2}} \) הוא בסך הכל 1, כך שההבדל לא מהותי. מכיוון שתמיד יוצא ש-\( s<l \) בכל העמודות, הרי ש-\( \frac{s^{2}}{l^{2}} \) הוא תמיד מספר בין 0 ל-1, ולכן האופן שבו קוראים את העמודה השמאלית ביותר הוא בתור שבר בבסיס 60. למשל, בשורה מספר 11 (מה שאצל נויגבאואר מסומן ב-13 כי הוא סופר גם את שורות הכותרת) הערך שכתוב בעמודה השמאלית הוא 33,45. אם אנחנו מפרשים את המספר הזה בתור שבר, אז אנחנו צריכים לחבר חזקות שליליות של 60, כלומר לחשב את

\( 33\cdot60^{-1}+45\cdot60^{-2}=\frac{33}{60}+\frac{45}{3600}=\frac{2025}{3600}=0.5625 \)

השלשה הפיתגורית של אותה שורה היא \( 60,45,75 \) (שהיא בעצם השלשה 3,4,5 ב”תחפושת” - כופלים כל אחד מהאיברים בשלשה ב-15), ועל כן \( \frac{s^{2}}{l^{2}}=\left(\frac{3}{4}\right)^{2}=0.5625 \). כלומר, אין ממש ספק ביחס לנוסחה של הערכים שמופיעים בעמודה השמאלית. התהיה היחידה היא האם היה אמור להיות \( 1. \) לפני כל אחד מהערכים שם (במקרה שבו הערך שם הוא \( \frac{d^{2}}{l^{2}} \)) וכל ה-1-ים הללו נשברו מהטבלה (כי, כזכור, החלק השמאלי אכן שבור).

אם תסתכלו לרגע על רשימת המספרים שבעמודה השמאלית, כנראה תשימו לב לתופעה מעניינת למדי שמתרחשת שם: המספרים מופיעים בעמודה בסדר יורד, ולא סתם בסדר יורד אלא בקצב די אחיד - אם נצייר גרף של הערכים הללו במרווחים קבועים נקבל קו כמעט ישר שעובר ביניהם. זו כבר גלישה לפרשנות, אבל נראה לי די ברור שזה לא מקרי ושזה מעיד על החשיבות של העמודה השמאלית (שהיא לכאורה עמודה “מיותרת” כי אפשר לחשב אותה מהאחרות). נחזור לזה בהמשך, כשנדבר על הפרשנויות.

אוקיי, הבנו מה הערכים המספריים בטבלה, אבל מה התרגום של הכותרות של העמודות? שוב, אני לא מבין בכך שום דבר ורק מצטט גדולים ממני: את העמודה הימנית ביותר אפשר לתרגם בתור “השם שלו” או “המקום שלו” - זה מתאים לכך שבעמודה הזו יש מספר סידורי. העמודה השניה מימין נקראת “ה-ib-si של האלכסון” ואילו השלישית מימין נקראת “ה-ib-si של הרוחב”. מה זה ib-si? זה לא לגמרי ברור. נויגבאואר אומר שלפעמים המשמעות של זה היא “השורש הריבועי” או “הצלע של הריבוע” אבל בדרך כלל משתמשים בביטוי כדי לתאר מספר שהוא תוצאה של חישוב או פתרון של תרגיל מסויים. זו דוגמה טובה לקושי האדיר שיש לנו להבין תגליות כאלו אפילו אם הן באות עם תוכן עניינים!

ואז מגיעה העמודה השמאלית ביותר, שבאה עם כותרת ארוכה משמעותית מהיתר. לרוע המזל, הכותרת הזו נפגעת מאחד מהפגמים של הלוח. נויגבאואר הסתבך עם התרגום של החלק הזה, ומאמרים חדשים יותר שיפרו אותו לאט לאט. בסוף מקבלים משהו בסגנון “ה-takiltum של האלכסון שממנו הוחסר 1 כך שהצד הקצר comes up’’ (אין לי מושג מה הצורה הטובה ביותר לתרגם comes up כאן, כך שאני משאיר את הביטוי האנגלי הזה שמוסכם על חלק מהמאמרים). מה זה takiltum? לא ברור; ככל הנראה זו דרך לומר “ריבוע” ועוד נחזור לזה אחר כך.

בזאת סיימנו להסביר מה בעצם התוכן של הלוח. אני מקווה שגם ברור בשלב הזה שהתוכן הזה מעניין. מעניין מאוד אפילו. לא סתם אומרים תגלית היסטורית חשובה ביותר. עכשיו צריך לעבור לדבר על החלק הבעייתי יותר - מה הפרשנות של הממצאים הללו. כלומר, לנסות לתת תשובות לשאלות כמו

1. מי יצר את הלוח הזה?
2. למה הוא יצר את הלוח? איזו מטרה הוא בא לשמש?
3. איך נוצר הלוח? באיזו שיטה מתמטית?

פרק שני, ובו אנחנו מייצרים שלשות פיתגוריות

בואו נתחיל מלדבר על הפרשנות שנויגבאואר נתן ללוח, כי הוא היה הראשון והפרשנות שלו היא עדיין הנפוצה ביותר שאני רואה בדיונים על הלוח. עד כמה שאני רואה, נויגבאואר לא נכנס לשאלת מי יצר את הלוח ולמה; אבל הוא מתאר שיטה שבה הוא היה עשוי להיווצר - השיטה הסטנדרטית לייצור שלשות פיתגוריות. השיטה הזו הולכת כך: בואו ניקח שני מספרים טבעיים כלשהם \( p>q \), ונגדיר \( a=p^{2}-q^{2},b=2pq,c=p^{2}+q^{2} \), אז קל לראות את הדבר הבא:

\( a^{2}+b^{2}=\left(p^{2}-q^{2}\right)^{2}+\left(2pq\right)^{2}= \)

\( p^{4}-2p^{2}q^{2}+q^{4}+4p^{2}q^{2}=p^{4}+2p^{2}q^{2}+q^{4}= \)

\( \left(p^{2}+q^{2}\right)^{2}=c^{2} \)

כלומר, מכל \( p>q \) טבעיים אנחנו מקבלים שלשה פיתגורית. אפשר להראות שכל שלשה פיתגורית תתקבל באופן הזה. השיטה הזו, בניסוח גאומטרי, מופיעה ב”יסודות” של אוקלידס (ספר X, טענה 29, למה 1) ולכן לפעמים זה נקרא “נוסחת אוקלידס”, אם כי לקרוא לזה בשם הזה, זה טיפה מטעה - כאמור, אצל אוקלידס הכל נוסח בצורה גיאומטרית ולא הייתה נוסחה אלגברית כפי שנתתי כאן. כל הרעיון של נוסחאות אלגבריות שכאלו היה זר ליוונים ונכנס למתמטיקה שלנו רק במאות האחרונות.

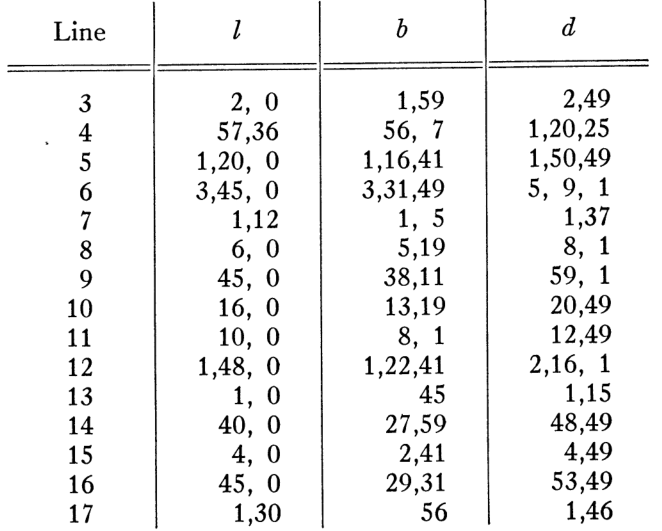
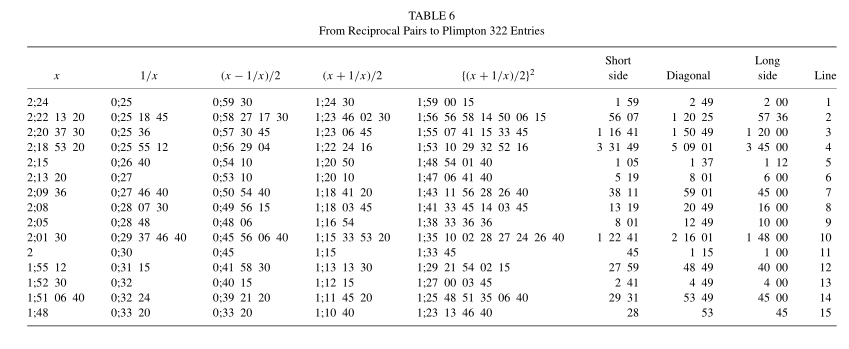
מה נויגבאואר עושה? ראשית הוא מציין את העובדה שתיארתי כבר, לפיה העמודה השמאלית ביותר ממוינת בסדר יורד כמעט לינארי. שנית, הוא אומר - בואו נכתוב שניה במפורש את העמודה ה”חסרה” של הערך של הצלע השלישית של המשולש. הנה הטבלה שלו (\( b,d \) הם מי שקראתי להם \( s,d \) קודם) עם המספרים בבסיס 60:

ועכשיו נויגבאואר אומר - היי תראו איזה יופי הערכים של \( l \) נראים ביחס לערכים של \( s,d \). הם הרבה יותר עגולים (ביחס לבסיס 60). מה קורה פה? ובכן, הוא מציע שכל המספרים התקבלו מהנוסחה עם \( p,q \) כאשר \( l=2pq \) תמיד. אם \( p,q \) שניהם “פשוטים” אז גם \( 2pq \) יהיה כזה (להבדיל מ-\( p^{2}+q^{2} \) ו-\( p^{2}-q^{2} \) שיכולים להיראות איכסה). למה נויגבאואר מתכוון ב”פשוטים”? למה שנקרא במתמטיקה מספרים רגולריים. בואו נראה דוגמא.

כאשר אני רוצה לכתוב את חצי, \( \frac{1}{2} \), בתור שבר עשרוני, מה שיוצא לי הוא \( 0.5 \). אם אני רוצה לכתוב את \( \frac{1}{5} \) כשבר עשרוני יוצא לי \( 0.2 \). אם אני רוצה לכתוב את \( \frac{1}{4} \) כשבר עשרוני יוצא לי \( 0.25 \) ואם אני רוצה לכתוב את \( \frac{1}{8} \) יוצא לי \( 0.125 \). לעומת זאת אם אני רוצה לכתוב את \( \frac{1}{3} \) כשבר עשרוני יוצאת לי הזוועה \( 0.333\dots \). מה ההבדל? בכל המקרים הראשונים, הייצוג העשרוני היה סופי. אחרי מספר ספרות הוא הסתיים (או, לחילופין, נמשך עד אינסוף עם רצף אפסים). לעומת זאת שליש לא מסתדר לי טוב - אני ממשיך עם ה-3 עד אינסוף. זה אמנם ייצוג מחזורי אבל הוא מרגיש פחות נחמד מאשר המספרים הקודמים. מה הוביל להבדל הזה? התשובה היא שבכל הדוגמאות בהתחלה, המספר במכנה הורכב מחזקות של 2 או של 5. לעומת זאת במקרה של \( \frac{1}{3} \) המכנה לא מקיים זאת. למה שזה יהיה חשוב? בואו נראה דוגמא: אם אני כופל את \( \frac{1}{4} \) ב-\( \frac{25}{25} \) (בסך הכל כפל ב-1) אני מקבל \( \frac{25}{100} \), ואת המספר הזה קל להמיר לייצוג עשרוני סופי - לוקחים את המונה ופשוט מחלקים אותו פעמיים ב-10, כלומר מזיזים את הנקודה העשרונית פעמיים שמאלה. מ-\( 25.0 \) אנחנו מגיעים ל-\( 0.25 \). באופן דומה עבור \( \frac{1}{8} \) אנחנו מקבלים \( \frac{1}{8}\cdot\frac{125}{125}=\frac{125}{1000}=0.125 \). במילים אחרות, קיבלנו ייצוג עשרוני סופי בגלל שיכלנו לכפול את המכנה במספר כלשהו ולקבל חזקה של 10. את 3 אין שום דרך לכפול במשהו ולקבל חזקה של 10: כי נניח ש-\( 3n=10^{k} \), אז אגף שמאל מתחלק על ידי 3 אבל אגף ימין לא מתחלק על ידי 3 אלא רק על ידי 2,5 ומכפלות שלהם.

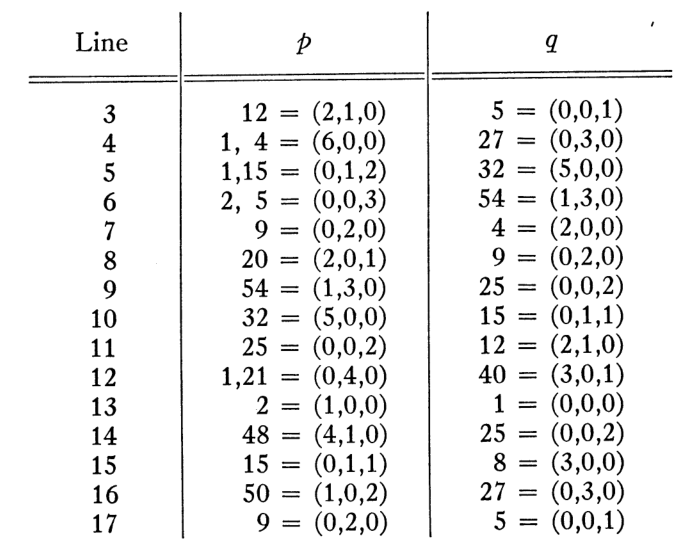
דבר דומה קורה בבסיס 60, אבל שם המצב קצת טוב יותר. בניגוד ל-10, שמתחלק רק על ידי 2 ו-5, עבור 60 יש לנו גם את 3 בתור מחלק. זה אומר שלכל מספר שהוא מכפלה של חזקות של 2,3,5 אנחנו נקבל ייצוג סקסגסימלי (“בבסיס 60”) סופי. נויגבאואר עכשיו אומר את הדבר המופלא הבא: אם נסתכל על ה-\( p,q \) שיוצרים את הטבלה של פלימפטון 322, נראה שכולם הם מספרים סקסגסימליים רגולריים. הוא טורח לחשב טבלה שלהם ולכתוב הצגה של כל אחד מהם בתור חזקות של \( 2,3,5 \): הכתיב \( \left(\alpha,\beta,\gamma\right) \) בא לתאר את המספר \( 2^{\alpha}3^{\beta}5^{\gamma} \).

זה מלמד אותנו משהו על קריטריון אפשרי של מי שיצר את הלוח - לתת רק שלשות פיתגוריות שנוצרות על ידי מספרים רגולריים. אבל איך אותו אדם ידע אילו \( p,q \) כדאי לו לבחור? בוודאי אם היעד שלו היה לייצר רשימה יורדת לינארית של ערכי \( \frac{d^{2}}{l^{2}} \)? ובכן, נויגבאואר אומר, בואו ניקח את הנוסחאות \( d=p^{2}+q^{2} \) ו-\( l=2pq \) ונציב אותן ב-\( \frac{d}{l} \). מה נקבל?

\( \frac{d}{l}=\frac{p^{2}+q^{2}}{2pq}=\frac{1}{2}\left(\frac{p}{q}+\frac{q}{p}\right) \)

הביטוי באגף ימין כולל את ההופכיים של \( p,q \) ולכן הייצוג שלו בבסיס 60 הוא סופי אם ורק אם \( p,q \) הם רגולריים. אם כן, אומר נויגבאואר, אם היוצר של הלוח רצה להבטיח שהעמודה השמאלית תהיה שבר בעל ייצוג סופי, הוא היה חייב לבחור \( p,q \) רגולריים כדי להבטיח זאת. זו גם השיטה שהוא מציע שבה נבנה הלוח - היוצר שלו בחר \( p,q \)-ים עבורם הוא כבר ידע את \( \frac{p}{q},\frac{q}{p} \) כך שהסכום שלהם יהיה קרוב ככל הניתן ל-\( \frac{d}{l} \) שהוא היה מעוניין בו, ואז בנה מ-\( p,q \) את השלשה הפיתגורית המתאימה.

המסקנה של נויבאואר הייתה שהבבלים הכירו את השיטה לייצור שלשות פיתגוריות שמתוארת אצל אוקלידס - כלומר, שהם הקדימו את אוקלידס ב-1,500 שנים. לא רע!

פרק שלישי, ובו איפכא מסתברא

נויגבאואר היה החלוץ, אבל לא מעט חוקרים באו אחריו. אני הולך להתעלם מכולם ולקפוץ מהר מהר קדימה, לשנת 2001, לזוג מאמרים שפירסמה אלינור רובסון, פרופסורית להיסטוריה בקולג’ האוניברסיטאי של לונדון. אפשר לקרוא את המאמרים כאן וכאן. התקציר שלהם פשוט - ההסבר של יצירת פלימפטון 322 באופן שנויגבאואר מתאר, וגם ההסבר (שלא נכנסתי אליו כרגע) של היצירה שלו בתור טבלה טריגונומטרית הם לא סבירים ולא מסתדרים עם הידע ההיסטורי שלנו; ואפשר לתת הסבר פשוט יותר לאופן שבו פלימפטון 322 נוצר. כזה שלא מניח שהבבלים הכירו נוסחאות ליצירה של שלשות פיתגוריות או השתמשו בטבלאות טריגונומטריות.

מכיוון שאלו מאמרים רחבים למדי, אין סיכוי שאוכל לעשות להם צדק כאן - אעביר רק את הרעיונות הכלליים. למען הסר ספק, אני חושב שאלו מאמרים מרתקים: הם ממחישים בצורה נפלאה עד כמה עבודת ה”בלשות” של ההיסטוריה של המתמטיקה היא בעייתית וכמה קל לתת לחשיבה המודרנית שלנו להיכנס לתמונה בצורה שגויה.

אז מה הבעיה עם הפרשנות של נויגבאואר? הנה כמה ראשי פרקים. שום דבר כאן הוא לא מוחלט, כמובן; רובסון מסכימה לחלוטין עם כך שמבחינה מתמטית הפרשנות של נויגבאואר היא תקפה לחלוטין. השאלה היא רק כמה היא מתאימה לקונטקסט ההיסטורי.

1. לוחות דומים לפלימפטון 322 נקראים משמאל לימין, אבל בסדר הזה לא ברור למה העמודה השמאלית קיימת בכלל ומה מטרתה. היא לא נחוצה לחישוב השלשות הפיתגוריות.
2. אם אכן הטבלה נוצרה בעזרת זוגות \( p,q \) שנכתבו בצד שמאל השבור שלה, הזוגות הללו לא מסודרים בסדר הגיוני כלשהו (כדוגמת המיון שמתבטא בעמודה השמאלית ביותר).
3. אין הסבר ברור למה דווקא אותם \( p,q \) שנבחרו (15 מתוך מאות אפשריים, בהנחה ש-\( p,q \) נלקחו מתוך טבלאות ידועות של מספרים הופכיים) נבחרו.
4. אין הסבר טוב לחלק מהשגיאות שנפלו במהלך החישוב, בפרט זו של שורה 2 (לכך אתייחס עוד מעט).
5. וכמובן, נקודת החוזק של פלימפטון 322 היא גם עקב האכילס שלו: אין לנו אינדיקציה אחרת להיכרות של הבבלים עם הנוסחה של אוקלידס לייצור שלשות פיתגוריות, מה שמעמיד בספק את האפשרות שהלוח נוצר באמצעותה.

נקודה 5 היא ככל הנראה הנקודה המעניינת ביותר כאן, כי זו דילמה שלא ברור איך אפשר להכריע אותה בצורה סבירה. אם גילינו ממצא שעבורו יש לנו פרשנות נפלאה שמעידה על ידע מתמטי מתקדם ביותר שלא ידענו שהיה קיים בתרבות הזו, האם זה אומר שהתרבות הייתה יותר מתקדמת משחשבנו, או שאולי אנחנו מפרשים לא נכון את הממצא? אין לי תשובה לזה.

הפרשנות השניה שרובסון מנסה לפסול היא הפרשנות שלפיה הלוח הוא טבלה טריגונומטרית. עדיין לא תיארתי את הפרשנות הזו, כי וריאציה עליה היא בדיוק מה שנמצא במאמר החדש שהוא הטריגר לפוסט הנוכחי ואני לא חושב שהטיעונים של רובסון רלוונטיים לגביו. רובסון אומרת, למשל, שאצל הבבלים עיגול נתפס לא בתור רדיוס מסתובב אלא בתור היקף שחוסם שטח, ועל פי הגישה הזו הם מחשבים שטח שלו וכדומה. זה טוב ויפה, אבל אני לא בטוח שנכון לומר שזה מה שטריגונומטריה או לוחות טריגונומטריים מתעסקים בו. אני אחזור לנקודה הזו כשנדבר על הפרשנות השלישית.

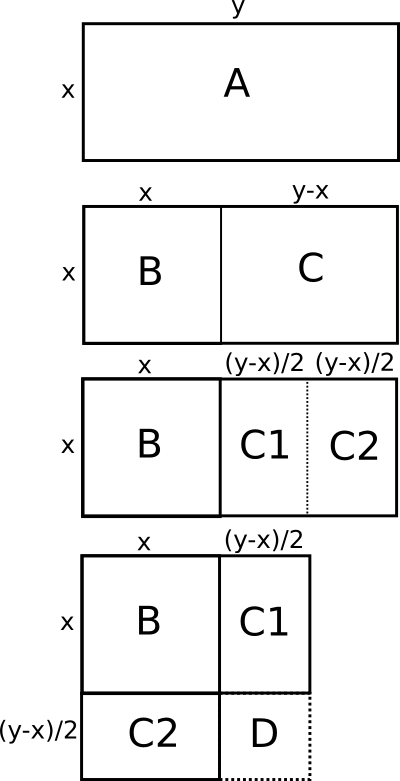
בואו נדבר עכשיו על הפרשנות שרובסון כן מאמצת (הרעיון המקורי אינו שלה והיא מייחסת אותו ל-Bruins ואחרים, אבל המאמרים שלה טורחים לספק לו קונטקסט רלוונטי). על פי רובסון, ייתכן שהלוח היה אוסף של תרגילי חשבון שבהם השתמשו בהוראה. יש לכך קונטקסט היסטורי סביר - נמצאו לוחות אחרים שבהם זה בדיוק מה שקורה. רובסון מביאה דוגמא של לוח אחר, שנקרא YBC 6967 (שימו לב: לוח שאינו פלימפטון 322) שכולל את התרגיל הבא, בניסוח מודרני: נניח ש-\( x,y \) הם “הופכיים” במובן זה שהמכפלה שלהם היא חזקה של 60 ושההפרש ביניהם הוא 7. מה ערכם? פתרון מודרני יגיד משהו כזה: נסמן \( y=\frac{60}{x} \) (הבחירה בהנחה ש-\( xy=60 \) היא שרירותית משהו אבל רובסון מנמקת אותה קצת, ומכל מקום זה מה שהולך בלוח) ונכתוב \( x-y=7 \). מהצבת המשוואה הראשונה בשניה נקבל \( x-\frac{60}{x}=7 \), נכפול ב-\( x \), נעביר אגף, נקבל \( x^{2}-7x-60=0 \), וכעת נשתמש בנוסחת השורשים ונקבל \( x_{1,2}=\frac{7\pm\sqrt{49+240}}{2}=\frac{7\pm17}{2}=12,-5 \). אם פוסלים את הפתרון השלילי נקבל \( x=12,y=5 \). זה כמובן פתרון נכון אבל השיטה שבה מצאנו אותו היא מודרנית למדי - שיטה אלגברית שלא הייתה מוכרת אצל הבבלים. הפתרון בלוח מתבסס על שיטת עבודה גאומטרית שביסודה היא דומה מאוד למה שעשינו - נוסחת השורשים נולדה ממנה, ואחד מהפוסטים האהובים עלי בבלוג מתאר את זה בדיוק. אני אפילו יכול למחזר את התמונה מהפוסט ההוא, שמתאר איך מתבצעת שיטת ההשלמה לריבוע:

אנחנו חושבים על \( x,y \) כאילו הם מייצגים מלבן שהשטח שלו הוא 60 - זו המשמעות הגאומטרית של \( xy=60 \). בתמונה אני מניח את ההפך מאשר בתרגיל - ש-\( x \) קטן מ-\( y \) (הוא הצלע הקטנה של המלבן). אפשר, אם כן, לחלק את המלבן לשני מלבנים: אחד, \( B \), שגם האורך וגם הרוחב שלו הוא \( x \), והשני, \( C \), שהרוחב שלו הוא \( x \) ואילו האורך שלו הוא \( y-x \). ה”מלבן” \( B \) הוא בעצם ריבוע כי אורך הצלעות שלו זהה. עכשיו נוקטים בתעלול הבא: לוקחים את המלבן \( C \) ומחלקים אותו לשני מלבנים ברוחב זהה: \( \frac{y-x}{2} \). נקרא להם \( C_{1},C_{2} \). לוקחים את \( C_{2} \), “חותכים אותו” מתוך המלבן הגדול ו”מדביקים” מחדש מתחת ל-\( B \). מקבלים מין צורה דמוית האות L מסובבת שכזו. הצורה הזו היא כמעט ריבוע בעצמה, אבל בפינה חסר משהו. את המשהו ש”חסר” מסמנים ב-\( D \). קל לראות שה-\( D \) הזה הוא בעצמו ריבוע, שאורך צלעו \( \frac{y-x}{2} \).

עכשיו, אנחנו יודעים שהשטח של ריבוע הוא הריבוע של אורך הצלע שלו. מכאן המילה “ריבוע” בהקשר של חזקה שנייה הגיעה. לכן השטח של הריבוע הגדול הוא \( \left(x+\frac{y-x}{2}\right)^{2} \). השטח הזה שווה לסכום השטחים של ארבעת המרובעים שבתמונה. והנה הטריק היפה: הסכום של שטחי ארבעת הריבועים שווה לסכום של שטח המלבן המקורי, שהוא כזכור 60, והריבוע המדומיין \( D \) שהשטח שלו הוא \( \left(\frac{y-x}{2}\right)^{2} \) שאותו קל לחשב. המציאה של \( x \) הופכת להיות, אם כך, האלגוריתם הבא:

1. בונים את הריבוע שאורך צלעו \( x+\frac{y-x}{2} \).
2. מחשבים את שטח הריבוע הזה באמצעות הנוסחה \( xy+\left(\frac{y-x}{2}\right)^{2} \).
3. מוציאים שורש לשטח וקבל את \( x+\frac{y-x}{2} \).
4. מחסירים את \( \frac{y-x}{2} \) מהתוצאה ומקבלים את \( x \). כדי לקבל את \( y \) אפשר להוסיף את \( \frac{y-x}{2} \) לתוצאה.

הבבלים לא עבדו עם \( x,y \). זה שוב פעם אנכרוניזם תרבותי לחשוב כך. יצורים כמו \( x,y \) שייכים לאלגברה שהגיעה אלפי שנים לאחר מכן. הלוח שרובסון מתארת עובד עם מקרה קונקרטי עם מספרים קונקרטיים - מספר וההופכי שלו שההפרש ביניהם הוא 7 וההנחה המובלעת היא ששטח המלבן שהם מגדירים הוא 60. התרגום של רובסון למה שהולך בלוח ההוא נשמע בערך כך (אני לא מתרגם במדויק, וההערות בסוגריים הן שלי):

אתה: שבור לחצי את ה-7 שבו המספר גדול מההופכי שלו ו-\( 3.5 \) (\( 3;30 \) אם אתם רוצים לעבוד בבסיס סקסגיסמלי) יופיע (זה החישוב של \( \frac{y-x}{2} \) של שלב 1). כפול את \( 3.5 \) ב-\( 3.5 \) ו-\( 12.25 \) (\( 12;15 \) בבסיס 60) יופיע (זה החישוב של \( \left(\frac{y-x}{2}\right)^{2} \) של שלב 2). הוסף את 60 ל-\( 12.25 \) שצץ (זהו \( xy+\left(\frac{y-x}{2}\right)^{2} \)) ו-\( 72.25 \) (\( 1,12;15 \) בבסיס 60) יופיע. מהו השורש של \( 72.25 \)? \( 8.5 \) (\( 8;30 \) בבסיס 60; זהו שלב 3). הנח שני עותקים של \( 8.5 \). חסר את \( 3.5 \) מאחד מהם (זה נותן את \( x \) בשלב 4) וחבר את \( 3.5 \) לאחד מהם (זה נותן את \( y \) בשלב 4). אחד הוא 12, השני הוא 5.

זו “דוגמא פתורה” שממחישה את השיטה הכללית. אחרי כמה תרגילים כאלו כבר מבינים את הרעיון. זו שיטת לימוד סבירה לגמרי שמאפשרת לבצע חישובים לא טריוויאליים גם ללא אלגברה ונוסחת השורשים, ובהחלט אפשר לראות אותה כאומרת שהבבלים “הכירו את נוסחת השורשים” אפילו שמעולם לא ניסחו אותה באופן אלגברי (למעשה, לא לגמרי הסברתי איך מגיעים לנוסחת השורשים משיטת ההשלמה לריבוע; זה בפוסט שקישרתי אליו).

אתם יכולים כמובן לתהות איך מוצאים את השורש בשלב 3; בטקסט המתורגם שציטטתי אין התייחסות לזה. הבבלים ככל הנראה ידעו להוציא שורשים ריבועיים בעזרת מה שנקרא “שיטת הרון” אבל אני לא רוצה להיכנס לכך בפוסט כי זה לא העניין כאן.

מה שמעניין פה הוא שהחישובים הרלוונטיים להשלמה בריבוע יוצרים שלשה פיתגורית על הדרך, כמעט בהיסח הדעת. בואו נראה את זה. נחזור עכשיו לדבר על המקרה של מספר \( x \) וההופכי שלו \( y \) שלו, כלומר \( xy=1 \) ולא \( xy=60 \) כמו בלוח לדוגמא שרובסון הביאה. כלומר, יש לנו בהתחלה מלבן עם אורכי צלעות \( x,\frac{1}{x} \) ושטח 1. אנחנו משלימים את המלבן הזה לריבוע על ידי כך שאנחנו גוזרים ממנו מלבן קטן \( C \) שאותו אנחנו מחלקים לשני מלבנים בגודל שווה. הרוחב של כל מלבן כזה הוא \( \left(x-\frac{1}{x}\right)/2 \) והאורך שלו הוא \( \frac{1}{x} \). אחרי שגזרנו את אחד מהמלבנים והעברנו אותו צד, אנחנו מקבלים ריבוע חדש, גדול יותר, שאורך הצלע שלו הוא \( \frac{1}{x}+\left(x-\frac{1}{x}\right)/2=\left(x+\frac{1}{x}\right)/2 \). בפרט נקבל שהשטח של הריבוע הגדול הזה הוא \( \left[\left(x+\frac{1}{x}\right)/2\right]^{2} \). שימו לב שהשטח הזה שווה לסכום השטח של המלבן המקורי - 1 - והשטח של הריבוע הדמיוני הקטן שיצרנו, שאורך הצלע שלו היה \( \left(x-\frac{1}{x}\right)/2 \). כלומר, בשיטת ההשלמה לריבוע נוצר השוויון הטריוויאלי \( 1+\left[\left(x-\frac{1}{x}\right)/2\right]^{2}=\left[\left(x+\frac{1}{x}\right)/2\right]^{2} \).

אם אנחנו עובדים עם מספרים קונקרטיים ולא עם נוסחאות, אז נקבל פה שני מספרים \( A,C \) כך ש-\( A^{2}+1=C^{2} \). המספרים \( A,C \) הללו הם לאו דווקא שלמים אבל הם רציונליים - יש גורם משותף \( B \) כך ש-\( AB,CB \) שניהם שלמים. אם כופלים בגורם המשותף הזה בריבוע את המשוואה \( A^{2}+1=C^{2} \) מקבלים \( \left(AB\right)^{2}+B^{2}=\left(CB\right)^{2} \). אם נסמן \( a=AB,b=B,c=BC \) קיבלנו שלשה פיתגורית \( a^{2}+b^{2}=c^{2} \). שימו לב איך קיבלנו אותה: לקחנו מספר ואת ההופכי שלו, חיברנו וחיסרנו אותם וחילקנו ב-2.

מצד אחד, השיטה הזו לא כל כך רחוקה ממה שנויגבאואר דיבר עליו: הוא עצמו אמר, כזכור, שצעד בדרך לבניית הרשימה שלו הוא מציאת \( p,q \) והתבוננות על \( \frac{1}{2}\left(\frac{p}{q}+\frac{q}{p}\right) \). אם נסמן \( x=\frac{p}{q} \) אז \( \frac{1}{x}=\frac{q}{p} \), כלומר את הביטוי הזה אפשר לכתוב בתור \( \frac{1}{2}\left(x+\frac{1}{x}\right) \) שראינו לפני רגע. מצד שני, נויגבאואר פוסל בספר שלו את ההנחה שהרשימה נוצרה על ידי מספרים הופכיים ולא נכנס לפירוט למה. הגישה שלו היא שהבבלים הכירו את הנוסחה הכללית לייצור שלשות פיתגוריות, ומה שרובסון מראה הוא ששלשות כאלו יכולות לצוץ גם בלי להכיר את הנוסחה/השיטה הזו, פשוט כתוצאה מביצוע השלמה לריבוע, שהיא תהליך שהבבלים הכירו היטב.

כדי לתת הסבר אפשרי כלשהו לאופן שבו צצו המספרים שבפלימפטון 322, רובסון נותנת רשימה של \( x \)-ים שמייצרים אותם. אנחנו מקבלים שהעמודה השמאלית ביותר המסתורית היא בדיוק \( \left[\left(x+\frac{1}{x}\right)/2\right]^{2} \), ואילו שתי העמודות הבאות (האיברים של השלשות) הם פשוט \( \left(x-\frac{1}{x}\right)/2 \) ו-\( \left(x+\frac{1}{x}\right)/2 \) כשהם מוכפלים בגורם המשותף כדי להפוך אותם משברים לשלמים.

זה עדיין לא מאפשר לנו לדעת בודאות איזה תרגיל, אם בכלל, פלימפטון 322 בא לתאר. בניגוד ל-YBC 6967 אין בו הוראות מפורטות לפתרון, והחלק השמאלי שלו חסר. אם, למשל, \( \left(x-\frac{1}{x}\right)/2 \) היה נתון, והמטרה הייתה למצוא את \( \left(x+\frac{1}{x}\right)/2 \) ולהציג את שניהם בתור שלמים, אז פתרון היה כולל את העלאת \( \left(x-\frac{1}{x}\right)/2 \), בריבוע, חיבור 1 לתוצאה, הוצאת שורש מהכל וקבלת \( \left(x+\frac{1}{x}\right)/2 \). בצורה הזו, אחרי השלב של “חיבור 1 לתוצאה” מקבלים את תוצאת הביניים \( \left[\left(x+\frac{1}{x}\right)/2\right]^{2} \), שהיא העמודה השמאלית ביותר של פלימפטון 322. יש עוד כל מני השערות שאפשר להעלות, אבל אין לנו דרך חד משמעית לבדוק אותן.

הנה הטבלה של רובסון:

העמודה הימנית השניה היא שם לצורך שלמות; היא לא באמת קיימת בלוח. כמו כן, כל ארבע העמודות השמאליות ביותר לא מופיעות בלוח וייתכן שהופיעו בלוח השלם, לפני שנשבר. אצל רובסון ה-\( x \)-ים הם בסדר יורד, והסדר הזה משרה את הסדר היורד על העמודה השמאלית ביותר של פלימפטון 322 - כלומר, זה עונה לתעלומה שנויגבאואר השאיר פתוחה (וגם מסביר למה זו העמודה השמאלית ביותר בלוח ולא ימנית יותר). כמובן, אין לנו שמץ של מושג למה דווקא ה-\( x \)-ים הללו נבחרו. חלקם מסובכים למדי ואני לא רואה סיבה טבעית לבחור דווקא אותם.

יתרון יפה של הפרשנות הזו הוא בכוח שלה להסביר את השגיאות הלא טריוויאליות שבלוח. ספציפית, יש שגיאות בשורה 15 ובשורה 2. בשורה 15 זה נראה שהערך באחת העמודות הוא חצי ממה שהוא צריך להיות, או ההפך - שהערך בעמודה השניה הוא פי 2 ממה שהוא צריך להיות. בשורה 2 השגיאה הרבה יותר מוזרה - נכתב שם \( 3,12,1 \) במקום \( 1,20,25 \) שהוא המספר הנכון. בשני המקרים, ההסבר (שרובסון נותנת אבל שייך לכותבים מוקדמים יותר, כלומר הוא כבר היה מבוסס למדי בשלב הזה) הוא שאלו שגיאות שנוצרו בשלב שבו כופלים בגורם משותף כדי לקבל מספרים שלמים (זוכרים? מה שתיארתי קודם בתור “בהינתן \( A^{2}+1=C^{2} \) אז נכפול ב-\( B \)…”). ההכפלה הזו כנראה בוצעה בשלבים - הכותב של הלוח (שעבד על טיוטה גסה ולא על פלימפטון 322 עצמו) קודם כפל ב-2, אחר כך ב-5, אחר כך שוב ב-2 וכן הלאה, לפי מה שהיה נוח לו באותו הרגע). אז במקרה של שורה 15 זה פשוט עניין של שלב אחד שבוצע בטעות פעם אחת יותר מדי עבור אחד מהערכים. עבור שורה 2, כפל פעמיים ב-12 של \( 1,20,25 \) מחזיר לנו \( 3,13,00,00 \). עכשיו, אם הכותב של הלוח העתיק בצורה שגויה מהטיוטה שלו, הוא היה עשוי להתבלבל ולחשוב שאחד מה-1-ים של ה-13 מרוחק מדי מהמספר עצמו ומייצג ספרה חדשה, 1. ככה זה נראה בפלימפטון 322:

תזיזו את ה-1 ההוא קצת שמאלה והוא יתחבר ל-12. נשמע קצת מופרז? ובכן, ההסבר של נויגבאואר לשגיאה של שורה 2 הרבה יותר מסובך מזה. יש משהו מאוד נחמד, לטעמי, בכך שהמקום שבו הכי טוב להעמיד למבחן את התיאוריות השונות לגבי אופן היווצרות הלוח הוא על ידי בחינת הטעויות שבו.

ועכשיו, אחרי ההסבר הזה שמצד אחד הוא מאוד נחמד ומצד שני קצת מצנן את ההתלהבות מהלוח, בואו נעבור לדבר על ההסבר החדש שעושה בדיוק ההפך.

פרק רביעי, ובו אנחנו מנסים להבין כמה חדש יש במאמר החדש

נתקלתי בפלימפטון 322 לראשונה כשקראתי ספר על ההיסטוריה של המתמטיקה אי שם ב-2006. הנושא עניין אותי בצורה לא סבירה וקראתי את שלל המאמרים בנושא, ובפרט את אלו של רובסון שהיו אז חדשים יחסית. ואז שכחתי מהנושא ולא התעסקתי בו עוד. רציתי כמה פעמים לכתוב עליו פוסט, אבל כפי שאתם רואים, לכתוב אפילו על מה שהיה קיים ב-2006 זה סיפור רציני למדי. הפוסט עד כה היה שטחי להחריד (גם כי אין מקום וגם כי כבר שכחתי את כל מה שהלך בו ועכשיו קראתי באופן לא מעמיק את המאמרים), אז זה פשוט לא יצא. מה הסיבה שבגללה עכשיו התיישבתי סוף סוף לכתוב פוסט על הנושא? שקרה הלא יאמן - הוא עלה לחדשות. בגלל מאמר חדש שכותרתו Plimpton 322 is Babylonian exact sexagesimal trigonometry ומציע פרשנות כלשהי למה שהולך בו.

מובן מאליו שבגלל מאמר עם אפקט מצנן כמו זה של רובסון לא היה סיכוי שפלימפטון 322 ייכנס לחדשות. אבל מאמר שטוען “פלימפטון 322 מראה שלבבלים הייתה טריגונומטריה יותר טובה מזו שלנו”? הו, זו כבר התלהבות. אפילו לאתרי החדשות שלנו זה הגיע. הנה אתר Ynet מתפעם: “מדענים מאוניברסיטה בסידני הצליחו כנראה לפתור חידה מתמטית שמסעירה את מוחותיהם של גאונים כבר עשרות שנים” הוא אומר (זו לא חידה מתמטית, זו חידה היסטורית). “על הלוח חרוט מעין “קוד משולש”, ועד כה לא הצליחו מדענים לפענח.” מתפעם המאמר מהאינדיאנה-ג’ונסיות של הנושא (שלשות פיתגוריות אינן “קוד משולש” והלוח עצמו פוענח לפני שנים). רוב שאר המאמר נותן ציטוטים של ד”ר דניאל מנספילד, אחד מהכותבים של המאמר החדש, שמנסה להציג אותו כתגלית ענקית. אוקיי. המאמר של Ynet (כמו רבים אחרים מסוגו) לא מזכיר את נויגבאואר, או את רובסון, או אף אחד מהמתמטיקאים וההיסטוריונים האחרים שחקרו את פלימפטון 322. במאמר של אתר nrg על הנושא מזכירים את אדגר בנקס, ה”אינדיאנה ג’ונס” שהשיג את הלוח מלכתחילה, אבל אין אף מילה על החוקר שגילה לראשונה שהלוח בכלל מעניין (נויגבאואר).

אני מקווה שבשלב הזה של הפוסט כבר ברור שפלימפטון 322 הוא לא “תעלומה” שאפשר “לפתור”. אפשר להציע פרשנויות. אין ממש דרך להכריע מהי הפרשנות הנכונה. כפי שכבר ראינו, האופן שבו נכון להכריע בין פרשנויות שונות הוא על פי הקשרים היסטוריים רחבים יותר. נראה לי לא נכון בעליל לבוא ולהגיד “היי תראו איזה לוח מגניב כנראה שכדי לייצר אותו היו צריכים לדעת את השיטה של אוקלידס לייצור שלשות פיתגוריות אז הנה למדנו משהו חדש על הידע המתמטי הבבלי”. בסקפטיות דומה צריך להתייחס לכל טיעון שמנסה לייחס יכולות מרשימות במיוחד כלשהן לפלימפטון 322. בעיקר אם אין להן גיבוי היסטורי בשום מקום.

אז מה יש במאמר החדש? ראשית כל, הוא כתוב לא רע בכלל. שנית, הוא נותן סקירה מאוד יפה של הרבה מהמאמרים הקודמים ומזכיר את כל מה שהזכרתי בפוסט הזה. כלומר, לא מדובר על חובבנים שבאו משום מקום ולא באמת מכירים את המאמרים של רובסון, למשל. המאמר מציע את האפשרות שכבר הוזכרה במאמרים קודמים והתעלמתי ממנה כאן שפלימפטון 322 יועד להיות בן 38 שורות ולא 15 שורות - כלומר, ה”שחזור” שלהם של פלימפטון 322 כולל עוד 23 שורות נוספות. פרט לכך, מה העמודות שלו? ובכן, בדיוק מה שיש אצל רובסון. אם להיות מדויקים יותר, אצל רובסון העמודות כללו את \( x \), את \( \frac{1}{x} \), ואז את \( \frac{1}{2}\left(x-\frac{1}{x}\right) \) ו-\( \frac{1}{2}\left(x+\frac{1}{x}\right) \) ואז את העמודות של פלימפטון 322. במאמר החדש משתמשים בסימון \( \beta=\frac{1}{2}\left(x-\frac{1}{x}\right) \) ו-\( \delta=\frac{1}{2}\left(x+\frac{1}{x}\right) \) וכוללים בתור שתי העמודות השמאליות ההיפותטיות את \( \beta,\delta \) (כלומר, בלי העמודות של \( x \) ו-\( \frac{1}{x} \)). הלוח כולו כולל, אם כך, את הדברים הבאים: \( \beta,\delta,\beta^{2},b,d \) כאשר \( b,d \) מתקבלים מ-\( \beta,\delta \) על ידי הכפלה בגורם משותף - גם בכך המאמר החדש מקבל את מה שאמרו לפניו, ובפרט את מה שמתואר אצל רובסון (דהיינו, ההסבר עבור השגיאות הוא אותו הסבר - אין פה משהו חדש). מי שרוצה לראות את השחזור של הלוח יכול למצוא אותו בטבלה 9 במאמר.

בתחילת חלק 5 של המאמר ניתן בו תיאור אלגוריתמי של האופן שבו הלוח היה עשוי להיווצר. יש שם התייחסות מעניינת (לא יודע עד כמה משהו בה חדש) לשאלה איך נבחרו הפרמטרים שעל פיהם לייצר את הלוח - לא עוברים על \( x \)-ים באופן שרירותי (כפי שנראה שקורה אצל רובסון) אלא על זוגות של \( r,s \) שמקיימים תכונות מסויימות כמו אצל נויגבאואר. ספציפית, עוברים על \( s \)-ים שמשתייכים לטבלה סטנדרטית כלשהי ואז בוחרים \( r \)-ים כך ש-\( \beta=\frac{1}{2}\left(\frac{r}{s}-\frac{s}{r}\right) \) יתאים תמיד לצלע הקצרה במשולש ישר הזווית המתקבל (זכרו שזה אכן מה שראינו שקורה - הצלע שלא כתובה במפורש בלוח היא תמיד הארוכה מבין שני הניצבים של המשולש). פרט לכך החישובים שמייצרים את הלוח הם אותם חישובים כמו אלו שראינו אצל נויגבאואר ורובסון.

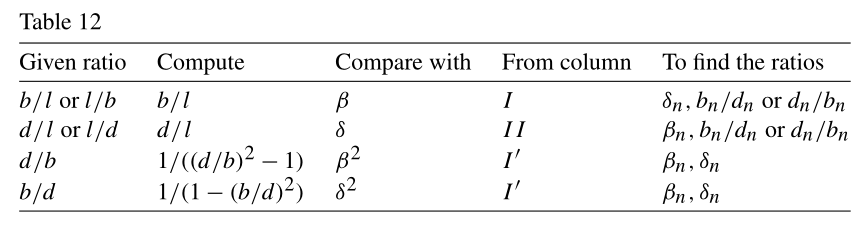
לב המאמר הוא ההצעה של המחברים שלו לראות את פלימפטון 322 בתור טבלה טריגונומטרית. מה זה אומר? ובכן, רובסון פסלה את האפשרות של התבססות על דברים כמו זוויות ורדיוסים של מעגלים וכדומה, אבל הדברים הללו הם לא הכרחיים לטריגונומטריה. בבסיס של הבסיס, הטריגונומטריה מתעסקת בשאלה הבאה: נתון משולש ישר זווית עם אורכי צלעות \( b\le l\le d \) ונניח שאנחנו יודעים את היחס בין זוג צלעות; מהם היחסים בין שני זוגות הצלעות האחרים? בלשון של הטריגונומטריה היוונית ה”רגילה” אנחנו רגילים להסתכל על שני פרטי מידע אחרים: אנחנו מניחים שאנחנו יודעים את הערך המדויק של אחת מהצלעות, ושאנחנו יודעים את אחת מהזוויות של המשולש פרט לזווית הישרה, ומכך אנו מסיקים את יתר אורכי הצלעות במשולש. אבל טריגונומטריה בבסיסה עוסקת ביחסים: אם \( \alpha \) היא הזווית שמול הצלע \( b \) אז \( \sin\alpha=\frac{b}{d} \) ו-\( \cos\alpha=\frac{l}{d} \) ואילו \( \tan\alpha=\frac{b}{l} \). כל הפונקציות הטריגונומטריות הללו הן דרך לייצג יחסים.

מה שהמאמר מציע, אם כן, הוא שפלימפטון 322 שימש בתור סוג של טבלה שבה אפשר היה לחפש את אחד היחסים והוא היה נותן כבר את היתר:

זה תיאור נחמד. בהנחה שהעמודות החסרות בפלימפטון 322 הן מה שהמאמר הציע (וכאמור, גם בפרשנות של רובסון, למשל, אלו העמודות) אז פלימפטון 322 יכל לשמש בתור סוג של טבלה טריגונומטרית שכזו. האם יש לנו אינדיקציה כלשהי, בפרט קונטקסט היסטורי נוסף מהסוג שרובסון מחפשת במאמר שלה, לכך שפלימפטון 322 שימש בתור טבלה טריגונומטרית שכזו? לחלוטין לא. המאמר אומר את זה במפורש בתחילת חלק 6:

There is no known historical evidence that confirms how P322(CR) was actually used. This is a question that must be answered by archeology, or by further discoveries on existing tablets. But we can open the possibility for a trigonometric interpretation

המאמר כן מנסה לשכנע אותנו שטבלה כזו הייתה יכולה להיות שימושית עבור הבבלים: הוא מציג בעיות שלקוחות מלוחות בבליים אחרים ומראה כיצד ניתן לפתור אותן (באופן מקורב) באמצעות פלימפטון 322 המשוחזר שלהם. את הדיון הזה הם מסיימים ב

These examples establish that P322(CR) contains enough information to solve practical geometric problems of the OB era, and hence could have been used as an exact sexagesimal trigonometric table. But if we accept this as a possibility then the immense power of the table becomes clear. We can exhibit this power by applying it to a wider range of problems, which renders our hypothesis more likely such a powerful trigonometric table is not created by accident.

שורת הסיום היא הטענה המעניינת ביותר כאן, כי היא עושה בדיוק את מה שרובסון מזהירה לא לעשות. ממש כשם שפלימפטון 322 לא מוכיחה שלבבלים הייתה היכרות עם נוסחת אוקלידס לשלשות פיתגוריות, כך צריך להיות מאוד זהירים לפני שמניחים שפלימפטון 322 מוכיח שהיה לבבלים בכלל מושג של טבלאות טריגונומטריות, אופן השימוש בהן וכדומה. יש כאן סכנה חמורה של גלישה לאנכרוניזם; אנחנו מכירים את המושגים הללו (נוסחת אוקלידס, טבלה טריגונומטרית) ולכן כשאנחנו רואים אצל הבבלים משהו דומה אנחנו מסיקים שגם הם הכירו את המושג הזה. אין שום ספק שזה היה ממש מגניב אם זה היה המצב, אבל דברים כאלו צריכים להיתמך על ידי ממצאים היסטוריים. במאמר אני לא רואה שיש כאלו, רק תיאוריות יפות.

שיהיה ברור - אין לי שום התנגדות לתיאוריות יפות. החיים כיפיים יותר עם תיאוריות יפות. אבל צריך להכיר בכך שזה כל מה שהן. בפרט כשכותרות העיתונים מדברים על התעלומה הגדולה של פלימפטון 322 ש”נפתרה סוף סוף”.

פרק חמישי, ובו מתגלה הטריגונומטריה הכי טובה אי פעם בדיוק בהחלט!!!!!

עכשיו אנחנו עוברים לחלק המעניין ביותר במאמר החדש - זה שמנסה לטעון שפלימפטון 322 המשוחזר מעיד על מתמטיקה בבלית שהיא טובה יותר מזו שבאה אלפי שנים אחריה. זה החלק שגרם לעיתונות לקפוץ בהתלהבות מעל הפופיק. אני מעדיף לא לצטט עיתונים או הודעות לעיתונות. המאמר עצמו אומר:

Having made the case that P322 is a trigonometric table, we now step well outside of OB mathematics to more recent times in order to make the further claim that P322 is superior in mathematical power to much later trigonometric tables.

אוקיי. אני זורם. מה הם אומרים? הם מבצעים השוואה לטבלה טריגונומטרית מודרנית הרבה יותר, מהמאה ה-14, של מדבה ההודי. הטבלה הזו כוללת את הסינוס של 24 זוויות, בקפיצות של \( \frac{1}{24} \) מ-90 מעלות בכל פעם (כלומר, קפיצה של \( 3.75 \) מעלות). הדרך לחשב סינוס בעזרת הטבלה היא קירוב, כמובן: מוצאים את המספר הקרוב ביותר לזווית שרוצים לחשב בתוך הטבלה ומסתכלים מה הערך שרשום שם. אותו דבר אם נתון לנו הערך של הסינוס ואנחנו רוצים למצוא את הזווית.

המאמר מציג את האופן שבו משתמשים בטבלה של מדהבה ובפלימפטון 322 כדי לפתור שתי בעיות פשוטות בטריגונומטריה. אני אתעסק כאן רק עם הראשונה כי לא היה לי כוח להיכנס כאן לפרטים של השניה. הבעיה הראשונה מתוארת ציורית על ידי רמפה שעולה אל זיגורט שגובהו 45 (לא חשוב 45 מה) ואורך הרמפה הוא 56. השאלה היא מה המרחק על הקרקע מבסיס הרמפה אל פסגת הזיגורט. שזו דרך מסובכת מאוד לומר - הנה משולש ישר זווית ונתון אחד מהאנכים והיתר. נא למצוא את אורך האנך השני. במילים אחרות, הבעיה הבסיסית של הטריגונומטריה.

המאמר פותר את הבעיה בשתי הדרכים ובאופן לא מפתיע פלימפטון 322 יוצא יותר מדויק. מייד מתעוררות השאלות הבאות:

1. האם הבעיה הומצאה עבור המאמר או שיש לה מקור היסטורי, כולל המספרים הספציפיים? התשובה ככל הנראה שלילית - אין רפרנס במאמר עד כמה שאני רואה.
2. האם יש במאמר סקירה כללית יותר של פתרון אותה בעיה עבור פרמטרים שונים? התשובה שלילית - אין כזו.
3. האם יש ערכים סבירים שעבורם אותו אלגוריתם בדיוק מוצא נצחון עבור הטבלה ההודית? התשובה חיובית. למשל עבור 20,24 או עבור 59,71.
4. מה יקרה אם אני אתכנת את זה בעצמי?

ובכן, לא התאפקתי וכתבתי קוד שעושה תחרות בין שני הלוחות על השאלה הזו, תוך שהוא מממש את אלגוריתם הפתרון שהוצע במאמר. צריך קצת להיזהר בבחירת הפרמטרים, כי פלימפטון 322 מטפל רק בזוויות בין 45 ל-90 (כלומר, אני צריך לבחור את \( d \) להיות לכל היותר עד סדר גודל של פי \( \sqrt{2} \) מ-\( b \)). במקרה הזה פלימפטון מנצח בערך ב-80 אחוז מהקלטים האקראיים שנתתי לו. מצד שני, לא ברור לי עד כמה אכן מדובר על יתרון שלא נובע מכוח גס פשוט: בטבלה המורחבת של פלימפטון יש 38 ערכים שמכסים את הזוויות מ-45 מעלות עד 90 מעלות - יוצא שלפעמים ההפרשים בין זוויות עוקבות הוא פחות ממעלה אחת. אצל הטבלה ההודית, לעומת זאת, יש רק 24 ערכים שמכסים את הטווח מ-0 מעלות עד 90 מעלות, בקפיצה קבועה. די מתבקש שטבלה עם רזולוציה טובה יותר תנצח יותר, כך שלא ברור לי מה בדיוק משווים פה - את הרזולוציה של הטבלה או תכונה מיוחדת אחרת?

אם ההשוואה היא לרזולוציה, עולה שאלה שבכלל לא קשורה לפלימפטון 322 אלא לטבלה ההודית - למה יש בה “רק” 24 ערכים? האם היה מסובך מדי לחשב 48? או שיש בה 24 ערכים כי הקירובים שהיא נתנה היו מספיק טובים לצרכים שלהם היא שימשה ולכן איש לא טרח לחשב משהו מפורט יותר? אין לשאלות הללו התייחסות במאמר. זו בעיה משמעותית, לטעמי - המאמר לא עונה לשאלות הבסיסיות שמתעוררות אצלי, והקונטקסט ההיסטורי שהוא מספק הוא דל מאוד.

לזכותו של המאמר ייאמר שהוא מתייחס לסיבות שבגללן פלימפטון 322 מנצח בעצמו. הוא מונה שלוש סיבות אפשריות: ראשית, את עניין ה-38 ערכים מול 24 שכבר הוזכר (אבל בלי להתייחס לשאלה אם בכלל סביר להעמיד את הלוח לתחרות מול לוח בעל 24 ערכים).

שנית, וזו נקודה טובה, הם אומרים שבלוח ההודי יש רק ערכי סינוס בזמן שבפלימפטון 322 יש את שלל היחסים בין כל הצלעות במשולש. זה בהחלט נכון אבל שוב מתעוררת השאלה - מה בעצם מנע להוסיף לטבלה ההודית גם את הערכים, נאמר, שלטנגנס? האם הייתה כאן מגבלה חישובית על יוצר הטבלה? לא נראה לי. לכן שוב נשאלת השאלה האם הטבלה ההודית היא “דלה” כזו בגלל שפשוט לא היה להם אכפת. דהיינו, הרמה המתמטית של ההודים הייתה טובה מספיק כדי לייצר טבלאות טובות בהרבה מפלימפטון 322, אבל לא הייתה להם סיבה לעשות זאת. זו עוד שאלה היסטורית ללא תשובה היסטורית במאמר.

הנקודה השלישית שהמאמר מעלה בתור תשובה לשאלה “למה פלימפטון 322 טוב יותר” היא שהטבלה של פלימפטון 322 היא מדויקת. למה הכוונה? אם תזכרו מה אמרנו כשהסתכלנו על הניתוח של נויגבאואר, הוא הצביע על כך שהשלשות הפיתגוריות נוצרו על ידי מספרים רגולריים בבסיס 60 - כאלו שההופכי שלהם הוא בעל ייצוג עשרוני סופי. זה אומר שכל הערכים שנמצאים בטבלה הם מדוייקים ולא מהווים קירוב. זאת להבדיל מהטבלה ההודית שבה הערכים הם מקורבים.

אם לומר את האמת, אני לא קונה את זה כל כך. גם שימוש בפלימפטון 322 מצריך קירוב - הרי על פי רוב המשולש שאנחנו עובדים איתו לא נמצא בטבלה, ואנחנו מחפשים את המשולש הכי קרוב אליו בטבלה. אז יש לנו שגיאת חישוב אוטומטית רק מעצם הדבר הזה. לנקודה הזו יש התייחסות לקראת סוף המאמר, כשמוכנס לתמונה המושג של אינטרפולציה. אינטרפולציה היא סוג קצת יותר חכם של קירוב: במקום לחפש את הערך הכי קרוב אלינו ולדבוק בו, לחפש את שני הערכים הקרובים ביותר אלינו ולהעריך מה הערך שאנחנו אמורים להחזיר על ידי סוג של ממוצע ביניהם. לא אכנס לפרטים יותר מדי כי זה לא כל כך חשוב - השורה התחתונה היא שהגישה הזו משפרת את איכות התשובות שפלימפטון 322 יכול לתת, והמאמר מנסה לבסס את הטענה שהבבלים הכירו את הרעיון של אינטרפולציה על ידי תיאור של לוח בבלי אחר. מדובר עדיין על קירוב, אבל קירוב טוב יותר מאשר קודם. בתרגיל השני, שלא נכנסתי לפתרון שלו, זה נותן עוד יתרון ממשי.

אני מודה שהייתי שמח לראות ניתוח מתמטי רציני של האיכות של פלימפטון 322 לעומת “המתחרים” ולא סתם כמה דוגמאות, אבל כזה דבר פשוט לא נמצא במאמר. אולי בעתיד.

פרק שישי, ובו כמה מילות סיכום ופרידה

המאמר החדש מסיים בשתי פסקאות שמרגישות לי מופרזות לגמרי:

P322 is historically and mathematically significant because it is both the first trigonometric table and also the only trigonometric table that is precise. Irrational numbers and their approximations are seen as essential to classical metrical geometry, but here we have shown they are not actually necessary for trigonometry. If the dice of history had fallen a different way, and the deep mathematical understanding of the scribe who created P322 not been lost, then very possibly ratio-based trigonometry would have developed alongside our angle-based approach.

This new interpretation of P322 significantly elevates the status of Babylonian mathematics, and the vast number of untranslated tablets are likely to contain many more surprises waiting to be found. The discovery of trigonometry is attributed to the ancient Greeks, but this needs to be reconsidered in light of the much earlier, computationally simpler and more precise Babylonian style of exact sexagesimal trigonometry. In addition to being historically significant, P322 also brings the founding assumptions of our own mathematical culture into perspective. Perhaps this different and simpler way of thinking has the potential to unlock improvements in science, engineering, and mathematics education today.

כשאני קורא את הטקסט הזה מייד קופצות לי שאלות - האם אנחנו באמת יודעים שזו טבלה טריגונומטרית? האם העובדה שהיא “מדוייקת” היא אכן חשובה? האם קירובים של מספרים אי רציונליים מפריעים למה שאנחנו עושים עם טריגונומטריה? האם אכן ניתן להסיק מהטבלה שליוצר שלה הייתה הבנה מתמטית “עמוקה”? האם אכן במהלך הדורות אנשים לא חשבו על האפשרות לתאר טריגונומטריה גם באמצעות יחסים? האם דרך החשיבה הזו אכן פשוטה יותר? האם משהו מכל זה רלוונטי לנו?

אני לא חושב שהמאמר מראה משהו מכל אלו. אני מעריך את האופטימיות וההתלהבות שלו, אבל אני הרבה יותר סקפטי ממנו. כמובן, אני לא האיש שיוכל לכתוב מאמר ביקורת של ממש כנגדו; יהיה מעניין לראות מה יאמרו בנושא המומחים. הפולמוס סביב פלימפטון 322 הרי מעולם לא נרגע לחלוטין ולעולם לא ייפתר לחלוטין; אנחנו כנראה רק בתחילת פרק חדש ומהנה לא פחות מקודמיו.

מכיוון שכולנו הלכנו לאיבוד בסבך האדיר של הדיון הזה, אני רוצה לסכם אותו בקצרה:

• פלימפטון 322 הוא לוח חרס בבלי קדום שמכיל 15 שורות שמתארות: אנך ויתר במשולש ישר זווית, ואת הריבוע של המנה של אחד מהם עם האנך השני. הלוח שבור וכנראה הכיל עוד עמודות. לעולם לא נמצא את החלק האבוד של הלוח או נבין מה היה ההקשר הרחב יותר שבו הוא נוצר, כי שוד עתיקות וכאלה.
• הפרשנות המקורית של הלוח הייתה שהוא נוצר על ידי שימוש בנוסחת אוקלידס ליצירת שלשות פיתגוריות ושזו הייתה מטרתו. הפרשנות הזו נראית נאיבית מדי כיום.
• פרשנות אחרת היא שהוא שימש כלוח תרגילים במתמטיקה והמספרים שעליו הם תוצאות ביניים של החישוב. בשיטה הזו אפשר לתת הסבר לא רע בכלל לאופן שבו המספרים בלוח נוצרו, כולל הסבר לטעויות שבו.
• הפרשנות החדשה שמציג המאמר מקבלת את אופן יצירת הלוח אבל טוענת שהוא בא לשמש מטרה אחרת - טבלה טריגונומטרית.
• אם הלוח הוא אכן טבלה טריגונומטרית, זו אכן טבלה מסוג שונה למדי מהטבלאות המקובלות, והיא מאפשרת חישובים ברמת דיוק טובה למדי.

האם הפרשנות החדשה פותרת תעלומה שמיטב המוחות המתמטיים שברו עליה את הראש? נראה לי כמו תיאור מופרז לגמרי. הפרשנות החדשה מתבססת מאוד חזק על כל הפרשנויות שקדמו לה והתוספת של המאמר אינה כה גדולה. זה הדבר שהכי מפריע לי בסיקור התקשורתי של התגלית - הרבה יותר רומנטי לדבר על החוקרים ההירואיים שפיצחו תעלומה שכל קודמיהם לא הבינו מה הולך בה, במקום להסתכל על התהליך ההדרגתי שהחל בנויגבאואר שבכלל הבין שיש כאן משהו מעניין ונתן את הניתוח המתמטי הבסיסי שכל הבאים אחריו התבססו עליו, והמשיך בשלל חוקרים אחרים - מתמטיקאים והיסטוריונים - שתרמו עוד נקודות התבוננות על התעלומה עד שכיום אנחנו מבינים אותה לא רע בכלל. התעלומה, זה הדבר שמעניין בסיפור הזה. לא פתרון מחץ זה או אחר.