משפט המספרים המחומשים

בפוסט הזה אני רוצה להוכיח את מה שנקרא משפט המספרים המחומשים. במבט ראשון המשפט נראה מוזר ולא ברור למה הוא מעניין במיוחד, ולכן הפוסט הקודם הוקדש לשימוש מעניין שלו - מציאת נוסחת נסיגה עבור פונקציית החלוקה. עם זאת, המטרה של הפוסט הנוכחי היא לעמוד בפני עצמו, כי המתמטיקה של הפוסט הקודם היא טכנית למדי ולא דומה כל כך למה שנדבר עליו הפעם, כך שחבל לוותר רק בגלל זה.

ראשית, מה זה מספר מחומש? זה מספר מהצורה \( \frac{k\left(3k-1\right)}{2} \) כאשר \( k \) הוא מספר טבעי חיובי. השם “מספר מחומש” מגיע מכך שצורה מוזרה שבה אפשר לקבל את המספרים היא לצייר סדרה של \( k \) מחומשים אחד בתוך השני, כשבמחומש ה-\( k \) יש בדיוק \( k \) נקודות על כל צלע, ואז לספור כמה נקודות יש בסך הכל. המחומש הראשון, זה עם נקודה אחת על כל צלע, הוא “מנוון” ונראה כמו נקודה בודדת:

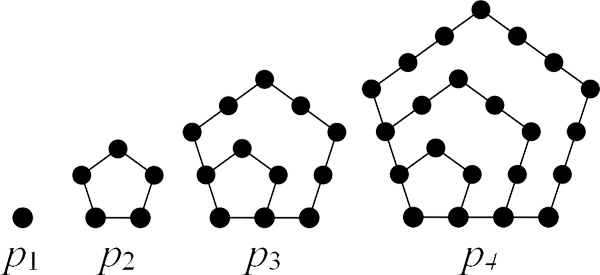
זו דרך די מוזרה להגדיר סדרת מספרים, ואני אכן לא אחזור אליה בכלל. יותר מכך - אני אדבר גם על המספרים שמתקבלים כשמציבים בתוך \( k \) ערכים שליליים; גם במקרה הזה מקבלים מספרים חיוביים. השיטה היא להציב מספר טבעי ואז את המינוס שלו, ואז את המספר הטבעי הבא וכן הלאה. הצבות של \( k=1,-1,2,-2,\dots \) מניבות את סדרת המספרים \( 1,2,5,7,12,15,22,26,\dots \).

הסיבה שהסדרה הזו מעניינת היא הנוסחה הבאה, שנקראת משפט המספרים המחומשים ובמבט ראשון ממש לא ברור מה היא אומרת בכלל:

\( \prod_{n=1}^{\infty}\left(1-x^{n}\right)=\sum_{k=-\infty}^{\infty}\left(-1\right)^{k+1}x^{\frac{k\left(3k-1\right)}{2}} \)

כפי שהצהרתי בפוסט הקודם, לטעמי זו אחת מהנוסחאות היפות במתמטיקה, אבל אין שום סיבה להתעמק בפרטים שלה כאן (את זה עשיתי בפוסט הקודם) - במקום זה אפשר לנסח את המשפט בצורה שקולה לגמרי שהרבה יותר קל להבין, ותהיה הרבה יותר רלוונטית לאופן שבו אוכיח את המשפט בפועל. בהינתן מספר טבעי \( n \), אפשר לדבר על הדרכים השונות להציג אותו בתור סכום של מספרים טבעיים חיוביים כך שאין מספר שמופיע פעמיים. בפוסט הזה אני אקרא בשם חלוקה להצגה כזו (באופן כללי “חלוקות” מתייחס גם למקרה שבו מספר יכול להופיע פעמיים). למשל, ל-4 יש שתי חלוקות: \( 4 \) עצמו, ו-\( 1+3 \). ה”חלוקה” \( 2+2 \) לא נחשבת כי המספר 2 מופיע בה פעמיים.

אפשר לתאר חלוקות בדרך ציורית בעזרת טבלת יאנג. טבלת יאנג כוללת בסך הכל כמה שורות של ריבועים, כשכל שורה לא ארוכה יותר מאלו שבאות מתחתיה. סכום הריבועים הכולל בטבלה הוא \( n \), והאורך של כל שורה מייצג את אחד מהאיברים בפירוק. הנה דוגמא עבור הפירוקים של 4:

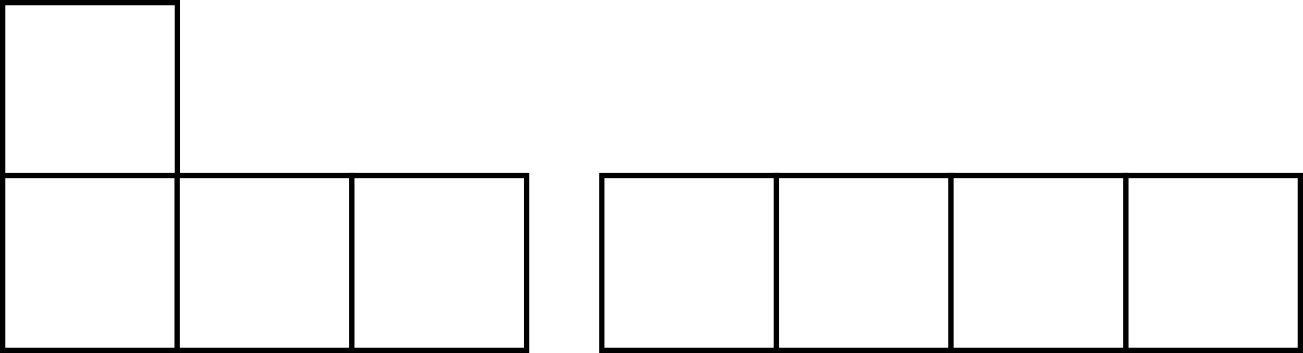
הכלל הנוסף של “אותו מספר לא מופיע פעמיים בפירוק” מתורגם אצלנו ל”בטבלת יאנג, כל שורה קצרה יותר מזו שמתחתיה”. לכן הטבלה הזו לא חוקית מבחינתנו:

מספר החלוקות של \( n \) הוא מספר טבלאות היאנג החוקיות שקיימות עבורו. עכשיו בואו נבדיל בין שני סוגי טבלאות: כאלו עם מספר זוגי של שורות, מה שאקרא לו “חלוקה זוגית”, וכאלו עם מספר אי-זוגי של שורות - “חלוקה אי-זוגית”. אסמן ב-\( p_{\text{odd}}\left(n\right) \) את מספר החלוקות האי-זוגיות של \( n \) וב-\( p_{\text{even}}\left(n\right) \) את מספר החלוקות הזוגיות. אנחנו יודעים ש-\( p_{\text{odd}}\left(n\right)+p_{\text{even}}\left(n\right) \) שווה למספר החלוקות של \( n \) בסך הכל; אבל למה שווה ההפרש, \( p_{\text{odd}}\left(n\right)-p_{\text{even}}\left(n\right) \)? ובכן, זה בדיוק התוכן של משפט המספרים המחומשים: הוא אומר שכמעט תמיד מספר החלוקות הזוגיות יהיה שווה למספר החלוקות האי-זוגיות, כלומר ההפרש ביניהם יהיה 0; המקרים היחידים שבהם זה לא יהיה כך יהיו עבור \( n \) שהוא מספר מחומש, ובמקרה הזה ההפרש יהיה פלוס-מינוס 1, כשהפלוס-או-מינוס נקבע על פי זוגיות ה-\( k \) שמגדיר את המספר. בכתיבה פורמלית:

\( p_{\text{odd}}\left(n\right)-p_{\text{even}}\left(n\right)=\begin{cases} 1 & n=\frac{k\left(3k-1\right)}{2},k\text{ odd}\\ -1 & n=\frac{k\left(3k-1\right)}{2},k\text{ even}\\ 0 & \text{else} \end{cases} \)

הנה דוגמאות לכל המקרים הללו. ראשית, 2. זה מספר מחומש שמתקבל על ידי \( k=1 \) האי-זוגי והפירוק היחיד שלו הוא 2; הפירוק \( 1+1 \) אינו חוקי כי 1 מופיע פעמיים. לכן מספר הפירוקים האי-זוגיים גדול ב-1 ממספר הפירוקים הזוגיים. כעת אל 7. זה מספר מחומש שמתקבל על ידי \( k=-2 \) הזוגי, כך שאנחנו מצפים שמספר הפירוקים הזוגיים שלו יהיה גדול ב-1 ממספר הפירוקים האי-זוגיים שלו. הנה כל הפירוקים:

\( 7,1+6,2+5,3+4,1+2+4 \)

יש לנו פה שלושה פירוקים זוגיים ושניים אי-זוגיים - כמו שהמשפט מבטיח.

עכשיו אל 8 שאיננו מספר מחומש בכלל ולכן אנחנו מצפים למספר שווה. הנה הפירוקים לכל גודל:

1: \( 8 \)

\( 2 \): \( 1+7,2+6,3+5 \)

3: \( 1+2+5,1+3+4 \)

יש לנו פה פירוק אחד מגודל 1 ושניים מגודל 3 - סה”כ שלושה מגודל אי זוגי, מה שמתקזז עם שלושה מגודל 2 הזוגי.

הרעיון ברור, אבל איך מוכיחים את המשפט? ההוכחה שאראה פה תהיה קומבינטורית ותיעזר בטבלאות יאנג; זו לא ההוכחה המקורית של אוילר אלא הוכחה שהתגלתה לקראת סוף המאה ה-19 על ידי פרנקלין האמריקאי (לא, לא פרנקלין הזה). הטריק הוא לסדר פירוקים זוגיים ואי זוגיים בזוגות, כשלכל היותר פירוק אחד נותר בודד. נעשה את זה על ידי הגדרת פונקציה שלוקחת פירוק ובונה ממנו פירוק חדש, עם מספר מחוברים שונה ב-1, כך שהפעלה נוספת של הפונקציה “מתקנת” את ההפעלה הקודמת וחוזרת לאיבר שממנו התחלנו. במילים אחרות, הפונקציה שלנו היא ההופכית של עצמה; מקיימת \( f\left(f\left(x\right)\right)=x \) לכל קלט. לפונקציה כזו קוראים אינבולוציה.

האינטואיציה של הבניה קלה להדהים כשמסתכלים עליה ציורית עם טבלאות יאנג. בואו נביט על טבלת היאנג של הפירוק \( 4+6+8+9+10 \) של \( 37 \):

אנחנו רוצים לבנות מהטבלה הזו טבלה שמייצגת מספר שונה ב-1 של מחוברים. כל מחובר מתאים לשורה בטבלת היאנג, כך ששתי דרכי הפעולה הטבעיות ביותר הן: או להוסיף שורה מעל השורה העליונה, שתיבנה מקוביות שניקח מהשורות האחרות; או להסיר את השורה העליונה ולחלק אותה לשורות האחרות. ואנחנו רוצים שהכלל שמכתיב לנו באיזו משתי הדרכים כדאי לנקוט יהיה כזה ש”הופך את עצמו” אחרי שימוש אחד. אז הנה הטריק: בואו נמספר ב-\( r \) את מספר הקוביות בשורה העליונה (“המחובר הקטן ביותר בסכום”) וב-\( s \) נמספר את האורך של האלכסון בצד ימין למטה של הטבלה. באיור אצבע את השורה העליונה בירוק ואת האלכסון באדום:

 

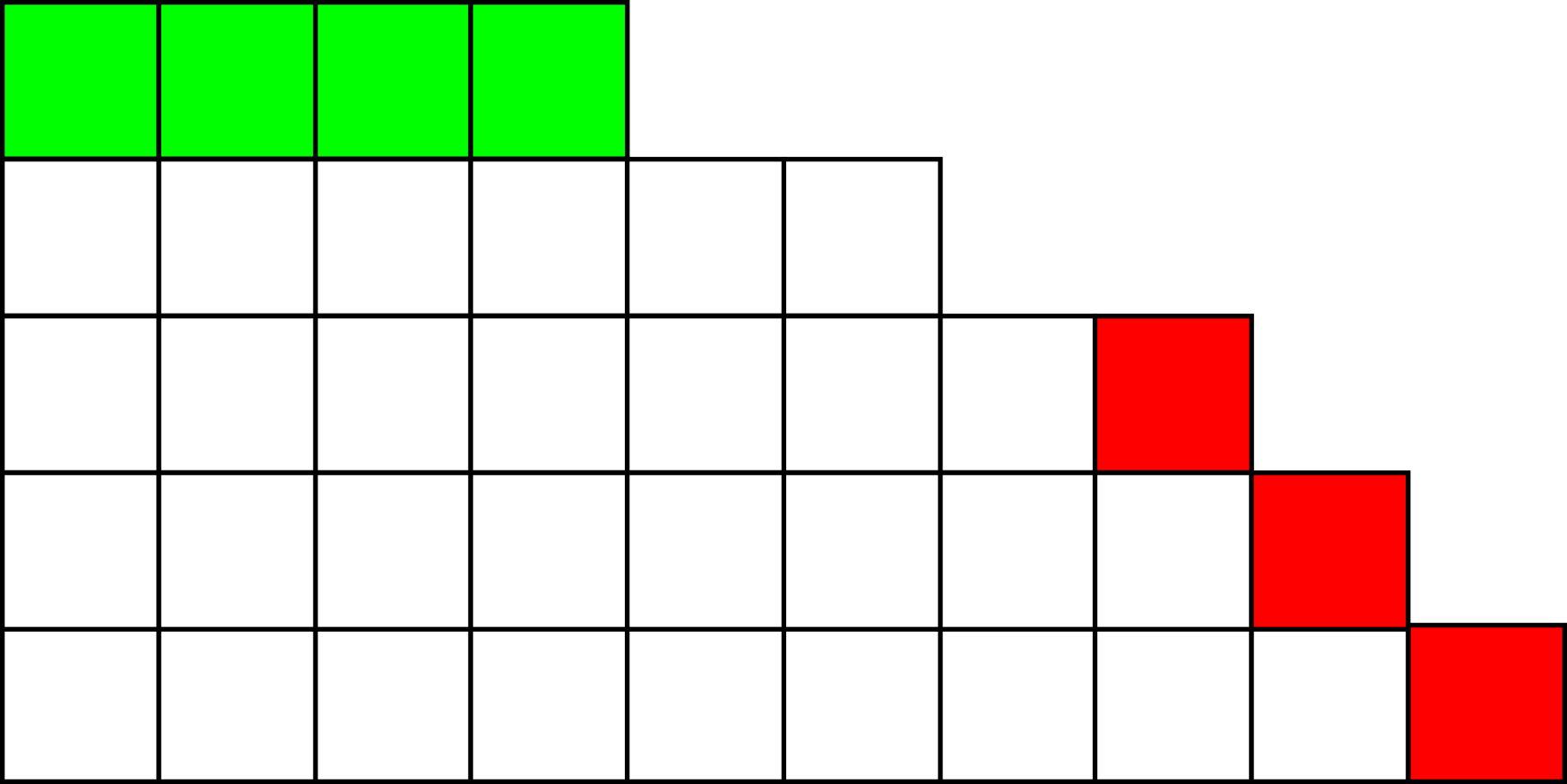
הגדרה פורמלית יותר של \( s \) היא זו: אורך הסדרה של המחוברים בסכום שמתחילה במחובר הגדול ביותר, עוברת עליהם מהגדול לקטן, ומסתיימת לפני האיבר הראשון ששונה מקודמו לפחות ב-2. והנה ניסוח עוד יותר פורמלי: אם נסמן חלוקה \( \lambda \) בתור \( \lambda=\left(\lambda_{1},\lambda_{2},\dots,\lambda_{k}\right) \) כך ש-\( \lambda_{1}>\lambda_{2}>\dots>\lambda_{k} \) אז \( r=\lambda_{k} \) ו-\( s \) הוא המספר הגדול ביותר עבורו מתקיים \( \left(\lambda_{1},\dots,\lambda_{s}\right)=\left(\lambda_{1},\lambda_{1}-1,\dots,\lambda_{1}-\left(s-1\right)\right) \).

ומה האינבולוציה עושה? אם \( r>s \) אז אנחנו מפרקים את האלכסון ובונים ממנו שורה חדשה מעל השורה העליונה; בגלל ש-\( r>s \) מובטח לנו שהשורה הזו תהיה קצרה מזו שמתחתיה, כדרוש. אם לעומת זאת \( r<s \) אנחנו מפרקים את השורה העליונה ובונים ממנה אלכסון חדש, כלומר מוסיפים קוביה אחת לכל \( r \) השורות הראשונות; מכיוון ש-\( r<s \) אנחנו יודעים שיש מספיק שורות כאלו.

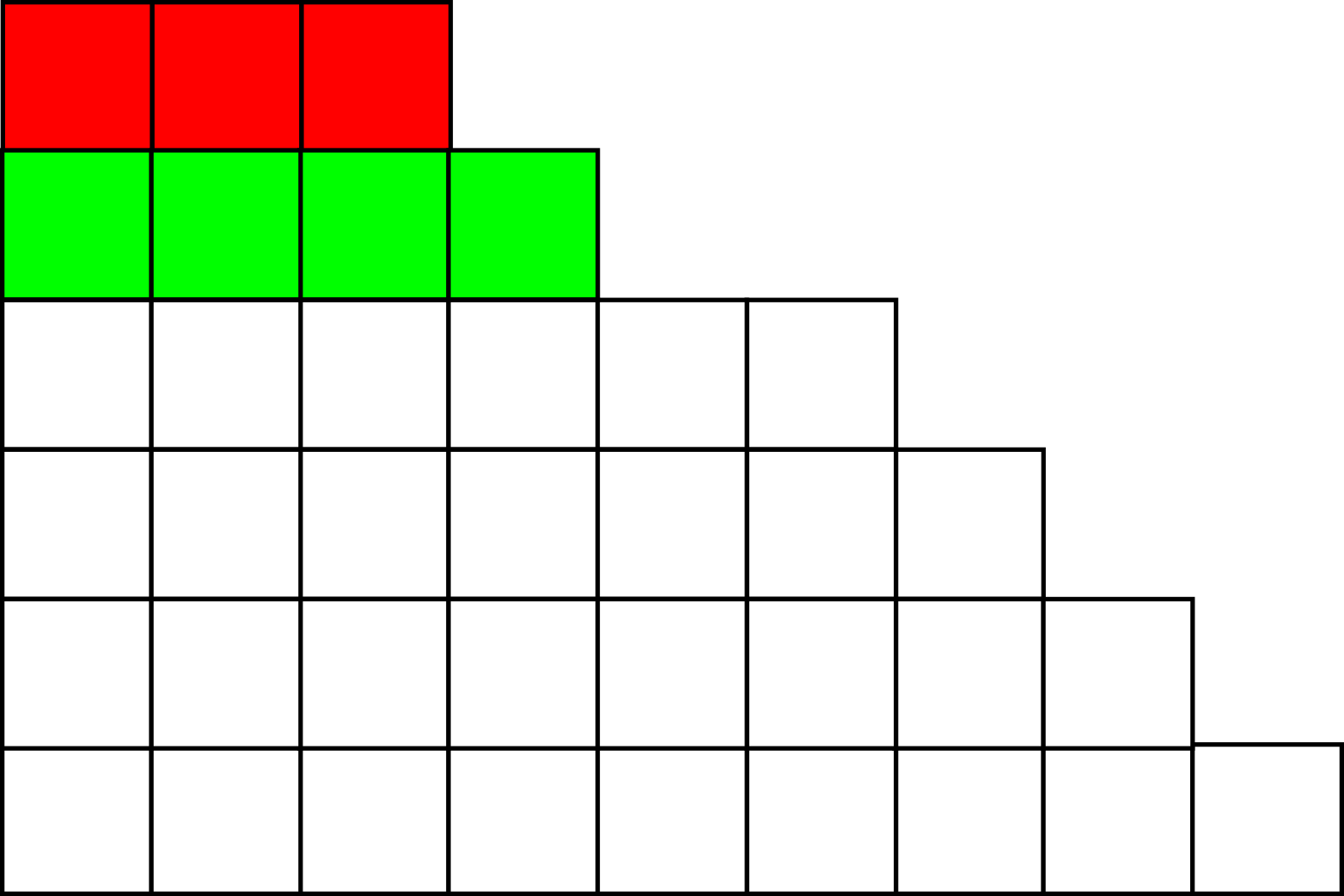
מתי עשויה להיות בעיה? במקרה שבו \( r=s \). כאן העסק עלול להתקלקל אבל לא חייב להתקלקל. בואו נראה דוגמא, שמתאימה ל-\( 3+6+8+9+10 \) של \( 36 \):

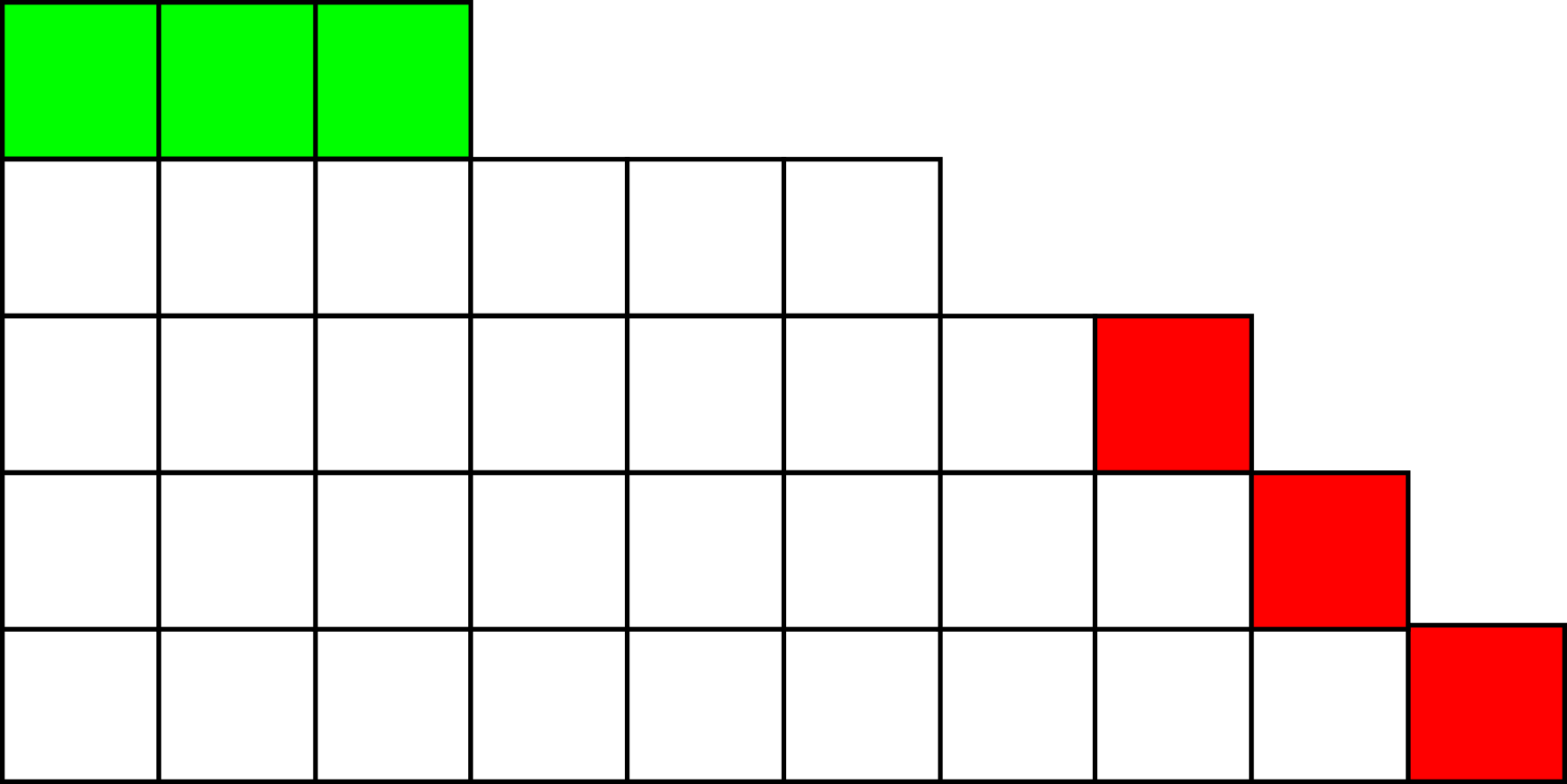
ברור שבמקרה הזה אי אפשר לייצר שורה חדשה, כי היא תהיה באותה אורך כמו זו שמתחתיה; חייבים לפרק את השורה הקיימת, ואז מקבלים את הפירוק \( 6+9+10+11 \):

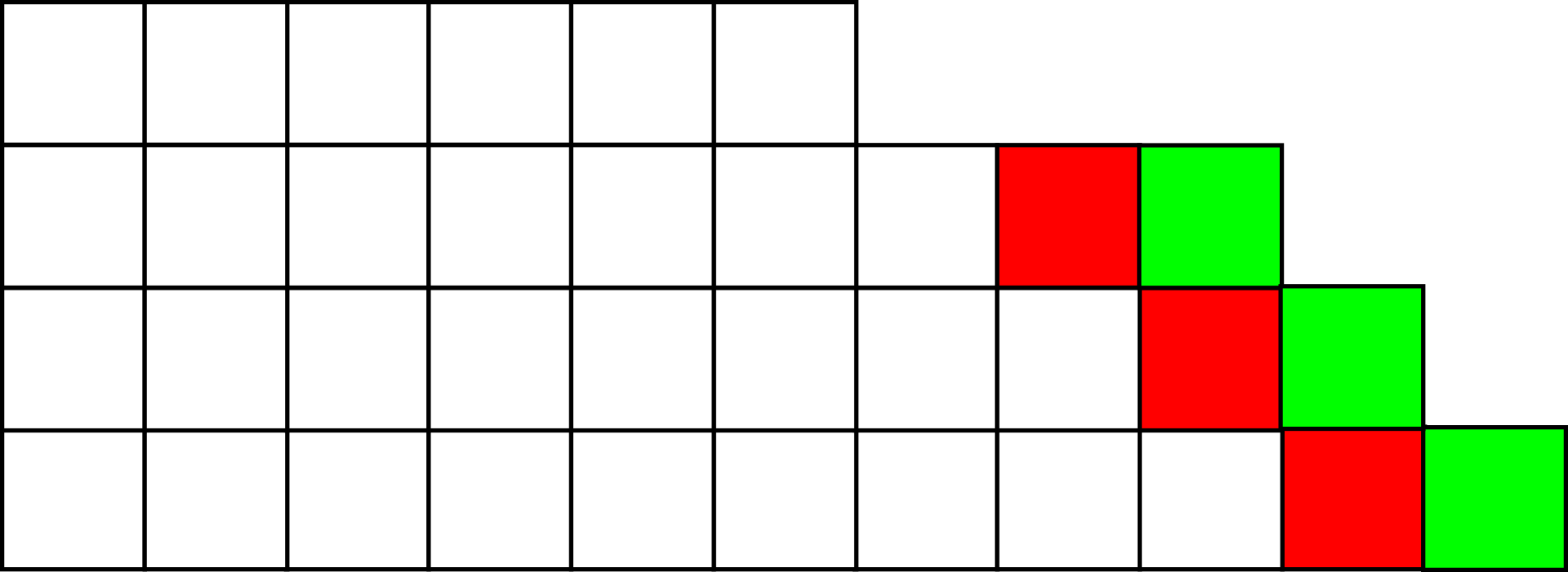
הפירוק הזה תקין לגמרי, וכשנפעיל עליו את האינבולוציה נחזור לסיטואציה המקורית והכל טוב. מתי כן הייתה עלולה לצוץ בעיה? רק אם לא היו לנו \( r \) שורות לחלק את הקוביות של השורה העליונה אליהן. מתי זה עלול לקרות? אנחנו הרי יודעים שיש לפחות \( s \) שורות, ואת המספר הכולל של השורות סימנתי ב-\( k \). כלומר \( r=s\le k \); לכן כדי שתוכל להיווצר בעיה, הכרחי שיתקיים \( s=k \): במצב הזה מכיוון שאנחנו מפרקים את השורה העליונה, אנחנו נשארים בסוף עם קוביה בודדת שאין לנו שורה להכניס אותה אליה.

איך נראית טבלה שבה \( s=k \)? היא תואמת כל חלוקה שבה הפער בין כל המחוברים הסמוכים הוא 1. למשל \( 1+2+3+4 \):

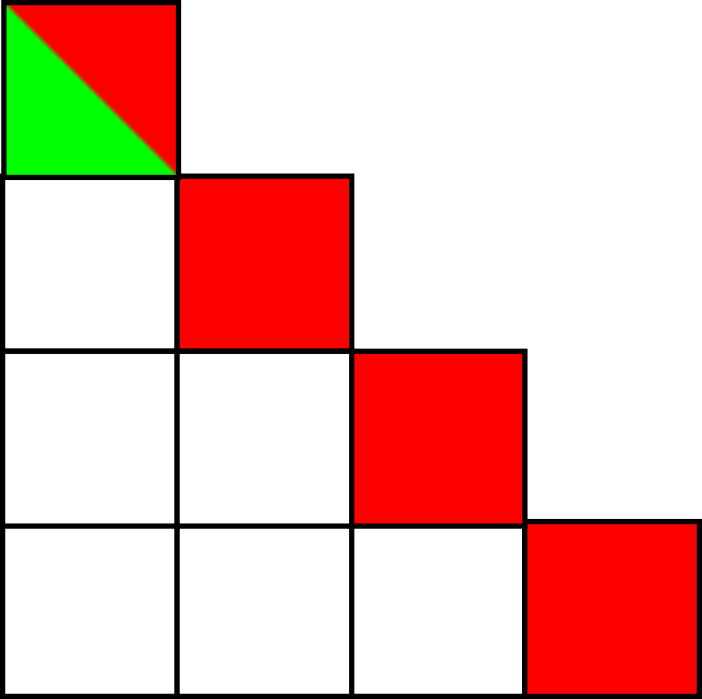
אבל כאן, כמובן, אין בעיה, כי \( r<s \) ולכן אפשר לפרק את השורה העליונה. לכן המקרה היחיד שבו יכולה להיות בעיה הוא זה שבו \( s=r=k \). למשל, הטבלה הזו:

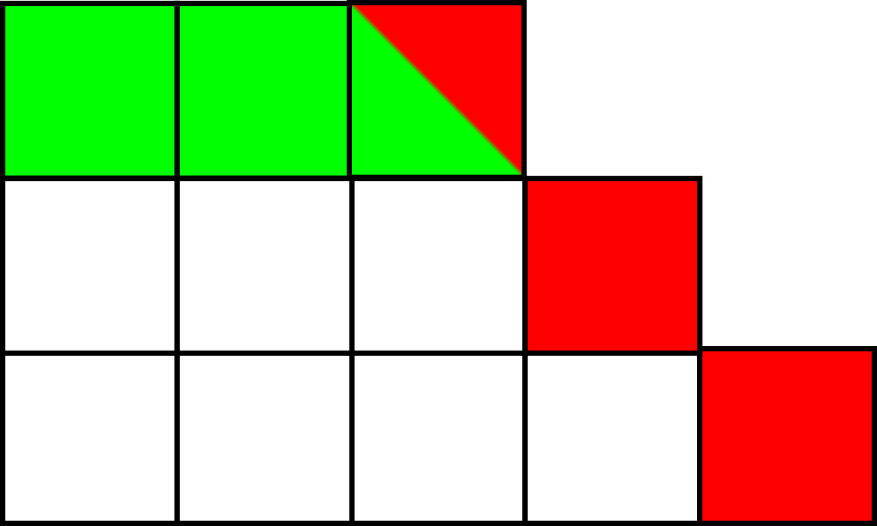
וכאן אנחנו אכן מקבלים מספר מחומש, \( 12 \). ובאופן כללי?

אם \( s=r=k \) אז החלוקה שלנו היא בהכרח מהצורה הבאה: \( \left(k,k+1,k+2,\dots,k+\left(k-1\right)\right) \). זה טור חשבוני פשוט במיוחד שאפשר לסכום “בשיטה של גאוס” - לשים לב שהסכום של המחובר הראשון והאחרון הוא \( 3k-1 \), וגם הסכום של המחובר השני והלפני אחרון, וכן הלאה, ויש בסך הכל \( k \) מחוברים ולכן \( \frac{k}{2} \) זוגות של מחוברים, ולכן הסכום הכולל הוא \( \frac{k\left(3k-1\right)}{2} \) - והופס, קיבלנו מספר מחומש! אבל שימו לב, רק עבור המקרה שבו \( k \) הוא חיובי, בינתיים. עכשיו גם ברור למה כאשר \( k \) אי-זוגי אז יש יותר חלוקות אי זוגיות מזוגיות, ואחרת ההפך; כי \( k \) הוא מספר השורות בטבלה, כלומר הזוגיות של \( k \) קובעת האם החלוקה שאין לה בת זוג היא זוגית או אי זוגית.

אז רגע, מה פספסנו? איך ערכים שליליים של \( k \) נכנסים לתמונה? ובכן, רימיתי אתכם קודם והשמטתי עוד מקרה קצה אחד. האם עליתם על הרמאות שלי? הבעיה היא במקרה שבו \( r>s \). במקרה הזה, כזכור, הרעיון הוא לפרק את האלכסון ולדחוף את האיברים שלו בשורה מעל העליונה; אבל כאן עלולה להיווצר בעיה אם גם השורה העליונה השתתפה באלכסון, כי אז כשאני מפרק את האלכסון אני מסיר ממנה איבר אחד. הנה מקרה שבו זה קורה:

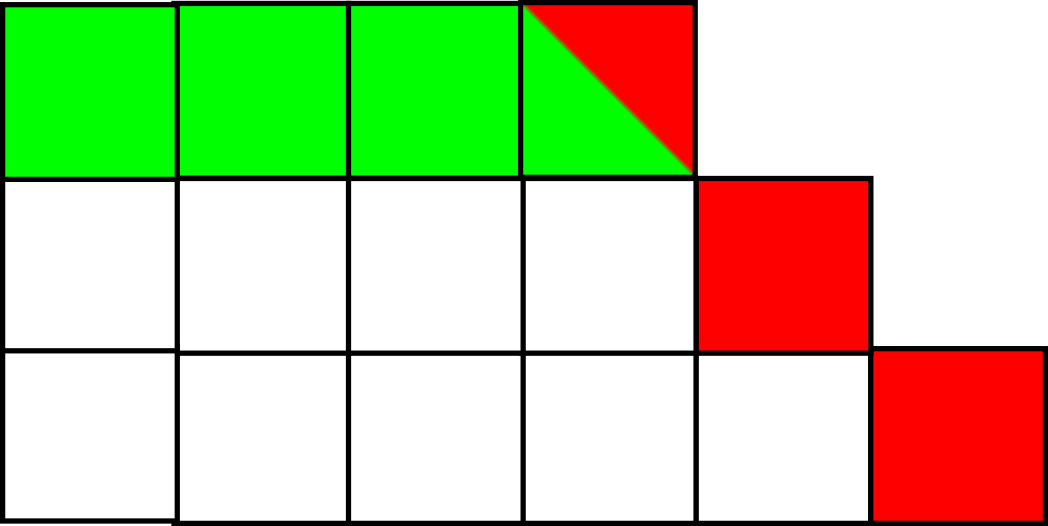
כאן האלכסון הוא מגודל 3 ולכאורה אין עם זה בעיה כי השורה העליונה היא מגודל 4, אבל כמובן - אחרי שנסיר את אברי האלכסון ניוותר עם שורה מגודל 3. לכן יכולה להיווצר בעיה בדיוק במקרה שבו \( r=s+1 \) ו-\( s=k \) (כי \( s=k \) פירושו “גם השורה העליונה משתתפת באלכסון). במקרה הזה, החלוקה היא מהצורה \( \left(k+1,k+2,\dots,k+k\right) \) והסכום יוצא \( \frac{k\left(3k+1\right)}{2} \). זה כמובן לא מתאים לנוסחה שלנו של מספר מחומש, אז אם רוצים לקבל את האחידות היפה בנוסחה שיש לנו, בואו נשים לב לכך ש-\( t\left(3t-1\right)=3t^{2}-t \) ולכן אם נגדיר \( t=-k \) נקבל

\( \frac{t\left(3t-1\right)}{2}=\frac{3t^{2}-t}{2}=\frac{3k^{2}+k}{2}=\frac{k\left(3k+1\right)}{2} \). זה מסביר את עניין המינוס ומסיים את ההוכחה.

נסכם מה הלך פה: הגדרתי אינבולוציה על קבוצת כל טבלאות יאנג הקיימות, למעט כמה מקרי קצה. האינבולוציה לא משנה את הגודל של הטבלה (מספר הריבועים שלה, ששווה לגודל המספר שאת החלוקה שלו הטבלה מייצגת) אבל היא כן משנה בדיוק ב-1 את מספר השורות שלה (מספר המחוברים בחלוקה). בצורה הזו אנחנו מקבלים התאמה חח”ע ועל בין החלוקות הזוגיות של מספר והחלוקות האי-זוגיות שלו, למעט במקרים שבהם לפחות אחת מטבלאות היאנג שלו משתייכת אל מקרי הקצה שהאינבולוציה לא יודעת לטפל בהם. ראינו שמקרי הקצה הללו מתרחשים בדיוק עבור מספרים מהצורה \( \frac{k\left(3k-1\right)}{2} \) עבור ערכים שלמים של \( k \); בפרט, אין שני מקרי קצה שמתרחשים עבור אותו גודל, כי לא קשה להראות שאין לאותו מספר טבעי שני ייצוגים שונים מהצורה \( \frac{k\left(3k-1\right)}{2} \) כאשר \( k \) שלם. זה יפה בפני עצמו, וזה עוד יותר יפה כשזוכרים שזה מה שמוביל בסופו של דבר לנוסחת הנסיגה המופלאה עבור פונקציית החלוקה שראינו בפוסט הקודם.