פרדוקס ברס ומנהרות הכרמל

כמו כל תושבי חיפה גם אני עוקב בעיון אחר הליך בנייתן של מנהרות הכרמל, שכעת עומדות על סף פתיחה. תקציר ללא-עוקבים: חיפה נמצאת על צ’ופצ’יק במישור החוף שבולט אל הים, והדרך עבור המגיעים מכביש החוף אל הקריות היא דרך חתחתים - או לנסוע לאורך החוף במלוא עיקולו של הצ’ופצ’יק, דרך מה שמכונה “העיר התחתית”, ולהיקלע לפקקים מכאן ועד להודעה חדשה; או לטפס על ההר עם ההגעה לחיפה במה שמכונה (בטעות) “דרך פרויד” המתעקלת והפקוקה-עד-המוות בשעות המתאימות, לחצות את חיפה לאורכה (במסלול הרבה יותר סביר מזה של העיר התחתית) ואז לרדת שוב לאזור צומת הצ’קפוסט הפקוקה מכאן ועד לנצח (אם כי בזכות גשר חדש ניתן לחלוף ביעף על חלקו הראשון של הצ’קפוסט). בקיצור, שתי דרכים שונות ושתיהן גרועות ביותר.

מנהרות הכרמל באות לפתור את כל הבלבלה הזו - במקום לטפס על ההר או לעקוף אותו, עוברים ישר דרכו. התחזיות מדברות על שמונה דקות נסיעה, בעוד שבשעות העומס כיום הנסיעה יכולה לקחת בקלות שעה. כמובן שאליה וקוץ בה - הכביש הוא כביש אגרה, כי הרי גם מי שטרחו לחפור את המנהרות צריכים להרוויח (ומבלי להיכנס לשאלה אם זה טוב או רע אפשר להסתפק באבחנה שהמנהרות נחצבו ועומדות להיפתח, ואילו על הרכבת התחתית של תל אביב חלמו כבר בזמנו של אלתרמן ויכולים להמשיך לחלום - אמנם, לא ברור לי אם בכלל ניתן לבנות בתל אביב רכבת תחתית נורמלית בהתחשב בסוג הקרקע, אבל זה כבר לבלוג אחר). עם זאת, היזמים טורחים להדגיש שהם טובים לכולם כולל מי שלא רוצה לשלם את האגרה: “ההערכה שלנו היא שהמנהרות יביאו לירידה של 15% בנסיעה בדרכים החלופיות, כך שגם לאותם נהגים (שלא ייסעו במנהרות) יהיו פחות פקקים”. ההערכה הזו נשמעת הגיונית ביותר - אם יש דרך חדשה ומהירה, האין זה מובן מאליו שהעומס ירד משאר הנתיבים?

אז זהו, שלא.

אין לי מושג מה יהיה במקרה של מנהרות הכרמל ואנו עומדים לגלות זאת בעצמנו בקרוב כך שלא אהיה שוטה ואנסה להתנבא; יותר מכך, אני מאמין ליזמים שכמות הפקקים אכן תרד. מנהרות הכרמל הן פשוט תירוץ להעלות לדיון את השאלה הכללית - האם בהינתן רשת תחבורה כלשהי, הוספת כביש תקל בהכרח על הפקקים - כלומר, תקטין את זמן הנסיעה הממוצע ברשת? והתשובה המפתיעה, שמכונה “פרדוקס ברס”, היא לא. הדוגמה הנגדית היא קצרה ופשוטה ולכן אציג אותה כאן במלואה.

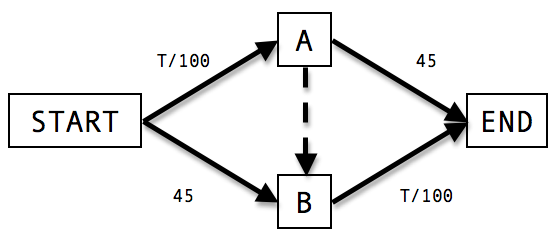
כרגיל, תמונה אחת שווה אלף מילים, אז הנה התמונה:

מה הולך כאן? נניח שהכניסה לחיפה היא נקודת ההתחלה, והקריות הן נקודת הסיום. מי שמגיע לחיפה צריך לבחור מה הוא מעדיף - לעלות על ההר בדרך פרויד המתפתלת, או לנסוע דרך העיר התחתית בכביש שמקיף את חיפה ומתארך עד אין קץ. הבה נניח את ההנחות (הלא ממש מציאותיות) הבאות: פרויד היא עליה מפותלת ובעייתית ותמיד לוקחת זמן רב - נניח, 45 דקות בין אם יש פקקים ובין אם אין (ממילא כולם נוסעים שם במהירות נמוכה). היא מסתיימת בנקודה שמסומנת ב-\( B \) בשרטוט, ואחרי שמגיעים לראש ההר עדיין צריכים לנסוע עד לצ’קפוסט. הנסיעה על ההר תלויה מאוד במצב התנועה - אם הכביש פנוי מרכבים אפשר לעבור אותה חיש קל - אפילו ב”0 דקות” (כמו שכבר הבנתם, המספרים פה שקריים לחלוטין - הרעיון הוא להתאים את עצמי לדוגמה). לעומת זאת ככל שמספר הרכבים שמנסים לנסוע דרך ההר גדל כך מספר הפקקים גדל באופן מחריד (החלק הזה דווקא מציאותי לגמרי…). התוצאה? אפשר להעריך שפרק הזמן שיקח לנהג לעבור את יתר הדרך על ההר הוא \( \frac{T}{100} \) דקות כאשר \( T \) הוא מספר הרכבים שמנסים לעבור דרך ההר בפרק הזמן הנוכחי. במילים אחרות, אם \( 4500 \) רכבים ינסו לעבור דרך ההר, גם קטע הדרך הזה יקח 45 דקות.

האלטרנטיבה היא כאמור לנסוע דרך העיר התחתית. אפשר לחלק גם את הדרך הזו לשניים - יש נסיעה קצרה בכניסה לחיפה עד לנקודה שמסומנת ב-\( A \), ואז נסיעה ארוכה לאורך כל העיר התחתית. נקרא לנקודה שאליה מגיעים בסיום הכניסה לחיפה בשם \( A \) ונניח שגם הנסיעה אליה תלויה במצב התנועה באותו אופן כמו הנסיעה על ההר: \( \frac{T}{100} \). לעומת זאת, העיר התחתית היא נסיעה במסלול ארוך ולא משנה מה, ולכן היא לוקחת תמיד 45 דקות (שוב, מספר לא מציאותי כי תמיד יש פקקים והמצב תמיד גרוע יותר). זה משלים את תמונת המצב הנוכחית.

נניח ש-4000 רכבים מנסים לעקוף את חיפה בדרך אל הצ’קפוסט. כמה זמן זה ייקח להם? ובכן, זה אולי לא נראה כך אך זוהי בעיה בתורת המשחקים. תורת המשחקים מנסה למדל מצבים שבהם מספר גורמים (“שחקנים”) צריכים לבחור בין כמה דרכי פעולה שונות ומנסה להעריך מה תהיה התוצאה. כאן יש לנו 4000 שחקנים, ומכיוון שהאינטרס היחיד שלהם הוא לעבור את העיר כמה שיותר מהיר, אנחנו מניחים שהם תמיד יבחרו בנתיב הנסיעה המהיר יותר. תורת המשחקים נכנסת לפעולה מכיוון שהשאלה “מהו הנתיב הקצר ביותר” תלויה בעצמה במה שהשחקנים עושים - כמה מהם בוחרים ללכת לאן. מה שאנחנו מחפשים הוא מצב של “שיווי משקל נאש” - מצב שבו דרכי הפעולה של כל השחקנים נקבעו להיות משהו מסויים וכל נהג, אם הוא יודע בדיוק מה עושים כל שאר הנהגים האחרים כרגע, לא ירגיש צורך לשנות את ההחלטה שלו עצמו.

הבה ונסמן את כמות האנשים שנוסעים דרך העיר התחתית ב-\( A \), ואת כמות האנשים שנוסעים דרך פרויד ב-\( B \). סה”כ \( A+B=4000 \). זמן הנסיעה של מי שנוסע בעיר התחתית הוא \( \frac{A}{100}+45 \), וזמן הנסיעה של מי שנוסע בפרויד הוא \( \frac{B}{100}+45 \). שיווי המשקל יתקבל כאשר הזמן שלוקחות הנסיעות הללו יהיה שווה, כלומר \( \frac{A}{100}+45=\frac{B}{100}+45 \), כלומר \( A=B=2000 \), ולכל נהג יקחו 65 דקות לעבור את חיפה. לא משהו, אבל זה מה יש.

כעת הוחלט לחצוב מנהרות צנועות יותר ממנהרות הכרמל - במקום לעבור את כל חיפה, חוצבים מהכניסה לחיפה (\( A \)) ועד להר למעלה, במקום שבו פרויד נגמר והמסע על ההר מתחיל (\( B \)). היתרון - המנהרה לא מתפתלת ומסתבכת אלא עולה בקו ישר ומהיר - כל כך מהיר שאפשר להניח שלוקח זמן 0 לעבור בה. מה כעת יהיה פרק הזמן שכל נהג מבלה במעבר חיפה?

הבה ונניח שאנחנו נהג שמתקרב לחיפה ושוקל מה לעשות - האם לנסוע לכיוון \( A \), או לכיוון \( B \)? מן הסתם, נעדיף לנסוע לכיוון \( A \) בכל מקרה. מדוע? כי אם מטרתנו היא להגיע ל-\( A \), אין שום טעם להגיע ל-\( B \); ואם מטרתנו היא להגיע ל-\( B \), אז עדיף לנו לבצע את העיקוף - קודם לנסוע ל-\( A \) ואז לנסוע במנהרה אל \( B \). מדוע? כי מכיוון שיש 4000 נהגים סך הכל, אז הזמן שאנו מבלים בדרך אל \( A \) יהיה לכל היותר 40 דקות ואז נגיע ל-\( B \) “בחינם”, בעוד שבעלייה הרגילה ל-\( B \) תמיד יידרשו לנו 45 דקות. בקיצור, הכביש החדש הפך את דרך פרויד לחסרת טעם לחלוטין. כולם ייסעו אל הנקודה \( A \) כי זה משתלם יותר ולא משנה מה.

אוקיי, אז הגענו ל-\( A \). כעת אפשר לעשות אחד משניים - או להקיף את חיפה דרך העיר התחתית ב-45 דקות, או לעלות אל ההר במנהרה החדשה ולנסוע דרך ההר. אנחנו שוב עושים את אותו חשבון - גם אם כל הרכבים ייסעו דרך ההר, זה ייקח לנו רק 40 דקות, שזה פחות מהעיר התחתית. אז אנחנו נוסעים דרך ההר - כלומר, קודם ל-\( B \) ואז לנקודת הסיום. מכיוון שכל הנהגים חושבים כמוני, כולם נוסעים באותה הדרך ולאף אחד לא משתלם לשנות זאת; ולכן כולנו נוסעים 80 דקות. יותר מאשר קודם!

טוב, תגידו, זה בגלל שהנהג הישראלי המצוי הוא אידיוט והולך על מה שנראה לו בתור הרווח המיידי למרות שזה פוגע בו. אם רק איזה אח גדול רחום היה מראה לו את האור ומסביר לו שעדיף שחצי מהנהגים ייסעו בדרך אחת וחצי בדרך האחרת, כמו קודם, הכל יסתדר. אלא שזה לא כך: נניח שאני נהג שמגיע זה עתה ויודע ששאר הנהגים אכן בוחרים להתפצל חצי-חצי. אז מה שאעשה יהיה להתחכם: אסע אל \( A \) במשך 20 דקות, אעלה במנהרה אל \( B \), ואז אסע מ-\( B \) והלאה גם כן 20 דקות, ואגיע למחוז חפצי ב-40 דקות בלבד - משתלם! רק מה, זה מעיד על כך שהמצב שבו כולם נוסעים או דרך \( A \) בלבד או דרך \( B \) בלבד אינו יציב; כמו שהשתלם לי להחליף, כולם יחליפו - ולכן שוב יקח לכולנו 80 דקות לנסוע בנתיב ה-\( A-B \) הזה. בקיצור, שום דבר לא יעזור - האינטרסים של הנהגים מכתיבים להם את דרך הנסיעה הגרועה הזו. שני הפתרונות היחידים הם להעיף לכל הרוחות את הכביש המיותר מ-\( A \) אל \( B \), או לאסור על כניסה לכבישים מסויימים לאחר שהצטבר עליהם עומס מסויים. המסקנה בכל אחד מהמקרים היא שכבר היה עדיף אם לא היו בונים את הכביש מ-\( A \) אל \( B \) מלכתחילה. וזה למרות שזה כביש נפלא ומהיר לכשעצמו.

כמו דברים רבים שמכונים “פרדוקס” (למשל “פרדוקס” יום ההולדת שהוזכר בפוסט הקודם) אין כאן באמת סתירה כלשהי. יש כאן פשוט תוצאה לא אינטואיטיבית, שממחישה בצורה יפה מאוד לטעמי איך ומדוע עלינו להיות זהירים מאוד עם הדברים שעליהם אנו אומרים “ברור”ו”קל לראות”. זה הכוח של המתמטיקה - היכולת לבצע ניתוח מדויק ופשוט של סיטואציות (מבלי צורך בבנייה של מאיץ חלקיקים השווה מיליארדים) שיכול להניב תוצאות שלחלוטין לא ציפינו להן.

והאם זה כך במנהרות הכרמל? כאמור, אני לא חושב כך. אני מאמין שהפקקים אכן ישתפרו בזכותן; כל מה שאני אומר הוא שאם כששמעתם “ההערכה שלנו היא שהמנהרות יביאו לירידה של 15% בנסיעה בדרכים החלופיות” פשוט הנהנתם בראשכם ואמרתם “ברור”, אז אני מקווה שכעת זה כבר לא כל כך ברור מאליו עבורכם (ואולי שזה יסייע לכם לאמץ את הספקנות והבדיקה העצמית כדרך חיים).