הוכחה לנוסחת אוילר לגרפים בעזרת גרפים אוילריים

המטרה שלי בפוסט הזה היא לקשר שני דברים בסיסיים בתורת הגרפים שאני מאוד מחבב אישית: נוסחת אוילר לגרפים מישוריים, והמושג של גרף אוילרי. ספציפית, אני הולך לתת הוכחה לנוסחת אוילר שמתבססת על גרפים אוילריים, תוך הסתייגות הולמת שזו לא באמת הוכחה פורמלית עד הסוף ואם ממש מתעקשים אפשר גם להציג אותה בלי המושג של גרף אוילרי אבל איפה הכיף פה. באנו היום לכייף.

כפי שאפשר לנחש, הפוסט הזה לא נועד לעמוד בפני עצמו והוא מניח שאתם מכירים את נוסחת אוילר לגרפים מישוריים וגרפים אוילריים. יש לי כאן פוסט על נוסחת אוילר וכאן פוסט על גרפים אוילריים, אבל אני כן אזכיר את מה שצריך לדעת. חוץ מגרפים. גרפים אני באמת הולך להניח שאתם יודעים וזהו.

נוסחת אוילר מדברת על גרפים מישוריים: גרפים שאפשר לצייר במישור בלי ששתי קשתות יחתכו זו את זו (הצמתים הם נקודות והקשתות הן קווים שמחברים את הנקודות; לאו דווקא קווים ישרים למרות שאפשר להראות שכל גרף מישורי אפשר לצייר עם קווים ישרים שכאלה). בשביל לדבר על נוסחת אוילר צריך גם לדרוש שהגרף המישורי יהיה קשיר - שיש מסלול שמחבר כל שני צמתים בו.

גרף אוילרי הוא גרף שאפשר לצייר מבלי להרים את העפרון מהדף - כזה שיש בו מסלול שעובר דרך כל הקשתות בדיוק פעם אחת. הנה דוגמא לגרף שיש בו גם את זה וגם את זה:

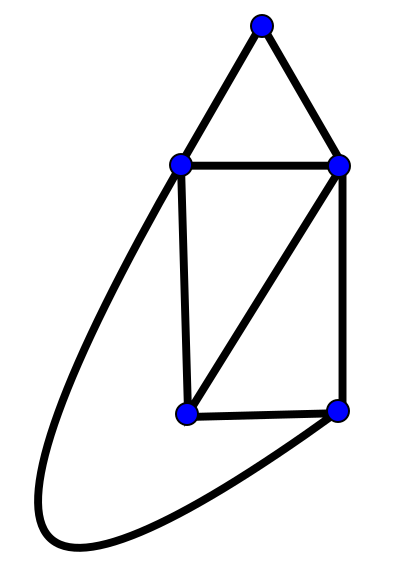
הגרף הזה הוא בעצם ציור הבית מחידת ה”האם אפשר לצייר בית עם איקס בתוכו מבלי להרים את העפרון מהדף” למעט זה שבמקום להשלים את האיקס בתוכו, הקשת שמחברת את הפינה הימנית-תחתונה והפינה השמאלית-עליונה עוברת מחוץ לבית כדי לא לחתוך את הקשת שעוברת בתוך הבית. זה מראה שהגרף הזה הוא מישורי, בנוסף לכך שהוא אוילרי. כפי שאפשר לנחש, הוא הולך לככב בהמשך הפוסט שלנו.

כשיש לנו ציור של גרף מישורי אפשר לדבר לא רק על הצמתים והקשתות שלו אלא גם על הפאות שלו - השטחים הסגורים שנתחמים על ידי הקשתות (המילה “פאות” מגיעה מההקשר המקורי של נוסחת אוילר, עבור פאונים; לא אדבר על כך בפוסט הזה):

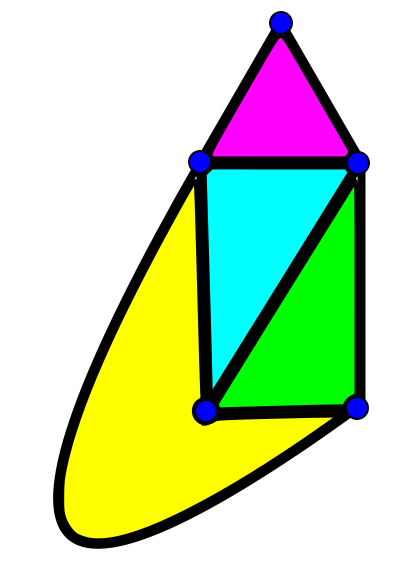
בתמונה הנוכחית צבעתי את הפאות בצבעים עליזים - ורוד, ירוק, כחול, צהוב ולבן. רגע, איפה הלבן כאן? ובכן, גם השטח ש”מחוץ” לגרף נחשב לאחת מהפאות שלו, “הפאה החיצונית”. כלומר, הצביעה העליזה שלי מראה לנו שלגרף יש חמש פאות. בנוסף לכך יש לו חמישה צמתים (הנקודות הכחולות) ויש לו שמונה קשתות (הקווים השחורים העבים שמחברים צמתים). אם נסמן את מספר הצמתים ב-\( V \), את מספר הקשתות ב-\( E \) ואת מספר הפאות ב-\( F \) נגלה שמתקיים

\( V-E+F=2 \)

והקשר הזה בין מספר הצמתים, הקשתות והפאות מתקיים תמיד, בכל גרף מישורי קשיר; זו נוסחת אוילר, שהיא ללא ספק אחת מהנוסחאות החביבות עלי במתמטיקה. המטרה שלי בפוסט הזה היא להוכיח שהיא אכן מתקיימת תמיד, בכל גרף מישורי קשיר (חייבים קשירות כי אחרת אפשר להגדיל את מספר הצמתים \( V \) בלי להשפיע על מספר הקשתות או הפאות, סתם על ידי הוספת צמתים מבודדים), אבל הוכחה היא מילה די גדולה בהקשר הזה - שנתפשר על “המחשה יפה”?

רגע, למה בעצם אני לא יכול לתת הוכחה של ממש? ובכן, כל המושג של “גרף מישורי” הוא די קשה מבחינה פורמלית. מה זה אומר “לצייר את הגרף במישור כך שאין חיתוכים”? צריך לערב כאן עולם מושגי חדש לגמרי - המישור \( \mathbb{R}^{2} \) ומה זה אומר “לצייר” בו משהו - זה אומר ליצור עקומות; עקומה היא פונקציה רציפה \( f:\left[0,1\right]\to\mathbb{R}^{2} \), ועכשיו צריך לדבר על חיתוך של עקומות, ועל מה זו בעצם פאה - רכיב קשירות נפרד של המישור כשמסירים ממנו את האיזורים שמכוסים על ידי עקומות? כל הדברים הללו מובילים אותנו אל משפט מפלצתי שנקרא משפט ז'ורדן ואומר (בנפנוף ידיים) שאם מציירים עיגול במישור אז הוא מפרק את המישור ל”בפנים” וה”בחוץ” של העיגול. זה משפט קשה עם הוכחה קשה. אז לא, אני לא אכנס לפורמליזם הזה פה ואפילו לא אנסה - בדיוק בשביל זה הבלוג נקרא “לא מדויק”.

הרעיון ב”הוכחה” שלי הוא פשוט ויפה וניתן לתיאור בפסקה אחת לפני שנדגים אותו בצורה מפורטת. אנחנו נצייר את הגרף המישורי שלנו מבלי להרים את העט מהדף, ונעקוב כל הזמן אחרי מספר הפאות הנוכחי. כל “צעד” שלנו כולל ציור של קשת אחת, ולכן אחרי \( E \) צעדים הציור יושלם. כשאנחנו רק מתחילים והציור ריק, יש לנו רק פאה אחת - הפאה החיצונית. מתי נוצרות פאות חדשות? בדיוק בצעדים שמחזירים אותנו לצומת שבה כבר היינו. כמה צעדים כאלו יש? אם יש \( E \) צעדים בסך הכל ולכן אנחנו מבקרים בסך הכל ב-\( E+1 \) צמתים במהלך הציור - הפלוס אחד מגיע מכך שאנחנו נמצאים בצומת כלשהי כבר בהתחלה, עוד לפני שציירנו קשת אחת. יש בסך הכל \( V \) צמתים ולכן אנחנו מבקרים ב-\( E+1-V \) צמתים יותר מפעם אחת. לכן מספר הפאות שמתווספות אל האחת הראשונית יהיה \( E+1-V \), כלומר \( F-1=E+1-V \), ואחרי העברת אגפים נקבל \( V-E+F=2 \).

איבדתן אותי? לא לדאוג, מייד תבוא דוגמא. לא איבדתן אותי אבל מעצבן אתכן שה”הוכחה” שלי עובדת רק אם הגרף המישורי שלי הוא גם במקרה על הדרך באופן ממוזל גרף אוילרי אבל בבירור רוב הגרפים המישוריים אינם כאלו? אז אני אגלה כבר עכשיו שזה פתיר בקלות רבה - קחו גרף מישורי כלשהו ופשוט שכפלו כל קשת פעמיים. גם לזה נחזור עם תמונות בהמשך.

בואו נעקוב אחרי תהליך הציור של התמונה לעיל, עם ספירה של מספר הקשתות והפאות בכל רגע נתון. כל חמשת הצמתים יופיעו כל הזמן - כלומר, \( V=5 \) הולך להיות קבוע. בהתחלה יש רק את הצמתים, ודמיינו שאנחנו עומדים בצומת הימני-תחתון ומחכים בהתרגשות לתחילת המסע שלנו בגרף:

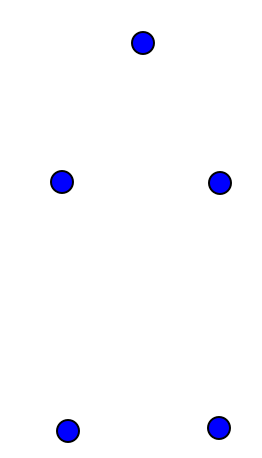
כאן \( E=0 \) ו-\( F=1 \) (כי הפאה החיצונית, הלבנה).

עכשיו נבצע את הצעד הראשון:

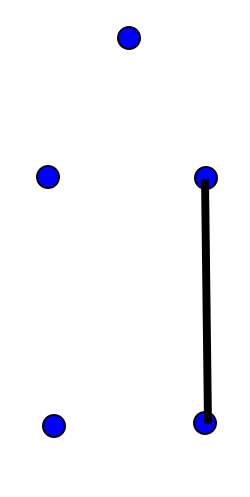
ועכשיו \( E=1 \) ו-\( F=1 \) נשאר כמו קודם - מכיוון שהקשת הגיעה לצומת שטרם ביקרנו בו, לא יצרנו פאה חדשה. אנחנו רואים שלבקר בצומת שטרם ביקרנו בו זה משעמם, אז בואו נבצע את כל יתר הצעדים הנדרשים כדי שנבקר בכל הצמתים; מרגע זה והלאה, כל צעד נוסף יצור פאה חדשה:

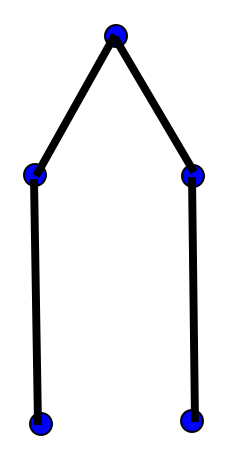
כרגע \( E=4 \) (כמספר הצמתים פחות אחד - לא מקרי, כמובן, הקשר \( E=V-1 \) מתקיים בכל עץ) ו-\( F=1 \). כלומר, כבר כרגע מתקיימת הנוסחה \( V-E+F=2 \), וזה לא מפתיע כי הגרף שקיבלנו כרגע הוא גם מישורי וגם קשיר (זוכרות? קשירות הייתה הכרחית בשביל נוסחת אוילר, בדיוק בגלל שצמתים מבודדים כמו בתמונות הקודמות לא משפיעים על \( E \) ועל \( F \) ואפשר להוסיף כמה מהם שרוצים). מה שיקרה מכאן ואילך הוא שכל צעד ישמר את הקשר הזה, \( V-E+F=2 \); כי כל צעד גם יוסיף קשת אחת (יגדיל את \( E \) ב-1) וגם יצור פאה חדשה (יגדיל את \( F \) ב-1). בואו נראה את זה קורה בפעם הראשונה:

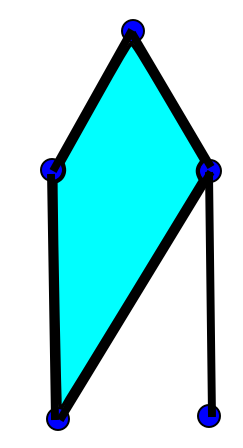
מה שנחמד פה הוא שהפאה שיצרנו לא מופיעה בתמונה הסופית, פשוט כי הצעד הבא מפרק אותה לשתי פאות:

ונראה לי שהרעיון ברור אז אני אצייר את שתי הקשתות הבאות ביחד:

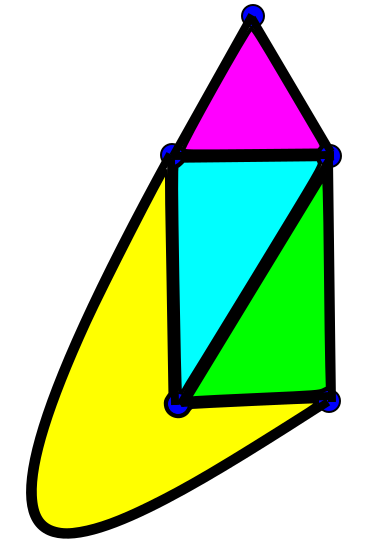
זה מסיים את ה”הוכחה”, אבל עדיין צריך להתייחס למקרה שבו הגרף המישורי שלנו איננו אוילרי, מה שמחזיר אותנו לשאלה בסיסית קצת יותר - מתי גרף הוא כן אוילרי? כאן נדרשים שני דברים. ראשית, שהגרף יהיה קשיר; אבל אנחנו מניחים שהגרף המישורי שלנו קשיר, כך שזה לא רלוונטי. שנית, צריך שהדרגה של כל צומת תהיה זוגית, פרט אולי לשני צמתים בדיוק. דרגה של צומת היא מספר הקשתות שנוגעות בו; מכיוון שבמסלול אוילרי בכל פעם שבה אנחנו נכנסים לצומת ו”שורפים” את הקשת שאיתה נכנסנו אנחנו גם יוצאים ממנו ו”שורפים” את הקשת שאיתה יצאנו, קל לראות שמספר הקשתות שמתאימות לכל צומת חייב להיות זוגי למעט בצמתי ההתחלה והסיום. האתגר הגדול יותר הוא להראות שזה גם תנאי מספיק לכך שיהיה מסלול אוילרי בגרף, אבל אני לא אעשה את זה כאן הפעם אלא רק אשתמש בזה.

בגלל שהקריטריון הזה לאוילריות של גרף הוא כל כך פשוט, אנחנו יכולים לנצל אותו ולהפוך גרף לאוילרי בקלי קלות - פשוט נכפיל את מספר הקשתות. הנה דוגמא:

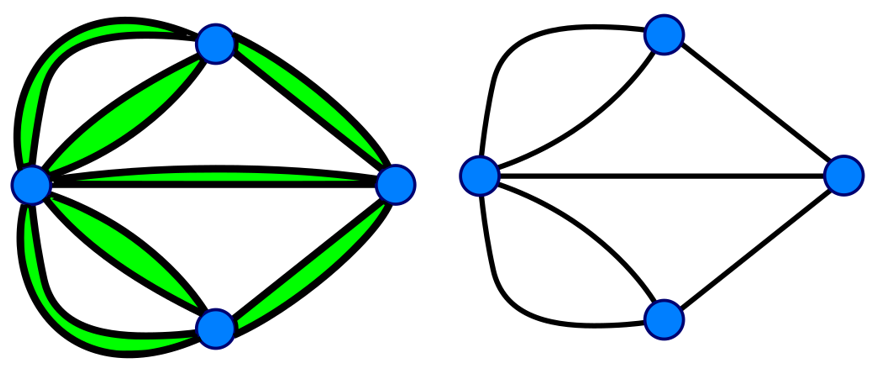
הגרף הימני הוא הגרף המפורסם של “בעיית הגשרים של קניגסברג” שאוילר פתר. כל הצמתים שם מדרגה אי זוגית ולכן הגרף אינו אוילרי, למרות שהוא בבירור מישורי ובבירור מקיים את נוסחת אוילר (\( V=4 \) ו-\( E=7 \) ו-\( F=5 \)). הגרף השמאלי הוא מה שקורה לגרף הימני כשאני לוקח כל קשת ומפצל אותה לשתיים. ההשפעה של הפיצול הזה על הגרף היא זו:

1. מספר הקשתות החדש בגרף הוא פי 2 מאשר בגרף הישן. אסמן זאת \( E^{\prime}=2E \).
2. מספר הצמתים בגרף החדש זהה למספר הצמתים בגרף הישן. אסמן זאת \( V^{\prime}=V \).
3. עבור כל קשת בגרף המקורי יצרנו פאה חדשה, של השטח ש"כלוא" בין שתי הקשתות החדשות שהחליפו את הקשת הזו - אני מסמן את הפאות החדשות בירוק. כלומר, \( F^{\prime}=F+E \).
4. הגרף החדש עכשיו אוילרי ולכן מקיים את נוסחת אוילר: \( V^{\prime}-E^{\prime}+F^{\prime}=2 \).

כל מה שנשאר לעשות הוא להציב במשוואה של 4 את המשוואות של 1-3. נקבל:

\( V-2E+\left(F+E\right)=2 \)

כלומר \( V-E+F=2 \), שזה מה שרצינו להוכיח, וסיימנו.

כפי שאמרתי קודם, ההוכחה הזו לא באמת נותנת נקודת מבט שונה מהותית על הנושא ביחס להוכחות הסטנדרטיות יותר שמשתמשות באינדוקציה וכדומה. סוג הטיעונים כמעט זהה. ההבדל העיקרי הוא שההוכחה הזו, לתחושתי, פשוט כיפית יותר.