ארבע פעולות החשבון - חיבור

אני רוצה לדבר על הבסיס של הבסיס של המתמטיקה - ארבע פעולות החשבון. חיבור, חיסור, כפל וחילוק. כולנו כנראה מכירים אותן, אבל אני רוצה לדבר גם על איך מבצעים אותן. כמובן, התשובה הפשוטה לכך היא “בעזרת מחשבון” ואני לגמרי בעד התשובה הזו כי מחשבונים חוסכים לנו זמן ומקטינים את הסיכוי לטעויות, אבל לפעמים יותר נוח לעשות את החשבון בראש או בעזרת דף ועט, לפעמים אפשר להפיק ממנו סוג של הנאה אסתטית, ולפעמים אפשר גם לספר סיפורים (שאין לי מושג אם הם נכונים או לא) על איך זה מפתח את החשיבה שלנו. אז בואו נניח שאנחנו רוצים לדעת איך לבצע ידנית את ארבע פעולות החשבון ונראה עד כמה זה נורא.

אני הולך לדבר רק על ארבע פעולות החשבון כשהן מופעלות על המספרים \( 0,1,2,3,\ldots \) וכן הלאה - מה שנקרא המספרים הטבעיים. אפשר לדבר עליהן גם בהקשר של מספרים שליליים ושברים וכדומה, אבל להבין אותן על המספרים הטבעיים זו נקודת המוצא להכל.

נפתח עם חיבור. אינטואיטיבית, לחבר שני כמויות של איברים זה לחשב כמה איברים יש כשכולם מעורבבים ביחד:

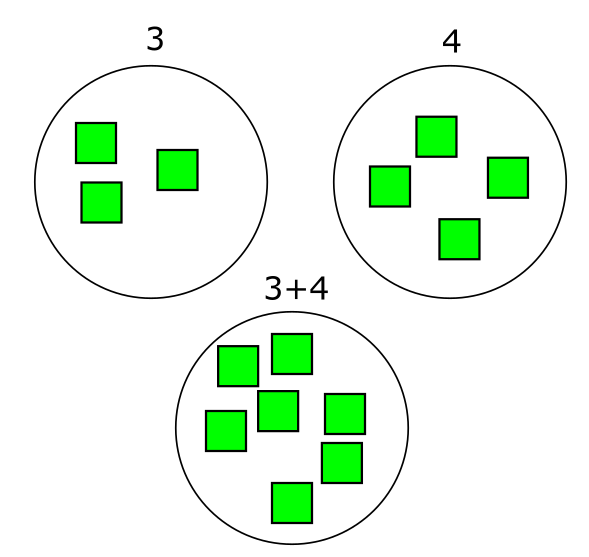
אם יש לנו קבוצה עם \( a \) איברים וקבוצה עם \( b \) איברים, ואנחנו מתחילים לספור את אברי הקבוצה הראשונה וכשאנחנו מסיימים אנחנו מתחילים לספור את אברי הקבוצה השניה בלי להתחיל מחדש את הספירה, אז הספירה תסתיים במספר \( a+b \). זה כל הרעיון, והוא פשוט למדי. עד כדי כך פשוט, שלא קשה להשתכנע שחיבור מקיים תכונות “נחמדות” כמו חוק החילוף שאומר ש-\( a+b=b+a \) וחוק הקיבוץ שאומר ש-\( \left(a+b\right)+c=a+\left(b+c\right) \).

ייתכן שזה לא מספיק טוב לאלו מכם שרוצים פורמליזם מתמטי מלא - אני לא לגמרי אכנס לכך כאן, אבל הנה הרעיון הבסיסי. אפשר לתאר את המספרים הטבעיים בעזרת המספר \( 0 \) ובעזרת פעולת העוקב, שלוקחת מספר טבעי ומחזירה את הבא אחריו. אסמן אותה ב-\( S \), ואז למשל \( 1=S\left(0\right) \) ו-\( 4=S\left(3\right) \) וכן הלאה. עכשיו אפשר להגדיר את פעולת החיבור באופן אינדוקטיבי, כלומר כזה שאומר “ראשית נגדיר מה זה חיבור עם 0, ואחר כך נגיד מה זה חיבור עם \( S\left(n\right) \) בהנחה שכבר הגדרתי חיבור עם \( n \)”. הנה ההגדרה:

• \( a+0=a \)
• \( a+S\left(n\right)=S\left(a+n\right) \)

אני לא אתעכב על ההגדרה או איך אפשר להתבסס עליה כדי להוכיח דברים כמו חוק החילוף; אני רק רוצה שנראה שאפשר להגדיר את זה פורמלית. עכשיו נעבור אל האקשן האמיתי - איך מחשבים את זה.

התשובה הלא נעימה היא שצריך מידה מסויימת של שינון. אפשר גם בלי, אבל בלי לזכור שום דבר בעל פה זה יוצא קשה למדי. מה שאני רוצה שנשנן הוא את התוצאות של חיבור מספרים בין 1 ל-10 זה עם זה. למשל, \( 8+5=13 \). איך אני מגיע למספר הזה אם אני לא יודע אותו ואין לי מחשבון או אינטרנט? ובכן, בשביל זה יש לרובנו 10 אצבעות: זוקפים מספר אצבעות ששווה למספר שאנחנו רוצים לחבר (5 בדוגמה שלי; תמיד יותר נוח לקחת את הקטן יותר), ומתחילים לקדם ב-1 את המספר השני. כלומר, אני אגיד “תשע” ואז אקפל אצבע אחת ויישארו 4; אגיד “עשר” ויישארו 3 אצבעות, וכן הלאה עד שאגיד “שלוש עשרה” ואסיים לקפל את כל האצבעות. זו שיטה לגיטימית לגמרי שנפוצה אצל ילדים וקרוב לודאי שגם אני הייתי נוקט בה אם לא הייתי זוכר בעל פה את כל תוצאות החיבור של מספרים בין 1 ל-10.

שיטה אחרת שאני מוצא את עצמי משתמש בה היא “לחבר ולחסר יחדיו”. נאמר שאני רוצה לחשב בראש את \( 8+5 \), מה שאני באמת עושה הוא זה: אומר “המממ, כדי להגיע מ-8 אל 10 צריך להוסיף לו 2, אז בואו נחסר 2 מ-5 ונקבל 3. קיבלתי ש-\( 8+5 \) זה אותו מספר כמו \( 10+3 \), וזה קל לי - זה 13”. כך אני זוכר יחסית בקלות את כל החיבורים האפשריים שגולשים מעל 10 - אבל אני לא מנסה לטעון שזו שיטה טובה במיוחד או כזו שתעבוד לכולם.

אפשר גם לרכז את כל זה בטבלה:

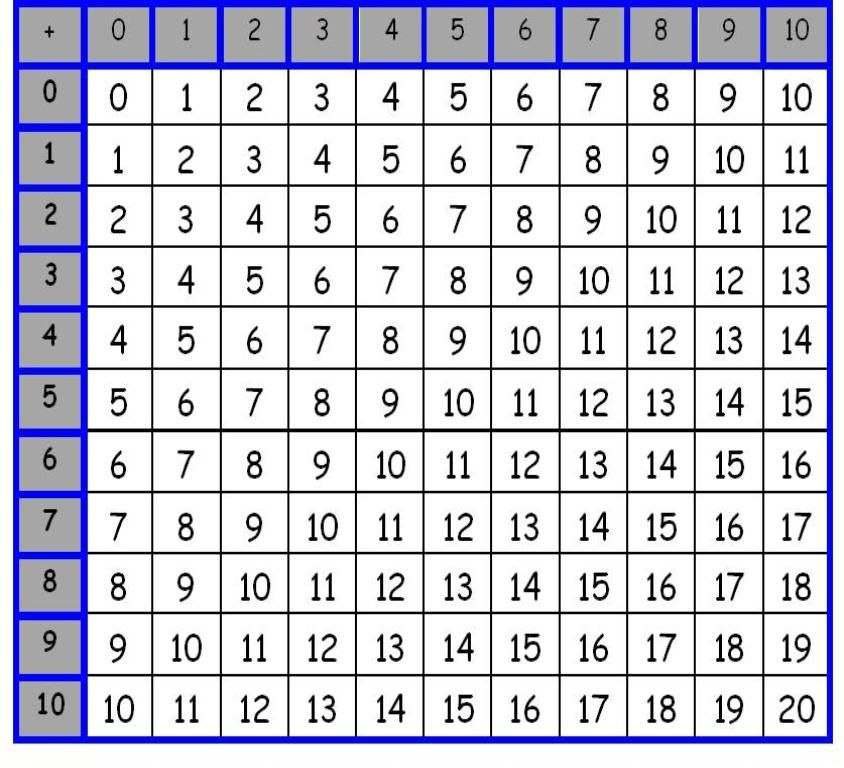
הבשורות הטובות הן שאם זוכרים את הטבלה הזו, אז אפשר לחבר כל שני מספרים טבעיים, לא משנה כמה גדולים, בכמות קטנה יחסית של מאמץ מנטלי בעזרת שיטה שנקראת חיבור ארוך או חיבור אנכי. בשיטה הזו כותבים את אחד המספרים מעל השני ומחברים “ספרה-ספרה”, החל מהספרה הקטנה ביותר. אני יכול פשוט להראות את זה, אבל אני רוצה קודם כל להסביר למה זה בכלל עובד. זה לא מובן מאליו שזה עובד - זה עובד בגלל שהשיטה שאיתה אנחנו מייצגים מספרים היא מגניבה. אם היינו מייצגים מספרים עם ספרות רומיות, זה היה יוצא קשה יותר.

מה המשמעות של מספר כמו \( 42 \) בשיטת הייצוג שלנו? ובכן, הוא אומר בעצם “שתיים ועוד ארבעים”. כלומר, הספרה 2 שמופיעה בצד ימין של המספר (ספרת האחדות) מייצגת את המספר “שתיים” בזמן שהספרה 4 שבצד שמאל (ספרת העשרות) מייצגת את המספר “ארבעים”. הרעיון הוא ש-42 בעצם מגדיר לנו מעין תרגיל חיבור: \( 2\cdot1+4\cdot10 \) (אני כותב כפל בעזרת נקודה, \( \cdot \) ולא בעזרת \( \times \) כי התרגלתי). באופן דומה, מספר בן שלוש ספרות כמו \( 513 \) מגדיר לנו את התרגיל \( 3\cdot1+1\cdot10+5\cdot100 \). באופן כללי, הרעיון הוא לכפול כל ספרה בחזקה של \( 10 \). קצת טריקי מצדי לדבר בשלב הזה על חזקות, שהן סוג של פעולת כפל, בהתחשב בכך שטרם הגעתי להגדרת כפל - אבל אני מניח שמי שקוראים את ההסבר מכירים ולו באופן אינטואיטיבי את המושג.

אם אני מסתכל על \( 2+3 \) אני פשוט אקבל \( 5 \) - חיבור של שתי ספרות אחדות החזיר לי ספרת אחדות חדשה. אבל ב-\( 5+8=13 \) קורה משהו יותר מתוחכם - בנוסף לספרת האחדות, נוצרת יש מאין גם ספרת עשרות. אנחנו נצטרך להתחשב ביצירה יש מאין הזו - זה מה שמוביל לסיבוך הטכני העיקרי בחיבור ארוך.

בואו נסתכל עכשיו על חיבור פשוט יחסית של שני מספרים בעלי שתי ספרות, \( 26+43=69 \). מה שקורה כאן הוא שאפשר לחשוב על החיבור הזה כאילו מחברים את ספרת האחדות של שני המספרים בנפרד, ואת ספרת העשרות של שניהם בנפרד. פורמלית מה שקורה כאן הוא זה:

\( \left(6\cdot1+2\cdot10\right)+\left(3\cdot1+4\cdot10\right)=\left(6\cdot1+3\cdot1\right)+\left(2\cdot10+4\cdot10\right) \)

ועכשיו אני מפעיל עוד תעלול שטרם תיארתי פורמלית ונקרא חוק הפילוג, ומקבל

\( 6\cdot1+3\cdot1=\left(6+3\right)\cdot1=9\cdot1 \)

\( 2\cdot10+4\cdot10=\left(2+4\right)\cdot10=6\cdot10 \)

ולכן המספר שהוא התוצאה יהיה \( 9\cdot1+6\cdot10 \), מה שאנחנו אכן כותבים בתור \( 69 \). אז הכל טוב ויפה - כדי לחבר את שני המספרים מספיק לחבר בנפרד את הספרות שלהם, ואת זה אנחנו כבר יודעים לעשות כי ספרות הן בין 0 ל-9 ויש לנו על נייר או בראש את “טבלת החיבור” של מספרים בתחום הזה.

כדי שזה יהיה קל, נהוג לכתוב את המספרים זה מעל זה, כך שכל עמודה בעצם כוללת את שתי הספרות שאנחנו רוצים לחבר:

\( \begin{array}{ccc} & 2 & 6\\ + & 4 & 3\\ \hline & 6 & 9 \end{array} \)

אותו דבר יעבוד גם עבור מספרים בני שלוש ספרות, או מאה ספרות, או כל דבר בסגנון. מספר פעולות החיבור הבסיסיות שנצטרך לעשות יהיה שווה למספר הספרות, וזה לא כל כך הרבה עבור רוב המספרים שאנחנו נתקלים בהם ביומיום.

עכשיו בואו נתחיל לסבך את העניינים. ראשית, מה אם שני המספרים שאנחנו רוצים לחבר אינם בעלי אותו מספר ספרות? למשל, \( 26+743 \). במקרה הזה אין קושי אמיתי - אפשר “להאריך” את המספר הקצר יותר על ידי הוספת הספרה 0, כלומר לכתוב את התרגיל בתור \( 026+743 \), ולקבל

\( \begin{array}{cccc} & 0 & 2 & 6\\ + & 7 & 4 & 3\\ \hline & 7 & 6 & 9 \end{array} \)

בפועל, כדי לחסוך לעצמנו אנרגיה, אנחנו לא טורחים לכתוב את ה-0-ים הללו שנמצאים בתחילת מספר, אז נכתוב:

\( \begin{array}{cccc} & & 2 & 6\\ + & 7 & 4 & 3\\ \hline & 7 & 6 & 9 \end{array} \)

המשמעות היא אותה משמעות - באנו לחבר את הספרות בעמודה ומצאנו שם רק ספרה אחת? נתייחס אל השניה בתור אפס.

בואו ניגש עכשיו לסיבוך המרכזי של חיבור ארוך - מה קורה אם יש זוג ספרות שמסתכם למספר שהוא 10 או יותר? למשל, \( 26+47 \). במקרה הזה, מה שעושים הוא הדבר הבא: קודם כל מחשבים את סכום שתי ספרות האחדות ומקבלים \( 13 \). עכשיו כותבים את 3 מתחת לזוג הספרות \( 6,7 \) ואילו את ה-\( 1 \) “נושאים למעלה” וכותבים מעל זוג הספרות הבא, \( 2,6 \). הוא הופך למספר חדש שמשתתף בתהליך החיבור - כלומר, מחברים שלוש ספרות בבת אחת. וכמו קודם - רושמים את התוצאה למטה, ואז היא הייתה גדולה או שווה ל-10, “נושאים” את ה-1 הנוסף הלאה. לכן הוא נקרא נשא (Carry).

ככה זה נראה:

\( \begin{array}{ccc} & 1\\ & 2 & 6\\ + & 4 & 7\\ \hline & 7 & 3 \end{array} \)

אני אישית מוצא שאני נמנע מלכתוב את ה-1 הנוסף הזה ופשוט זוכר אותו בזמן שאני מבצע את החיבור של הספרות הבאות, אבל אין חוקים פה - הכתיבה של ה-1 למעלה נועדה לעזור לנו, ואם היא עוזרת לנו - כדאי להשתמש בה.

עכשיו, בואו נסבך עוד קצת - מה קורה אם יש תרגיל חיבור שבו יש נשא גם בספרות האחרונות במספר? אז במקרה הזה נקבל חיבור של הנשא 1 עם שתי הספרות 0. נדגים את זה עם \( 76+47 \):

\( \begin{array}{cccc} & 1 & 1\\ & 0 & 7 & 6\\ + & 0 & 4 & 7\\ \hline & 1 & 2 & 3 \end{array} \)

ועוד דוגמא אחרונה - מה קורה אם מצטרף נשא לשתי ספרות שלבדן מסתכמות ל-9? אז עכשיו עם הנשא נגיע ל-10 ולכן נכתוב 0 למטה ונישא את 1 הלאה. נדגים זאת עם \( 76+24 \):

\( \begin{array}{cccc} & 1 & 1\\ & 0 & 7 & 6\\ + & 0 & 2 & 4\\ \hline & 1 & 0 & 0 \end{array} \)

עכשיו אפשר לקחת את זה צעד אחד קדימה. הנשא כבר גרם לי לסכם שלושה איברים באותה עמודה; זה מראה שאין בעיה עקרונית להשתמש בחיבור ארוך גם כדי לחבר שלושה או יותר מספרים. למשל את \( 23+34+56 \) אפשר לחבר כך:

\( \begin{array}{cccc} & 1 & 1\\ & & 2 & 3\\ & & 3 & 4\\ + & & 5 & 6\\ \hline & 1 & 1 & 3 \end{array} \)

כשמחברים שלושה מספרים, הנשא עשוי לצאת 2 ולא 1; זה לא ממש משנה את מה שעושים בפועל. בואו נראה את החישוב הזה עבור הדוגמא \( 18+28+38 \) שבה חיבור ספרת האחדות של המספרים נותן \( 24 \):

\( \begin{array}{ccc} & 2\\ & 1 & 8\\ & 2 & 8\\ + & 3 & 8\\ \hline & 8 & 4 \end{array} \)

עבור חיבור של מספר גדול יותר של מספרים אפר לקבל נשא שגדול מ-2. אם נחבר המון מספרים אנחנו עלולים לקבל נשא שהוא לפחות 10 - במקרה הזה פשוט כותבים את הספרות הבאות בעמודות הבאות בתור; אבל זו סיטואציה שהסיכוי שתצוץ בפועל היא אפסית כי בחישובים עם כל כך הרבה מספרים בבת אחת אולי עדיף לפצל את החישוב באמצע ממילא.

אם כן, זו שיטת החיבור הארוך - נשאר לי רק להסביר למה זה עובד בעצם. כבר הראיתי את זה בערך קודם עם חוק הפילוג, אבל לא נכנסתי למקרה שבו סכום ספרות יוצא גדול מ-10 ולכן נזקקים לנשא. בואו נדבר על זה עכשיו.

נחזור אל הדוגמא שלי של \( 26+47 \). אם אני כותב כמו קודם את 26 בתור \( 6\cdot1+2\cdot10 \) ואת 47 בתור \( 7\cdot1+4\cdot10 \) ומחבר, אני מקבל:

\( \left(7+6\right)\cdot1+\left(4+2\right)\cdot10 \)

כלומר, אני מקבל:

\( 13\cdot1+6\cdot10 \)

עכשיו, מה ש”מפריע” לי פה הוא שה-13 שמוכפל ב-1 הוא מספר שגדול מ-9, כלומר הוא לא ספרה. אז אני לוקח את \( 13 \) הזה וכותב אותו בתור \( 3\cdot1+10\cdot1 \), ואז אני מקבל:

\( \left(3\cdot1+1\cdot10\right)\cdot1+6\cdot10=3\cdot1+\left(6+1\right)\cdot10 \)

ה-\( 6+1 \) באגף ימין הוא בדיוק החיבור של הנשא (1) לתוצאת החיבור של שאר הספרות (6).

בואו נראה עכשיו עוד דוגמא אחת לסיום שתחדד עוד עניין קטן - החיבור \( 50+80=130 \). במקרה הזה ספרת האחדות היא 0 אז אני פשוט אשמיט אותה. מה שאנחנו מקבלים הוא

\( 5\cdot10+8\cdot10=13\cdot10 \)

ועכשיו אני כותב \( 13=3\cdot1+1\cdot10 \) ומקבל

\( \left(3\cdot1+1\cdot10\right)\cdot10=3\cdot10+1\cdot100 \)

שימו לב מה קרה פה - ההכפלה ב-10 הפכה את המספר 13 שהיה בסוגריים, למספר 130 שבתוצאה הסופית. כשעושים חיבור ארוך, ההכפלות הללו באות לידי ביטוי במיקום של מספרים - ככל שמספר מופיע יותר לכיוון שמאל, כך הוא מוכפל בחזקה גדולה יותר של 10. אפשר לראות את זה כאן:

\( \begin{array}{cccc} & 1\\ & & 5 & 0\\ + & & 8 & 0\\ \hline & 1 & 3 & 0 \end{array} \)

ה-1 שמופיע למעלה הוא ה-\( 1\cdot100 \) מהחישוב שהראיתי קודם, והוא נמצא במקום השלישי מימין - אפשר היה לכתוב שני אפסים מימינו ואז היה ברור שמדובר בעצם על 100.

אם כן, זה כל מה שיש לי לומר בשלב הזה על חיבור; בפעם הבאה ננסה להפוך את היוצרות ולדבר על חיסור.