ארבע פעולות החשבון - חיסור

בפוסט הקודם דיברתי על פעולת החיבור של מספרים טבעיים והפעם אני רוצה לדבר על הפעולה ה”משלימה” לה - חיסור. למה אני אומר “משלימה”? כי אם חיבור עונה לנו על השאלה “לאן הגענו מ-\( a \) אחרי שהלכנו עוד מרחק \( b \)?” אז חיסור עונה לנו על השאלה “אם הגענו מ-\( a \) אל \( b \), כמה הלכנו?”. או במשוואה, אם חיבור עונה על השאלה מהו \( x \) בביטוי \( a+b=x \), אז חיסור עונה על השאלה מהו \( x \) בביטוי \( a+x=b \).

אפשר לתאר את זה גם בצורה ציורית: נניח שהייתה לנו קבוצה עם 7 איברים, ומהם מחקתי שלושה; כמה נשארו לנו?

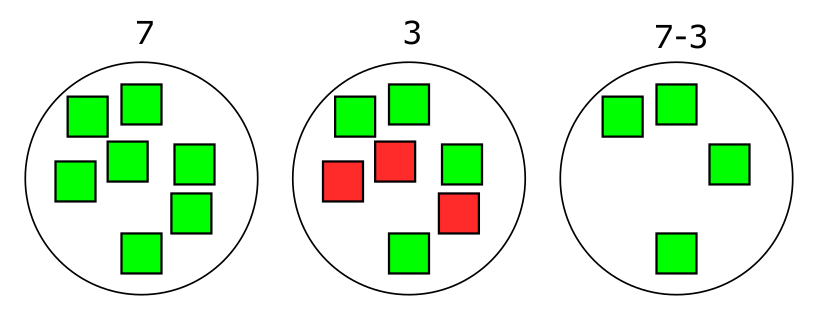
גם פה, יש לנו חיבור בתחפושת: זו השאלה המשלימה לשאלה כמה איברים אדומים צריך להוסיף לקבוצה הימנית כדי לקבל את הקבוצה השמאלית.

אפשר לתת לחיסור הגדרה פורמלית יותר אם מכניסים למשחק את המספרים השליליים ואז לחסר את \( b \) מ-\( a \) זה בסך הכל לחבר אל \( a \) את המספר הנגדי שמתאים ל-\( b \) (מה שאנחנו מסמנים בתור המספר \( -b \)), אבל בפוסט הזה אני רוצה להתמקד במספרים הטבעיים אז לא ארחיב יותר על העניין הזה. הנקודה שצריך לזכור היא שחיסור הוא מושג שהיה קיים במשך אלפי שנים גם בלי להזדקק לקיום המספרים השליליים (שהפכו לחלק סטנדרטי מהמשחק המתמטי בשלב מאוחר יחסית) וגם אצל ילדים בימינו נלמד בדרך כלל עצמאית לפני שמגיעים אל השליליים; למעשה, השליליים נותנים לנו את התשובה לשאלה מה קורה אם מחסרים מ-\( a \) מספר שגדול ממנו - אבל גם על זה אני לא הולך לדבר הפעם! (התשובה: אם \( b \) גדול מ-\( a \) אז אפשר לחשב קודם כל את \( b-a \) ואז לקחת את המספר הנגדי לתוצאה שקיבלנו).

חיסור שונה מחיבור בכך שחוק החילוף וחוק הקיבוץ הנחמדים לא מתקיימים לנו: \( a-b\ne b-a \) זה כמעט ברור (\( a-b \) הוא הנגדי של \( b-a \) כמו שאמרתי לפני רגע). את כשלון חוק הקיבוץ קל לראות עם דוגמא: \( \left(9-6\right)-3=3-3=0 \) ולעומת זאת \( 9-\left(6-3\right)=9-3=6 \). אם כן, כשיש שתי פעולות חיסור, הסוגריים חשובים.

השאלה האמיתית שאני רוצה לענות עליה בפוסט הזה, בדומה לפוסט הקודם, היא איך לחשב חיסור. כאן דווקא יש דמיון לא מבוטל לחיבור ולשיטת החיבור הארוך שהראיתי בפוסט הקודם, אבל הענינים טיפה יותר מסובכים.

ראשית, מה צריך לזכור בעל פה? פחות או יותר את התוצאות של חיסור מספר בין 0 ל-9 מכל אחד מהמספרים שגדולים ממנו בין 0 ל-19. למשל, לזכור ש-\( 9-6=3 \) אבל גם ש-\( 13-7=6 \). אין לי טריק טוב איך לזכור את התוצאות הללו מלבד להתעסק איתן מספיק, אבל אפשר לבצע את החיסור הזה בראש בעזרת תשע אצבעות: כדי לחשב את \( 13-7 \), למשל, אני אזקוף 7 אצבעות, ואז אתחיל לקפל אותן ועל כל אצבע שאני מקפל אני ארד צעד אחד החל מ-13. כלומר אני אגיד “13” (כשיש לי 7 אצבעות מוצגות), “12” (אחרי שקיפלתי את הראשונה ונשארתי עם 6) וכך הלאה עד “6” (אחרי שקיפלתי את האצבע האחרונה).

בשביל לראות חיסור ארוך, בואו ניזכר איך עבד חיבור ארוך

\( \begin{array}{ccc} & 5 & 3\\ + & 2 & 1\\ \hline & 7 & 4 \end{array} \)

הרעיון פה היה לכתוב את המספרים \( 53 \) ו-\( 21 \) זה מעל זה, ואז לעבור על הספרות שלהם מימין לשמאל, לחבר כל זוג ספרות ולכתוב את התוצאה למטה. זה עובד בדיוק באותו אופן גם עם חיסור:

\( \begin{array}{ccc} & 5 & 3\\ - & 2 & 1\\ \hline & 3 & 2 \end{array} \)

\( 3-1=2 \) ומכאן שהספרה הימנית בתוצאה היא 2, ואילו \( 5-2=3 \) ומכאן שהספרה השמאלית בתוצאה היא 3. עד כאן הכל טוב. הסיבוך מתחיל כשהספרה העליונה קטנה יותר מהספרה התחתונה.

ראשית, בואו ניזכר מה עשיתי כשהיה סיבוך בחיבור. שם הסיבוך מגיע מסיבה שונה: מכך שסכום שתי הספרות הוא לפחות 10 ולכן לא ניתן לייצג אותו על ידי ספרה בודד. הטריק במקרה הזה היה “להגלות” את ספרת העשרות אל העמודה הבאה, שם היא תתווסף לחיבור:

\( \begin{array}{ccc} & 1\\ & 5 & 3\\ + & 2 & 7\\ \hline & 8 & 0 \end{array} \)

כאן \( 3+7=10 \) אז כתבנו את ה-0 בתור הספרה שלנו, ואת ה-1 העברנו הלאה, להתחבר עם ה-5 וה-2.

בחיסור התעלול הוא הפוך: במקום להוסיף 1 לסכום עבור הספרות שמשמאל, אנחנו מחסרים 1 מהן, כדי להוסיף לספרות שלנו 10 - אפשר לומר שאנחנו לווים משהו מהספרות שמשמאל. כדי לראות איך זה עובד, בואו נסתכל לרגע על הדוגמא \( 53-27 \): כאן אם נבצע את החיסור \( 3-7 \) נקבל \( -4 \) וזו לא ספרה בין 0 ל-9. לכן אני משנה קצת את החשיבה שלי על התרגיל. במקום לומר ש-

\( 53-27=\left(3-7\right)\cdot1+\left(5-2\right)\cdot10 \)

אני אומר לעצמי שאת ה-5 הזה אפשר לכתוב בתור \( \left(4+1\right)\cdot10 \) ואז את ה-\( 1\cdot10 \) הזה אני יכול להוסיף אל החגיגה של \( \left(3-7\right)\cdot1 \), ולקבל

\( 53-27=\left(10+3-7\right)\cdot1+\left(4-2\right)\cdot10 \)

זה מה שעושים באופן כללי: בכל צעד של החיסור אנחנו מחסרים מהספרה העליונה את התחתונה. אם העליונה גדולה או שווה לתחתונה, הכל טוב. אם היא קטנה יותר, אנחנו מוסיפים לה 10 ומקטינים את הספרה העליונה שמשמאלה ב-1. ומה אם אין ספרה מצד שמאל? במקרה הזה יוצא שחיסרנו את המספר הגדול יותר מהקטן וזה לא הולך לעבוד - צריך לחסר את הקטן מהגדול.

עכשיו לשאלה המאתגרת באמת - איך כותבים את זה? ובכן, התשובה הנאיבית היא “מה שעובד לכם”. הנה איך אני עושה חיסור כזה:

\( \begin{array}{ccc} & 1\\ & 5 & 3\\ - & 2 & 7\\ \hline & 2 & 6 \end{array} \)

מה הולך פה? ראשית, אני מתרגם אוטומטית בראש את \( 3-7 \) לכך שצריך לכתוב את הספרה 6 למטה (כלומר, עובר מלחשוב על 3 בתור \( 3 \) אל לחשוב עליו בתור \( 13 \); ואם תרצו, אני מבצע חיסור מודולו 10 בראש). שנית, אני בלי שום בושה כותב 1 מעל \( 5 \) מתוך מוסכמה עם עצמי שאבין שצריך לחסר את ה-1 הזה מה-5, יחד עם ה-2 שאנחנו כבר ככה מחסרים ממנו. לרוב אני אפילו משמיט את כתיבת ה-1 הזה ופשוט זוכר שצריך לחסר 2 מ-4 במקום מ-5.

גישה אחרת היא פשוט למחוק את המספרים הסוררים ולכתוב גרסה תקינה שלהם (13 במקום 3, 4 במקום 5):

\( \begin{array}{ccc} & 4 & 13\\ & \require{cancel}\cancel{5} & \require{cancel}\cancel{3}\\ - & 2 & 7\\ \hline & 2 & 6 \end{array} \)

זו נראית לי גישה טובה כדי לצמצם טעויות, לפחות עד שמתרגלים לטכניקה. היא כמובן די מכוערת, אבל אסתטיקה היא לא היעד שלנו בחיסור ארוך אלא להצליח לפתור את התרגיל!

ובכן, זה כל מה שהיה לי להגיד על חיסור - הכיף האמיתי יגיע בפוסט הבא, כשנגיע לכפל.