ארבע פעולות החשבון - כפל

בשני הפוסטים הקודמים דיברתי על פעולות החיבור והחיסור של מספרים טבעיים והפעם הגענו אל פעולת הכפל. כאן העניינים מתחילים להסתבך מבחינה טכנית ואני מצהיר מראש שלא אוכל לעשות יותר מאשר לגרד את קצה הקרחון - יש הרבה טריקים ושיטות לביצוע של כפל בצורה מהירה ויעילה, שלרוב מתבססות על תעלולים קונקרטיים שאפשר להפעיל במקרים מסויימים; אני לא אדבר על זה כאן אלא אציג את השיטה ה”כללית”, שעובדת סבבה בהינתן נייר ועט והיכרות עם לוח הכפל.

בתור התחלה, מה זה כפל בכלל? הדרך הפשוטה ביותר לתאר כפל של מספרים טבעיים היא בתור סוג של “חיבור מקוצר”. להגיד “7 כפול שתיים” זה בעצם לעשות \( 7+7 \). להגיד “7 כפול שלוש” זה בעצם לעשות \( 7+7+7 \) וכן הלאה. לומר “\( a \) כפול \( b \)” זה בעצם לחבר \( b \) עותקים של המספר \( a \) זה עם זה. את “\( a \) כפול \( b \)” אני מסמן ב-\( a\times b \) או לפעמים ב-\( a\cdot b \) או אפילו משמיט את הנקודה לגמרי וכותב \( ab \) כשאני לא חושש מבלבול. בטקסטים מתמטיים מתקדמים נפוצה יותר הגישה של \( a\cdot b \) או \( ab \), אבל כשרק מתחילים את הלימוד משתמשים בדרך כלל ב-\( a\times b \) ובו אדבוק הפעם.

אפשר לתאר כפל ויזואלית באופן הבא: אם יש לנו \( a \) משבצות, ואנחנו מסדרים אותן בעמודה ואז יוצרים \( b \) עותקים של העמודה הזו, אנחנו מקבלים טבלה עם \( a\times b \) משבצות - מספר המשבצות בטבלה של \( a \) שורות ו-\( b \) עמודות.

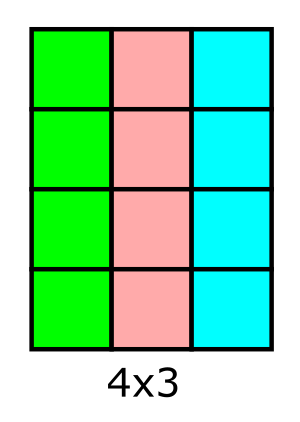
נקודת המבט של הטבלה הזו נחמדה במיוחד כי אם אנחנו לוקחים את הטבלה ומסובבים אותה ב-90 מעלות, אנחנו מקבלים טבלה אחרת שבה מספרי השורות והעמודות התחלפו אבל מספר המשבצות נותר ללא שינוי, וזה עוזר לנו לקבל אינטואיציה לכך ש-\( a\times b=b\times a \) - מה שנקרא חוק החילוף של כפל.

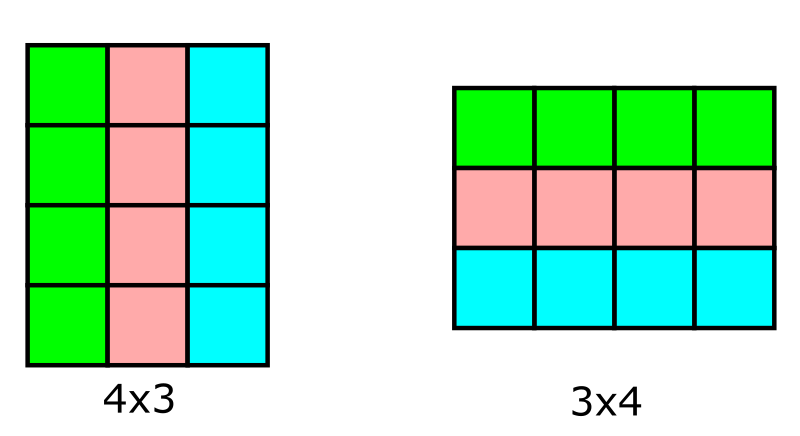
את ההמחשה בעזרת שורות ועמודות שיוצרות טבלה אפשר להעביר גם למכפלה \( a\times b\times c \) של שלושה מספרים - אפשר לחשוב על \( a\times b \) כאילו הם בונים טבלה של קוביות עם \( a \) שורות ו-\( b \) עמודות, ואז אנחנו חוזרים על הטבלה הזו במשך \( c \) קומות ומקבלים מעין מגדל קוביות. באותה מידה יכלנו להתחיל עם עמודה באורך \( b \) וגובה \( c \) ואז לחזור עליה במשך \( a \) שורות, והיינו מקבלים את אותו הדבר, כלומר \( \left(a\times b\right)\times c=a\times\left(b\times c\right) \) - אין חשיבות לשאלה אם קודם מחשבים את הכפל \( a\times b \) ואז כופלים ב-\( c \) או שקודם מחשבים את \( b\times c \) ואז כופלים ב-\( a \). זה מה שנקרא חוק הקיבוץ של הכפל.

הכלל האחרון והאהוב ביותר יקרוץ לכל מי ששברו אי פעם חבילת שוקולד. בואו ניקח טבלה עם \( a \) שורות ונשבור אותה במקום כלשהו על ידי קו אנכי, כך שמתקבלות שתי טבלאות - האחת עם \( a \) שורות ו-\( b \) עמודות, והשניה עם \( a \) שורות (אותו מספר שורות!) ו-\( c \) עמודות:

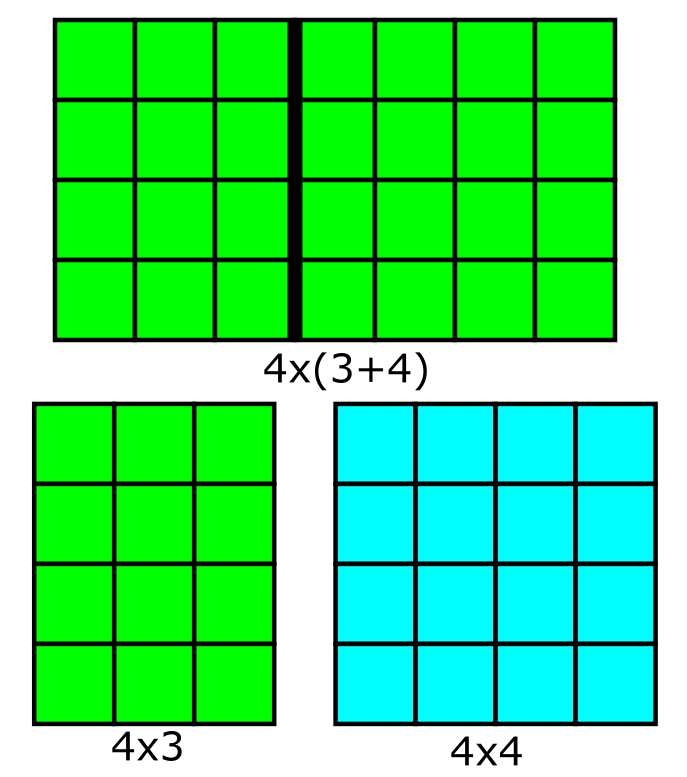
בטבלה המקורית היו \( a \) שורות ו-\( b+c \) עמודות, ולכן היו בה בסך הכל \( a\times\left(b+c\right) \) משבצות. אחרי הפירוק קיבלנו שתי טבלאות - אחת עם \( a\times b \) משבצות והשניה עם \( a\times c \) משבצות. בשתי הטבלאות גם יחד יש \( a\times b+a\times c \) משבצות, כך שקיבלנו את השוויון הבא:

\( a\times\left(b+c\right)=\left(a\times b\right)+\left(a\times c\right) \)

השוויון הזה נקרא חוק הפילוג, יחד עם הכלל המאוד דומה לו הבא:

\( \left(a+b\right)\times c=\left(a\times c\right)+\left(b\times c\right) \)

והסיבה שהוא כל כך חשוב לי היא הקשר בין כפל וחיבור שאנחנו רואים כאן. השיטה שאציג עבור “כפל ארוך” תתבסס בצורה חזקה מאוד על הכלל הזה. הנה דוגמא פשוטה: כמה זה \( 7\times23 \)? הטריק שרבים מאיתנו ינקטו בו כדי לחשב את זה יהיה לפרק את \( 23 \) ל-\( 3+20 \). עכשיו, אפשר לחבר את \( 7 \) לעצמו שלוש פעמים כדי לקבל ש-\( 7\times2=14 \) ו-\( 7\times3=21 \). אם \( 7\times2=14 \) אז הטריק הוא להכפיל את שני האגפים ב-10; כשכופלים מספר ב-10 זה מתבטא בכך שמוסיפים לו את הספרה 0 מימין, כלומר \( 7\times20=140 \). לכן \( 7\times23=7\times20+7\times3=140+21=161 \).

מה הלך פה? זה עדיין לא היה קל, אבל זה עירב כמה צעדי בסיס מוגבלים יחסית. ראשית, היינו צריכים לדעת את תוצאת הכפל של \( 7 \) במספרים 2,3; שנית, היינו צריכים לדעת את הטריק של “לכפול ב-10 מוסיף 0”. לבסוף, היינו צריכים לדעת לבצע חיבור. אלו גם שלושת המרכיבים של כפל ארוך באופן כללי:

• לדעת לכפול כל זוג מספרים בין 0 ל-9 ("לוח הכפל")
• להשתמש באופן מובלע בטריק הוספת האפסים (בפועל זה מתבטא בכתיבת מספרים כשהם מוזחים הצידה, כפי שאראה עוד מעט)
• לדעת לחבר מספרים באמצעות שיטת החיבור הארוך.

חיבור ארוך הוא יחסית פשוט לביצוע וטריק הוספת האפסים הוא פשוט מאוד; החור השחור בסיפור הזה הוא לוח הכפל:

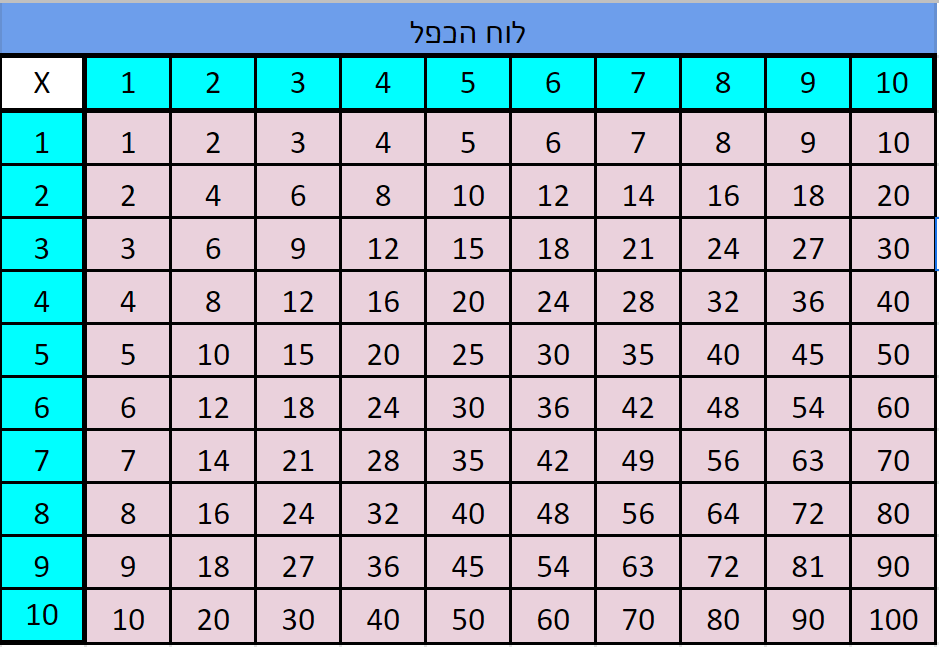
לזכור את לוח הכפל זה קשה. אצל חלקנו הוא טבוע בראש מילדות ולכל זוג מספרים המכפלה שלהם עולה בראש מייד, כברק; למזלי כך זה המצב אצלי. אצל אחרים חלק מהלוח מסתדר יפה מאוד אבל יש בו חורים לא ברורים שלא נסתמים גם אם חוזרים שוב ושוב עליהם; אצל אחרים פשוט אי אפשר לזכור את הדבר הארור הזה. אז יש שיטות וטריקים שמאפשרים לחשב חלק מהמקרים במהירות - אנסה להציג קצת מקצה הקרחון הזה בהמשך. בינתיים בואו נראה איך לבצע כפל ארוך בהינתן שיש לנו את לוח הכפל.

כפל ארוך כותבים בדומה לחיבור ארוך - מסדרים את שני המספרים זה מעל זה, ספרה-ספרה:

\( \begin{array}{ccc} & 2 & 3\\ \times & & 7\\ \hline \\ \end{array} \)

עכשיו, אני נוקט בגישה הבאה: קודם כל כופל את ה-7 שלמטה ב-3 שמייד מעליו, וכותב את התוצאה (שהושגה באמצעות לוח הכפל) למטה:

\( \begin{array}{ccc} & 2 & 3\\ \times & & 7\\ \hline & 2 & 1 \end{array} \)

עכשיו אני עובר לכפול את ה-7 בספרה הבאה בתור אחרי 3, כלומר ב-2; זה משהו שונה ממה שהיה בחיבור ארוך שבו חיברנו רק שתי ספרות שהאחת הייתה מעל השניה. את התוצאה של הכפל של 2 ב-7 (שהושגה, שוב, באמצעות לוח הכפל) אני כותב בשורה חדשה מתחת לשורה של ה-21, אבל כשהיא מוזחת צעד אחד שמאלה. למה? זה בדיוק אפקט ה”לכפול ב-10 זה כמו לכתוב 0 מצד ימין” שאצלנו מתבטא בהזחה בלי כתיבת ה-0 במפורש:

\( \begin{array}{ccc} & 2 & 3\\ \times & & 7\\ \hline & 2 & 1\\ 1 & 4 \end{array} \)

עכשיו אנחנו מחברים את שתי השורות שקיבלנו:

\( \begin{array}{cccc} & & 2 & 3\\ & \times & & 7\\ \hline & & 2 & 1\\ + & 1 & 4\\ \hline & 1 & 6 & 1 \end{array} \)

טוב ויפה, אבל עכשיו העניינים מסתבכים בשתי צורות אפשריות: ראשית, המספר שלמעלה עלול לכלול שלוש ספרות או יותר; שנית, המספר שלמטה עלול לכלול שתי ספרות או יותר. קודם כל נטפל במקרה הראשון, שהוא בסך הכל לחזור על הצעד שעשינו עוד פעם, עם שתי הזחות שמאלה, וחיבור של שלושה מספרים באמצעות חיבור ארוך:

\( \begin{array}{ccccc} & & 4 & 2 & 3\\ & \times & & & 7\\ \hline & & & 2 & 1\\ & & 1 & 4\\ + & 2 & 8\\ \hline & 2 & 9 & 6 & 1 \end{array} \)

זה עובד, אבל זה מתחיל להיות מסורבל. אם למספר למעלה יהיו ארבע ספרות כבר יהיו לנו ארבעה מספרים לחבר, וכן הלאה. ואם חושבים על זה לרגע - כל המספרים הללו הולכים להיות רק בני שתי ספרות, כי הם מתקבלים מהכפלת שני מספרים בין 0 ל-9. אז אפשר לחסוך הרבה מקום על ידי עוד קצת מאמץ ושימוש בשיטת “נשא” שדומה לזו של חיבור ארוך רק מסובכת טיפה יותר.

הנה מה שאני עושה עבור המכפלה \( 423\times7 \): ראשית אני כופל בראש את \( 3 \) ב-\( 7 \) ומקבל 21. אני כותב 1 מתחת לקו, וזוכר בראש 2. אפשר גם לכתוב את ה-2 מעל המספר העליון, כמו שעושים בחיבור עם נשא:

\( \begin{array}{cccc} & & 2\\ & 4 & 2 & 3\\ \times & & & 7\\ \hline & & & 1 \end{array} \)

עכשיו אני עובר לכפול את 7 ב-2, מקבל בראש את התוצאה 14, ואז מוסיף לה 2, שהוא הנשא שכתוב למעלה. אני מקבל 16, ואז אני כותב את ה-6 למטה ומעביר את ה-1 הלאה:

\( \begin{array}{cccc} & 1\\ & 4 & 2 & 3\\ \times & & & 7\\ \hline & & 6 & 1 \end{array} \)

לבסוף אני כופל את ה-7 ב-4, מקבל 28, מוסיף את הנשא 1 ומקבל 29, וכותב את שניהם למטה:

\( \begin{array}{cccc} & 4 & 2 & 3\\ \times & & & 7\\ \hline 2 & 9 & 6 & 1 \end{array} \)

זהו, בצורה הזו לא הייתי צריך לכתוב את כל המספרים ואז לסכום אותם - עשיתי את זה “על הדרך”, בעזרת שיטת הנשא. סיימנו עם הבעיה של הכפלת מספר עם מספר ספרות כלשהו במספר בן ספרה אחת. אבל מה קורה כשרוצים לכפול במספר בן שתי ספרות?

בואו ננסה את מזלנו עם המכפלה \( 23\times97 \). חוק הפילוג עוזר לנו גם כאן: \( 23\times97=23\times90+23\times7 \). כלומר, אנחנו צריכים לקחת את \( 23\times7 \) שאנחנו כבר יודעים לחשב, ואיכשהו להוסיף למשחק גם את \( 23\times90 \), שזה אותו דבר כמו \( 23\times9 \) רק עם הזחה של צעד אחד שמאלה מראש. כלומר, מה שאני אעשה יהיה לכתוב שתי שורות ולחבר אותן: השורה הראשונה תוקדש למכפלה \( 23\times7 \) והשניה תוקדש למכפלה \( 23\times90 \). קודם כל אכתוב את השורה הראשונה:

\( \begin{array}{ccc} & 2 & 3\\ \times & 9 & 7\\ \hline 1 & 6 & 1 \end{array} \)

איך חישבתי את זה? בדיוק כמו קודם - אני לא אחזור שוב על התהליך. אבל עכשיו בואו נכתוב במפורש מה קורה בשורה השניה. קודם כל אני כופל את 9 ב-3 ומקבל 27, שמתוכם אני אשמור את 2 להיות נשא ואילו את 7 אכתוב למטה, אבל שימו לב איזה למטה: אני מתחיל לכתוב אותו מתחת ל-9, כלומר בהזחה של צעד אחד שמאלה - זה בגלל שאני לא כופל את 23 ב-9 אלא כופל אותו בעצם ב-90 (הזחה שמאלה של התוצאה כמוה בדיוק ככפל ב-10). אני אקבל:

\( \begin{array}{ccc} & 2\\ & 2 & 3\\ \times & 9 & 7\\ \hline 1 & 6 & 1\\ & 7 \end{array} \)

עכשיו אני כופל את 9 ב-2 ומוסיף את הנשא, שהיה גם כן 2 - אני מקבל \( 18+2=20 \), ולכן אני כותב 20 למטה:

\( \begin{array}{cccc} & & 2\\ & & 2 & 3\\ & \times & 9 & 7\\ \hline & 1 & 6 & 1\\ 2 & 0 & 7 \end{array} \)

עדיין לא סיימתי. עכשיו צריך לחבר את שני המספרים שכתבתי, כפי שעושים בחיבור ארוך:

\( \begin{array}{ccccc} & & & 2 & 3\\ & & \times & 9 & 7\\ \hline & & 1 & 6 & 1\\ + & 2 & 0 & 7\\ \hline & 2 & 2 & 3 & 1 \end{array} \)

וזה בעצם הרעיון כולו. כשאני כופל שני מספרים (מתי זה קרה לאחרונה, בעצם?) אני כותב את הקטן מתחת לגדול; הרי לכל ספרה של המספר התחתון אני מוסיף עוד מספר לחיבור הארוך, כך שאני רוצה שיהיו כמה שפחות ספרות כאלו. כמובן, אין שום דבר קדוש בבחירה השרירותית הזו; אפשר להחליט גם שבכלל כופלים את הספרות של המספר העליון במספר התחתון ומחברים את התוצאות; אין דרך אחת “נכונה”.

זה לכאורה מסיים את מה שיש לי לומר על כפל ארוך, אבל עדיין נשאר העניין הפעוט הזה של לוח הכפל. כאמור, יש הרבה טריקים כדי לזכור אותו ולא אציג אותם כאן, אבל כן אנסה להראות איך אני מנסה לייצר אותו בכמה שפחות מאמץ גם בלי לזכור שום דבר בעל פה. נתחיל, אם כן, מלוח ריק:

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1\\ 2\\ 3\\ 4\\ 5\\ 6\\ 7\\ 8\\ 9\\ 10 \end{array} \)

בגלל חוק החילוף, הלוח הולך להיות סימטרי - מה שיש בשורה של 3 והעמודה של 7 יהיה זה ה למה שיש בשורה 7 והעמודה 3, אבל אני עדיין אמלא את שניהם. נתחיל עם מה שקל מאוד למלא - כפל ב-1 וכפל ב-10. כפל ב-1 פשוט לא משנה את המספר שבו כופלים, וכפל ב-10 מתבטא בסך הכל בהוספת 0 מימין למספר שבו כופלים:

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & & & & & & & & & 20\\ 3 & 3 & & & & & & & & & 30\\ 4 & 4 & & & & & & & & & 40\\ 5 & 5 & & & & & & & & & 50\\ 6 & 6 & & & & & & & & & 60\\ 7 & 7 & & & & & & & & & 70\\ 8 & 8 & & & & & & & & & 80\\ 9 & 9 & & & & & & & & & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

כפל ב-2 גם הוא לא עניין מסובך כל כך אם אנחנו יודעים חיבור - זה בסך הכל לחבר את המספר שכופלים ב-2 עם עצמו, וזה אחד מהדברים שאני צריך לזכור בעל פה כדי לבצע חיבור. אפשר לעשות את זה בעזרת אצבעות הידיים, כמו שאמרתי בפוסט על חיבור. אם כן, נמלא גם את 2:

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\ 3 & 3 & 6 & & & & & & & & 30\\ 4 & 4 & 8 & & & & & & & & 40\\ 5 & 5 & 10 & & & & & & & & 50\\ 6 & 6 & 12 & & & & & & & & 60\\ 7 & 7 & 14 & & & & & & & & 70\\ 8 & 8 & 16 & & & & & & & & 80\\ 9 & 9 & 18 & & & & & & & & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

עוד דבר פשוט יחסית הוא כפל ב-5. להכפיל ב-5 זה בעצם אותו הדבר כמו להכפיל ב-10 ואז לחלק ב-2, או בניסוח אחר - לקחת את המספר שאותו כופלים ב-5, לחלק אותו ב-2 ולכפול את התוצאה ב-10. זה אומר שאם כופלים מספר זוגי ב-5 מקבלים את החצי של המספר הזה כפול 10 - למשל, 8 כפול 5 שווה ל-4 כפול 10, כלומר ל-40. אם לעומת זאת כופלים ב-5 מספר אי זוגי זה אומר שצריך לקחת את המספר הזה, לחלק ב-2 ולהתעלם מהשבר שמתקבל, לכפול ב-10 ולהוסיף 5 לתוצאה. כלומר, בשביל 7 כפול 5 אנחנו נחלק את 7 ב-2, נקבל תוצאה של 3 ועוד משהו שנתעלם ממנו, נכפול את ה-3 ב-10 ונקבל 30 ולכל זה נוסיף 5 ונקבל 35. כך לפחות קל עבורי לחשוב על זה. נמלא גם את זה בטבלה:

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\ 3 & 3 & 6 & & & 15 & & & & & 30\\ 4 & 4 & 8 & & & 20 & & & & & 40\\ 5 & 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 & 45 & 50\\ 6 & 6 & 12 & & & 30 & & & & & 60\\ 7 & 7 & 14 & & & 35 & & & & & 70\\ 8 & 8 & 16 & & & 40 & & & & & 80\\ 9 & 9 & 18 & & & 45 & & & & & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

המספר האחרון שיחסית קל לי לחשב כפולות שלו הוא 9. זה קצת לא אינטואטיבי, כי 9 נראה קצת מפחיד בהתחלה, אבל הוא מערב טריק פשוט ומקסים. באופן כללי, כשכופלים מספר ב-9, הסכום של הספרות בתוצאה חייב להתחלק ב-9. עכשיו, אנחנו כופלים ב-9 רק מספרים בין 1 ל-10, מה שאומר שהתוצאה היא מספר בן שתי ספרות (אפשר לחשוב על \( 1\times9 \) בתור \( 09 \)). זה אומר שאנחנו יודעים בדיוק מה תהיה הספרה השניה אם אנחנו יודעים את הראשונה - מה שמשלים אותה ל-9. כלומר, אחרי 09 יגיע 18, ואז 27, ואז 36 וכן הלאה - בכל פעם ספרת העשרות גדלה וספרת האחדות קטנה.

עוד דרך פשוטה למדי לזכור את זה היא שלכפול משהו ב-9 זה בסך הכל לכפול אותו ב-10, ואז לחסר אותו עצמו מהתוצאה. למשל, 7 כפול 9 זה בעצם 70 פחות 7, כלומר 63. שילוב שני הטריקים הללו הקל עלי מאוד לזכור את הכפולות של 9. בואו נוסיף גם אותן לטבלה.

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\ 3 & 3 & 6 & & & 15 & & & & 27 & 30\\ 4 & 4 & 8 & & & 20 & & & & 36 & 40\\ 5 & 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 & 45 & 50\\ 6 & 6 & 12 & & & 30 & & & & 54 & 60\\ 7 & 7 & 14 & & & 35 & & & & 63 & 70\\ 8 & 8 & 16 & & & 40 & & & & 72 & 80\\ 9 & 9 & 18 & 27 & 36 & 45 & 54 & 63 & 72 & 81 & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

ו… המצב לא רע! בעצם נשארו לנו רק 15 מכפלות “קשות” לזכור, אבל גם עבור 4 ו-6 יש טריק פשוט יחסית שנובע מהקרבה של שניהם ל-5. רוצים להכפיל משהו ב-4? תכפילו אותו ב-5 ותפחיתו אותו מהתוצאה (כמו שגם ב-9 הפחתנו). רוצים להכפיל משהו ב-6? תכפילו אותו ב-5 ותוסיפו אותו לתוצאה. כך יוצא ש-3 כפול 4 זה בעצם 15 פחות 3, כלומר 12; ו-4 כפול 4 הוא 20 פחות 4, כלומר 16, וכן הלאה. עבור 6 אנחנו מקבלים ש-7 כפול 6 הוא בעצם 35 ועוד 7, כלומר 42, וכן הלאה. הבה ונוסיף אותם לטבלה:

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\ 3 & 3 & 6 & & 12 & 15 & 18 & & & 27 & 30\\ 4 & 4 & 8 & 12 & 16 & 20 & 24 & 28 & 32 & 36 & 40\\ 5 & 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 & 45 & 50\\ 6 & 6 & 12 & 18 & 24 & 30 & 36 & 42 & 48 & 54 & 60\\ 7 & 7 & 14 & & 28 & 35 & 42 & & & 63 & 70\\ 8 & 8 & 16 & & 32 & 40 & 48 & & & 72 & 80\\ 9 & 9 & 18 & 27 & 36 & 45 & 54 & 63 & 72 & 81 & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

נשארו לנו בעצם רק ארבעה דברים: ראשית, מה שמקבלים כשכופלים את 3 בעצמו, מה שמקבלים כשכופלים את 7 בעצמו ומה שמקבלים כשכופלים את 8 בעצמו; מה שנקרא, הריבוע שלהם. אין לי שיטת קסם לזכור אותם, אבל יש טריק נחמד שמערב אותם שהכי קל לזכור באמצעות התמונה הזו:

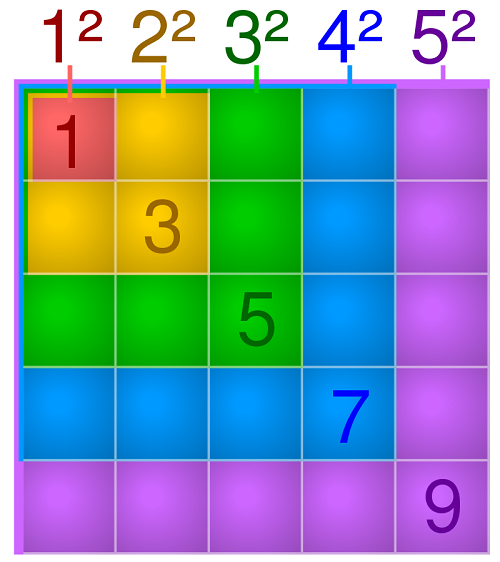
הרעיון הוא כזה: השטח האדום כולל ריבוע 1. השטח הצהוב כולל 3 ריבועים, וביחד עם השטח האדום יוצא 4 ריבועים - והמספר 4 הוא בדיוק \( 2^{2} \) (זה הסימון עבור “2 בריבוע”, כלומר \( 2\times2 \)). השטח הירוק כולל 5 ריבועים נוספים - אם נחבר אותם לשטח הקיים נקבל \( 4+5=9 \) ריבועים, ו-\( 9=3^{2} \) (כלומר, \( 3\times3 \)). באופן הזה זה נמשך: אחרי שמחברים 7 ל-9 שכבר קיבלנו מקבלים את \( 4^{2} \), ואחרי שמחברים אליו 9 מקבלים את \( 5^{2} \) וכן הלאה. בצורה שבה האיור מציג את זה, ברור למה מקבלים מספר שהוא ריבוע - כי כל הוספת שכבה חדשה משלימה את כל הריבועים עד כה לצורה של ריבוע-של-ריבועים שאורך הצלע שלו נקבל על ידי אורך הצלע של השכבה החדשה.

כך למשל, אחרי שמוסיפים את 7, אנחנו מקבלים ריבוע חדש שאורך הצלע שלו הוא 4 ריבועים. למה 4? בואו נסתכל על הריבועים הכחולים שהוספנו - יש שורה עם 4 ריבועים ועמודה עם 4 ריבועים ויש להם משבצת משותפת אחת - בסך הכל אנחנו מקבלים אורך צלע שהוא 7 חלקי 2 כשהתוצאה מעוגלת כלפי מעלה. כך זה יקרה גם באופן כללי.

אם כן, דרך אחת (לאו דווקא טובה!) לחשוב על \( 3\times3 \) היא בתור “\( 2^{2} \) ועוד 5”. אפשר כמובן לשאול איך אני יודע שזה ועוד 5 וזה נובע מהחשבון שעשיתי קודם - אני פשוט לוקח את המספר שאני רוצה לכפול בעצמו (כלומר 3), כופל אותו ב-2 ומפחית 1. בצורה הזו אני יכול לחשוב על \( 7\times7 \) בתור “\( 6^{2} \) ועוד 13” כלומר \( 36+13=49 \), ועל \( 8\times8 \) בתור \( 7^{2} \) ועוד 15, כלומר \( 49+15=64 \). בואו נוסיף גם את המספרים הללו לטבלה:

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\ 3 & 3 & 6 & 9 & 12 & 15 & 18 & & & 27 & 30\\ 4 & 4 & 8 & 12 & 16 & 20 & 24 & 28 & 32 & 36 & 40\\ 5 & 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 & 45 & 50\\ 6 & 6 & 12 & 18 & 24 & 30 & 36 & 42 & 48 & 54 & 60\\ 7 & 7 & 14 & & 28 & 35 & 42 & 49 & & 63 & 70\\ 8 & 8 & 16 & & 32 & 40 & 48 & & 64 & 72 & 80\\ 9 & 9 & 18 & 27 & 36 & 45 & 54 & 63 & 72 & 81 & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

צריך לטפל גם ב-3 כפול 7 וב-3 כפול 8 שעד כה הזנחתי - ואין לי דרך קלה לזכור את זה מעבר ללחבר 7 לעצמו 3 פעמים וכך גם עם 8, או לחסר 3 מ-30 פעמיים (בשביל כפל ב-8) או שלוש פעמים (בשביל כפל ב-7). נקבל את \( 21 \) ואת \( 24 \):

\( \begin{array}{c|cccccccccc} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 2 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20\\ 3 & 3 & 6 & 9 & 12 & 15 & 18 & 21 & 24 & 27 & 30\\ 4 & 4 & 8 & 12 & 16 & 20 & 24 & 28 & 32 & 36 & 40\\ 5 & 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 & 45 & 50\\ 6 & 6 & 12 & 18 & 24 & 30 & 36 & 42 & 48 & 54 & 60\\ 7 & 7 & 14 & 21 & 28 & 35 & 42 & 49 & & 63 & 70\\ 8 & 8 & 16 & 24 & 32 & 40 & 48 & & 64 & 72 & 80\\ 9 & 9 & 18 & 27 & 36 & 45 & 54 & 63 & 72 & 81 & 90\\ 10 & 10 & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \end{array} \)

וזה מותיר אותנו עם מכפלה בודדת, אחת ויחידה, רועצת החשבון, האימה הטהורה: \( 7\times8=56 \). את המכפלה הזו אין לי דרך לזכור מלבד פשוט לזכור אותה… לא, זה לא מדויק. אני יכול לזכור ש-\( 7\times9=63 \) ואז לחסר 7 מהתוצאה ולדעתי זה גם מה שאני עושה אינסטנקטיבית כשאני לא בטוח בעצמי. ועדיין, זו מכפלה קשה יותר מכל האחרות - לא סתם היא שרדה אצלי לסוף, וכבר ראיתי אנשים שאומרים שמבחינתם זה חור שחור. לא משנה עד כמה זה “בסך הכל מספר אחד לזכור”. גם אני, כשכתבתי עכשיו את הפוסט הזה, היססתי לשניה לפני שכתבתי 56. קורה.

אם כן, זה מה שיש לי לומר על כפל ארוך - זה לא קל, אבל אני מקווה שזה גם לא קשה ומפחיד כפי שאולי זה נראה ממבט ראשון. זה משאיר אותנו רק עם האתגר הגדול ביותר - חילוק ארוך. אליו אגיע בפוסט הבא.