מה בעצם הולך בטריגונומטריה בתיכון? (חלק ה’ - משפט הקוסינוסים)

אנחנו מתקדמים יפה מאוד בסדרת הפוסטים שלי שמטרתה להבין את הנוסחאות הטריגונומטריות:

בפעם הקודמת ראינו את משפט הסינוסים וכעת נדבר על משפט הקוסינוסים. למשפט הזה אין קשר ישיר למשפט הסינוסים והוא לא “גרסה של משפט הסינוסים רק עם קוסינוסים” אלא זה משהו שונה למדי - סוג של הכללה של משפט פיתגורס. אז בואו ניזכר מהו משפט פיתגורס. לשם כך נזדקק למשולש ישר זווית - איך לא. כל מה שאנחנו עוסקים הוא כל היום להתעסק במשולשים ישרי זווית.

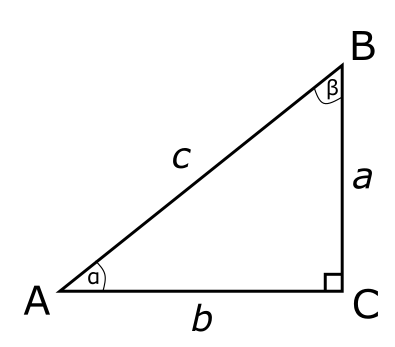
אם כן, בואו נסתכל על משולש ישר זווית שהיתר שלו היא מאורך \( c \) והצלעות האחרות הן מאורך \( a,b \). משפט פיתגורס אומר ש-\( a^{2}+b^{2}=c^{2} \). יש שלל שיטות להוכיח אותו אבל נעזוב את זה רגע. בואו נסתכל עכשיו על משולש כללי, כזה שאינו ישר זווית:

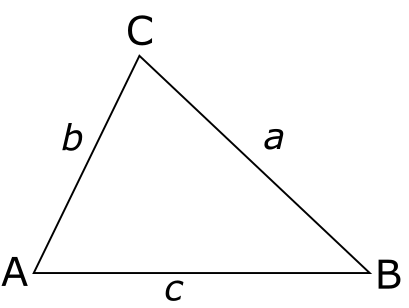
בואו נקרא לזווית \( \angle ACB \) שמול \( AB \) בשם \( \gamma \). אז משפט הקוסינוסים אומר את הדבר הבא:

\( a^{2}+b^{2}-2ab\cos\gamma=c^{2} \)

אם המשולש הוא ישר זווית, כלומר \( \gamma=90^{\circ} \), אז \( \cos\gamma=0 \) ולכן הביטוי \( -2ab\cos\gamma \) מתאפס ואנחנו חוזרים למקרה הרגיל של משפט פיתגורס. אבל אם המשולש אינו ישר זווית, אנחנו רואים שמשפט פיתגורס מתקיים עם “תיקון” שמתחשב בזווית בין הצלעות \( AC \) ו-\( BC \). ייתכן שהביטוי \( ab\cos\gamma \) נראה מוכר; זה מה שנקרא המכפלה הסקלרית של שתי הצלעות, אבל אני לא אכנס לזה בפוסט.

השימושיות של המשפט ברורה - אם משולש נתון לנו באמצעות אורכי שתי צלעות והזווית ביניהם, אנחנו יכולים להסיק ממנו את אורך הצלע השלישית; זה דומה למה שקרה במשפט הסינוסים, שם היכרות עם צלע אחד ושתי זוויות נתנה לנו את היתר.

איך מוכיחים את המשפט? ובכן, אם אתן עוקבות אחרי סדרת הפוסטים הזו מתחילתה, אתן כבר יודעות מה הולך לבוא כרגע! כן! הנה הוא בא! האנך מגיע! אוי לאאאא!

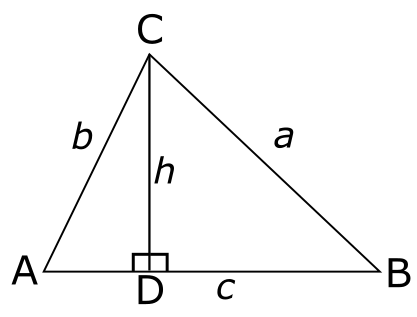
כן, זה המצב. אני יודע לעשות רק טריק אחד ואיכשהו הוא פותר לי את הכל שוב ושוב. וזה דבר טוב! זה מראה שיחסית קל להגיע אל כל הנוסחאות הללו. עדיין, איך האנך עוזר לנו כאן? ובכן, אם נסמן את הזווית \( \angle CAB \) ב-\( \alpha \) ואת \( \angle ABC \) ב-\( \beta \), כרגיל, נקבל את האורכים של \( AD \) ושל \( BD \) באופן הבא:

\( \left|AD\right|=b\cos\alpha \)

\( \left|BD\right|=a\cos\beta \)

וזה נחמד מאוד כי \( \left|AB\right|=c \) הוא סכום של שני אלו:

עכשיו, אנחנו רוצים להגיע אל \( c \) בריבוע; דרך אחת לעשות זאת היא להכפיל את שני אגפי המשוואה ב-\( c \) ולקבל

\( c^{2}=ac\cos\beta+bc\cos\alpha \)

אני רוצה גם את \( a^{2},b^{2} \) אז אני יכול להתבסס על כך שאפשר לעשות את אותו חישוב בדיוק גם עבורם, ולקבל

\( a^{2}=ab\cos\gamma+ac\cos\beta \)
\( b^{2}=ab\cos\gamma+bc\cos\alpha \)

עכשיו, בואו נחבר את שתי המשוואות הללו:

\( a^{2}+b^{2}=2ab\cos\gamma+\left(ac\cos\beta+bc\cos\alpha\right) \)

בבירור הגורם בסוגריים הוא פשוט \( c^{2} \) ולכן אחרי שנעביר אגף נקבל

\( a^{2}+b^{2}-2ab\cos\gamma=c^{2} \)

וזה מה שרצינו להוכיח. ממש פשוט! אולי אפילו פשוט מדי! שוב פעם הנחתי באופן מובלע שהאנך שאני מוריד יהיה בתוך המשולש. צריך גם לטפל במקרה שבו זה לא קורה.

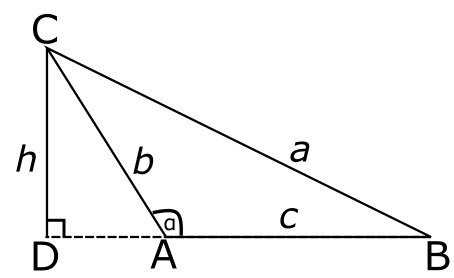
ובכן, ראינו את המקרה הזה גם בפוסט הקודם על משפט הסינוסים, והטריק שם היה שאפשר לקבל את \( \left|AB\right| \) הפעם באמצעות הפרש: \( \left|AB\right|=\left|BD\right|-\left|AD\right| \). האם אנו יודעים לחשב את שני האיברים שבאגף ימין? ובכן, \( \left|BD\right|=a\cos\beta \) (על פי המשולש \( BCD \)) ו-\( \left|AD\right|=b\cos\left(180^{\circ}-\alpha\right) \) (על פי המשולש \( ACD \)). עכשיו, בפוסט הקודם הסתמכנו על כך ש-\( \sin\left(180^{\circ}-\alpha\right)=\sin\alpha \) אבל בקוסינוסים זה לא הולך ככה אלא עם סימן מינוס:

\( \cos\left(180^{\circ}-\alpha\right)=-\cos\alpha \)

ולכן נקבל

\( \left|AD\right|=b\cos\left(180^{\circ}-\alpha\right)=-b\cos\alpha \)

\( \left|AB\right|=a\cos\beta+b\cos\alpha \)

בדיוק כמו שקרה במקרה הקודם, ומכאן ההוכחה ממשיכה כרגיל.

רגע, זה הכל? ובכן, כן, זה כמעט וסיים לנו את כל דף הנוסחאות ואני חייב להודות שזה היה ממש קל, יחסית. מה נשאר לנו? להבין את החלק בדף הנוסחאות שמדבר על רדיאנים. אז נכון שיש לי פוסט בנושא אבל הוא נכתב לפני שנים רבות ולא יזיק לכתוב עוד אחד אם אנחנו כבר כאן; זה יהיה בפעם הבאה.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: