מה בעצם הולך בטריגונומטריה בתיכון? (חלק ו' - רדיאנים)

בסדרת הפוסטים שלי על נוסחאות טריגונומטריות כבר כיסינו את כל הנוסחאות שבדף הנוסחאות שלי, למעט שתי אלו שמזכירות רדיאנים:

אז בואו נדבר על מה זה רדיאנים. בפשטות, רדיאן היא יחידת מידה לזווית שבמובן מסויים היא “טבעית” ומועיל להשתמש בה. החוק להמרה בין יחידת המידה הסטנדרטית שלנו, שנקראת מעלה ובין רדיאן הוא זה: מעלה אחת שווה ל-\( \frac{\pi}{180}\approx0.01745\ldots \) רדיאנים. זה נראה… חסר כל פשר? מצוין, עד סוף הפוסט הזה נבין את הכל, אני מקווה, וזה לא יהיה קשה במיוחד.

מכיוון שאנו עוסקים בהגדרות בסיסיות, כדאי לחזור לבסיס של הבסיס ולתהות מה זו בעצם “זווית”. הרעיון בזווית הוא שיש לנו שני קווים שמחוברים בקודקוד משותף, והזווית בין שניהם היא כמות הסיבוב שנדרשת כשמסובבים אחד מהם כדי שיגיע אל השני.

האיור קצת מטעה כי הרי אפשר לסובב את הקווים בכמה דרכים: אפשר לסובב את הקו התחתון נגד כיוון השעון עד שיגיע אל העליון, ולכמות הסיבוב הזו אני קורא \( \alpha \); ואפשר גם לסובב את העליון עם כיוון השעון עד שיגיע לתחתון וגם כמות הסיבוב הזו תהיה \( \alpha \), אבל אפשר גם ללכת בדרך הארוכה ולסובב את הקו התחתון עם כיוון השעון - הוא יעשה סיבוב מאוד ארוך אבל בסוף יגיע לקו השני, וגם כמות הסיבוב הזו היא זווית שבין שני הקווים. לכן כשמגדירים זווית כדאי שיהיה ברור לאיזו מהזוויות האפשריות הכוונה; כמעט תמיד אין סכנה לבלבול (למשל, לא הייתה כזו בכל הדברים שעשינו עד כה בסדרת הפוסטים הזו).

“כמות סיבוב” נשמע כמו מושג כמעט אבסטרקטי; איך מודדים כמות של סיבוב? גישה אחת היא לתת איזו יחידת מידה לסיבוב שלם שבסופו חוזרים לאותו מקום, ואז לדבר על חלקים של הסיבוב הזה - למשל, רבע סיבוב שלם הוא מה שאנחנו קוראים לו “זווית ישרה”. כשעובדים במעלות זו הגישה שבה משתמשים, ועוד אחזור לכך. אבל יש עוד גישה שגם היא טבעית למדי ותהיה לנו שימושית מאוד. בואו נקשר את מדידת הזווית למדידה של מרחק - המרחק שאנחנו עוברים בזמן הסיבוב.

בואו נשחק את המשחק הבא: ניקח את שני הקווים שלנו ונדביק מכחול בצבע אדום לקצה של אחד מהם. נסובב אותו אל הקו השני ובחזרה, ונבדוק איך נראית הצורה שהמכחול צייר. זה מה שנראה:

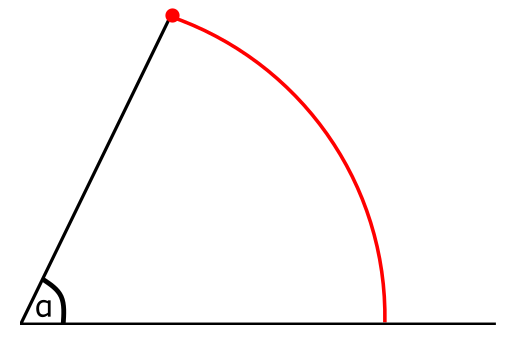
הקו האדום הוא קשת, חלק ממעגל. המשותף לכל הנקודות על הקשת הזו הוא שהמרחק שלהן מנקודת החיבור של שני הקווים שלנו זהה - הוא שווה לאורך של הקו העליון, שהוא הרדיוס של המעגל שאת חלקו ציירתי. מה שנחמד עם קשת כזו הוא שזה גודל שאפשר למדוד - למשל, עם חוט שיכול להתאים את עצמו לצורת הקשת ואחר כך להימתח לקו ישר שאותו קל למדוד עם סרגל. אז אפשר לנסות להגדיר את גודל הזווית \( \alpha \) בתור האורך של הקשת האדומה. אבל צריך להיזהר פה - האורך של הקשת הזו תלוי באורך של הרדיוס שאנחנו מסובבים. ככל שהקו יותר ארוך, הקשת האדומה תהיה גדולה יותר עבור אותה זווית סיבוב בדיוק. כמה גדולה יותר היא תהיה? אם נכפיל את אורך הרדיוס פי 2, גם אורך הקשת יגדל פי 2. על זה אומרים שאורך הקשת פרופורציוני לאורך הרדיוס.

לא לגמרי טריוויאלי להוכיח שאורך הקשת פרופורציוני לאורך הרדיוס, אבל זו כנראה אחת מהתוצאות המתמטיות המוכרות ביותר, במובלע. כמעט כל אדם מכיר את הקבוע המתמטי \( \pi \). מה הקבוע הזה מייצג? את היחס בין היקף מעגל (כלומר, אורך הקשת של “סיבוב שלם”) לקוטר שלו (כלומר, פעמיים הרדיוס). העובדה ש-\( \pi \) הוא קבוע שלא תלוי באורך הרדיוס של המעגל היא לב העניין פה; היא אומרת שאם ניקח את אורך הקשת של סיבוב שלם ונחלק ברדיוס של המעגל, נקבל תמיד את הערך \( 2\pi \) (כי אם היינו מחלקים בקוטר, שגדול פי 2, היינו מקבלים \( \pi \)). ולכן אם ניקח חצי סיבוב נקבל \( \pi \), ואם ניקח רבע סיבוב נקבל \( \frac{\pi}{2} \) וכדומה.

אם כן, זו ההגדרה של מדידת זוויות ברדיאנים: בהינתן זווית, קחו מעגל שבו הזווית הזו היא זווית מרכזית (כלומר, נקודת המפגש בין שני הקווים שיוצרים את הזווית היא בדיוק מרכז המעגל), קחו את הקשת שנשענת על הזווית הזו, כלומר את החלק מהמעגל ש”כלוא” בין שני הקווים שיוצרים את הזווית, וחלקו אותה ברדיוס המעגל - כלומר באורך של הקווים שיוצרים את הזווית עד לנקודה שבה הם נוגעים במעגל. בתמונה (הקצת עקומה) הזו זה הגודל \( \frac{S}{R} \), אורך הקו האדום חלקי אורך הקו הכחול:

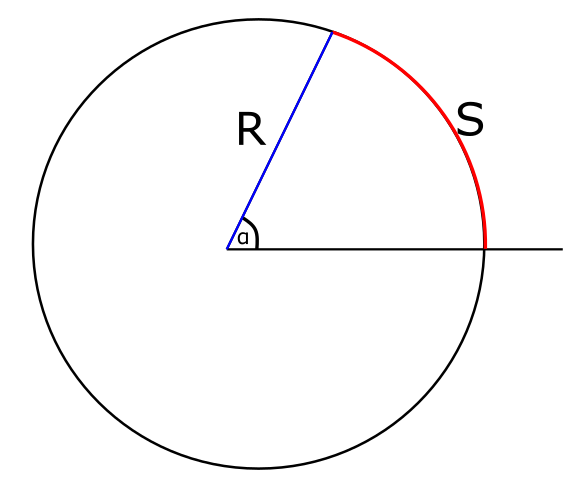
אספקט מעניין של ההגדרה הזו היא שהמספר שמתקבל הוא נטול יחידות. למה הכוונה? ובכן, נניח שאנחנו מודדים אורך בסנטימטרים, אז האורך של המעגל אינו נטול יחידה; הוא בעל היחידה “ס”מ”. אבל אם אנחנו מחלקים את האורך של שני דברים ששניהם נספרים בס”מ, התוצאה תהיה מספר שהוא לא ס”מ בעצמו - אנחנו אומרים “היקף המעגל גדול פי \( 2\pi \) מרדיוס המעגל” ולא “היקף המעגל גדול פי \( 2\pi \) ס”מ מרדיוס המעגל” (זו אמירה חסרת משמעות). זו אחת הסיבות שאוהבים מדידה ברדיאנים - היא לא מכניסה יחידת מידה שרירותית נוספת למערכת המדידה שלנו.

עכשיו, אחרי שקצת התפוגג הערפל סביב מה זה רדיאן, בואו נדבר על מה זה מעלות. כאשר מודדים סיבוב במעלות, הרעיון הוא שסיבוב שלם, שבסופו חוזרים לנקודת ההתחלה, הוא בדיוק מגודל \( 360 \) מעלות, ואנחנו מסמנים שמספר מציין מעלות על ידי עיגול קטן למעלה, כלומר \( 360^{\circ} \). מאיפה הגיעה השיטה הזו? למה דווקא 360 ולא 17? ובכן, לגבי מקורות השיטה התשובה היא שאנחנו לא באמת יודעים. היא מלווה אותנו כבר משחר המין האנושי והשתמשו בה במקומות שונים באופן כנראה בלתי תלוי, ומשם היא הגיעה אל יוון העתיקה שבה נולדה המתמטיקה כפי שאנו מכירים כיום. יש שיטות נוספות למדידת זוויות פרט למעלות ורדיאנים אבל הן הרבה, הרבה פחות נפוצות ולא אדבר עליהן כאן (דרך אלגנטית להסתיר את זה שאני לא באמת יודע שום דבר מעניין לומר עליהן).

עם זאת, אפשר להעלות שתי הצדקות לשימוש במספר 360. ראשית, מספר הימים בשנה הוא 365 כך ש-360 הוא קירוב לא רע אליו. זה לכשעצמו מפחית מהשרירותיות של השימוש במספר הזה (“יום” ו”שנה” הם מושגים אובייקטיביים שנובעים מתופעות אסטרונומיות במערכת של כדור הארץ והשמש; אין כאן החלטה אנושית שרירותית). אבל אז אפשר לשאול למה 360 ולא 365. היתרון הגדול של 360 הוא בכך שזה מספר עם המון מחלקים שלמים. 360 מתחלק ב-24 המספרים הבאים ללא שארית:

\( 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180,360 \)

המשמעות של התחלקות כזו היא שאפשר לדבר על הרבה חלקים של סיבוב באמצעות מספר שלם: למשל, “שליש סיבוב” הוא 120 מעלות; “אחד חלקי תריסר סיבוב” הוא \( 30 \) מעלות, וכן הלאה. אם מקבלים את זה שיותר נוח לנו לחשוב ולעבוד עם מספרים שלמים מאשר עם שברים (ולי לכל הפחות נוח יותר) זה מסביר את השימושיות של מספר כמו 360, שמצד אחד הוא לא עד כדי כך גדול ומצד שני באמת שיש לו המון מחלקים.

אפשר לפרמל מתמטית את ה”המון מחלקים” הזה. מגדירים במתמטיקה “מספר פריק במיוחד” בתור מספר שיש לו יותר מחלקים מאשר כל מספר שבא לפניו. הנה המספרים הפריקים במיוחד הראשונים:

\( 1,2,4,6,12,24,36,48,60,120,180,240,360 \)

פרט ל-360 אפשר לראות ברשימה הזו עוד ידידים שרירותיים-לכאורה של המין האנושי: ה-24 שאנחנו נעזרים בו כדי לחלק את היממה (תופעה אסטרונומית אובייקטיבית) ל-24 שעות (חלוקה שרירותית לגמרי) וה-60 שאנחנו נעזרים בו כדי לחלק את השעות לדקות ואת הדקות לשניות. אפשר גם לחזק עוד יותר את ההגדרה של “המון מחלקים” אל “המון מחלקים ביחס לגודל המספר” (אבל לא אכנס לפרטים הטכניים של זה, זה לא כזה מעניין) ועדיין 360 יככב ברשימה (אבל 24 לא, ולכן אני לא אוהב ללכת בכיוון הזה!).

עכשיו, מה הקשר בין מעלות ורדיאנים? במעלות, המספר שמתאר “סיבוב שלם” הוא 360 שהוא כאמור מספר שרירותי שכנראה נבחר כי הוא יפה. ברדיאנים, המספר שמתאר “סיבוב שלם” הוא \( 2\pi \) שנבחר בגלל שזה היחס בין היקף של מעגל שלם ובין הרדיוס שלו. זה אומר שמתקיים הקשר הבא בין מעלות ורדיאנים: \( 360^{\circ}=2\pi \). כלומר, כדי לדעת לכמה רדיאנים שווה מעלה אחת, נחלק ב-360 ונקבל \( 1^{\circ}=\frac{2\pi}{360}=\frac{\pi}{180}\approx0.01745\ldots \) שזה המספר שהראיתי בתחילת הפוסט. אין שום טעם לזכור את המספר הזה; כשרוצים להמיר ממעלות לרדיאנים אפשר פשוט לחלק ב-180 ולכפול ב-\( \pi \). למשל, זווית של \( 90^{\circ} \) תהפוך ל-\( \frac{\pi}{2} \). הכיוון ההפוך קצת יותר קל - מחלקים ב-\( \pi \) (מה שלרוב מפשט את העניינים כי זוויות קונקרטיות ברדיאנים נתונות לרוב בתור \( \pi \) כפול משהו) וכופלים ב-180. למשל, \( \frac{\pi}{4} \) יהפוך ל-\( 45^{\circ} \).

אני כבר רגיל לשימוש ברדיאנים וכשאני רואה משהו כמו \( \frac{\pi}{2} \) המוח שלי אוטומטית חושב על “זווית של 90 מעלות”, אבל התרגום האוטומטי הזה גם ממחיש שאני רגיל לחשוב במעלות על הכל. לטעמי מעלות הן יחידת מידה סבבה לגמרי. אני מאוד אוהב אותן וזה לא מקרי שהשתמשתי בהן בכל סדרת הפוסטים הזו. אבל היה מקום אחד בסדרת הפוסטים שבו אמרתי שחד משמעית אי אפשר להשתמש בהן - טורי הטיילור של הפונקציות הטריגונומטריות. בואו נזכיר אחד מהם:

\( \sin x=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\ldots \)

מה שקורה בנוסחה הזו הוא ש-\( x \) משמש אותנו בשני תפקידים שונים: מצד שמאל, \( x \) הוא “הדבר הזה שתוקעים לתוך סינוס ומקבלים מספר”. פונקציית הסינוס יודעת לזהות אם הקלט שלה נתון במעלות או בצורה אחרת ולהוציא פלט מתאים (הטהרנים יכתוב \( \sin^{\circ} \) כדי לתאר את הפונקציה שמקבלת את הקלט במעלות - ברשותכם, אוותר על זה). בצד ימין אין שום דבר כזה - \( x \) כאן הוא מספר שמעלים בחזקה כלשהי ומחברים ומחסרים וכדומה. באגף ימין אין שום “עיבוד מקדים” של \( x \). אם נבחר שיטת מדידה של 400 מעלות במעגל במקום 360 מעלות (וקיימת כזו), ההבדל הזה בין 360 ו-400 לא יבוא לידי ביטוי בשום צורה באגף ימין. כלומר, מלכתחילה אין סיבה להניח שאגף ימין יעבוד עם שיטת מדידה שרירותית כלשהי. ה”קסם” הוא שעבור שיטת המדידה שמשתמשת ברדיאנים זה כן יעבוד. אבל למה? ובכן, זה ידרוש ממני גלישה לפרטים טכניים שאני לא מניח שתכירו, אבל לא חייבים להבין אותם עד הסוף; זו הזדמנות טובה להכיר את הקיום של המושגים הללו גם בלי להבין לגמרי מהם.

אם כן, אנחנו רוצים להבין איך מוכיחים את הנוסחה \( \sin x=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\ldots \). פרטי ההוכחה של הנוסחה הזו גוררים אותנו לשטח של חשבון דיפרנציאלי ואינטגרלי, ואני לא אכנס לפרטים אבל כן אספר שההוכחה מסתמכת בצורה חזקה על מושג שנקרא נגזרת: בפרט, על כך שמתקיימת הנוסחה \( \sin^{\prime}x=\cos x \). הנוסחה הזו גם כן נכונה אך ורק כאשר \( x \) נתון ברדיאנים ולא במעלות. ואת הנוסחה הזו מוכיחים בעזרת הגבול הבא: \( \lim_{x\to0}\frac{\sin x}{x}=1 \) שגם הוא נכון רק ברדיאנים ולא במעלות. הגבול הזה הוא לב הסיפור - הוא הבסיס של כל החשבון הדיפרנצאלי והאינטגרלי של פונקציות טריגונומטריות אם אנחנו בוחרים להגדיר אותן בגישה שראינו עד כה (כאמור, יש גישה להגדיר את סינוס באמצעות \( \sin x=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\ldots \) וזו דווקא גישה די טובה).

אבל רגע, מה זה בכלל “גבול”? ובכן, אין צורך להציג את ההגדרה המלאה עבור הביטוי \( \lim_{x\to0}\frac{\sin x}{x}=1 \) (זו לא הגדרה פשוטה - ההגדרה של גבול היא אולי הדבר הכי קשה לעיכול כשמתחילים ללמוד מתמטיקה באוניברסיטה). מספיק אם נגיד שהרעיון הוא שכאשר \( x \) קטן, אז \( \sin x \) מאוד קרוב אליו במובן הזה שהיחס בין שניהם הוא כמעט זהה (זהירות! אם למשל \( x=0.00001 \) אבל \( \sin x=0.000000000001 \) אז בוודאי שהמרחק בין שני המספרים הללו הוא קטן כי שניהם קטנים; אבל היחס בין שניהם הוא גדול יחסית).

יש לי פוסטעל האופן שבו מוכיחים את הגבול הזה, ובפוסט מופיע האיור הבא, שמשתמשים בו כחלק מההוכחה:

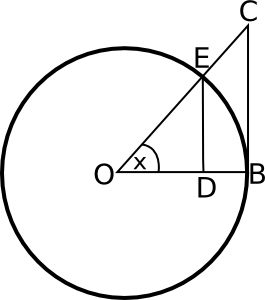
באיור הזה המעגל הוא מעגל היחידה, כלומר מעגל מרדיוס 1. הזווית \( x \) נמדדת ברדיאנים, כלומר אורך הקשת \( EB \) הוא \( x \) (כי אורך הקשת חלקי אורך הרדיוס שווה \( x \), אבל אורך הרדיוס הוא 1). הקו \( ED \) שווה ל-\( \sin x \), והטענה \( \lim_{x\to0}\frac{\sin x}{x}=1 \) אומרת שככל שהזווית \( x \) קטנה יותר, כך הקו \( ED \) הולך ומתקרב באורכו אל הקשת \( EB \). זה מאוד אינטואיטיבי; הרי הקשת הזו מתחילה בתור קו אנכי שעולה למעלה מהנקודה \( B \), כמו ש-\( ED \) עולה למעלה מהנקודה \( D \), אבל ככל שמתקדמים למעלה כך הקו של הקשת מתעקל שמאלה, אל עבר \( E \). ככל שהזווית קטנה יותר, ההתעקלות שמאלה קטנה יותר. זו אינטואיציה בלבד; ההוכחה האמיתית מסובכת יותר (אפילו הרבה יותר, כפי שאפשר לראות מהחפירות שלי בפוסט ההוא).

בשביל מה זה טוב? בשביל לראות איפה מתרחש ה”קסם” שגורם לרדיאנים להיות יחידת המידה שבגללה הנוסחאות במתמטיקה יוצאות יפות כל כך. אם היינו עובדים במעלות ולא ברדיאנים, מה היה משתנה? כדי לעבור ממעלות לרדיאנים צריך, כזכור, לכפול ב-\( \pi \) ולחלק ב-180; היינו מקבלים משהו כזה:

\( \sin x^{\circ}=\frac{\pi x}{180}-\frac{\pi^{3}x^{3}}{3!180^{3}}+\frac{\pi^{5}x^{5}}{5!180^{5}}-\frac{\pi^{7}x^{7}}{7!180^{7}}+\ldots \)

אפשר, כמובן, לחיות גם עם נוסחאות כאלו - אבל הן בהחלט מרגישות מסורבלות מדי שלא לצורך. עם רדיאנים הנוסחאות יוצאות פשוטות, וזו סיבה מרכזית למה אוהבים אותם כל כך בחלקים מסויימים של המתמטיקה.

עכשיו אפשר לחזור אל דף הנוסחאות:

מה שנקרא שם “אורך קשת של \( \alpha \) רדיאנים” הוא בעצם ההגדרה: אם אורך הקשת שנשענת על זווית \( \alpha \) הוא \( l \) ורדיוס המעגל שבו הקשת נמצאת הוא \( R \), אז \( \alpha=\frac{l}{R} \) הייתה ההגדרה של הזווית ברדיאנים. נכפול ב-\( R \) ונקבל את \( l=\alpha R \).

שטח גזרה זה כבר מושג שלא תיארתי, אבל קל לתאר. בואו נחזור לאיור שראינו קודם:

הגזרה שמתאימה לזווית \( \alpha \) היא השטח ש”נגזר” מתוך המעגל אם חותכים את שני הקווים ש-\( \alpha \) כלואה ביניהם ומקבלים משולש פיצה מתאים. איך אפשר לדעת מה השטח של משולש הפיצה הזה? ובכן, צריך לדעת בשביל זה את הנוסחה לשטח עיגול: השטח של עיגול עם רדיוס \( R \) הוא \( \pi R^{2} \). מהעיגול הזה חתכנו חתיכה כלשהי, אז צריך לחלק את השטח הכולל במספר שמתאים לחתיכה שחתכנו. אם למשל היינו חותכים בדיוק רבע עיגול, מה שמתאים לזווית \( \frac{\pi}{2} \), אז שטח הגזרה המתאים היה \( \frac{\pi R^{2}}{4} \). אם היינו חותכים חצי עיגול, כלומר זווית של \( \pi \), אז שטח הגזרה המתאים היה \( \frac{\pi R^{2}}{2} \). אפשר לראות פה את המגמה. באופן כללי, אם הזווית היא \( \alpha \), אז היא מתארת חיתוך של בדיוק \( \frac{\alpha}{2\pi} \) מהעיגול (היחס בין \( \alpha \) ובין “סיבוב שלם” שהוא \( 2\pi \)) ולכן נקבל שטח גזרה של \( \pi R^{2}\cdot\frac{\alpha}{2\pi}=\frac{\alpha R^{2}}{2} \), וזה מה שמופיע בנוסחה השניה.

בזאת, למרבה השמחה, סיימנו לטפל בכל דף הנוסחאות! ראינו את ההסבר לכל נוסחה שמופיעה בו! האם סיימנו בזאת עם טריגונומטריה תיכונית? לחלוטין לא! למעשה, לא דיברתי עדיין על פונקציית הטנגנס, שהיא אחד מהדברים החשובים ביותר שאפשר לדבר עליהם בהקשר הזה. אבל זה יהיה בפעם הבאה.