חישוב קוונטי: אלגוריתם הערכת פאזה

מה זה בכלל ובשביל מה זה טוב?

האלגוריתם הקוונטי שאני רוצה להציג בפוסט הזה, אלגוריתם הערכת פאזה, הוא פשוט קסם. מה שהוא עושה הוא קסם. האופן שבו הוא עושה את זה הוא קסם. האופן שבו זה משתלב עם התמרת פורייה הקוונטית שעליה דיברתי בפוסט הקודם הוא קסם. הדבר היחיד שאינו קסם, חוץ מההוכחה הפורמלית שהכל עובד והיא טכנית למדי, הוא להבין בשביל מה זה טוב. אז אני אשתמש באותו תירוץ שהשתמשתי בו בפוסט על התמרת פורייה הקוונטית - זה הכלי המרכזי שבו משתמש האלגוריתם של שור לפירוק לגורמים. למעשה, אפשר לחשוב על כל החלק הקוונטי באלגוריתם של שור בתור מקרה פרטי של אלגוריתם הערכת פאזה. אבל בשביל זה באמת צריך להסביר מה זה האלגוריתם הזה ומה הוא עושה.

הרעיון בהערכת פאזה הוא זה: נניח שיש לנו מרחב על \( m \) קיוביטים, כלומר \( \mathbb{C}^{2^{m}} \), ועל המרחב הזה מוגדר לנו אופרטור אוניטרי \( U:\mathbb{C}^{2^{m}}\to\mathbb{C}^{2^{m}} \), ואני מניח שלאופרטור הזה יש וקטור עצמי, \( \left|u\right\rangle \). עכשיו, הערכים העצמיים של אופרטורים אוניטריים הם תמיד מנורמה 1, אז אפשר לכתוב את הערך העצמי שמתאים ל-\( \left|u\right\rangle \) בתור \( e^{2i\pi\cdot\varphi} \), כאשר המספר \( \varphi \) נקרא הפאזה של הערך העצמי. המטרה שלנו היא לחשב את \( \varphi \), עד רמת דיוק מסויימת שנוכל לשלוט עליה ולהגדיל אותה כרצוננו; אבל מכיוון שתמיד נקבל מספר רציונלי ו-\( \varphi \) עשוי להיות אי רציונלי, גם ברמת דיוק גבוהה עדיין ייתכן שנקבל רק הערכה של הערך של \( \varphi \), ומכאן שם האלגוריתם.

זה אלגוריתם מעניין למדי כבר בשלב הזה, כי הוא עושה משהו שלא ראינו עד כה - מחשב ערך מספרי כלשהו ומחזיר אותו לנו. לא לגמרי ברור איך עושים את זה, או למה זה חשוב; עד סוף הפוסט אני מקווה שחלק מהערפל הזה קצת יתבהר, אבל לשימושים לא נגיע הפעם.

אלגוריתם הערכת פאזה, תיאור פורמלי וקסום

אבני הבניין שמהן אנו בונים את אלגוריתם הערכת הפאזה הן שלוש: קודם כל, אנו נעזרים ב-\( n \) קיוביטים שמאותחלים ל-\( \left|0^{n}\right\rangle \), כאשר \( n \) מתאר את רמת הדיוק שלנו - אנחנו הולכים לקבל כפלט מספר בן \( n \) ספרות בינאריות אחרי הנקודה שהוא קירוב של \( \varphi \) (ואם \( \varphi \) עצמו ניתן לתיאור מדויק באמצעות \( n \) ספרות בינאריות אחרי הנקודה, נקבל אותו במדויק). שנית, אנו נעזרים ב-\( t \) קיוביטים נוספים שהמצב שלהם בתחילת האלגוריתם הוא \( \left|u\right\rangle \), הוקטור העצמי שאת הפאזה שלו מחפשים (בפוסט על האלגוריתם של שור נראה שלא באמת חייבים לדעת את \( \left|u\right\rangle \)). לבסוף, אנחנו מניחים שיש לנו יכולת לבנות מעגל שמחשב את \( U \), אבל יותר מזה - גם את \( U^{2},U^{4},U^{8},\ldots \) וכדומה, עבור חזקות \( U^{2^{t}} \) עם \( t\ge0 \). למה רק חזקות של 2? כי נראה שהן יספיקו לנו כדי לחשב את כל החזקות של \( U \) שנזדקק להן.

בהינתן שיש לנו את כל אלו (וזו לא הנחה טריוויאלית), אלגוריתם הערכת הפאזה די קל לתיאור קונספטואלי. אני אקרא לקיוביטים שאותחלו ל-\( \left|0^{n}\right\rangle \) בשם “הרגיסטר הראשון” ולקיוביטים שמהווים את \( \left|u\right\rangle \) בשם “הרגיסטר השני”, וכעת מה שעושים הוא:

מפעילים \( H \) על כל אברי הרגיסטר הראשון.
מפעילים את הטרנספורמציה \( \left|k\right\rangle \left|u\right\rangle \mapsto\left|k\right\rangle U^{k}\left|u\right\rangle \) על שני הרגיסטרים.
מפעילים את \( \text{QFT}_{N}^{\dagger} \) על הרגיסטר הראשון.
מודדים את הרגיסטר הראשון. תוצאת המדידה תהיה הקירוב המבוקש.

בתור מין מעגל סכמטי, זה נראה כך:

אבל כרגע רב הנסתר על המרובה. להפעיל \( H \) על אברי הרגיסטר הראשון - את זה אנחנו כבר מבינים, וגם יודעים שזה מייצר לנו את המצב \( \left|+^{n}\right\rangle \). אבל איך מבצעים את הטרנספורמציה \( \left|k\right\rangle \left|u\right\rangle \mapsto\left|k\right\rangle U^{k}\left|u\right\rangle \) ומה זה \( \text{QFT}_{N}^{\dagger} \)? נתחיל מהשני. בפוסט הקודם על התמרת פורייה תיארנו מעגל שמחשב את \( \text{QFT}_{N} \). הסימון \( \text{QFT}_{N}^{\dagger} \) פשוט מייצג את הטרנספורמציה ההופכית. קל לחשב אותה, כי חישוב קוונטי שלא מערב מדידות הוא הפיך - פשוט לוקחים את המעגל של \( \text{QFT}_{N} \) ושמים את כל השערים שלו בסדר הפוך. פורמלית, מה שמשתמשים בו בהערכת פאזה הוא לא “התמרת פורייה הקוונטית” אלא “התמרת פורייה הקוונטית ההפוכה”, ועוד מעט ייפול לנו גם האסימון למה.

השאלה השניה היא איך מחשבים את \( \left|k\right\rangle \left|u\right\rangle \mapsto\left|k\right\rangle U^{k}\left|u\right\rangle \), וכאן זה הולך להיות דומה מאוד למה שקרה בהתמרת פורייה הקוונטית. כל כך דומה, שאני ממליץ בחום לחזור ולקרוא את הפוסט ההוא למי שדילגו עליו (מצד שני, אולי זה פשוט יותר כאן, ויקל על מי שנתקעו בפוסט ההוא?)

כזכור, אנחנו אוהבים ייצוג בינארי של מספרים. הייצוג הבינארי של מספר \( k \) הוא ייצוג בתור \( k=\sum_{t=1}^{n}2^{n-t}k_{t} \) כך ש-\( k_{t}\in\left\{ 0,1\right\} \). עכשיו, אפשר לפרק העלאה כללית בחזקת \( k \) למכפלה של העלאות בחזקות של 2:

\( U^{k}=U^{\sum_{t=1}^{n}2^{n-t}k_{t}}=\prod_{t=1}^{n}U^{2^{n-t}k_{t}}=\prod_{k_{t}=1}U^{2^{n-t}} \)

אז האפקט שאנחנו רוצים הוא בעצם:

\( \left|k_{1}k_{2}\ldots k_{n}\right\rangle \left|u\right\rangle \mapsto\left|k_{1}k_{2}\ldots k_{n}\right\rangle \prod_{k_{t}=1}U^{2^{n-t}}\left|u\right\rangle \)

ראינו משהו דומה לזה בפוסט על פורייה, ושם הטריק שלנו היה שאפשר לעבור מסכום של \( 2^{n} \) איברים שכל אחד מהם הוא מכפלה של \( n \) קיוביטים (כלומר, הסכום הוא על כל המכפלות האפשריות) אל מכפלה טנזורית של \( n \) הקיוביטים שכל אחד מהם הוא בסופרפוזיציה של בדיוק שני מצבים. אני ארצה לעשות את זה גם כאן, אבל בגלל שמעורבים פה שני רגיסטרים קוונטיים שונים, אחד עם \( \left|k_{1}k_{2}\ldots k_{n}\right\rangle \) ואחד עם \( \left|u\right\rangle \), זה יותר מסובך - אני צריך להוציא החוצה את \( \left|u\right\rangle \) איכשהו, וקל לי לעשות את זה כי \( \left|u\right\rangle \) הוא וקטור עצמי של \( U \) ולכן הפעולה של \( U \) עליו מתורגמת לכפל בסקלר, ואת הסקלר אני יכול להעביר אל \( \left|k_{1}k_{2}\ldots k_{n}\right\rangle \):

\( \left|k_{1}k_{2}\ldots k_{n}\right\rangle \prod_{k_{t}=1}U^{2^{n-t}}\left|u\right\rangle =\left|k_{1}k_{2}\ldots k_{n}\right\rangle \prod_{k_{t}=1}e^{2\pi i\varphi\cdot2^{n-t}}\left|u\right\rangle = \)

\( \prod_{k_{t}=1}e^{2\pi i\varphi\cdot2^{n-t}}\left|k_{1}k_{2}\ldots k_{n}\right\rangle \left|u\right\rangle \)

עכשיו בואו נעשה טריק כמו בפורייה: ראשית ניקח סכום של כל \( 2^{n} \) מצבי הבסיס \( \left|k_{1}k_{2}\ldots k_{n}\right\rangle \). הוא יצטרך להיות משוקלל, כלומר נחלק אותו ב-\( \frac{1}{2^{n/2}} \). נקבל שצריך להגיע אל

\( \frac{1}{2^{n/2}}\sum_{k=0}^{2^{n}-1}\prod_{k_{t}=1}e^{2\pi i\varphi\cdot2^{n-t}}\left|k_{1}k_{2}\ldots k_{n}\right\rangle \left|u\right\rangle = \)

\( =\frac{1}{2^{n/2}}\bigotimes_{t=1}^{n}\left(\left|0\right\rangle +e^{2\pi i\varphi\cdot2^{n-t}}\left|1\right\rangle \right)\left|u\right\rangle \)

\( =\bigotimes_{t=1}^{n}\left(\frac{\left|0\right\rangle +e^{2\pi i\varphi\cdot2^{n-t}}\left|1\right\rangle }{\sqrt{2}}\right)\left|u\right\rangle \)

מה שאנחנו רואים פה הוא שאפשר לחשוב על היעד שלנו בתור משהו שבו \( \left|u\right\rangle \) המקורי לא השתנה, אבל ברגיסטר הראשון הקיוביט ה-\( t \) התחלף מ-\( \left|0\right\rangle \) תמים אל \( \frac{\left|0\right\rangle +e^{2\pi i\varphi\cdot2^{n-t}}\left|1\right\rangle }{\sqrt{2}} \). איך משיגים אפקט כזה? ראשית, כמו שאמרתי כבר, מפעילים \( H \) בהתחלה על כל הקיוביטים ברגיסטר הזה - זה מעביר כל אחד מהם אל \( \frac{\left|0\right\rangle +\left|1\right\rangle }{\sqrt{2}} \). עכשיו רק צריך להכניס את הפאזה \( e^{2\pi i\varphi\cdot2^{n-t}} \) לתוך המקדם של \( \left|1\right\rangle \) מבלי לגעת ב-\( \left|0\right\rangle \). את זה אפשר לעשות עם שער מותנה. מה שאני רוצה שיקרה הוא

\( \left|0\right\rangle \left|u\right\rangle \mapsto\left|0\right\rangle \left|u\right\rangle \)
\( \left|1\right\rangle \left|u\right\rangle \mapsto\left|1\right\rangle U^{2^{n-t}}\left|u\right\rangle =e^{2\pi i\varphi\cdot2^{n-t}}\left|1\right\rangle \left|u\right\rangle \)

אז אני הולך להפעיל שער \( U^{2^{n-t}} \) שמותנה בקיוביט ה-\( t \)-י. ככה זה הולך להיראות:

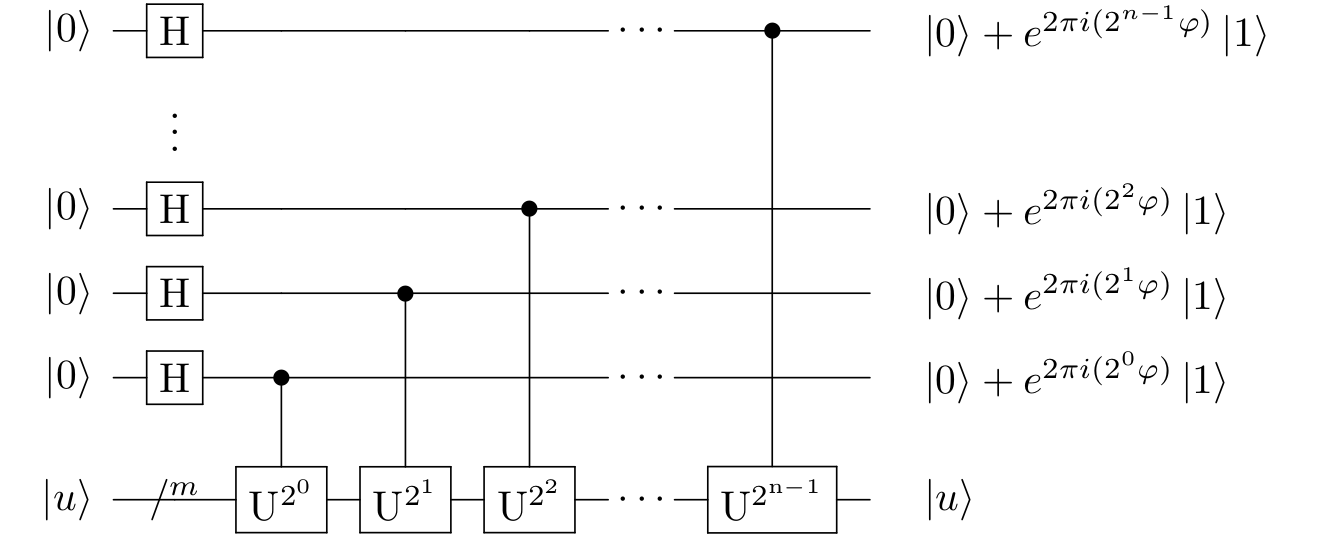
אפשר כמובן לשאול איך בונים שערי \( U^{2^{t}} \) מותנים בפועל - זו שאלה שאלגוריתם הערכת הפאזה עצמו לא מתעסק בה; הוא אומר “אם \( U \) הוא נחמד ואתם יכולים לבנות את השערים הללו עבורו, אז אפשר להפעיל הערכת פאזה” אבל בשימוש ספציפי, כמו אלגוריתם שור, אכן נצטרך להסביר איך לעשות את זה.

שימו לב שעל פניו, קורה כאן משהו מוזר מאוד: אחרי שערי ה-\( H \) בהתחלה, לכאורה על שערי הרגיסטר הראשון לא מופעל שום דבר שמשנה אותם - רק שערים שמותנים בהם. והרגיסטר השני? מופעלים עליו \( U^{j} \)-ים, אבל בגלל ש-\( \left|u\right\rangle \) הוא וקטור עצמי של \( U \) זה לא משנה את \( \left|u\right\rangle \) - רק מכפיל אותו בסקלר כלשהו, ואחר כך אנחנו בכל מקרה לא מודדים את \( \left|u\right\rangle \) אז לכאורה הסקלר אמור “להיעלם”. מה הולך כאן? זה נראה כמו קסם - מעגל שלא עושה כלום ומחשב בדיוק את מה שהוא אמור.

כמובן שאין פה קסם - הסקלר של \( \left|u\right\rangle \) לא הולך להיעלם אלא להצטבר בצורה חכמה בתוך הסופרפוזיציה שמהווים אברי הרגיסטר הראשון. איך זה ייתכן, אם אנחנו לא פועלים עליהם? ובכן, אין דבר כזה בחישוב קוונטי, לומר בנחרצות כזו שאנחנו לא פועלים על משהו; שערים מותנים הם לא משהו שפועל על כל קיוביט בנפרד אלא על זוג קיוביטים ביחד, וצריך לחשוב על ההשפעה שלהם בתור משהו שמשפיע על שני הקיוביטים הללו יחד. כבר ראינו איך זה בא לידי ביטוי פורמלי.

עכשיו אנחנו קרובים בצורה מפתיעה לסיום ההבנה של “למה זה עובד”. נשאר רק דבר אחד, בעצם. בואו נסתכל על מצב הרגיסטר הראשון אחרי סיום ריצת המעגל:

\( \bigotimes_{t=1}^{n}\frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i\varphi\cdot2^{n-t}}\left|1\right\rangle \right) \)

ובוא נזכיר לעצמנו מה עשתה התמרת פורייה הקוונטית, בפוסט הקודם:

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)=\bigotimes_{t=1}^{n}\frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.j_{n-t+1}\ldots j_{n}}\left|1\right\rangle \right) \)

הדמיון בין שני הביטויים עצום, והוא יגדל עוד יותר אם נזכיר לעצמנו מה בעצם הולך בביטוי \( \varphi\cdot2^{n-t} \). הפאזה \( \varphi \) עצמה היא מספר בין 0 ל-1, כלומר אפשר לכתוב \( \varphi=0.\varphi_{1}\varphi_{2}\ldots \) בייצוג בינארי. עכשיו, לכפול את זה ב-\( 2^{n-t} \) פירושו “להזיז שמאלה” את הספרות \( n-t \) צעדים, ומכיוון שכל זה קורה במעריך של \( e^{2\pi i} \), הספרות שמשמאל לנקודה הבינארית פשוט ייעלמו (זה היה הטריק המרכזי שלנו בהתמרת פורייה הקוונטית). אז מה שבעצם הגענו אליו הוא

\( \bigotimes_{t=1}^{n}\frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.\varphi_{n-t+1}\ldots\varphi_{n}\ldots}\left|1\right\rangle \right) \)

עכשיו, אם \( \varphi=0.\varphi_{1}\varphi_{2}\ldots\varphi_{n} \) הוא ייצוג מדויק של \( \varphi \) באמצעות \( n \) ספרות בינאריות, אז מה שקיבלנו הוא בדיוק

\( \bigotimes_{t=1}^{n}\frac{1}{\sqrt{2}}\left(\left|0\right\rangle +e^{2\pi i0.\varphi_{n-t+1}\ldots\varphi_{n}}\left|1\right\rangle \right)=\text{QFT}_{N}\left(\left|\varphi_{1}\varphi_{2}\ldots\varphi_{n}\right\rangle \right) \)

ולכן, אם אחרי המעגל שכבר הראינו אנחנו מוסיפים \( \text{QFT}_{N}^{\dagger} \), נסיים במצב הקוונטי הבודד \( \left|\varphi_{1}\varphi_{2}\ldots\varphi_{n}\right\rangle \), וכשנמדוד אותו נקבל את סדרת הספרות \( \varphi_{1}\varphi_{2}\ldots\varphi_{n} \) בהסתברות 1.

זה ממש קסם.

ועכשיו לחלק הפחות קסום

אם אפשר לייצג את הפאזה \( \varphi \) בעזרת \( n \) ספרות בינאריות, האלגוריתם עובד מושלם. אבל אם אי אפשר לייצג כך את הפאזה, הכל הופך ליותר מסובך וטכני. במקרה הזה בודאות לא נוכל לקבל את \( \varphi \) במדויק ולכן בכל מקרה נקבל קירוב שלו; אנחנו רוצים להשתכנע שגם במקרה הזה, בהסתברות טובה נקבל קירוב טוב.

אני הולך להיכנס לפרטים הטכניים של הניתוח עד הסוף, אבל מי שמתייאשים באמצע לא חייבים לסבול; אפשר לקפוץ לתחילת החלק הבא שבו אסכם את כל מה שצריך לדעת.

בשביל הניתוח במקרה הזה, יהיה לנו יותר נוח לחשוב על ייצוג המצב בתור סכום של \( N=2^{n} \) מחוברים. אז בואו ניזכר מה קורה בשני השלבים הראשונים:

\( \left|0^{n}\right\rangle \left|u\right\rangle \mapsto\frac{1}{2^{n/2}}\sum_{k=0}^{2^{n}-1}\left|k\right\rangle \left|u\right\rangle \mapsto\frac{1}{2^{n/2}}\sum_{k=0}^{2^{n}-1}\left|k\right\rangle U^{k}\left|u\right\rangle = \)

\( =\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{2\pi i\varphi\cdot k}\left|k\right\rangle \left|u\right\rangle \)

עכשיו, מה הפעלת \( \text{QFT}_{N}^{\dagger} \) עושה? כזכור

\( \text{QFT}_{N}\left(\left|j\right\rangle \right)\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}e^{\frac{2\pi i}{N}jk}\left|k\right\rangle \)

כדי לקבל את \( \text{QFT}_{N}^{\dagger} \) אפשר פשוט להפעיל צמוד מרוכב על אגף ימין; הדבר היחיד שהוא עושה הוא להחליף את \( i \) (המספר המרוכב \( i \); זה לא אינדקס) ב-\( -i \). אז בואו נכתוב את זה - ואני גם אחליף את הסימונים של מצבי הקלט והפלט, כך שהקלט יהיה דווקא \( k \) והפלט דווקא \( j \), כי עדיין קונספטואלית אני הופך את הסדר, וזה גם מתאים לשימוש שתכף אבצע בזה:

\( \text{QFT}_{N}^{\dagger}\left(\left|k\right\rangle \right)\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}e^{-\frac{2\pi i}{N}jk}\left|j\right\rangle \)

ולכן הפעלת \( \text{QFT}_{N}^{\dagger} \) על המצב שהגענו אליו ברגיסטר הראשון תניב

\( \text{QFT}_{N}^{\dagger}\left(\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{2\pi i\varphi\cdot k}\left|k\right\rangle \right)= \)

\( \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{2\pi i\varphi\cdot k}\text{QFT}_{N}^{\dagger}\left(\left|k\right\rangle \right)= \)

\( =\frac{1}{N}\sum_{k=0}^{N-1}\sum_{j=0}^{N-1}e^{2\pi i\varphi\cdot k}e^{-2\pi i\cdot\frac{jk}{N}}\left|j\right\rangle = \)

\( =\frac{1}{N}\sum_{j=0}^{N-1}\sum_{k=0}^{N-1}e^{2\pi i\left(\varphi-\frac{j}{N}\right)k}\left|j\right\rangle \)

קיבלנו פה סופרפוזיציה של הרבה מצבים; כדי להבין מה ההסתברות שמדידה תעלה בגורל מצב \( \left|j\right\rangle \) נסתכל על המקדם שלו, מה שאני מכנה האמפליטודה שלו ומסמן \( \alpha_{j} \); ההעלאה בריבוע של הערך המוחלט של האמפליטודה תיתן לנו את ההסתברות ש-\( \left|j\right\rangle \) יעלה בגורל. באופן כללי האמפליטודה הזו תהיה

\( \alpha_{j}=\frac{1}{N}\sum_{k=0}^{N-1}e^{2\pi i\left(\varphi-\frac{j}{N}\right)k} \)

האם אפשר לפשט את זה קצת? בהחלט, יש לנו פה טור הנדסי! אם נזכור את חוקי החזקות: \( e^{ab}=\left(e^{a}\right)^{b} \) אפשר לראות שבעצם קיבלנו פה את הסכום

\( \alpha_{j}=\frac{1}{N}\sum_{k=0}^{N-1}\left[e^{2\pi i\left(\varphi-\frac{j}{N}\right)}\right]^{k} \)

וזה טור הנדסי, כלומר ביטוי מהצורה \( \sum_{k=0}^{N-1}q^{k} \) כאשר במקרה שלנו \( q=e^{2\pi i\left(\varphi-\frac{j}{N}\right)} \). עכשיות למרות שמדגדג לי, לא אחזור על האופן שבו מוצאים את הסכום של טור הנדסי - יש לי פוסט על זה. פשוט צריך לזכור ש-

\( \sum_{k=0}^{N-1}q^{k}=\frac{q^{N}-1}{q-1}=\frac{1-q^{N}}{1-q} \)

(עברתי לצורה השניה כי היא קצת יותר אינטואיטיבית במקרה כמו שלנו שבו \( \left|q\right|<1 \))

ולכן במקרה שלנו נקבל

\( \alpha_{j}=\frac{1}{N}\left(\frac{1-e^{2\pi i\left(\varphi-\frac{j}{N}\right)\cdot N}}{1-e^{2\pi i\left(\varphi-\frac{j}{N}\right)}}\right)=\frac{1}{N}\left(\frac{1-e^{2\pi i\left(N\varphi-j\right)}}{1-e^{2\pi i\left(\varphi-j/N\right)}}\right) \)

זו האמפליטודה עבור מצב \( j \) כללי. בואו ניקח אחד ספציפי שטוב לנו במיוחד: ניקח מספר \( b \) שנותן לנו את הקירוב הטוב ביותר ל-\( \varphi \) מלמלטה שכולל \( n \) ספרות בינאריות. כלומר, ניקח \( 0\le b<N \) שמקיים ש-\( \frac{b}{N}=0.b_{1}b_{2}\ldots b_{n} \), \( \frac{b}{N}\le\varphi \) ו-\( \delta=\left|\varphi-\frac{b}{N}\right|=\varphi-\frac{b}{N} \) הוא מינימלי ביחס לדרישות הללו.

אנחנו לא יודעים, כמובן, מהו \( \delta \) אבל ברור ש-\( 0\le\delta\le\frac{1}{N} \) (כי אם \( \frac{1}{N}<\delta \) אפשר להגדיל את \( b \) ב-\( \frac{1}{N}=\frac{1}{2^{n}} \) על ידי חיבור 1 לספרה הכי פחות משמעותית בו ולקבל קירוב טוב יותר מ-\( b \)).

לא כל כך קל לחסום מלמטה את ההסתברות לקבל את \( b \) או דברים שקרובים אליו, אז נעשה את ההפך - נחסום מלמעלה את ההסתברות לקבל דברים שרחוקים מ-\( b \).

לשם כך בואו נכניס לתמונה עוד סימון. נזכור ש-\( 0\le b<N \), ולכן אפשר לתאר אברים אחרים בתחום הזה בתור \( b+d\text{ mod }N \) כאשר \( d\in\mathbb{Z} \) הוא מספר שלם כלשהו. למשל, אם \( N=8 \) ו-\( b=5 \) אז \( b+4=1 \) ו-\( b+\left(-7\right)=6 \) וכדומה. אני אשתמש ב-\( \beta_{d} \) כדי לסמן את האמפליטודה של איבר שמיוצג כך, כלומר

\( \beta_{d}=\alpha_{b+d\left(\text{mod }N\right)} \)

עכשיו השאלה היא כזו: נניח ש-\( e \) הוא מספר חיובי כלשהו שבא לציין את “סף הרגישות לשגיאה” שלנו - ככל שהוא קטן יותר כך גודל השגיאות שאנחנו מוכנים לסבול הוא קטן יותר. פורמלית, אם \( m \) הוא התוצאה שהאלגוריתם החזיר לנו, אנחנו מתחילים לכעוס אם \( \left|m-b\right|>e \) (שימו לב ש-\( \left|m-b\right| \) הוא לא כמה שאנחנו רחוקים מ-\( \varphi \); לניתוח של זה נגיע בהמשך).

אם כן, מה ההסתברות שלנו לקבל במדידה \( m \) בעייתי שכזה? בשביל זה אפשר להסתכל על כל ה-\( \beta_{d} \)-ים כך ש-\( d\notin\left[-e,e\right] \), כל עוד אני לא לוקח \( d \) גדול או קטן מדי עד שהוא כבר עושה סיבוב מסביב ל-\( N \) וחוזר שוב לתחום \( \left[-e,e\right] \). לצורך זה אני אקח את כל ה-\( d \)-ים שמקיימים או \( e+1\le d\le\frac{N}{2} \) או \( -\frac{N}{2}<d\le-\left(e+1\right) \). זה יבטיח שאני תופס את כל האיברים ה”בעייתיים” ולא לוקח איברים לא בעייתים, אלא אולי במקרי קיצון מוזרים וגם בהם הטעות הזו יכולה רק להיות לרעתנו (כי היא תנפח את ההסתברות לקבל משהו לא טוב) אבל הניתוח שלנו יצליח בכל מקרה.

אם כן, פורמלית:

\( p\left(\left|m-b\right|>e\right)\le\sum_{-N/2<d<-e}\left|\beta_{d}\right|^{2}+\sum_{e<d\le N/2}\left|\beta_{d}\right|^{2} \)

כדי לעשות משהו מועיל עם הביטוי הזה אני צריך למצוא חסם מלמעלה על \( \left|\beta_{d}\right|^{2} \), כלומר חסם מלמעלה על \( \left|\beta_{d}\right| \), כלומר חסם מלמעלה על

\( \left|\beta_{d}\right|=\frac{1}{N}\frac{\left|1-e^{2\pi i\left(N\varphi-\left(b+d\right)\right)}\right|}{\left|1-e^{2\pi i\left(\varphi-\left(b+d\right)/N\right)}\right|} \)

ההחלפה של \( j \) ב-\( b+d \) כאן בלי להכניס איזה \( \text{mod}N \) היא לא טריוויאלית לגמרי; היא מוצדקת בכך שכפולה של \( N \) במעריך של האקספוננט פשוט מובילה לתוספת כמות שלמה של \( 2\pi i \), שמתורגם ל-1; בשלב הזה כבר השתמשנו בזה כמה פעמים ואני מקווה שזה ברור.

עכשיו, את המונה קל לחסום מלמעלה:

\( \left|1-e^{2\pi i\left(N\varphi-b+d\right)}\right|\le2 \)

אז המונה קל, אבל את המכנה:

\( \left|1-e^{2\pi i\left(\varphi-\left(b+d\right)/N\right)}\right| \)

צריך לחסום מלמטה. זה דורש קצת יותר. ראשית, בואו נחזיר לתמונה את

\( \delta=\varphi-\frac{b}{N} \)

והביטוי שצריך לחסום יהפוך אל

\( \left|1-e^{2\pi i\left(\delta-d/N\right)}\right| \)

עכשיו, \( \varphi-\frac{b+d}{N}=\delta-\frac{d}{N} \).

מכיוון ש-\( -\frac{N}{2}<d \) אז \( -\frac{N}{2}+1\le d \), כלומר \( -\frac{1}{2}+\frac{1}{N}\le\frac{d}{N} \). בנוסף לכך \( \delta\le\frac{1}{N} \) ולכן נקבל

\( \delta-\frac{d}{N}\le\frac{1}{N}+\frac{1}{2}-\frac{1}{N}=\frac{1}{2} \)

ובאופן קצת יותר קל גם

\( \delta+\frac{d}{N}\ge0-\frac{1}{2}=-\frac{1}{2} \)

מה שנותן לנו

\( -\pi\le2\pi\left(\delta-d/N\right)\le\pi \)

בשביל מה זה טוב? כי בואו נסתכל שניה על הביטוי \( 1-e^{i\theta}=1-\cos\theta-i\sin\theta \) כאשר \( -\pi\le\theta\le\pi \). אני אצטרך קצת נוסחאות טריגונומטריות כדי לפשט אותו:

\( 1-\cos\theta=2\sin^{2}\frac{\theta}{2} \)
\( \sin\theta=2\sin\frac{\theta}{2}\cos\frac{\theta}{2} \)

לשמחתי אני סוף סוף יכול לומר שיש לי פוסט שמוכיח את הנוסחאות הללות ולכן לא אסביר אותן כאן שוב, אבל הן מפשטות יפה את הביטוי שלנו:

\( 1-\cos\theta-i\sin\theta=2\sin^{2}\frac{\theta}{2}-2i\sin\frac{\theta}{2}\cos\frac{\theta}{2}=2\sin\frac{\theta}{2}\left(\sin\frac{\theta}{2}-i\cos\frac{\theta}{2}\right) \)

לכאורה זה יותר מסובך, אבל ערך מוחלט יפשט לנו את העניינים. בכללי, \( \left|a+bi\right|=\sqrt{a^{2}+b^{2}} \), ותוך ניצול העובדה ש-\( \sin^{2}\alpha+\cos^{2}\alpha=1 \), נקבל

\( \left|2\sin\frac{\theta}{2}\left(\sin\frac{\theta}{2}-i\cos\frac{\theta}{2}\right)\right|=2\left|\sin\frac{\theta}{2}\right|\left|\sin\frac{\theta}{2}-i\cos\frac{\theta}{2}\right|=2\left|\sin\frac{\theta}{2}\right| \)

עכשיו, בתחום \( 0\le x\le\frac{\pi}{2} \) סינוס מקיימת תכונה נחמדה מאוד: היא קעורה, כלומר הערכים שלה בין שתי נקודות גדולים יותר מהקו הישר שמחבר את שתי הנקודות הללו. נקודות הקצה של התחום הן \( \left(0,0\right) \) (ראשית הצירים) ו-\( \left(\frac{\pi}{2},1\right) \) (הקצה הימני של תחום העלייה של סינוס, כשהיא מגיעה ל-1 ומתחילה ליפול) ולכן הקו הישר המחבר את שתי הנקודות הללו הוא \( y=\frac{2}{\pi}x \), ואנו מקבלים ש-\( \sin x\ge\frac{2}{\pi}x \), כלומר בתחום הזה שבו הכל חיובי, \( \left|\sin x\right|\ge\frac{2}{\pi}\left|x\right| \).

עבור \( -\frac{\pi}{2}\le x\le0 \) זה טיפה יותר מסובך כי \( \left|x\right|=-x \) במקרה הזה. עכשיו, \( \sin x \) היא פונקציה אנטי-סימטרית, כלומר \( \sin\left(-x\right)=-\sin x \), ולכן עבור \( -\frac{\pi}{2}\le x\le0 \) נקבל

\( \left|\sin x\right|=-\sin x=\sin\left(-x\right)\ge\frac{2}{\pi}\left(-x\right)=\frac{2}{\pi}\left|x\right| \)

ולכן קיבלנו את אי-השוויון \( \left|\sin x\right|\ge\frac{2}{\pi}\left|x\right| \) עבור כל \( -\frac{\pi}{2}\le x\le0 \).

עכשיו, אם \( -\pi\le\theta\le\pi \) אז \( -\frac{\pi}{2}\le\frac{\theta}{2}\le\frac{\pi}{2} \) ולכן אנו מקבלים

\( \left|1-e^{i\theta}\right|=2\left|\sin\frac{\theta}{2}\right|\ge2\cdot\frac{2}{\pi}\left|\frac{\theta}{2}\right|=\frac{2}{\pi}\left|\theta\right| \)

ואפשר להתקדם הלאה. כזכור, אנחנו באמצע חסימה מלמטה של הביטוי

\( \left|1-e^{2\pi i\left(\delta-d/N\right)}\right| \)

תוך שאנחנו יודעים ש-

\( -\pi\le2\pi\left(\delta-d/N\right)\le\pi \)

כלומר, במקרה הזה \( \theta=2\pi\left(\delta-d/N\right) \), ולכן נקבל

\( \left|1-e^{2\pi i\left(\delta-d/N\right)}\right|\ge4\left|\left(\delta-d/N\right)\right| \)

עכשיו נחזור אל הדבר שממנו התחלנו - אנחנו מנסים לחסום מלמטה את הערך המוחלט של \( \beta_{d} \), שהיא האמפליטודה של תוצאה “לא טובה” בערכי ה-\( d \) שאנו מסתכלים עליהם. תוך שימוש באי השוויון שהוכחנו זה עתה, נקבל

\( \left|\beta_{d}\right|\le\frac{1}{N}\frac{2}{\left|1-e^{2\pi i\left(\delta-d/N\right)}\right|}\le\frac{1}{N}\frac{2}{4\left|\left(\delta-d/N\right)\right|}=\frac{1}{4}\frac{1}{\left|\left(N\delta-d\right)\right|} \)

וקיבלנו חסם על ההסתברות הכוללת לתוצאה “רעה”:

\( p\left(\left|m-b\right|>e\right)\le\sum_{-N/2\le d<e}\left|\beta_{d}\right|^{2}+\sum_{e<d\le N/2}\left|\beta_{d}\right|^{2} \)

\( \le\frac{1}{4}\left[\sum_{-N/2<d<-e}\frac{1}{\left(N\delta-d\right)^{2}}+\sum_{e<d\le N/2}\frac{1}{\left(N\delta-d\right)^{2}}\right] \)

כן, כן, זה עדיין נראה מחריד ונצטרך לעבוד עוד כדי לפשט את זה. זו דרך החדו”א - כל הזמן מוצאים מה לפשט במחיר של \( \le \) נוסף בדרך. עכשיו אפשר להתעסק עם ה-\( \delta \) הזה שלמטה שהמהות שלו היא להיות קטן. כמה קטן? \( 0\le\delta\le\frac{1}{N} \), כלומר \( 0\le N\delta\le1 \). זה אומר שאפשר להעלים את \( N\delta \) מתוך \( \left(N\delta-d\right)^{2} \) בצורה יחסית פשוטה - אבל כרגיל, נצטרך להיזהר. קודם כל נפתח סוגריים

\( \left(N\delta-d\right)^{2}=\left(N\delta\right)^{2}-2\left(N\delta\right)d+d^{2}=\left(N\delta\right)\left[N\delta-2d\right]+d^{2} \)

אם \( d<0 \) אז גם \( N\delta+2d>0 \) ולכן \( \left(N\delta-d\right)^{2}>d^{2} \), כלומר \( \frac{1}{\left(N\delta-d\right)^{2}}<\frac{1}{d^{2}} \). זה מטפל באיברים של הסכום השמאלי.

אם \( d>0 \), כלומר \( d\ge1 \) נעשה משהו אחר: נשתמש בכך ש-\( N\delta\le1 \) ולכן \( N\delta-d\le1-d \). עכשיו, שני האגפים בביטוי הזה הם שליליים (כי \( d\ge1 \)) ולכן כשנעלה אותם בריבוע כיוון האי שוויון יתהפך ונקבל \( \left(N\delta-d\right)^{2}\ge\left(1-d\right)^{2} \), ולכן \( \frac{1}{\left(N\delta-d\right)^{2}}\le\frac{1}{\left(1-d\right)^{2}} \).

לסיכום, קיבלנו את הצעד הבא בחסימה של הביטוי שלנו:

\( p\left(\left|m-b\right|>e\right)\le\frac{1}{4}\left[\sum_{-N/2<d<-e}\frac{1}{d^{2}}+\sum_{e<d\le N/2}\frac{1}{\left(d-1\right)^{2}}\right] \)

אנחנו כבר לקראת הסוף! התעלול הבא הוא לאחד את שני הסכומים לסכום אחד כי בעצם מופיעים בהם כמעט אותם איברים בדיוק: בשמאלי מופיע \( \frac{1}{d^{2}} \) לכל \( -\frac{N}{2}<d<-e \) ובשני מופיע \( \frac{1}{\left(d-1\right)^{2}} \) לכל \( e<d\le\frac{N}{2} \). כלומר, בשניהם מופיעים כל האיברים

\( \frac{1}{\left(e+1\right)^{2}},\frac{1}{\left(e+2\right)^{2}},\ldots,\frac{1}{\left(N/2-1\right)^{2}} \)

ובנוסף בימני מופיע גם \( \frac{1}{e^{2}} \). אז בואו ניקח 2 כפול סכום כל האיברים הללו:

\( p\left(\left|m-b\right|>e\right)\le\frac{1}{2}\sum_{d=e}^{N/2-1}\frac{1}{d^{2}} \)

זה כבר סכום ממש פשוט. טריק סטנדרטי כדי לחסום סכומים כאלו הוא לעבור מסכום לאינטגרל, ב”מחיר” של הגדלה קטנה של התחום התחתון:

\( \sum_{d=e}^{N/2-1}\frac{1}{d^{2}}\le\int_{e-1}^{N/2-1}\frac{1}{x^{2}}dx \)

זה עובד כי מאחר ו-\( \frac{1}{x^{2}} \) היא פונקציה יורדת, המינימום שלה מתקבל בסוף כל קטע, והאינטגרל של פונקציה על קטע כלשהו גדול או שווה למינימום שלה כפול אורך הקטע. במילים אחרות, \( \int_{d-1}^{d}\frac{1}{x^{2}}dx\ge\frac{1}{d^{2}}\cdot1 \), ובצורה הזו אנחנו יכולים לחסום את כל אברי הסכום \( \sum_{d=e}^{N/2-1}\frac{1}{d^{2}} \) על ידי חתיכות אינטגרלים מתאימות.

למה לעבור לאינטגרל עזר לנו? כי אינטגרלים יותר קל לנו לחשב במדויק:

\( \int_{e-1}^{N/2-1}\frac{1}{x^{2}}dx=\left[-\frac{1}{x}\right]_{e-1}^{N/2-1}=\frac{1}{e-1}-\frac{1}{N/2-1}\le\frac{1}{e-1} \)

ולכן קיבלנו סוף כל סוף

\( p\left(\left|m-b\right|>e\right)\le\frac{1}{2\left(e-1\right)} \)

וזה… ביטוי די פשוט!

סיכום רגוע יותר של כל העניין

עשיתי הרבה חישובים טכניים בחלק הקודם, אבל אפשר לסכם אותם בצורה די פשוטה: הראינו שההסתברות לקבל באלגוריתם הערכת הפאזה תוצאה לא טובה חסומה על ידי \( \frac{1}{2\left(e-1\right)} \), כש-\( e \) הוא פרמטר שמשמש אותנו להערכת רמת הדיוק שלנו. רמת הדיוק תלויה לא רק בערך המספרי של \( e \) אלא גם במספר הקיוביטים שאנחנו משתמשים בו ברגיסטר הראשון, \( n \). בואו ניכנס עכשיו להסבר יותר מפורט של מה שזה אומר.

המושג שאנחנו מדברים עליו הוא “רמת דיוק של \( k \) ספרות אחרי הנקודה”. בואו ניתן דוגמא פשוטה עם מספרים בייצוג עשרוני. אם \( a=0.2513 \) הוא מספר, ואנחנו מסתכלים על קירוב שלו ברמת דיוק של שתי ספרות אחרי הנקודה, הכוונה היא לכל מספר \( b \) כך ש-\( \left|a-b\right|\le0.01 \). אז למשל, \( a=0.25 \) הוא מספר כזה, אבל גם \( 0.2433 \), למרות שהוא לא מדויק בספרה השניה אחרי הנקודה, גם אם נעגל את המספר לשתי ספרות ונקבל \( 0.24 \). באופן כללי, דיוק ב-\( k \) ספרות אחרי הנקודה פירושו \( \left|a-b\right|\le\frac{1}{10^{k}} \), אבל בהקשר שלנו, שבו המספרים מיוצגים בבסיס בינארי, הכוונה היא ל-\( \left|a-b\right|\le\frac{1}{2^{k}} \).

נניח שאנחנו רוצים לקבל רמת דיוק של \( k \) ספרות אחרי הנקודה בהסתברות טובה יחסית. ברור שאנחנו חייבים להקצות לפחות \( n \) קיוביטים לרגיסטר הראשון, אחרת אין לנו מספיק ספרות בשביל דיוק של \( k \) ספרות. כל קיוביט נוסף מעבר לכך שנקצה לרגיסטר הראשון יעזור לנו לשפר את ההסתברות לקבלת תוצאה טובה, אז בואו נכתוב \( n=k+p \), כאשר \( p \) הם “הקיוביטים הנוספים לצורך שיפור ההסתברות” ובסוף נראה מה יוצאת ההסתברות כתלות ב-\( p \).

מה שכבר ראינו הוא שיש מספר טבעי \( b \) כלשהו כך ש-\( \frac{b}{2^{n}} \) קירוב טוב של \( \varphi \), במובן זה ש-\( \left|\frac{b}{2^{n}}-\varphi\right|\le\frac{1}{2^{n}} \), והיתרון של ה-\( b \) הזה היה שיכלנו לחסום את המרחק של תוצת אלגוריתם הערכת הפאזה ממנו: האלגוריתם מחזיר מספר טבעי \( m \) (שאנחנו חושבים עליו בתור דרך אחרת לכתוב את המספר \( \frac{m}{2^{n}} \) שהוא הקירוב של \( \varphi \) שאנו מחפשים) שההסתברות שיקיים \( \left|m-b\right|>e \) קטנה או שווה ל-\( \frac{1}{2\left(e-1\right)} \) שהזכרתי קודם. היופי הוא שה-\( e \) נתון לבחירתנו בהתאם למה שנוח לנו.

אם אנחנו רוצים דיוק של \( k \) ספרות, מה שנעשה הוא להגדיר \( e=2^{n-k}-1 \). אם \( \left|m-b\right|\le e \) אז

\( \left|\frac{m}{2^{n}}-\varphi\right|\le\left|\frac{m}{2^{n}}-\frac{b}{2^{n}}\right|+\left|\frac{b}{2^{n}}-\varphi\right|=\frac{1}{2^{n}}\left|m-b\right|+\left|\frac{b}{2^{n}}-\varphi\right|\le \)

\( \le\frac{1}{2^{n}}\left(2^{n-k}-1\right)+\frac{1}{2^{n}}=\frac{2^{n-k}}{2^{n}}=\frac{1}{2^{k}} \)

וזה בדיוק מה שרצינו. כעת, מה הסתברות הכישלון, כלומר ההסתברות שלא ניפול על \( m \) טוב שכזה, בהינתן ה-\( e \) שבחרנו? ראשית, ההסתברות היא לכל היותר \( \frac{1}{2\left(e-1\right)} \). כעת, נציב \( e=2^{n-k}-1 \) ונקבל את הסתברות הכישלון

\( \frac{1}{2\left(2^{n-k}-2\right)}=\frac{1}{2\left(2^{p}-2\right)} \)

עבור \( p=0,1 \) מקבלים תוצאה שהיא שלילית או אינסוף - זה מפני שהחישוב עבור \( e \) הניח במובלע שהוא לא מספר 0 או 1 בעצמו. אבל עבור \( p=2 \) מקבלים כבר תוצאה הגיונית - \( \frac{1}{4} \). עבור \( p=3 \) מקבלים \( \frac{1}{12} \), עבור \( p=4 \) מקבלים \( \frac{1}{28} \) וכן הלאה - ככל שמוסיפים יותר קיוביטים, ההסתברות לקבל הערכה לא טובה שואפת אקספוננציאלית לאפס. אנחנו כמובן רוצים לדעת עד כמה זה שואף לאפס - מה צריך להיות \( p \) אם אנחנו רוצים להקטין את הסתברות הכשלון כרצוננו? אז יהא \( \varepsilon>0 \) מספר כלשהו. כדי שהסתברות הכישלון תהיה קטנה מ-\( \varepsilon \) צריך להתקיים

\( \frac{1}{2\left(2^{p}-2\right)}\le\varepsilon \)

נכפול את שני האגפים ב-\( 2^{p}-2 \) ונחלק ב-\( \varepsilon \) ונקבל

\( 2^{p}-2\ge\frac{1}{2\varepsilon} \)

נעביר את \( 2 \) אגף:

\( 2^{p}\ge2+\frac{1}{2\varepsilon} \)

ניקח \( \lg \) (לוגריתם על בסיס 2) לשני האגפים ונקבל

\( p\ge\lg\left(2+\frac{1}{2\varepsilon}\right) \)

וזו הנוסחה שרצינו: אם אנחנו רוצים להבטיח הסתברות כישלון קטנה מ-\( \varepsilon \), נזדקק ל-\( \left\lceil \lg\left(2+\frac{1}{2\varepsilon}\right)\right\rceil \) קיוביטים (זה הסימן לערך מוחלט עליון, לעגל כלפי מעלה) וזאת בנוסף ל-\( k \) הקיוביטים שאמרנו ש”חייבים”.

אז לסיכום הכולל: כדי לקבל באלגוריתם הערכת הפאזה קירוב עם דיוק של \( k \) ספרות בינאריות אחרי הנקודה בהסתברות של לפחות \( 1-\varepsilon \) צריך להשתמש ב-

\( n=k+\left\lceil \lg\left(2+\frac{1}{2\varepsilon}\right)\right\rceil \) קיוביטים.

זה סוגר את האלגוריתם, אבל עדיין נותרה השאלה הפתוחה - בשביל מה זה טוב? והאלגוריתם של שור נותן לזה תשובה מוחצת וחד משמעית, ועוד מעז לעשות את זה עם שימוש יפהפה ולא טריוויאלי בכלל בהערכת פאזה, כך שנחכה עם זה לפוסט הבא.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: