אסימפטוטות, חלק ב’: הדברים שמתקרבים להיות קשים ואולי גם מגיעים לשם

מבוא ותזכורת

בפוסט הקודם דיברתי על מה זו אסימפטוטה של פונקציה. אינטואיטיבית זה קו ישר כלשהו שהפונקציה מתקרבת אליו עוד ועוד כשהגרף שלה “הולך לאינסוף”. בפוסט הזה גם אציג את ההגדרה הפורמלית והלא אינטואיטיבית, אבל אשמור את זה לסוף - בינתיים אני רוצה לראות עוד פונקציות קונקרטיות והאסימפטוטות האפשריות שלהן. כזכור, בפוסט הקודם דיברתי על שני סוגים של פונקציות: פולינומים ופונקציות רציונליות.

פולינום היה פונקציה מהצורה \( p\left(x\right)=a_{n}x^{n}+\ldots+a_{1}x+a_{0} \) כאשר \( n \) הוא מספר טבעי כלשהו שנקרא מעלת הפולינום ו-\( a_{n}\ne0 \) הוא מספר שנקרא המקדם המוביל של הפולינום. עבור פולינומים ראינו שפשוט אין להם אסימפטוטות; זה היה מקרה פשוט מדי.

השלב הבא היה פונקציות רציונליות שהן פונקציות מהצורה \( f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)} \) כאשר \( p,q \) שניהם פולינומים. למשל \( \frac{1}{x} \) שהייתה דוגמת האב טיפוס שלי ל”פונקציה עם אסימפטוטות”. עבור פונקציות כאלו ראינו שני דברים:

האסימפטוטות האנכיות (אסימפטוטות שהן קו אנכי, למעלה-למטה) היו הקווים מהצורה \( x=a \) כאשר \( a \) היה שורש של \( q\left(x\right) \) (משהו שמאפס את הפולינום \( q\left(x\right) \) שבמכנה). זה לא עבד לכל שורש; רק לכאלו שלא איפסו את \( p\left(x\right) \). עבור כאלו שאיפסו גם את המונה וגם את המכנה היה צורך לחלק ב-\( x-a \) ולבדוק שוב.
האסימפטוטות האופקיות (אסימפטוטות שהן קו אופקי, ימינה-שמאלה) היו זהות גם כשהפונקציה הלכה לאינסוף וגם כשהלכה למינוס אינסוף, כלומר הייתה רק אסימפטוטה אופקית אחת לכל היותר. אם \( q\left(x\right) \) היה ממעלה גדולה מ-\( p\left(x\right) \), האסימפטוטה הזו הייתה \( y=0 \); אם \( p\left(x\right) \) היה ממעלה גדולה מ-\( q\left(x\right) \) לא היו אסימפטוטות (הפונקציה \( f\left(x\right) \) פשוט "בורחת" לאינסוף/מינוס אינסוף כש-\( x \) הולך לשם), ואם הם היו ממעלה שווה אז האסימפטוטה הייתה \( y=\frac{a_{n}}{b_{n}} \) כאשר \( a_{n} \) המקדם המוביל של \( p\left(x\right) \) ו-\( b_{n} \) המקדם המוביל של \( q\left(x\right) \).

אפשר לחשוב על המקרה של פולינומים בתור מקרה פשוט למדי של פונקציות רציונליות: במקום לדבר על פולינום \( p\left(x\right) \) אפשר לדבר על הפונקציה הרציונלית \( \frac{p\left(x\right)}{q\left(x\right)} \) כאשר \( q\left(x\right)=1 \) - פולינום קבוע ממעלה 0. מקרה 1 לא יכול להתקיים פה כי אין ערך שאפשר להציב ב-\( q\left(x\right) \) ולקבל 0, ומקרה 2 נופל תחת “\( p\left(x\right) \) ממעלה גדולה מ-\( q\left(x\right) \) (כי מעלת \( q\left(x\right)=0 \)) למעט המקרה שבו גם \( p\left(x\right) \) הוא קבוע ואז הפונקציה עצמה היא קו אופקי, ולכן מהווה את האסימפטוטה של עצמה (זה מקרה טריוויאלי כל כך שלא טרחתי להתייחס אליו קודם; בדרך כלל לא בודקים אסימפטוטות של קווים ישרים).

יופי. עכשיו, מה קורה עם פונקציות מסובכות אחרות, שאינן פונקציות רציונליות?

אסימפטוטות שמערבות שורשים

נתחיל עם פונקציה פשוטה יחסית - פונקציית השורש ריבועי. שורש ריבועי של מספר \( x \) הוא מספר אי שלילי \( a \) כך ש-\( a^{2}=x \); מסמנים זאת \( a=\sqrt{x} \). יש כאן שתי נקודות שצריך לשם לב אליהן:

אם \( x \) שלילי, אין לו שורש ריבועי. אין מספר ממשי \( a \) כך ש-\( a^{2}=-1 \), כי במספרים ממשיים כל מספר כפול עצמו יוצא אי-שלילי. השימוש שלי במילה "ממשיים" מרמז שיש סוג אחר של מספרים, מספרים מרוכבים, שבהם הסיטואציה מורכבת יותר ויש שורשים גם למספרים שליליים, אלא שאני לא אדבר עליהם כאן; הניתוח של פונקציות מרוכבות הוא משמעותית יותר מסובך ממה שנעשה כאן. לכן מבחינתנו, אם מה שבתוך השורש הוא שלילי, השורש פשוט לא מוגדר.
למספרים חיוביים יש למעשה שני שורשים ריבועים. למשל \( 2^{2}=4 \) אבל גם \( \left(-2\right)^{2}=4 \). גם באופן כללי - אם \( a^{2}=x \) אז גם \( \left(-a\right)^{2}=x \). בגלל שהשורשים תמיד באים בזוגות כאלו של מספר/מינוס שלו, הקונבנציה שאנחנו עובדים איתה היא שכשמוציאים שורש למספר, כלומר כותבים \( a=\sqrt{x} \), אז \( a \) תמיד יהיה השורש האי-שלילי. לפעמים, כשרוצים לדבר על שני השורשים יחד, משתמשים בסימון \( \pm \). כך למשל בנוסחת השורשים לפתרון משוואה ריבועית מהצורה \( ax^{2}+bx+c \): הנוסחה היא \( x_{1,2}=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \), וכאן מתייחסים לשני השורשים האפשריים של \( b^{2}-4ac \).

תמונה אחת כידוע שווה אלף מילים - חזרתי על זה שוב ושוב בפוסט הקודם. אז הנה תמונה של \( f\left(x\right)=\sqrt{x} \):

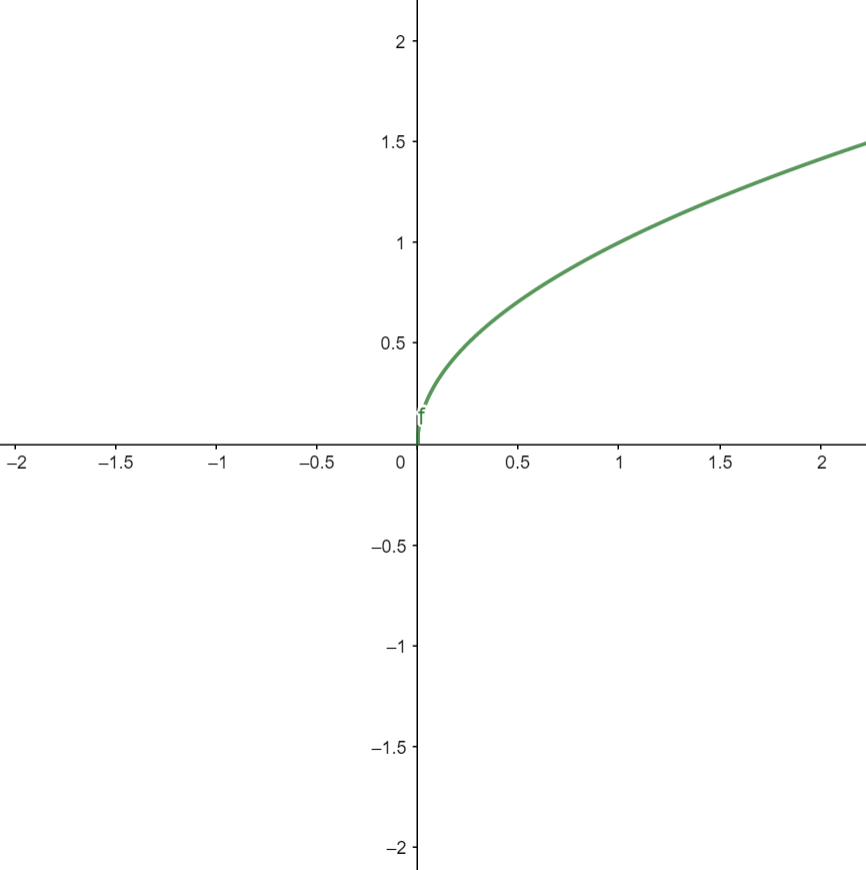
והתמונה הזו… שווה מעט מאוד! כמעט כלום! אנחנו רואים ש-\( f\left(x\right) \) נקטעת בפתאומיות ב-\( x=0 \) (כי כאמור, היא לא מוגדרת לערכים קטנים יותר) אבל אין לה שם אסימפטוטה (הפונקציה לא בורחת לאינסוף), ובאשר למה שקורה כש-\( x\to\infty \)? אי אפשר להבין כלום מהאיור. נראה שהפונקציה עולה, אבל בצורה “מתמתנת” שכזו (השם הפורמלי הוא פונקציה קעורה, אבל זה לא חשוב). אז מה קורה? התשובה היא ש-\( f\left(x\right)\underset{x\to\infty}{\to}\infty \) ואפשר לראות את זה יחסית בקלות: נניח ש-\( y=a \) זו אסימפטוטה של הפונקציה עם \( a\ge0 \) (עבור \( a<0 \) ברור שזו לא תהיה אסימפטוטה - הפונקציה לא מתקרבת לשם בכלל), ונסתכל על \( x=\left(a+1\right)^{2} \). אז \( f\left(x\right)=\sqrt{\left(a+1\right)^{2}}=a+1 \). כלומר, מתישהו \( f\left(x\right) \) כבר בגובה \( 1 \) מעל הקו \( y=a \) ובהמשך היא רק תמשיך לעלות עוד ועוד, אז הקו הזה הוא לא אסימפטוטה.

האמת היא ש-\( \sqrt{x} \) לא כל כך שונה מפולינומים בהיבט שמעניין אותנו. הנה דרך טובה להכניס אותו למשחק: אני מניח שאנחנו כבר מכירים את חוקי החזקות, שאומרים ש-\( x^{a}\cdot x^{b}=x^{a+b} \) וגם ש-\( \left(x^{a}\right)^{b}=x^{ab} \). בהתחלה, החוקים הללו מוגדרים רק עבור חזקות שהן מספרים טבעיים, אבל אם מניחים לרגע שהן מוגדרות גם עבור שברים, אז מייד רואים שצריך להתקיים \( x^{\frac{1}{2}}\cdot x^{\frac{1}{2}}=x^{1}=x \). כלומר, אם יש משמעות לביטוי \( x^{\frac{1}{2}} \) ואנחנו חושבים עליו בתור מספר \( a=x^{\frac{1}{2}} \), אז בפרט צריך להתקיים \( a^{2}=x \), כלומר \( a \) הוא אחד מהשורשים של \( x \). זה מוביל אותנו להגדרה \( x^{\frac{1}{2}}=\sqrt{x} \), וזו הגדרה מועילה למדי כי החוקים שראינו קודם על פונקציות רציונליות ופולינומים עובדות גם עבור \( x \) בחזקה שהיא שבר.

אל מה אני מתכוון? ובכן, במקום לדבר על \( f\left(x\right)=\sqrt{x} \) אפשר לדבר על הפונקציה הרציונלית \( f\left(x\right)=\frac{x^{\frac{1}{2}}}{1} \), והחוקים שראינו קודם עבור פונקציות רציונליות תקפים גם כאן ומראים לנו מייד שאין אסימפטוטה (כי המעלה של המונה, \( \frac{1}{2} \), גדולה ממעלת המכנה 0).

אפשר לטפל כך גם בסיטואציות מסובכות יותר. שורש \( n \)-י של \( x \) הוא המספר האי שלילי שמקיים \( a^{n}=x \), ומסמנים את זה \( a=\sqrt[n]{x} \) או, בגישה שלנו, \( a=x^{\frac{1}{n}} \). ובאופן הכי כללי, \( x^{\frac{k}{n}} \) הוא סימון מקוצר של \( \sqrt[n]{x^{k}} \). אלו לא פולינומים, אבל אלו עדיין חזקות של \( x \) שאפשר להשוות את גודלן לחזקות אחרות של \( x \).

אם כן, נראה שכל תוספת השורשים הזו לא שינתה שום דבר מהותי ביחס למה שכבר ראינו.

אז זהו, שלא.

בואו נסתכל לרגע על הפונקציה \( f\left(x\right)=\frac{x}{\sqrt{x^{2}+4}} \). כאן העסק מתחיל להסתבך, כי השורש הוא לא על \( x \) בודד אלא על ביטוי שלם. ומבט אחד בגרף של הפונקציה יבהיר לנו שאנחנו לא ברציוקנזס יותר:

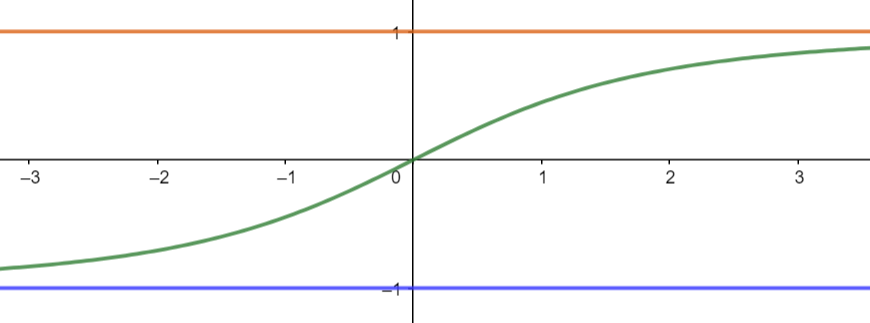
מה קורה כאן? ראשית, הפונקציה מוגדרת לכל \( x \), כי הביטוי שבתוך השורש, \( x^{2}+4 \), הוא תמיד חיובי. יותר מכך, הוא שווה לפחות 4, ולכן השורש יהיה לפחות 2 ולכן המכנה לא יתאפס. שנית, לפונקציה יש שתי אסימפטוטות אופקיות שונות זו מזו: \( y=1 \) מימין ו-\( y=-1 \) משמאל.

מה האינטואיציה למה שקורה כאן? ובכן, \( \sqrt{x^{2}+4} \) זה משהו שהוא “בערך כמו” \( x \) מבחינת קצב הגידול שלו, כי השורש מקזז את ה-\( x^{2} \) שיש בפנים. מכיוון שהמכנה הוא \( x \) בעצמו, קיבלנו מקרה שדומה לזה של מונה ומכנה מאותה מעלה, ולכן האסימפטוטות נקבעות לפי מנת המקדמים המובילים. כאן העסק מתחיל להיות שונה. כאשר \( x\to\infty \) המונה הוא חיובי וגם המכנה הוא חיובי ואין פלא שמתקרבים אל 1, אז כאשר \( x\to-\infty \) קורה משהו שלא קרה קודם. המונה יהיה שלילי, אבל המכנה יהיה חיובי, בגלל שפונקציית השורש תמיד מחזירה את הערך החיובי. זה שונה לגמרי ממה שקרה בפונקציות רציונליות רגילות, שבהן אם גם המונה וגם המכנה היו שניהם מאותה מעלה, אז שניהם היו שליליים ביחד (אם המעלה הייתה אי זוגית) או ששניהם היו חיוביים ביחד (אם המעלה הייתה זוגית). כאן המונה שלילי והמכנה חיובי, ולכן התוצאה שאנחנו מקבלים היא אסימפטוטה \( y=-1 \). ה-\( 1 \) הוא עדיין מה שנובע מהיחס בין המקדם המוביל של המונה לזה של המכנה (אם למשל במונה היה \( 3x \) אז האסימפטוטות היו \( y=\pm3 \)), אבל הסימן השלילי שלו זה הדבר החדש שיכול לקרות כאן.

זה לכאורה מסיים עם \( f\left(x\right)=\frac{x}{\sqrt{x^{2}+4}} \) אבל מרגיש לי מוזר לעצור פה. נפנפתי מאוד בידיים לגבי “\( \sqrt{x^{2}+4} \) זה בערך אותו סדר גודל כמו \( x \)” ואני מרגיש שזה זמן טוב להראות נימוק יותר משכנע, גם בלי לגלוש לפורמליזם המלא. אם כן, הבה ונראה מה עושים בחדו”א כדי להתמודד עם סיטואציות כאלו.

המהות של חדו”א היא פשוטה: לחסום, לחסום, לחסום. אם יש לנו ביטוי מסובך, אבל אנחנו יכולים להראות שהוא “כלוא” בין שני ביטויים פשוטים בהרבה, אנחנו מאוד שמחים. במקרה שלנו, ראשית נשים לב לכך ש-\( x^{2}\le x^{2}+4 \), ולכן \( \sqrt{x^{2}}\le\sqrt{x^{2}+4} \) (כאן אני משתמש בכך ששורש היא פונקציה עולה; ככל שמגדילים את הקלט שלה, גם הפלט גדל). אם אני מניח ש-\( x>0 \), שזה מה שהולך לקרות בסיטואציה שבה \( x\to\infty \), אז \( \sqrt{x^{2}}=x \), כלומר קיבלתי \( x\le\sqrt{x^{2}+4} \). זה חסם בכיוון אחד.

מצד שני:

\( x^{2}+4\le x^{2}+4x+4=\left(x+2\right)^{2} \)

כאן השתמשתי בכך שאני כבר מכיר את הנוסחה \( \left(x+a\right)^{2}=x^{2}+2ax+a^{2} \). מה המטרה שלי? למה הוספתי משהו ל-\( x^{2}+4 \) כדי לקבל ביטוי שכולו בריבוע? כמובן, כדי להיפטר מהשורש המעצבן הזה. קיבלתי:

\( \sqrt{x^{2}+4}\le\sqrt{\left(x+2\right)^{2}}=x+2 \)

אם כן, קיבלתי בסך הכל

\( x\le\sqrt{x^{2}+4}\le x+2 \)

זה כבר ממש מועיל. בואו ניזכר לרגע בחוק לגבי אי שוויונים שמערבים שברים: אם \( x\le y \) אז \( \frac{1}{y}\le\frac{1}{x} \), כלומר כיוון האי-שוויון “מתהפך” אם מחלקים. לכן אי השוויון \( x\le\sqrt{x^{2}+4}\le x+2 \) שלנו הופך אל

\( \frac{1}{x}\ge\frac{1}{\sqrt{x^{2}+4}}\ge\frac{1}{x+2} \)

וכדי שנקבל באמצע את \( f\left(x\right)=\frac{x}{\sqrt{x^{2}+4}} \) אני כופל ב-\( x \) את הכל. מכיוון שאני מניח ש-\( x\ge0 \) (כזכור, אנחנו כרגע במקרה של \( x\to\infty \)) כיווני אי השוויון לא מתהפכים, וקיבלתי

\( \frac{x}{x+2}\le\frac{x}{\sqrt{x^{2}+4}}\le\frac{x}{x} \)

עכשיו, \( \frac{x}{x}=1 \), ומה בדבר \( \frac{x}{x+2} \)? זו פונקציה רציונלית רגילה עם מונה ומכנה ששניהם ממעלה 1 ועם מקדם מוביל 1, ולכן \( \frac{x}{x+2}\underset{x\to\infty}{\to}1 \). אז מה שקיבלנו הוא שהפונקציה \( \frac{x}{\sqrt{x^{2}+4}} \) “כלואה” בין שתי פונקציות ששתיהן שואפות ל-1. לדבר כזה יש שם בחדו”א - משפט הסנדוויץ'. הוא אומר שאם יש לנו פונקציה ש”כלואה” בין שתי פונקציות ששואפות שתיהן לאותו גבול, גם הפונקציה שבאמצע שואפת לאותו הגבול. בכתיב קצת יותר פורמלי, אם \( g_{1}\left(x\right)\le f\left(x\right)\le g_{2}\left(x\right) \) וגם \( g_{1}\left(x\right)\to L \) ו-\( g_{2}\left(x\right)\to L \) אז גם \( f\left(x\right)\to L \).

אז במקרה הנוכחי קיבלנו ש-\( \frac{x}{\sqrt{x^{2}+4}}\underset{x\to\infty}{\to}1 \). זו הדרך הפורמלית להוכיח שהאסימפטוטה הימנית היא \( y=1 \) (היא לא מלאה כי לא הוכחתי את משפט הסנדוויץ’, אבל מן הסתם לא צריך להוכיח אותו בכל פעם שבה באים לחשב אסימפטוטה).

אני אסתכן עכשיו בטרחנות ואעשה את החישוב הדומה גם עבור \( x\to-\infty \) פשוט כי עד עכשיו נפנפתי הרבה בידיים ואני רוצה שנראה בצורה מדויקת למה זה יוצא \( y=-1 \).

אם כן, אני מניח עכשיו ש-\( x<0 \). המקום הראשון שבו החישובים שעשיתי קודם “נשברים” הוא במעבר שלי מ-\( \sqrt{x^{2}}\le\sqrt{x^{2}+4} \) אל \( x\le\sqrt{x^{2}+4} \). אם \( x<0 \) אז זה פשוט לא נכון ש-\( x=\sqrt{x^{2}} \), כי מה שפונקציית השורש מחזירה הוא תמיד השורש החיובי. מכיוון ש-\( x<0 \) הוא לא השורש החיובי של \( x^{2} \), אבל הוא כן מינוס השורש החיובי הזה. כלומר, אני יכול לכתוב \( x=-\sqrt{x^{2}} \) ולהתקדם מכאן: מ-\( \sqrt{x^{2}}\le\sqrt{x^{2}+4} \) אני מסיק \( -x\le\sqrt{x^{2}+4} \).

עבור הכיוון השני, המעבר \( x^{2}+4\le x^{2}+4x+4 \) כבר לא נכון כי כאשר \( x<0 \) אז \( 4x<0 \), אבל מצד שני \( -4x>0 \) אז אני יכול לכתוב

\( x^{2}+4\le x^{2}-4x+4=\left(-x+2\right)^{2} \)

ומכיוון שהביטוי \( \left(-x+2\right) \) חיובי אני יכול לכתוב \( \sqrt{\left(-x+2\right)^{2}}=-x+2 \). קיבלתי

\( -x\le\sqrt{x^{2}+4}\le-x+2 \)

ואחרי שניקח את ההופכי של כולם, נקבל

\( -\frac{1}{x}\ge\frac{1}{\sqrt{x^{2}+4}}\ge-\frac{1}{x+2} \)

ועכשיו אני כופל את זה ב-\( x \). הפעם \( x<0 \) ולכן כיוון אי השווינים כן מתהפך:

\( -\frac{x}{x}\le\frac{x}{\sqrt{x^{2}+4}}\le-\frac{x}{x+2} \)

ועכשיו יש לי שוב את כלל הסנדוויץ’, אבל הפעם כששתי הפונקציות בצדדים שואפות אל \( -1 \), מה שמסיים את ההוכחה.

יופי, התקדמנו! אנחנו גם קצת יותר מתורגלים בעבודה עם שורשים, וגם ראינו כלי רציני שאפשר להשתמש בו כדי לחשב אסימפטוטות אופקיות. כאן עולה כמובן השאלה - האם זה כלי שאפשר להשתמש בו בבית הספר? אני מודה שאני לא יודע. אני חושד שלא, ושהתיאור ה”אינטואיטיבי” הוא מה שאמורים להסתמך עליו, בנוסף אולי להצבה של ערכים גדולים וקטנים של \( x \) ובחינה של מה קורה.

אסימפטוטות שמערבות לוגריתמים

עכשיו בואו נסבך את התמונה על ידי סוג חדש של פונקציה שטרם הזכרתי - לוגריתמים. יש לי פוסט על לוגריתמים אז אני אזכיר רק בקצרה מה הם: אם \( x=10^{a} \) אז \( \log x=a \). כלומר, \( \log \) של מספר כלשהו אומר “באיזו חזקה צריך להעלות את 10 כדי לקבל את \( x \)?”. כאן החזקה יכולה להיות כל מספר - חיובי, שלילי, שלם, שבר, אפילו \( \pi \).

ההגדרה של \( \log \) שהצגתי מתבססת על 10, אבל 10 הוא מספר די שרירותי - אנחנו משתמשים בו כנראה כי יש לנו 10 אצבעות, אבל אין מניעה לדבר על לוגריתמים שמדברים על העלאה בחזקה של מספרים אחרים. למספר שבודקים כמה צריך להעלות אותו בחזקה קוראים בסיס הלוגריתם. אנחנו ראינו לוגריתם שהבסיס שלו הוא 10, אבל עוד סוג מאוד נפוץ הוא לוגריתם על בסיס 2, שקיבל סימון משלו: \( \lg \). כך למשל \( \lg256=8 \) כי \( 2^{8}=256 \). ואפשר להשתמש בעוד בסיסים גם אם אין להם סימון מיוחד: למשל, \( \log_{6}36 \) הוא הסימון ללוגריתם על בסיס 6 של 36, וזה שווה 2, כי \( 6^{2}=36 \). מה שכן קריטי הוא שהבסיס יהיה תמיד מספר גדול מ-1 כי כשמעלים בחזקה מספרים קטנים או שווים מ-1 מתחילות להתרחש כל מני מהומות שאין לנו כוח אליהן.

אבל עזבו אתכם מבסיס 2, או 6, או 10. יש בסיס אחד שבשימוש נרחב משמעותית יותר מכל בסיס אחר: בסיס שהוא המספר \( e=2.718281828459\ldots \), מה שכמובן מעורר שאלת “מה הולך פה?!” אצל מי שרואים את זה בפעם הראשונה.

במקום לכתוב \( \log_{e} \) אנחנו כותבים \( \ln \), וזה יהיה הסימון שבו אני אשתמש בהמשך כל הזמן. לפני שאסביר למה אנחנו משתמשים ב-\( \ln \) הזה ולא סתם ב-\( \log \) אני אתחיל עם להבהיר שזה לא משנה באיזה לוגריתם אנחנו משתמשים כי כולם פחות או יותר אותו הדבר. אחת התוצאות הבסיסיות על לוגריתמים היא השוויון \( \log_{a}b=\frac{\ln b}{\ln a} \), שאומר שבעצם, לכל \( a \) אפשרי, הלוגריתם על בסיס \( a \) הוא “כמו \( \ln \) רק כפול איזה קבוע”. למשל, עבור \( a=10 \), אנחנו מקבלים ש-\( \log b=\left(\frac{1}{\ln10}\right)\ln b \), כלומר כדי לחשב את \( \log b \) אנחנו מחשבים את \( \ln b \) ופשוט כופלים במספר הקבוע \( \frac{1}{\ln10} \).

אז למה בעצם להשתמש במספר מוזר כמו \( e \) זה הדבר הנכון? יש הרבה גישות שונות שבהן הוא צץ, אבל אני אלך על הישירה ביותר - זו שמערבת את מושג הנגזרת שלומדים בחדו”א ומתאר את קצב השינוי של פונקציות. אם אנחנו גוזרים את \( \ln x \) אנחנו מקבלים את הנגזרת הנחמדה \( \frac{1}{x} \). אם לעומת זאת אנחנו גוזרים לוגריתם בבסיס אחר \( a \), כלומר את \( \log_{a}x \), אנחנו מקבלים \( \frac{1}{x\ln a} \) - משתרבב לנו פנימה עוד איזה קבוע. באופן דומה אפשר לדבר על מה שנקרא פונקציה אקספוננציאלית שהיא פונקציה מהצורה \( f\left(x\right)=a^{x} \) - כזו שבו לוקחים את \( x \) ובמקום להעלות אותו בחזקה כמו שעושים בפולינומים, להשתמש בו דווקא בתור המעריך של חזקה שהבסיס שלה הוא מספר \( a \) נתון מראש. אז גם בפונקציה כזו, הנגזרת שלה תהיה \( a^{x}\ln\left(a\right) \) - מוכפלת בקבוע. אם אנחנו בוחרים \( a=e \) אז נקבל שהנגזרת של \( e^{x} \) היא \( e^{x} \) עצמה - הפונקציה היחידה ששווה לנגזרת שלה. למעשה, זו דרך פופולרית להגדיר את \( e \): מוכיחים (עם כלים מתקדמים יחסית בחדו”א) שקיימת רק פונקציה אחת \( f\left(x\right) \) ששווה לנגזרת של עצמה ומקיימת \( f\left(0\right)=1 \), ואז מגדירים \( e=f\left(1\right) \) ומוכיחים שהפונקציה הזו מתנהגת כמו \( e^{x} \).

נחזור לעניין שלשמו התכנסנו - אסימפטוטות. כרגיל, הכי טוב להסתכל קודם כל על הגרף של \( \ln x \) כדי לקבל תחושה מה קורה פה:

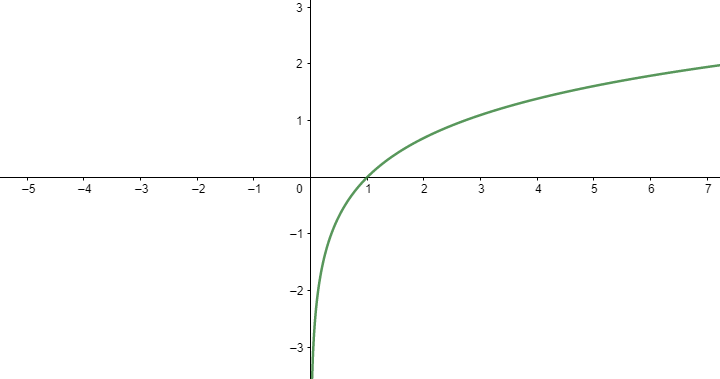
מה שאפשר לראות פה מייד הוא שכאשר הפונקציה מתקרבת אל \( x=0 \) היא צוללת בחדות למטה - יש לה אסימפטוטה אנכית. הסיבה לכך היא שככל שמספר קרוב יותר לאפס, כך גם החזקה שבה צריך להעלות את \( e \) כדי לקבל אותו היא נמוכה יותר (את אפס עצמו אי אפשר להשיג אף פעם, ולכן הפונקציה לא מוגדרת ב-\( x=0 \)). לעומת זאת, כשמסתכלים מה קוה עם \( x\to\infty \) הסיטואציה דומה למה שקרה עם שורש - לא ברור אם יש אסימפטוטה אופקית או לא. קצת מחשבה מראה שלא יכולה להיות כזו: אם נסתכל על \( y=a \), אז קיימת חזקה כלשהי של \( e \) שמקיימת \( e^{x}>a \) (כי ככל שמגדילים את \( x \) כך \( e^{x} \) גדל באופן בלתי חסום) ולכן עבור \( x=\ln a \) ומעלה, הפונקציה תחצה את \( y=a \) ותמשיך להתרחק ממנו.

במקרה של שורש ראינו שאפשר לחשוב עליו בתור \( x^{\frac{1}{2}} \) ולהשוות אותו עם פולינומים. עבור לוגריתם הסיטואציה קצת שונה - כל ביטוי מהצורה \( x^{a} \) עבור \( a>0 \) גדל “יותר מהר” מ-\( \ln x \). כלומר, אם יש לנו \( \frac{\ln x}{x} \), אז כש-\( x\to\infty \) הביטוי הזה ישאף לאפס. לעומת זאת, השאיפה ל-\( -\infty \) של \( \ln x \) כש-\( x\to0^{+} \) חזקה יותר מכל פולינום, כך ש-\( \frac{\ln x}{x}\underset{x\to0^{+}}{\to}-\infty \).

מאיפה אני יודע את הדברים הללו? לצערי, אין לי כאן כלל סנדוויץ’ לשלוף; ההוכחות שאני מכיר מתבססות על כלי חזק בחדו”א שנקרא כלל לופיטל ומשתמש בנגזרות, שזה מושג שאני לא ממש נכנס אליו כאן. ניאלץ פשוט לקבל את הטענות הללו כנכונות.

בואו נראה עכשיו משהו קצת יותר מסובך כדי להבין את העיקרון הכללי של איך לטפל בדברים מסובכים (אבל כמובן, מה שיש בפוסטים הללו לא מספיק; צריך לתרגל עוד ולראות עוד דוגמאות): הפונקציה \( \ln\left(x^{2}-4\right) \). פונקציה כזו נקראת “הרכבה” - אנחנו לוקחים את הפולינום \( x^{2}-4 \) ו”מרכיבים” אותו על הפונקציה \( \ln \). כלומר, במקום ה-\( x \) הרגיל שהוא קלט של \( \ln \), מה ש-\( \ln \) מקבלת הוא את כל הפולינום.

כזכור, \( \ln x \) בכלל לא מוגדר אם \( x\le0 \). אז \( \ln\left(x^{2}-4\right) \) בכלל לא מוגדר אם \( x^{2}-4\le0 \), כלומר אם \( x^{2}\le4 \), כלומר אם \( -2\le x\le2 \). האסימפטוטה של \( \ln x \) צצה כש-\( x \) שואף אל 0, אז עבור \( \ln\left(x^{2}-4\right) \) היא תצוץ כש-\( x^{2}-4 \) ישאף אל אפס. בפונקציה נחמדה כמו פולינום קל לדעת מתי היא שואפת לאנשהו - בודקים באיזו נקודה היא שווה בדיוק לאותו משהו, ואז כששואפים לנקודה הזו, הפונקציה שואפת למשהו (ה”נחמדות” הזו נקראת רציפות; כל הפולינומים רציפים, פונקציות רציונליות רציפות בכל נקודה שבה הן מוגדרות, שורשים, לוגריתמים וגם פונקציות טריגונומטריות - כולן רציפות!).

\( x^{2}-4=0 \) בדיוק כאשר \( x=\pm2 \), ולכן כש-\( x\to2^{+} \) ו-\( x\to-2^{-} \) הפונקציה תשאף אל \( -\infty \) וקיבלנו שתי אסימפטוטות אנכיות, ב-\( x=\pm2 \). למה כתבתי \( x\to2^{+} \)? הפלוס הזה אומר שאני שואף אל 2 מצד ימין - מהצד החיובי שלה - כי מהצד השמאלי הפונקציה לא מוגדרת. בדומה גם עבור \( -2 \) שאליה אני שואף מצד שמאל.

אגב, מה קורה עם הפונקציה \( f\left(x\right)=e^{x} \)? האם לה יש אסימפטוטות? אם נציץ בגרף שלה נגלה שהיא נראית כאילו לקחנו את הגרף של \( \ln x \), סובבנו אותו 90 מעלות נגד כיוון השעון, ואז בנוסף לכל הצרות גם שיקפנו בראי:

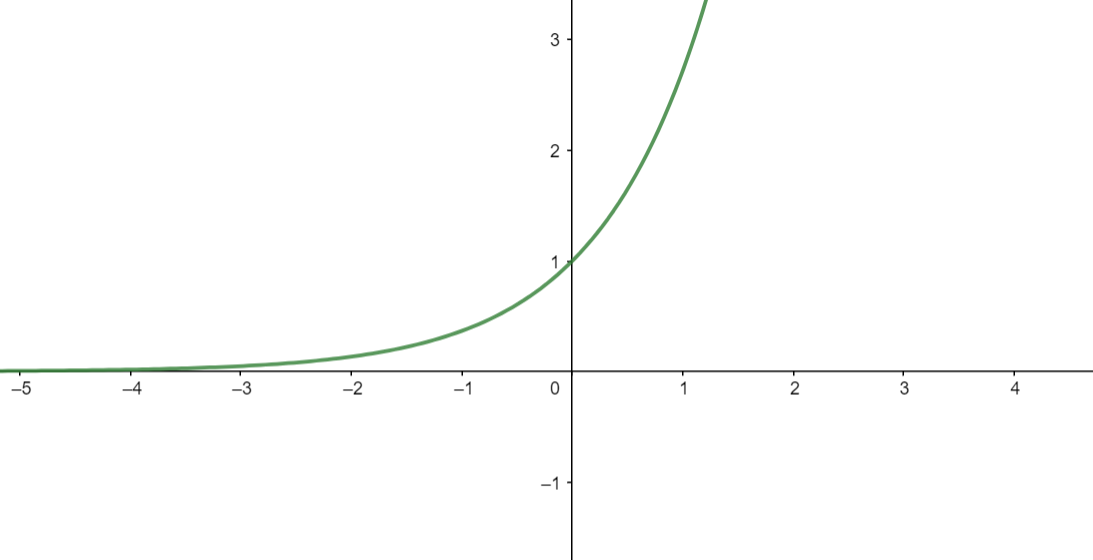
הדמיון הזה לא מקרי; הוא נובע מכך ש-\( e^{x} \) ו-\( \ln x \) הן פונקציות הופכיות זו לזו, כלומר אם מפעילים אחת ואז את השניה חוזרים לערך המקורי. הקטע הזה של “הגרף מתקבל מסיבוב ושיקוף” נכון באופן כללי לכל זוג פונקציות הופכיות.

עכשיו, כאשר \( x\to\infty \) הגרף של \( e^{x} \) מתנהג כמו החלק הלא אסימפטוטי של הגרף של \( \ln x \) - כל מה שקורה הוא ש-\( e^{x}\to\infty \) ואין פה אסימפטוטה. אבל כאשר \( x\to-\infty \) יש לנו את האסימפטוטה האופקית \( y=0 \), בדיוק כמו שב-\( \ln x \) הייתה לנו האסימפטוטה האנכית \( x=0 \) (הסיבוב ב-90 מעלות המדובר הופך אסימפטוטה אנכית לאופקית).

אסימפטוטות שמערבות פונקציות טריגונומטריות

יש לי פוסטים על טריגונומטריה, אז בואו ניגש מייד לעסק: שתי הפונקציות המרכזיות שלנו הן סינוס וקוסינוס, \( \sin x,\cos x \), שהן פונקציות מחזוריות שנעות בין \( 1 \) ובין \( -1 \), ובעצם נראות אותו דבר בדיוק חוץ מזה שאחת היא הזזה של השניה:

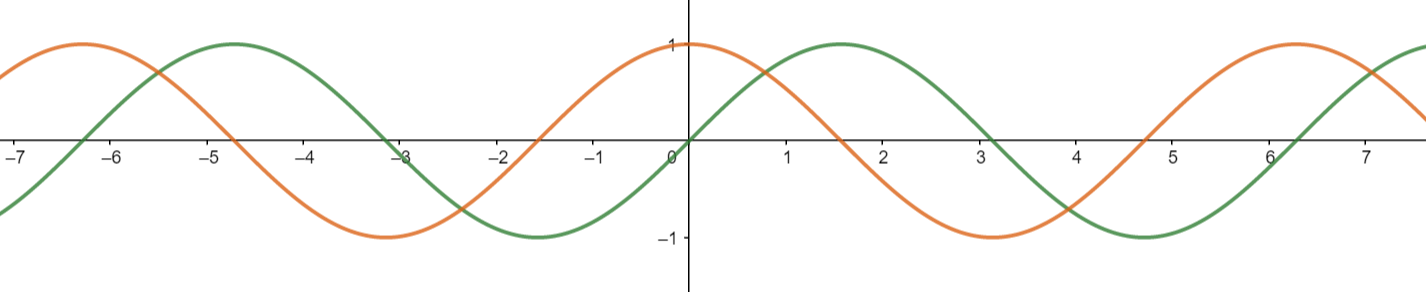
הפונקציה שעוברת בראשית הצירים היא סינוס, וזו שב-\( x=0 \) שווה 1 דווקא היא קוסינוס. אלו פונקציות מרכזיות במתמטיקה ובחיים ובהכל, אבל נראה שהרלוונטיות שלהן לדיון האסימפטוטות היא כמעט אפסית - הן בוודאי לא שואפות לשום נקודה קונקרטית כש-\( x \) שואף לאינסוף, והן לא “מתפוצצות” עם אסימפטוטה אנכית. בפוסט הקודם ראינו שהסיטואציה שלהן כשמערבים אותן בפונקציות רציונליות היא בעייתית יותר: \( \frac{\sin x}{x} \) הידועה לשמצה היא פונקציה שבסביבות \( 0 \) שואפת ל-1 ואין לה אסימפטוטה, ואילו כאשר \( x \) שואף לאינסוף היא שואפת לאפס. אינטואיטיבית, הסיבה לכך היא שקרוב מאוד לאפס, \( \sin x \) מתנהגת מאוד דומה ל-\( x \), אבל הדמיון הזה הולך לאיבוד לחלוטין אחרי שמתרחקים קצת מאפס.

ושוב, אפשר לשאול - איך מוכיחים את זה? בפרט, איך מוכיחים ש-\( \frac{\sin x}{x}\underset{x\to0}{\to}1 \)? באופן אולי מפתיע, זו הוכחה מאוד לא פשוטה (יש לי פוסט שמסביר מה בעצם הבעיה פה) והגבול הלכאורה תמים הזה הוא בעצם בעל חשיבות קריטית לחדו”א של פונקציות טריגונומטריות; עליו מתבססים כשמחשבים את הנגזרות שלהן.

אם כן, אין משהו מעניין לומר על אסימפטוטות וטריגונומטריה… רגע, חכו חכו. יש עוד פונקציה טריגונומטרית אחת שלא הזכרתי - טנגנס. היא מוגדרת פשוט בתור \( \tan x=\frac{\sin x}{\cos x} \). עכשיו, הקוסינוס שבמכנה מתאפס די הרבה וכשזה קורה הסינוס לא נמצא בסביבות אפס בכלל, כלומר אנחנו הולכים לקבל אסימפטוטה. ולא אחת, אלא הרבה - בגלל המחזוריות של סינוס וקוסינוס, גם האסימפטוטות של טנגנס יהיו מחזוריות. ככה זה נראה:

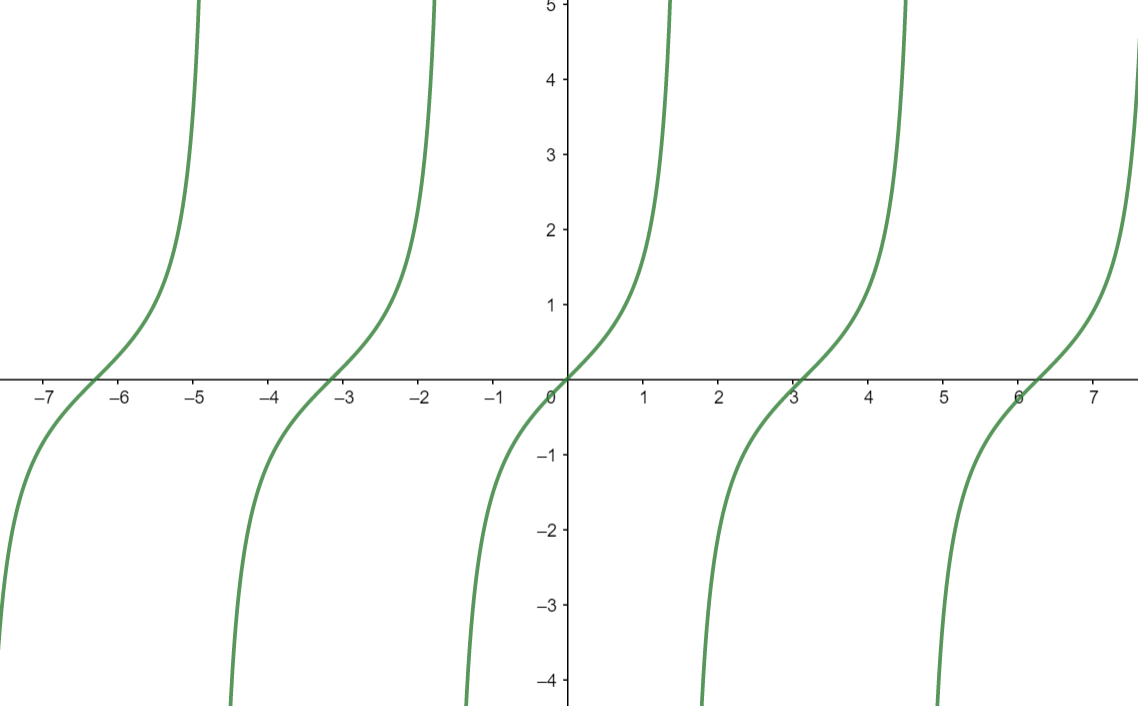
טנגנס היא פונקציה שחוזרת על עצמה הרבה פעמים, ובכל פעם כזו הצד השמאלי שלה שואף ל-\( -\infty \) והימני שואף ל-\( \infty \). באילו נקודות זה קורה? ובכן, יש פיצוץ בכל פעם שבה המכנה של \( \frac{\sin x}{\cos x} \) שואף לאפס. ומתי זה קורה? כאמור, \( \cos x \) רציפה, אז זה קורה בדיוק כש-\( x \) שואף לערך שבו \( \cos x=0 \). ומתי זה קורה? ובכן, זה מצריך אותי להכניס לתמונה את הקבוע המפורסם השני של המתמטיקה: \( \pi=3.14159265359 \). איך הוא קשור?

ובכן, הנה דרך אפשרית אחת לחשוב על קוסינוס: נצייר מעגל עם רדיוס 1, נעמוד עליו בנקודה \( \left(1,0\right) \) (הימנית ביותר) ואז נתחיל ללכת עליו נגד כיוון השעון ונסמן את המרחק שהלכנו עד כה ב-\( x \). בכל רגע נתון אפשר לעצור ולבדוק לאן הגענו. נניח שהגענו לקואורדינטה \( \left(a,b\right) \) כלשהי; אז \( a=\cos x \).

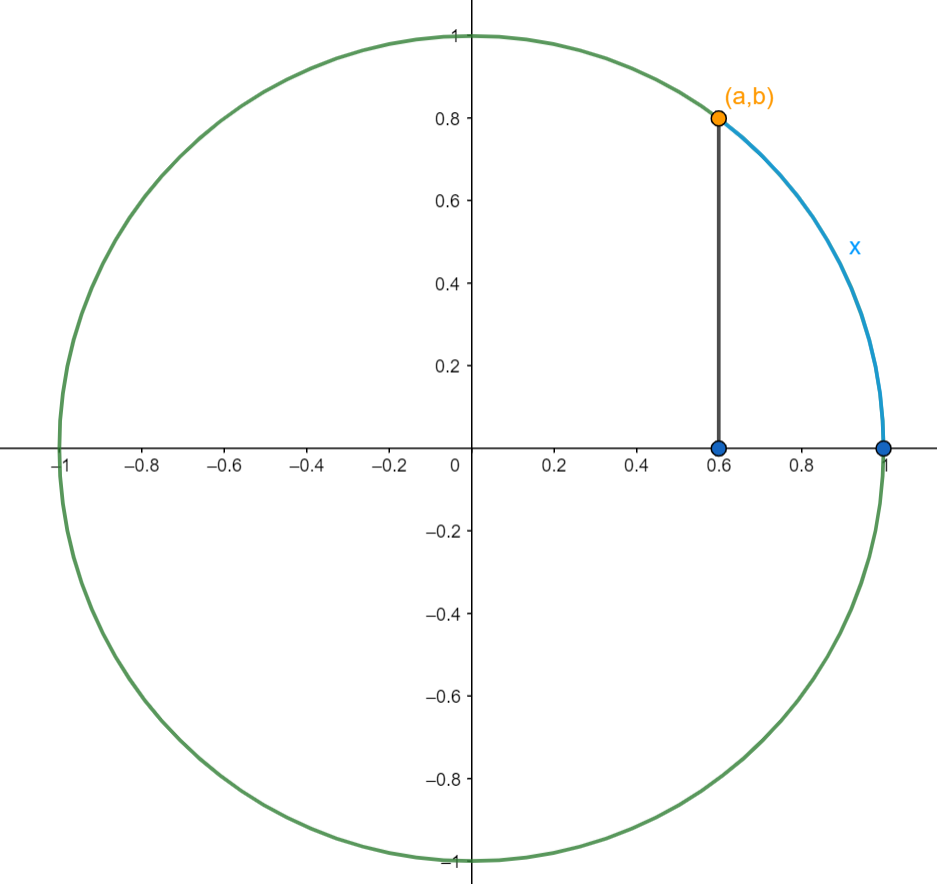
זו לא הדרך הכי מיידית לתאר קוסינוס, אבל היא בהחלט נכונה ועובדת, ומאפשרת לנו לראות מה הקשר של \( \pi \) לכל זה. בבסיסו, \( \pi \) הוא היחס בין היקף מעגל והקוטר שלו: אם למעגל יש רדיוס 1 אז הקוטר שלו הוא 2, ולכן ההיקף שלו הוא \( 2\pi \). זה היקף של מעגל שלם, ולכן היקף של רבע מעגל הוא \( \frac{\pi}{2} \). הפעם הראשונה בטיול שלנו על המעגל שבה אנחנו מגיעים לקואורדינטה \( \left(a,b\right) \) עם \( a=0 \) (כלומר, חוצים את ציר \( y \)) היא כאשר השלמנו טיול על רבע מעגל בדיוק: \( \cos\left(\frac{\pi}{2}\right)=0 \). הפעם השניה היא כשהשלמנו סיבוב על חצי המעגל שמצד שמאל של ציר \( y \); חצי מעגל הוא מאורך \( \pi \) כך שקיבלנו \( \cos\left(\frac{\pi}{2}+\pi\right)=0 \), וזה הולך להימשך - בכל פעם, אחרי שאנחנו מבצעים עוד מסע באורך \( \pi \) נגיע אל ציר \( y \). ולכן באופן כללי אפשר לכתוב \( \cos\left(\frac{\pi}{2}+\pi k\right)=0 \) וזה לכל \( k\in\mathbb{Z} \) (גם עבור מספרים שליליים זה עובד!) לכן האסימפטוטות של \( \tan x \) יהיו בנקודות \( x=\frac{\pi}{2}+\pi k \) הללו.

זה מספיק כדי להבין את הרעיון הבסיסי של התעסקות עם פונקציות טריגונומטריות, אבל כמובן שתמיד יש סיבוכים. למשל, אם \( f\left(x\right)=\frac{\cos x}{\cos x+1} \), מה קורה כאן? במונה ובמכנה יש \( \cos x \) וזה אולי קצת מזכיר את המקרה של \( \frac{x}{x+1} \) שיש לו אסימפטוטות אופקיות, אבל במקרה של הפונקציות הטריגונומטריות זה לא קורה כי כזכור, \( \cos x \) מזפזפת לה בין \( 1 \) ובין \( -1 \) ולכן ההתנהגות שלה כש-\( x \) שואף לאינסוף לא שונה מההתנהגות שלה בסביבות \( x=0 \).

מה עם אסימפטוטות אנכיות? כאן צריך לראות מתי \( \cos x+1=0 \), כלומר \( \cos x=-1 \), וזו כבר משוואה שונה מזו שדיברתי עליה קודם, אבל הרעיון הוא דומה: \( \cos x=-1 \) אם אחרי ה”טיול” על המעגל הגענו אל הנקודה \( \left(-1,0\right) \) (זו הנקודה היחידה על המעגל שקואורדינטת ה-\( x \) שלה היא \( -1 \)). מכיוון שהתחלנו בדיוק בצד השני של המעגל, הגענו לנקודה הזו אחרי מרחק \( \pi \), כלומר \( \cos\left(\pi\right)=-1 \). כמו כן, אנחנו חוזרים לנקודה הזו כל \( 2\pi \) צעדים (ולא כל \( \pi \) צעדים כי כאמור - יש רק נקודה אחת כזו, להבדיל מהמקרה הקודם שבו היו שתי נקודות עם קואורדינטת ה-\( x \) המתאימה שהמרחק ביניהן על המעגל היה בדיוק \( \pi \)). לכן יש אסימפטוטה אופקית בכל הנקודות \( x=\pi+2k\pi \).

ומה ההסבר הפורמלי לכל זה?

אני רוצה לעשות “תם ולא נשלם”, כי הפוסט הזה הציג את הרעיונות הכלליים של אסימפטוטות אבל בוודאי שלא נכנס לכל החישובים והסיטואציות האפשריות, כולל אלו שרואים בבית הספר; ועדיין, אני מקווה שהוא עוזר מספיק כדי לקבל את המושג הראשוני של מה הולך כאן בכלל ומי הנפשות הפועלות.

אבל אני לא רוצה לסיים בלי להציג את הפורמליזם האמיתי שעומד מאחורי כל זה, פשוט כי אני זוכר כמה הפריע לי, כתלמיד תיכון שקרא ספרי מתמטיקה, שפטרו דברים כמו הגדרת הגבול ב”לא נוכל כאן להציג את הגדרת הגבול” ואז המשיכו להשתמש בגבולות כמו כלום, כמו שעשינו כאן. אז אני אכתוב פה הסברים קצרים ותמציתיים יחסית; יש לי פוסטים מלאים יותר בנושאים הללו.

המושג הבסיסי שעליו כל נושא האסימפטוטות מתבסס הוא מושג הגבול. גבול של פונקציה מתאר “לאן הפלט של הפונקציה הולך כשהקלט הולך למקום ספציפי”. ההגדרה המדויקת של גבול היא לא קלה לעיכול ולכן נמנעים ממנה בבתי הספר, אבל קל לכתוב את כולה בשורה אחת:

אומרים ש-\( f\left(x\right) \) שואפת לגבול \( L \) כאשר \( x \) שואף ל-\( x_{0} \) ומסמנים את זה בתור \( f\left(x\right)\underset{x\to_{x0}}{\to}L \), או בסימון החביב עלי יותר שהסתרתי עד כה, \( \lim_{x\to x_{0}}f\left(x\right)=L \), אם:

לכל \( \varepsilon>0 \) קיים \( \delta>0 \) כך שאם \( \left|x-x_{0}\right|<\delta \) אז \( \left|f\left(x\right)-L\right|<\varepsilon \)

או במילים: לכל אפסילון גדול מאפס אנחנו יכולים למצוא דלתא גדול מאפס, כך שאם המרחק של \( x \) מ-\( x_{0} \) קטן מדלתא, אז המרחק של \( f\left(x\right) \) מ-\( L \) קטן מאפסילון.

כשאנחנו מתעסקים עם אסימפטוטות, אנחנו עובדים עם הכללה של ההגדרה הזו שגם מערבת את מושג האינסוף. בחדו”א נזהרים לא להגדיר דברים תוך התייחסות לאינסוף בתור מספר, אלא בתור סימון בלבד, וזה יוביל אותנו לכמה הגדרות שהן כולן באותה הרוח:

\( \lim_{x\to\infty}f\left(x\right)=L \) אם לכל \( \varepsilon>0 \) קיים \( M>0 \) כך שאם \( x>M \) אז \( \left|f\left(x\right)-L\right|<\varepsilon \)
\( \lim_{x\to-\infty}f\left(x\right)=L \) אם לכל \( \varepsilon>0 \) קיים \( M>0 \) כך שאם \( x<-M \) אז \( \left|f\left(x\right)-L\right|<\varepsilon \)
\( \lim_{x\to x_{0}}f\left(x\right)=\infty \) אם לכל \( M>0 \) קיים \( \delta>0 \) כך שאם \( \left|x-x_{0}\right|<\delta \) אז \( f\left(x\right)>M \)
\( \lim_{x\to x_{0}}f\left(x\right)=-\infty \) אם לכל \( M>0 \) קיים \( \delta>0 \) כך שאם \( \left|x-x_{0}\right|<\delta \) אז \( f\left(x\right)<-M \)

את זה אפשר לסבך עוד יותר - שגם השאיפה של \( x \) תהיה לאינסוף/מינוס אינסוף וגם הפונקציה עצמה שואפת לאינסוף תוך כדי, ואפשר גם לדבר על שאיפה “חד צדדית” ל-\( x_{0} \), למשל \( x\to x_{0}^{+} \) אומר שבמקום הדרישה \( \left|x-x_{0}\right|<\delta \) שבעצם אומרת \( x_{0}-\delta<x<x_{0}+\delta \), תהיה לנו רק הדרישה \( x_{0}<x<x_{0}+\delta \), וכדומה.

אם יש לנו שתי פונקציות \( f\left(x\right),g\left(x\right) \), אפשר לדבר גם על המרחק ביניהן לכל \( x \): זה פשוט \( \left|f\left(x\right)-g\left(x\right)\right| \). הדבר הזה הוא בעצמו פונקציה של \( x \); אני יכול למשל לסמן \( h\left(x\right)=\left|f\left(x\right)-g\left(x\right)\right| \). עכשיו, אם \( \lim_{x\to\infty}h\left(x\right)=0 \), המשמעות היא שהפונקציות \( f,g \) “שואפות אחת לשניה” כש-\( x \) שואף לאינסוף. אני אחשוב על \( f \) בתור הפונקציה הרגילה שלנו ועל \( g \) בתור קו ישר, ועולה השאלה - איך בעצם נראית פונקציה של קו ישר? התשובה פשוטה: \( g\left(x\right)=mx+a \), כאשר הקבוע \( m \) נקרא השיפוע של הישר ואילו \( a \) היא נקודת החיתוך עם ציר \( y \) (כי \( g\left(0\right)=a \), ו-\( x=0 \) בדיוק כשאנחנו עוברים דרך ציר \( y \)).

עד עכשיו ראינו שני סוגים של קווים: ראשית, קווים אופקיים, שבהם \( m=0 \); ושנית, קווים אנכיים שבהם… אה… \( m=\infty \)? לא אמרתי לפני רגע שאסור לי לעשות משהו כזה? ובכן, כן; קווים אנכיים הם סוג של יוצאים מן הכלל כי הם הקווים היחידים שאינם פונקציות. בפונקציה, לכל קואורדינטת \( x \) יש ערך בודד של \( y \) שמתאים לה; אבל בקו אנכי לכל הנקודות אותה קואורדינטת \( x \). העניין הוא שלא חייבים להשתמש בפונקציות כדי לתאר אובייקטים גאומטריים; הדרך הכללית לתאר אותם היא באמצעות משוואה.

על הפונקציה \( y=mx+a \) אפשר לחשוב גם בתור משוואה, \( y-mx-a=0 \). זה מוביל אותנו להגדרה ה”כללית” של ישר: אוסף הפתרונות \( \left(x,y\right) \) של משוואה מהצורה \( Ax+By+C=0 \) כאשר \( A,B,C \) הם פרמטרים. בפרט, אוסף הפתרונות של המשוואה \( x=a \) הוא ישר - הישר האנכי שחותך את ציר \( x \) בנקודה \( a \).

אם אנחנו רוצים לבדוק האם יש לפונקציה אסימפטוטה אופקית כש-\( x \) שואף לאינסוף, אנחנו בעצם בודקים האם קיים \( a \) כך ש-\( \left|f\left(x\right)-g\left(x\right)\right|\underset{x\to\infty}{\to}0 \) עבור \( g\left(x\right)=a \), כלומר האם \( \left|f\left(x\right)-a\right|\underset{x\to\infty}{\to}0 \). אם נפתח את הגדרת הגבול בצורה מלאה נראה שאנחנו שואלים האם לכל \( \varepsilon>0 \) קיים \( M \) כך שאם \( x>M \) אז \( \left|f\left(x\right)-a-0\right|<\varepsilon \) שזה בעצם אותו הדבר בדיוק כמו לומר ש-\( f\left(x\right)\underset{x\to\infty}{\to}a \). במילים אחרות, הבעיה של מציאת אסימפטוטה אופקית לפונקציה היא בדיוק אותה בעיה כמו לבדוק האם לפונקציה קיים גבול באינסוף. אולי זו הסיבה למה מאז שהתחלתי ללמוד חדו”א באוניברסיטה לא זכור לי שדיברו על אסימפטוטות יותר - פשוט מדברים על גבולות וזהו.

בשביל אסימפטוטה אנכית אנחנו צריכים לבדוק האם קיים \( a \) שעבורו \( \lim_{x\to a^{\pm}}f\left(x\right)=\pm\infty \) (הפלוס/מינוס כאן אומר “או זה או זה”; יש 4 שילובים אפשריים של כיוון השאיפה אל \( a \) והאם הפונקציה שואפת לאינסוף או מינוס אינסוף).

לפונקציה יש לכל היותר שתי אסימפטוטות אופקיות - אחת לכיוון \( \infty \) והשניה לכיוון \( -\infty \). זאת מכיוון שהגבול של פונקציה בשאיפה לנקודה מסויימת או לאינסוף הוא יחיד, בהנחה שהוא קיים. לעומת זאת כפי שראינו עם טנגנס, יכולות להיות אינסוף אסימפטוטות אנכיות - כי פונקציה יכולה לשאוף לאינסוף בכמה נקודות שונות (בכל נקודה כזו הגבול הוא עדיין יחיד - אינסוף).

אז האם סיימנו? לא!

בונוס: עוד אסימפטוטות!

ההגדרה הפורמלית שנתתי מאפשרת לי לדבר על משהו שעד עכשיו הסתרתי לגמרי - יש גם אסימפטוטות שאינן אופקיות או אנכיות אלא משופעות; כל קו ישר יכול לתפקד בתור אסימפטוטה. בואו נראה דוגמא - הפונקציה \( f\left(x\right)=\frac{x^{3}+2x}{x^{2}+7} \):

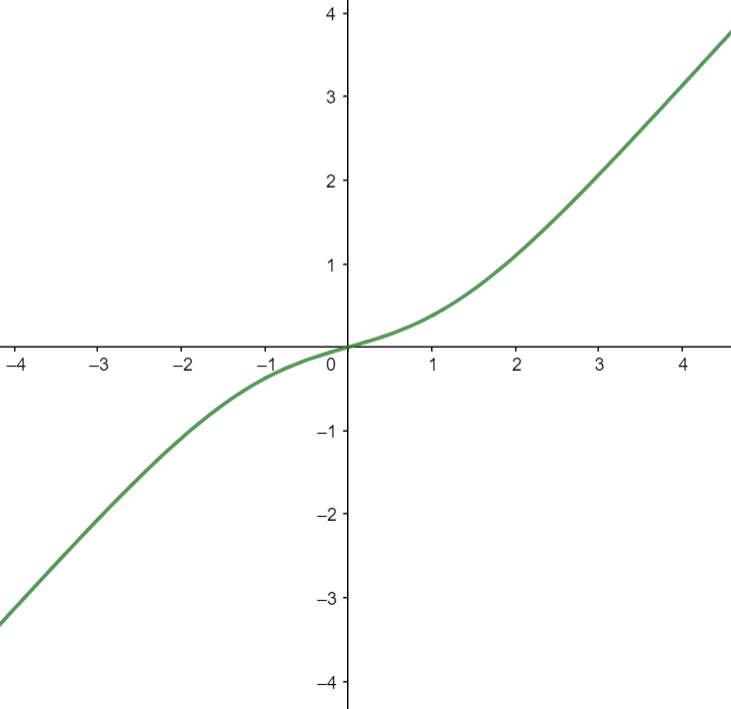
נראה שבשאיפה לאינסוף הפונקציה הופכת להיות כמעט קו ישר, שכמובן שואף לאינסוף. בואו נראה טריק שיאפשר לי להוכיח ש-\( g\left(x\right)=x \) היא אכן אסימפטוטה: ראשית, שימו לב לכך ש-\( x^{3}+2x=x\left(x^{2}+7\right)-5x \) (עשיתי פה משהו שנקרא חלוקת פולינומים ולא קשה יותר מסתם חילוק ארוך אחרי שמתרגלים). כלומר, אני יכול לכתוב

\( \frac{x^{3}+2x}{x^{2}+7}=\frac{x\left(x^{2}+7\right)-5x}{x^{2}+7}=x-\frac{5x}{x^{2}+7} \)

בואו נשווה את הפונקציה הזו לקו הישר \( g\left(x\right)=x \):

\( \left|f\left(x\right)-g\left(x\right)\right|=\left|x-\frac{5x}{x^{2}+7}-x\right|=\left|-\frac{5x}{x^{2}+7}\right| \)

ואנחנו כבר יודעים שהביטוי הזה שואף לאפס כי המכנה ממעלה גדולה מהמונה.

כדי שהטריק הזה יעבוד, נזקקנו לכך שהמעלה של המונה \( \frac{x^{3}+2x}{x^{2}+7} \) תהיה גדולה מהמעלה של המכנה בדיוק ב-1. אם הייתה פחות גדולה, הייתה לנו אסימפטוטה לא משופעת או שום אסימפטוטה בכלל; ואם הייתה יותר גדולה אז טריק החלוקה של פולינומים היה משאיר אותי עם \( x^{2} \) פחות משהו, או חזקה גבוהה יותר - והיא לא הייתה מתבטלת עם ה-\( x \) של \( g\left(x\right) \).

הדוגמה שנתתי היא קצת מנוונת, כי יוצא שהאסימפטוטה עוברת דרך ראשית הצירים. בואו נראה דוגמא שבה זה לא קורה, אבל לפני כן נבין איך מוצאים אסימפטוטה כזו באופן כללי. נניח שנתונה לנו פונקציה \( f\left(x\right) \) ואנחנו רוצים למצוא מה האסימפטוטה ב-\( x\to\infty \) (עבור \( -\infty \) זה יהיה אותו רעיון). בואו נניח שיש אסימפטוטה כזו, \( g\left(x\right)=mx+a \) כך שמתקיים \( \left|f\left(x\right)-g\left(x\right)\right|\to0 \). אני רוצה איכשהו למצוא את \( m,a \); הנה טריק שיעזור לי לעשות את זה. אם אני לוקח את \( g\left(x\right) \) ומחלק אותו ב-\( x \), התוצאה תהיה \( \frac{g\left(x\right)}{x}=m+\frac{a}{x} \), והביטוי הזה בבירור שואף ל-\( m \) כאשר \( x \) שואף לאינסוף; אם \( f\left(x\right) \) שואפת אל \( g\left(x\right) \) כאשר \( x \) שואף לאינסוף אני מצפה שההתנהגות של \( \frac{f\left(x\right)}{x} \) תהיה דומה וגם הוא ישאף אל \( m \).

כדי להוכיח פורמלית ש-\( \lim_{x\to\infty}\frac{f\left(x\right)}{x}=m \) אנחנו צריכים לקחת \( \varepsilon>0 \) ולהראות שקיים \( M>0 \) כך שאם \( x>M \) אז \( \left|\frac{f\left(x\right)}{x}-m\right|<\varepsilon \). לצורך כך, אני אשתמש בטכניקת הוכחה סופר-נפוצה בחדו”א: אני אפרק את הביטוי \( \left|\frac{f\left(x\right)}{x}-m\right| \) לסכום של שני ביטויים, שאת שניהם אני יכול לחסום. אני אעשה את זה עם הטריק של לחבר ולחסר את \( \frac{g\left(x\right)}{x} \) בתוך הביטוי, מה שנותן לי

\( \left|\frac{f\left(x\right)}{x}-m\right|=\left|\frac{f\left(x\right)}{x}-\frac{g\left(x\right)}{x}+\frac{g\left(x\right)}{x}-m\right| \)

\( \left|\frac{f\left(x\right)}{x}-\frac{g\left(x\right)}{x}+\frac{g\left(x\right)}{x}-m\right|\le\left|\frac{f\left(x\right)}{x}-\frac{g\left(x\right)}{x}\right|+\left|\frac{g\left(x\right)}{x}-m\right| \)

כדי לחסום כל ביטוי בנפרד, בואו נזכור אילו גבולות כבר יש לנו:

\( \lim_{x\to\infty}\left|f\left(x\right)-g\left(x\right)\right|=0 \)

\( \lim_{x\to\infty}\frac{g\left(x\right)}{x}=m \)

כדי “להפעיל” גבול אני בוחר אפסילון כלשהו ומקבל בחזרה \( M \) כך שאם \( x>M \) אז הפונקציה קרובה לגבול עד כדי אפסילון. לי, כזכור, יש כבר \( \varepsilon \) שהוא ה”אתגר” שאני צריך לענות עליו כשאני מוכיח ש-\( \lim_{x\to\infty}\frac{f\left(x\right)}{x}=m \), אז אני יכול לבחור את מה להעביר לשני הגבולות הללו בצורה שתתאים לי. מכיוון שאני הולך לחבר את שניהם, אני רוצה שהסכום הכולל שלהם יהיה קטן מ-\( \varepsilon \), אז אני אוכל לנסות להקטין אותם כך ששניהם קטנים מ-\( \frac{\varepsilon}{2} \).

הגבול הראשון נותן לי קיום של \( M_{1} \) כך שאם \( x>M_{1} \) אז \( \left|f\left(x\right)-g\left(x\right)-0\right|<\frac{\varepsilon}{2} \).

הגבול השני נותן לי קיום של \( M_{2} \) כך שאם \( x>M_{2} \) אז \( \left|\frac{g\left(x\right)}{x}-m\right|<\frac{\varepsilon}{2} \).

עכשיו מגיע תעלול סטנדרטי: אני אגדיר \( M=\max\left\{ M_{1},M_{2}\right\} \) וכעת אם \( x>M \) אז הוא בו זמנית גדול מ-\( M_{1},M_{2} \) ולכן שני אי השוויונים למעלה מתקיימים עבורו בו זמנית.

יש סיבוך טכני אחד קטן: אני צריך שיתקיים \( \left|\frac{f\left(x\right)-g\left(x\right)}{x}\right|<\frac{\varepsilon}{2} \), אבל מה שיש לי הוא \( \left|f\left(x\right)-g\left(x\right)\right|<\frac{\varepsilon}{2} \). למרבה המזל, אם \( x>1 \) אז \( \left|\frac{f\left(x\right)-g\left(x\right)}{x}\right|<\left|f\left(x\right)-g\left(x\right)\right|<\frac{\varepsilon}{2} \) וזה מה שאני רוצה - אבל בשביל זה אני חייב לדרוש שיתקיים \( x>1 \). למרבה השמחה אני באמת שולט על זה - במקום להגדיר \( M=\max\left\{ M_{1},M_{2}\right\} \) אני אגדיר \( M=\max\left\{ M_{1},M_{2},1\right\} \) ואקבל את מה שרציתי.

אם כן, לסיכום:

\( \left|\frac{f\left(x\right)}{x}-m\right|\le\left|\frac{f\left(x\right)}{x}-\frac{g\left(x\right)}{x}\right|+\left|\frac{g\left(x\right)}{x}-m\right|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon \)

זה מה שרציתי להוכיח.

אם כן, בהינתן פונקציה \( f\left(x\right) \) שיש לה אסימפטוטה משופעת \( mx+a \) ב-\( x\to\infty \) גילינו איך למצוא את השיפוע \( m \) שלה. אבל איך מוצאים את \( a \)? ובכן, המשמעות של זה ש-\( mx+a \) היא אסימפטוטה של \( f\left(x\right) \) הוא שמתקיים \( \left|f\left(x\right)-mx-a\right|\to0 \) אם חושבים על ההגדרה רגע רואים שזה אותו הדבר כמו לומר \( \left|f\left(x\right)-mx\right|\to a \), לכן כל מה שצריך לעשות הוא לחשב גם את הגבול הזה וסיימנו למצוא את האסימפטוטה.

אם לא קיימת אסימפטוטה, האם חישובי הגבולות שהצגתי עדיין יכולים “בטעות” לתת לנו אסימפטוטה שלא קיימת? ובכן, לא. ייתכן שאין אסימפטוטה אבל החישוב של \( \lim_{x\to\infty}\frac{f\left(x\right)}{x} \) יניב איזה גבול \( m \), זה בהחלט יכול לקרות. אבל אם הגבול \( \left|f\left(x\right)-mx\right| \) קיים ושווה \( a \) זה מוכיח ש-\( \left|f\left(x\right)-mx-a\right|\to0 \) שאומר בדיוק שהקו \( mx+a \) הוא אסימפטוטה של \( f\left(x\right) \). אם לעומת זאת הגבול \( \left|f\left(x\right)-mx\right| \) לא קיים, אז אכן אין אסימפטוטה.

בואו נראה עכשיו דוגמא קונקרטית - הפונקציה \( f\left(x\right)=\frac{2x^{2}+3x+1}{x} \). ראשית, \( \frac{f\left(x\right)}{x}=\frac{2x^{2}+3x+1}{x^{2}}\to2 \) (זה הטריק הרגיל של מנת המקדמים המובילים של המונה והמכנה) אז \( m=2 \).

שנית, \( f\left(x\right)-mx=\frac{2x^{2}+3x+1}{x}-2x=\frac{3x+1}{x} \) ולכן \( \left|f\left(x\right)-mx\right|\to3 \), וקיבלנו את האסימפטוטה \( y=2x+3 \).

כאן אני הולך לעצור - כיסינו את המושגים הבסיסיים וקצת את האופן שבו משתמשים בהם, אבל עם דוגמאות וטכניקות קונקרטיות לחישוב אסימפטוטות בסיטואציות שונות ומשונות - עם זה אפשר להמשיך עד אינסוף.

נהניתם? התעניינתם? אם תרצו, אתם מוזמנים לתת טיפ: